Photonic spin-selective perfect absorptance on planar metasurfaces driven by chiral quasi-bound states in the continuum
Hongju
Li
 a,
Hongmiao
Zhou
a,
Gangao
Wei
a,
Hangsheng
Xu
a,
Meng
Qin
*a,
Jianqiang
Liu
b and
Feng
Wu
a,
Hongmiao
Zhou
a,
Gangao
Wei
a,
Hangsheng
Xu
a,
Meng
Qin
*a,
Jianqiang
Liu
b and
Feng
Wu
 c
c
aSchool of Physics, Hefei University of Technology, Hefei, Anhui 230009, China. E-mail: qinm@hfut.edu.cn
bSchool of Science, Jiujiang University, Jiujiang 332005, China
cSchool of Optoelectronic Engineering, Guangdong Polytechnic Normal University, Guangzhou 510665, China
First published on 2nd March 2023
Abstract
Optical metasurfaces with high-quality-factor resonances and selective chirality simultaneously are desired for nanophotonics. Here, an all-dielectric planar chiral metasurface is theoretically proposed and numerically proved to support the astonishing symmetry-protected bound state in the continuum (BIC), due to the preserved π rotational symmetry around the z axis and up-down mirror symmetry simultaneously. Importantly, such BIC is a vortex polarization singularity enclosed by elliptical eigenstate polarizations with non-vanishing helicity, owing to the broken in-plane mirror symmetry. Under the oblique incidence, companied by the BIC transforming into a quasi-BIC (Q-BIC), the strong extrinsic chirality manifests. Assisted by the single-port critical coupling, the planar metasurface can selectively and near-perfectly absorb one circularly polarized light but non-resonantly reflect its counterparts. The circular dichroism (CD) approaching 0.812 is achieved. Intriguingly, the sign of CD (namely, the handedness of the chiral metasurface) can be flexibly manipulated only via varying the azimuthal angle of incident light, due to the periodic helicity sign flip in eigen polarizations around the BIC. Numerical results are consistent with the coupled-mode theory and multipole decomposition method. The spin-selective metasurface absorber empowered by the physics of chiral Q-BICs undoubtedly may promise various applications such as optical filters, polarization detectors, and chiral imaging.
Introduction
Symmetry is ubiquitous in the natural world. The symmetry in physics always describes the invariance of laws or geometries through a particular transformation pathway. Despite the beauty of symmetry, the study of symmetry breaking1 has been important both scientifically and technologically in various areas. One such example is the chirality induced by complete breaking of mirror symmetry.2 Chirality refers to an intrinsic property of a given object that cannot be brought to coincide with its mirror image by translation or rotation operator,3,4 and is particularly important in pharmaceutics, biomedicine, and spectroscopy. The chiral phenomenon in optics is known as chiroptics,5 which is originated from the interaction between circularly polarized light with different helicities and chiral objects. Chiroptics is manifested by a difference in amplitude, phase, and field distribution, when left- and right-circularly polarized light illuminate individually.6 As a consequence, the new physical terms including optical activity,7 circular birefringence,8 and circular dichroism (CD),9 have been proposed to characterize the distinguishable chiroptical responses. Chiral optical absorption, as an enduring branch of chiral light–matter interaction,10–12 has found significant applications in polarization imaging, photodetection, filtering, and many other fields. Chiral absorption in natural materials is extremely weak, due to the small size of molecular structure relative to the wavelength of incident light.13,14 The structures with geometric chiral properties on length scales comparable with the wavelength of incident light are desired to realize strong chiroptical absorption.15 Artificial metamaterials16,17 with unit cells on sub-wavelength scale that is typically much larger than the size of molecular naturally have received burgeoning amount of interest recently. Benefiting from the flexible structure design and strong near-field enhancement, various metal-based chiral metamaterial absorbers have been successively proposed by breaking the mirror symmetry in the propagation direction.18 Examples include the double-layered L-shaped copper antennas,19 bi-layered fourfold twisted T-shaped structure,20 four rotated twisted closed ring resonators,21 and so on. Beyond the three-dimensional metamaterials,22,23 the two-dimensional counterparts (which are also referred as metasurfaces24–27) with broken in-plane mirror symmetry are capturing interest, because they do not require very demanding nanofabrication techniques. Examples include the double-rectangle gold bars,28,29 η-shaped silver resonators,30 Z-shaped silver antennas,31 and other planar chiral structures.32 Although the metal-based chiral metamaterials can near-perfectly absorb one circularly polarized light but non-resonantly reflect its counterparts, the quality factor (Q-factor) of absorption peaks and the extremum of CD are limited by the inevitable Ohmic loss and heating problem in metals.33 Importantly, once the metamaterial with a specific shape is fabricated, its handedness and the sign of CD are irrevocable.6 Hence, the realization of chiral metasurface absorbers with high Q-factor and tunable spin selectivity simultaneously is urgent.The symmetry-protected bound states in the continuum (BICs)34–38 on all-dielectric planar metasurfaces, to the best of our knowledge, may provide a feasible way to achieve such desired chiral absorbers. On the one hand, the BICs are identified as non-radiating eigenvalues of electromagnetic wave equation above the light cone.39 The nearly real eigenfrequency mode,40 characterized by an unbounded Q-factor and vanishing linewidth, indicates that the ideal BICs will be invisible in absorptance spectra and cannot be externally accessed.41 Fortunately, the small perturbation from breaking in the mirror symmetry of metasurfaces not only enables the symmetry-protected BICs to be transformed into externally accessible quasi-BICs (Q-BICs)42–47 with ultrahigh Q-factors but also may give rise to the chiral response.48–52 On the other hand, the BICs have been proved to be vortex centers in the polarization directions of far-field radiation.53 The winding structure of polarization states in the momentum space offers a new avenue to modulating polarization. Especially, due to the appearance of circularly polarized states induced by in-plane symmetry breaking, modulating the handedness of a chiral metasurface supporting the original symmetry-protected BICs is possible.54–56 Therefore, the planar metasurface supporting a symmetry-protected BIC enclosed by elliptical eigenstate polarizations with non-vanishing helicity in momentum space is an ideal candidate to obtain chiral absorbers with ultrahigh Q-factors and actively tunable spin selectivity simultaneously.
Here, two pairs of parallel and staggered silicon bars are orthogonally placed to form a planar metasurface. The preserved π rotational symmetry around the z axis (C2z) and simultaneously the up-down mirror symmetry along the z direction (σz) ensure the metasurface to support the fantastic symmetry-protected BIC. The additional breaking in the in-plane mirror symmetry leads to that the vortex polarization singularity at the BIC is enclosed by elliptical eigenstate polarizations with non-vanishing helicity. Under the oblique incidence, not only is the symmetry-protected BIC transformed into a Q-BIC with high Q-factor but also the strong extrinsic chirality emerges. Assisted by the single-port critical coupling, this planar metasurface thus can near-perfectly absorb one circularly polarized light but non-resonantly reflect its counterparts. Accompanied by the realization of chiral absorption, the CD approaching 0.812 is observed. Intriguingly, the sign of CD (namely, the handedness of the chiral metasurface) can be actively manipulated only via varying the azimuthal angle of incident light, due to the periodic helicity sign flip in eigen polarizations around the Γ point at the first Brillouin zone. Numerical results are in excellent agreement with the coupled-mode theory (CMT) and multipole decomposition method. The spin-selective metasurface perfect absorber empowered by the physics of BICs undoubtedly may find utility in optical filters, polarization detectors, and imaging display.
Structure and principle
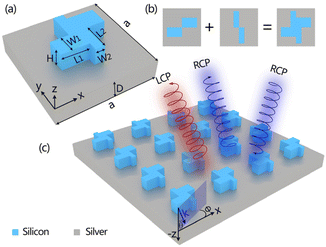
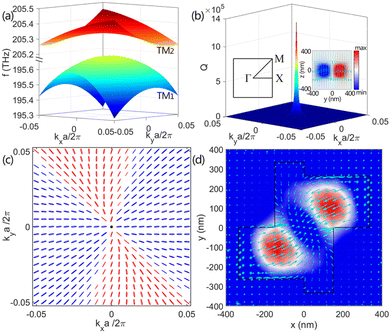
Fig. 1 shows the schematic illustration of the designed chiral metasurface on a metallic substrate. The unit cell comprises two pairs of parallel and staggered rectangular silicon bars, which are orthogonally placed and intersect at the origin, as displayed in Fig. 1(b). The schematic drawing of unit cell with detailed geometry definitions is shown in Fig. 1(a). The width and length of two identical rectangular silicon bars along x axis are denoted by W1 and L1, respectively. Similarly, the width and length of the silicon bars along y axis are marked by W2 and L2, respectively. The thickness of all silicon bars is H. The period of the fabricated silicon metasurface arranging in a square lattice is a, and the thickness of metallic substrates is D. To simplify the absorption mechanism, the metallic substrate with thickness of D = 400 nm is considered. This thickness is much larger than the penetration depth of electromagnetic waves so that the investigated structure is degraded into a single-port system without the transmission channel. Certainly, in addition to the ultra-thickness metallic substrate, an all-dielectric Bragg mirror can enable this structure to work as a single-port system in principle. Such simple single-port system permits the use of critical coupling to obtain the potential perfect absorption.57–59Firstly, the eigenmodes of an isolated periodic metasurface made from lossless silicon with a refractive index of n = 3.478 are numerically analyzed by using the finite element method. The optimized geometric parameters are H = 360 nm, W1 = 260 nm, W2 = 148 nm, L1 = L2 = 330 nm, and a = 800 nm. The W1 ≠ W2 ≠ L1 indicates that the metasurface maintains the C2z symmetry and σz symmetry simultaneously, but suffers from the loss of in-plane mirror symmetry. In theory, the combination of C2z symmetry and the σz symmetry is the sufficient condition for a stable symmetry-protected BIC.53 In the implementation, the eigenfrequency solver in COMSOL Multiphysics software is utilized to calculate the eigenmodes. The Floquet periodic boundary conditions are applied in the x and y directions to determine the in-plane wavevectors (kx, ky), and the perfectly matched layers are used in the z direction to absorb the radiation wave. Here, we restrict the discussion to transverse-magnetic-like eigenmodes as they have much higher Q-factors than transverse-electric-like modes in the wavelength range of interest. To select the transverse magnetic (TM) eigenstates, a perfect electric conductor as boundary condition is set at the middle of the metasurface. Two TM band structures with real parts of eigenfrequencies in the first Brillouin zone are shown in Fig. 2(a). The first Brillouin zone of a square lattice is schematically shown in the left inset of Fig. 2(b). Comparison of two TM band structures exhibits that the TM1 mode with a relatively flat band at the Γ point has smaller imaginary parts of complex eigenfrequencies expressed by f = f0 + jη, in which the real part f0 is the resonance frequency and the imaginary part η represents the leakage rate. In other words, the TM1 eigenmode possesses higher Q-factor, which is defined as 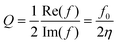 . The calculated Q-factors for the TM1 band at the first Brillouin zone are shown in Fig. 2(b). It is interesting to note that the radiative Q-factor diverges at the Γ point, indicating the occurrence of a symmetry-protected BIC (also referred as the Γ-state BIC).36
. The calculated Q-factors for the TM1 band at the first Brillouin zone are shown in Fig. 2(b). It is interesting to note that the radiative Q-factor diverges at the Γ point, indicating the occurrence of a symmetry-protected BIC (also referred as the Γ-state BIC).36
Another hard evidence for a symmetry-protected BIC is that the vortex polarization singularity occurs at the Γ point in the eigen polarization map of the TM1 band, as indicated by the black dot in Fig. 2(c). The magnetic field profiles of the BIC at different slices are shown in the Fig. 2(d) and the right inset of Fig. 2(b), respectively. Combination of mode profiles indicates that the BIC can be treated as a pair of anti-parallel magnetic dipoles along the x axis. Assisted by the C2 group symmetry analysis,60,61 we can further understand the perfectly confined BIC. As shown in Fig. 2(d), the magnetic field of the BIC at the Γ point is even under the π rotation around the incident direction (the z axis). However, for Γ point of the reciprocal space, the one and only radiation channel for the sub diffractive regime is the plane wave propagating along the z axis, and its electromagnetic fields, meanwhile, should be odd under the same C2z operator. Due to the symmetry mismatch between the mode profile inside the metasurface and that of the external propagating wave, the TM1 eigenmode cannot be excited by any linearly polarized plane waves under normal incidence, and thus behaves as a typical symmetry-protected BIC that cannot be accessed externally.
Another striking feature in Fig. 2(d) is that the field profile has a spatial inversion symmetry, which will allow the local response to be birefringent.49 In combination with the lack of any in-plane mirror symmetry, the metasurface will manifest the inherent planar chirality,62–64 and the intrinsic BIC thus is enclosed by vortex elliptical eigen polarizations with non-vanishing helicity, as already shown in Fig. 2(c). The helicity sign periodically flips around the Γ point. The opposite helicity of eigen polarizations along the x and y directions is observed. Under the oblique incidence of circularly polarized light, the symmetry-protected BIC will be transformed into a chiral Q-BIC with high Q-factor. The planar metasurface thus manifests the strong extrinsic chirality. More importantly, the periodic helicity sign flip of the Q-BIC around the Γ point in the momentum space will promise a feasible way of only by changing the azimuthal angle of circularly polarized light under oblique incidence to actively modulate the handedness of the chiral metasurface, as indicated in Fig. 1(c).
Simulation and discussion
To verify the potential spin-dependent optical response of the chiral metasurface driven by the physics of BIC, the chiral absorber enabled by the single-port system is comprehensively investigated. The metallic substrate is assumed to be silver whose relative permittivity is characterized by the typical Drude model εm(ω) = ε∞ − ωp2/(ω2 + jωγ).65–67 Here, we consider the ε∞ = 3.7, ωp = 9.1 eV, and γ = 0.018 eV at the near-infrared region. Other parameters are same as those used for Fig. 2. Without the transmission, the Jones matrix of reflection coefficient (r) under circular polarization basis is enough for illustrating the chiral absorption response.68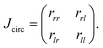 | (1) |
Here, the subscripts r and l represent the right-handed polarization (RCP) and left-handed polarization (LCP), respectively. The rij (i = r, l and j = r, l) stands for the reflection coefficient of output polarization i from input polarization j. The absorptance of the incident LCP and RCP lights can be respectively expressed as
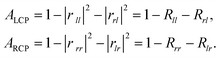 | (2) |
The Rij = |rij|2 is the reflection of the system. Additionally, to highlight the chirality of the metasurface, the CD is defined as the reflection difference and is described as49
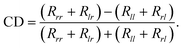 | (3) |
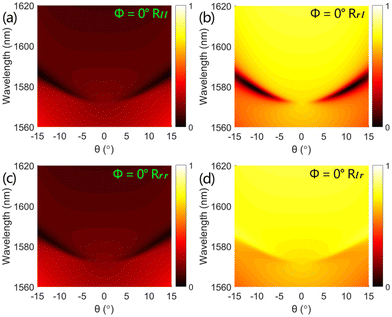
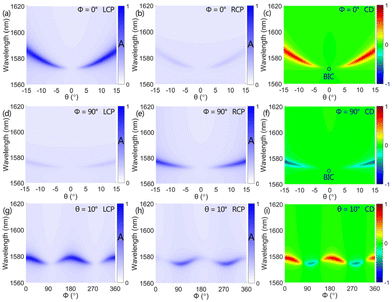
The evolution of simulated reflection spectra of all Jones matrix elements by continuously varying incident angle θ along the x direction (Φ = 0°) is shown in Fig. 3. We note that all incident lights are totally reflected at the normal incidence (θ = 0°), indicating that there is no resonant mode excited on the metasurface in this case. Under the oblique incidence, however, an obvious dip appears at the co-polarized reflection spectra (Rll and Rrr), as shown in Fig. 3(a) and (c), respectively. Meanwhile, as the |θ| increases, the reflection dip gradually drops with expanded linewidth and its resonant wavelength experiences a redshift. Such observation is the direct evidence for the transformation of an unobservable BIC to the accessible Q-BIC. Notably, in addition to the nearly same reflection spectra for the co-polarized Rll and Rrr, the striking difference in the cross-polarized reflection spectra (Rrl and Rlr) is observed in Fig. 3(b) and (d). Based on the eqn (2), the chiral absorption will be achieved on the metasurface under the oblique incidence. The calculated absorptance spectra as a function of θ are shown in Fig. 4. Comparison of Fig. 4(a) and (b) suggests that companied by the appearance of chiral Q-BIC resonance under the oblique incidence, the metasurface indeed can strongly absorb left-circularly polarized (LCP) light, whereas non-resonantly reflect the right-circularly polarized (RCP) light. As excepted, with the |θ| increasing, the absorptance peak of LCP light gradually arises with expanded linewidth and its spectral position tends to exhibit a redshift simultaneously. The calculated CD spectra are shown Fig. 4(c). The CD as high as 0.812 is observed. Therefore, the strong external chirality empowered by the Q-BIC resonance on the planar metasurface is achieved.
Fig. 4(d) and (e) demonstrate the absorptance spectra as a function of incident angle θ varying along the y direction (Φ = 90°). In stark contrast to the results in Fig. 4(a) and (b), the metasurface strongly absorbs RCP light and non-resonantly reflects the LCP light, when the incident angle varies along the y direction (Φ = 90°). Compared to the Fig. 4(c), as a result, the sign flip of CD is observed in the Fig. 4(f). The combination of Fig. 4(c) and (f) suggests that the planar metasurface driven by the chiral Q-BIC resonance can exhibit opposite handedness only by varying the incident angle along x and y directions, respectively. Such superior spin selectivity can be attributed to the opposite helicity of eigen polarizations along the kx and ky directions, as shown in Fig. 2(c). Therefore, we can selectively modulate the handedness of the chiral metasurface by changing the azimuthal angle of the incident light, according to the helicity of eigen polarizations around the Γ point at the first Brillouin zone. The absorptance and CD spectra as a function of the azimuthal angle Φ are presented in Fig. 4(g)–(i). The incident angle is fixed at θ = 10° to observably excite the Q-BIC resonance. As expected, the azimuthal angle of incident light indeed behaves as a key factor to switch the handedness of the chiral metasurface. As the Φ evolves from 0 to 360°, the opposite varying trend is observed at the absorptance spectra of LCP and RCP light, as shown in Fig. 4(g) and (h), respectively. The periodic sign flip of CD thus is achieved with the increase of Φ, as shown in Fig. 4(i). The observation in Fig. 4(i) matches well with the helicity sign flip of the eigen polarizations around the Γ point in Fig. 2(c). Empowered by the abundant physics of BIC on the planar metasurface, hence, we not only realize a chiral absorber but also can actively manipulate its handedness only through handily varying the azimuthal angle of the incident light, unlike the conventional ways where fabricating a new structure would be essential for switching the handedness.
We also confirm the chiral Q-BIC on the metasurface by the multipole decomposition method.69–72 The five leading multipole moments including electric dipole (ED) moment 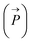 , magnetic dipole (MD) moment
, magnetic dipole (MD) moment 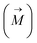 , toroidal dipole (TD) moment
, toroidal dipole (TD) moment 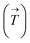 , electric quadrupole (EQ) moment
, electric quadrupole (EQ) moment 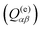 , and magnetic quadrupole (MQ) moment
, and magnetic quadrupole (MQ) moment 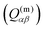 are calculated by using the expressions.69
are calculated by using the expressions.69
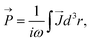 | (4) |
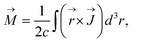 | (5) |
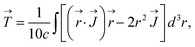 | (6) |
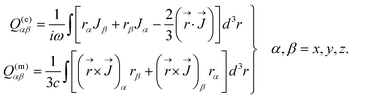 | (7) |
Here, c is the speed of light in vacuum and ω is its angular frequency. The 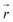 is the distance vector from the origin to point (x, y, z) in the Cartesian coordinate. The
is the distance vector from the origin to point (x, y, z) in the Cartesian coordinate. The 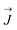 is the displacement current density within a unit cell of the chiral silicon metasurface. The far-field scattered energy from multipole excitation is respectively calculated by72
is the displacement current density within a unit cell of the chiral silicon metasurface. The far-field scattered energy from multipole excitation is respectively calculated by72
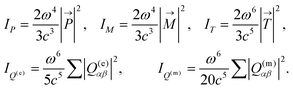 | (8) |
Without loss of generality, the oblique incidence with θ = 10° and Φ = 0° as an example is considered. As already shown in Fig. 4(a), under the illumination of LCP light, the Q-BIC resonance is excited at θ = 10° and the nearly perfect absorptance peak is observed at the wavelength of 1581 nm. On the contrary, without the excitation of the Q-BIC resonance on the metasurface, the incident RCP light is almost completely reflected, as shown Fig. 4(b). Scattered powers of five leading multipoles on the chiral metasurface under LCP and RCP illumination are demonstrated in Fig. 5(a) and (b), respectively. For the illumination of LCP light with θ = 10° and Φ = 0°, the excited Q-BIC resonance primarily dominated by the MD is observed in Fig. 5(a), which is consistent with the result from the eigenmode analysis in Fig. 2 where the BIC is characterized by a pair of anti-parallel magnetic dipoles along the x axis. For the illumination of RCP light in Fig. 5(b), however, the contributions from the multipoles are suppressed at the wavelength of 1581 nm, and thus the excitation of a Q-BIC resonance is prohibited. Therefore, the extrinsic chiral response of the metasurface is again verified to be attributed to the chiral Q-BIC resonance, which is primarily dominated by the MD and is only excited by one circularly polarized light at a time.
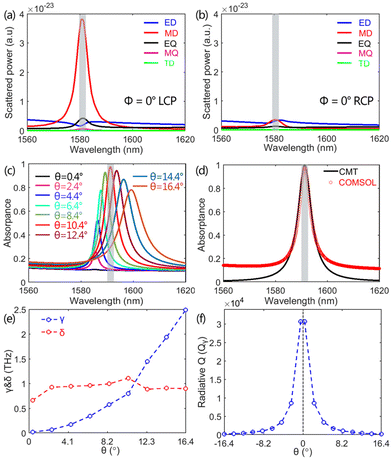 | ||
| Fig. 5 Scattered energy of five leading multipoles of the chiral metasurface under LCP (a) and RCP (b) illumination with θ = 10° and Φ = 0°. (c) The evolution of absorptance spectra of LCP light on the incident angle varying from 0.4° to 16.4° in intervals of 2° along the x direction (Φ = 0°). The other parameters are same as those used in Fig. 2, except for the a = 846 nm. (d) The CMT-fitted and numerically simulated absorptance spectra at critical coupling of θ = 10.4°. (e) The calculated radiative loss rate γ and dissipative loss rate δ for different θ. (f) The calculated radiative Q-factor (Qγ) for different θ. | ||
In addition, it is well known that the radiative Q-factor of the Q-BIC resonance gradually decreases as the incident angle increases, due to the expanded leakage channel. Therefore, the linewidth of the absorptance peak enabled by the Q-BIC expands gradually with the incident angle increasing, as already shown in Fig. 4(a). Particularly, we observe that the absorptance intensity increases at the beginning and then decreases as the incident angle increases, according to the enlarged absorptance spectra in Fig. 5(c). In the Fig. 5(c), the absorptance spectra for the incident angle increasing from 0.4° to 16.4° in intervals of 2° are demonstrated. The absorptance intensity increases as the θ increases from 0.4° to 10.4°, and reaches a maximum at θ = 10.4°. The further increase in the θ, however, leads to the decrease of absorptance intensity. The proposed single-port system permits the use of the versatile CMT73–75 to reveal the unusual behavior in the absorptance intensity induced by the change in θ.
When the intrinsic Q-BIC is excited by the LCP light under the oblique incidence of Φ = 0°, the dynamic equations for the single-port system are described by74
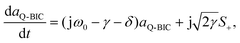 | (9) |
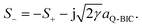 | (10) |
Here, aQ-BIC and ω0 denote the amplitude and frequency of the Q-BIC, respectively. The j stands for the imaginary unit. The γ and δ represent the radiative loss rate and dissipative loss rate of the Q-BIC, respectively. The S+ and S− stand for the amplitudes of input and output waves, respectively. Using the general frequency domain e+jωt to isolate the S−/S+, the reflection coefficient of the system is expressed as
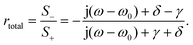 | (11) |
The absorptance of the system is obtained by ALCP = 1 − |rtotal|2 and thus is expressed as
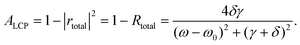 | (12) |
The eqn (12) shows that the maximum absorptance at the resonant frequency of ω0 is determined by the γ and δ. It is expressed as
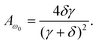 | (13) |
The half-maximum absorptance at the resonant frequency ω1 is
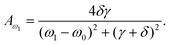 | (14) |
Because of the Aω0 = 2Aω1, the full width at half maximum (Γ) is obtained by
| Γ = 2|ω1 − ω0| = 2(γ + δ). | (15) |
The total Q-factor of the absorptance peak is defined by
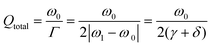 | (16) |
Similarly, the radiative and dissipative Q-factors can be respectively calculated by
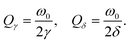 | (17) |
The eqn (13) shows that the realization of perfect absorptance at the resonant frequency of ω0 is possible, when the γ = δ occurs. The γ = δ suggests that the energy is coupled into the system at the same rate as that of the dissipation, and thus is defined as the critical coupling.74 Besides the critical coupling, the γ < δ is defined as the under coupling, whereas the γ > δ is defined as the over coupling. At the under coupling of γ < δ, the reflection coefficient at the resonant frequency ω0 is expressed as
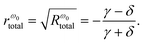 | (18) |
In combination with the eqn (16) and (17), we can obtain the radiative Q-factor (Qγ) and dissipative Q-factor (Qδ).
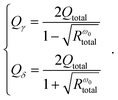 | (19) |
At the over coupling of γ > δ, the reflection coefficient at the resonant frequency ω0 is expressed as
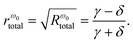 | (20) |
The Qγ and Qδ are expressed as
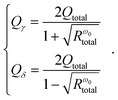 | (21) |
The calculated radiative loss rate γ and dissipative loss rate δ for different incident angles are shown in Fig. 5(e). They are extracted from the absorptance spectra in Fig. 5(c) by using the eqn (16)–(21). Considering the BIC-driven chiral metasurface absorber, the radiative channel of the symmetry-protected BIC opens under the oblique incidence, and thus, the ideal BIC is turned into a leaky resonance (Q-BIC). With the incident angle increasing, the radiative loss rate γ of the Q-BIC increases from zero to finite values, as indicated by the blue curve in Fig. 5(e). However, the dissipative loss of the Q-BIC is ascribed to the neighboring metallic substrate, because the silicon metasurface is treated as lossless. Thus, the dissipative loss rate δ is considered to nearly remain unchanged as the incident angle increases, as demonstrated by the red curve in Fig. 5(e). Interestingly, with the incident angle increasing, the crossing between γ and σ appears at θ = 10.4°, indicating the occurrence of critical coupling. Therefore, the system successively experiences the under coupling, critical coupling, and over coupling, as the θ varies from 0.4° to 16.4°. As expected, we observe that the absorptance intensity increases as the θ increases from 0.4° to 10.4° and reaches a maximum at θ = 10.4° in Fig. 5(c). When the θ further increases, the system drops into the over coupling region and the perfect absorptance is destructed. The simulated result is in excellent agreement with that obtained by the CMT. As a specific example, the nearly perfect absorptance at the critical coupling is fitted very well by the CMT in the Fig. 5(d). We also show the calculated radiative Q-factor as a function of incident angle in Fig. 5(f). As a characteristic feature of an ideal symmetry-protected BIC,34 the inverse quadratic law between Qγ and the asymmetric parameter θ is observed.
So far, assisted by the physics of chiral Q-BIC and the single-port critical coupling, the chiral perfect absorber with tunable spin selectivity is successfully realized. The established planar microfabrication techniques,76–78 such as the electron beam lithography companied by the processes of deposition, patterning, lift-off, and etching, are competent for the construction of such planar silicon metasurface. The robustness of the chiral perfect absorptance is also investigated via changing the structural parameters including W1, L1, H, and a. The chiral metasurface under LCP illumination with θ = 10° and Φ = 0° as an example is considered. The nearly perfect absorption spectrum is obtained, as shown in Fig. 4(a). Fig. 6(a)–(d) show the evolution of absorptance spectra on the W1, L1, H, and a, respectively. Because the chiral response is empowered by the Q-BIC resonance evolved from an ideal symmetry-protected BIC, the chiral absorptance will remain unchanged as long as the C2z symmetry and σz symmetry are preserved by the metasurface. Additionally, the Q-BIC resonance is characterized by a pair of anti-parallel magnetic dipoles along the x axis, and its field is mainly confined in the two silicon bars arranging in the x direction, as shown in Fig. 2(d). The circular electric field within the y–z cross section of silicon bars arranging in the x direction is also observed in the right inset of Fig. 2(b). Therefore, at a fixed incident angle, the wavelength of the Q-BIC resonance will be determined by the width W1 and height H of the silicon bars arranging in the x direction. The changes in other structural parameters including a, L1, and W2, will have little effect on the resonant wavelength of the Q-BIC. Simulated results confirm the qualitative analysis mentioned above. As shown in Fig. 6(a) and (c), the spectral position of the absorptance peak indeed tends to exhibit a redshift with the width W1 and height H increasing, respectively. The expected robustness of absorptance spectra with the L1 and a individually varying is also witnessed in Fig. 6(b) and (d), respectively.
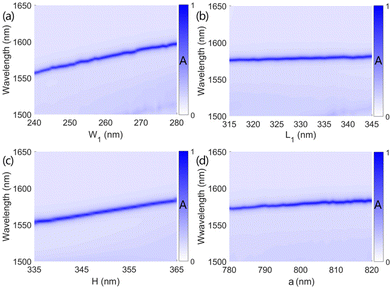 | ||
| Fig. 6 The dependence of absorptance spectra on structural parameters. Absorptance spectra as a function of W1 (a), L1 (b), H (c), and a (d), respectively. Other simulated details are identical to those used in Fig. 5(a), except the variable parameter in each subfigure. | ||
Conclusions
In summary, we have both theoretically and numerically investigated the photonic spin-selective absorptance on a planar metasurface enabled by the chiral Q-BIC. The total absorptance of one circularly polarized light but non-resonantly reflection of its counterparts is realized. The CD up to 0.812 is observed. Intriguingly, the spin selectivity of the chiral metasurface and the corresponding sign of CD can be handily modulated only via varying the azimuthal angle of the incident light, instead of fabricating a new structure. All numerical observes are consistent with those obtained by the CMT and multipole decomposition method. The robustness of the chiral perfect absorptance under the changes in the structural parameters is also comprehensively demonstrated. The chiral metasurface perfect absorber with actively tunable handedness undoubtedly may find utility in optical filters, polarization detectors, and imaging display.Author contributions
Hongju Li: conceptualization, software, data curation, formal analysis, investigation, methodology, writing – original draft, funding acquisition. Hongmiao Zhou: writing – review and editing. Gangao Wei: writing – review and editing. Hangsheng Xu: writing – review and editing. Meng Qin: writing – review and editing, supervision, funding acquisition. Jianqiang Liu: software, writing – review and editing. Feng Wu: writing – review and editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (grants no. 61805064 and 12104105), the Fundamental Research Funds for the Central Universities of China (grants no. PA2021KCPY0052, JZ2021HGQA0259, and JZ2021HGTA0143), and the Start-up Funding of Guangdong Polytechnic Normal University (grant no. 2021SDKYA033).References
- F. Strocchi, Symmetry Breaking, Springer-Verlag, Berlin, 2005 Search PubMed.
- L. Kelvin, Baltimore Lectures on Molecular Dynamics and the Wave Theory of Light, C. J. Clay and Sons, London, 1904 Search PubMed.
- T. Mori, Chem. Rev., 2021, 121, 2373 CrossRef CAS PubMed.
- B. Semnani, J. Flannery, R. Al Maruf and M. Bajcsy, Light: Sci. Appl., 2020, 9, 23 CrossRef CAS PubMed.
- M. Ren, E. Plum, J. Xu and N. I. Zheludev, Nat. Commun., 2012, 3, 833 CrossRef PubMed.
- A. Lininger, G. Palermo, A. Guglielmelli, G. Nicoletta, M. Goel, M. Hinczewski and G. Strangi, Adv. Mater., 2022, 2107325 CrossRef PubMed.
- H. Liu, D. A. Genov, D. M. Wu, Y. M. Liu, Z. W. Liu, C. Sun, S. Zhu and X. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073101 CrossRef.
- N. Engheta and D. L. Jaggard, IEEE Antennas Propag. Soc. Newsl., 1988, 30, 6 Search PubMed.
- M. Decker, M. W. Klein, M. Wegener and S. Linden, Opt. Lett., 2007, 32, 856 CrossRef CAS PubMed.
- M. Qiu, L. Zhang, Z. Tang, W. Jin, C. W. Qiu and D. Y. Lei, Adv. Funct. Mater., 2018, 28, 1803147 CrossRef.
- E. Plum and N. I. Zheludev, Appl. Phys. Lett., 2015, 106, 221901 CrossRef.
- Z. Wang, H. Jia, K. Yao, W. Cai, H. Chen and Y. Liu, ACS Photonics, 2016, 3, 2096 CrossRef CAS.
- Z. Tang, Chiral Nanomaterials: Preparation, Properties and Applications, John Wiley & Sons, Hoboken, NJ, USA, 2018 Search PubMed.
- Y. Wen, M. Q. He, Y. L. Yu and J. H. Wang, Adv. Colloid Interface Sci., 2021, 289, 102376 CrossRef CAS PubMed.
- Y. Luo, C. Chi, M. Jiang, R. Li, S. Zu, Y. Li and Z. Fang, Adv. Opt. Mater., 2017, 5, 1700040 CrossRef.
- S. Xiao, T. Wang, T. Liu, C. Zhou, X. Jiang and J. Zhang, J. Phys. D: Appl. Phys., 2020, 53, 503002 CrossRef CAS.
- V. A. Fedotov, M. Rose, S. L. Prosvirnin, N. Papasimakis and N. I. Zheludev, Phys. Rev. Lett., 2007, 99, 147401 CrossRef CAS PubMed.
- W. Ma, F. Cheng and Y. Liu, ACS Nano, 2018, 12, 6326 CrossRef CAS PubMed.
- M. Li, L. Guo, J. Dong and H. Yang, J. Phys. D: Appl. Phys., 2014, 47, 185102 CrossRef.
- Y. Cheng, H. Chen, J. Zhao, X. Mao and Z. Cheng, Opt. Mater. Express, 2018, 8, 1399 CrossRef CAS.
- D. B. Stojanović, G. Gligorić, P. P. Beličev, M. R. Belić and L. Hadžievski, IEEE J. Sel. Top. Quantum Electron., 2020, 27, 4700506 Search PubMed.
- J. Peng, X. He, C. Shi, J. Leng, F. Lin, F. Liu, H. Zhang and W. Shi, Phys. E, 2020, 124, 114309 CrossRef CAS.
- X. He and W. Cao, Opt. Mater. Express, 2023, 13, 413 CrossRef.
- V. A. Fedotov, P. L. Mladyonov, S. L. Prosvirnin, A. V. Rogacheva, Y. Chen and N. I. Zheludev, Phys. Rev. Lett., 2006, 97, 167401 CrossRef CAS PubMed.
- R. Zhang, Q. Zhao, X. Wang, K. M. Lau, T. K. Yung, J. Li and W. Y. Tam, Nanophotonics, 2022, 11, 495 CrossRef.
- M. V. Gorkunov, A. A. Antonov and Y. S. Kivshar, Phys. Rev. Lett., 2020, 125, 093903 CrossRef CAS PubMed.
- M. V. Gorkunov, A. A. Antonov, V. R. Tuz, A. S. Kupriianov and Y. S. Kivshar, Adv. Opt. Mater., 2021, 9, 2100797 CrossRef CAS.
- L. Ouyang, W. Wang, D. Rosenmann, D. A. Czaplewski, J. Gao and X. Yang, Opt. Express, 2018, 26, 31484 CrossRef CAS PubMed.
- H. Tang, D. Rosenmann, D. A. Czaplewski, X. Yang and J. Gao, Opt. Express, 2022, 30, 20063 CrossRef CAS PubMed.
- B. Tang, Z. Li, E. Palacios, Z. Liu, S. Butun and K. Aydin, IEEE Photonics Technol. Lett., 2017, 29, 295 CAS.
- W. Li, Z. J. Coppens, L. V. Besteiro, W. Wang, A. O. Govorov and J. Valentine, Nat. Commun., 2015, 6, 8379 CrossRef CAS PubMed.
- Z. Shen, X. Fang, S. Li, W. Yin, L. Zhang and X. Chen, Opt. Lett., 2022, 47, 505 CrossRef CAS PubMed.
- Z. Wang, F. Cheng, T. Winsor and Y. Liu, Nanotechnology, 2016, 27, 412001 CrossRef PubMed.
- K. Koshelev, S. Lepeshov, M. Liu, A. Bogdanov and Y. Kivshar, Phys. Rev. Lett., 2018, 121, 193903 CrossRef PubMed.
- M. Kang, S. Zhang, M. Xiao and H. Xu, Phys. Rev. Lett., 2021, 126, 117402 CrossRef CAS PubMed.
- J. Jin, X. Yin, L. Ni, M. Soljačić, B. Zhen and C. Peng, Nature, 2019, 574, 501 CrossRef CAS PubMed.
- X. Y. He, F. T. Lin, F. Liu and W. Z. Shi, Nanophotonics, 2022, 11, 4705 CrossRef CAS.
- R. M. Saadabad, L. Huang and A. E. Miroshnichenko, Phys. Rev. B, 2021, 104, 235405 CrossRef.
- C. W. Hsu, B. Zhen, J. Lee, S. L. Chua, S. G. Johnson, J. D. Joannopoulos and M. Soljačić, Nature, 2013, 499, 188 CrossRef CAS PubMed.
- A. Kodigala, T. Lepetit, Q. Gu, B. Bahari, Y. Fainman and B. Kanté, Nature, 2017, 541, 196 CrossRef CAS PubMed.
- H. M. Doeleman, F. Monticone, W. den Hollander, A. Alù and A. F. Koenderink, Nat. Photonics, 2018, 12, 397 CrossRef CAS.
- R. Chai, W. Liu, Z. Li, H. Cheng, J. Tian and S. Chen, Phys. Rev. B, 2021, 104, 075149 CrossRef CAS.
- Z. Liu, Y. Xu, Y. Lin, J. Xiang, T. Feng, Q. Cao, J. Li, S. Lan and J. Liu, Phys. Rev. Lett., 2019, 123, 253901 CrossRef CAS PubMed.
- X. Wang, J. Duan, W. Chen, C. Zhou, T. Liu and S. Xiao, Phys. Rev. B, 2020, 102, 155432 CrossRef CAS.
- S. Yang, C. Hong, Y. Jiang and J. C. Ndukaife, ACS Photonics, 2021, 8, 1961 CrossRef CAS.
- M. Gandolfi, A. Tognazzi, D. Rocco, C. De Angelis and L. Carletti, Phys. Rev. A, 2021, 104, 023524 CrossRef CAS.
- D. R. Abujetas, Á. Barreda, F. Moreno, A. Litman, J. M. Geffrin and J. A. Sánchez-Gil, Laser Photonics Rev., 2020, 15, 2000263 CrossRef.
- J. Wu, X. Xu, X. Su, S. Zhao, C. Wu, Y. Sun, Y. Li, F. Wu, Z. Guo, H. Jiang and H. Chen, Phys. Rev. Appl., 2021, 16, 064018 CrossRef CAS.
- T. Shi, Z. L. Deng, G. Geng, Y. Zeng, G. Hu, A. Overvig, J. Li, C. W. Qiu, A. Alù, Y. S. Kivshar and X. Li, Nat. Commun., 2022, 13, 4111 CrossRef CAS PubMed.
- X. Yin, J. Jin, M. Soljačić, C. Peng and B. Zhen, Nature, 2020, 580, 467 CrossRef CAS PubMed.
- X. Zhang, Y. Liu, J. Han, Y. Kivshar and Q. Song, Science, 2022, 377, 1215 CrossRef CAS PubMed.
- S. Wan, K. Wang, F. Wang, C. Guan, W. Li, J. Liu, A. Bogdanov, P. A. Belov and J. Shi, Opt. Lett., 2022, 47, 3291 CrossRef PubMed.
- B. Zhen, C. W. Hsu, L. Lu, A. D. Stone and M. Soljačić, Phys. Rev. Lett., 2014, 113, 257401 CrossRef PubMed.
- W. Liu, B. Wang, Y. Zhang, J. Wang, M. Zhao, F. Guan, X. Liu, L. Shi and J. Zi, Phys. Rev. Lett., 2019, 123, 116104 CrossRef CAS PubMed.
- A. Overvig, N. Yu and A. Alù, Phys. Rev. Lett., 2021, 126, 073001 CrossRef CAS PubMed.
- Y. Chen, W. Chen, X. Kong, D. Wu, J. Chu and C. W. Qiu, Phys. Rev. Lett., 2022, 128, 146102 CrossRef CAS PubMed.
- J. R. Piper and S. Fan, ACS Photonics, 2014, 1, 347 CrossRef CAS.
- Y. Liu, A. Chadha, D. Zhao, J. R. Piper, Y. Jia, Y. Shuai, L. Menon, H. Yang, Z. Ma, S. Fan, F. Xia and W. Zhou, Appl. Phys. Lett., 2014, 105, 181105 CrossRef.
- J. Wang, A. Chen, Y. W. Zhang, J. P. Zeng, Y. F. Zhang, X. H. Liu, L. Shi and J. Zi, Phys. Rev. B, 2019, 100, 075407 CrossRef CAS.
- S. Xiao, M. Qin, J. Duan, F. Wu and T. Liu, Phys. Rev. B, 2022, 105, 195440 CrossRef CAS.
- C. W. Hsu, B. Zhen, A. D. Stone, J. D. Joannopoulos and M. Soljačić, Nat. Rev. Mater., 2016, 1, 16048 CrossRef CAS.
- Z. Cao, J. Chen, S. Deng and H. Chen, Nanoscale, 2022, 14, 3849 RSC.
- Z. C. Li, W. W. Liu, H. Cheng, S. Q. Chen and J. G. Tian, Opt. Lett., 2016, 41, 3142 CrossRef CAS PubMed.
- X. Ma, C. Huang, M. Pu, Y. Wang, Z. Zhao, C. Wang and X. Luo, Appl. Phys. Lett., 2012, 101, 161901 CrossRef.
- J. Park, H. Kim and B. Lee, Opt. Express, 2008, 16, 413 CrossRef PubMed.
- H. Li, B. Chen, M. Qin and L. Wang, Opt. Express, 2020, 28, 205 CrossRef CAS PubMed.
- T. Hu, Y. Wang, L. Wu, L. Zhang, Y. Shan, J. Lu, J. Wang, S. Luo, Z. Zhang, L. Liao, S. Wu, X. Shen and Z. Chen, Appl. Phys. Lett., 2017, 110, 051101 CrossRef.
- C. Menzel, C. Rockstuhl and F. Lederer, Phys. Rev. A, 2010, 82, 053811 CrossRef.
- T. Kaelberer, V. A. Fedotov, N. Papasimakis, D. P. Tsai and N. I. Zheludev, Science, 2010, 330, 1510 CrossRef CAS PubMed.
- Y. He, G. Guo, T. Feng, Y. Xu and A. E. Miroshnichenko, Phys. Rev. B, 2018, 98, 161112(R) CrossRef.
- P. D. Terekhov, V. E. Babicheva, K. V. Baryshnikova, A. S. Shalin, A. Karabchevsky and A. B. Evlyukhin, Phys. Rev. B, 2019, 99, 045424 CrossRef CAS.
- H. Li, G. Wei, H. Zhou, H. Xiao, M. Qin, S. Xia and F. Wu, Phys. Rev. B, 2022, 105, 165305 CrossRef CAS.
- W. Suh, Z. Wang and S. Fan, IEEE J. Quantum Electronics., 2004, 40, 1511 CAS.
- W. Yin, Z. Shen, S. Li, Y. Cui, F. Gao, H. Hao, L. Zhang and X. Chen, Opt. Express, 2022, 30, 32162 CrossRef CAS PubMed.
- H. Li, M. Qin, L. Wang, X. Zhai, R. Ren and J. Hu, Opt. Express, 2017, 25, 31612 CrossRef CAS PubMed.
- G. Yang, S. U. Dev, M. S. Allen, J. W. Allen and H. Harutyunyan, Nano Lett., 2022, 22, 2001 CrossRef CAS PubMed.
- K. I. Okhlopkov, A. Zilli, A. Tognazzi, D. Rocco, L. Fagiani, E. Mafakheri, M. Bollani, M. Finazzi, M. Celebrano, M. R. Shcherbakov, C. De Angelis and A. A. Fedyanin, Nano Lett., 2021, 21, 10438 CrossRef CAS PubMed.
- A. A. Popkova, I. M. Antropov, G. I. Tselikov, G. A. Ermolaev, I. Ozerov, R. V. Kirtaev, S. M. Novikov, A. B. Evlyukhin, A. V. Arsenin, V. O. Bessonov, V. S. Volkov and A. A. Fedyanin, Laser Photonics Rev., 2022, 16, 2100604 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |