Carbon nanowires made by the insertion-and-fusion method toward carbon–hydrogen nanoelectronics

Abstract

Carbon nanowires (CNWs), long linear carbon chains encapsulated inside carbon nanotubes, exhibit sp hybridization characteristics as one of one-dimensional nanocarbon materials. The research interests on CNWs are accelerated by the successful experimental syntheses from the multi-walled to double-walled until single-walled CNWs recently but the formation mechanisms and structure–property relationships of CNWs remain poorly understood. In this work, we studied the insertion-and-fusion formation process of CNWs at an atomistic level using ReaxFF reactive molecular dynamics (MD) and density functional theory (DFT) calculations with particular focus on the hydrogen (H) adatom effects on the configurations and properties of carbon chains. The constrained MD shows that short carbon chains can be inserted and fused into long carbon chains inside the CNTs due to the van der Waals interactions with little energy barriers. We found that the end-capped H atoms of carbon chains may still remain as adatoms on the fused chains without C–H bond breaking and could transfer along the carbon chains via thermal activation. Moreover, the H adatoms were found to have critical effects on the distribution of bond length alternation as well as the energy level gaps and magnetic moments depending on the varied positions of H adatoms on the carbon chains. The results of ReaxFF MD simulations were validated by the DFT calculations and ab initio MD simulations. The diameter effect of the CNTs on the binding energies suggest that multiple CNTs with a range of appropriate diameters can be used to stabilize the carbon chains. Different from the terminal H of carbon nanomaterials, this work demonstrated that the H adatoms could be used to tune the electronic and magnetic properties of carbon-based electronic devices, opening up the door toward rich carbon–hydrogen nanoelectronics.

---

1. Introduction

As one of true one-dimensional (1D) allotropes of carbon with sp hybridization, carbyne has attracted increasing interest due to its outstanding mechanical properties such as extremely high stiffness and Young's modulus as well as tunable electronic properties and thermal properties predicted theoretically.^1–4 However, the isolated carbyne is unlikely to exist at ambient conditions due to the tendency to form more stable sp² or sp³ hybridized nanocarbons via crosslinking reactions and cycloaddition.^5–7 The key to successful experimental synthesis of carbyne is to utilize confinement or constraint for stabilization. Although carbyne-like linear carbon chains (LCCs) can be stabilized by end-capped functional groups and graphyne-type materials,^8,9 the lengths of LCCs are still very limited.^10–12 The preparation of stable long LCCs (LLCCs) remained as a barrier for the property investigations and applications. The synthesis of carbon nanowires (CNWs) utilizing carbon nanotube (CNT) confinement provide a reliable approach for the bulk production of LLCCs.¹³ The CNWs can be regarded as LLCCs encapsulated inside the hollow core of CNTs. The confinement of CNTs offers an effective protection for LLCCs to avoid the crosslinking reactions, making the stable existence of carbyne possible.¹⁴

According to the number of layers of outer CNTs, CNWs can be classified as single-walled carbon nanowires (SWCNWs), double-walled carbon nanowires (DWCNWs), and multi-walled carbon nanowires (MWCNWs).¹⁵ Since MWCNWs were first discovered in 2003 by Zhao et al.,¹³ the synthesis and preparation of CNWs have achieved significant progress. In 2006, Endo et al. observed the carbon chains induced resonant Raman mode located at 1855 cm⁻¹ in DWCNTs after heat treatment.¹⁶ Using the arc discharge technique in a He atmosphere, Cazzanelli et al. prepared MWCNWs in 2007 and discussed the temperature-driven phase transition of LCCs.¹⁷ Using H arc discharge production of DWCNTs followed by high-temperature treatments, Shi et al. grow LLCCs successfully inside the DWCNTs, leading to the formation of DWCNWs in 2011.¹⁸ Zhao et al. investigated the fusion reactions of linear C₁₀H₂ molecules and realized the high temperature induced formation and growth of LLCCs inside the DWCNTs in 2011.¹⁹ Later, the pressure induced Raman spectrum changes of LLCCs inside the multi-walled CNTs (MWCNTs) were reported by Andrade et al.²⁰ Until 2015, the existence of LLCCs within the innermost nanotubes of MWCNTs was confirmed via cross section image by Andrade et al., providing unambiguous evidence to the long-standing debate on the existence of CNWs.²¹ Furthermore, Shi et al. reported very long LCCs composed of more than 6000 carbon atoms stabilized by the confinement of DWCNTs.¹⁴

The continuous improvement for the high-yield growth of MWCNWs drive the further researches on LLCCs and carbyne.^15,22–24 The existence of outer CNTs influences the structures and physical properties of LLCCs and thus hinders the direct characterization of LLCCs.²² The SWCNWs make the direct measurements of many properties of LLCCs possible. In 2018, Shi et al. reported the extraction of SWCNWs from DWCNWs.²⁵ The successful separation of SWCNWs offered a possibility toward the isolation of LCCs from CNTs. Toma et al. presented the preparation of SWCNWs, DWCNWs, and MWCNWs using electrical arc discharge techniques.²⁶ Chang et al. synthesized SWCNWs by insertion followed by the heat treatment of polyynes inside the SWCNTs at 700 °C, providing a controllable method for the mass-production of SWCNWs with diameters ranging between 7.0–9.5 Å.²⁷ The great successes achieved in the synthesis and preparation of CNWs provide the opportunities for the property investigations in experiments, such as the electronic properties,^28,29 mechanical properties,³⁰ and vibrational characteristics.^31,32

The computational study at an atomistic level provides fundamental understanding on the properties of CNWs. Chen et al. calculated the electronic and transport properties of SWCNWs using tight-binding (TB) method and revealed the effect of encapsulated LCCs on (8, 0) SWCNT.³³ CNWs have been studied extensively via density functional theory (DFT) including structural and electronic properties,^29,34–38 mechanical properties,³⁶ and optical properties.³⁹ In 2016, Shi et al. predicted and confirmed experimentally that the optimum diameter of CNT is about 7.1 Å for the growth of LLCCs.¹⁴

Molecular dynamics (MD) enables the simulations of dynamic evolutions on large systems over long time scales and thus provide crucial dynamic information at a lower cost compared with DFT calculations. In 2011, Zhao et al. investigated the fusion reactions of LCCs inside the DWCNTs using TB-MD simulations.¹⁹ Moreover, the effect of pressures,²⁰ temperatures, diameters of CNT,⁴⁰ and catalysts⁴¹ on the formation of LCCs inside CNTs were also studied using reactive force field (ReaxFF) method. The simulations focused on the possibilities of the formation of CNWs from the thermodynamics point of view was also reported by our group previously using ReaxFF.²⁷ Although the growth process of LLCCs inside CNTs has been investigated both experimentally and theoretically,^{19,20,22,40–42} the formation mechanisms especially the detailed dynamics of growth process and refined configurations of carbon chains inside CNTs are still elusive from kinetic point of view.

Regarding to the H effects on nanocarbon materials, most existing simulations focus on the edge H atoms if any that intrinsically exist to saturate the dangling bonds of the edge carbon atoms. The single C atom^43,44 and carbon dimer^45,46 without H atoms have often been used as the precursors and building blocks in the simulations of nanocarbon growth. The ignorance of H atoms is understandable because the naked C atoms without H are more easily to bind and grow to bigger species at short time scale of simulations, plus the simplicity of configuration construction avoiding the introduction of additional degree of freedom. This H-free assumption has been considered valid for years since the final products often do not have internal H adatoms or are not carefully confirmed due to the challenge of locating light H atoms in experiments. Theoretically speaking, it would be energetically favorable that H adatoms turn the C–C orbital hybridization of 1 D carbon chains from original sp to the more stable sp² locally. However, what process can lead to the formation of the H adatom configurations and what the consequence of these H adatoms on the configurations, electronic, and magnetic properties are still poorly understood. Specifically, the effects of the residual H adatoms on fused LCCs have not yet been fully explored.

In this work we carried out reactive MD simulations of the formation mechanisms of CNWs using ReaxFF force field with the parameters developed in our group. ReaxFF force fields, one of most widely used reactive force field, have been extensively applied to study the chemical reactions of various organic and inorganic systems, especially for hydrocarbon systems that mainly involve C–H bond breaking and formation.^47–52 Both the insertion and the fusion reactions of carbon chains inside CNTs were investigated using constrained MD simulations, respectively. The evolution of configurations during the fusion process of carbon chains inside CNTs were described by ReaxFF MD simulations followed by the verification of DFT calculations. Our simulations demonstrated that carbon chains can move into the CNTs and then fuse together spontaneously when the diameters of the CNTs favor the attractions of van der Waals (vdW) interactions. The effects of end-capped H atoms and H adatoms after chain fusion were particularly studied. We found that the H adatoms diffuse along carbon chain dynamically without C–H bond breaking, making the end C–C fusion energetically more easily. The effects of the diameters of the CNTs were also investigated. The insertion-and-fusion mechanisms of CNWs formation provide a theoretical basis for optimizing the experimental synthesis, characterization, and applications of CNWs. Different from the terminal H used for saturation, the H adatoms of carbon chains can be used as an effective tuning strategy for the so-called carbon–hydrogen nanoelectronics.

2. Computational methods

All the MD simulations reported in this work were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)⁵³ package with a ReaxFF module.^54,55 In the MD simulations we used the all-carbon ReaxFF reactive force field ReaxFF_C-S22 developed for various carbon allotropes in our group recently. The detailed description of ReaxFF_C-S22 will be described elsewhere. Firstly, energy minimization for the studied systems were carried out at 0 K. Then constrained MD were performed by fixing the distance between the given constraint atoms. The temperature was ramped up to the target value within 1.0 ps in a canonical (NVT) ensemble followed by the equilibrium NVT-MD simulations for 500 ps. The temperatures were controlled using the Nosé-Hoover thermostat.⁵⁶ The statistical results were analyzed for the last 200 ps trajectories. The experimental synthesis of CNWs was reported by Chang et al. where the heat treatment was operated at 700 °C,²⁷ so the temperature of 973 K was used in the MD simulations of this work.

The other constraint simulation methods are discussed and compared as follows: (1) the frozen atom method would fix the full coordinates of atoms that could introduce more artificial effects on the energy barriers since the end atoms may rotate before fusion. In our constrained MD, only the distances were fixed and the atoms were allowed to move freely that minimized the artificial effects. (2) Nudged elastic band (NEB) method is more suitable to find minimum energy paths with saddle points for complex reaction paths.^57,58 The CNW formation has well-defined 1D reaction coordinate with little energy barriers that has more clear physical insights into the formation mechanism. (3) the constrained MD is equivalent to scan the potential energy surface along the most critical one-dimensional (1D) migration direction in a flexible way. The confinement of CNTs reduced the degrees of freedom of the carbon chains, leading to the reaction path limited to the quasi 1D case. Therefore, the distance constraint MD is a suitable method to study 1D fusion dynamics in this work.

Density functional theory (DFT) calculations and ab-initio molecular dynamics (AIMD) simulations were carried out using The Vienna Ab-initio Simulation Package (VASP).⁵⁹ Projector augmented wave (PAW) pseudopotentials⁶⁰ were applied to represent the electron–ion interactions. The generalized gradient approximation (GGA) in a form of Perdew–Burke–Ernzerhof (PBE) was chosen for the exchange–correlation functional.⁶¹ vdW interactions corrections were considered using the DFT-TS method.⁶² A kinetic energy cutoff of 600 eV was employed for the plane-wave basis functions. The first Brillouin zone (BZ) integration was performed using the Monkhorst–Pack scheme⁶³ and 1 × 1 × 1 k-point mesh was utilized. Periodic boundary conditions were applied with a vacuum region greater than 15 Å. Magnetic moments were considered to describe the systems with lone pair electrons. In the DFT calculations, a convergence criterion of 1 × 10⁻⁶ eV was adopted for the total energy difference in the self-consistent field iterations. All the atomic positions except for the constraints if any were fully optimized until the Hellmann–Feynman force component on each atom was less than 0.005 eV Å⁻¹. In AIMD simulations, NVT dynamics was conducted at 973 K for 3.0 ps with a 1.0 fs time step. The temperature control was achieved by using the Nosé–Hoover thermostat.⁵⁶ The convergence criterion for the total energy difference in self-consistent field calculations was 1 × 10⁻⁵ eV. The results were analyzed statistically for the last 1.0 ps.

3. Results and discussion

3.1 Insertion process of CNW formation

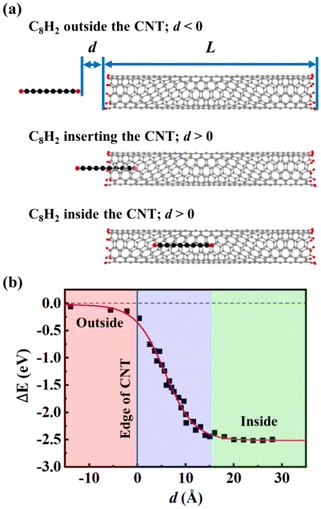
To understand the insertion mechanism of CNWs, we simulated the process of inserting a C₈H₂ chain into (6, 5) CNT at 973 K. The host (6, 5) CNT had a finite length of about 50 Å whose edges were saturated with H atoms. The constrained MD were performed by fixing the distance (d) between the end of C₈H₂ and the edge of the CNT. Then, we define d < 0 when the C₈H₂ is located outside the CNT while d > 0 when the C₈H₂ moves into the CNT [Fig. 1(a)]. Using the infinite large separation as a reference, the relative energies of CNT and chain systems were plotted as a function of separation d during the insertion process [Fig. 1(b)]. When the C₈H₂ was located far from the CNT, there is little interaction between C₈H₂ and CNT, indicated by the small relative energies close to the reference energy. When the C₈H₂ approached the CNT edge (d = 0), the relative energy of the system began to drop due to the attractive vdW interactions between C₈H₂ and CNT. As the chain was moving into the CNT, the relative energy of the system decreased linearly because of the larger vdW interactions associated with the more inserted carbon atoms. The distance of vdW interactions was ∼3.8 Å between the C₈H₂ and the CNT wall, same as the empty CNT before the insertion. When the C₈H₂ moved into the CNT completely (d ≈ 15 Å), the system reached its lowest energy (ΔE = −2.50 eV), meaning that the vdW interaction energy is ∼0.3 eV/C atom between the C chain and the CNT. The energy profile during the insertion process indicates that carbon chains can be inserted into the CNTs with little energy barrier if the diameters of the CNT favor the attractive vdW interactions.

Fig. 1 (a) Snapshots of a C₈H₂ insertion into the (6, 5) CNT. (b) Relative energy profile during the insertion process with an infinite separation as a reference. The total energy of C₈H₂ inside the CNT was 2.50 eV lower than that outside the CNT.

3.2 Fusion process of CNW formation

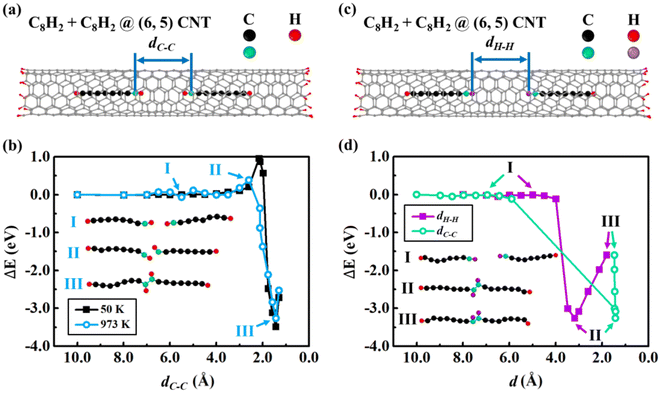
Since the insertion of a carbon chain into CNTs is energetically barrierless, multiple carbon chains may be absorbed into one CNT. We now studied the fusion process of two carbon chains inside (6, 5) CNT by constrained MD. We considered various constraint conditions to examine the fusion process. By fixing the distance (d_C–C) between two end C atoms of the C₈H₂ chains [Fig. 2(a)], we performed constrained MD at 50 K and 973 K, respectively. The relative energies were plotted as functions of d_C–C [Fig. 2(b)]. The energy remains unchanged when d_C–C is between 10.0–3.5 Å, indicating that there is little interaction between two C₈H₂ chains far each other. As d_C–C decreased further, the repulsive interactions between the two end-capped H atoms of the chains led to the energy increase of the system. The maximum energy barrier was 0.39 eV when d_C–C = 2.6 Å. As the d_C–C decreased further, the energy suddenly dropped mainly due to the attraction between two end C atoms of the C₈H₂ chains. The two constrained end C atoms overcame the energy barrier and formed C–C covalent bond, leading to the coalescence of two C₈H₂ chains into a C₁₆H₄ chain inside (6, 5) CNT. The minimum energy of the coalesced C₁₆H₄ at (6, 5) CNT was −3.26 eV when d_C–C = 1.4 Å, indicating that the fusion energy from C–C bond formation is approximately 10 times larger than the insertion vdW interaction ∼0.3 eV/C atom. The two end-capped H atoms still kept their bindings with the end C atoms at the middle of the chain. The system energy increased again if d_C–C decreased further mainly due to the repulsive interaction between the too close end-capped carbon atoms. To examine the temperature effect, we also simulated the fusion process at a low temperature 50 K. The trend of the energy changes at 50 K is similar to that at 973 K except that the energy barrier at 50 K is 0.57 eV higher when d_C–C = 2.2 Å. As shown in Fig. 2(b), the higher temperature would facilitate the fusion process starting at further distance with lower energy barrier. At high temperature the large kinetic energy prompts the rotation of C–H bonds that favors the C–C bond formation in the fusion reactions. The energy barriers in Fig. 2(b) were mainly caused by the repulsive interactions between H atoms.

Fig. 2 (a) Schematic model of the fusion process of two C₈H₂ chains inside (6, 5) CNT. The distance (d_C–C) between two end carbon atoms of the C₈H₂ chains was constrained (in green). (b) Relative energies as functions of d_C–C at 50 K and 973 K. (c) The distance (d_H–H) between two end-capped H atoms of the C₈H₂ chains was constrained (in purple). (d) Relative energies as functions of d_H–H at 973 K. The insets in (b) and (d) are typical configurations during the fusion process, and the CNTs are hidden for clear visual inspection.

To examine the influences of the different reaction coordinates on the minimum energy paths, we considered other possible constrained pairs atoms during fusion processes, e.g., H–H and C–H pairs besides the C–H pairs discussed above. We carried out the constrained MD by fixing the distance between two end-capped H atoms of the C₈H₂ chains (d_H–H) [Fig. 2(c)]. The relative energies were plotted as functions of the constrained d_H–H and corresponding non-fixed d_C–C in Fig. 2(d). The energies remained unchanged when d_H–H = 10.0–4.0 Å due to little interactions between the two far separated chains. Different from the case of the C–C constraint, however, there was little fusion energy barriers under H–H constraints. This comparison implied that the small energy barriers under the C–C constraint might come from the hindrance of H–H repulsion during the C–C fusion. When d_H–H is large [stage I in Fig. 2(d)], both the end C–H bonds are parallel to the carbon chains. As d_H–H decreased to 3.2 Å [stage II in Fig. 2(d)], the H–H repulsion and thermal vibration rotated the two C–H bonds to the opposite directions to minimize H–H repulsion. The C–H bond rotation facilitated the C–C fusion and the non-fixed d_C–C decreased suddenly from 5.9 Å to 1.4 Å, reaching the optimal equilibrium C–C bond length of sp² hybridization. If d_H–H decreased further, the energy increased due to the repulsive interaction between the closed H atoms while d_C–C remained the same since the completion of the C–C bond formation.

In the fusion simulations discussed above, the ends of carbon chains were saturated using H atoms that is a reasonable model in low-temperature experiments. CNWs also can be synthesized in vacuum and inert gas at high temperatures^19,24,64 where carbon chains may also exist without end caps. To examine the fusion reactions without the end-capped H atoms, we performed constrained MD simulations along the other reaction coordinates (Fig. S1†): (1) the distance of C–H bond between C₈H and C₈H₂ chain; (2) the distance of C–C bond between two C₈H chains. The end C atom of the C₈H chain was not saturated by H before fusion. The C chains with unsaturated end C atoms fused more early at further distances with much larger energy drop compared with the C chains with the H saturated ends. There are always little energy barriers for the fusion of C chains despite with saturated or unsaturated ends.

3.3 Configurations of carbon chains with hydrogen adatoms

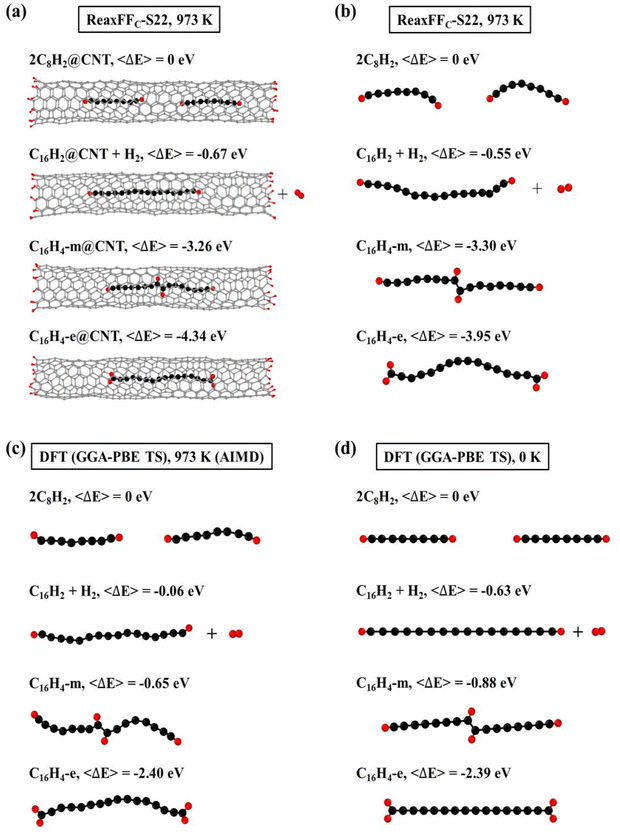
Since carbon chains can be inserted into the CNTs and subsequently fused together, the configurations of fused carbon chains inside CNT need to be clarified upon the understanding of the insertion-and-fusion process. Several typical configurations of carbon chains inside a finite (6, 5) CNT were considered [Fig. 3(a)]. The isolated carbon chains without CNTs were also calculated for comparison [Fig. 3(b)]. In general, the fused carbon chain is thermodynamically more stable than that of two separated C₈H₂ chains inside CNT (2C₈H₂@CNT) [Fig. 3(a)]. Specifically, the energy of a C₁₆H₂ chain inside CNT plus an isolated H₂ (C₁₆H₂@CNT + H₂) is 0.67 eV lower than that of 2C₈H₂@CNT, in consistent with our previous calculations.²⁷ The energies of C₁₆H₄ chains inside the CNT were even lower, despite the two H adatoms sit at the middle of the chain (C₁₆H₄-m) or transfer to the ends of the chain (C₁₆H₄-e). Moreover, C₁₆H₄-e@CNT is the most thermodynamically stable configuration with the relative energy of −4.34 eV. This indicated that the fusion reactions of carbon chains inside CNT did not necessarily break C–H bonds and produced H₂ molecules as most previous theory and experiments assumed. Instead, the short C chains preferred to form C₁₆H₄ chains without C–H bond breaking. The results of the isolated carbon chains had the similar trends [Fig. 3(b)] except that the carbon chains would bend without the confinement of the CNT. These are consistent with our previous results that CNTs can provide the radial confinement to prevent polyyne molecules from crosslinking reactions and offer an alignment effect along the narrow axial channel, increasing the probability of end-to-end fusion reactions of carbon chains.²⁷ The AIMD simulations and DFT calculations were also performed on the isolated carbon chains, and the qualitatively similar results [Fig. 3(c) and (d)] further validated the conclusions obtained by the ReaxFF MD simulations.

Fig. 3 ReaxFF MD simulations of various configurations of (a) carbon chains inside a finite (6, 5) CNT and (b) isolated carbon chains at 973 K. (c) AIMD simulations and (d) DFT calculations of various typical configurations of isolated carbon chains at 973 K and 0 K, respectively.

It has been commonly believed that the fusion of C chains involves the C–H bond breaking that produces an isolated H atom. The two isolated H atoms then form a H₂ molecule that moves out of CNT eventually. However, our simulations found that the C–H bonds did not necessarily break and the H atoms remained on the C chains as H adatoms. To confirm this prediction, we further carried out MD and DFT calculations on the effects of C–H bond breaking that are often ignored previously. Fig. 3(a) and (b) show the ReaxFF NVT-MD simulations at 973 K on the C chains with and without C–H bond breaking and CNTs, respectively. Compared with the two separated C₈H₂ chains, the separated C₁₆H₂ and H₂ system had lower energies in spite of the existence of CNTs. However, if the C–H bonds did not break, the C₁₆H₄ chains had even lower energies. Moreover, the C₁₆H₄ configuration where H adatoms are all located at the chain ends (dubbed C₁₆H₄-e) was much more stable than the configuration having H adatoms in the middle (dubbed C₁₆H₄-m). The results of AIMD by DFT at 973 K [Fig. 3(c)] and DFT at 0 K [Fig. 3(d)] both supported and validated the trends predicted by ReaxFF MD in Fig. 3(a) and (b), confirming that the order of stability remained the same despite quantitative difference due to temperature effects. The residual H adatoms were also found in the C₂H₂ addition process during the formation of graphene, the so-called “Add and Dehydrogenate” (ADh) mechanism.⁶⁵

The long carbon chains would not fuse with the edge or the wall of carbon nanotubes based on the discussions as follows. (1) Chain-edge fusion: The insertion of chain into the tube core is energetically barrierless as shown in the energy profile in Fig. 1. Also, the chain insertion was driven by the significant energy drop due to the attractive vdW interaction between chain and tube. On the other hand, the chain is hard to fuse with the edge because the chain end would have H–H repulsion with the saturated edges of CNT. In CNW the energy barrier would be overcome and collision probability would increase due to the confinement effects inside CNTs plus the activation energy provided by the high temperature heat treatment. Without the geometry confinement of CNT, the collision probability between chain and edge would become extremely low, so the chain-edge fusion could hardly occur from both thermodynamic and kinetic points of view. (2) Chain-wall fusion: The fusion between chain end and tube wall is energetically unfavorable mainly because the chain would deviate from the optimal parallel alignment along the tube axis that maximizes the attractive vdW interaction. The chain-wall fusion would make the end C atoms of chain changed from sp to sp² hybridization with downhill energy and the C atom of wall changed from sp² to sp³ hybridization with uphill energy. The fusion-induced energy changes during C_chain–C_wall bond formation are smaller than the dominated energy penalty of misalignment of long carbon chains off the tube axis, further confirmed by the calculations below.

To examine the possibility of the fusion reactions between carbon chains and CNT tube, we carried out several additional MD simulations on C₁₆H₂ fusion with the (6, 5) CNT wall [Fig. S2(c)–(e) of ESI†]. The result shows that the chain-wall fusion configuration (C₁₆-CNT + 2H₂) with two generated H₂ molecules was unfavorable with very high positive energies, confirming again that the H₂ generation is unlikely [Fig. S2(d) of ESI†]. The chain-wall fusion configuration with one H₂ molecule [C₁₆H₂-CNT + H₂ in Fig. S2(c) of ESI†] had higher energy than the encapsulated chain configuration (C₁₆H₂@CNT + H₂) [Fig. S2(b) of ESI†]. The chain-wall fusion configuration without H₂ generation [Fig. S2(e) of ESI†] was energetically less favorable than the capsulated chain configurations [Fig. 3(a)]. It is possible that the very short carbon chain fuse with the CNT wall. Liu et al.³⁴ reported that small carbon species with dangling bonds including carbon chains and graphene sheets could react with the wall atoms of CNT.

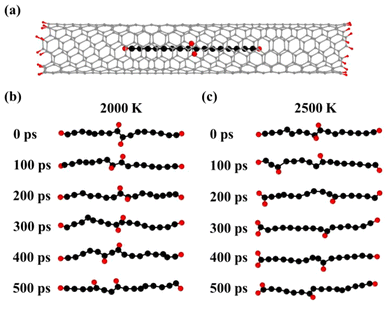
To examine the stability of H adatoms, we explored the effect of higher temperatures on C₁₆H₄-m@(6, 5) CNT with the H adatoms located at the joint positions of the two short chains [Fig. 4(a)]. The temperature of the systems increased linearly to 2000 K and 2500 K, respectively, at a rate of 1.0 K fs⁻¹. Then the NVT-MD simulations were performed for 500 ps. The snapshots of the MD trajectories at 2000 K and 2500 K were shown in Fig. 4(b) and (c), respectively, where the CNTs were hidden for clear visual inspection. At 2000 K [Fig. 4(b)], the H adatoms vibrated at the joint positions at the first 300 ps. Between 300–400 ps, one of the H adatoms transferred to form a bond with the other C atom. Subsequently, the H adatom transferred to another C atom again between 400–500 ps. The H transfer along the chain was driven by the thermal vibration of the system. In the MD simulations at a higher temperature 2500 K [Fig. 4(c)], the C–H bonds broke and formed more frequently and the H adatoms migrated more easily along the fused carbon chain, leading to one H atom moving from the center to the end. The H adatom transferred to and remained at the end of the C chain, while the other H adatom continued to move along the C chain. Statistically speaking, the other H atom may eventually migrate to the end of chain. These high temperature MD simulations demonstrated the thermodynamic limits shown in Fig. 3(a). However, only the MD simulations at very high temperatures and very long times could lead to the complete migration of H atoms going from the center to the ends, which may not be easily realized at the experimental conditions. Therefore, we believe the H migrations are most likely incomplete and the H atoms are distributed separately along the carbon chains at the experimental conditions. The thermodynamically stable configuration with two H at each end of carbon chain may be obtained by other experimental approaches with higher energy input in future.

Fig. 4 (a) Schematic model of a C₁₆H₄-m chain inside a finite (6, 5) CNT. Typical configurations during the NVT-MD simulations at (b) 2000 K and (c) 2500 K, respectively. The CNTs were hidden in (b) and (c) for clear visual inspection.

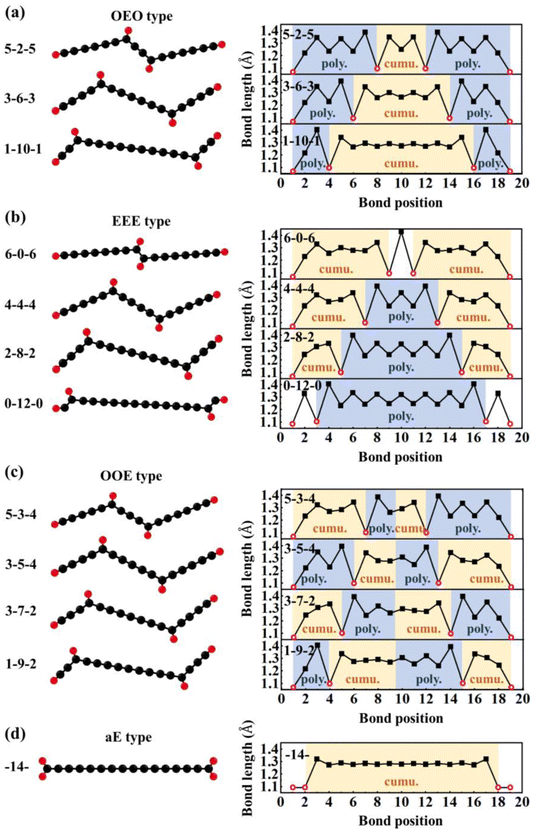
The diffusion dynamics predicted by ReaxFF MD were further validated by DFT calculations at 0 K on a series of H adatom positions on the chains (Fig. 5). Moreover, DFT calculations were carried out to study the H adatom effects on the electronic and magnetic properties of the C chains [Fig. 6(a) and (b)]. The energy levels of the carbon chains with the typical H adatom configurations are shown in Fig. S3 in the ESI.† The binding of the H adatoms with C atoms after C–C bond formation led to local sp² hybridization at the joint position. Such local hybridization change from sp to sp² would have a long-range domino effect, e.g., inducing alternative single and triple C–C bonds between the neighboring C atoms that propagate along the C chain. To describe the various configurations with different H atom origins, the H adatoms are denoted as aH type while the terminal H atom as tH type. According to the H origin types and their positions, we can classify various configurations into several categories as follows.

Fig. 5 Typical configurations of C chains with H adatoms: (a) OEO type, (b) EEE type, (c) OOE type, and (d) aE type of C₁₆H₄ chains and corresponding bond length distributions optimized by DFT. The solid black squares represent the C–C bond length while the open red circles represent the C–H bond length.

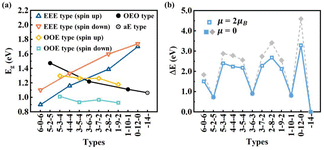Fig. 6 (a) HOMO–LUMO gaps and (b) relative DFT energies of typical types of C₁₆H₄ chains including OEO, EEE, OOE, and aE types.

(1) Odd-Even-Odd (OEO) type: The Odd-Even-Odd (OEO) type of configurations is defined if the number of C atoms (N_C) between C-tH and C-aH is odd leading to the polyyne type with alternative single and triple C–C bonds, and the N_C between the two middle C-aH atoms is even leading to the cumulene type with all double C–C bonds, e.g., 5–2–5, 3–6–3, 1–10–1 where the numbers represent the N_C of different segments excluding the C atoms binding to the tH or aH [Fig. 5(a)]. The OEO types of configurations are energetically stable without magnetic moments. The OEO types have the cumulene middle segments with all double C–C bonds responsible for electron conduction. If aH atoms are transferred gradually to the ends of C chains, N_C of the cumulene segments increased while those of the polyyne segments decreased [Fig. 5(a)]. These changes of bond length alternation (BLA) reduced the HOMO–LUMO gaps [solid circles in Fig. 6(a)] that would increase their electron conductivity. On the other hand, the intensity of Raman spectrum may decrease because the Raman spectra are contributed by the segments of the polyyne type between the C-aH and C-tH atoms. These OEO types are probably the low energy configurations observed in the experiments.

(2) Even-Even-Even (EEE) type: The Even-Even-Even (EEE) type of configuration is defined if N_C between C-tH and C-aH is even leading to the cumulene type with all double C–C bonds, and N_C between the two middle C-aH atoms is even leading to the polyyne type with alternative single and triple C–C bonds, e.g., 6–0–6, 4–4–4, 2–8–2, 0–12–0 [Fig. 5(b)]. The EEE types of configurations are energetically less stable and exhibit magnetic moments. If the aH atoms transfer to the ends, the cumulene segments became shorter while the polyyne segments became longer [Fig. 5(b)]. These changes of BLA increased HOMO–LUMO gaps [up and down triangles in Fig. 6(a)] that may reduce electron conductivities. The intensity of Raman spectra may be enhanced because Raman spectra are determined by the segments of polyyne type between the two C-aH atoms. The non-magnetic OEO type and magnetic EEE type could be switched by the H transfer via temperature control experimentally.

(3) Odd-Odd-Even (OOE) or Even-Odd-Odd (EOO) type: The Odd-Odd-Even (OOE) type of configuration is defined if N_C between C-tH and C-aH is odd on one side while N_C between C-tH and C-aH is even on the other side, and N_C between the two middle C-aH atoms is odd [Fig. 5(c)]. In the OOE types of configurations the C–C bonding exhibit alternative cumulene and polyyne types, e.g., 5–3–4, 3–5–4, 3–7–2, 1–9–2 [Fig. 5(c)]. The OOE types of configurations are energetically less stable and also exhibit magnetic moments [Fig. 6(a) and (b)]. If the aH atoms transfer to the ends, the cumulene and the polyyne segments switched each other that kept HOMO–LUMO gaps having little change [Fig. 5(c)]. Accordingly, the electron conductivity and Raman intensity may not change. These alternative cumulene and polyyne segments may play a role of P–N junctions in nanoelectronics and thus be used to control direction of electric current.

(4) All-Even (aE) type: The All-Even (aE) type of configuration is defined if the tH and aH atoms are bound to the same end C atoms simultaneously and the N_c between the C-aH (or C-tH) atoms are even, e.g., dubbed -14- [Fig. 5(d)]. The aE type of configurations has the cumulene bonding type with all double C–C bonds that are Raman inactive modes. The aE type of chains is energetically most stable but the H adatom transfer to the end C atoms needs to overcome high energy barriers between 1.28–2.48 eV [Fig. 6(b)]. The mild experimental conditions most likely lead to metastable H adatoms sitting in the middle of the carbon chains.

According to analyses above, every H adatom transfer along the C chain could cause the changes of configurations as well as HOMO–LUMO gaps and magnetic moments. The experimental confirmation on the existence of H on the carbon chain was challenging using conventional electron microscopy or C–H vibration spectrum method. However, the H-induced changes of electronic and magnetic properties may be possibly to be measured and verified experimentally. On the other hand, one may induce H transfer via temperature control or other methods that in turn tunes the electronic and magnetic properties. Therefore, it is possible to use hydrogen adatoms to tune the properties of carbon-based nanoelectronics devices that can be called carbon–hydrogen (C–H) nanoelectronics. The future sizes of electronic circuits would reduce to below one nm that makes the precise doping control extremely hard if not impossible. The designed H adatoms in C–H nanoelectronics provide a new strategy to tune the electronic properties of nanomaterials without the needs of doping. The hydrogen adatom tuning strategy may be applied to other nanocarbon materials and their associated electronic or magnetic devices.

3.4 Diameter effects on the binding energies of carbon nanowires

We calculated previously²⁷ the binding energies of C₁₆H₂ chains inside finite CNTs with various diameters and chirality using ReaxFF_CHO-2016.⁵¹ The MD simulations show that (6, 5) CNT with a diameter of 7.6 Å is optimal for growing carbon chains. In this work we performed calculations on the CNT diameter effects using in-house developed ReaxFF_C-S22 at 300 K to examine the effects of force field parameters. As shown in Fig. 7(a), the binding energy curves of C₁₆H₂ chains as functions of CNT diameters were qualitatively similar between ReaxFF_C-S22 and ReaxFF_CHO-2016 and both predicted the minimum energy at the CNT diameter of 7.6 Å. The quantitative differences include that ReaxFF_C-S22 predicted the larger depth of energy well −4.51 eV and harder repulsion at short distance. The MD results confirmed again that it is thermodynamically stable for carbon chains to be inserted into the CNTs whose diameters are favorable for the vdW interactions despite the chirality and metallic/semiconducting properties, consistent with experimental results.²⁷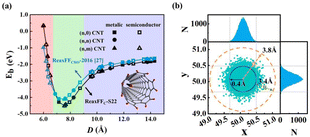

Fig. 7 (a) Binding energies of C₁₆H₂ chain inside finite CNTs with various diameters and chirality calculated by ReaxFF_CHO-2016²⁷ and ReaxFF_C-S22, respectively. The inset is the schematic model of a C₁₆H₂ chain inside a finite (6, 5) CNT. (b) The projected positions of all C atoms of C₁₆H₂ chain at every MD step and the corresponding histogram of probability distribution of x- and y-coordinates.

The optimal CNT for insertion predicted in this work was (6, 5) CNT with a diameter of 7.6 Å, larger than the diameter 7.1 Å predicted by DFT previously.¹⁴ The DFT prediction at 0 K did not consider temperature effects and the distortion of flexible C chains. The H adatoms would induce the local kink distortion of straight chains due to the sp² hybridizations. The thermal energy at finite temperatures in MD simulations caused C₁₆H₂ chains to vibrate and distort to some extent. There should be a “free” moving zone for the easier vibration and distortion of flexible chains in the CNT cores satisfying overall optimal vdW interactions between the distorted chains and CNTs. To characterize quantitatively the size of free moving zone of chains, we projected the positions of all C atoms of C₁₆H₂ chains at every MD step onto the x–y plane as plotted in Fig. 7(b). The histogram of probability distribution of x- and y-coordinates were plotted in the top and right panels, respectively. The Gaussian functions were used to fit the probability distribution of the coordinates. According to the predicted optimal CNT radius 3.8 Å and the ideal vdW interlayer distance of graphite 3.4 Å, the core of free moving zone core should have an average optimal radius of 0.4 Å. Our MD trajectory analyses show that the free moving zone with R = 0.4 Å encompasses 97% maximum height of Gaussian distribution functions and 98% occurrence probability of C chain atoms [Fig. 7(b)]. These mean that the majority of C chain atoms stay within the free moving zone except that a very few atoms move into the repulsive vdW region via thermal energy.

The MD simulations show that the CNTs with the radii slightly larger than the ideal vdW interaction distance still can protect and prevent the carbon chains from crosslinking reactions. The free moving zone allows the carbon chains to have enough room for vibration and distortion but not to rearrange themselves to form sp² configurations. If the tube diameter is too large, the CNT lose its confinement effect and carbon chains tend to form sp² carbon materials via crosslinking reactions. On the other hand, if the tube diameter is too small, the carbon chains are hard to be inserted into the tube due to repulsion.

Our MD simulations suggest that both ReaxFF_C-S22 and ReaxFF_CHO-2016 predicted the similar optimal diameters of CNW, confirming further the main conclusion in this study is less sensitive to the force field parameters. More importantly, this work reported two new results: (1) More accurate ReaxFF_C-S22 predicted the deeper energy well and harder repulsion at short distance of CNWs compared with ReaxFF_CHO-2016; (2) We proposed the existence of “free” moving zone of carbon chains at the center of SWCNT while most previous studies assumed the single ideal CNT radius with optimal vdW interaction. The CNTs with the radii slightly larger than the ideal vdW interaction distance suggested that the choices of CNT diameters can be broader in the insertion-and-fusion experimental preparation, providing a guidance for the CNT precursor selection in the experimental synthesis of CNWs. Indeed the SWCNWs prepared in the experiments are observed to have a range of diameters between 7.0–9.5 Å.²⁷

4. Conclusions

This work studied the insertion and fusion processes of carbon chains inside CNTs by ReaxFF molecular dynamics and DFT calculations, providing theoretical evidence of insertion of carbon chains into CNTs to form carbon nanowires, consistent with recent experimental synthesis. Our MD simulations show that the thermodynamically optimal CNTs have a free moving zone to encapsulate the distorted carbon chains that leads to a range of candidate CNT diameters for the carbon chain insertion. The constrained MD simulations show that both the insertion and fusion processes are energetically barrierless, indicating that the formation of carbon nanowire is kinetically a spontaneous process.

The analyses of configurations of fused carbon chains show that the end-capped H of short C chains remained as residual adatoms on the fused C chains rather than the C–H bond breaking and formation of H₂. The H adatoms could transfer along the C chains via thermal activation. Depending on the varied positions of H adatoms on the C chains, there are several distribution types of bond length alternation, leading to the different HOMO–LUMO energy gaps and magnetic moments. Therefore, the electronic and magnetic properties of carbon chains can be tuned accordingly upon the H adatom transfer. The H adatoms discussed in this work have rich configurations, bonding characteristics, and influences on electronic and magnetic properties different from the terminal H of carbon nanomaterials for the saturation of the dangling bonds. This work provides a theoretical basis for the design of novel carbon–hydrogen nanoelectronic devices in future.

Author contributions

Fu Liu: investigation, formal analysis, visualization, writing – original draft; Qingqing Wang: discussion – force field and MD methods; Yuchao Tang: discussion – MD method and analyses; Wan Du: discussion – MD method and analyses; Weiwei Chang: discussion – experiments; Zewei Fu: resources – funding support; Xinluo Zhao: resources – discussion – experiments; Yi Liu: conceptualization, supervision, formal analysis, writing – review & editing.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by Key Program of Science and Technology of Yunnan Province (Grant No. 202002AB080001-2), Yunnan Province “Ten Thousand Talents Plan” Industrial Technology Leading Talent Program (No. YNWR-CYJS-2017-056), Key Research Project of Zhejiang Laboratory (No. 2021PE0AC02), and Shanghai Technical Service Center for Advanced Ceramics Structure Design and Precision Manufacturing (No. 20DZ2294000). The authors acknowledge the Beijing Super Cloud Computing Center, Hefei Advanced Computing Center, and MGI at Shanghai University for providing HPC resources.

References

1. M. Liu, V. I. Artyukhov, H. Lee, F. Xu and B. I. Yakobson, Carbyne from first principles: Chain of C atoms, a nanorod or a nanorope, ACS Nano, 2013, 7, 10075–10082,  DOI:10.1021/nn404177r.
2. X. Liu, G. Zhang and Y.-W. Zhang, Tunable mechanical and thermal properties of one-dimensional carbyne chain: Phase transition and microscopic dynamics, J. Phys. Chem. C, 2015, 119, 24156–24164,  DOI:10.1021/acs.jpcc.5b08026.
3. C. S. Casari, M. Tommasini, R. R. Tykwinski and A. Milani, Carbon-atom wires: 1-D systems with tunable properties, Nanoscale, 2016, 8, 4414–4435,  10.1039/C5NR06175J.
4. S. Tongay, R. T. Senger, S. Dag and S. Ciraci, Ab initio electron transport calculations of carbon based string structures, Phys. Rev. Lett., 2004, 93, 136404,  DOI:10.1103/PhysRevLett.93.136404.
5. C. S. Casari, A. Li Bassi, L. Ravagnan, F. Siviero, C. Lenardi, P. Piseri, G. Bongiorno, C. E. Bottani and P. Milani, Chemical and thermal stability of carbyne-like structures in cluster-assembled carbon films, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075422,  DOI:10.1103/PhysRevB.69.075422.
6. F. Cataldo, Stability of polyynes in air and their degradation by ozonolysis, Polym. Degrad. Stab., 2006, 91, 317–323,  DOI:10.1016/j.polymdegradstab.2005.04.046.
7. R. H. Baughman, Dangerously seeking linear carbon, Science, 2006, 312, 1009–1110,  DOI:10.1126/science.1125999.
8. R. H. Baughman, H. Eckhardt and M. Kertesz, Structure-property predictions for new planar forms of carbon: Layered phases containing sp² and sp atoms, J. Chem. Phys., 1987, 87, 6687–6699,  DOI:10.1063/1.453405.
9. F. Liu, X. Tang, W. Du, B. Chi, X. Zhao and Y. Liu, Radial and axial vibration modes of graphyne nanotubes, Mater. Today Commun., 2022, 31, 103610,  DOI:10.1016/j.mtcomm.2022.103610.
10. W. A. Chalifoux and R. R. Tykwinski, Synthesis of polyynes to model the sp-carbon allotrope carbyne, Nat. Chem., 2010, 2, 967–971,  DOI:10.1038/nchem.828.
11. J. A. Januszewski and R. R. Tykwinski, Synthesis and properties of long [n]cumulenes (n ≥ 5), Chem. Soc. Rev., 2014, 43, 3184–3203,  10.1039/C4CS00022F.
12. L. Fang, T. Zhu, W. Chang, Y. Liu and X. Zhao, Purification of polyynes via carbides, Carbon, 2021, 179, 28–32,  DOI:10.1016/j.carbon.2021.04.032.
13. X. Zhao, Y. Ando, Y. Liu, M. Jinno and T. Suzuki, Carbon nanowire made of a long linear carbon chain inserted inside a multiwalled carbon nanotube, Phys. Rev. Lett., 2003, 90, 187401,  DOI:10.1103/PhysRevLett.90.187401.
14. L. Shi, P. Rohringer, K. Suenaga, Y. Niimi, J. Kotakoski, J. C. Meyer, H. Peterlik, M. Wanko, S. Cahangirov, A. Rubio, Z. J. Lapin, L. Novotny, P. Ayala and T. Pichler, Confined linear carbon chains as a route to bulk carbyne, Nat. Mater., 2016, 15, 634–639,  DOI:10.1038/nmat4617.
15. Y. Zhang, J. Zhao, Y. Fang, Y. Liu and X. Zhao, Preparation of long linear carbon chain inside multi-walled carbon nanotubes by cooling enhanced hydrogen arc discharge method, Nanoscale, 2018, 10, 17824–17833,  10.1039/C8NR05465G.
16. M. Endo, Y. A. Kim, T. Hayashi, H. Muramatsu, M. Terrones, R. Saito, F. Villalpando-Paez, S. G. Chou and M. S. Dresselhaus, Nanotube coalescence-inducing mode: A novel vibrational mode in carbon systems, Small, 2006, 2, 1031–1036,  DOI:10.1002/smll.200600087.
17. E. Cazzanelli, M. Castriota, L. S. Caputi, A. Cupolillo, C. Giallombardo and L. Papagno, High-temperature evolution of linear carbon chains inside multiwalled nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 121405,  DOI:10.1103/PhysRevB.75.121405.
18. L. Shi, L. Sheng, L. Yu, K. An, Y. Ando and X. Zhao, Ultra-thin double-walled carbon nanotubes: A novel nanocontainer for preparing atomic wires, Nano Res., 2011, 4, 759–766,  DOI:10.1007/s12274-011-0132-y.
19. C. Zhao, R. Kitaura, H. Hara, S. Irle and H. Shinohara, Growth of linear carbon chains inside thin double-wall carbon nanotubes, J. Phys. Chem. C, 2011, 115, 13166–13170,  DOI:10.1021/jp201647m.
20. N. F. Andrade, A. L. Aguiar, Y. A. Kim, M. Endo, P. T. C. Freire, G. Brunetto, D. S. Galvão, M. S. Dresselhaus and A. G. Souza Filho, Linear carbon chains under high-pressure conditions, J. Phys. Chem. C, 2015, 119, 10669–10676,  DOI:10.1021/acs.jpcc.5b00902.
21. N. F. Andrade, T. L. Vasconcelos, C. P. Gouvea, B. S. Archanjo, C. A. Achete, Y. A. Kim, M. Endo, C. Fantini, M. S. Dresselhaus and A. G. Souza Filho, Linear carbon chains encapsulated in multiwall carbon nanotubes: Resonance Raman spectroscopy and transmission electron microscopy studies, Carbon, 2015, 90, 172–180,  DOI:10.1016/j.carbon.2015.04.001.
22. C. Kang, K. Fujisawa, Y. Ko, H. Muramatsu, T. Hayashi, M. Endo, H. J. Kim, D. Lim, J. H. Kim, Y. C. Jung, M. Terrones, M. S. Dresselhaus and Y. A. Kim, Linear carbon chains inside multi-walled carbon nanotubes: Growth mechanism, thermal stability and electrical properties, Carbon, 2016, 107, 217–224,  DOI:10.1016/j.carbon.2016.05.069.
23. Y. Zhang, W. Chang, Y. Liu, T. Maruyama and X. Zhao, High-yield growth of multi-walled carbon nanowires by magnetic field controlled arc technique, Carbon, 2020, 158, 672–680,  DOI:10.1016/j.carbon.2019.11.039.
24. X. Li, Y. Zhang, Y. Wu and L. Shi, Pressure-tailored synthesis of confined linear carbon chains, J. Appl. Phys., 2021, 129, 064302,  DOI:10.1063/5.0035854.
25. L. Shi, K. Yanagi, K. Cao, U. Kaiser, P. Ayala and T. Pichler, Extraction of linear carbon chains unravels the role of the carbon nanotube host, ACS Nano, 2018, 12, 8477–8484,  DOI:10.1021/acsnano.8b04006.
26. S. Toma, K. Asaka, M. Irita and Y. Saito, Bulk synthesis of linear carbon chains confined inside single-wall carbon nanotubes by vacuum discharge, Surf. Interface Anal., 2019, 51, 131–135,  DOI:10.1002/sia.6590.
27. W. Chang, F. Liu, Y. Liu, T. Zhu, L. Fang, Q. Li, Y. Liu and X. Zhao, Smallest carbon nanowires made easy: Long linear carbon chains confined inside single-walled carbon nanotubes, Carbon, 2021, 183, 571–577,  DOI:10.1016/j.carbon.2021.07.037.
28. L. Shi, P. Rohringer, M. Wanko, A. Rubio, S. Waßerroth, S. Reich, S. Cambré, W. Wenseleers, P. Ayala and T. Pichler, Electronic band gaps of confined linear carbon chains ranging from polyyne to carbyne, Phys. Rev. Mater., 2017, 1, 075601,  DOI:10.1103/PhysRevMaterials.1.075601.
29. X. Yang, C. Lv, Z. Yao, M. Yao, J. Qin, X. Li, L. Shi, M. Du, B. Liu and C. Shan, Band-gap engineering and structure evolution of confined long linear carbon chains@double-walled carbon nanotubes under pressure, Carbon, 2020, 159, 266–272,  DOI:10.1016/j.carbon.2019.12.057.
30. K. Sharma, N. L. Costa, Y. A. Kim, H. Muramatsu, N. M. Barbosa Neto, L. G. P. Martins, J. Kong, A. R. Paschoal and P. T. Araujo, Anharmonicity and universal response of linear carbon chain mechanical properties under hydrostatic pressure, Phys. Rev. Lett., 2020, 125, 105501,  DOI:10.1103/PhysRevLett.125.105501.
31. S. Heeg, L. Shi, L. V. Poulikakos, T. Pichler and L. Novotny, Carbon nanotube chirality determines properties of encapsulated linear carbon chain, Nano Lett., 2018, 18, 5426–5431,  DOI:10.1021/acs.nanolett.8b01681.
32. C. D. Tschannen, G. Gordeev, S. Reich, L. Shi, T. Pichler, M. Frimmer, L. Novotny and S. Heeg, Raman scattering cross section of confined carbyne, Nano Lett., 2020, 20, 6750–6755,  DOI:10.1021/acs.nanolett.0c02632.
33. J. Chen, L. Yang, H. Yang and J. Dong, Electronic and transport properties of a carbon-atom chain in the core of semiconducting carbon nanotubes, Phys. Lett. A, 2003, 316, 101–106,  DOI:10.1016/S0375-9601(03)01132-0.
34. Y. Liu, R. O. Jones, X. Zhao and Y. Ando, Carbon species confined inside carbon nanotubes: A density functional study, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125413,  DOI:10.1103/PhysRevB.68.125413.
35. Y. Wang, Y. Huang, B. Yang and R. Liu, Structural and electronic properties of carbon nanowires made of linear carbon chains enclosed inside zigzag carbon nanotubes, Carbon, 2006, 44, 456–462,  DOI:10.1016/j.carbon.2005.08.026.
36. Y. Wang, Y. Huang, B. Yang and R. Liu, Crystal orbital study on carbon chains encapsulated in armchair carbon nanotubes with various diameters, Carbon, 2008, 46, 276–284,  DOI:10.1016/j.carbon.2007.11.043.
37. A. Tapia, L. Aguilera, C. Cab, R. A. Medina-Esquivel, R. de Coss and G. Canto, Density functional study of the metallization of a linear carbon chain inside single wall carbon nanotubes, Carbon, 2010, 48, 4057–4062,  DOI:10.1016/j.carbon.2010.07.011.
38. H. Bai, W. Qiao, Y. Zhu and Y. Huang, Crystal orbital study on the combined carbon nanowires constructed from linear carbon chains encapsulated in zigzag double-walled carbon nanotubes, Curr. Appl. Phys., 2015, 15, 342–351,  DOI:10.1016/j.cap.2015.01.008.
39. F. Bonabi, S. J. Brun and T. G. Pedersen, Excitonic optical response of carbon chains confined in single-walled carbon nanotubes, Phys. Rev. B, 2017, 96, 155419,  DOI:10.1103/PhysRevB.96.155419.
40. Y. Deng and S. W. Cranford, Mapping temperature and confinement dependence of carbyne formation within carbon nanotubes, Carbon, 2019, 141, 209–217,  DOI:10.1016/j.carbon.2018.09.054.
41. U. Khalilov, C. Vets and E. C. Neyts, Catalyzed growth of encapsulated carbyne, Carbon, 2019, 153, 1–5,  DOI:10.1016/j.carbon.2019.06.110.
42. E. Ganz, A. B. Ganz, L. Yang and M. Dornfeld, Carbon nanotube-carbyne composite: A nanoreactor in a quasi-1D liquid state, Comput. Mater. Sci., 2018, 149, 409–415,  DOI:10.1016/j.commatsci.2018.03.020.
43. Z. Xu, T. Yan, G. Liu, G. Qiao and F. Ding, Large scale atomistic simulation of single-layer graphene growth on Ni(111) surface: Molecular dynamics simulation based on a new generation of carbon–metal potential, Nanoscale, 2016, 8, 921–929,  10.1039/C5NR06016H.
44. J. Dong, H. Wang, H. Peng, Z. Liu, K. Zhang and F. Ding, Formation mechanism of overlapping grain boundaries in graphene chemical vapor deposition growth, Chem. Sci., 2017, 8, 2209–2214,  10.1039/C6SC04535A.
45. L. Xu, Y. Jin, Z. Wu, Q. Yuan, Z. Jiang, Y. Ma and W. Huang, Transformation of carbon monomers and dimers to graphene islands on Co(0001): Thermodynamics and kinetics, J. Phys. Chem. C, 2013, 117, 2952–2958,  DOI:10.1021/jp400111s.
46. Z. Xu, T. Yan and F. Ding, Atomistic simulation of the growth of defect-free carbon nanotubes, Chem. Sci., 2015, 6, 4704–4711,  10.1039/C5SC00938C.
47. T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, The ReaxFF reactive force-field: Development, applications and future directions, npj Comput. Mater., 2016, 2, 15011,  DOI:10.1038/npjcompumats.2015.11.
48. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: A reactive force field for hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409,  DOI:10.1021/jp004368u.
49. K. D. Nielson, A. C. T. van Duin, J. Oxgaard, W. Deng and W. A. Goddard, Development of the ReaxFF reactive force field for describing transition metal catalyzed reactions, with application to the initial stages of the catalytic formation of carbon nanotubes, J. Phys. Chem. A, 2005, 109, 493–499,  DOI:10.1021/jp046244d.
50. K. Chenoweth, A. C. T. van Duin and W. A. Goddard, ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation, J. Phys. Chem. A, 2008, 112, 1040–1053,  DOI:10.1021/jp709896w.
51. C. Ashraf and A. C. T. van Duin, Extension of the ReaxFF combustion force field toward syngas combustion and initial oxidation kinetics, J. Phys. Chem. A, 2017, 121, 1051–1068,  DOI:10.1021/acs.jpca.6b12429.
52. L. Liu, Y. Liu, S. V. Zybin, H. Sun and W. A. Goddard, ReaxFF-lg: Correction of the ReaxFF reactive force field for London dispersion, with applications to the equations of state for energetic materials, J. Phys. Chem. A, 2011, 115, 11016–11022,  DOI:10.1021/jp201599t.
53. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19,  DOI:10.1006/jcph.1995.1039.
54. H. M. Aktulga, J. C. Fogarty, S. A. Pandit and A. Y. Grama, Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques, Parallel Comput., 2012, 38, 245–259,  DOI:10.1016/j.parco.2011.08.005.
55. A. K. Rappe and W. A. Goddard, Charge equilibration for molecular dynamics simulations, J. Phys. Chem. B, 1991, 95, 3358–3363,  DOI:10.1021/j100161a070.
56. G. J. Martyna, M. L. Klein and M. Tuckerman, Nosé–Hoover chains: The canonical ensemble via continuous dynamics, J. Chem. Phys., 1992, 97, 2635–2643,  DOI:10.1063/1.463940.
57. G. Mills and H. Jónsson, Quantum and thermal effects in H₂ dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems, Phys. Rev. Lett., 1994, 72, 1124–1127,  DOI:10.1103/PhysRevLett.72.1124.
58. G. Mills, H. Jónsson and G. K. Schenter, Reversible work transition state theory: Application to dissociative adsorption of hydrogen, Surf. Sci., 1995, 324, 305–337,  DOI:10.1016/0039-6028(94)00731-4.
59. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50,  DOI:10.1016/0927-0256(96)00008-0.
60. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
62. A. Tkatchenko and M. Scheffler, Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data, Phys. Rev. Lett., 2009, 102, 073005,  DOI:10.1103/PhysRevLett.102.073005.
63. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
64. C. S. Casari, C. S. Giannuzzi and V. Russo, Carbon-atom wires produced by nanosecond pulsed laser deposition in a background gas, Carbon, 2016, 104, 190–195,  DOI:10.1016/j.carbon.2016.03.056.
65. R. Chen, F. Liu, Y. Tang, Y. Liu, Z. Dong, Z. Deng, X. Zhao and Y. Liu, Combined first-principles and machine learning study of the initial growth of carbon nanomaterials on metal surfaces, Appl. Surf. Sci., 2022, 586, 152762,  DOI:10.1016/j.apsusc.2022.152762.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr00386h

---