Exhaustive classification and systematic free-energy profile study of single-stranded DNA inter-overhang migration†
Hon Lin
Too
ab and
Zhisong
Wang
 *ab
*ab
aNUS Graduate School for Integrative Science and Engineering, National University of Singapore, Singapore 117542. E-mail: phywangz@nus.edu.sg
bDepartment of Physics, National University of Singapore, 2 Science Drive 3, Singapore 117542
First published on 11th July 2023
Abstract
Migration of a short single-stranded DNA (ssDNA) between DNA overhangs is a basic molecular process that is widely used in dynamic DNA nanotechnology. The migration rate is sensitive to migration gaits, and limits the speed of dynamic DNA systems like DNA nanowalkers and other functional devices. Here, we identify and exhaustively classify all possible inter-overhang migration gaits of a ssDNA into only four categories based on their intrinsic symmetry. Using the oxDNA package, we conduct a systematic computational study for a typical migrator-overhang system to identify the lowest-energy pathway for all four migration categories. The one-dimensional free-energy profile along this pathway allows a parameter-free estimation of migration rates for all the four categories by the first passage time theory plus benchmarking from experimental rates available for one migration category. The obtained rates indicate a big room to improve DNA nanowalkers’ speed above 1 μm per minute. The free-energy profile for each migration category possesses distinct and robust symmetric patterns, which largely decide local barriers, trapping states, and thereby a migration's rate-limiting processes and capacity for directional bias. This study thus provides a unified symmetry-based framework to analyze and optimize ssDNA migrations in kinetics, bias capacity, and structural design for better dynamic DNA nanotechnology.
1 Introduction
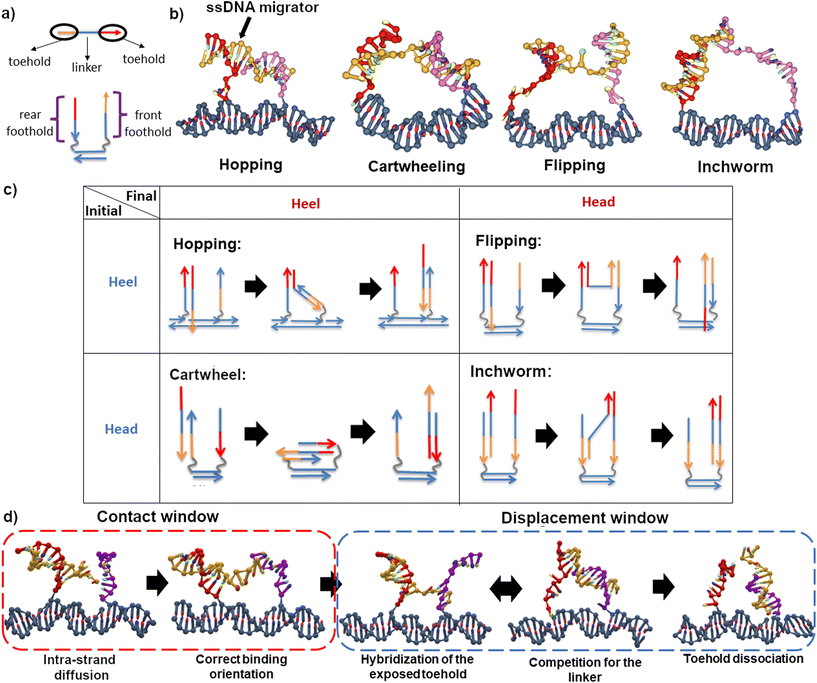
Migration of a short single-stranded DNA (ssDNA) on an array of DNA overhangs is a basic molecular process that is widely used in dynamic DNA nanotechnology. Such a minimal ssDNA migrator automatically displaces itself between two nearby single-stranded DNA overhangs (often called footholds) due to their dynamic competition to hybridize with the migrator. This automatic inter-overhang mobility has become a key element of numerous dynamic DNA nanosystems, especially DNA molecular motors.1 Placed on an array of overhang footholds, a ssDNA migrator readily becomes a molecular walker that, despite no energy input, can move back and forth randomly along the overhang track. Long-range translocation far beyond nearby overhangs has been demonstrated for such energy-free and directionless ssDNA molecular walkers.2,3 The ssDNA migrators have also been converted into directional molecular walkers4,5 when an energy supply is supplied to cut the overhang footholds upon the migrator-foothold hybridization. This leads to so-called bridge-burning DNA walkers as the cutting triggers a downhill migration to a nearby intact foothold to give the walker a unique direction, but all the footholds will be successively damaged to lose the track function. The ssDNA migrators continue to be a crucial component for advanced non-bridge-burning DNA molecular walkers fully qualified as molecular motors, which are often double-stranded bipeds with two ssDNA migrators as legs. Either ssDNA migrator still does automatic migration between two adjacent overhangs which combine to form a composite binding site, and the inter-overhang migration is amplified into the bipedal walker's long-range directional translocation along a linear array of composite sites.Following the schematic illustrations in Fig. 1a, a ssDNA migrator typically consists of three segments – a head toehold, a heel toehold, and an intermediate linker. A toehold is classified based on its relative distance to the track – the heel toehold is closer to the track compared to the head toehold. The gait is categorized based on the position change of migrator's exposed toehold that starts a forward migration from one overhang to another. For a ssDNA migrator, there are only two possible starting states – a heel starting state and a head starting state. In the heel starting state, the heel toehold is exposed; while in the head starting state, the head toehold is exposed. After a successful migration, the exposed toehold binds to the second overhang at a foothold domain near the track and becomes a heel toehold (the heel state) or at the foothold domain far away from the track to become a head toehold (the head state). Thus, all imaginable inter-overhang ssDNA migrations can be classified into only four migration gaits, namely hopping (heel to heel), flipping (heel to head), cartwheeling (head to heel) and inchworm (head to head), as summarized in Fig. 1b and c. This classification is exhaustive as the backward reverse of the four migration types recovers either each other (e.g. hopping → inchworm) or itself (e.g. flipping and cartwheeling).
The flipping migration is used in light-powered DNA bipedal motors (with the migrator's heel6 or head7,8 segment linking the motor's intermediate duplex bridge). The hopping migration is used in an autonomous chemically fueled motor9,10 and is later adapted into a light-powered motor.11 The inchworm migration is used in bridge-burning DNA walkers4,5 and many later variations12–14 and applications.15–17 The cartwheeling migration is used for a directionless DNA walker3 that uses this single type of migration for long-range translocation along an overhang track on a DNA origami platform. Another directionless DNA walker2 combined the inchworm and hopping migration to achieve long-range translocation and thereby a robotic cargo-sorting task on a DNA origami platform.
Considering the wide application of inter-overhang ssDNA migration in dynamic DNA nanotechnology, understanding this basic process becomes important. The migration gait is often the most crucial rate-limiting factor for DNA walkers and other dynamic DNA nanosystems because the local binding geometry of DNA directly affects the diffusion rate, hybridization rate, dissociation rate and the chemical fuel invasion rate.3,7,9,18–21 Therefore, an exhaustive study on all possible migration gaits is necessary to rationally design and optimize the migrator's performance. Computer simulation may be the most pragmatic approach to exhaustively study the inter-overhang migration due to its ability to identify structural change that may not be easily detected by experiments. The oxDNA simulation package,22,23 an effective computational package based on a coarse-grained DNA model, has been widely used to study non-equilibrium processes such as the hybridization of DNA,24,25 the walking of a bipedal DNA walker9,26–28 and a burning bridge motor.29 The basic physical properties of the ssDNA and dsDNA have been extensively studied by oxDNA, with the predicted radius of gyration30 and persistence length22,31,32 consistent with experimental data and all-atom simulations. The free-energy profile of different migration gaits as a function of design and operation parameters such as nucleotide sequences, inter-foothold distance, temperature and salt concentration9,26–28 are easily obtainable from the simulation. The free-energy profile can be used to infer reaction pathways, estimate the migration rate for each gait, and study how each design and operation parameter affects the rate.
In this study, we report a systematic oxDNA computational study for the four migration categories, which exhaustively cover all possible inter-overhang ssDNA migration in broad dynamic DNA nanotechnology. The free-energy profile of each migration is extracted through the umbrella sampling method and the lowest energy pathway is studied. The inter-overhang migration rate is estimated from the first passage theory of a diffusion-controlled reaction.33 Overall, we found that the migration gait affects the inter-overhang migration rate differently. Strategies to optimize the inter-overhang migration rate should therefore consider the migration gait.
2 Methodology
2.1 Simulation method
All simulations were run on oxDNA2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 force field, sequence-averaged interaction at 24 °C and 0.1 M [Na+] salt concentration. oxview34 was used for initial structure design, generation and visualization. Virtual Move Monte Carlo (VMMC)35 was employed to sample the states visited by the system. To overcome the large transition barrier, the free-energy profile is extracted through the umbrella sampling method.36 The iterative reweighting method is employed to ensure the data is well-sampled. More details on the simulation method can be found in the ESI.†
31 force field, sequence-averaged interaction at 24 °C and 0.1 M [Na+] salt concentration. oxview34 was used for initial structure design, generation and visualization. Virtual Move Monte Carlo (VMMC)35 was employed to sample the states visited by the system. To overcome the large transition barrier, the free-energy profile is extracted through the umbrella sampling method.36 The iterative reweighting method is employed to ensure the data is well-sampled. More details on the simulation method can be found in the ESI.†
To sample the geometrical configuration of specific intermediate states, a few molecular dynamics (MD) simulations were performed on the oxDNA public server.37 A mutual trap force field is introduced to all the binding nucleotides to ensure the system stays in the state of interest. All MD simulations were conducted in NVT ensemble, with a time step of dt = 3.03 fs for at least 5 × 108 simulation steps.
The schematic of the studied migrators is presented in Fig. 1a. The nucleotide sequences used are presented in Fig. S2 and S3.† The migrator is 15 nucleotides (nt) long and is divided into 3 equally long segments. Its performance is studied on 2 different tracks – a 10 base pair (bp) long and a 20bp long dsDNA track. Here, the track length refers to the inter-foothold distance (either 10bp or 20bp). A track can be designed to be either isoenergetic or downhill. An isoenergetic track consists of equally long front and rear footholds (10nt). On the other hand, a downhill track has an asymmetric foothold length. Since the ssDNA migrator prefers to be fully bound, the asymmetry creates an energetically favorable environment for forward migration, hence the name downhill. In this study, the inchworm migrator is the only migrator operating on a downhill track (15nt front foothold, 10nt rear foothold).
Process-wise, a successful migration starts from the intra-strand diffusion of the exposed toehold at the rear foothold, followed by the hybridization of the toehold to the front foothold, the competition between both footholds for the linker, and finally the dissociation of toehold from the rear foothold (see Fig. 1d). To effectively study these processes, the simulation is broken down into two windows – the contact window and the displacement window. The reaction coordinate in the contact window is the contact distance x between the toehold's tip and the front foothold. The free-energy in this window is defined as
G(x) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p(x)) ln(p(x)) | (1) |
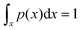 .
.
Here, we assume that the toehold hybridizes with the foothold when xmin = 1.7 nm since this distance is smaller than the natural binding distance between a pair of nucleotides, which is 2.0 nm. The relative free-energy with respect to the reference state ΔG(x) is obtained from the following formula
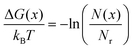 | (2) |
| ΔGfc = −ΔGmin | (3) |
The displacement window captures the hybridization process after a contact is formed. Its reaction coordinate is defined by two parameters – the total number of migrator's nucleotide bound to the rear foothold nr and the total number of migrator's nucleotide bound to the front foothold nf. The free-energy G(nf, nr) is defined as
G(nf,nr) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p(nf,nr)) ln(p(nf,nr)) | (4) |
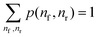 . The relative free-energy with respect to the reference state ΔG(nf, nr) is obtained from the following formula
. The relative free-energy with respect to the reference state ΔG(nf, nr) is obtained from the following formula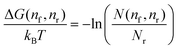 | (5) |
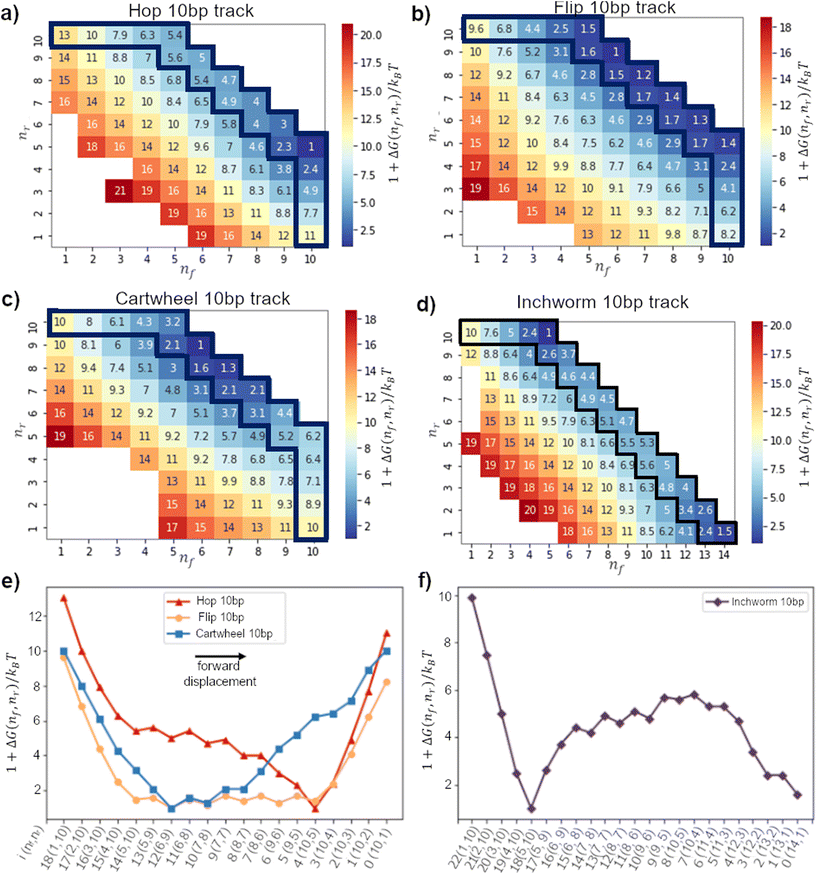
In this window, a migrator starts from the initial state (nf, nr) = (1, 10) and ends at (10, 1) (or (14, 1) for the downhill track). Therefore, to obtain the 1D lowest energy pathway, we search for the minimum path sum in the 2D free-energy landscape. The minimum path sum for each gait is highlighted in Fig. 3a–d and Fig. S6–S9.† We refer the readers to the ESI† for more details on the method to obtain the minimum path sum.
2.2 Bending angle between neighboring nucleotides
In the oxDNA model, a DNA is treated as a string of rigid nucleotides. The position and orientation of each nucleotide are described by 3 vectors – a center of mass vector, a backbone-nucleobase vector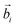 , and a normal vector that is perpendicular to the nucleotide's plane. In this work, the bending angle between neighboring nucleotides θi,i+1 is defined as the angle between their backbone-base vectors (see Fig. S5a†).
, and a normal vector that is perpendicular to the nucleotide's plane. In this work, the bending angle between neighboring nucleotides θi,i+1 is defined as the angle between their backbone-base vectors (see Fig. S5a†).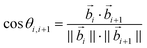 | (6) |
Since the DNA is a helix structure, the natural bending angle between a pair of neighboring nucleotides is around 36°. In this study, a strong bending occurs when the average bending angle between any nucleotide pair is larger or equal to 90°, i.e. 〈θi,i + 1〉 ≥ 90°.
2.3 Reaction rate calculation
The contact rate kcontact is the inverse of average time taken for a migrator to reach xmin. According to the first passage time theory by Szabo et al.,33 the contact rate can be approximated as: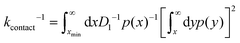 | (7) |
The displacement rate kdisplace is the inverse of average time for a migrator to displace from the rear foothold to the front foothold on the lowest energy pathway immediately after first contact. Since the reaction coordinate is discrete, the displacement rate can be approximated as
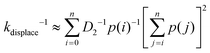 | (8) |
3 Results and discussion
3.1 Free-energy profile analysis for all migration gaits
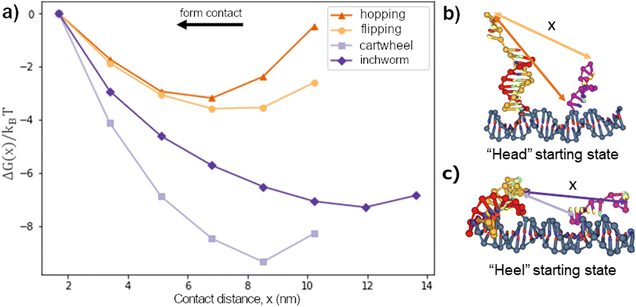
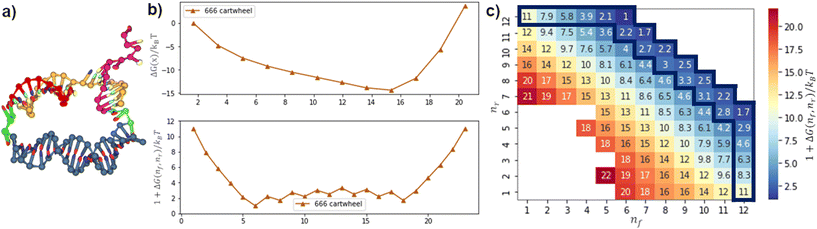
We first considered the free-energy profile in the contact window. Fig. 2a shows the free-energy of 4 different gaits as a function of contact distance x on a 10bp track. The first-contact free-energy ΔGfc increases in the order of hopping ≈ flipping < downhill inchworm < cartwheeling. Overall, a gait with an exposed heel toehold requires a lower first-contact free-energy compared to those with an exposed head toehold. This is because the exposed head toehold has a rigid duplex beneath that keeps it away from the front foothold (see Fig. 2b vs. c).The hopping gait has a significantly lower ΔGfc than its counterpart, inchworm, due to the difference in their starting states. This asymmetry means a hopping migrator requires a larger energetic cost to backward migrate after a successful forward migration since it is harder for the inchworm gait to form contact. The difference in energetic cost provides a natural directional bias to the hopping gait as far as the first contact is concerned. On the other hand, gaits which are the backward reverse of themselves (cartwheel and flip) have no such bias.
Fig. 3a–d show the displacement free-energy landscapes on a 10bp track. In general, the minimum is located at the state where the migrator is fully bound to both footholds (i.e. nf + nr = 15). The 1D lowest-energy pathways in Fig. 3e and f elucidate some common features for all migration gaits. Firstly, the 5 consecutive transitions from the (1,10) state to the (5,10) state is normally a downhill process. This corresponds to the zippering of exposed toehold to the front foothold. Secondly, if the track is isoenergetic, the free-energy of the initial and final states is similar. Thirdly, for all isoenergetic tracks, there is an inevitable uphill curve near the end of inter-overhang migration. This energy barrier corresponds to the energetic cost to dissociate the toehold from the rear foothold.
The biggest difference between the gaits lies in the competition phase – where the front and rear footholds compete for the migrator's linker. This phase largely determines if the lowest-energy profile is symmetrical. In this phase, the free-energy can form a flat plateau or a sharp energy well. The toehold mediated strand displacement (TMSD) mechanism in a cartwheel migrator flattens the free-energy during the competition process,19,38 which is observed on a 20bp track (see Fig. 4g). The flat plateau makes the free-energy profile highly symmetrical. However, on a short 10bp track, this symmetry is broken. This is because the track-migrator binding induces a strong internal tension, which forces the migrator to bend (see Fig. S4†). This bending increases the difficulty for the front foothold to invade the linker. Therefore instead of a flat plateau, an energy well is observed.
The flipping migrator's free-energy profile is highly symmetrical due to the flat plateau in the competition phase. The symmetry comes from the unique “U”-shaped configuration when the migrator is fully bound to both footholds (see Fig. S5a†). The “U”-shaped configuration induces a strong bending on the migrator. To verify this, we plotted the 2D bending angle histogram in (8,7) and (10,5) states. Both plots show there is at least a nucleotide pair with a mean bending angle greater than 90°. Similar strong bending is unavoidable in (8,7), (10,5) and other fully bound states, thus the symmetrical free-energy profile.
On the other hand, a hopping migrator contains a sharp minimum at the (10,5) state. The sharp minimum located near the end of the lowest-energy pathway breaks the symmetry of its free-energy profile. To understand this, we analyzed the migrator bending angle distribution of the (5,10) and (10,5) state. From Fig. S5e and f,† the (5,10) state contains a nucleotide pair with strong bending (larger than 125°), but this geometrical feature is not found in the (10,5) state. The absence of strong bending in the (10,5) state is energetically favored, hence the formation of a sharp minimum. The sharp minimum indicates that a hopping migrator contains a well-defined intermediate structure. This feature may be useful for structure-based selective control of migration.
Since the inchworm gait is the backward reverse of the hopping gait, the inchworm free-energy profile is the mirror image of its counterpart. On a downhill track, the inchworm free-energy profile contains a sharp minimum located at the (5,10) state and is immediately followed by an energy barrier before completely dissociating from the rear foothold. Again, the bending angle distribution of the migrator is plotted (see Fig. S5h†). For the (5,10) state, 30°–40° is the most common bending angle across all nucleotide pairs, indicating the lack of strong bending. This makes the (5,10) state the energetically most favorable state. The fully bound intermediate states after the (5,10) state show a clear sign of strong bending (see Fig. S5i† for (9,6) state), which is energetically unfavorable. Such energetic difference at the beginning and middle of the reaction pathway breaks the symmetry in its free-energy profile.
3.2 Migrator optimization strategy differs from gait to gait
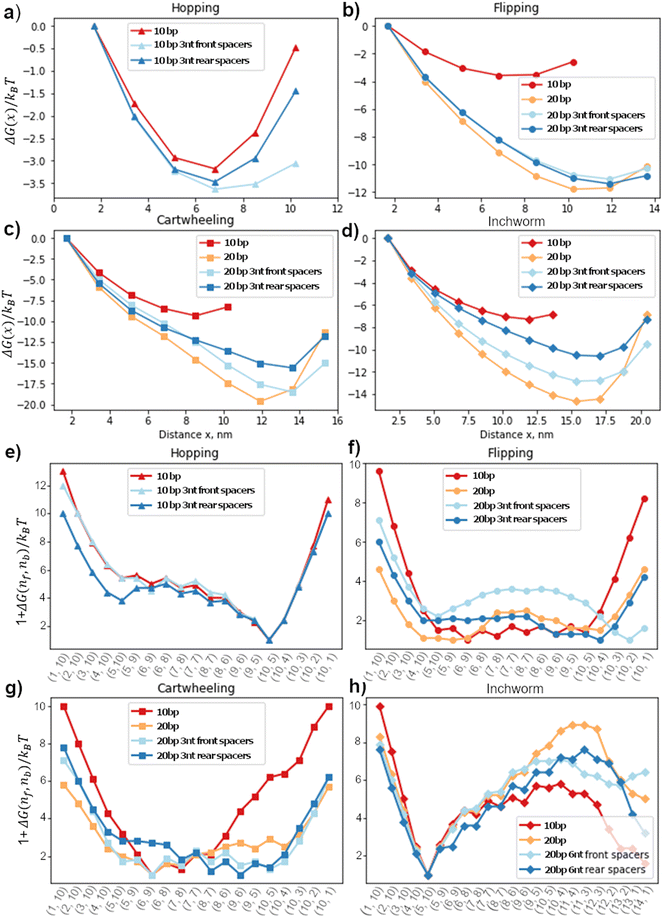
Since the free-energy profile is sensitive towards the local geometry, the energy profile can be tuned by changing the inter-foothold distance, migrator length or introducing spacers between the footholds and track. The goal of this section is to understand how these design parameters affect the free-energy profile. Here, we fixed the migrator's length and focused on the effect of inter-foothold distance and spacer.Fig. 4a–d show the free-energy profile in the contact window. In general, the larger the inter-foothold distance, the larger the free-energy ΔGfc to form first contact. Hopping is the only gait that could not initiate first contact when the inter-foothold distance increases to 20bp. This gait has the shortest reach, which is why in the cargo sorting robot, the rear foothold is designed to have unusually long rear spacers (11nt long) to ensure the first contact can be initiated when it conforms to the hopping gait.2
The rear spacers are more effective in decreasing ΔGfc of both cartwheel and inchworm migrators compared to the front foothold. To initiate first contact, the head starting migrators bend the joint between the rear foothold and the track. They suffer from a larger energetic penalty to initiate first contact. Therefore, the conformation flexibility provided by the rear spacers will be more effective in reducing ΔGfc. On the other hand, both flipping and hopping migrators do not bend as much as they are already parallel to the track. Therefore, their ΔGfc are not sensitive towards the spacers location.
The displacement window's free-energy landscape is also sensitive to the local geometry. Fig. 4e–h show the 1D lowest-energy reaction pathway of all 4 gaits on different tracks. In general, a longer inter-foothold distance decreases the energy to dissociate the toehold from the rear foothold. The reduction is probably contributed by the larger internal tension on a longer track. However, for a downhill inchworm migrator, its dissociation energy increases significantly on a longer track. This energy barrier can be reduced by introducing spacers to the track (Fig. 4h). We found that the 6nt front spacers track is more effective in lowering the energy barrier than the track with 6nt rear spacers.
The free-energy profile of a cartwheeling migrator during its competition phase is flatter on a longer inter-overhang distance. This is consistent with the TMSD free-energy profile without any geometrical constraint38 because the TMSD is more efficient when the migrator's linker is straight to ease the front foothold invasion. The flat free-energy profile on a 20bp track in the competition phase, followed by a sharp increase in the dissociation phase is also consistent with the experiment by Li et al.3 They found that the transition rate between the intermediate states in the competition phase are high, but the dissociation rate from the rear foothold is significantly lower and is therefore the rate-limiting process of this migration gait.
3.3 Rate estimation
The computed free-energy profiles in Fig. 4 allow the estimation of migration rates via the first-passage time theory (Methods). However, the contact window and the displacement window have different effective diffusion coefficients (D1 and D2 in eqn (7) and (8)) that are not well determined from experiments. The contact rate depends on the intra-chain diffusion coefficient for the ssDNA migrator, i.e., D1 in eqn (7). For such intra-nucleotide diffusion, a measured coefficient of D1–1.4 × 104 nm2 s−1 is reported in ref. 39. Table 1 gives the contact rate for the four types of migrations estimated using this measured D1 value and the free-energy profiles in Fig. 4a–d. The displacement rate depends on the effective diffusion coefficient of the hybridization, strand displacement and strand dissociation, i.e., D2 in eqn (7), which is largely unknown. The contact rate and displacement rate combine to determine the total migration rate, which is ∼0.04 s−1 as reported from a recent single-molecule study by Li et al.3 for an 18nt-long migrator cartwheeling migrator over 20bp inter-overhang gap. Exploiting this measured rate for a common benchmark, we can have a reasonably reliable rate estimation for all four migration types as follows.| Gait | Track | k contact (nm2 s−1) | ||
|---|---|---|---|---|
| Flip | 10bp | 2.5 × 102 | 2.5 × 104 | 9.0 × 100 |
| 20bp | 8 × 10–2 | 1.0 × 101 | 2.0 × 102 | |
| 20bp 3nt front spacers | 2 × 10–1 | 2.3 × 101 | 2.0 × 103 | |
| 20bp 3nt rear spacers | 1 × 10–1 | 1.7 × 101 | 4.0 × 102 | |
| Cartwheel | 10bp | 2.3 × 100 | 1.8 × 102 | 3.0 × 100 |
| 20bp | 6 × 10–5 | 8 × 10–3 | 1.2 × 102 | |
| 20bp 3nt front spacers | 2 × 10–4 | 2 × 10–2 | 7.2 × 101 | |
| 20bp 3nt rear spacers | 3 × 10–3 | 3 × 10–1 | 8.0 × 101 | |
| 20bp Li et al. 18nt migrator3 | 7 × 10–3 | 1 | 1 | |
| Downhill inchworm | 10bp | 8.3 × 100 | 7.5 × 102 | 1.4 × 102 |
| 20bp | 4 × 10–3 | 5 × 10–1 | 5.0 × 100 | |
| 20bp 6nt front spacers | 2 × 10–2 | 3.0 × 100 | 1.9 × 101 | |
| 20bp 6nt rear spacers | 2 × 10–1 | 2.5 × 101 | 1.7 × 101 | |
| Hop | 10bp | 3.7 × 102 | 4.3 × 104 | 3.0 × 100 |
| 10bp 3nt front spacers | 1.8 × 102 | 2.4 × 104 | 7.0 × 100 | |
| 10bp 3nt rear spacers | 2.4 × 102 | 3.1 × 104 | 6.0 × 100 |
We first carry out the same oxDNA simulation for the measured cartwheeling migration (18nt migrator over 20bp inter-overhang gap) to obtain its free-energy profiles for the contact window and for the energy-minimum pathway for the displacement window (Fig. 5). Then we apply the same first-passage time formula (eqn (7) and (8)) to the free-energy profiles, yield the rates for the two windows as the function of diffusion coefficients D1 and D2. By a crude but reasonable approximation, the two diffusion coefficients may be assumed to be independent of the migration gaits, inter-overhang distance and migrator length. As a consequence, the ratio of computed contact rates between any migration and the measured migration is independent of the uncertain diffusion coefficient D1. Similarly, the ratio of computed displacement rates between any migration and the measured migration is independent of the uncertain diffusion coefficient D2. The two rate ratios, which are given in Table 1, allow a parameter-free cross-migration rate comparison for each window on the same footing. Perhaps more importantly, the two rate ratios also allow quantitative estimation of the magnitude of total rates for all the migrations based on the benchmark of the experimentally measured cartwheeling rate.
Taking the rate ratios for the contact window and displacement window as  and
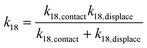
and  , we have the total rates k15 and k18 satisfying
, we have the total rates k15 and k18 satisfying 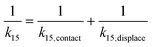 and
and 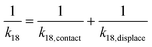 as a complete migration is the diffusive contact followed by displacement (Fig. 1d). Hence total rates for a 15nt migrator k15 and for the experimentally measured 18nt cartwheeling migrator k18 are
as a complete migration is the diffusive contact followed by displacement (Fig. 1d). Hence total rates for a 15nt migrator k15 and for the experimentally measured 18nt cartwheeling migrator k18 are
 | (9) |
 | (10) |
 | (11) |
If γ1 > γ2, the ratio 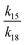 has a lower limit by replacing γ2 in its denominator with γ1 and a upper limit by replacing γ1 in its denominator with γ2, namely
has a lower limit by replacing γ2 in its denominator with γ1 and a upper limit by replacing γ1 in its denominator with γ2, namely 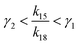 . Similarly, the ratio follows
. Similarly, the ratio follows 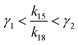 if γ1 < γ2 and
if γ1 < γ2 and 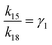 if γ1 = γ2. Thus, the ratios in Table 1 yield the absolute rate over a certain range for all the migration based on the experimentally reported rate3 of k18 ∼ 0.04 s−1. Considering the 10bp inter-overhang gap, the resultant rates are 0.36 s−1 < k15,flip < 1.0 × 103 s−1 for the flipping, 0.12 s−1 < k15,cw < 7.2 s−1 for the cartwheeling, 5.6 s−1 < k15,inchworm < 30 s−1 for the downhill inchworm, and 0.12 s−1 < k15,hop < 1.7 × 103 s−1 for the hopping. These lower limits are a conservative but reliable experiment-informed estimate of practically accessible rates for the four types of migration over the same 10bp inter-overhang gap, i.e., 0.36 s−1 for the flipping, 0.12 s−1 for the cartwheeling, 5.6 s−1 for the downhill inchworm, and 0.12 s−1 for the hopping.
if γ1 = γ2. Thus, the ratios in Table 1 yield the absolute rate over a certain range for all the migration based on the experimentally reported rate3 of k18 ∼ 0.04 s−1. Considering the 10bp inter-overhang gap, the resultant rates are 0.36 s−1 < k15,flip < 1.0 × 103 s−1 for the flipping, 0.12 s−1 < k15,cw < 7.2 s−1 for the cartwheeling, 5.6 s−1 < k15,inchworm < 30 s−1 for the downhill inchworm, and 0.12 s−1 < k15,hop < 1.7 × 103 s−1 for the hopping. These lower limits are a conservative but reliable experiment-informed estimate of practically accessible rates for the four types of migration over the same 10bp inter-overhang gap, i.e., 0.36 s−1 for the flipping, 0.12 s−1 for the cartwheeling, 5.6 s−1 for the downhill inchworm, and 0.12 s−1 for the hopping.
3.4 Migration speed, and practically accessible speed of DNA nanowalkers
The lower limits obtained in this study for the total migration rates (Table 1, rightmost column) provide a reliable experiment-calibrated estimation of accessible speed for DNA walkers, including both ssDNA walkers and bipedal walkers. Considering again the 15nt migrator over the 10bp inter-overhang gap, the lower rate limits times the inter-overhang distance (∼3.4 nm) yield the realistic migration speed for the four types of ssDNA migrators as ∼73 nm min−1 for the flipping, 24 nm min−1 for the cartwheeling, ∼1.1 × 103 nm min−1 for the downhill inchworm, and ∼24 nm min−1 for the hopping. These migration speed values, which are for a single inter-overhang migration step, offer directly a realistic upper bound for the speed of bridge-burning and directionless DNA nanowalkers as the two types of walkers are typically made of a ssDNA migrator with its on-track walking implemented by a single type of inter-overhang migration (now over a linear array of often equal-spaced overhangs). As for advanced track-walking bipedal DNA motors, their steps are typically completed by an energy-driven dissociation of the motor's rear leg from a two-legged motor-track binding state, followed by forward inter-overhang migration of the front leg within a bi-overhang site and the biased binding of the rear leg to a front site. Among the three molecular processes, the inter-overhang migration is often the rate-limiting process as the leg dissociation rate is readily promoted beyond the migration rate (e.g., 0.12 s−1–5.6 s−1 for the 15nt migrator over 10bp gap) by the externally controlled rate for energy supply (e.g., high fuel concentration40 or strong light irradiation6), and the forward leg binding rate also can reach41 a high level of 10 s−1–100 s−1 for small nanowalkers. Hence the above migration speed values also offer a conservative and realistic upper bound for the overall speed of advanced bipedal DNA motors, i.e., from ∼24 nm min−1 up to ∼1.1 × 103 nm min−1.The reported DNA nanowalkers are already near the low end of the above speed range (i.e., ∼24 nm min−1) but still far away from the high end (i.e., ∼1.1 × 103 nm min−1). An autonomous chemically fueled DNA bipedal motor9 adopting the hopping migration achieves a speed of ∼8 nm min−1 as found by a recent single-molecule mechanical study10 using magnetic tweezers. This motor speed is not far from the ∼24 nm min−1 migration speed for the hopping. A bridge-burning ssDNA walker adopting the downhill inchworm migration reaches a speed of ∼6 nm min−1 as found by a single-molecule imaging study42 using atomic force microscopy. The latest autonomously chemically fueled DNA bipedal motor43 based on the cartwheeling migration achieves ∼30 nm min−1 speed. This goes beyond the conservative estimation of ∼24 nm min−1 migration speed for cartwheeling likely because the motor adopts a downhill cartwheeling instead of the isoenergetic cartwheeling in this study. Overall, there exists a big room to further improve DNA nanowalkers up to the predicted speed of ∼1.1 × 103 nm min−1, which is ∼40 times lower than the speed of a fast archetypal biological molecular motor called kinesin44 (∼800 nm s−1). Practical accessibility of the target speed of ∼1.1 × 103 nm min−1, i.e., ≤20 nm s−1, is also supported by the single-molecule mechanical study for the hopping-based DNA bipedal motor. The single-motor trajectories from this study10 show, though often with long inter-step pause, fast individual steps – sometimes less than 0.2 seconds per ∼16 nm step. This experimental finding concurs with the present computational study for the conclusion that the DNA migration kinetics is fast enough to support DNA nanowalkers up to the speed of 1000 nm min−1, especially for DNA motors with good directionality.
This study provides guidelines for accelerating inter-overhang migration for faster DNA nanowalkers. Adapting the four types of isoenergetic migration into downhill migration can accelerate the migration non-trivially, as evidenced from the higher migration speed for the downhill inchworm migrator than the other three isoenergetic migrators. The parameter-free cross-migration comparison for the contact window or the displacement window reveals more mechanistic insights. When the inter-overhang gap widens from 10bp to 20bp for the flipping and cartwheeling migrators (all 15nt long), the contact rate decreases but the displacement increases as shown by the rates normalized to that of the common benchmarking 18nt migrator (i.e., rate ratios k15,contact/k18,contact and k15,displace/k18,displace in Table 1). The trend is clear – a longer foothold distance increases the gap for the first contact to reduce the contact rate, but also increases the intra-migrator tension that helps to dissociate the migrator from the rear foothold (hence increasing the displacement rate). Thus, the speed optimization for the flipping and cartwheeling migration involves a trade-off between the contact window and the displacement window. For the downhill inchworm, both the contact rate and the displacement rate decrease with the widening inter-overhang gap. This may be attributed to the higher energy barrier for the 20bp inter-overhang gap than the 10bp gap for both the contact and displacement windows (Fig. 4d and h). Thus, a good strategy to accelerate this type of migration is to reduce the foothold distance.
3.5 From inter-overhang migration to directional bias of bipedal DNA nanowalkers
A bipedal DNA walker may have its two legs as two ssDNA migrators, often of the same type and with their heads or heels connecting to the intermediate duplex bridge of the bipedal walker. The two overhangs supporting the migrations in this study, if arranged repeatedly into a linear periodic array, form the track for the bipedal walker. If the walker has one leg binding to such a bi-overhang site and the other leg mobile above the track, the inter-site migration of the track-bound leg may place the other leg closer to the front site but further from the rear site, resulting in a directional bias (i.e., preferential forward leg binding) for the bipedal walker. Such a bias, which amplifies45,46 a small local displacement within a single binding site into long-range inter-site directional walking, has been found in biological bipedal molecular motors (e.g., kinesin,47 myosin V48) and also implemented in artificial DNA molecular motors6–11,27,49,50 through the inter-overhang migrations on an ad hoc basis. This study now allows an exhaustive counting of all migration types capable of the bias. At first glance, all four types of migration provide the bias whether the ssDNA migrator's head or heel segment is linked to the other mobile leg of a bipedal walker since the average location of the migrator's head (or heel) is displaced forward over a distance equivalent of the inter-overhang gap d0 (assuming, for sake of general discussion, the walker's direction always follows the forward direction of inter-overhang migrations shown in Fig. 1c).However, the magnitude of this bias differs between the migration types, and is sensitive to their free-energy profiles, migrator-overhang binding structure, and the migrator's linkage to the other leg of a motor. The hopping migration, if fully completed as illustrated in Fig. 1c, provides a rather big and robust bias because the most forward location of the migrator's heel is also displaced forward by a distance ∼d0, and the same is true for the migrator's head via back-and-forth swing of the migrator-overhang duplex after migration. Similar biases are provided by the inchworm migration due to virtually the same displacement for the most forward location of the migrator's head or heel. However, the hopping migration may be paused at the trapping state near the final stage (corresponding to the potential well in Fig. 4e), in which the migrator-overhang binding structure has the migrator's heel segment near the bottom of the front overhang but the head segment still bound with the first overhang and tilted backward (see Fig. 1b, leftmost plot; also consistent with an early study51). The trapping state retains the forward bias if the migrator's heal segment is linked to the other leg, but produces a slight backward bias if the head segment is linked to the other leg. This is consistent with an autonomous chemically fuelled DNA bipedal motor8,9,27 (also a latter light-powered version11) that exploits the trapping state of the hopping migration (with the ssDNA migrator leg's head linked to the other migrator leg) and indeed shows a weak backward bias in absence of fuels (but overcome by a chemomechanical coupling effect9,11 in presence of fuels). The inchworm migration has a trapping state too but near the early stage (corresponding to the potential well in Fig. 4h), with the migrator being bound with the first overhang almost entirely (see migrator-overhang binding structure in Fig. 2b, rightmost plot). Regardless of the inchworm migrator's linkage to the other leg, the trapping state largely delays the forward bias until the migration further proceeds for the migrator's full dissociation from the first overhang (e.g., by downhill migration).
Compared to the hopping and cartwheeling migration, the flipping migration provides an even better bias if the ssDNA migrator's heel is linked to the other mobile leg, because the heel's most forward location is displaced by ∼d0 plus the length of post-migration migrator-overhang duplex. The same migration provides a reduced bias if the migrator's head is linked to the other leg, because the migration-induced displacement for the head's most forward location is roughly equal to the length of pre-migration migrator-overhang duplex minus d0. Similarly, the cartwheeling provides a reduced bias with the migrator's head linked to the other leg but a good bias with the heel linked to the other leg (near the best bias for the flipping). The flipping and cartwheeling migration have no well-defined trapping state due to their flat free-energy profiles (Fig. 4f and g, except for cartwheeling at small inter-overhang gap). Nevertheless, the best bias for the two types of migration is still delayed until the migrator's full dissociation from the first overhang. Fig. 1b shows the typical intermediate migrator-overhang binding structures that hold the migrator largely before the front overhang. This structural pattern is rather stable before the full migration although the migrator's base pairs with the two overhangs may change dynamically due to the flat free-energy profile (with the total number of base pairs roughly fixed, see the horizontal axis for Fig. 4f and g). The flipping-based bias is consistent with the forward leg binding bias observed in two light-powered DNA bipedal motors, which use the flipping ssDNA legs with either heal-to-heel connection6,49,50 or head-to-head connection7,8,27 through the intermediate duplex.
As seen in Fig. 4e–h, the free-energy profile pertinent to directional biases is reversely asymmetric between the hopping and inchworm migration, but mostly flat and symmetric for the flipping and cartwheeling. These symmetric patterns are rather robust regardless of parameter changes (e.g. inter-overhang gap, spacers under overhangs, isoenergetic or downhill). These stable symmetric patterns in the free-energy profiles are largely decided by the intrinsic symmetry of the different migration gaits: the reverse of flipping or cartwheeling is itself but the reverse of hopping is inchworm and vice versa. These distinct and robust symmetric patterns of free-energy profiles largely decide intermediate states or trapping states and their structures, thus forming a conceptually clear basis for designing and analyzing biases and overall directionality52–54 of advanced bipedal DNA motors. We note that the speed of a DNA nanowalker is determined not only by the DNA migration kinetics but also by the walker's overall directionality. As a consequence, a directional DNA walker has a higher speed than a directionless DNA walker even if both walkers possess the same level of DNA kinetics. Therefore, improving the speed of DNA nanowalkers requires not only faster DNA kinetics but also better biases and directionality. Furthermore, the distinct symmetric patterns of the one-dimensional free-energy profiles, which correspond to the lowest-energy pathways pertinent to the migration kinetics, also largely decide local barriers and rates. Hence the often complex task of rate optimization can be conveniently guided by modulating the symmetric patterns of the free-energy profiles along the lowest-energy pathways by adjusting design parameters. Altogether, this study provides a unified symmetry-based conceptual framework for computation-aided and sequence-dependent optimization of DNA migration kinetics and biases (i.e. through the chain of oxDNA computed two-dimensional free-energy landscape → identified lowest-energy pathway, the associated one-dimensional free-energy profile, and symmetry analysis → intermediate states, structures and barriers → rates and biases). This conceptual framework covers all possible ssDNA inter-overhang migrations, classified exhaustively into four categories that each possess distinct symmetries in gaits and in free-energies along the lowest-energy pathways.
4 Conclusions
In summary, all possible types of inter-overhang migration of ssDNA migrators, which play a key role in DNA nanowalkers and wider dynamic DNA nanotechnology, are exhaustively identified based on their intrinsic gait symmetry, and classified into only four categories. The free-energy landscape for all four migration categories is obtained from realistic sequence-dependent simulation for typical migrator-overhang systems. The free-energy landscape allows the lowest-energy migration pathway to be identified, yielding a one-dimensional free-energy profile along the pathway that is pertinent to the migration kinetics. Using an experimentally measured migration rate as a benchmark, a parameter-free estimation of migration rates is achieved for all four migration categories. The resultant rates are compatible with reported DNA nanowalkers and indicate a big room to further improve the present DNA nanowalkers – up to a speed above 1 μm per minute. This speed is practically accessible for DNA walkers, especially directional DNA bipedal nanomotors. This target speed is only ∼40 times below the speed of the fastest biological molecular motor (kinesin), and suffices for many real-world nanotechnological applications. Besides, the free-energy profile along the lowest-energy migration pathway is found to possess distinct and robust symmetric patterns for the four migration categories due to their intrinsic gait symmetry. The symmetric patterns along the lowest-energy migration pathways largely decide local barriers, intermediate trapping states and their structures, and thereby affect not only migration rates but also directional biases (both important for speed of advanced bipedal DNA motors, which typically use two ssDNA migrators as legs). This study thus provides a symmetry-based unified framework to analyze all possible inter-overhang ssDNA migrations, and guide their optimization in energetics, kinetics and structures for better DNA nanowalkers and many more dynamic DNA nanotechnological systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Ministry of Education of Singapore under Grant No. A-0008378-00-00, A-8000628-00/01-00, and A-8000982-00-00 (to Z. S. Wang).References
- Z. Wang, R. Hou and I. Y. Loh, Nanoscale, 2019, 11, 9240–9263 RSC.
- A. J. Thubagere, W. Li, R. F. Johnson, Z. Chen, S. Doroudi, Y. L. Lee, G. Izatt, S. Wittman, N. Srinivas and D. Woods, et al. , Science, 2017, 357, eaan6558 CrossRef PubMed.
- J. Li, A. Johnson-Buck, Y. R. Yang, W. M. Shih, H. Yan and N. G. Walter, Nat. Nanotechnol., 2018, 13, 723–729 CrossRef CAS PubMed.
- J. Bath, S. J. Green and A. J. Turberfield, Angew. Chem., Int. Ed., 2005, 44, 4358–4361 CrossRef CAS PubMed.
- Y. Tian, Y. He, Y. Chen, P. Yin and C. Mao, Angew. Chem., 2005, 117, 4429–4432 CrossRef.
- J. Cheng, S. Sreelatha, R. Hou, A. Efremov, R. Liu, J. R. van der Maarel and Z. Wang, Phys. Rev. Lett., 2012, 109, 238104 CrossRef PubMed.
- I. Y. Loh, J. Cheng, S. R. Tee, A. Efremov and Z. Wang, ACS Nano, 2014, 8, 10293–10304 CrossRef CAS PubMed.
- Y. Chiang, S. Tsai, S. Tee, O. Nair, I. Loh, M. Liu and Z. Wang, Nanoscale, 2018, 10, 9199–9211 RSC.
- M. Liu, J. Cheng, S. R. Tee, S. Sreelatha, I. Y. Loh and Z. Wang, ACS Nano, 2016, 10, 5882–5890 CrossRef CAS PubMed.
- X. Hu, X. Zhao, I. Y. Loh, J. Yan and Z. Wang, Nanoscale, 2021, 13, 13195–13207 RSC.
- X. R. Liu, X. Hu, I. Y. Loh and Z. Wang, Nanoscale, 2022, 14, 5899–5914 RSC.
- M. You, Y. Chen, X. Zhang, H. Liu, R. Wang, K. Wang, K. R. Williams and W. Tan, Angew. Chem., Int. Ed., 2012, 51, 2457–2460 CrossRef CAS PubMed.
- T.-G. Cha, J. Pan, H. Chen, J. Salgado, X. Li, C. Mao and J. H. Choi, Nat. Nanotechnol., 2014, 9, 39–43 CrossRef CAS PubMed.
- K. Yehl, A. Mugler, S. Vivek, Y. Liu, Y. Zhang, M. Fan, E. R. Weeks and K. Salaita, Nat. Nanotechnol., 2016, 11, 184–190 CrossRef CAS PubMed.
- H. Peng, X.-F. Li, H. Zhang and X. C. Le, Nat. Commun., 2017, 8, 1–13 CrossRef CAS PubMed.
- K. Lund, A. J. Manzo, N. Dabby, N. Michelotti, A. Johnson-Buck, J. Nangreave, S. Taylor, R. Pei, M. N. Stojanovic and N. G. Walter, et al. , Nature, 2010, 465, 206–210 CrossRef CAS PubMed.
- S. Piranej, A. Bazrafshan and K. Salaita, Nat. Nanotechnol., 2022, 17, 514–523 CrossRef CAS PubMed.
- Y. Gao, L. K. Wolf and R. M. Georgiadis, Nucleic Acids Res., 2006, 34, 3370–3377 CrossRef CAS PubMed.
- D. Y. Zhang and E. Winfree, J. Am. Chem. Soc., 2009, 131, 17303–17314 CrossRef CAS PubMed.
- S. A. Mortimer, M. A. Kidwell and J. A. Doudna, Nat. Rev. Genet., 2014, 15, 469–479 CrossRef CAS PubMed.
- W. F. Lima, B. P. Monia, D. J. Ecker and S. M. Freier, Biochemistry, 1992, 31, 12055–12061 CrossRef CAS PubMed.
- T. E. Ouldridge, A. A. Louis and J. P. Doye, J. Chem. Phys., 2011, 134, 085101 CrossRef PubMed.
- T. E. Ouldridge, Coarse-grained modelling of DNA and DNA self-assembly, Springer Science & Business Media, 2012 Search PubMed.
- T. E. Ouldridge, A. A. Louis and J. P. Doye, Phys. Rev. Lett., 2010, 104, 178101 CrossRef PubMed.
- T. E. Ouldridge, P. Šulc, F. Romano, J. P. Doye and A. A. Louis, Nucleic Acids Res., 2013, 41, 8886–8895 CrossRef CAS PubMed.
- T. E. Ouldridge, R. L. Hoare, A. A. Louis, J. P. Doye, J. Bath and A. J. Turberfield, ACS Nano, 2013, 7, 2479–2490 CrossRef CAS PubMed.
- Q. Yeo, I. Loh, S. Tee, Y. Chiang, J. Cheng, M. Liu and Z. Wang, Nanoscale, 2017, 9, 12142–12149 RSC.
- D. C. Khara, J. S. Schreck, T. E. Tomov, Y. Berger, T. E. Ouldridge, J. P. Doye and E. Nir, Nucleic Acids Res., 2018, 46, 1553–1561 CrossRef CAS PubMed.
- P. Šulc, T. E. Ouldridge, F. Romano, J. P. Doye and A. A. Louis, Nat. Comput., 2014, 13, 535–547 CrossRef.
- S. Naskar and P. K. Maiti, J. Mater. Chem. B, 2021, 9, 5102–5113 RSC.
- B. E. Snodin, F. Randisi, M. Mosayebi, P. Šulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir and A. A. Louis, et al. , J. Chem. Phys., 2015, 142, 234901 CrossRef PubMed.
- A. Sengar, T. E. Ouldridge, O. Henrich, L. Rovigatti and P. Šulc, Front. Mol. Biosci., 2021, 8, 693710 CrossRef CAS PubMed.
- A. Szabo, K. Schulten and Z. Schulten, J. Chem. Phys., 1980, 72, 4350–4357 CrossRef CAS.
- E. Poppleton, J. Bohlin, M. Matthies, S. Sharma, F. Zhang and P. Šulc, Nucleic Acids Res., 2020, 48, e72–e72 CrossRef CAS PubMed.
- S. Whitelam and P. L. Geissler, J. Chem. Phys., 2007, 127, 154101 CrossRef PubMed.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- E. Poppleton, R. Romero, A. Mallya, L. Rovigatti and P. Šulc, Nucleic Acids Res., 2021, 49, W491–W498 CrossRef CAS PubMed.
- N. Srinivas, T. E. Ouldridge, P. Šulc, J. M. Schaeffer, B. Yurke, A. A. Louis, J. P. Doye and E. Winfree, Nucleic Acids Res., 2013, 41, 10641–10658 CrossRef CAS PubMed.
- M. I. Wallace, L. Ying, S. Balasubramanian and D. Klenerman, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 5584–5589 CrossRef CAS PubMed.
- J. Fu, Y. R. Yang, A. Johnson-Buck, M. Liu, Y. Liu, N. G. Walter, N. W. Woodbury and H. Yan, Nat. Nanotechnol., 2014, 9, 531–536 CrossRef CAS PubMed.
- D. Fan, W. Zheng, R. Hou, F. Li and Z. Wang, Biochemistry, 2008, 47, 4733–4742 CrossRef CAS PubMed.
- S. F. Wickham, M. Endo, Y. Katsuda, K. Hidaka, J. Bath, H. Sugiyama and A. J. Turberfield, Nat. Nanotechnol., 2011, 6, 166–169 CrossRef CAS PubMed.
- S. Winna, H. L. Too, A. Tommy, X. R. Liu, I. Y. Loh and Z. Wang, 2023. to be published.
- K. Visscher, M. J. Schnitzer and S. M. Block, Nature, 1999, 400, 184–189 CrossRef CAS PubMed.
- W. Zheng, D. Fan, M. Feng and Z. Wang, Phys. Biol., 2009, 6, 036002 CrossRef PubMed.
- Z. Wang, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 17921–17926 CrossRef CAS PubMed.
- S. Rice, A. W. Lin, D. Safer, C. L. Hart, N. Naber, B. O. Carragher, S. M. Cain, E. Pechatnikova, E. M. Wilson-Kubalek and M. Whittaker, et al. , Nature, 1999, 402, 778–784 CrossRef CAS PubMed.
- Y. Xu and Z. Wang, J. Chem. Phys., 2009, 131, 12B621 Search PubMed.
- J. Cheng, S. Sreelatha, I. Y. Loh, M. Liu and Z. Wang, Methods, 2014, 67, 227–233 CrossRef CAS PubMed.
- M. Liu, R. Hou, J. Cheng, I. Y. Loh, S. Sreelatha, J. N. Tey, J. Wei and Z. Wang, ACS Nano, 2014, 8, 1792–1803 CrossRef CAS PubMed.
- S. R. Tee, X. Hu, I. Y. Loh and Z. Wang, Phys. Rev. Appl., 2018, 9, 034025 CrossRef CAS.
- A. Efremov and Z. Wang, Phys. Chem. Chem. Phys., 2011, 13, 6223–6233 RSC.
- A. Efremov and Z. Wang, Phys. Chem. Chem. Phys., 2011, 13, 5159–5170 RSC.
- Z. Wang, R. Hou and A. Efremov, J. Chem. Phys., 2013, 139, 035105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional discussion on the iterative reweighting umbrella sampling method and the minimum path sum used in this study, Migrator-track sequence and supporting figures Fig. S1–S9. See DOI: https://doi.org/10.1039/d3nr01058a |
| This journal is © The Royal Society of Chemistry 2023 |