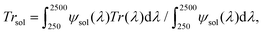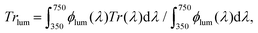Spinodal decomposition introduces strain-enhanced thermochromism in polycrystalline V_1−xTi_xO₂ thin films

Abstract

Processes of self-organization play a key role in the development of innovative functional nanocomposites, allowing, in particular, the transformation of metastable solid solutions into multilayers by activating spinodal decomposition instead of layer-by-layer film growth. We report the formation of strained layered (V,Ti)O₂ nanocomposites in thin polycrystalline films using a spinodal decomposition. Already during the growth of V_0.65Ti_0.35O₂ films, spinodal decomposition was detected while producing atomic-scale disordered V- and Ti-rich phases. Post-growth annealing enhances compositional modulation, arranges the local atomic structures of the phases, and yields periodically layered nanostructures that resemble superlattices. The coherent interfacing of the V- and Ti-rich layers results in the compression of the V-rich phase along the c-axis of the rutile structure and enables strain-enhanced thermochromism. The latter is characterized by a simultaneous decrease in the temperature and width of the metal–insulator transition in the V-rich phase. Our results provide proof-of-concept for an alternative strategy to develop VO₂-based thermochromic coatings by introducing strain-enhanced thermochromism into polycrystalline thin films.

---

1 Introduction

Ordering matter by self-organization and self-assembly underlies numerous natural processes and opens vast opportunities in various technologies ranging from energy and environment to electronics and healthcare.^1,2 Among other self-organization phenomena, spinodal decomposition (SD) holds special significance because of its inherent ability to assemble nanoscale phase-separated materials from initially homogeneous crystalline solids, soft matter, and liquids. In contrast to the traditional growth of new phases by nucleation, spinodal ordering emerges in a metastable solution that is sufficiently far from equilibrium, as a regular compositional wave appearing in response to thermodynamic stimuli.³ The most prominent feature of SD is its capacity to assemble anisotropic condensed matter into ordered multilayers or even superlattices (SLs) without layer-by-layer epitaxy.^4–6

A notable example of SD ordering is provided by the strongly anisotropic VO₂–TiO₂ system.⁷ The compositional wave in V_1−xTi_xO₂ propagates along the c-axis of the rutile structure (c_R), producing a layered nanocomposite with alternating V- and Ti-rich phases. Strain minimization is achieved by interfacing layers along the a(b)-axis, where the lattice mismatch is smaller. By applying post-growth annealing, (V,Ti)O₂ nanocomposites have been fabricated in bulk polycrystalline materials,^7,8 single crystals,⁹ epitaxial films of various orientations grown on TiO₂ ^10–13 and Al₂O₃ substrates,^14–16 and, lately, polycrystalline films.¹⁷ Furthermore, coherently strained SLs have been demonstrated by the enhancement of uphill diffusion during epitaxial growth on TiO₂(001).¹⁸

Ordered (V,Ti)O₂ multilayers are particularly intriguing because of the strongly dissimilar electronic properties of the constituent oxides. TiO₂ is a wide-bandgap insulator, whereas VO₂ is a strongly correlated material with coupled metal–insulator (MI) and structural (tetragonal–monoclinic) phase transitions.¹⁹ Sharp, reversible, and tunable ultrafast changes in electrical resistivity and optical constants make VO₂ highly promising for a wide variety of switching and sensing devices.²⁰ In particular, because of its close to room temperature T_MI = 341 K and strong modulation of near-infrared (NIR) optical transmittance, VO₂ has been considered for a long time as the most favorable candidate for thermochromic coatings in energy-efficient “smart” windows.²¹

However, the research and development of thermochromic VO₂-based coatings are still in “the infancy”, because the following characteristics should be achieved simultaneously: (1) T_MI ∼ 20 ÷ 25 °C; (2) solar transmittance modulation, ΔT_sol > 10%; and (3) integral luminous transmission, Tr_lum > 60%.²² In addition, the MI transition should be sharp, with as narrow a thermal hysteresis loop as possible.²³ For several decades, research has primarily focused on two strategies: (1) reduction of T_MI by doping²⁴ and (2) increasing Tr_lum by implementing a nanothermochromic concept, based on the embedment of VO₂ nanoparticles into a transparent matrix,²⁵ or by combining both strategies.²⁶ Consequently, the issue of ineffective switching behaviour remains unaddressed, and reliable VO₂-based thermochromic coatings are still unavailable. Moreover, VO₂ doping is accompanied by degradation of the NIR transmittance switching owing to the broadening of the MI transition. The vital demand for an alternative strategy for tailoring NIR switching has recently resulted, for instance, in the hybridization of VO₂ films with plasmonic TiN nanoparticles.²⁷

Herein, we propose an alternative strategy based on strain-driven reduction of the T_MI and the width of the MI transition. Coherent epitaxial strains have been widely exploited to tune the functional characteristics of transition metal oxides, including VO₂.^28,29 In contrast to doping, compressive strain along the c_R-axis results in a reduction in T_MI without an undesirable broadening of the MI transition.^30,31 Unfortunately, the use of strain engineering for tuning T_MI is intimately linked to epitaxial growth, which is inapplicable to thermochromic coatings, as they must be deposited on an amorphous glass substrate. In the VO₂–TiO₂ system, the necessity for epitaxial growth can, in principle, be overcome using a strained layered nanocomposite formed by the SD process, which must be executed in a thin polycrystalline film. To date, the optical and thermochromic properties of (V,Ti)O₂-based nanocomposites have been studied exclusively for epitaxial films.^12,14 However, strong elastic coupling (clamping) of the epitaxial film and substrate makes strain-enhanced thermochromism unattainable.

In this study, we performed SD in polycrystalline thin films of V_1−xTi_xO₂ grown on fused quartz substrates, examining thus spinodal ordering inside small grains with a lateral size D < 100 nm.

The composition of the solid solution was adjusted to x = 0.35, that is to the center of the miscibility gap for the VO₂–TiO₂ system, which is known to be optimal for SD.⁷ Next, post-growth annealing was performed to accomplish decomposition. The structural and thermochromic properties of the as-grown and annealed films were studied to disclose the SD features in the fine grains and to estimate the potential of our strategy for the fabrication of thermochromic coatings.

2 Experimental details

Thin film samples were grown using a solution-based chemical technique of metalorganic aerosol deposition³² (MAD), which is founded on the pyrolysis of precursors at the surface of a heated substrate. The deposition system was equipped with a pneumatic nebulizer (MEINHARD®) for spray flux generation and various controllers and sensors to regulate deposition parameters such as substrate temperature, T_sub, Ar and O₂ gas flows, spray flux intensity, pressure etc. To stabilize the V⁴⁺ valence state, the growth of VO₂ and V_1−xTi_xO₂ films was performed under oxygen-deficient conditions by using a mixture of Ar and O₂ gases. Regardless of the gas mixture composition, the total pressure inside the chamber was maintained at 750 mbar to ensure a constant distribution of the spray over the substrate. OV(acac)₂ and Ti(O-i-Pr)₂(TMHD)₂ precursors were dissolved in dimethylformamide with a concentration of 0.05 M l⁻¹ for fabrication of pure-phase VO₂ and TiO₂ films, respectively; a mixture of the precursors was employed for deposition of V_1−xTi_xO₂ films. The 10 × 10 × 0.5 mm substrates of 2-side polished fused quartz were used for the deposition of polycrystalline films. Additionally, Al₂O₃(0001) substrates were utilized for the optimization of VO₂ synthesis. To prevent vanadium over-oxidation, spinodal decomposition of the V_0.65Ti_0.35O₂ films was performed by annealing in a pure Ar atmosphere at a pressure of 1000 mbar.

The surface morphology of the films was characterized using either a Zeiss Leo Supra 35 field-emission gun scanning electron microscope (SEM) or a Park System XE7 atomic force microscope (AFM). The composition of the solid-solution films was estimated by energy dispersive X-ray (EDX) elemental analysis using the same SEM. Using a Bruker D8 Advance diffractometer (Cu_Kα radiation), the thickness of the films was determined from X-ray reflection (XRR) oscillations by plotting the reflection intensity versus the momentum transferred perpendicular to the sample, which is defined by 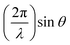; the roughness of thick polycrystalline films was too high to determine their thickness by XRR.

The microstructure of the films and the local V/Ti chemical composition were analyzed using a FEI TITAN 80-300 environmental transmission electron microscope (TEM) operating at 300 kV and equipped with a Gatan imaging filter (Quantum 965 ER). Bright-field (BF) and high-angle annular dark field (HAADF) images were acquired in the scanning TEM (STEM) mode after the collection of electron energy-loss spectra (EELS). The analysis of crystalline phases was performed by X-ray diffraction (XRD) using a Malvern Panalytical Empyrean 2 diffractometer (λ = 1.54098 Å) in grazing incidence mode (θ = 0.5°). A dedicated X-ray server³³ was used to estimate the residual strains in polycrystalline V_1−xTi_xO₂ films by numerically fitting the XRD patterns. To simulate peak broadening, the XRD patterns were represented as a sum of reflections from numerous individual grains by varying their parameters (grain size, number of compositional layers, and their thickness) around the average values, which were determined using TEM. Micro-Raman analysis was carried out at room temperature in a backscattering geometry with a continuous wave Nd:YAG laser (λ = 532 nm) using a confocal Raman microscope (LabRAM HR Evolution, Horiba JobinYvon); to avoid significant heating of the sample, the laser power was reduced down to 0.2 mW.

The electrical resistivity of the samples was measured using the four-electrode method (silver paint contacts) at temperatures ranging from 300 to 400 K in a physical property measurement system (PPMS, Quantum Design) with a heating/cooling rate of 2 K min⁻¹. Temperature-dependent optical transmission at wavelengths of 400–2500 nm was measured using a custom-assembled setup based on: (1) two spectrometers (Maya2000Pro for 165–1100 nm and NIRQuest512-2.5 for 900–2500 nm, both by OceanOptics); (2) the corresponding Vis and NIR light sources (DH-2000 and HL-2000-FHSA, both by OceanInsight); and (3) the temperature-controlled stage (THMS350V, Linkam Scientific) for mounting samples. The integrated solar transmittance (250–2500 nm) was calculated as follows:

where T(λ) represents the transmittance at wavelength λ and ψ_sol is the solar irradiance spectrum for an air mass of 1.5. The solar modulation ability was calculated as follows:

ΔTr_sol = ΔTr_{sol, lT} − ΔTr_{sol, hT},

where lT and hT represent 25 °C and 100 °C, respectively. The integral luminous transmittance (350–750 nm) was calculated using the equations:
where φ_lum is the standard luminous efficiency of photopic vision.

3 Results and discussion

3.1 Thin film growth and annealing

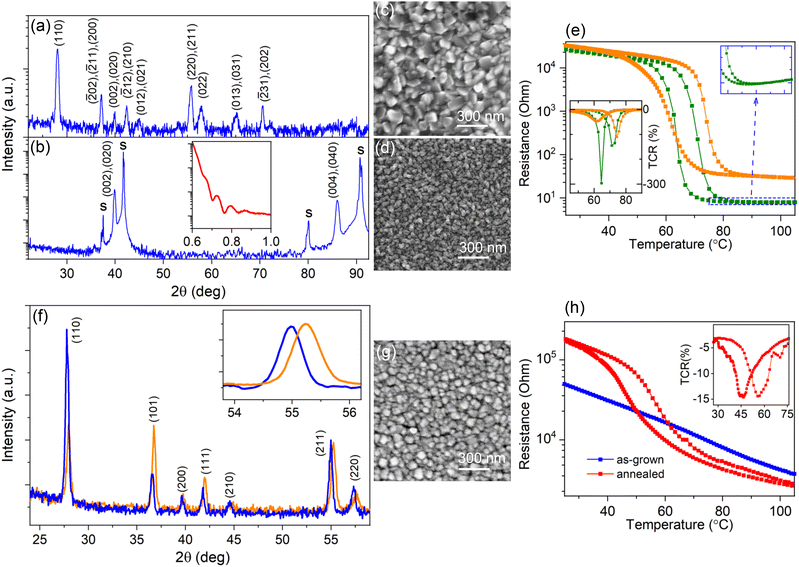
Because of the abundant vanadium valences ranging from 2⁺ to 5⁺, over 20 oxide phases can be produced.³⁴ Therefore, the growth conditions for the pure-phase VO₂ synthesis were firstly optimized and these conditions were further applied to prepare the V_1−xTi_xO₂ solid solution. The growth parameters of VO₂ are interrelated, and a higher T_sub or deposition rate requires an increase in oxygen content.³⁵ Subsequently, we optimized VO₂ synthesis by regulating O₂ flow only, as the most sensitive parameter, keeping fixed the rest of them: (1) Ar + O₂ gas flow at 1000 cm³ min⁻¹, (2) T_sub = 470 °C, and (3) deposition rate at 1 nm s⁻¹. XRD analysis of crystalline phases, used for a prior optimization, shows that for the O₂ flow below 10 cm³ min⁻¹ all XRD peaks belong to the monoclinic VO₂ phase, forming typical patterns for polycrystalline (Fig. 1a) and (010)-oriented (Fig. 1b) films grown on fused quartz and Al₂O₃(0001), respectively. Precise tuning of the O₂ flow was then carried out by measuring the temperature-dependent resistance, R(T), because the value of T_MI and the form of the hysteresis loop proved to be more sensitive to the VO₂ off-stoichiometry. Thereby, we found that only a narrow O₂ flow interval of around 4 cm³ min⁻¹ ensures a pure-phase VO₂ synthesis. That is, an O₂ content of 0.4% provides both the anion-to-cation stoichiometry and the utilization of organic remains; the latter is imperative for the MAD technique, which involves the combustion of an organic solvent and precursor ligands.³⁶

Fig. 1 Characterization of VO₂ and V_1−x Ti_xO₂ thin films. XRD patterns of VO₂ films grown on (a) fused quartz and (b) Al₂O₃(0001) substrates (the sapphire peaks are denoted by s); the inset in (b) shows the XRR oscillations of the 83 nm-thick film. SEM images of VO₂ films grown on (c) fused quartz and (d) Al₂O₃(0001) substrates. (e) Temperature-dependent resistance of VO₂ films grown on Al₂O₃(0001) (olive) and fused quartz (orange) substrates; the insert shows the thermal coefficients of resistance, TCR(T) = 100% × (1/R)(dR/dT). The magnified area in (e) demonstrates the metallic conductivity of the VO₂ film grown on Al₂O₃(0001). (f) XRD patterns of two V_1−xTi_xO₂ films with x₁ = 0.26 (orange) and x₂ = 0.43 (blue); the inset demonstrates shifting of the (211)-peak with x. (g) SEM image of 180 nm-thick V_0.65Ti_0.35O₂ films grown on fused quartz substrate. (h) Temperature-dependent resistance of as-grown (blue) and annealed (red) at 530 °C for 1 hour V_0.65Ti_0.35O₂ film; the inset shows TCR(T) of the annealed film.

SEM images of the VO₂ films grown under the optimized conditions on fused quartz and Al₂O₃(0001) substrates are presented in Fig. 1c and d, respectively. Both surfaces are composed of densely packed grains, but their average sizes are quite different: they reach D ∼ 120 nm in the polycrystalline film and D ∼ 40 nm in the single-oriented film of the same thickness. The smoother surface of the oriented film on sapphire allowed us to determine the film thickness of d ∼ 83 nm by XRR (the insert on Fig. 1b). The R(T) curves shown in Fig. 1e reveal the same T_MI = 68 °C both for the polycrystalline and the single-oriented films; here T_MI was determined as a middle temperature between TCR(T) minima (see the inset in Fig. 1e). However, the width, sharpness, and amplitude of the hysteresis loops are predictably different because of the large contribution of irregular grain boundaries in the polycrystalline material. The obtained T_MI value exactly fits the tabulated value for pristine VO₂.¹⁹ The observed metallic behavior above T_MI in the single-oriented film (see the zoomed area of the R(T) curve in Fig. 1e) confirms the achievement of pure-phase VO₂ synthesis.

Titanium is less prone to phase variation, displaying a valence state of 4+ for all oxygen pressures that are higher than the minimum value required for stoichiometric TiO₂ formation. Therefore, before V_1−xTi_xO₂ deposition, we verified the formation of TiO₂ under the optimal conditions for synthesizing pure-phase VO₂, i.e. under ∼0.4% oxygen in an Ar + O₂ atmosphere. The obtained films were insulating with a sheet resistance above 10⁸ Ω. Fig. S1† presents the results of characterization for a TiO₂ film grown on a fused quartz substrate. The AFM image in Fig. S1a† demonstrates the typical surface of a polycrystalline film comprising grains with an average size of D ∼ 60 nm. This surface morphology was sufficiently smooth to develop XRR oscillations (see Fig. S1b†) and to determine the film thickness d = 34 nm. All XRD peaks in Fig. S1c† belong to the rutile TiO₂ structure, confirming thus the formation of TiO₂ under O₂ content of 0.4%.

To fabricate V_1−xTi_xO₂, a specified quantity of the V precursor was replaced with the Ti precursor, maintaining the integral molarity of the mixed precursor solutions and all other growth conditions constant. A fast cooling rate of ∼100 °C min⁻¹ was applied after film growth to freeze out the metastable state of the obtained solid solution. Fig. 1f shows the XRD patterns of the two V_1−xTi_xO₂ films with different Ti contents. One can see that, regardless of the Ti/V precursor ratio, XRD reveals peaks belonging to the solid solution only. The texture shifts towards the (110)-orientation with an increase in the Ti-content, but all peaks correspond to the rutile structure and are located between those seen for pristine VO₂ and TiO₂. This result is in line with rutile structure formation at x > 0.2 in the bulk polycrystals.⁷ According to Vegard's law, the compositions of the V_1−xTi_xO₂ films in Fig. 1f correspond to x₁ = 0.26 and x₂ = 0.43. By tuning the Ti/V ratio we obtained the solid solution with nominal value of x = 0.35 required for further SD processing. In Fig. 1g the SEM image shows the surface morphology of a 180 nm-thick V_0.65Ti_0.35O₂ film with an average grain size of D ∼ 120 nm. The EDX spectrum in Fig. S2† corresponds to the metal stoichiometry of V_0.66Ti_0.34, confirming thus the compositional analysis performed by XRD.

The SD was then activated by a step-by-step increase in either the temperature or duration of post-growth annealing. We observed that the surface morphology and average composition of the solid solution films remained unchanged (not shown) during all annealing cycles. However, the R(T) dependence changed after exposure to 530 °C for 1 h, transforming from a gradual dependence into a hysteresis loop, as shown in Fig. 1h. The observed resistance switching suggests the onset of the MI transition in the V_0.65Ti_0.35O₂ film owing to the appearance of the V-rich phase. It is worth noting that our attempts to further increase either the temperature or duration of annealing resulted in deterioration of the R(T) hysteresis loop. In comparison with the R(T) dependence in Fig. 1e for the optimized VO₂, the resistance switching of annealed V_0.65Ti_0.35O₂ in Fig. 1h is shifted towards a lower temperature, implying an essential difference between the emerged V-rich phase and the pure-phase VO₂.

3.2 TEM analysis

The microstructures of the as-grown and annealed V_0.65Ti_0.35O₂ films were analyzed by TEM and compared with that of pure VO₂ polycrystalline film. The top row in Fig. 2 presents the plan-view BF STEM images of VO₂ (a), as-grown (b), and annealed (c) V_0.65Ti_0.35O₂. In contrast to VO₂, a periodic alternation of bright and dark stripes appeared in both V_0.65Ti_0.35O₂ samples. The cross-sectional BF STEM image shown in Fig. 2d also reveals the striped microstructure of the annealed V_0.65Ti_0.35O₂ film. The V- and Ti-rich layers appear in the BF images as dark and bright strips, respectively. In bulk polycrystalline materials, the alternation of bright and dark bands indicates the separation of the V- and Ti-rich phases that emerge as a result of SD.⁷ Note that the striped microstructure can be observed by TEM only in the grains for which the direction of compositional modulation coincides with the image plane. In otherwise oriented grains, the elemental contrast is screened by the overlapping layers. By choosing correctly oriented grains, the estimated thickness of the individual layers is equal to ∼8 nm for the Ti-rich layers and ∼12 nm for the V-rich ones. The observed layered nanostructures contain stacking faults and “curved” layers, which result from the irregular shape of the crystallites and a limited number of layers embedded in the nano-sized grains.

Fig. 2 TEM analysis of VO₂ and V_0.65Ti_0.35O₂ films grown on fused quartz substrates. Plan-view BF STEM images of (a) VO₂, (b) as-grown, and (c) annealed V_0.65Ti_0.35O₂ films. (d) Cross-sectional BF STEM image of annealed V_0.65Ti_0.35O₂ films. HAADF-STEM images and respective EELS maps of as-grown (e) and annealed (f) V_0.65Ti_0.35O₂ films; V is marked as orange and Ti as blue.

Thus, TEM analysis confirmed the realization of SD in the small crystallites of thin polycrystalline films. Moreover, it was revealed that a layered nanocomposite also forms in the as-grown V_0.65Ti_0.35O₂ film, pointing out that SD occurs even during film growth. The presence of a layered structure signifies the spinodal nature of phase separation during growth; the alternative process of phase separation through nucleation and growth can only yield nanodot or nanopillar-embedded composites due to the isotropy of adatom surface mobility on the amorphous substrates. The development of SD during film growth has been predicted theoretically³⁷ and observed experimentally in epitaxial (V,Ti)O₂ films.¹⁸ However, the observed here nanoscale phase separation in the as-grown V_0.65Ti_0.35O₂ contradicts the gradual R(T) behavior in the as-grown sample (see Fig. 1h), apparently contrasting with a robust hysteresis loop appeared after the annealing. The lack of resistance switching in the as-grown films can be rationalized by comparing the elemental compositions of the V- and Ti-rich layers before and after annealing. HAADF STEM images with corresponding the EELS elemental maps are shown in Fig. 2e and f for the as-grown and annealed V_0.65Ti_0.35O₂ films, respectively. The bright and dark strips in the HAADF STEM image correspond to the V (red) and Ti (blue) areas, respectively, in the EELS elemental maps. The Ti content in the as-grown film corresponds to x = 0.41 in the Ti-rich layers and x = 0.24 in the V-rich ones. After annealing, the degree of compositional modulation becomes notably higher: x = 0.45 (Ti-rich) and x = 0.19 (V-rich). It was established⁷ that the value of x < 0.2 is necessary for efficient V–V dimerization, which is an essential prerequisite of the MI transition in VO₂. Thus, the observed compositional modulation in the as-grown film, i.e. V_0.76Ti_0.24O₂, is insufficient for V–V dimerization and the onset of MI transition. Post-growth annealing resulted in the formation of V_0.81Ti_0.19O₂ layers with a sufficiently high concentration of V for the manifestation of a pronounced MI transition in R(T) dependence.

3.3 XRD analysis

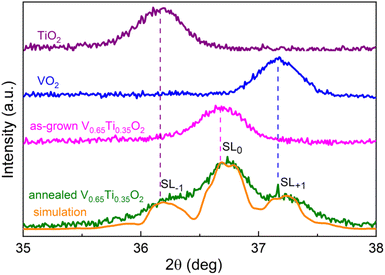
XRD patterns in Fig. S3† reveal a broadening of the (101), (111), and (211) peaks after post-growth annealing, whereas the (110), (200), and (210) peaks remain unchanged. Because broadening was detected only for (hkl)-peaks with l = 1, the compositional modulation is directed along the c_R-axis⁷ and is independent of the grain orientations. In Fig. 3 a detailed XRD pattern near the broadened (101)-peak of V_0.65Ti_0.35O₂ is shown together with the corresponding peaks of the VO₂ and TiO₂ films. Two important changes induced by annealing can be observed: (1) the (101)-peak shifts toward a larger 2θ-angle; and (2) two small peaks appear symmetrically on both sides of the main (101)-peak. The observed shift indicates either a change in the film composition or a strained state of the layered nanocomposite. According to the EDX data, the average film composition did not change after the annealing. Therefore, we can attribute this shift to a decrease in the c-lattice parameter from 0.2250 to 0.2247 nm, which indicates residual compressive strain. The reason for compression is the coherent interfacing of the V- and Ti-rich layers along the a(b)-axis in the presence of a lattice mismatch (0.86% between pristine VO₂ and TiO₂). Coherent interfacing results in compressive and tensile strains along the c_R-axis in the V- and Ti-rich layers, respectively. The overall shift of the main peak to a larger 2θ-angle means that shrinking c_R in V-rich layers overcomes its expansion in Ti-rich layers. Note that the as-grown V_0.65Ti_0.35O₂ film appears to be unstrained, and this state coexists with a level of compositional modulation that is insufficient to exhibit a hysteresis loop in the R(T) dependence.

Fig. 3 Normalized XRD patterns next to the (101) peaks of TiO₂ (purple), VO₂ (blue), as-grown (magenta), and annealed (olive) V_0.65Ti_0.35O₂ films grown on fused quartz substrates. Simulated XRD (orange) of polycrystalline film with grains comprised V_0.81Ti_0.19O₂/V_0.55Ti_0.45O₂ superlattices. The positions of the (101) peaks are indicated by the vertical dashed lines in the respective colors.

The appearance of two minor peaks after annealing (Fig. 3) was more intriguing. In principle, by stopping the SD process at the initial stage, it is possible to acquire an XRD pattern comprising both the initial peak of the solid solution and two minor peaks, which correspond to the incipient V- and Ti-rich phases. However, TEM analysis revealed a significant degree of phase separation even before and, especially, after the annealing of V_0.65Ti_0.35O₂. Moreover, the angular distance between the main and minor peaks is too large; the minor peak at a larger 2θ-angle corresponds to a compressed pure phase of VO₂, but the EELS analysis established a V-rich phase composition of V_0.81Ti_0.19O₂. Therefore, another origin for the minor peaks must be supposed. Because the minor peaks appear at equal distances from the main one, we suppose that these peaks represent satellites SL₋₁ and SL₊₁ of the main superlattice peak SL₀. That is, the appearance of minor peaks points to the right periodicity of V_0.81Ti_0.19O₂ and V_0.55Ti_0.45O₂ layers. By applying Schuller's formula³⁸ for superlattices Λ = λ/(sin θ_n − sin θ_n−1), a superlattice period Λ = 20.6 nm was determined. This value agrees very well with the sum of the V- and Ti-rich layer thicknesses, i.e. 12 + 8 = 20 nm, as observed by TEM (Fig. 2). By numerically fitting the XRD patterns, we estimated the individual values of the residual strains in the V- and Ti-rich layers. The best agreement between the simulated and experimental curves in Fig. 3 was achieved at the same value of the lattice strain parameter, Δc/c = 0.01 ÷ 0.014, in both layers. Considering that compressed V-rich layers are 1.5 times thicker than tensile Ti-rich layers, the average lattice parameter of the whole SL decreases and the position of the central SL₀ peak shifts toward a higher 2θ-angle.

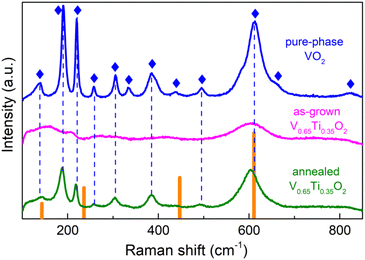
3.4 Raman analysis

Despite the considerable compositional modulation, SL peaks were absent in the as-grown V_0.65Ti_0.35O₂ films. Therefore, along with the quantitative enhancement of the compositional modulation revealed by TEM, post-growth annealing results in a distinct structural transformation. Raman spectroscopy allows us to elucidate this transformation. Fig. 4 shows the Raman spectra of a V_0.65Ti_0.35O₂ film before and after annealing, as well as the spectrum of a pure-phase VO₂ film and reference data for rutile TiO₂.³⁹ Almost all phonon modes of monoclinic VO₂ ⁴⁰ were identified in the spectrum of the VO₂ film. The spectrum of the annealed V_0.65Ti_0.35O₂ film reproduces most of the VO₂ modes, but with a shift towards smaller wavenumbers, e.g., the A_g mode shifts from 613 cm⁻¹ to 602 cm⁻¹. This shift is caused by the formation of a solid solution because the replacement of V with Ti increases the bond length at almost identical binding energies of the Ti–O and V–O bonds.⁴¹

Fig. 4 Room-temperature micro-Raman spectra acquired on the pure-phase VO₂ film (blue), as-grown (magenta), and annealed (green) at 530 °C for 1 hour V_0.65Ti_0.35O₂ films grown on fused quartz substrates. Diamonds indicate the tabulated VO₂ modes. The vertical dashed lines show the correspondence between the lines in the VO₂ and V_0.65Ti_0.35O₂ spectra. The orange strips denote the positions and relative intensities of rutile TiO₂ lines.

The Raman spectrum of the as-grown V_0.65Ti_0.35O₂ film, which lacks almost all phonon modes, differs drastically from those measured for VO₂ and annealed V_0.65Ti_0.35O₂ films. It consists of only a 602 cm⁻¹ mode, which is broader and weaker than that of the annealed V_0.65Ti_0.35O₂ film. Because XRD reveals robust crystallinity in the as-grown film, we cannot attribute such strong damping of almost all phonon modes to an amorphous state of V_0.65Ti_0.35O₂. It is likely that the observed contradiction between XRD and Raman spectroscopy is caused by the different probing scales of these methods. Raman spectroscopy is sensitive to the local atomic-scale coordination, which is determined mainly by the nearest neighbors and to a lesser extent by the next to nearest-neighbor atoms, i.e. the probing scale is ∼1–2 unit cells.⁴² The coherence scattering length of XRD in polycrystalline materials is limited by the size of the crystallites. By applying Scherrer's formula L = 0.9λ/β cos θ, where L is the crystallite size, λ is the X-ray wavelength, β is the full width at half maximum of the diffraction peak, the estimated average grain size in the V_0.65Ti_0.35O₂ film is L ≈ 50 unit cells. This size exceeds the probing scale of Raman spectroscopy by many times. Therefore, the observed contradiction can be explained by the difference between the local atomic structure and long-range or mesoscopic structure (crystallite). The local disorder in the metastable V_0.65Ti_0.35O₂ solid solution stems from the inhomogeneous distribution of Ti and V atoms during growth. The alloying-induced disorder was frozen by the fast cooling after film growth, producing thus numerous local microphases with various arrangements of V–Ti atomic chains. Raman spectroscopy is able to detect vibrational modes from similar micro-phases developing in a random solid solution.⁴³ In our case, the overlapping of slightly displaced vibrational modes from different microphases results in the observed broadening of the most intensive A_g-peak and damping of the rest of peaks with a smaller intensity. Hence, the results of Raman spectroscopy allowed us to conclude that upon annealing, the random solid solutions in the V- and Ti-rich layers underwent a structural transformation into short-range ordered states.

3.5 Optical transmittance

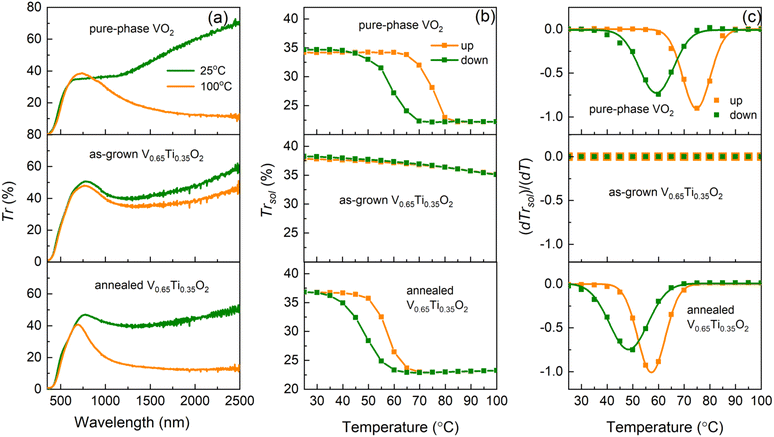
Using R(T) measurements, we detected the onset of the MI transition in the V_0.65Ti_0.35O₂ film after annealing. However, percolative transport through the two-phase nanocomposite, where only V-rich layers undergo the MI transition, causes smearing of the hysteresis loop in R(T). Optical transmittance measurements allowed us to uncover the characteristics of the MI transition in the V-rich phase and to elucidate the thermochromic properties of the (V,Ti)O₂-nanocomposite. Fig. 5 presents the temperature-dependent Vis–NIR optical transmittance of a pure VO₂ film in comparison with the as-grown and annealed V_0.65Ti_0.35O₂ films.

Fig. 5 Optical properties of 83 nm-thick VO₂ films (top panels) in comparison with 180 nm-thick as-grown (middle panels) and annealed (bottom panels) V_0.65Ti_0.35O₂ films all deposited on fused quartz substrates. (a) Vis–NIR transmittance spectra at 25 and 100 °C. (b) Temperature-dependent integral solar transmittance in the 250 ÷ 2500 nm range of wavelengths. (c) Derivatives of integral solar transmittance: experimental points and Gaussian fittings.

The Vis–NIR transmittance spectra in Fig. 5a were measured well below (25 °C) and above (100 °C) the standard T_MI = 68 °C for pristine VO₂. The spectra of the VO₂ film demonstrate a typical transition-induced change in the NIR transmittance, ΔTr = 38% at 1700 nm, for a film thickness d = 83 nm. The as-grown 180 nm-thick V_0.65Ti_0.35O₂ film exhibited a negligible change, ΔTr = 7%. However, the emergence of MI transition after annealing led to an increase in ΔTr to 29%. Fig. 5b shows the temperature-dependent integral solar transmittance, ΔTr_sol, for wavelengths λ = 250–2500 nm for the VO₂ and V_0.65Ti_0.35O₂ films shown in Fig. 5a. The main MI transition characteristics (T_MI, width, and amplitude of the hysteresis loop) are shown in Fig. 5c by plotting the derivative dTr_sol/dT and fitting the curves using Gaussians. Here, T_MI is determined as the middle temperature between the derivative minima for the heating and cooling curves. The pure VO₂ film demonstrated a tabulated MI transition temperature, T_MI = 68 °C, confirming the value evaluated from R(T) in Fig. 1e. The solar modulation ability, ΔTr_sol = 12%, and width of the thermal hysteresis loop, ΔT_MI = T_MI (heating) − T_MI (cooling) = 16 °C, agree well with those reported for high-quality polycrystalline VO₂ films of comparable thickness.⁴⁴ The as-grown V_0.65Ti_0.35O₂ film demonstrates a lack of hysteresis behavior similar to the R(T) measurements, exhibiting a weak gradual decrease of T_sol with temperature and a low solar modulation ΔTr_sol = 3%, which appears because of the variation in the optical constants with temperature. In contrast, the onset of the MI transition in the V-rich layers after annealing led to a pronounced hysteresis loop, which demonstrated a reduced T_MI of 53 °C, a decreased ΔT_MI of 9 °C, and an enhanced ΔTr_sol of 14%.

The observed change in ΔTr_sol can be interpreted as a result of the increased VO₂ content in the 180 nm-thick V_0.65Ti_0.35O₂ film compared to that in the 83 nm-thick pure-phase VO₂ film. However, the simultaneous decrease in T_MI and ΔT_MI can only be caused by compressive strains in the V-rich layers because simple alloying of VO₂ with TiO₂ leads to an extended transition at elevated T_MI.⁴⁵ The emergence of strain-enhanced optical characteristics after annealing was in full agreement with the formation of a strained superlattice-like microstructure, as revealed by XRD. The lack of the substrate clamping effect causes the independence of interfacial strains on the grain orientation and leads to a reduction of T_MI by 15 °C, which substantially exceeds the 5–6 °C reduction observed in the presence of the clamping effect in epitaxial films.¹⁵

Despite the ∼40% excess in VO₂ content, the V_0.65Ti_0.35O₂ and VO₂ films possess almost the same values of Tr_lum, 29.0 and 28.9%, respectively. According to the nanothermochromic concept, VO₂ nanoparticles embedded in a transparent dielectric host provide a higher Tr_lum than VO₂ films of an equivalent thickness.²⁵ In our case, the layers of a more transparent TiO₂-rich phase produced the nanothermochromic effect, maintaining Tr_lum at the same value despite an increase in the equivalent VO₂ thickness.

3.6 Discussion

We established that spinodal decomposition can be performed in small grains of thin polycrystalline V_1−xTi_xO₂ films in the same manner as in bulk materials and epitaxial films. In addition to a basic similarity, two essential differences were observed: (1) SD develops simultaneously with film growth, producing a significant phase separation in the as-grown V_0.65Ti_0.35O₂ films, and (2) post-growth annealing results in the formation of strained superlattice-like (V,Ti)O₂ nanostructures.

An in situ SD during film growth has already been observed in epitaxial (V,Ti)O₂ films when the c_R-axis coincides with the film growth direction.¹⁸ In our case, the direction of compositional modulation was irrelevant to the grain orientation, and the SD was identical to that in the bulk materials. We suppose that enhanced surface adatom diffusion is responsible for SD during growth, whereas bulk diffusion occurs under post-grown annealing. The enhancement of surface diffusion stems from the main peculiarities of MAD growth: (1) being a chemical technique, MAD operates under near-equilibrium growth conditions, promoting surface diffusion; (2) the pyrolysis of precursors such as β-diketonates of V and Ti is an exothermic reaction, resulting in an additional increase in the surface temperature, which leads to an extra enhancement of surface diffusion. However, adatom diffusion is kinetically limited by deposition rate. As a result, phase separation during growth was incomplete, yielding an insufficient concentration of V to achieve the MI transition in V-rich layers. Moreover, Raman spectroscopy revealed a disordered state in the as-grown solid solutions, with an inhomogeneous local distribution of V and Ti atoms. Such random solid solutions possess diffused interfaces; thus, they are inconsistent with the formation of strained nanocomposites via coherent interfacing between layers. Therefore, neither superlattice-like nanostructure nor MI transition were observed in the as-grown V_0.65Ti_0.35O₂ films.

The activation of bulk diffusion by post-growth annealing results in predictable strengthening of the compositional modulation, yielding also strained superlattice-like nanostructures. This is the most remarkable feature revealed by XRD analysis in the thin polycrystalline V_0.65Ti_0.35O₂ films. The corresponding transformation of the optical properties, i.e. a simultaneous decrease in T_MI and ΔT_MI, confirms the strained state after annealing. In principle, the formation of SLs is the conventional termination step of the SD process.⁴ Nevertheless, suitable conditions for SL formation are hardly accessible because of (1) the pinning of compositional waves at various structural imperfections and (2) the development of new phases by concurrent processes of nucleation. We suppose that in our case, a fine grain size, D ∼ 30–100 nm, facilitates the formation of superlattices. In bulk materials, the result of SD is determined by the superposition of numerous compositional waves initiated in different parts of a large crystalline grain, D > 0.5 μm for bulk polycrystals⁷ or mm-size single crystals.⁹ For a grain size of only several tens of nanometers, it is plausible to suppose that a single compositional wave propagates over the entire crystallite, forming a superlattice-like structure of just a few periods.

As a moderate SD level has been obtained during film growth, it raises the question of whether a higher level of compositional modulation can be achieved during growth without a considerable increase in substrate temperature. This is a key challenge for the practical application of (V,Ti)O₂-based nanocomposites as thermochromic coatings because the thermal budget of smart window fabrication is limited by the glass transition temperature. We obtained an enhanced surface adatom mobility during growth at T_sub = 470 °C. To activate bulk diffusion, we applied post-growth annealing at 530 °C, exceeding thus the deposition temperature by 60 °C only. We believe that further enhancement of surface diffusion during film growth can be achieved either (1) by overcoming the kinetic limitation using a reduced deposition rate or (2) by preventing the formation of foreign phase inclusions, which interrupt the diffusion flux. The latter stems from the fact that the SD in bulk polycrystals can be activated at temperatures as low as 400 °C (ref. 7) and the most probable structural defects in the VO₂–TiO₂ system are related to VO₂ off-stoichiometry. Thus, in our case, we can assign the necessity for higher temperatures to the unbalanced cation–anion stoichiometry, owing to the partial replacement of V by Ti. Indeed, the degree of V oxidation may be reduced because a higher oxygen consumption is required for the utilization of organic residues³⁶ for the Ti precursor, Ti(O-i-Pr)₂(TMHD)₂, which contains four organic ligands, in contrast with only two ligands in the V-precursor, OV(acac)₂. According to the Ellingham diagrams, a large difference in the formation energies favors TiO₂ stabilization over VO₂ in the case of an oxygen deficiency.

Through optical measurements, we revealed a simultaneous improvement in several thermochromic parameters. These enhancements encompass the reduction of T_MI and ΔT_MI, as well as the presence of the nanothermochromic effect due to more transparent Ti-rich layers. Well-established strategies are often effective in enhancing a specific parameter only, however, this improvement generally comes at the cost of degradation in the others.⁴⁶ For instance, the incorporation of doping elements, particularly W, is undoubtedly an effective strategy for reducing T_MI to the desired range of 20 ÷ 25 °C, but it results in a broader transition. Similarly, nanothermochromism is a superior way for increasing luminous transmittance up to the required values of Tr_lum > 60%, but this method also fails to address the issue of switching behaviour. By comparing our proposed approach with the aforementioned strategies, we can deduce that SD-assisted formation of strained (V,Ti)O₂-based nanocomposites is a promising method for the development of thermochromic coatings. While thermochromic parameters (T_MI = 53 °C, ΔTr_sol = 14%, Tr_lum = 29%) achieved in this study are still quantitatively insufficient, the demonstrated potential to simultaneously enhance several crucial factors, such as MIT temperature, luminous transmittance, and switching behavior, through a single strategy provides a promising foundation for future research.

The process of spinodal decomposition encounters a notable restriction in the thickness and composition of the resulting layers due to the necessity for preserving initial V_1−xTi_xO₂ composition near x = 0.35. This constraint imposes limitations on the potential strain-induced enhancements. Nonetheless, our polycrystalline films have not yet reached the same level of decomposition as one achieved in bulk materials. In order to lower the T_MI, it is necessary to achieve a higher degree of compositional modulation during SD-process. We believe that by increasing the compositional modulation and using a heterostrain detached from the substrate, the T_MI can be downshifted to the required temperatures. The sharpness and width of the NIR transmittance switching can also be advanced by increasing the compressive strain in the V-rich layers. If the nanothermochromic increase of Tr_lum by the Ti-rich layers will be insufficient due to limitations on their maximum thickness, a further advance could be achieved by adding a third oxide component, such as ZnO, which is transparent and structurally unmixable with the VO₂–TiO₂ system. The interrelation between the structure and composition-dependent properties of (V,Ti)O₂-based nanocomposites is quite complex, and to fulfill all requirements for thermochromic coatings simultaneously, experimental work on nanocomposite metamaterials will strongly benefit from a predictive numerical simulation of their optical properties.

4 Conclusion

Overall, using spinodal decomposition, we demonstrated the formation of strained superlattice-like nanocomposites in thin polycrystalline films of V_0.65Ti_0.35O₂. Starting during growth with the formation of atomic-scale disordered V- and Ti-rich layers, spinodal decomposition is completed by subsequent post-growth annealing, producing sharp heterointerfaces between the layers and creating a superlattice-like nanocomposite inside crystalline grains. Elastically coupled heterointerfaces between V- and Ti-rich layers generate lattice misfit strains, which compress the VO₂-rich phase along the c-axis of the rutile structure and yield a strain-enhanced thermochromism with a simultaneous reduction in the temperature of the MI transition and narrowing of the hysteresis loop. In addition, the layers of the TiO₂-rich phase promote luminous transmittance, according to the nanothermochromic concept. However, to meet the strict requirements for thermochromic coatings quantitatively, further improvements must be made based on thorough optimization of the entire fabrication process.

Author contributions

A. B. conceived of the original idea and drafted the manuscript. A. B. and O. S. designed the thin film deposition system. O. S. fabricated the samples. O. S. and A. B. carried out the characterizations of the samples. V. R. performed TEM analysis. S. V. carried out XRD analysis. J. W. performed Raman spectroscopy. K. S. performed optical measurements. A. B., O. S., and V. M. contributed to the interpretation of the results. V. M. contributed to the final version of the manuscript and supervised the project. All authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding by the Deutsche Forschungsgemeinschaft via the CRC 1073, project Z02, by STCU project no. 6133, and by NARD(ANCD) project no. 20.80009.5007.12 and the use of equipment in the “Collaborative Laboratory and User Facility for Electron Microscopy” (CLUE) are gratefully acknowledged.

References

1. G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
2. Z. Chai, A. Childress and A. A. Busnaina, ACS Nano, 2022, 16, 17641–17686.
3. J. W. Cahn, Acta Metall., 1961, 9, 795–801.
4. P. Venezuela, J. Tersoff, J. A. Floro, E. Chason, D. M. Follstaedt, F. Liu and M. G. Lagally, Nature, 1999, 397, 678–681.
5. S. Gallardo-Hernández, I. Martinez-Velis, M. Ramirez-Lopez, Y. Kudriatsev, A. Escobosa-Echavarria, S. L. Morelhao and M. Lopez-Lopez, Appl. Phys. Lett., 2013, 103, 192113.
6. Y. Horibe, M. Ishimatsu, S. Takeyama, S. Mori, M. Kudo, M. Auchi, M. Tanaka and Y. Murakami, Appl. Phys. Lett., 2019, 115, 232401.
7. Z. Hiroi, H. Hayamizu, T. Yoshida, Y. Muraoka, Y. Okamoto, J. Yamaura and Y. Ueda, Chem. Mater., 2013, 25, 2202–2210.
8. M. Ogata, K. Kadowaki, M. Ijiri, Y. Takemoto, K. Terashima, T. Wakita, T. Yokoya and Y. Muraoka, J. Eur. Ceram. Soc., 2017, 37, 3177–3183.
9. Z. Hiroi, T. Yoshida, J. Yamaura and Y. Okamoto, APL Mater., 2015, 3, 062508.
10. Z. Chen, X. Wang, Y. Qi, S. Yang, J. A. N. T. Soares, B. A. Apgar, R. Gao, R. Xu, Y. Lee, X. Zhang, J. Yao and L. W. Martin, ACS Nano, 2016, 10, 10237–10244.
11. Y. Muraoka, F. Yoshii, T. Fukuda, Y. Manabe, M. Yasuno, Y. Takemoto, K. Terashima, T. Wakita and T. Yokoya, Thin Solid Films, 2020, 698, 137854.
12. Y. Zheng, Z. Chen, H. Lu, Y. Cheng, X. Chen, Y. He and Z. Zhang, Nanoscale, 2021, 13, 7783–7791.
13. T. Fukuda, Y. Takemoto, T. Wakita, T. Yokoya and Y. Muraoka, Thin Solid Films, 2022, 751, 139210.
14. G. Sun, H. Zhou, X. Cao, R. Li, M. Tazawa, M. Okada and P. Jin, ACS Appl. Mater. Interfaces, 2016, 8, 7054–7059.
15. G. Sun, X. Cao, Y. Yue, X. Gao, S. Long, N. Li, R. Li, H. Luo and P. Jin, Sci. Rep., 2018, 8, 5342.
16. Y. Matsuura, F. Yoshii, T. Otsuka, K. Kadowaki, M. Ijiri, Y. Takemoto, K. Terashima, T. Wakita, T. Yokoya and Y. Muraoka, J. Eur. Ceram. Soc., 2018, 38, 5043–5050.
17. Y. Muraoka, K. Takeda, Y. Takemoto, T. Wakita and T. Yokoya, Thin Solid Films, 2023, 769, 139749.
18. J. Park, G.-Y. Kim, K. Song, S.-Y. Choi and J. Son, NPG Asia Mater., 2019, 11, 1868.
19. F. J. Morin, Phys. Rev. Lett., 1959, 3, 34–36.
20. K. Liu, S. Lee, S. Yang, O. Delaire and J. Wu, Mater. Today, 2018, 21, 875–896.
21. S. Babulanam, T. Eriksson, G. Niklasson and C. Granqvist, Sol. Energy Mater., 1987, 16, 347–363.
22. J. Houska, J. Appl. Phys., 2022, 131, 110901.
23. M. E. A. Warwick, I. Ridley and R. Binions, Open J. Energy Effic., 2013, 02, 75–88.
24. X. Geng, T. Chang, J. Fan, Y. Wang, X. Wang, Y. Sun, P. Selvarajan, C. Liu, C.-H. Lin, X. Wang, J. Yang, Z. Cheng, K. Kalantar-Zadeh, X. Cao, D. Wang, A. Vinu, J. Yi and T. Wu, ACS Appl. Mater. Interfaces, 2022, 14, 19736–19746.
25. S.-Y. Li, G. A. Niklasson and C. G. Granqvist, J. Appl. Phys., 2010, 108, 063525.
26. T. Paik, S.-H. Hong, E. A. Gaulding, H. Caglayan, T. R. Gordon, N. Engheta, C. R. Kagan and C. B. Murray, ACS Nano, 2014, 8, 797–806.
27. Q. Hao, W. Li, H. Xu, J. Wang, Y. Yin, H. Wang, L. Ma, F. Ma, X. Jiang, O. G. Schmidt and P. K. Chu, Adv. Mater., 2018, 30, 1705421.
28. N. B. Aetukuri, A. X. Gray, M. Drouard, M. Cossale, L. Gao, A. H. Reid, R. Kukreja, H. Ohldag, C. A. Jenkins, E. Arenholz, K. P. Roche, H. A. Dürr, M. G. Samant and S. S. P. Parkin, Nat. Phys., 2013, 9, 661–666.
29. B. Zhi, G. Gao, X. Tan, P. Chen, L. Wang, S. Jin and W. Wu, Mater. Res. Express, 2014, 1, 046402.
30. Y. Muraoka and Z. Hiroi, Appl. Phys. Lett., 2002, 80, 583–585.
31. Y. Yang, X. Mao, Y. Yao, H. Huang, Y. Lu, L. Luo, X. Zhang, G. Yin, T. Yang and X. Gao, J. Appl. Phys., 2019, 125, 082508.
32. A. Belenchuk, O. Shapoval, V. Roddatis, V. Bruchmann-Bamberg, K. Samwer and V. Moshnyaga, Appl. Phys. Lett., 2016, 109, 232405.
33. S. Stepanov, J. Appl. Crystallogr., 2021, 54, 1530–1534.
34. H. A. Wriedt, Bull. Alloy Phase Diagrams, 1989, 10, 271–277.
35. K. Shibuya and A. Sawa, AIP Adv., 2015, 5, 107118.
36. N. Li, Y.-H. A. Wang, M. N. Iliev, T. M. Klein and A. Gupta, Chem. Vap. Deposition, 2011, 17, 261–269.
37. I. Daruka and J. Tersoff, Phys. Rev. Lett., 2005, 95, 076102.
38. I. K. Schuller, Phys. Rev. Lett., 1980, 44, 1597–1600.
39. H. Ma, J. Yang, Y. Dai, Y. Zhang, B. Lu and G. Ma, Appl. Surf. Sci., 2007, 253, 7497–7500.
40. K. Shibuya and A. Sawa, J. Appl. Phys., 2017, 122, 015307.
41. Z. Zhang, Y. Gao, L. Kang, J. Du and H. Luo, J. Phys. Chem. C, 2010, 114, 22214–22220.
42. E. Liarokapis, Phys. C, 2000, 341–348, 2185–2188.
43. M. N. Iliev, V. G. Hadjiev and V. G. Ivanov, J. Raman Spectrosc., 1996, 27, 333–342.
44. H.-C. Ho, Y.-C. Lai, K. Chen, T. D. Dao, C.-H. Hsueh and T. Nagao, Appl. Surf. Sci., 2019, 495, 143436.
45. Y. Wu, L. Fan, Q. Liu, S. Chen, W. Huang, F. Chen, G. Liao, C. Zou and Z. Wu, Sci. Rep., 2015, 5, 9328.
46. Y. Cui, Y. Ke, C. Liu, Z. Chen, N. Wang, L. Zhang, Y. Zhou, S. Wang, Y. Gao and Y. Long, Joule, 2018, 2, 1707–1746.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr01350b

‡ Present address: GFZ German Research Centre for Geosciences, Telegrafenberg D-14473 Potsdam, Germany.

§ Present address: IFW Dresden, Helmholtzstraße 20, D-01069 Dresden, Germany.

---