Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sequence-dependent folding of monolayered DNA origami domains†
Sabrina
Gambietz
,
Lena J.
Stenke
and
Barbara
Saccà
 *
*
Center of Medical Biotechnology (ZMB) and Center for Nanointegration Duisburg Essen (CENIDE), University Duisburg-Essen, 45141 Essen, Germany. E-mail: barbara.sacca@uni-due.de
First published on 11th July 2023
Abstract
Current models of DNA origami folding can explain the yield of the assembly process and the isomerization of the structure upon the application of mechanical forces. Nevertheless, the role of the sequence in this conformational transformation is still unclear. In this work, we address this question by performing a systematic thermodynamic study of three origami domains that have an identical design but different sequence contents. By comparing the thermal stability of the domains in various settings and measuring the extent of isomerization at equilibrium (both at the global and single-molecule levels), we extract the contribution to folding given by the sequence and propose thermal criton maps of the isomers to rationalize our findings. Our data contribute to a deeper understanding of DNA origami assembly by considering both the topological- and thermal-dependent properties of the sites of initial folding. While the former are responsible for the mechanical aspects of the process, the latter justify the observed sequence-dependent conformational preferences, which appear evident in simple origami structures but remain typically undisclosed in large and more intricate architectures.
Introduction
The DNA origami method relies on the folding of a long single-stranded DNA scaffold into a pre-designed shape using hundreds of complementary short staple strands.1 This method, first established in 2006, rapidly evolved in terms of the complexity of the structures attainable and their applications,2–4 but the molecular mechanisms underlying the assembly process became increasingly clearer only many years later.5–17 Currently, the most comprehensive and widely accepted description of DNA origami folding founds on the concept of cooperativity.5–7,10 According to this model, the formation of a DNA origami structure is cooperatively driven by three contributions: the first term originates from the progressive reduction in the entropic penalty associated with the formation of scaffold loops. When a staple binds to discontinuous portions of the scaffold, a loop is formed and the number of configurational microstates of the system, and thus its entropy, decreases. Concurrently, the distances between the domains of the remaining unbound portions of the scaffold become shorter, lowering the entropic cost for binding of the next staples.9 A second contribution is given by base stacking. Once adjacent DNA helices stack, they align, and by doing so, they facilitate the binding and coaxial stacking of the incoming staples.15 Finally, base hybridization contributes to the assembly process by guiding the initial inter-molecular recognition between a portion of a staple and its complementary sequence in the scaffold. Binding of the remaining staple sub-sequences occurs intra-molecularly and is favored by the increased spatial proximity of the interacting species.11 Hence, once the initial binding events take place, the cooperative assembly of a DNA origami is driven by entropic and energetic contributions of progressively lower cost, with the nucleation sites most probably occurring in the regions of the nascent structure that promote the formation of shorter scaffold loops (entropically favored) and/or the hybridization of longer staple/scaffold stretches (enthalpically favored). This model has been successfully applied to explain, and in some cases even to predict, the efficiency of the assembly process, that is, the yield of the intended structure over misfolded or partially assembled by-products. This helped, for example, to rationalize not only the impact of staple design on the success of the assembly,18,19 but also the effect of buffer composition, type and concentration of ions, as well as temperature ramps, on the stability and reconfigurability of DNA origami structures.20,21 In all these cases, the outcome of the assembly is either a correctly or a non-correctly folded form, with the well-formed shape being the one expected from the design. A special case is represented by monolayered DNA origami structures, which are composed of a regular pattern of intertwined Holliday junctions (HJs). These structures typically fold in quantitative yields; however, they can appear in two distinct and well-folded conformations (folds). This peculiar phenomenon, i.e., the formation of two distinct origami conformers from the same set of staples, was first observed in small origami tubular structures22 and is reminiscent of the multifarious assembly displayed by natural biopolymers.23 A few studies, including ours, have shown that these conformers are obtained one from the other by exchanging the strands that stack at the crossovers of the constituent HJs.16,17,24 Whereas in one conformer (here referred to as the canonical form, can), antiparallel stretches of scaffold strands are kept in place by staple crossovers, in its isomerized form (here called iso), antiparallel stretches of staples are joined by scaffold crossovers, resulting in two shapes of equal area but different aspect ratios (Fig. 1a). Previous studies have shown that the interconversion between these conformers can be triggered by the addition of strands or the application of mechanical forces at the edges of the structure, where the scaffold inverts its direction and forms loops.16,24,25 The topological strain generated at these sites initiates a local rearrangement of HJs, which is allosterically propagated to the entire architecture. Interestingly, the sequence of the strands that trigger or undergo a transformation was either not investigated or shown to be irrelevant, suggesting that the role of the nucleobase sequence in DNA origami folding is minimal, as indeed observed for more complex origami constructs.26 Conversely, we have recently shown that, at equilibrium, the ratio between the two conformers of a monolayered DNA origami structure is strongly affected, yet in a complicated and still unknown fashion, by the nucleobase composition of the staple strands, even at sites that are distant from the edges.17 A recent study from others27 has confirmed the important role of the sequence in the conformational preference of immobile HJs, revealing the structural origin of this phenomenon.28–37 Nevertheless, in agreement with our observations, ordered assemblies of HJs have shown a long-range sequence-to-structure relationship, which is still difficult to decipher. These data suggest that the sequence of the strands forming a regular pattern of HJs, that is, a simple monolayered DNA origami domain, may indeed affect the folding path, resulting in the preferential assembly of one conformational species. This sequence-to-structure relationship is therefore an intrinsic property of DNA origami domains, which may remain undisclosed during the folding of larger and more intricate three-dimensional structures.In this work, we address this question by investigating the folding of three DNA origami domains that have an identical design (and thus identical topology- and entropy-related features) but different staple sequences (i.e. distinct base stacking- and hybridization-dependent properties). Our structures are sufficiently small (ca. 2.400 bp) to simplify the problem but large enough to undergo cooperative assembly and are therefore ideal model systems to tackle the question of sequence-dependent conformational preference in DNA origami structures. We performed a systematic and comparative thermodynamic study of these constructs in various design scenarios and used atomic force microscopy to determine the ratio between the two conformers at equilibrium. We then used optical tweezers to stretch individual origami domains of different sequence contents at identical positions and confirmed that the mechanical response of the structure strongly depends on the thermal stability of the microregion to which the force is applied, i.e. ultimately on its sequence content.
Given the numerous sequence permutations of individual domains, attempting to analyze the impact of these mutations using traditional methods becomes not only time-consuming but also practically impossible. To overcome this challenge, we introduced thermal criton maps as qualitative tools for integrating two types of information embedded in the design of monolayered DNA origami domains. The first type of information is provided by the routing of the scaffold and describes the topological/mechanical contributions to folding. The second type of information is given by the sequence of the staples, which mostly govern the thermal-dependent features of the assembly process. Accordingly, we define topological and thermal nucleation sites (NS) as the possible sites of initial folding. Both types of NS may simultaneously occur and possibly compete in the earliest phase of the assembly, with the former typically initiating at scaffold loops and the latter originating in the staple/scaffold duplex regions of high thermal stability. When scaffold loops are mechanically strained, the formation of thermal NS in the regions of the nascent structure that are far from (or at) the scaffold loops results in preferential folding, respectively, in the can (or iso) conformer. Although in all intermediate scenarios, the ratio of conformational states is still difficult to predict, our study merges diverse experimental observations into a unified vision and adds new insights into the complexity of the events occurring during DNA origami assembly.
Results and discussion
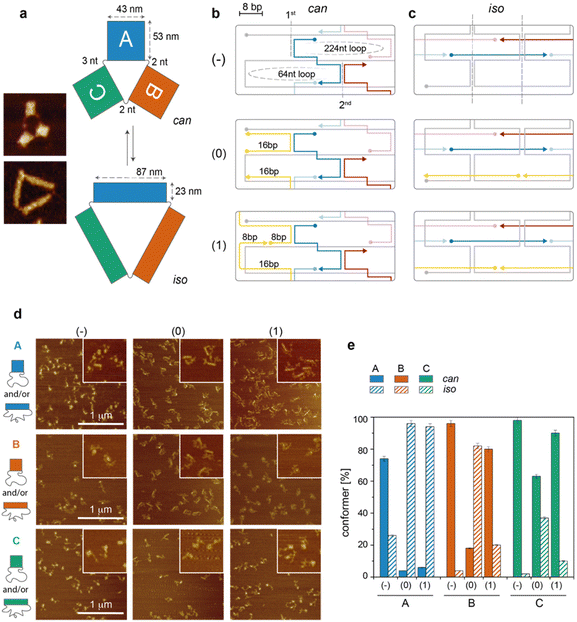
The DNA origami structure under study relies on a previous work from us:17 briefly, a long single-stranded DNA is folded into three monolayered origami domains (called A, B and C) using an identical design of staples. Since the staples of each domain hybridize to different portions of the scaffold, the three sets of staples, associated with A, B and C, respectively, are different (Fig. 1a). Moreover, the domains are physically separated by two or three unpaired scaffold bases, allowing the assembly and manipulation of each domain individually. Each domain has been prepared in three versions (indicated as −, 0 and 1), which differ in the extent of mechanical stress at the edges of the structure, leading to a total of nine possible constructs (Fig. 1b and c). Each construct is partitioned between two conformers, can and iso (Fig. 1a). The can conformer has a square-like shape (43 nm × 53 nm) while the iso conformer has approximatively the same area but a different aspect ratio, resulting in a rectangular shape (87 nm × 23 nm). In our previous investigation, we reported the existence of a sequence-dependent conformational preference. Here, we aimed at understanding the reason for this phenomenon. We thus performed a systematic and comparative study of all constructs at various levels of molecular detail and correlated the thermodynamic and single-molecule data obtained for each construct with the fraction of can and iso forms at equilibrium, as revealed by atomic force microscopy (AFM, Fig. 1d and e).The cooperativity model applied to individual DNA origami domains
We first analyzed the folding of our structures according to a simplified version of the cooperativity model for planar and small DNA origami domains.10 We then compared our expectations with the experimental data obtained and enlarged the model to make it more general and capable of explaining the observed isomerization phenomenon. Briefly, the cooperative model of DNA origami folding states that the free energy of structure formation (ΔGfold) depends mainly on three contributions according to eqn (1):| ΔGfold = ΔGloop + ΔGstack + ΔGhybr | (1) |
The free energy of loop formation (ΔGloop) contains an entropic (ΔSloop) contribution and an enthalpic (ΔHloop) contribution that scale with the length of the loop in an opposite fashion. Indeed, while the formation of shorter loops is less entropically disfavoured, the elastic energy cost for bending them becomes prohibitively high, especially if the loops are partially bound to staples, thus increasing their persistence length. ΔGstack and ΔGhybr are the energetic contributions to folding due, respectively, to base stacking at the crossovers of adjacent HJs and base hybridization between the staples and their complementary stretches in the scaffold.
To summarize, the three edge designs of an individual domain should feature almost identical ΔGstack and ΔGhybr contributions and differ mostly in the ΔGloop term, with the latter including an entropic term dependent on the length of the enclosed scaffold loops and an elastic term related to the flexibility of these loops. While the length of the scaffold loops is identical to the three edge designs, the unfavourable elastic term in the (0) and (1) constructs, when compared to the (−) analogues, is supposed to hamper full hybridization and bending of the staples at the edges of the can form. This may presumably trigger the progressive reconfiguration of the nascent structure in the alternative iso form (Fig. 1c). According to this hypothesis, we expect to observe, for each individual DNA origami domain, an extent of can-to-iso isomerization that scales with the following order of edge type: (−) < (1) ≤ (0).
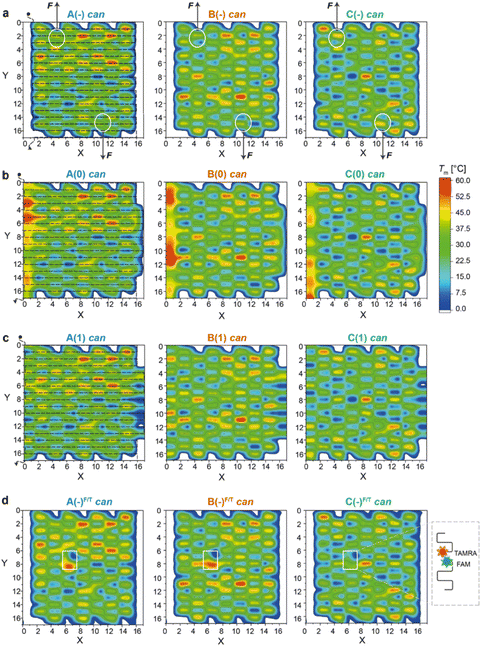 | ||
| Fig. 2 Thermal maps of DNA origami domains (in the can state). Thermal maps were generated considering the longest and continuous linear duplexes (critons) of each DNA origami domain, either in the absence of edges (a) or in the presence of edges of type 0 (b) or type 1 (c). Insertion of FAM- and TAMRA-labelled staples slightly changes the length and sequence of critons in the central region of each domain (d). Critons are identified by a (x,y,z) coordinate, which indicates the position (x) of the criton along the helix (y) with a color-coded Tm (z). The routing of the scaffold in the can form (dashed line, left panels) starts at position (0,0) and terminates at position (0,17). FRET reporters were located at positions (7,8) and (6,7) of the can form (white boxes in d; FRET reporters of the iso form are illustrated in Fig. S15†). Staple strands at positions (5,1) and (11,16) were prolonged with DNA handles for trapping the can form of the A(−), B(−) and C(−) domains between two beads of a dual optical tweezer and their response to the application of a mechanical force was investigated (white circles in (a)). | ||
Thermal vs. topological nucleation sites
Thermal maps were generated by dissecting the origami design into “critons”. A criton is here defined as a continuous and linear duplex of maximal length, i.e., the portion of each double helix of the origami domain that is not interrupted by nicks, turns, or crossovers. Accordingly, in both the can and iso forms, each staple of the core is composed of three critons, respectively 8, 16, and 8 bp long (Fig. S1b and S2b†). Left-side edges of type 0, in both conformational states, are instead composed of two critons of equal length (16 bp long; Fig. S3†), while edges of type 1 are made of three critons (8, 16 and 8 bp long) in the can form and two critons (24 and 8 bp long) in the iso form (Fig. S4†). The melting temperature (Tm) of every criton was estimated using the OligoAnalyzer™ tool (available online at idtdna.com). The thermal maps of each fold were generated by assigning a Tm value to each criton at position x along the y helix, with Tm indicated by a color-coded scale along the z-axis. In this way, every origami fold is represented by a unique set of critons, with a criton being the elementary unit of the map identified by a (x,y,z) spatial coordinate.By tracing the routing of the scaffold on top of each thermal map, the position of high Tm critons with respect to the edges of the structure can be easily visualized (Fig. 2a–c and Fig. S5† for the corresponding iso forms). Regions of thermally stable critons (in red) are supposed to form in the initial phase of the assembly, when the temperature is still high, and will be here referred to as thermal nucleation sites. Our structures are too small to prove (for example, by AFM) that these sites are indeed the first to form; however, our assumption is justified by previous studies on larger DNA origami structures.8,11 These studies clearly demonstrated that regions of high thermal stability are the first to assemble or the last to disassemble. Conversely, topological NS can be idealized as nuclei of assembly whereby staples link together portions of the scaffold that are near each other. These regions typically correspond to the edges of the structure, where the scaffold inverts its direction and forms loops.9 In our design, the edges suffer from a high mechanical strain, which is supposed to trigger the conformational transition of the entire domain from the intended can to the alternative iso form.17 Thus, in our vision, while thermal NS are mostly governed by enthalpic factors, topological NS are mostly entropically driven. It is their combination (and compromise) that defines the preferential assembly path.
As shown in Fig. 2a (left panel), the thermal map of domain A(−) features several sparse critons with Tm >50 °C (red spots in the region defined by 8 < x < 16 and 0 < y < 6), with some high Tm critons touching the left-side edges of the structure (x = 3). The number and density of thermal NS decrease in domain B(−) and are drastically reduced in C(−) (middle and right panel, respectively), with the latter showing only one localized high Tm criton in the center of the core (x,y = 9,8) and mostly low Tm critons in the rest of the structure.
The addition of edge staples leads to the appearance of high Tm regions at the left-side scaffold loops, particularly for constructs A(0) and B(0) (Fig. 2b, left and middle panels), whereas a lower effect is observed for type (1) constructs (Fig. 2c). According to our hypothesis, the co-localization of thermal and topological NS, i.e., the formation of mechanically strained edges at the beginning of the assembly process, should favor the iso state to escape the strain accumulated during folding. Hence, by extending the cooperativity model of DNA origami folding with our concept of thermal and topological nucleation sites, we expect to find a fraction of isomerized structures that – for a given domain – is larger for the edges of type 0, when compared to the edges of type 1 and no-edges, with domain A displaying the highest extent of the iso state and domain C mostly retaining the can state.
AFM imaging of equilibrium structures
For each construct, the distribution of can vs. iso conformers, upon equilibration at 20 °C, was estimated by AFM, counting a statistically significant number of structures (Fig. 1d, e and Tables S1–S4†). We observed that the extent of isomerization notably increased in the presence of edges of type 0, particularly for domains A and B (96% and 82% isomerization, blue and orange striped bars, respectively, in Fig. 1e), with domain C being instead the most resilient structure in the can state (37% isomerization, green striped bars). The formation of edges of type 1 resulted in strong isomerization only for domain A (94% iso), with all other constructs displaying less than 20% iso forms. The surprisingly high extent of iso forms in A(1) might be due to the vicinity of several high Tm critons in the top half of the can structure. This would reinforce the triggering effect of edge staples through the cooperative participation of nearby regions. In general, the AFM results suggest that the extent of isomerization significantly scales with the energetic cost of loop formation (no edges < edges type 1 < edges type 0; cfr. striped bars in Fig. 1e) and with the presence of thermally stable critons at these sites (C < B < A; cfr. striped bars in Fig. 1e). This is in perfect match with our expectations from the application of the cooperativity model described above, additionally refined with the thermal maps of the domains.Of special note is the presence of a small fraction of iso state (26%) in domain A(−). As mentioned earlier, the thermal map of A(−) displays a set of critons (at x = 3) that are supposed to affect the initial phase of the assembly process (Tm >46 °C). These critons belong to staples that are located next to the scaffold turns and, even in the absence of edge staples, may moderately suffer from mechanical strain, explaining the partial isomerization of this domain. The same set of staples in B(−) and C(−) shows instead only one or two critons of moderate Tm with all other critons characterized by low Tm values, suggesting a late involvement of these staples in the assembly process and a growing front that propagates from regions of the structure far from the iso-triggering edges. In agreement with this idea, the extent of iso forms in B(−) and C(−) is almost negligible (Fig. 1e). From the AFM imaging data, we conclude that the sequence-dependent isomerization of monolayered DNA origami domains can be satisfactorily explained by extending the cooperativity model of origami folding with the notions obtained by the application of the thermal criton map of the structure.
Global thermal properties of DNA origami domains
We then investigated the folding/unfolding of the origami constructs at the global level. For this purpose, a SYBR Green solution was added to a mixture of origami strands, as previously described,38 and the assembly/disassembly of each individual domain (and their totality) was monitored by measuring the intensity of the fluorescence signal emitted by a DNA staining dye upon a cooling/heating cycle at ± 0.08 °C min−1. The normalized thermal profiles obtained for the nine origami constructs are reported in Fig. 3 (for the entire origami structure in the three edge versions see Fig. S6 and Table S5†). As expected, the data show variable extents of thermal hysteresis in all cases, with the folding curves (blue lines) being shifted to slightly lower temperatures than the corresponding unfolding curves (red lines). The first derivatives of the thermal data (dθ/dT, bottom panels in Fig. 3) better evidence the thermal features of the process, with each peak indicating the folding/unfolding of a region of the domain and the steepness of the peak proportional to the degree of cooperativity of the transition. In the following sections, we focus our analysis on the differential data for the cooling profiles (blue lines), since these are more truly representative of the process of interest, that is, the assembly and folding of several strands into one or two origami conformer(s).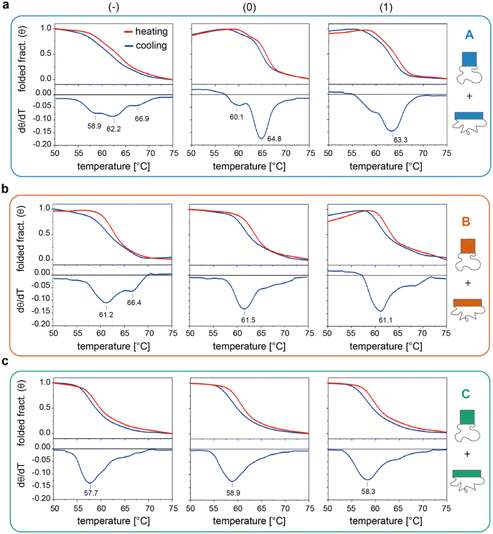 | ||
| Fig. 3 Global thermal properties of DNA origami domains. Folding and unfolding of the individual DNA origami domains (a to c, for A, B and C, respectively) in all three possible edge designs (−, 0 and 1, left to right panels) were monitored upon cooling (blue lines) and heating (red lines) a solution of scaffold and staples at −/+0.08 °C min−1. The solution was pre-stained with SYBR Green and the extent of folding was evaluated by measuring the change in the fluorescence emission signal of the dye over temperature, as previously reported.38 First derivatives of cooling processes (lower panels) were used to compare the nine constructs with respect to their folding features. Note that the method cannot distinguish between the two conformational species of each domain and reflects the global thermal behavior of the entire structure. Thermal curves shown are the average of five replicates. | ||
The profiles of the constructs lacking the edge staples (Fig. 3a–c, left panels) indicate that although folding of C(−) proceeds through one broad transition at about 58 °C, the formation of B(−) features two transitions centered at ca. 61 °C and 66 °C, while domain A(−) is characterized by a complex thermal profile with multiple transitions occurring between 59 °C and 67 °C (Tables S1–S4†). Interestingly, as shown in Fig. 2a, C(−) features an isolated high Tm criton (>55 °C) located in the center of the structure, while two to three regions of high Tm can be identified in B(−) (top and middle of the domain), with A(−) characterized instead by a larger distribution of high and moderate Tm critons sparsely located on the top half of the structure. Thus, to a first approximation, it appears that the number and stability of the thermal transitions of a DNA origami domain are related to the number and stability of the sub-domains discernible in the corresponding thermal map.
The situation becomes more complicated in the presence of edge staples (Fig. 3a–c, middle and right panels). Indeed, while domains C(0) and C(1) still show a single and relatively broad peak at ca. 58 °C (Fig. 3c), the thermal profiles of B(0) and B(1) slightly change, despite maintaining a major transition at ca. 61 °C (Fig. 3b). In contrast, the addition of edge staples results in a complete reshape of the thermal profile of domain A, with the appearance of a cooperative transition at high Tm (ca. 65 °C and 63 °C; Fig. 3a for (0) and (1) constructs, respectively). We attribute this change to the formation of the iso form in the quasi totality of the structures (Fig. 1e, blue bars). Finally, for a given edge design, the effect of sequence content on the global thermal stability of the structure consistently follows the order C < B < A, in full agreement with our expectations.
Thermal properties of individual DNA origami conformers
We then applied the FRET strategy reported in our previous study17 to monitor the assembly/disassembly of the conformers associated with each origami domain (Fig. S7†). Since each domain can appear in two conformational states, the nine constructs analyzed in this study (3 domains with 3 edge types) may give rise to a maximum of 18 distinct folds. FRET experiments were performed by labelling the DNA origami domain of interest, with the other two domains being folded but unlabelled. For domain A, we demonstrated that the melting/cooling behaviour is not significantly affected by the folding/unfolding of the other two domains (Table S2†), suggesting that each domain can be analyzed as an independent structure. Measurements were performed in triplicate at four different temperature scan rates (ranging between ± 0.08 °C min−1 and ± 2.6 °C min−1) for a total of more than 120 thermal profiles (Fig. S8–S14†). Each domain in the can form was labelled at positions (7,8) and (6,7) with a FAM and TAMRA fluorophore, respectively, while positions (12,2) and (12,3) were chosen to label the corresponding iso forms (rectangular white insets in Fig. 2d and Fig. S15†). The averaged FRET thermal profiles of domains A(−), B(−) and C(−), all in the can form and acquired at 0.08 °C min−1, are reported in Fig. 4a to c, respectively. The extent of hysteresis and the Tm values for the cooling and heating process of all constructs at the same scan rate are given in Fig. 4d and e, respectively.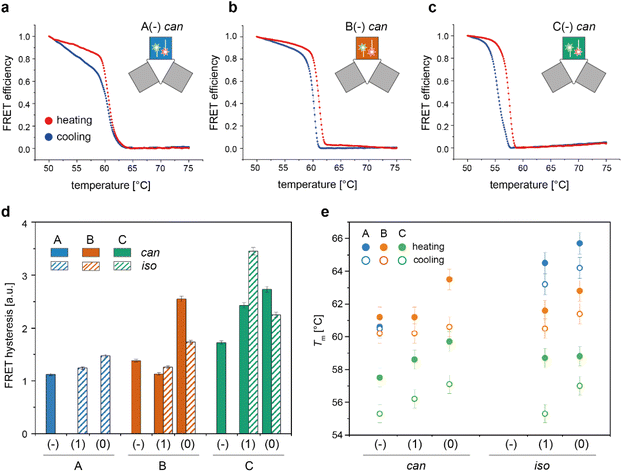 | ||
| Fig. 4 Thermal properties of individual DNA origami conformers. Folding and unfolding of the can and iso states of each DNA origami domain in all possible edge versions were monitored by bulk FRET spectroscopy using FRET reporters specific for each conformational state, as previously described.17 (a–c) Representative normalized thermal profiles of the no-edge domains in the can form. Thermal curves shown are the average of at least four replicates. (d) The extent of thermal hysteresis was evaluated by measuring the area included between the heating (red line) and cooling (blue line) profiles for both the can (plain bars) and iso states (striped bars) of each domain (blue, orange and green bars, for A, B and C domains, respectively). A(−) in the iso state was not considered due to its anomalous FRET thermal profile (Fig. S8 and S9†). (e) Melting temperature (Tm) of each conformer, evaluated as the temperature value for which the first derivative of the heating (full circles) or cooling (empty circles) profiles assumes a maximum or a minimum, respectively. Error bars indicate standard deviations and are within 1% of the average value. | ||
A closer look at the FRET data enabled to identify the following aspects: first, appreciable FRET signals (at least >5% of the maximal FRET value observed) were visible only for those species that were significantly populated at equilibrium, in good agreement with the AFM results. Accordingly, no signal was monitored for A(0) and A(1) in the can state, and iso forms were not measurable for the domains lacking the edge staples, with the exception of A(−), which was indeed present in about 26% of the end products (Fig. S8 and S9†). Second, the assembly process was highly cooperative but irreversible in all cases, with the degree of hysteresis increasing from A to B to C, independently of the edge design and conformational state of the origami structure (blue, orange, and green bars in Fig. 4d and Fig. S14†). Again, this result may be well understood by observing the thermal maps of the structures. In domain A(−), the FRET dyes are located in a region of the structure which is densely populated by high Tm critons, some of them located nearby the strained scaffold loops (Fig. 2d, left panel; Fig. S15† for the corresponding map of the iso form). Folding of this region is therefore supposed to occur at high temperatures (blue dots Fig. 4e) and in a cooperative fashion (plain blue bars in Fig. 4d), with the concurrent and competitive initiation of both the can and iso assembly routes probably leading to an anomalous biphasic profile observed in the FRET experiments (Fig. S8 and S9†).
Conversely, domains B and C are labeled in isolated regions of moderate and low thermal stability, respectively (Fig. 2d, middle and right panels). Hence, their formation is expected to occur at comparatively lower temperatures and over a wider interval, resulting in FRET curves with lower Tm (orange and green dots in Fig. 4e) and a larger degree of hysteresis than the corresponding A domains with the same edge design (orange and green bars in Fig. 4d). A last feature of our FRET data is that the values of Tm consistently follow the order C < B < A for the same edge design, with the thermal stability of different edge versions of the same domain following the order (−) < (1) ≤ (0) in both the can and iso states (Fig. 4e). These data are in good agreement with the conclusions drawn by global thermal analysis and indicate that, although FRET reporters are typically indicative of the structural properties of the surrounding region, the small dimensions of our DNA origami domains and their compactness allow for sensing the conformational change of the entire construct.
Altogether, our thermal data indicate that many aspects of DNA origami folding, including the conformational preference of small domains, may be better understood through a combined approach that merges considerations from the cooperativity model of origami assembly with the information gathered by the thermal criton maps of the structures.
Single-molecule force measurements
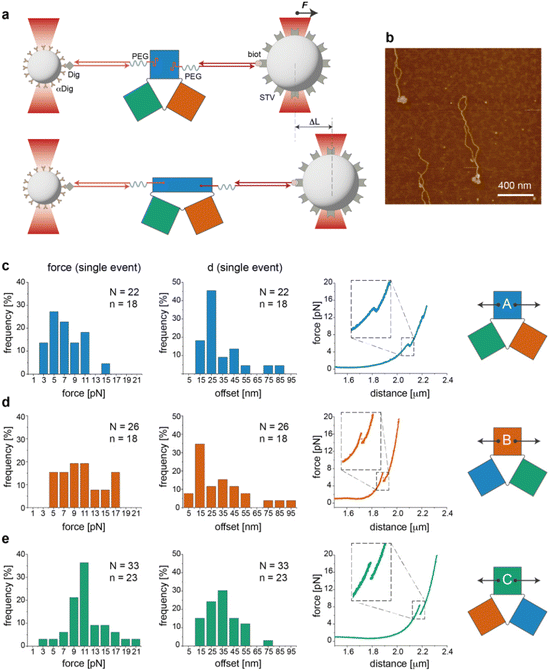
We then performed a last set of experiments to verify whether the sequence-dependent information encoded in the thermal maps may explain the different mechanical responses of topologically identical origami domains exposed to the same local forces. This may offer a way to interpret the observed conformational preferences as a consequence of sequence-dependent mechanical effects. For this purpose, we modified each individual domain (in the no-edge version only) with two double-stranded DNA handles positioned at opposite sides of the structure (Fig. S1†) and trapped a single molecule of each construct (mostly in the can form) between two beads of a dual optical tweezer (Fig. 5, the experimental procedure is fully reported in the ESI and Fig. S16–S33†). Since the anchoring positions are the same in the three domains and the latter are topologically identical, the mechanical response of each domain to the same stretching force will be influenced solely by the strength with which the handles are attached to the origami structure, i.e., ultimately by the local sequence environment in the direct vicinity of the anchoring point. We performed a representative comparative study for only one pair of handles placed at positions (5,1) and (11,16) of constructs A(−), B(−) and C(−) in the can form (white circles in Fig. 2a). The force–distance (F–d) curves show a complex pattern in all constructs, with multiple events at varying F–d values, and stretching profiles often ending with stripping of the tether at forces >25–30 pN (representative curves in Fig. S25 and S26†), in agreement with previously reported data on relatively small DNA origami structures.16,39 We then decided to focus our comparative analysis solely on the first transition event (Fig. 5c–e, right panels). Indeed, this event appeared as a “signature” of the domain, characterized by rather reproducible and specific F–d features, which we attributed to the initial partial isomerization of the structure in the region around the point of handle attachment. Domain A(−) exhibited a force profile of moderately broad distribution, centered at about 5–7 pN and a distance offset (i.e., extension of the structure during application of the force) of ca. 25 nm (Fig. 5c, left and middle panels). Domain B(−) featured a much broader force distribution profile ranging from 5 to 17 pN and a less defined distance offset, with a maximal frequency at ca. 15 nm (Fig. 5d, left and middle panels).Finally, C(−) showed a narrow distribution of forces centered at about 11 pN and a distance offset centered at ca. 35 nm (Fig. 5e, left and middle panels). These results suggest that domain C(−) is the most resistant to mechanical stretching, followed by domain A(−) and finally B(−), which instead respond in a relatively weak and heterogeneous manner to the application of a stretching force. Again, these data find a logic explanation in the thermal maps, as the points of DNA handle attachment are situated in regions of different local thermal stabilities (white circles in Fig. 2a and Fig. S1†) with an average Tm of ca. 47 °C in C(−), followed by regions of lower Tm in A(−) and B(−) (ca. 39 °C and 38 °C, respectively). Using different staples for attachment of the handles resulted in different force–distance curves (Fig. S29 and S30†), while introducing sequence deletions in different regions of a given domain led to variable conformer ratios, depending on the type of edge design and the location of the lacking staples (Fig. S31–S33†). These data again confirm that single “point mutations” in a relatively small DNA origami structure may result in large changes of mechanical properties and in distinct conformational preferences.
Conclusions
The folding of a small monolayered DNA origami structure is a complex process mediated by the interplay of energetic and entropic factors, which depend (i) on the topological features of scaffold routing and (ii) on the sequence information at these and nearby sites. Our study shows that, combining the topology-dependent information provided by scaffold routing with the thermal stability map constructed on critons, many of the sequence-dependent folding features occurring in simple patterns of connected HJs can be explained. Such a sequence-to-structure relationship is an intrinsic property of DNA origami domains, which becomes evident in small and topologically malleable structures but is rarely observed in more complex architectures, where multiple forces are in play in a much more intricate fashion.We propose that both topological and thermal properties of the nascent structure contribute to the formation of the initial nuclei of origami assembly, upon which multiple growing fronts may emerge and possibly compete or combine into one dominant folding path. We have previously observed that the presence of mechanically strained scaffold loops in the canonical (can) design may result in the appearance of an alternative iso conformer, with the conformers being related one to the other by the global isomerization of all constituent HJs. Which of the two states will dominate at equilibrium depends on its probability to nucleate and propagate to the rest of the structure. Here, we propose that when topologically frustrated scaffold loops feature a high Tm, these sites will be probably the first regions to nucleate, forcing the structure to adopt the alternative iso conformation to escape the mechanical stress that accumulates at the edges during folding (as in A(0), A(1), or B(0)). If thermal NS and topological NS are instead located in different regions of the nascent structure, i.e., when the regions of high thermal stability are located far from the mechanically strained scaffold loops, the can conformer will have a higher chance to nucleate and propagate, eventually becoming the predominant species at equilibrium (this is the case for B(−), C(−) or C(1)). In all intermediate scenarios, characterized by edges of moderate Tm and/or thermal NS located sparsely within the structure (as in A(−), B(1) and C(0)), the fate of the assembly is more difficult to predict besides the fact that both conformers will be present.
Hence, our study adds an important piece of information to the problem of DNA origami conformational preference, namely, the information encoded in the sequence. This information guides the initial molecular recognition among the individual components of the assembly mixture and, together with the entropic and elastic energy contributions to polymer bending, can provide a more general model of folding for monolayered DNA origami domains. This extended model can in part rationalize data on regular patterns of HJs that cannot be fully explained considering only the entropic aspects of the problem, i.e., those aspects related to the topology and mechanical properties of the origami construct. Nevertheless, more complex scenarios, as, for example, the presence of both conformers in a comparable amount or the occurrence of long-range sequence-to-structure relationships, are still difficult to explicate and might be too complicated to be addressed with the current knowledge. More experiments and simulation studies are probably needed to improve our understanding of DNA origami self-assembly. Moreover, label-free methods40 could be applied to better reveal the role played by the sequence of individual staples, without the need for using intercalators or fluorophore dyes. This, together with refined theoretical models, may help to predict or even create new origami folds in a rational manner.
Experimental
Materials
Oligonucleotides for origami assembly (Merck) were diluted in ddH2O (100 mM) and stored at −20 °C until use. FAM- and TAMRA-modified oligonucleotides were purchased from IDT in HPLC purification grade and used as received after dissolution in ddH2O. The M13mp18 ssDNA scaffold was amplified in E. coli XL1-Blue (Agilent Technologies) from template phage DNA (Affymetrix). Buffers used were 1× TEMg12.5 (20 mM Tris base, 2 mM EDTA, 12.5 mM MgCl2, pH 7.6); 1× TBEMg12.5 (40 mM Tris base, 20 mM boric acid, 2 mM EDTA, 12.5 mM magnesium acetate, pH 8); anti-blinking buffer (1× TEMg12.5 supplemented with 2 mM Trolox (Sigma)); and oxygen scavenger buffer (anti-blinking buffer supplemented with 100 mM D-glucose (Carl Roth) and 2.000 U ml−1 Catalase (Sigma)). Activating pyranose oxidase (Sigma) was prepared as a 30 mM solution in 1× anti-blinking buffer. C-trap® buffers were filtered before use.DNA origami design and assembly
DNA origami constructs were designed using caDNAno software (https://www.cadnano.org) and assembled using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 molar ratio between the scaffold (10 nM) and each of the staple strands in 1× TEMg12.5 buffer. Thermal annealing was performed in a thermocycler Mastercycler nexus gradient (Eppendorf) at a constant cooling rate (−1 °C min−1) from 80 °C to 20 °C.
10 molar ratio between the scaffold (10 nM) and each of the staple strands in 1× TEMg12.5 buffer. Thermal annealing was performed in a thermocycler Mastercycler nexus gradient (Eppendorf) at a constant cooling rate (−1 °C min−1) from 80 °C to 20 °C.
Electrophoretic mobility assays
The reaction mixtures were controlled for correct assembly by agarose gel electrophoresis with 1% agarose (Biozyme) in 1× TBEMg12.5 for 2 h at 80 V. Gel chambers were submerged in an ice-water bath and used at 4 °C. A 1 kbp ladder (Carl Roth) was added to control the size of the construct. Gels were imaged with a Typhoon FLA 9000 (GE Healthcare Lifescience) using a laser scanner at a resolution of 100 μm per pixel. Upon detection in the FAM and TAMRA channels, gels were stained with ethidium bromide and imaged under UV illumination.Atomic force microscopy
5 μl of sample was applied to a freshly cleaved mica surface (Plano GmbH) and allowed to adsorb for 5 min at room temperature. After rinsing with ddH2O, the sample was dried under gentle air flow and scanned in ScanAsyst mode using a MultiModeTM microscope (Bruker) equipped with a Nanoscope V controller. Cantilevers with sharpened pyramidal tips (ScanAsystAir, Bruker) were used for scanning. To reduce bias and ensure reproducibility, images were acquired at different spots on a mica surface. Image analysis was performed using NanoScope Analysis software 1.9.Ensemble fluorescence and FRET spectroscopy
The temperature-dependent folding and unfolding of the origami samples were monitored with a CFX96 real time system (BioRad) by measuring the change in the fluorescence emission signal at 522 nm upon excitation at 498 nm. SYBR Green (SG; Jena Bioscience) experiments were performed as previously reported.38 For individual DNA origami domains, a 60 nM SG solution was added to a mixture containing 20 nM scaffold and 100 nM staple strands in 1× TEMg12.5 buffer. Thermal experiments on the entire construct were performed using 160 nM SG. Five replicates of each sample were equilibrated at 70 °C for 10 h and further cooled from 70 °C to 50 °C at 0.08 °C min−1. Upon 5 min equilibration at 50 °C, melting was carried out up to 70 °C at the same temperature scan rate. Control samples, including scaffold-only, staples-only or buffer-only, were prepared to correct for the background signal. A solution containing a thermally stable hairpin (sequence 5′-CGCTCGCGGACCGCTGAGTGAGGATACCTCACTCAGCGGTCCGCGAGCG-3′; Tm >70 °C) was used as an internal standard for “non-melted” regions. Temperature-dependent FRET experiments were performed on solutions containing 50 nM scaffold in the presence of 5-fold staple strands (for the assembly of all domains) and 2-fold fluorescently labelled strands (for reporting the folding/unfolding of a specific domain). Two distinct pairs of FAM- and TAMRA-labelled strands were used to monitor either the formation of the can or iso form, as previously described.17 A control sample, containing only the FAM-labelled strand, was prepared for calculation of the FRET efficiency E = (ID − IDA)/ID (with ID and IDA being the fluorescence emission intensity of the donor fluorophore in the absence and presence of the acceptor dye, respectively). Moreover, an identical unlabelled sample was used as a reference to correct for possible other sources of signal change. At least four replicates of each sample were prepared and cooling was performed from 75 °C to 50 °C at one of four distinct temperature scan rates (± 0.08 °C min−1, ± 0.7 °C min−1, ± 1.3 °C min−1, and ± 2.6 °C min−1), followed by rapid cooling to 20 °C. Melting of the sample was performed upon an initial preheating to 50 °C for 5 min, followed by a 50 °C to 75 °C gradient at the same temperature scan rate used for cooling. After each cooling run, 5 μl of sample were taken from the assembly mixture and further characterized by agarose gel electrophoresis and/or AFM to prove the correct folding of the structure. Analysis of the data was done using OriginPro (v. 22, OriginLab Corporation, Northampton, MA, USA).Single-molecule force measurements
Two double-stranded DNA handles for trapping and stretching experiments at a dual optical tweezer (C-trap®, LUMICKS) were produced by PCR amplification of the pET28a(+) plasmid. For each handle, the reverse primers consisted of a 21-nt sequence, carrying a digoxigenin- (left handle) or a biotin group (right-handle) at its 5′-end. The forward primers were 53-nt long sequences composed of a 21-nt sequence that hybridizes to the plasmid, a central C18 PEG spacer and a 32-nt long single-stranded overhang for integration of the handle into the DNA origami structure. Each handle is 3083 bp long. A control tether (6198 bp) was prepared by hybridization of two handles at complementary 32-nt long extensions. A reference double-stranded DNA tether (6163 bp), lacking the central PEG spacers, was obtained from PCR amplification of the M13mp18 RF I plasmid (New England Biolabs). PCR reactions were carried out in a volume of 50 μl using a Phusion HF PCR kit (Thermo Fisher Scientific). Reaction aliquots were pooled, purified from contaminants by ethanol precipitation and further analyzed by agarose-gel electrophoresis. Handles were isolated by extracting the desired band from the gel, further washed with a NucleoSpin PCR clean-up kit (Macherey-Nagel) and finally purified by an additional ethanol precipitation. Attachment of both handles to the origami structure was performed in a one-step annealing procedure using 10-fold excess handles for up to a 10 nM origami assembly mixture and cooling the solution from 80 °C to 20 °C at a scan rate of −1 °C min−1. After assembly, the sample was concentrated to 40 μl using ultracentrifugal filters (Merck, cut-off >50 kDa), analyzed and purified by agarose gel electrophoresis and recovered using Freeze′N′Squeeze (BioRad) columns. All origami tethers were checked by AFM prior to single-molecule force experiments. Polystyrene beads (Biozol), coated either with streptavidin (stv; ø = 1.5–1.9 μm) or anti-digoxigenin (α-dig; ø = 0.7–0.9 μm), were sonicated in buffer directly before usage. Measurements were performed in 1× TEMg12.5 buffer containing Trolox and a freshly prepared oxygen-scavenging system (2.000 U ml−1 catalase, 100 mM glucose and 30 mM pyranose oxidase). A 1 μl solution of the purified origami sample at 0.3 nM concentration was incubated for 5 min at room temperature with 5 μl of a 0.1% suspension of α-dig coated beads. After the addition of 500 μl buffer, the mixture was introduced into the flow cell and a single α-dig coated bead was optically trapped by a laser beam. Injection of a preparation of STV-coated beads (1 μl of a 1% SVT-bead suspension in 1 ml 1× TEMg12.5) enabled rapid binding of the origami sample at the biotinylated handle and the consequent formation of an origami tether between two beads. Bead calibration was implemented in Bluelake (Version: 2.0) using power spectrum analysis and was performed for every caught bead pair. Force (F) versus extension (d) traces were recorded at 10 nm sec−1 without flow and the first transition event was analyzed by fitting the experimental F–d curve to an extended worm-like chain model according to Odijk41,42 (eqn (2)) using a Jupyter notebook python script from LUMICKS: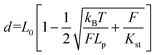 | (2) |
Author contributions
SG and BS conceived the project. SG performed the experimental work and analyzed the data, with the support from LJS. BS supervised the project. The manuscript was written with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project has been realized with financial support from the DFG (project SA 1952/5-1 to B. S. and the large instrumentation program INST 20876/346-1 FUGG to B. S.). We are thankful to Dr Roman Renger and Dr Philip Rauch (LUMICKS, The Netherlands) for their assistance in the experimental set up of the optical tweezer and the initial data analysis and elaboration. We are grateful to Dana Bludau and Isabel Feldmann for their assistance in the acquisition of single-molecule force measurements.References
- P. W. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- F. Hong, F. Zhang, Y. Liu and H. Yan, Chem. Rev., 2017, 117, 12584–12640 CrossRef CAS PubMed.
- S. Dey, C. Fan, K. V. Gothelf, J. Li, C. Lin, L. Liu, N. Liu, M. A. D. Nijenhuis, B. Saccà, F. C. Simmel, H. Yan and P. Zhan, Nat. Rev. Methods Primers, 2021, 1, 13 CrossRef CAS.
- X. Chang, Q. Yang, J. Lee and F. Zhang, Curr. Top. Med. Chem., 2022, 22, 652–667 CrossRef CAS PubMed.
- J. M. Arbona, J. Elezgaray and J. P. Aime, EPL, 2012, 100, 28006 CrossRef.
- J. M. Arbona, J. P. Aime and J. Elezgaray, J. Chem. Phys., 2012, 136, 065102 CrossRef PubMed.
- J. M. Arbona, J. P. Aime and J. Elezgaray, J. Chem. Phys., 2013, 138, 015105 CrossRef PubMed.
- J. Song, J. M. Arbona, Z. Zhang, L. Liu, E. Xie, J. Elezgaray, J. P. Aime, K. V. Gothelf, F. Besenbacher and M. Dong, J. Am. Chem. Soc., 2012, 134, 9844–9847 CrossRef CAS PubMed.
- K. E. Dunn, F. Dannenberg, T. E. Ouldridge, M. Kwiatkowska, A. J. Turberfield and J. Bath, Nature, 2015, 525, 82–86 CrossRef CAS PubMed.
- F. Dannenberg, K. E. Dunn, J. Bath, M. Kwiatkowska, A. J. Turberfield and T. E. Ouldridge, J. Chem. Phys., 2015, 143, 165102 CrossRef PubMed.
- J. L. Wah, C. David, S. Rudiuk, D. Baigl and A. Estevez-Torres, ACS Nano, 2016, 10, 1978–1987 CrossRef PubMed.
- J. M. Majikes, J. A. Nash and T. H. LaBean, Nanoscale, 2017, 9, 1637–1644 RSC.
- J. M. Majikes, P. N. Patrone, A. J. Kearsley, M. Zwolak and J. A. Liddle, ACS Nano, 2021, 15, 3284–3294 CrossRef CAS PubMed.
- J. Wang, Y. Wei, P. Zhang, Y. Wang, Q. Xia, X. Liu, S. Luo, J. Shi, J. Hu, C. Fan, B. Li, L. Wang, X. Zhou and J. Li, Nano Lett., 2022, 22, 7173–7179 CrossRef CAS PubMed.
- A. Cumberworth, D. Frenkel and A. Reinhardt, Nano Lett., 2022, 22, 6916–6922 CrossRef CAS PubMed.
- P. Shrestha, T. Emura, D. Koirala, Y. Cui, K. Hidaka, W. J. Maximuck, M. Endo, H. Sugiyama and H. Mao, Nucleic Acids Res., 2016, 44, 6574–6582 CrossRef PubMed.
- R. Kosinski, A. Mukhortava, W. Pfeifer, A. Candelli, P. Rauch and B. Sacca, Nat. Commun., 2019, 10, 1061 CrossRef PubMed.
- S. Ramakrishnan, L. Schärfen, K. Hunold, S. Fricke, G. Grundmeier, M. Schlierf, A. Keller and G. Krainer, Nanoscale, 2019, 11, 16270–16276 RSC.
- X. Wei, J. Nangreave, S. Jiang, H. Yan and Y. Liu, J. Am. Chem. Soc., 2013, 135, 6165–6176 CrossRef CAS PubMed.
- M. Hanke, E. Tomm, G. Grundmeier and A. Keller, ChemBioChem, 2023, 24, e202300338 CrossRef CAS PubMed.
- A. Bednarz, S. M. Sonderskov, M. Dong and V. Birkedal, Nanoscale, 2023, 15, 1317–1326 RSC.
- M. Endo, S. Yamamoto, T. Emura, K. Hidaka, N. Morone, J. E. Heuser and H. Sugiyama, Angew. Chem., Int. Ed., 2014, 53, 7484–7490 CrossRef CAS PubMed.
- A. Murugan, Z. Zeravcic, M. P. Brenner and S. Leibler, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 54–59 CrossRef CAS PubMed.
- J. Song, Z. Li, P. Wang, T. Meyer, C. Mao and Y. Ke, Science, 2017, 357, eaan3377 CrossRef PubMed.
- Y. Cui, R. Chen, M. Kai, Y. Wang, Y. Mi and B. Wei, ACS Nano, 2017, 11, 8199–8206 CrossRef CAS PubMed.
- F. Schneider, N. Moritz and H. Dietz, Sci. Adv., 2019, 5, eaaw1412 CrossRef CAS PubMed.
- C. R. Simmons, T. MacCulloch, M. Krepl, M. Matthies, A. Buchberger, I. Crawford, J. Sponer, P. Sulc, N. Stephanopoulos and H. Yan, Nat. Commun., 2022, 13, 3112 CrossRef CAS PubMed.
- X. Li, H. Wang and N. C. Seeman, Biochemistry, 1997, 36, 4240–4247 CrossRef CAS PubMed.
- S. A. McKinney, A. C. Declais, D. M. Lilley and T. Ha, Nat. Struct. Biol., 2003, 10, 93–97 CrossRef CAS PubMed.
- S. Zhang, T. J. Fu and N. C. Seeman, Biochemistry, 1993, 32, 8062–8067 CrossRef CAS PubMed.
- S. Zhang and N. C. Seeman, J. Mol. Biol., 1994, 238, 658–668 CrossRef CAS PubMed.
- R. M. Clegg, A. I. Murchie and D. M. Lilley, Biophys. J., 1994, 66, 99–109 CrossRef CAS PubMed.
- L. A. Marky, N. R. Kallenbach, K. A. McDonough, N. C. Seeman and K. J. Breslauer, Biopolymers, 1987, 26, 1621–1634 CrossRef CAS PubMed.
- A. I. Murchie, R. M. Clegg, E. von Kitzing, D. R. Duckett, S. Diekmann and D. M. Lilley, Nature, 1989, 341, 763–766 CrossRef CAS PubMed.
- N. C. Seeman, J. H. Chen and N. R. Kallenbach, Electrophoresis, 1989, 10, 345–354 CrossRef CAS PubMed.
- T. J. Fu, Y. C. Tse-Dinh and N. C. Seeman, J. Mol. Biol., 1994, 236, 91–105 CrossRef CAS PubMed.
- D. M. Lilley, Q. Rev. Biophys., 2000, 33, 109–159 CrossRef CAS PubMed.
- J. P. Sobczak, T. G. Martin, T. Gerling and H. Dietz, Science, 2012, 338, 1458–1461 CrossRef CAS PubMed.
- P. Shrestha, S. Jonchhe, T. Emura, K. Hidaka, M. Endo, H. Sugiyama and H. Mao, Nat. Nanotechnol., 2017, 12, 582–588 CrossRef CAS PubMed.
- H. Ijas, T. Liedl, V. Linko and G. Posnjak, Biophys. J., 2022, 121, 4800–4809 CrossRef CAS PubMed.
- T. Odijk, Macromolecules, 1995, 28, 7016–7018 CrossRef CAS.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Biophys. J., 1997, 72, 1335–1346 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: DNA design, FRET melting curves, preparation of DNA handles and DNA origami tethers, additional force–distance traces, supplementary tables and a list of DNA sequences. See DOI: https://doi.org/10.1039/d3nr02537c |
| This journal is © The Royal Society of Chemistry 2023 |