Understanding the reactivity and selectivity of Diels–Alder reactions involving furans

Abstract

The reactivity and endo/exo selectivity of the Diels–Alder cycloaddition reactions involving furan and substituted furans as dienes have been computationally explored. In comparison to cyclopentadiene, it is found that furan is comparatively less reactive and also less endo-selective in the reaction with maleic anhydride as the dienophile. Despite that, both the reactivity and the selectivity can be successfully modified by the presence of substituents at either 2- or 3-positions of the heterocycle. In this sense, it is found that the presence of strong electron-donor groups significantly increases the reactivity of the system while the opposite is found in the presence of electron-withdrawing groups. The observed trends in both the reactivity and selectivity are analyzed quantitatively in detail by means of the activation strain model of reactivity in combination with the energy decomposition analysis methods.

---

1. Introduction

The Diels–Alder (DA) [4 + 2] cycloaddition reaction¹ plays a crucial role in synthetic organic chemistry because it can construct complex architectures, with up to four stereocenters, in a single reaction step.^2,3 Due to its high atom-efficiency, adhering to the fundamental principles of green chemistry,^4–6 this specific reaction has been applied to the synthesis of a wide variety of target molecules including complex natural products and species with potential applications in materials science and medicinal chemistry.^2,7

In this sense, the DA reactions involving furan and furan derivatives as the diene partner are receiving considerable attention recently^8,9 since furanics constitute renewable platform molecules to produce, among other interesting systems, responsive materials^10–13 or drug delivery species.^14,15 As many other pericyclic reactions,¹⁶ the reactivity trends of the DA cycloadditions involving furans have been traditionally rationalized in terms of the Frontier Molecular Orbital (FMO)¹⁷ theory and Woodward–Hoffmann rules.¹⁸ However, some deficiencies of these conceptual frameworks have been identified¹⁹ which indicate that other factors, different from FMO interactions, may be responsible for both the observed reactivity trends and selectivity patterns. For instance, we recently found, with the help of the activation strain model (ASM)²⁰ of reactivity in combination with the Energy Decomposition Analysis (EDA)²¹ method, that the catalysis of various fundamental transformations in organic chemistry, such as Diels–Alder,²² Michael addition²³ and Alder–ene reactions,²⁴ is not, as widely accepted, caused by enhancing FMO interactions. Instead, the physical mechanism behind the acceleration induced by the catalyst is a significant reduction of the Pauli repulsion between the key occupied molecular orbitals of the reactants. These examples, which belong to the recently introduced Pauli-repulsion lowering concept,²⁵ nicely illustrate that the traditionally used FMO arguments can be misleading, particularly in DA cycloaddition reactions.

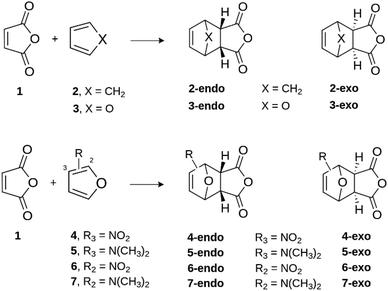
For this reason, herein we shall also apply the ASM-EDA approach to investigate quantitatively in detail the so far not fully understood factors controlling both the reactivity and selectivity in the Diels–Alder reactions involving furan and furan derivatives as dienes.⁸ To this end, we will first compare the parent reaction between furan and maleic anhydride with the analogous parent reaction involving cyclopentadiene (Scheme 1). Then, we will explore the analogous processes involving furans substituted at either 2- or 3-position of furan because the presence of electron-donor or electron-withdrawing groups at such positions has been shown to significantly affect both the reactivity and endo/exo selectivity of the process.²⁶ However, the reasons behind the influence of these substituents on the transformation remain unclear as well.

Scheme 1 Overview of Diels–Alder [4 + 2] cycloaddition reactions studied in this work.

2. Methods

2.1 Activation strain model and energy decomposition analysis

The activation strain model of reactivity (ASM, also called the distortion/interaction approach^20b) is a fragmented-based method to understanding chemical processes, in which the reaction barriers are described and understood in terms of the original reactants.²⁰ More specifically, this model considers the rigidity of the reactants as well as the extent to which the reactants must deform during the reaction, plus their capability to interact as the reaction proceeds. Thus, the potential energy surface, ΔE(ζ), is decomposed in two terms along the reaction coordinate ζ (eqn (1)):

ΔE(ζ) = ΔE_strain(ζ) + ΔE_int(ζ) (1)

In this equation, ΔE_strain(ζ) stands for the strain energy associated with the structural deformation the reactants undergo from their equilibrium structure to the geometry they adopt during the reaction at a specific point on the reaction coordinate. The term ΔE_int(ζ) accounts for the chemical interaction between the increasingly deformed reactants along the reaction coordinate.

The reaction coordinate ζ is defined as the projection of the Intrinsic Reaction Coordinate (IRC) onto the forming C⋯C distance between the carbon atoms of the diene and dienophile. This reaction coordinate undergoes a well-defined change in the course of the reaction from the dissociation limit to the equilibrium C–C distance in the transition state.²⁷

Within the Energy Decomposition Analysis (EDA) method,²¹ the interaction ΔE_int(ζ) between the strained reactants can be further decomposed into the following chemically meaningful terms (eqn (2)):

ΔE_int(ζ) = ΔE_Pauli(ζ) + ΔV_elstat(ζ) + ΔE_orb(ζ) (2)

herein, ΔV_elstat(ζ) is the classical electrostatic interaction between the unperturbed charge distributions of the deformed reactants and is usually attractive. The Pauli repulsion term, ΔE_Pauli(ζ), comprises the destabilizing interaction between occupied closed-shell orbitals of the fragments due to de Pauli's exclusion principle. The orbital interaction ΔE_orb(ζ) accounts for charge transfer (interaction between occupied orbitals on one moiety with unoccupied orbitals on the other, including HOMO–LUMO interactions) and polarization (empty-occupied orbital mixing on one fragment due to the presence of another fragment).

2.2 Computational details

Geometry optimizations of the stationary points generated by the Diels–Alder reactions of this study were performed without symmetry constraints using the Gaussian16 suite of programs²⁸ employing the hybrid meta-GGA M06-2X ²⁹ functional together with the triple-ζ basis set def2-TZVPP.³⁰ The nature of the stationary points on the potential energy surface was checked by harmonic vibrational frequency calculations. Minima have positive definite Hessian matrices whereas the transition states show only one negative eigenvalue in their diagonalized force constant matrices, and their associated eigenvectors were confirmed to correspond to the motion along the reaction coordinate under consideration using the Intrinsic Reaction Coordinate (IRC) method.³¹ Energy refinements were carried out by means of single-point calculations at the accurate DLPNO-CCSD(T)³² approach with the def2-TZVPP basis set using the ORCA 5.0 program.³³ This level is denoted DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP.

The program package ADF^34,35 was used for EDA calculations using the M06-2X/def2-TZVPP optimized geometries at the same DFT level with a triple-ζ-quality basis set using uncontracted Slater-type orbitals (STOs) augmented by two sets of polarization functions with a frozen-core approximation for the core electrons.³⁶ Auxiliary sets of s, p, d, f, and g STOs were used to fit the molecular densities and to represent the Coulomb and exchange potentials accurately in each SCF cycle.³⁷ Scalar relativistic effects were incorporated by applying the zeroth-order regular approximation (ZORA).³⁸ This level of theory is denoted ZORA-M06-2X/TZ2P//M06-2X/def2-TZVPP.

3. Results and discussion

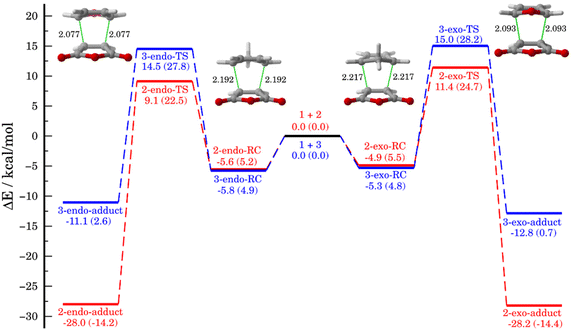
We first compared the Diels–Alder cycloaddition reactions between the maleic anhydride (1) and cyclopentadiene (2) with the analogous process involving furan (3, Scheme 1). Table 1 lists the relative energies, with zero-point energy corrections, for the endo and exo pathways obtained at the DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP level of theory whereas Fig. 1 depicts the corresponding reaction profiles including the relative free energies (within parentheses) computed at the same level.

Fig. 1 Relative energies of the stationary points, including the zero-point energies (in kcal mol⁻¹), on the potential energy surface for the 1 + 2 (red) and 1 + 3 (blue) reactions, calculated at DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP. Values within parentheses refer to relative free energy computed at the same level of theory. Bond distances in the corresponding transition states are given in angstroms.

Table 1 Relative energies with zero-point energy correction, calculated at DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP^a level of theory for the reactions between maleic anhydride (1), cyclopentadiene (2), and furan (3). All values are in kcal mol⁻¹

Reactions	endo pathway			exo pathway
	RC	TS	Adduct	RC	TS	Adduct
a Zero-point energy correction included at M06-2X/def2-TZVPP.
1 + 2	−5.6	9.1	−28.0	−4.9	11.4	−28.2
1 + 3	−5.8	14.5	−11.1	−5.3	15.0	−12.8

---

As shown in Fig. 1, both cycloaddition reactions begin from an initial van der Waals reactant complex, RC (whose formation becomes endergonic when entropic effects are considered), which evolves to the corresponding cycloadducts in a concerted manner through the corresponding six-membered cyclic transition state (TS). From the data in Fig. 1, it becomes clear that whereas the cycloaddition involving cyclopentadiene selectively produces the thermodynamically less stable endo-cycloadduct under kinetic control (ΔΔG^‡ = 2.2 kcal mol⁻¹), the analogous reaction involving furan is only slightly endo-selective in view of the much lower endo–exo barrier difference (ΔΔG^‡ = 0.4 kcal mol⁻¹). Please note that our DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP energies are in excellent agreement with previous experimental (ΔΔG^‡ = 2.5 kcal mol⁻¹, for the 1 + 2 reaction)³⁹ and theoretical data (ΔΔG^‡ = 0.6 kcal mol⁻¹, for the 1 + 3 reaction),²⁶ which supports the selected method for this study. In addition, it becomes evident that furan is less reactive than cyclopentadiene in their reactions with maleic anhydride in view of the higher barriers computed for both endo/exo approaches (ΔΔG^‡ = 5.3 kcal mol⁻¹ for the endo pathway). Moreover, whereas the cycloaddition involving cyclopentadiene is irreversible, the analogous process involving furan is clearly reversible, which is consistent with previous studies.⁸

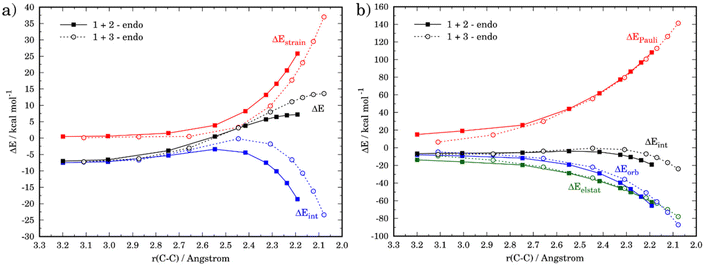
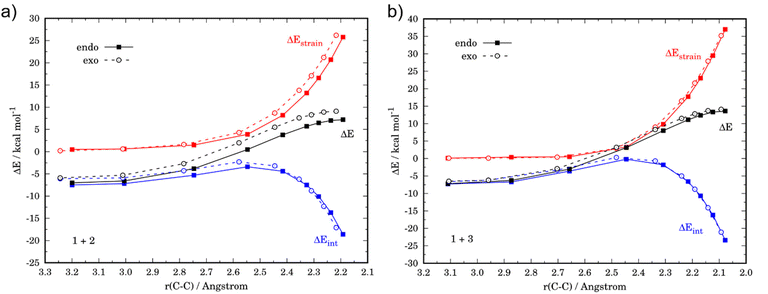
Although the lower reactivity of furan can be initially ascribed to the loss of aromaticity of the heterocycle during the transformation, we applied next the activation strain model of reactivity (ASM) to quantitatively understand the origin of this reactivity trend. To this end, we compared the favored endo-pathways for both cycloadditions involving cyclopentadiene and furan. Fig. 2a shows the computed activation strain diagrams (ASDs) for both reactions from the initial stages of the transformation to the respective transition states and projected onto the C⋯C bond-forming distances.²⁷ From the data in Fig. 2a, the (1 + 3) reaction presents a less destabilizing strain energy compared to the (1 + 2), and therefore the ΔE_strain term is not all responsible for the reactivity trend. At variance, the cycloaddition involving cyclopentadiene benefits from a much stronger interaction energy between the deformed along the entire reaction coordinate and particularly at the transition state region. Therefore, the lower reactivity of furan can be exclusively ascribed to a less stabilizing interaction between the reactants during the transformation as compared to the analogous process involving cyclopentadiene.

Fig. 2 Comparative activation strain analyses (a), computed at the M06-2X/def2-TZVPP level, and the energy decomposition analysis (b), computed at the ZORA-M06-2X/TZ2P//M06-2X/def2-TZVPP level, for the endo pathways of the Diels–Alder cycloaddition reactions between the maleic anhydride (1) and cyclopentadiene (2, solid lines) and furan (3, dashed lines), projected onto the C⋯C bond-forming distance.

The origin of the stronger interaction energy between the deformed reactants for (1 + 2) can be better interpreted with the help of the energy decomposition analysis (EDA). Fig. 2b illustrates the evolution of the EDA terms along the reaction coordinate for both reactions. Interestingly, both the Pauli repulsion and the electrostatic attractions are rather similar for both processes which indicates that the orbital interactions become the only differentiating factor between both reactions. Indeed, the ΔE_orb term is clearly more stabilizing for the process involving cyclopentadiene along the entire reaction coordinate. For instance, at the same consistent C⋯C bond-forming distance of 2.2 Å, the difference in the orbital term (ΔΔE_orb = 9.4 kcal mol⁻¹) nearly matches that of the interaction energy (ΔΔE_int = 9.9 kcal mol⁻¹).

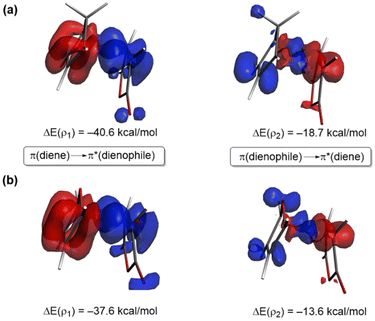
To comprehend the reasons behind the stronger orbital interactions computed for the reaction involving maleic anhydride and cyclopentadiene, we applied the natural orbital for chemical valence (NOCV)⁴⁰ extension of the EDA method. This approach allows us to not only identify but also quantify the main orbital interactions contributing to the ΔE_orb term. Fig. 3 depicts the deformation densities (Δρ) of the pairwise main orbital interactions between the interacting fragments and the corresponding stabilization energies, ΔE(ρ), for the Diels–Alder cycloaddition reactions between maleic anhydride (1) and cyclopentadiene (2) and furan (3). Within the NOCV method, two main orbital interactions are identified, namely the direct π-HOMO(diene) → π*-LUMO(dienophile) and the reverse π-HOMO(dienophile) → π*-LUMO(diene), denoted as ρ₁ and ρ₂, respectively. Not surprisingly, the direct interaction ρ₁ is stronger than the reverse interaction ρ₂, which is consistent with the normal electronic demand nature of both Diels–Alder reactions. Interestingly, both molecular orbital interactions are comparatively weaker for the 1 + 3 cycloaddition (see ΔE(ρ) values in Fig. 3, computed at the same consistent C⋯C bond-forming distance of 2.2 Å), which translates into the computed less stabilizing ΔE_orb and weaker ΔE_int and ultimately, the decreased reactivity (i.e. higher barrier) computed for the process involving furan.

Fig. 3 Plot of the deformation densities (Δρ) of the pairwise orbital interactions between the interacting fragments and the corresponding stabilization energies, ΔE(ρ), for the Diels–Alder cycloaddition reactions between maleic anhydride (1), cyclopentadiene (2, (a)), and furan (3, (b)), computed at the same consistent C⋯C bond-forming distance of 2.2 Å. All data have been computed at the ZORA-M06-2X/TZ2P//M06-2X/def2-TZVPP level.

We then addressed the remarkable difference in endo/exo selectivity in these processes, i.e. while the cycloaddition involving cyclopentadiene is completely endo-selective (ΔΔG^‡ = 2.2 kcal mol⁻¹), the analogous process involving furan is not selective (ΔΔG^‡ = 0.5 kcal mol⁻¹, see above). Fig. 4 shows the corresponding ASDs for both approaches in both cycloadditions. In agreement with previous calculations,⁴¹ the endo-selectivity in the parent 1 + 2 reaction does not result from the interaction energy, which becomes rather similar for both approaches, but exclusively derives from a less destabilizing strain energy for the endo-approach (Fig. 4a). This is mainly due to the unfavorable steric arrangement occurring between the methylene and oxygen moieties of cyclopentadiene and maleic anhydride. The replacement of the methylene group by an oxygen atom in furan should reduce this unfavorable interaction, which is nicely confirmed in the corresponding ASD (Fig. 4b). Indeed, this crucial strain energy is only slightly less destabilizing for the endo-approach of the process involving furan, which results in the observed lack of selectivity in the 1 + 3 reaction.

Fig. 4 Comparative activation strain analyses for the endo and exo pathways of the Diels–Alder cycloaddition reactions between the maleic anhydride (1) and cyclopentadiene (2, a) and furan (3, b), projected onto the C⋯C bond-forming distance. All data have been computed at the M06-2X/def2-TZVPP level.

Once we analyzed the reactivity and selectivity of the prototype Diels–Alder reactions, we then focused on the factors defining the reactivity and endo/exo selectivity of the analogous cycloaddition reactions involving substituted furans. To this end, we evaluated the effects of the extreme situations represented by the systems having a strong electronic withdrawing (–NO₂) or a strong donating (–NMe₂) substituent placed at either 3- (compounds 4 and 5) or 2- (compounds 6 and 7) positions of furan (see Scheme 1). Table 2 lists the relative electronic and free energies, computed for the endo and exo pathways of the corresponding reactions with maleic anhydride, obtained at the DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP level.

Table 2 Relative energies with zero-point energy correction, calculated at DLPNO-CCSD(T)/def2-TZVPP//M06-2X/def2-TZVPP level of theory for the reactions of the maleic anhydride (1) with 3-nitrofuran (4), N,N-dimethylfuran-3-amine (5), 2-nitrofuran (6), N,N-dimethylfuran-2-amine (7). Values within parentheses refer to relative free energy computed at the same level of theory. All values are given in kcal mol⁻¹

Reactions	endo pathway			exo pathway
	RC	TS	Adduct	RC	TS	Adduct
1 + 4	−4.8 (5.5)	18.3 (31.6)	−8.9 (4.7)	−4.8 (5.5)	17.1 (30.4)	−11.9 (1.7)
1 + 5	−7.9 (4.1)	7.0 (20.3)	−19.1 (−5.7)	−7.6 (3.4)	9.0 (22.0)	−20.4 (−6.8)
1 + 6	−6.2 (3.7)	16.1 (29.5)	−12.0 (1.6)	−6.9 (3.8)	17.1 (30.7)	−13.4 (0.5)
1 + 7	−8.8 (2.7)	8.0 (21.2)	−13.3 (0.8)	−8.4 (2.7)	7.1 (20.6)	−11.5 (2.9)

---

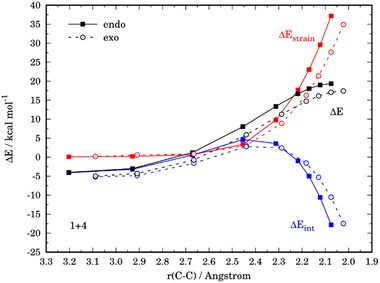
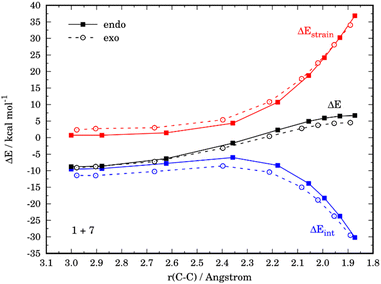
Similar to the parent reaction involving furan, in all cases the cycloadditions also proceed concertedly through the corresponding six-membered transition states (see Fig. S1 in the ESI†). Data gathered in Table 2 show that, compared to unsubstituted furan, the presence of an electron-donating group leads to an enhancement of the reactivity (i.e. the cycloaddition proceeds with a lower barrier) regardless of the position of the substituent. At variance, the reactivity is reduced (i.e. the cycloaddition proceeds with a higher barrier) in those systems having the acceptor NO₂ group. Strikingly, the endo/exo selectivity strongly depends on both the nature of the substituent and its relative position. For instance, the exo-cycloadduct derived from 3-nitrofuran (4) is favored both thermodynamically (ΔΔG = 3.0 kcal mol⁻¹) and kinetically (ΔΔG^‡ = −1.2 kcal mol⁻¹), while the analogous NMe₂-system (5) favors the formation of the corresponding endo-cycloadduct under kinetic control (ΔΔG^‡ = 1.7 kcal mol⁻¹). The opposite is found when the substituents are placed in position 2, i.e. 2-nitrofuran (6) kinetically favors the corresponding endo-adduct (ΔΔG^‡ = 1.2 kcal mol⁻¹), whereas 7 slightly favors the exo-adduct (ΔΔG^‡ = 0.6 kcal mol⁻¹).

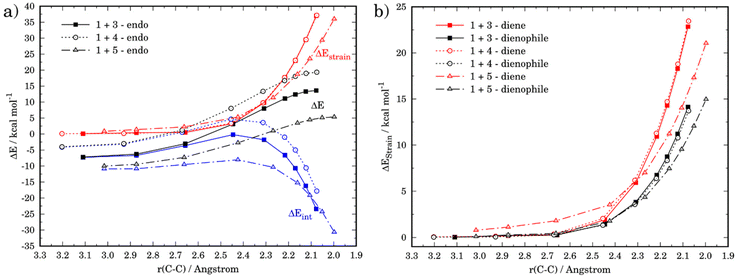
The ASM was again applied to first understand the computed reactivity trend (NO₂ < H < NMe₂) for the reactions of the maleic anhydride with substituted furans. To this end, we compared the processes involving the parent furan 3 and 3-substituted furans 4 and 5 focusing exclusively on the corresponding endo-approaches to enable a direct comparison between the different cycloadditions. Fig. 5a presents the corresponding ASDs for these reactions once again from the beginning of the process up to the respective transition state and projected onto the shortest C⋯C bond-forming distance.²⁷ From the data in Fig. 5a, it becomes clear that the lower reactivity of the nitro-derivative 4 compared to furan results exclusively from a less stabilizing interaction energy along the entire transformation (the strain energy of both systems is nearly identical). The cycloaddition involving the NMe₂-derivate 5 (which exhibits the lowest barrier) benefits from both a stronger interaction and, in addition, from a less stabilizing strain energy, which is translated in the enhanced reactivity of this system. The partitioning of the ΔE_strain term into the contributions of the individual reactant indicates that the required distortion of both reagents is clearly lower for the process involving 5 as compared to the parent furan 3 or its nitro-derivative 4. This is directly related to the higher asynchronicity of the 1 + 5 cycloaddition. As shown in Fig. 6, which shows the optimized transition structures of the endo-pathways for (1 + 4) and (1 + 5) reactions, the asynchronicity is markedly higher for the reaction involving N,N-dimethylfuran-3-amine (5) (Δr^TS_CC = 0.235 Å), compared to the involving 3-nitrofuran (4) (Δr^TS_CC = 0.013 Å).⁴² A higher degree of asynchronicity typically implies that the corresponding transition state is reached earlier and, consequently, the energy penalty to adopt the TS geometry is lower.^22,24

Fig. 5 (a) Comparative activation strain diagrams for the endo-pathways of the cycloaddition reactions between maleic anhydride (1) and furan (3) (solid lines), 3-nitrofuran (4) (dotted lines), and N,N-dimethylfuran-3-amine (5) (dashed lines). (b) Decomposition of the total strain into contributions coming from each reactant. All results are obtained at M06-2X/def2-TZVPP level of theory.

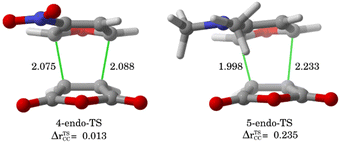Fig. 6 Optimized the endo-pathway transition structures for (1 + 4) and (1 + 5) reactions, as well as the degree of the asynchronicity (Δr^TS_CC).

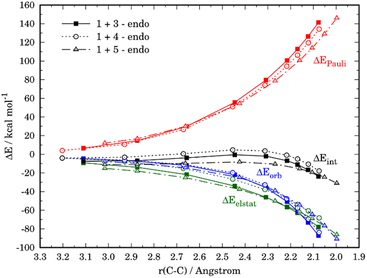
The crucial role of the ΔE_int term in the reactivity of substituted furans was also evaluated with the help of the EDA method. Fig. 7 illustrates the evolution of the individual EDA terms for the considered (endo)-cycloadditions along the reaction coordinate. The presence of the NO₂-group in 4 leads, as expected, not only to weaker orbital interactions with the dienophile as compared to furan but also to much less stabilizing electrostatic attractions. For instance, at the same C⋯C bond-forming distance of 2.1 Å, the differences in the orbital term (ΔΔE_orb = 3.4 kcal mol⁻¹) and electrostatic attractions (ΔΔE_elstat = 9.7 kcal mol⁻¹) favor the reaction 1 + 3. As a consequence, the interaction between the deformed reactants is weaker for the reaction involving 4 which results in the observed reduced reactivity. At variance, the enhanced interaction computed for the process involving 5 derives almost exclusively from a less destabilizing Pauli repulsion (mainly between the occupied orbitals π-HOMO−1 of the diene and the π-HOMO of the dienophile) along the entire transformation, and particularly, at the transition state region.

Fig. 7 Comparative energy decomposition analyses of the Diels–Alder for the endo-pathways of the cycloaddition reactions between maleic anhydride (1) and furan (3) (solid lines), 3-nitrofuran (4) (dotted lines), and N,N-dimethylfuran-3-amine (5) (dashed lines).

For completeness, we finally investigated the endo/exo selectivity reversal induced by the substituent. We first considered the processes involving 3-nitrofuran (4), which kinetically favors the formation of the corresponding exo-cycloadduct (see above). From the comparative ASDs in Fig. 8, it can be concluded that, although the exo-pathway exhibits a stronger interaction at the beginning of the process, it is the less destabilizing strain the decisive factor favoring the exo-approach. This is again related to the extent of the asynchronicity of the process, which is higher in the exo-pathway (Δr^TS_CC = 0.149 Å) than in the endo-pathway (Δr^TS_CC = 0.013 Å).

Fig. 8 Comparative activation strain analyses for the endo and exo pathways of the Diels–Alder cycloaddition reactions between the maleic anhydride (1) and 3-nitrofuran (4), projected onto the C⋯C bond-forming distance. All data have been computed at the M06-2X/def2-TZVPP level.

At variance, for the process involving N,N-dimethylfuran-2-amine (7), we found that the only reason behind the slight preference for the exo-cycloadduct is the interaction energy, which becomes stronger for the exo-approach along the entire reaction coordinate (Fig. 9). According to the EDA, this is due exclusively to a less destabilizing Pauli repulsion in the exo-pathway. As instance, at the same consistent C⋯C bond-forming distance of 1.9 Å, the differences in the orbital term (ΔΔE_orb = 2.1 kcal mol⁻¹) and electrostatic attractions (ΔΔE_elstat = 3.2 kcal mol⁻¹), which favor the endo-approach, are compensated by the lower Pauli repulsion computed for the exo-pathway (ΔΔE_Pauli = 6.5 kcal mol⁻¹).

Fig. 9 Comparative activation strain analyses for the endo and exo pathways of the Diels–Alder cycloaddition reactions between the maleic anhydride (1) and N,N-dimethylfuran-2-amine (7), projected onto the C⋯C bond-forming distance. All data have been computed at the M06-2X/def2-TZVPP level.

4. Conclusions

In summary, this computational study provides quantitative insights into the factors controlling the reactivity and selectivity of the Diels–Alder cycloaddition reactions involving furans as the diene partner. In comparison to cyclopentadiene, it is found that furan is comparatively less reactive in the reaction with maleic anhydride because it exhibits weaker orbital interactions with the dienophile (both the direct π-HOMO(diene) → π*-LUMO(dienophile) and the reverse π-HOMO(dienophile) → π*-LUMO(diene), in almost the same extent). While the process involving cyclopentadiene is endo-selective, the analogous reaction involving furan is practically non-selective. Interestingly, the presence of the NMe₂-donor group in the heterocycle (either at 2- or 3-position) significantly increases the reactivity of the system whereas the opposite is found in the presence of a strong electron-withdrawing group (NO₂). The enhanced reactivity of the NMe₂-derivates results from the combination of a less destabilizing Pauli repulsion together with a lower strain resulting from a higher asynchronicity. At variance, the lower reactivity of the nitro-counterparts exclusively results from a reduced interaction between the deformed reactants. Finally, the endo/exo selectivity strongly depends on both the nature and the position of the substituents, leading to a clear endo/exo selectivity reversal for the process involving 3-nitrofuran and N,N-dimethylfuran-2-amine.

Author contributions

Tiago Vinicius Alves: conceptualization, calculations, formal analysis, writing – original draft. Israel Fernández: supervision, conceptualization, project administration, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Spanish MCIN/AEI/10.13039/501100011033 (grants PID2019-106184GB-I00 and RED2018-102387-T). T. V. A. acknowledges the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brazil (CAPES) for the visiting professor scholarship (CAPES-PrInt – 88887.803486/2023-00).

References

1. A. Diels and K. Alder, Justus Liebigs Ann. Chem., 1928, 460, 98.
2. (a) F. Fringuelli and A. Taticchi, The Diels–Alder Reaction: Selected Practical Methods, Wiley, Hoboken, 2002. See also: (b) S. Sankararaman, Pericyclic Reactions – A Textbook: Reactions, Applications and Theory, Wiley, Weinheim, 2005.
3. K. N. Houk, F. Liu, Z. Yang and J. I. Seeman, Angew. Chem., Int. Ed., 2021, 60, 12660.
4. P. T. Anastas and J. C. Warner, Green Chemistry: Theory and Practice, Oxford University Press, Oxford, New York, 1998.
5. B. M. Trost, Angew. Chem., Int. Ed. Engl., 1995, 34, 259.
6. R. A. Sheldon, Pure Appl. Chem., 2000, 72, 1233.
7. (a) K. C. Nicolaou, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668; (b) K.-I. Takao, R. Munakata and K.-I. Tadano, Chem. Rev., 2005, 105, 4779; (c) M. Juhl and D. Tanner, Chem. Soc. Rev., 2009, 38, 2983; (d) J.-A. Funel and S. Abele, Angew. Chem., Int. Ed., 2013, 52, 3822.
8. For a recent review, see: R. C. Cioc, M. Crockatt, J. C. van der Waal and P. C. A. Bruijnincx, Angew. Chem., Int. Ed., 2022, 61, e202114720.
9. Selected reviews: (a) A. E. Settle, L. Berstis, N. A. Rorrer, Y. Roman-Leshklv, G. T. Beckham, R. M. Richards and D. R. Vardon, Green Chem., 2017, 19, 3468; (b) F. A. Kucherov, L. V. Romashov, G. M. Averochkin and V. P. Ananikov, ACS Sustainable Chem. Eng., 2021, 9, 3011; (c) J. M. J. M. Ravasco and R. F. A. Gomes, ChemSusChem, 2021, 14, 3047.
10. H. Sun, C. P. Kabb, M. B. Sims and B. S. Sumerlin, Prog. Polym. Sci., 2019, 89, 61.
11. M. Vauthier, L. Jierry, J. C. Oliveira, L. Hassouna, V. Roucoules and F. B. Gall, Adv. Funct. Mater., 2019, 29, 1806765.
12. A. Gandini, Prog. Polym. Sci., 2013, 38, 1.
13. Y.-L. Liu and T.-W. Chuo, Polym. Chem., 2013, 4, 2194.
14. M. Gregoritza and F. P. Brandl, Eur. J. Pharm. Biopharm., 2015, 97, 438.
15. T. Elschner, F. Obst and T. Heinze, Macromol. Biosci., 2018, 18, 1800258.
16. K. N. Houk, Acc. Chem. Res., 1975, 8, 361.
17. (a) K. Fukui and H. Fujimoto, Bull. Chem. Soc. Jpn., 1967, 40, 2018; (b) K. Fukui, Angew. Chem., Int. Ed. Engl., 1982, 21, 801.
18. R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Verlag, Chemie, GmbH, Weinheim, 1970.
19. See, for instance: (a) S. D. Kahn, C. F. Pau, L. E. Overman and W. J. Hehre, J. Am. Chem. Soc., 1986, 108, 7381; (b) C. Spino, H. Rezaei and Y. L. Dory, J. Org. Chem., 2004, 69, 757; (c) B. R. Ussing, C. Hang and D. A. Singleton, J. Am. Chem. Soc., 2006, 128, 7594; (d) D. H. Ess, G. O. Jones and K. N. Houk, Adv. Synth. Catal., 2006, 348, 2337.
20. (a) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953; (b) K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070; (c) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649. See also: (d) I. Fernández, in Discovering the Future of Molecular Sciences, ed. B. Pignataro, Wiley-VCH, Weinheim, 2014, pp. 165–187.
21. (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, Vol. 15, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, pp. 1–86; (b) M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43; (c) I. Fernández, in Applied Theoretical Organic Chemistry, ed. D. J. Tantillo, World Scientific, New Jersey, 2018, pp. 191–226.
22. (a) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2020, 59, 6201; (b) P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Chem. Sci., 2020, 11, 8105; (c) S. Portela, J. J. Cabrera-Trujillo and I. Fernández, J. Org. Chem., 2021, 86, 5317.
23. T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2019, 58, 8922.
24. H. A. Rodríguez, D. A. Cruz, J. I. Padrón and I. Fernández, J. Org. Chem., 2023, 88, 11102.
25. T. A. Hamlin, F. M. Bickelhaupt and I. Fernández, Acc. Chem. Res., 2021, 54, 1972.
26. Y. Qiu, J. Phys. Org. Chem., 2015, 28, 370.
27. This critical reaction coordinate undergoes a well-defined change throughout the reaction and has successfully been used in the past for the analysis of other pericyclic reactions. See, for instance: (a) I. Fernández, Phys. Chem. Chem. Phys., 2014, 16, 7662; (b) I. Fernández, Eur. J. Org. Chem., 2018, 1394; (c) I. Fernández, Chem. Sci., 2020, 11, 3769. See also ref. 22–25.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
29. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
30. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
31. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
32. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
33. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
34. G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
35. ADF2020, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, https://www.scm.com.
36. J. G. Snijders, P. Vernooijs and E. J. Baerends, At. Data Nucl. Data Tables, 1981, 26, 483.
37. J. Krijn and E. J. Baerends, Fit Functions in the HFS-Method, Internal Report (in Dutch), Vrije Universiteit, Amsterdam, The Netherlands, 1984.
38. (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783; (c) E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943.
39. L. M. Stephenson, D. E. Smith and S. P. Current, J. Org. Chem., 1982, 47, 4170.
40. M. P. Mitoraj, A. Michalak and T. A. Ziegler, J. Chem. Theor. Comput., 2009, 5, 962.
41. I. Fernández and F. Matthias Bickelhaupt, J. Comput. Chem., 2014, 35, 371.
42. For a recent study on the origin of the asynchronicity in related Diels–Alder reactions see: P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2021, 23, 20095.

---

Footnote

† Electronic supplementary information (ESI) available: Figure S1 and Cartesian coordinates and electronic energies. See DOI: https://doi.org/10.1039/d3ob01343j

---