Exploring the computational design of anionic spin-crossover systems†
Laia
Navarro
 and
Jordi
Cirera
and
Jordi
Cirera
 *
*
Departament de Química Inorgànica i Orgànica and Institut de Recerca de Química Teòrica i Computacional, Universitat de Barcelona, Diagonal 645, 08028 Barcelona, Spain. E-mail: jordi.cirera@qi.ub.es
First published on 4th November 2022
Abstract
In this work, a systematic study on how the ligand design in the anionic spin-crossover system [Fe(OEt-L1-pH)(NCS)3]− can be used to achieve a high degree of tuning of its transition temperature (T1/2) is presented. Our calculations correctly reproduce the experimentally reported data and allow us to gain further and systematic insight on how to tune up or down the T1/2 value. The axial thiocyanate ligand can be replaced by similar groups (NCO−, NCSe− and NCBH3−) that allows for a large change in the T1/2 value, while a much finer degree of tuning can be achieved by functionalizing the para position of the pyridine groups. Altogether, [Fe(OEt-L1-pH)(NCS)3]− offers a unique platform to explore how ligand design can be realized to prepare new anionic SCO materials with tailored properties.
1. Introduction
Switchable or stimuli responsive materials1 are currently an active research area due to their potential technological applications in sensors,2–4 molecular machines,5 nanodevices,6 energy storage7,8 and self-healing materials,8 among others. Among such types of materials, spin-crossover (SCO) systems,9–14 which can switch reversibly between two alternative electronic states close in energy, are quite appealing systems due to their intrinsic behavior as molecular level switches.15–18 This transition, which can be triggered by changing the temperature, and also with pressure or electromagnetic radiation,19,20 comes with remarkable changes in the physical properties of the system, such as changes in the magnetic moment, color, or structural distortions.21,22 For all of the above reasons, many SCO systems have been characterized over the last century. This phenomenon was originally reported by Cambi in 1931 for Fe(III) coordination compounds,23 but this field rapidly grew and expanded to other transition metals,24 and eventually expanded also to systems with higher nuclearity25–27 and even coordination polymers which exhibit SCO transitions and are sensitive to the nature of their guest molecules.28–31The field of SCO is vastly dominated by six coordinated Fe(II) compounds,32–35 in which the transition is often induced by controlling the external temperature. The temperature with equal populations of both spin-states is defined as the transition temperature (T1/2) and is a key parameter for the physical characterization of SCO systems,36 but also a key factor in terms of making such systems operational, because in principle, one might like to preselect the temperature at which the SCO transition occurs. This is, however, a quite challenging task from the experimental point of view. Even though major progress has been made in this field, understanding how to modulate the transition temperature using ligand design is a major challenge in the rational design of new SCO systems with tailored properties. Because of this intrinsic problem, the use of computational tools has helped in gaining insight into how to modulate the transition temperature in SCO systems, using a broad range of electronic structural methods at different levels of theory as well as machine learning protocols.37–44
Most SCO systems are either neutral or positively charged, but very few of them have been reported having a total negative charge.45–62 The lack of more anionic SCO systems is somehow problematic because such systems are key components in the design of fluorescent multifunctional materials and conducting switchable materials. Thus, the synthesis of new anionic SCO systems with tailored properties is an important target towards the rational design of multifunctional materials that can be operated at specific temperatures.18,63 For this reason, we decided to study in detail the anionic SCO system [Fe(OEt-L1-pH)(NCS)3]− (L1 = tris(pyridin-2-yl)ethoxymethane),54 which allows for an important degree of chemical functionalization in the molecular skeleton, aiming to study the impact of such changes on the spin-state energy gap of the system, the corresponding transition temperatures, and the overall spin-crossover behavior of such systems. In this paper, we investigate the effect that three different possible sites, in which chemical functionalization can be applied, have on T1/2 of the family of the [Fe(R1-L1-pH)(L2)3]− (R1 = O–R or CH2–R, with R = H, –Me, –Et, –nPr and nBu, R2 = –NH2, –OH, –OMe, –Me, –F, –H, –Cl, –Br, –CF3 and –NO2, and L2 = NCO−, NCS−, NCSe− and NCBH3−) anionic SCO systems. First, we will present the results from our computational studies, which will be later discussed in terms of the electronic structure of the analyzed systems. Finally, conclusions and outlook will be reported.
2. Computational details
All density functional calculations (DFT) have been carried out with the Gaussian 16 (revision B0.1)64 electronic structure package with a 10−8 convergence criterion for the density matrix elements, using the latest triple-ζ basis set with polarization functions for all elements (def2-TZVP).65 For all systems, the exchange correlation functional TPSSh has been used, which has been recently reported as the most accurate one towards transition metal ions d4–d7 in terms of the spin-state energy gaps.66 However, the calculation of spin-state energy gaps using density functional theory methods is a quite challenging problem.67–70 Therefore, a benchmark study on the [Fe(OEt-L1-pH)(NCS)3]− system was performed, showing that only TPSSh and OPBE71,72 among several exchange/correlation functionals provide the correct spin-state energy gap (see the ESI†). Finally, the TPSSh functional,73 a hybrid version of the TPSS74meta-GGA functional with 10% of exact exchange Hartree-Fock, was chosen due to its overall performance towards SCO systems. The corresponding vibrational analysis was performed for all optimized structures to ensure that they were global minima along the potential energy surface. The transition temperatures (T1/2) were estimated using the thermochemistry quantities obtained in the vibrational analysis. To study the d-MOs energy gap in low-spin systems (S = 0), n-electron valence perturbation theory (NEVPT2)75 calculations were performed using the Orca 4.0 computer code.76 In these calculations, we employed the def2TZVPP basis set, including the corresponding auxiliary basis set for the correlation and Coulomb fitting. The active space contains the 5 d-orbitals of the metal and 6 electrons, and the ab initio ligand-field theory (AILFT) approach was employed to extract the related orbitals.773. Results
As indicated above, few anionic spin-crossover systems have been reported in the literature.45–62 Among them, the Fe(II) compound [Fe(OEt-L1-pH)(NCS)3]− (L1 = tris(pyridin-2-yl)ethoxymethane) offers us the possibility of studying how different chemical modifications on the ligand can be harvested to modify the physical properties of the compound allowing for, in principle, a fine degree of tuning of T1/2.54 In Fig. 1, we show the molecular structure of the parent compound and a schematic depiction of the system with three sites in which chemical modifications can be applied in order to alter the ligand field around the metal center, and thus its SCO properties. Such sites are the R1 group (ethoxy in the original system), the R2 group, which is at the para position of the pyridine groups (a H atom in the parent molecule), and finally the L2 ligand, which is a NCS− group in the original molecule. Therefore, one can systematically study the effect of modifying such sites on the spin-state energy gap in the system. Overall, the system of study can be labelled with the generic formula [Fe(R1-L1-pR2)(L2)3]−, which denotes the three positions in which we will apply chemical modifications to the molecule.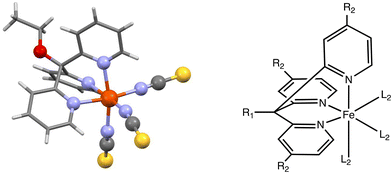 | ||
| Fig. 1 Left, the [Fe(OEt-L1-pH)(NCS)3]− (OEt-L1-pH = tris(pyridin-2-yl)ethoxymethane) molecule.54 Right, a schematic drawing of the system of study indicating the different functionalization sites. | ||
First, we studied the effect of replacing the thiocyanate (NCS−) ligand by similar ligands, such as the selenocyanate and cyanoborohydride ligands (NCSe− and NCBH3−), which are stronger ligand field substituents than the original NCS−, and we also tested the cyanate ligand (NCO−), a weaker one, to get a broader picture of the effect that L2 has on the SCO properties of the [Fe(OEt-L1-pH)(L2)3]− system. The results are summarized in Table 1.
From the above results, one can see that the experimentally reported trends for [Fe(OEt-L1-pH)(NCS)3]− and [Fe(OEt-L1-pH)(NCBH3)3]− are properly reproduced (see the ESI†),53 with a similar shift in the computed T1/2 as has been observed for previous calculations in SCO systems using the TPSSh functional.37,66
Next, we modified the R1 group while keeping R2 = H and L2 = NCS−. Two sets of substituents have been studied: first, alkane groups, starting from the smallest one (R1 = H) and up to the n-butyl group; secondly, alkoxide groups, starting from R1 = OH and up to the n-butoxy group. The results are summarized in Table 2.
| [Fe(R1-L1-pH)(NCS)3]− | ΔE | ΔH | ΔS | T 1/2 |
|---|---|---|---|---|
| a The average value of reported T1/2. | ||||
| R1 = H | 8.32 | 7.02 | 23.82 | 295 |
| R1 = Me | 10.48 | 9.15 | 23.50 | 389 (290) |
| R1 = Et | 6.97 | 5.63 | 24.66 | 228 (338) |
| R1 = nPr | 9.22 | 7.83 | 22.01 | 356 (298) |
| R1 = nBu | 9.34 | 7.97 | 23.84 | 334 (315) |
| R1 = OH | 9.03 | 7.70 | 23.32 | 330 (132) |
| R1 = OMe | 7.92 | 6.59 | 26.47 | 249 (245) |
| R1 = OEt | 6.94 | 5.59 | 24.67 | 226 (170a) |
| R1 = OnPr | 9.42 | 8.00 | 23.15 | 346 |
| R1 = OnBu | 7.12 | 5.75 | 24.39 | 236 |
At this point, we did some control calculations to evaluate if the inclusion of the counterions was required. From Table S2 in the ESI,† it is possible to find a family of systems that have been characterized with three different counterions. The [Fe(Me-L1-pH)(NCS)3]− system has been studied using [NMe4]+, [NBu4]+ and [PPh4]+ as counterions. The experimental T1/2 value for such systems (313, 330 and 290 K respectively) seems to indicate that the impact of the counterion is minor, but we computed the corresponding [Fe(Me-L1-pH)(NCS)3][C] systems (C = [NMe4]+, [NBu4]+ or [PPh4]+) to evaluate the impact of adding the counterion in the calculations. Once the spin-state energy gap was corrected for the basis set superposition error, the computed values are quite similar across the whole series and slightly higher than the computed value for the anionic species (see S7 in the ESI†), indicating that the effect of the counterion is minimal. To further evaluate if the counterions were affecting the predicted trends, we also computed the whole series for [Fe(Me-L1-pH)(L2)3][NMe4] (L2 = NCO−, NCS−, NCSe− and NCBH3−) and compared the trend with the one computed for the anionic families of [Fe(Me-L1-pH)(L2)3]− and [Fe(OEt-L1-pH)(L2)3]− systems (see S7 in the ESI†). These results show that the critical difference between both systems arises from replacing a Me group by an OEt group at the R1 position of the ligand, which has a much larger effect than doing the calculations with counterions. In fact, the experimentally reported shift for T1/2 between [Fe(Me-L1-pH)(NCS)3][NMe4] (T1/2 = 135 K) and [Fe(Me-L1-pH)(NCS)3][NMe4] (T1/2 = 313 K) is 178 K, a quite close value to the one computed for the [Fe(Me-L1-pH)(L2)3]− and [Fe(OEt-L1-pH)(L2)3]− anionic systems (163 K), thus reinforcing the idea that the calculations grasp the nature of the changes in the ligand field strength around the Fe(II) metal center. More importantly, in all cases the computed value with or without cations is quite similar.
Finally, we studied the effect that the para-substitution of the pyridine groups has on the SCO properties of the [Fe(OEt-L1-pR2)(L2)3]− systems. Here, we have been able to deal with two chemical functionalizations at the same time. For each L2 ligand, we studied several p-groups (R2 = –NH2, –OH, –OMe, –Me, –F, –H, –Cl, –Br, –CF3 and –NO2), covering from electron withdrawing groups (EWG) to electron donating groups (EDG). The results are summarized in Table 3, and the whole set of thermochemical data can be found in the ESI.†
| [Fe(OEt-L1-pR2)(NCX)3]− | NCS− | NCSe− | NCBH3− | |||
|---|---|---|---|---|---|---|
| ΔE | T 1/2 | ΔE | T 1/2 | ΔE | T 1/2 | |
| R2 = NH2 | 2.26 | 21 | 5.02 | 180 | 9.95 | 343 |
| R2 = OH | 5.19 | 143 | 6.72 | 211 | 10.37 | 367 |
| R2 = OMe | 5.30 | 167 | 6.85 | 221 | 10.67 | 381 |
| R2 = Me | 6.51 | 200 | 7.92 | 251 | 11.87 | 515 |
| R2 = F | 5.37 | 157 | 6.79 | 213 | 10.97 | 378 |
| R2 = H | 6.94 | 226 | 8.32 | 281 | 12.28 | 441 |
| R2 = Cl | 6.41 | 197 | 7.76 | 247 | 11.96 | 405 |
| R2 = Br | 6.51 | 201 | 7.86 | 250 | 12.09 | 411 |
| R2 = CF3 | 7.61 | 251 | 8.89 | 294 | 13.26 | 458 |
| R2 = NO2 | 6.37 | 229 | 8.50 | 309 | 14.53 | 504 |
4. Discussion
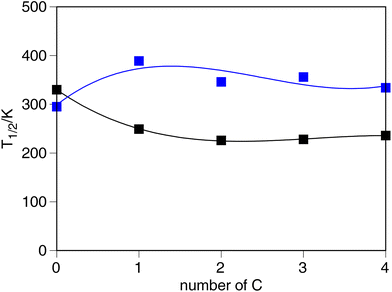
As can be seen from above, significant changes in the SCO properties can be observed upon the chemical modifications applied to the [Fe(R1-L1-pR2)(L2)3]− system. In the following section, we will discuss the origin of such changes and its trends, and the effect that such changes have on the ligand field splitting of the metal center.To begin with, the length of the R1 (R1 = O–R or CH2–R, R = –H, –Me, –Et, –nPr and –nBu) [Fe(R1-L1-pH)(NCS)3]− system could be envisioned as a potential first place for tuning of the SCO properties in such molecules. However, aside from the fact that O-donor and C-donor substituents have a different effect on T1/2, being the C-donors the ones that lead to higher T1/2, the value of the transition temperature seems to be, at least from the electronic point of view, mostly independent of the length of the R chain. This can be observed in Fig. 2, in which the dependence of T1/2 on the number of C atoms in the side chain becomes independent from each other. The O-donor groups tend to reach a stable value of 235 K, while the C-donor groups lead to a larger T1/2 value of 356 K. So, even though different behaviors are observed between the C-donor and the O-donor, no dependence on the length of the –R group for the R1 substituent can be outlined. These results are consistent with experimental studies on how the alkane/alkanoic side chains affect T1/2.78 We must stress at this point that although no significant electronic effects are observed, the length of this side chain (particularly for long chains) can play an important role in the crystal packing, thus modulating the overall shape of the spin-transition, but from the electronic point of view, the length of the side chain seems to have a minimal impact on the SCO properties of the [Fe(R1-L1-pR2)(L2)3]− systems.
On the other hand, it is clear that changing L2 in the [Fe(OEt-L1-pH)(L2)3]− systems will have a major impact on the ligand field splitting of the FeII metal center. The increasing ligand strength, NCO− < NCS− < NCSe− < NCBH3−, appears to be clearly reflected in the progressive shift in the computed T1/2 value, as has been observed experimentally for some of these systems.53 A nice correlation between the ligand f factor,79 which measures the ligand strength, and the computed T1/2 can be outlined, as seen in Fig. 3. The magnitude of the d-MO splitting can be properly quantified by the Ab Initio Ligand Field Theory (AILFT) method to analyze the output from NEVPT2 calculations on the optimized geometries for all [Fe(OEt-L1-pH)(L2)3]− low-spin systems. The computed Δ against the ligand f factor also reflects the increasing gap among the d-based MOs (see the ESI†), from 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 to 18
200 to 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 between the weakest (NCO−) and the strongest (NCBH3−) ligand. As has been reported for similar systems, the increasing gap is due to the loss of the partial antibonding character among the t2g orbitals. This set of orbitals, which are non-bonding for the perfect octahedron with six σ-donor ligands, gains antibonding character due to the presence of π-type orbitals from the NCX− ligands that can interact in a π-antibonding fashion with the dxz, dyz and dxy orbitals. However, as the L2 ligand becomes stronger, these π-type orbitals move down in energy, thus effectively decreasing the interaction of the d-MOs that regain non-bonding character and leading to larger Δ values. In Fig. 4, we plotted the HOMO for the [Fe(OEt-L1-pH)(L2)3]− systems (L2 = NCO−, NCS−, NCSe− and NCBH3−) to illustrate such effects.
200 cm−1 between the weakest (NCO−) and the strongest (NCBH3−) ligand. As has been reported for similar systems, the increasing gap is due to the loss of the partial antibonding character among the t2g orbitals. This set of orbitals, which are non-bonding for the perfect octahedron with six σ-donor ligands, gains antibonding character due to the presence of π-type orbitals from the NCX− ligands that can interact in a π-antibonding fashion with the dxz, dyz and dxy orbitals. However, as the L2 ligand becomes stronger, these π-type orbitals move down in energy, thus effectively decreasing the interaction of the d-MOs that regain non-bonding character and leading to larger Δ values. In Fig. 4, we plotted the HOMO for the [Fe(OEt-L1-pH)(L2)3]− systems (L2 = NCO−, NCS−, NCSe− and NCBH3−) to illustrate such effects.
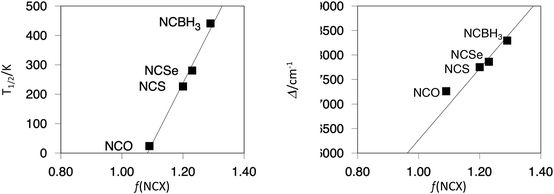 | ||
| Fig. 3 Correlation between the ligand f factor and the computed T1/2 (left), and the computed Δ (right) values. | ||
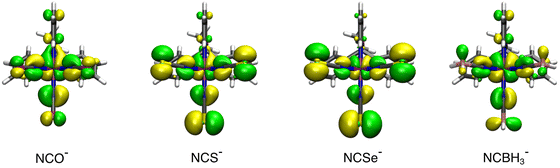 | ||
| Fig. 4 Isosurfaces for the HOMO d-based MOs on the [Fe(OEt-L1-pH)(L2)3]− systems (L2 = NCO−, NCS−, NCSe− and NCBH3−) (0.03 au−3/2 isovalue contour). | ||
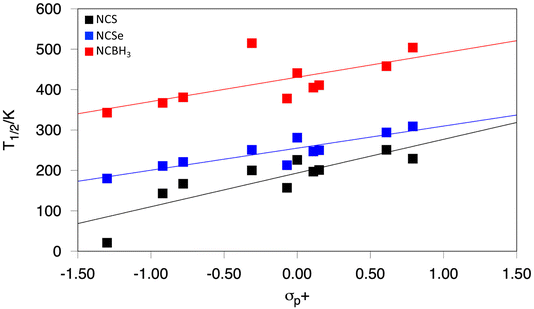
Another way of tuning T1/2, in a more subtle way, is using electron donating groups (EDGs) or electron withdrawing groups (EWGs) as substituents at the para position of the pyridine ring. This effect has been already reported in other SCO systems and shows T1/2 shifts towards higher values as the EDG character of the para-substituent increases. We decided to study how such substitutions impact the SCO properties and functionalized the pyridine group of the OEt-L1-pR2 ligand (R2 = –NH2, –OH, –OMe, –Me, –F, –H, –Cl, –Br, –CF3 and –NO2) in the [Fe(OEt-L1-pR2)(NCS)3]− system. As expected, EWGs lead to smaller values of T1/2, and this parameter can be tuned up by replacing the R2 group with a stronger EDG substituent. In fact, a correlation with the Hammett σp+ parameter80 (or the σp constant, see the ESI†) can be outlined (Fig. 5), in agreement with this behavior, as has been previously observed for other SCO systems.81–87 This trend thus allows for a fine tuning degree of T1/2 for the [Fe(OEt-L1-pR2)(NCS)3]− system, and we decided to explore if a similar behavior would occur for the other [Fe(OEt-L1-pR2)(L2)3]− systems. Our results show that, actually, a very similar degree of fine tuning is observed regardless of the L2 ligand (L2 = NCS−, NCSe−, and NCBH3−), meaning that one can select a specific range of temperatures using L2 and later on select a much finer degree of tuning of T1/2via the R2 substituent of the pyridine ligands. A similar trend is also observed for NCO−, but the weaker nature of this ligand makes, in the majority of cases, the system a high-spin system, and only the strongest EDG has an impact on increasing T1/2 (see the ESI†).
5. Conclusions
In this work, the TPSSh functional has been used to analyze the SCO properties of the [Fe(OEt-L1-pH)(NCS)3]− system, one of the few anionic SCO molecules reported in the literature. In order to expand this family of compounds and design systems with specific physical properties, we used our computational methodology to study the effect that different functionalizations will have on the spin-state energy gap for different members of the [Fe(R1-L1-pR2)(L2)3]− family, in which several chemical modifications over the basic molecular structure have been studied. Functionalization of R1 does lead to some differences, but the length of the aliphatic chain seems to play a minor role in the modulation of T1/2. In any case, the role of this side chain cannot be overlooked in terms of modifying the SCO properties through crystal packing effects. On the other hand, by changing the L2 ligands one can access a broad range of transition temperatures that can later be fine-tuned using the R2 groups of the pyridine ligand. Our results show that a two-knob model can be outlined, in which one can select a higher or lower T1/2 value by using different L2 ligands and achieve a much precise value of such a quantity through the pyridine functionalization at the para position. All trends can be understood in terms of the electronic structure of the studied systems, and several correlations have been outlined that predict the changes that T1/2 will experience upon ligand modification. We believe that our results will be of great help in the future design of new anionic SCO systems that can be operated at specific transition temperatures.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
J. C. thanks the Spanish MICINN for a Ramón y Cajal research contract (RYC2018-024692-I), the Spanish MICINN research grant (PID2020-115165GB-I00) and the Spanish Structures of Excellence María de Maeztu program (MDM-2017-0767). L. N. is grateful for a PREDOCS-UB 2019 grant (5760700-Institut de Química Teòrica i Computacional).References
- M. W. Urban, in Handbook of Stimuli–Responsive Materials, ed. M. W. Urban, Wiley, 2011. DOI:10.1002/9783527633739.
- P. Qin, S. Okur, C. Li, A. Chandresh, D. Mutruc, S. Hecht and L. Heinke, A Photoprogrammable Electronic Nose with Switchable Selectivity for VOCs Using MOF Films, Chem. Sci., 2021, 12, 15700–15709, 10.1039/d1sc05249g.
- M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Bidirectional Chemo-Switching of Spin State in a Microporous Framework, Angew. Chem., Int. Ed., 2009, 48(26), 4767–4771, DOI:10.1002/anie.200806039.
- A. Darabi, P. G. Jessop and M. F. Cunningham, CO2-Responsive Polymeric Materials: Synthesis, Self-Assembly, and Functional Applications, Chem. Soc. Rev., 2016, 45(15), 4391–4436, 10.1039/C5CS00873E.
- I. Aprahamian, The Future of Molecular Machines, ACS Cent. Sci., 2020, 6(3), 347–358, DOI:10.1021/acscentsci.0c00064.
- D. Natelson, Nanostructures and Nanotechnology, Cambridge University Press, 2015. DOI:10.1017/CBO9781139025485.
- C. Sun, C. Wang and R. Boulatov, Applications of Photoswitches in the Storage of Solar Energy, ChemPhotoChem, 2019, 3(6), 268–283, DOI:10.1002/cptc.201900030.
- A. Goulet-Hanssens, F. Eisenreich and S. Hecht, Enlightening Materials with Photoswitches, Adv. Mater., 2020, 32(20), 1905966, DOI:10.1002/adma.201905966.
- M. A. Halcrow, in Spin-Crossover Materials, ed. M. A. Halcrow, John Wiley & Sons Ltd, Oxford, UK, 2013. DOI:10.1002/9781118519301.
- G. Molnár, S. Rat, L. Salmon, W. Nicolazzi and A. Bousseksou, Spin Crossover Nanomaterials: From Fundamental Concepts to Devices, Adv. Mater., 2018, 30(5), 1703862, DOI:10.1002/adma.201703862.
- P. Gütlich, Spin Crossover - Quo Vadis?, Eur, J. Inorg. Chem., 2013, 2013(5–6), 581–591, DOI:10.1002/ejic.201300092.
- P. Gütlich and H. A. Goodwin, Spin Crossover in Transition Metal Compounds III, Topics in Current Chemistry, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004. vol. 235. DOI:10.1007/b96439.
- K. Senthil Kumar and M. Ruben, Emerging Trends in Spin Crossover (SCO) Based Functional Materials and Devices, Coord. Chem. Rev., 2017, 346, 176–205, DOI:10.1016/j.ccr.2017.03.024.
- P. Gütlich, A. B. Gaspar and Y. Garcia, Spin State Switching in Iron Coordination Compounds, Beilstein J. Org. Chem., 2013, 9, 342–391, DOI:10.3762/bjoc.9.39.
- M. C. Muñoz and J. A. Real, Thermo-, Piezo-, Photo- and Chemo-Switchable Spin Crossover Iron(II)-Metallocyanate Based Coordination Polymers, Coord. Chem. Rev., 2011, 255(17–18), 2068–2093, DOI:10.1016/j.ccr.2011.02.004.
- M. A. Halcrow, Structure: Function Relationships in Molecular Spin-Crossover Complexes, Chem. Soc. Rev., 2011, 40(7), 4119, 10.1039/c1cs15046d.
- I. Boldog, A. B. Gaspar, V. Martínez, P. Pardo-Ibañez, V. Ksenofontov, A. Bhattacharjee, P. Gütlich and J. A. Real, Spin-Crossover Nanocrystals with Magnetic, Optical, and Structural Bistability near Room Temperature, Angew. Chem., Int. Ed., 2008, 47(34), 6433–6437, DOI:10.1002/anie.200801673.
- B. Benaicha, K. Van Do, A. Yangui, N. Pittala, A. Lusson, M. Sy, G. Bouchez, H. Fourati, C. J. Gómez-García, S. Triki and K. Boukheddaden, Interplay between Spin-Crossover and Luminescence in a Multifunctional Single Crystal Iron(II) Complex: Towards a New Generation of Molecular Sensors, Chem. Sci., 2019, 10(28), 6791–6798, 10.1039/C9SC02331C.
- P. Gütlich, A. B. Gaspar, Y. Garcia and V. Ksenofontov, Pressure Effect Studies in Molecular Magnetism, C. R. Chim., 2007, 10(1–2), 21–36, DOI:10.1016/j.crci.2006.09.011.
- J. A. Real, A. B. Gaspar and M. C. Muñoz, Thermal, Pressure and Light Switchable Spin-Crossover Materials, Dalton Trans., 2005,(12), 2062, 10.1039/b501491c.
- S. Alvarez, Relationships between Temperature, Magnetic Moment, and Continuous Symmetry Measures in Spin Crossover Complexes, J. Am. Chem. Soc., 2003, 125(22), 6795–6802, DOI:10.1021/ja0283450.
- M. Oppermann, F. Zinna, J. Lacour and M. Chergui, Chiral Control of Spin-Crossover Dynamics in Fe(II) Complexes, Nat. Chem., 2022, 14(7), 739–745, DOI:10.1038/s41557-022-00933-0.
- L. Cambi and L. Szegö, Über Die Magnetische Susceptibilität Der Komplexen Verbindungen, Ber. Dtsch. Chem. Ges. (A and B Series), 1931, 64(10), 2591–2598, DOI:10.1002/cber.19310641002.
- J. Olguín, Unusual Metal Centres/Coordination Spheres in Spin Crossover Compounds, Coord. Chem. Rev., 2020, 407(15), 213148, DOI:10.1016/j.ccr.2019.213148.
- K. S. Murray, Advances in Polynuclear Iron(II), Iron(III) and Cobalt(II) Spin–Crossover Compounds, Eur. J. Inorg. Chem., 2008, 2008(20), 3101–3121, DOI:10.1002/ejic.200800352.
- R. W. Hogue, S. Singh and S. Brooker, Spin Crossover in Discrete Polynuclear Iron(II) Complexes, Chem. Soc. Rev., 2018, 47(19), 7303–7338, 10.1039/C7CS00835J.
- E. Breuning, M. Ruben, J.-M. Lehn, F. Renz, Y. Garcia, V. Ksenofontov, P. Gütlich, E. Wegelius and K. Rissanen, Spin Crossover in a Supramolecular Fe4II [2 × 2] Grid Triggered by Temperature, Pressure, and Light, Angew. Chem., Int. Ed., 2000, 39(14), 2504–2507, DOI:10.1002/1521-3773(20000717)39:14<2504::AID-ANIE2504>3.0.CO;2-B.
- X.-W. Zhu, D. Luo, X.-P. Zhou and D. Li, Imidazole-Based Metal-Organic Cages: Synthesis, Structures, and Functions, Coord. Chem. Rev., 2022, 455, 214354, DOI:10.1016/j.ccr.2021.214354.
- H.-Y. Li, S.-N. Zhao, S.-Q. Zang and J. Li, Functional Metal–Organic Frameworks as Effective Sensors of Gases and Volatile Compounds, Chem. Soc. Rev., 2020, 49(17), 6364–6401, 10.1039/C9CS00778D.
- M. Nakaya, R. Ohtani and S. Hayami, Guest Modulated Spin States of Metal Complex Assemblies, Eur. J. Inorg. Chem., 2020, 2020(39), 3709–3719, DOI:10.1002/ejic.202000553.
- C. Bartual-Murgui, A. Akou, C. Thibault, G. Molnár, C. Vieu, L. Salmon and A. Bousseksou, Spin-Crossover Metal–Organic Frameworks: Promising Materials for Designing Gas Sensors, J. Mater. Chem. C, 2015, 3(6), 1277–1285, 10.1039/C4TC02441A.
- Y.-C. Chuang, C.-T. Liu, C.-F. Sheu, W.-L. Ho, G.-H. Lee, C.-C. Wang and Y. Wang, New Iron(II) Spin Crossover Coordination Polymers [Fe(μ-Atrz)3]X2·2H2O (X = ClO4−, BF4−) and [Fe(μ-Atrz)(μ-Pyz)(NCS)2]·4H2O with an Interesting Solvent Effect, Inorg. Chem., 2012, 51(8), 4663–4671, DOI:10.1021/ic202626c.
- D. C. Ashley and E. Jakubikova, Ironing out the Photochemical and Spin-Crossover Behavior of Fe(II) Coordination Compounds with Computational Chemistry, Coord. Chem. Rev., 2017, 337, 97–111, DOI:10.1016/j.ccr.2017.02.005.
- H. S. Scott, R. W. Staniland and P. E. Kruger, Spin Crossover in Homoleptic Fe(II) Imidazolylimine Complexes, Coord. Chem. Rev., 2018, 362, 24–43, DOI:10.1016/j.ccr.2018.02.001.
- P. Gütlich, Y. Garcia and H. A. Goodwin, Spin Crossover Phenomena in Fe(Ii) Complexes, Chem. Soc. Rev., 2000, 29(6), 419–427, 10.1039/b003504l.
- O. Kahn, Molecular Magnetism, VCH, 1993 Search PubMed.
- J. Cirera and F. Paesani, Theoretical Prediction of Spin-Crossover Temperatures in Ligand-Driven Light-Induced Spin Change Systems, Inorg. Chem., 2012, 51(15), 8194–8201, DOI:10.1021/ic300750c.
- J. Cirera and E. Ruiz, Theoretical Modeling of the Ligand-Tuning Effect over the Transition Temperature in Four-Coordinated Fe-II Molecules, Inorg. Chem., 2016, 55(4), 1657–1663, DOI:10.1021/acs.inorgchem.5b02564.
- A. Rudavskyi, C. Sousa, C. de Graaf, R. W. A. Havenith and R. Broer, Computational Approach to the Study of Thermal Spin Crossover Phenomena, J. Chem. Phys., 2014, 140(18), 184318, DOI:10.1063/1.4875695.
- S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Thermal Spin Crossover in FeII and FeIII. Accurate Spin State Energetics at the Solid State, Phys. Chem. Chem. Phys., 2020, 22(9), 4938–4945, 10.1039/D0CP00162G.
- J. Cirera and E. Ruiz, Computational Modeling of Transition Temperatures in Spin-Crossover Systems, Comments Inorg. Chem., 2019, 39(4), 216–241, DOI:10.1080/02603594.2019.1608967.
- J. P. Janet, L. Chan and H. J. Kulik, Accelerating Chemical Discovery with Machine Learning: Simulated Evolution of Spin Crossover Complexes with an Artificial Neural Network, J. Phys. Chem. Lett., 2018, 9(5), 1064–1071, DOI:10.1021/acs.jpclett.8b00170.
- L. Navarro, F. Rodriguez and J. Cirera, Controlling the Spin-Crossover Behavior of the [Cr(Indenyl)2] Family via Ligand Functionalization, Dalton Trans., 2021, 50(25), 8704–8710, 10.1039/D1DT00481F.
- D. Vidal, J. Cirera and J. Ribas-Arino, Accurate Calculation of Spin-State Energy Gaps in Fe(III) Spin-Crossover Systems Using Density Functional Methods, Dalton Trans., 2021, 50(47), 17635–17642, 10.1039/D1DT03335B.
- W. Phonsri, B. A. I. Lewis, G. N. L. Jameson and K. S. Murray, Double Spin Crossovers: A New Double Salt Strategy to Improve Magnetic and Memory Properties, Chem. Commun., 2019, 55(93), 14031–14034, 10.1039/C9CC07416C.
- W. Phonsri, D. S. Macedo, B. A. I. Lewis, D. F. Wain and K. S. Murray, Iron(III) Azadiphenolate Compounds in a New Family of Spin Crossover Iron(II)–Iron(III) Mixed-Valent Complexes, Magnetochemistry, 2019, 5(2), 37, DOI:10.3390/magnetochemistry5020037.
- V. Gómez, S. de Pipaón, C. Maldonado-Illescas, P. Waerenborgh, J. C. Martin, E. Benet-Buchholz, J. Galán-Mascarós and J. R, Easy Excited-State Trapping and Record High TTIESST in a Spin-Crossover Polyanionic FeII Trimer, J. Am. Chem. Soc., 2015, 137(37), 11924–11927, DOI:10.1021/jacs.5b07879.
- N. Hirosawa, Y. Oso and T. Ishida, Spin Crossover and Light-Induced Excited Spin-State Trapping Observed for an Iron(II) Complex Chelated with Tripodal Tetrakis(2-Pyridyl)Methane, Chem. Lett., 2012, 41(7), 716–718, DOI:10.1246/cl.2012.716.
- M. Yamasaki and T. Ishida, Spin-Crossover Thermal Hysteresis and Light-Induced Effect on Iron(II) Complexes with Tripodal Tris(2-Pyridyl)Methanol, Polyhedron, 2015, 85, 795–799, DOI:10.1016/j.poly.2014.10.013.
- M. Yamasaki and T. Ishida, Heating-Rate Dependence of Spin-Crossover Hysteresis Observed in an Iron(II) Complex Having Tris(2-Pyridyl)Methanol, J. Mater. Chem. C, 2015, 3(30), 7784–7787, 10.1039/C5TC00926J.
- T. Ishida, T. Kanetomo and M. Yamasaki, An Iron(II) Complex Tripodally Chelated with 1,1,1-Tris(Pyridin-2-Yl)Ethane Showing Room-Temperature Spin-Crossover Behaviour, Acta Crystallogr., Sect. C: Struct. Chem., 2016, 72(11), 797–801, DOI:10.1107/S2053229616004174.
- A. Kashiro, K. Some, Y. Kobayashi and T. Ishida, Iron(II) and 1,1,1-Tris(2-Pyridyl)Nonadecane Complex Showing an Order–Disorder-Type Structural Transition and Spin-Crossover Synchronized over Both Conformers, Inorg. Chem., 2019, 58(12), 7672–7676, DOI:10.1021/acs.inorgchem.9b01146.
- E. Cuza, S. Benmansour, N. Cosquer, F. Conan, S. Pillet, C. J. Gómez-García and S. Triki, Spin Cross-Over (SCO) Anionic Fe(II) Complexes Based on the Tripodal Ligand Tris(2-Pyridyl)Ethoxymethane, Magnetochemistry, 2020, 6(2), 26, DOI:10.3390/magnetochemistry6020026.
- E. Cuza, C. D. Mekuimemba, N. Cosquer, F. Conan, S. Pillet, G. Chastanet and S. Triki, Spin Crossover and High-Spin State in Fe(II) Anionic Polymorphs Based on Tripodal Ligands, Inorg. Chem., 2021, 60(9), 6536–6549, DOI:10.1021/acs.inorgchem.1c00335.
- S. Murata, K. Takahashi, T. Sakurai, H. Ohta, T. Yamamoto, Y. Einaga, Y. Shiota and K. Yoshizawa, The Role of Coulomb Interactions for Spin Crossover Behaviors and Crystal Structural Transformation in Novel Anionic Fe(III) Complexes from a π-Extended ONO Ligand, Crystals, 2016, 6(5), 49, DOI:10.3390/cryst6050049.
- K. Takahashi, K. Kawamukai, M. Okai, T. Mochida, T. Sakurai, H. Ohta, T. Yamamoto, Y. Einaga, Y. Shiota and K. Yoshizawa, A New Family of Anionic Fe III Spin Crossover Complexes Featuring a Weak-Field N2O4 Coordination Octahedron, Chem. – Eur. J., 2016, 22(4), 1253–1257, DOI:10.1002/chem.201504883.
- C. Cook, F. Habib, T. Aharen, R. Clérac, A. Hu and M. Murugesu, High-Temperature Spin Crossover Behavior in a Nitrogen-Rich Fe III -Based System, Inorg. Chem., 2013, 52(4), 1825–1831, DOI:10.1021/ic301864d.
- Z.-Y. Li, J.-W. Dai, Y. Shiota, K. Yoshizawa, S. Kanegawa and O. Sato, Multi-Step Spin Crossover Accompanied by Symmetry Breaking in an Fe III Complex: Crystallographic Evidence and DFT Studies, Chem. – Eur. J., 2013, 19(39), 12948–12952, DOI:10.1002/chem.201302272.
- S. Floquet, N. Guillou, P. Négrier, E. Rivière and M.-L. Boillot, The Crystallographic Phase Transition for a Ferric Thiosemicarbazone Spin Crossover Complex Studied by X-Ray Powder Diffraction, New J. Chem., 2006, 30(11), 1621–1627, 10.1039/B605326B.
- S. Floquet, M.-L. Boillot, E. Rivière, F. Varret, K. Boukheddaden, D. Morineau and P. Négrier, Spin Transition with a Large Thermal Hysteresis near Room Temperature in a Water Solvate of an Iron(III) Thiosemicarbazone Complex, New J. Chem., 2003, 27(2), 341, 10.1039/b207516d.
- S. K. Karuppannan, A. Martín-Rodríguez, E. Ruiz, P. Harding, D. J. Harding, X. Yu, A. Tadich, B. Cowie, D. Qi and C. A. Nijhuis, Room Temperature Conductance Switching in a Molecular Iron(III) Spin Crossover Junction, Chem. Sci., 2021, 12(7), 2381–2388, 10.1039/D0SC04555A.
- M. Yamada, M. Ooidemizu, Y. Ikuta, S. Osa, N. Matsumoto, S. Iijima, M. Kojima, F. Dahan and J.-P. Tuchagues, Interlayer Interaction of Two-Dimensional Layered Spin Crossover Complexes [FeIIH3LMe ][FeIIL Me ]X (X - = ClO4-, BF3-, PF6-, AsF6-, and SbF6 -; H3L, Inorg. Chem., 2003, 42(25), 8406–8416, DOI:10.1021/ic034439e.
- E. Coronado, J. R. Galán-Mascarós, C. J. Gómez-García and V. Laukhin, Coexistence of Ferromagnetism and Metallic Conductivity in a Molecule-Based Layered Compound, Nature, 2000, 408(6811), 447–449, DOI:10.1038/35044035.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. B.01, Gaussian, Inc., Wallingford, CT 2016 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305, 10.1039/b508541a.
- J. Cirera, M. Via-Nadal and E. Ruiz, Benchmarking Density Functional Methods for Calculation of State Energies of First Row Spin-Crossover Molecules, Inorg. Chem., 2018, 57(22), 14097–14105, DOI:10.1021/acs.inorgchem.8b01821.
- M. Swart, Accurate Spin-State Energies for Iron Complexes, J. Chem. Theory Comput., 2008, 4(12), 2057–2066, DOI:10.1021/ct800277a.
- M. Swart, Spin States of (Bio)Inorganic Systems: Successes and Pitfalls, Int. J. Quantum Chem., 2013, 113(1), 2–7, DOI:10.1002/qua.24255.
- K. P. Kepp, Theoretical Study of Spin Crossover in 30 Iron Complexes, Inorg. Chem., 2016, 55(6), 2717–2727, DOI:10.1021/acs.inorgchem.5b02371.
- K. P. Jensen and J. Cirera, Accurate Computed Enthalpies of Spin Crossover in Iron and Cobalt Complexes, J. Phys. Chem. A, 2009, 113(37), 10033–10039, DOI:10.1021/jp900654j.
- N. C. Handy and A. J. Cohen, Left-Right Correlation Energy, Mol. Phys., 2001, 99(5), 403–412, DOI:10.1080/00268970010018431.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78(7), 1396 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. M. Tao and J. P. Perdew, Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes, J. Chem. Phys., 2003, 119(23), 12129–12137, DOI:10.1063/1.1626543.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401, DOI:10.1103/PhysRevLett.91.146401.
- C. Angeli, R. Cimiraglia and J. P. Malrieu, N-Electron, Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants, J. Chem. Phys., 2002, 117(20), 9138–9153, DOI:10.1063/1.1515317.
- F. Neese, Software Update: The ORCA Program System, Version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1327, DOI:10.1002/wcms.1327.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Covalency and Chemical Bonding in Transition Metal Complexes: An Ab Initio Based Ligand Field Perspective, Coord. Chem. Rev., 2017, 344, 2–25, DOI:10.1016/j.ccr.2017.03.018.
- A. Kashiro, W. Kohno and T. Ishida, Odd–Even Effect on the Spin-Crossover Temperature in Iron(II) Complex Series Involving an Alkylated or Acyloxylated Tripodal Ligand, Inorg. Chem., 2020, 59(14), 10163–10171, DOI:10.1021/acs.inorgchem.0c01296.
- C. K. Jørgensen, Modern Aspects of Ligand Field Theory, North-Holland Publishing, 1971 Search PubMed.
- C. Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91(2), 165–195, DOI:10.1021/cr00002a004.
- M. F. Tweedle and L. J. Wilson, Variable Spin Iron(III) Chelates with Hexadentate Ligands Derived from Triethylenetetramine and Various Salicylaldehydes. Synthesis, Characterization, and Solution State Studies of a New 2T .Dblarw. 6A Spin Equilibrium System, J. Am. Chem. Soc., 1976, 98(16), 4824–4834, DOI:10.1021/ja00432a023.
- J.-F. Létard, C. Carbonera, J. A. Real, S. Kawata and S. Kaizaki, Photomagnetism of a Series of Dinuclear Iron(II) Complexes, Chem. – Eur. J., 2009, 15(16), 4146–4155, DOI:10.1002/chem.200802171.
- I. Prat, A. Company, T. Corona, T. Parella, X. Ribas and M. Costas, Assessing the Impact of Electronic and Steric Tuning of the Ligand in the Spin State and Catalytic Oxidation Ability of the Fe II (Pytacn) Family of Complexes, Inorg. Chem., 2013, 52(16), 9229–9244, DOI:10.1021/ic4004033.
- K. Cook, L. J. Kulmaczewski, R. Mohammed, R. Dudley, S. Barrett, S. A. Little, M. A. Deeth, R. J. Halcrow and M. A, A Unified Treatment of the Relationship Between Ligand Substituents and Spin State in a Family of Iron(II) Complexes, Angew. Chem., Int. Ed., 2016, 55(13), 4327–4331, DOI:10.1002/anie.201600165.
- A. Kimura and T. Ishida, Pybox-Iron(II) Spin-Crossover Complexes with Substituent Effects from the 4-Position of the Pyridine Ring (Pybox = 2,6-Bis(Oxazolin-2-Yl)Pyridine), Inorganics, 2017, 5(3), 52, DOI:10.3390/inorganics5030052.
- H.-C. Liang, Y. Pan, H.-L. Zhu, Y.-S. Meng, C.-H. Liu, T. Liu and Y.-Y. Zhu, The Substituent Effect on the Spin-Crossover Behaviour in a Series of Mononuclear Fe(II) Complexes from Thio-Pybox Ligands, Inorg. Chem. Front., 2022, 9(10), 2343–2352, 10.1039/D2QI00208F.
- R. Kulmaczewski, M. J. Howard and M. A. Halcrow, Influence of Ligand Substituent Conformation on the Spin State of an Iron(II)Di(Pyrazol-1-Yl)Pyridine Complex, Dalton Trans., 2021, 50(10), 3464–3467, 10.1039/D1DT00590A.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2qi02163c |
| This journal is © the Partner Organisations 2023 |