Open Access Article
Open Access ArticleAsymmetry-enhanced 59Co NMR thermometry in Co(III) complexes†
Ökten
Üngör
 ,
Stephanie
Sanchez
,
Tyler M.
Ozvat
,
Stephanie
Sanchez
,
Tyler M.
Ozvat
 and
Joseph M.
Zadrozny
and
Joseph M.
Zadrozny
 *
*
Department of Chemistry, Colorado State University, Fort Collins, Colorado 80523, USA. E-mail: joe.zadrozny@colostate.edu
First published on 23rd October 2023
Abstract
Design strategies for molecular thermometers by magnetic resonance are essential for enabling new noninvasive means of temperature mapping for disease diagnoses and treatments. Herein we demonstrate a new design strategy for thermometry based on chemical control of the vibrational partition function. To do so, we performed variable-temperature 59Co NMR investigations of four air-stable Co(III) complexes: Co(accp)3 (1), Co(bzac)3 (2), Co(tBu2-acac)3 (3), and Co(acac)3 (4) (accp = 2-acetylcyclopentanonate; bzac = benzoylacetonate; tBu2-acac = 2,2,6,6-tetramethyl-3,5-heptanedionate and acac = acetylacetonate). We discovered 59Co chemical shift temperature sensitivity (Δδ/ΔT) values of 3.50(2), 3.39(3), 1.63(3), and 2.83(1) ppm °C−1 for 1–4, respectively, at 100 mM concentration. The values observed for 1 and 2 are new records for sensitivity for low-spin Co(III) complexes. We propose that the observed heightened sensitivities for 1 and 2 are intimately tied to the asymmetry of the accp and bzac ligands versus the acac and tBu2-acac ligands, which enables a larger number of low-energy Raman-active vibrational modes to contribute to the observed Δδ/ΔT values.
Introduction
Thermometry by magnetic resonance imaging, which utilizes nuclear magnetic resonance (NMR) technology, is a powerful technique for noninvasive monitoring of temperature.1–3 This capability is important in biomedical treatments, e.g. monitoring the progression of thermal ablation of tumors. Moreover, the technique is also important for simply achieving a deeper fundamental understanding of internal temperature regulation in the body, which is poorly understood and still yielding new insights to this day.4 Designing molecular probes that enable high temperature/spatial resolution in vivo is an essential component of improving thermometer capabilities.One method for temperature detection via NMR utilizes a temperature-dependent chemical shift. This technique can use protons (1H),5–719F,8,913C,10,11 and 31P.12,13 Yet, the temperature sensitivities of these systems are often low, <1 ppm °C−1 (e.g, 0.01 ppm °C−1 for 1H in H2O,6 or 0.012 ppm °C−1 in 19F as perfluorotributylamine9). A related technique, PARACEST (PARAmagnetic Chemical Exchange Saturation Transfer), can imbue a temperature dependence to the 1H chemical shift of bulk water through hyperfine coupling in open-shell lanthanide complexes.14,15 These strategies also generally produce temperature sensitivities of ca. 1 ppm °C−1.
The 59Co nucleus in low-spin Co(III) complexes is a particularly attractive alternative system for chemical-shift-based thermometry applications.16 The 59Co nucleus is 100% naturally abundant, exhibits a nuclear spin of I = 7/2, has a high receptivity (ca. 30% that of 1H), and displays a wide reported chemical shift (δ) window (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm), which reflects an exquisite sensitivity of δ to electronic structure and the ligand field splitting (Δo).17,18 Importantly, the 59Co nucleus also typically yields a large temperature-dependent chemical shift, Δδ/ΔT, of 1–3 ppm °C−1 in magnitude, which stems from the temperature dependence of Δo. In 1980, Levy and co-workers set the record for Δδ/ΔT with Co(acac)3 (acac = acetylacetonate), which displayed a 3.15 ppm °C−1 Δδ/ΔT for the 59Co nucleus.19
000 ppm), which reflects an exquisite sensitivity of δ to electronic structure and the ligand field splitting (Δo).17,18 Importantly, the 59Co nucleus also typically yields a large temperature-dependent chemical shift, Δδ/ΔT, of 1–3 ppm °C−1 in magnitude, which stems from the temperature dependence of Δo. In 1980, Levy and co-workers set the record for Δδ/ΔT with Co(acac)3 (acac = acetylacetonate), which displayed a 3.15 ppm °C−1 Δδ/ΔT for the 59Co nucleus.19
A target sensitivity of ca. 10 ppm °C−1 for 59Co is ideal to balance the typical wide linewidths of the peaks, and the gradient range in an MRI scanner, and avoid the need for retuning the instrument mid-measurement. A molecule to reach this target parameter should ideally also be air stable to facilitate biomedical imaging applications. In light of these requirements, the recently reported20 record (>100 ppm °C−1) sensitivities in [(CpCo(OP(OR)2)3)2]Co+ (R = Me, Et, tBu) are too large. The complexes are also air sensitive, and these two properties together limit applicability. Separately, one complex that is closer to the 10 ppm °C−1 goal, [tBu(PNP)Fe–H], exhibits thermal sensitivities of 14 ppm °C−1 (1H)21 and 34 ppm °C−1 (31P)22 though these molecules are also, unfortunately, air sensitive. Hence, design strategies to maximize Δδ/ΔT in an air-stable compound remains a key target of fundamental understanding.
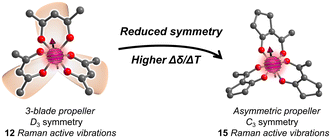
We recently proposed a route to a higher Δδ/ΔT through designing the vibrational partition function. In this strategy, the target parameter for higher Δδ/ΔT is a larger number of low-energy symmetric (Raman-active) vibrational modes.23 A group-theory analysis of the CoO6 coordination shell of Co(acac)3 reveals 15 possible vibrations, but local D3 symmetry ensures that only 12 of these are Raman active (Fig. 1). We hypothesized that the 3 lost vibrations could be diminishing the partition function, and, hence, lowering Δδ/ΔT. We hypothesized that a system with asymmetric bidentate ligands would lower local point group symmetry to C3 (or lower), symmetries where all vibrations are Raman active, and hence ensure a higher partition function and thus higher Δδ/ΔT.
Herein we report the synthesis and 59Co NMR characterization of a set of Co(III) complexes with asymmetric analogues of the acac ligand: Co(accp)3 (1, accp = 2-acetylcyclopentanonate), Co(bzac)3 (2, bzac = benzoylacetonate), Co(tBu2-acac)3 (3, tBu2-acac = 2,2,6,6-tetramethyl-3,5-heptanedionate) and Co(acac)3 (4, acac = acetylacetonate), Fig. 2. We hypothesized that the ligands of 1 and 2 would enforce a higher Δδ/ΔT than the original report of Co(acac)3.19 We show that this asymmetry-focused design strategy based on maximizing the vibrational partition function can indeed be harnessed to raise Δδ/ΔT.
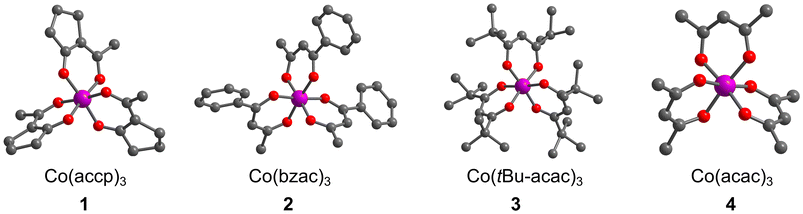 | ||
| Fig. 2 The crystal structures of the Co(III) complexes studied in this manuscript. Structures of 2–4 are taken from previous reports.24–26 H atoms are omitted for clarity. Color scheme; Co: violet, O: red, C: gray. | ||
Results and discussion
Syntheses and molecular structures
Compounds 1–4 are all pseudooctahedral, low-spin Co(III) complexes. Single crystals of 1 were grown by slow evaporation from acetonitrile (MeCN), and the structures of 2–4 were previously reported24–26 – all are shown in Fig. 2. All complexes exhibit six-coordinate inner coordination shells with 6 donor O atoms. Average Co–O bond distances are 1.88(2) Å for 1, which are in the range of reported average distances of 1.81(2), 1.86(1), and 1.90(2) for 2–4. The average O–Co–O bite angle for 1 is 89.2(2)°, close to 90.04(13), 92.3(2), and 92.9(3)° for 2–4, respectively. Continuous-shape-measurement analyses were also performed to check for geometric structural trends.27,28 For an idealized octahedral Oh geometry, SHAPE scores are 0. The scores for 1–4 are 0.34, 0.28, 0.08 and 0.37, respectively, indicating that all four complexes closely resemble perfect octahedral geometry.The ligands in 1–4 direct the molecular point group of the complex. In 3 and 4, which have C2v-symmetric acac and tBu2-acac ligands, the local coordination environments of the Co(III) ions are D3 symmetry. In contrast, 1 and 2, which have asymmetric ligands, have two possible forms. If the ligands in these complexes are all oriented similarly, then local C3 symmetry is possible, resulting in a fac isomer. If one of the ligands is flipped in orientation relative to the other two, the local symmetry is C1 (the mer isomer). In the single-crystal diffraction data, only the mer isomer is observed for 1. However, in the structure of 2 one of the bzac ligands is disordered and hence the mer and fac isomers are both present in the single crystal.24
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 (600 nm) give 1–4 deep green colors in solution, and these are likely d–d transitions, specifically the 1A1g to 1T2g transition.29–31 All molecules also give more intense (ca. 250 M−1 cm−1) peaks at much higher energies; 29
700 cm−1 (600 nm) give 1–4 deep green colors in solution, and these are likely d–d transitions, specifically the 1A1g to 1T2g transition.29–31 All molecules also give more intense (ca. 250 M−1 cm−1) peaks at much higher energies; 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 30
000 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 for 1 and 4. These same high-energy transitions are very broad for 3, spanning 28
600 cm−1 for 1 and 4. These same high-energy transitions are very broad for 3, spanning 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 571 to 33
571 to 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 cm−1. Lastly, two transitions of this type are observed for 2 at 34
333 cm−1. Lastly, two transitions of this type are observed for 2 at 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965 and 38
965 and 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 cm−1. These high-energy transitions are likely ligand π–π* transitions.32
610 cm−1. These high-energy transitions are likely ligand π–π* transitions.32
The energies of the low-energy peaks and the d6 Tanabe–Sugano diagram33 allowed us to quantify Δo, which increases in order from 1 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 cm−1) to 4 (16
502 cm−1) to 4 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 850 cm−1) to 2 (16
850 cm−1) to 2 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 852 cm−1) to 3 (16
852 cm−1) to 3 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 cm−1). The value of 4 is consistent with the literature value,29 whereas the values for the other three have not been previously reported. In all, these values suggest generally weak ligand fields for the Co(III) ions and control for the possibility of substantial ligand field differences causing the observed trends in Δδ/ΔT.
885 cm−1). The value of 4 is consistent with the literature value,29 whereas the values for the other three have not been previously reported. In all, these values suggest generally weak ligand fields for the Co(III) ions and control for the possibility of substantial ligand field differences causing the observed trends in Δδ/ΔT.
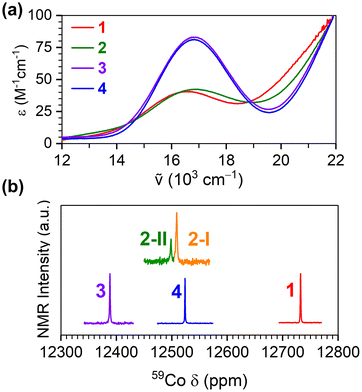
For all four complexes, the 59Co NMR chemical shift varied within 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 to 12
400 to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ppm (Fig. 3b). These values are within the range of 59Co NMR peaks of previously reported all-oxygen-bound octahedral Co(III) complexes.16 An important feature of the 59Co NMR spectra of 2 is the presence of two peaks. We note that prior DFT calculations and 1H NMR analyses of 2 reveal both fac and mer isomers to be stable,34 and disorder in the crystal structure of 2 indicates the presence of both isomers. We tentatively assign the two 59Co NMR peaks to the respective isomers as 2-I (for mer) and 2-II (for fac). This assignment is based on literature references indicating that the fac isomer exhibits greater shielding, narrower linewidth and lower signal intensity.34,35 We note that only one peak is observed for 1, suggesting that only one isomer is present, which is consistent with the lack of any disorder in the crystal structure. Finally, the known correlation of 59Co chemical shifts to Δo17 indicates the magnitude of Δo increases in the order of 1 < 4 < 2 < 3, in agreement with the lowest-energy peak in the UV-vis data above.
800 ppm (Fig. 3b). These values are within the range of 59Co NMR peaks of previously reported all-oxygen-bound octahedral Co(III) complexes.16 An important feature of the 59Co NMR spectra of 2 is the presence of two peaks. We note that prior DFT calculations and 1H NMR analyses of 2 reveal both fac and mer isomers to be stable,34 and disorder in the crystal structure of 2 indicates the presence of both isomers. We tentatively assign the two 59Co NMR peaks to the respective isomers as 2-I (for mer) and 2-II (for fac). This assignment is based on literature references indicating that the fac isomer exhibits greater shielding, narrower linewidth and lower signal intensity.34,35 We note that only one peak is observed for 1, suggesting that only one isomer is present, which is consistent with the lack of any disorder in the crystal structure. Finally, the known correlation of 59Co chemical shifts to Δo17 indicates the magnitude of Δo increases in the order of 1 < 4 < 2 < 3, in agreement with the lowest-energy peak in the UV-vis data above.
We also conducted diffuse-reflectance spectroscopy (DRS) on these compounds for comparison between solution and solid-state electronic structures and, by proxy, physical structure. The diffuse reflectance spectra (Fig. S2†), transformed from reflectance to the Kubelka–Munk parameter F(R), have generally sharper features than the solution phase UV-vis spectra. For 1–4, two to three peaks noticeable below 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The energies of the lowest-energy peaks increase in order from 2 (13
000 cm−1. The energies of the lowest-energy peaks increase in order from 2 (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 cm−1) to 4 (13
626 cm−1) to 4 (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 633 cm−1) to 3 (13
633 cm−1) to 3 (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 cm−1) to 1 (14
645 cm−1) to 1 (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 004 cm−1) in the solid-state, but are generally close in energy, like the solution-phase UV-vis data. This general similarity leads us to conclude there are no large differences structurally from compound to compound in solution, at least with respect to the CoO6 coordination shell. However, the lowest-energy peaks are also generally lower than solution-phase values. This distinction, and other differences in the data, suggests the possibility of small structural changes in the solution phase, though we note the colors of the compounds in the solid state and the solutions are strikingly similar (Fig. S2†), suggesting a lack of gross changes to coordination geometry/structure/oxidation state, consistent with the general chemical stabilities of low-spin Co(III) ion bound by chelating ligands.36
004 cm−1) in the solid-state, but are generally close in energy, like the solution-phase UV-vis data. This general similarity leads us to conclude there are no large differences structurally from compound to compound in solution, at least with respect to the CoO6 coordination shell. However, the lowest-energy peaks are also generally lower than solution-phase values. This distinction, and other differences in the data, suggests the possibility of small structural changes in the solution phase, though we note the colors of the compounds in the solid state and the solutions are strikingly similar (Fig. S2†), suggesting a lack of gross changes to coordination geometry/structure/oxidation state, consistent with the general chemical stabilities of low-spin Co(III) ion bound by chelating ligands.36
We tested the matrix sensitivity of the 59Co thermal responses of 1–4 through variable-solvent (see Tables S3–S7†) and variable-concentration studies (see Tables S13, S14 and Fig. S8, S12, S16 and S25†). We selected a variety of solvents: CHCl3, CH2Cl2, CD2Cl2, MeOH, DMSO and 1,2,4-trichlorobenzene (TCB), based on variance in physical properties such as polarity (from 2.2 to 47 for solvent TCB and DMSO, respectively) and viscosity (from 0.43 cP for CH2Cl2 to 32.9 cP for TCB).38 Notably, 1–4 are not water-soluble and, hence, were not tested in aqueous solutions. The 59Co NMR peak and its temperature sensitivity differed in each solvent (see Table S2†). The highest 59Co Δδ/ΔT values were observed for 1, 2-I, 2-II, and 4 in CDCl3, 2.71(1), 2.69(1), 2.64(2), and 2.78(1) ppm °C−1 and 3, 2.00(3) ppm °C−1, in MeOH (see Tables S3–S7 and Fig. S7, S11, S15, S19 and S22†). Among these, the sensitivity of 3 was found to be the lowest of 1–4 in each solvent. In 2–4, only slight changes (ca. 0.4 ppm °C−1) were observed in Δδ/ΔT with deuteration and no effect for 1.
The origin of the solvent sensitivity likely stems from an impact from the solvent cage, though it is unclear precisely how that mechanism functions. In Co(III) amine complexes, solvent dependence of Δδ/ΔT has been suggested to result from hydrogen-bonding interaction with donor solvents.39 In 1–4, there are no hydrogen bonding possibilities, which precludes that interaction as one of importance for Δδ/ΔT. There are also no apparent direct relationships between Δδ/ΔT and polarity or viscosity of the solvent (Fig. S28 and S29†). Finally, we recognize that the solvent dependence is counterintuitive on the basis of sterics because of the variation of the chemical shift of 3 with solvent, which is wider than 1, 2, and 4. One might expect, given the steric congestion afforded by the tBu functional groups, that 3 should have the weakest solvent dependence, yet it does not, in agreement with some previous observations by Kanakubo.37
Variable-temperature 59Co NMR spectra were collected on 1–4 at 1, 10, and 100 mM, revealing changes in the chemical shift and its temperature sensitivity with concentration (Fig. 4 and Fig. S7, S11, S15†). The 59Co peak for compounds 1–4 in a 100 mM solution exhibited a downfield shift in the range of approximately 1–3 ppm compared to a 1 mM solution. Notably, the value of Δδ/ΔT changed significantly, particularly for compound 1, increasing to 3.50(2) ppm °C−1, at the increased concentration (Fig. 4). A similar trend is observed for 2, where the Δδ/ΔT value increased from 2.70(2) to 3.23(2) ppm °C−1 for 2-I, and from 2.64(2) to 3.26(4) ppm °C−1 for 2-II. Similarly, the Δδ/ΔT value increased from 1.55(4) to 1.63(3) ppm °C−1 for 3. Lastly, in 4 the 59Co peak position appears significantly less dependent on concentration; only a small increase was observed in the sensitivity, from 2.78(2) to 2.83(2) ppm °C−1. To the best of our knowledge, the observed value of 3.50 ppm °C−1 for 1 establishes a record for temperature sensitivity not only among closed-shell Co(III) complexes, but for all closed-shell species.
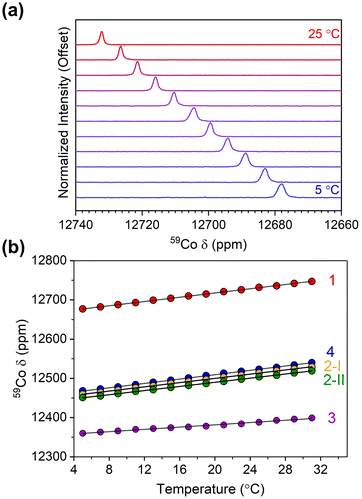 | ||
| Fig. 4 (a) Variable-temperature 59Co NMR for 1 in CDCl3 at 100 mM concentration. (b) Peak positions for 1–4 as a function of temperature at 100 mM concentration in CDCl3. | ||
The origin of the concentration dependence of Δδ/ΔT needs further investigation. It is reasonable to propose aggregation effects enhance the temperature sensitivity on account of the observed concentration dependence. However, there is no clear chemical difference in 1–4 that presents the possibility of aggregation in an intuitive way, e.g. functional groups for hydrogen bonding or open coordination sites. Furthermore, if such interactions exist, they are likely not magnetic in nature because they would be too weak. For instance, the dipole–dipole interaction between two 59Co nuclei held at 7.47(1) Å apart (from the structure of 1, the closest Co⋯Co distance in the crystal structures of 1–4 and likely closest possible distance in solution) is calculated to be only ca. 0.3 Hz (∼6 ppm), significantly smaller than the total ranges observed (ca. 80 ppm, see Fig. 4). An alternative explanation of the concentration dependence is that aggregation is modifying how the individual 59Co nuclei interact with the solvent cage. Changes in this interaction may induce changes in the electric field gradient at the cobalt nucleus,40–43 which might also contribute to the concentration dependence of the chemical shift. Dynamic light scattering experiments as a function of concentration and solvent suggest that some degree of aggregation may be happening (see ESI†), though these changes do not trend with Δδ/ΔT, or any other magnetic resonance characteristic, across all studied concentrations and solvent choice. Note, finally, that the test of viscosity dependence of Δδ/ΔT through the variable-solvent studies appears to disprove a mechanism stemming directly from increased viscosity of the higher-concentration solvents, or simply slower molecular motion in solution from aggregation.
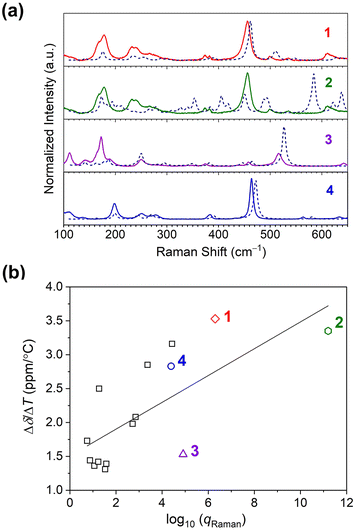 | ||
| Fig. 5 (a) Room-temperature Raman spectra collected on microcrystalline samples of 1–4. All spectra are baseline corrected. The dotted lines indicate the calculated spectra for the complexes. (b) The relationship between the 59Co temperature sensitivity (Δδ/ΔT) and total vibrational partition function of Raman modes, qRaman, for 1–4 (colored data points), and other Co(III) complexes (square data points). The linear correlation by R2 is 0.49. Data for the other complexes are taken from ref. 15. | ||
Computational analysis of the vibrational spectra enabled assignment of the observed modes in the Raman spectra and comparison with Δδ/ΔT. The experimental spectra match the predicted spectra closely (see Fig. 5a). Experimentally, the most intense modes in all species are symmetric Co–O bond stretching modes (“breathing” modes). These modes are observed at 456 cm−1 for 1, and in the region of 563–568 cm−1 for 2. For the symmetric complexes, this band is observed at 517 and 463 cm−1 for 3 and 4, respectively. Bands below 200 cm−1 are mainly related to torsional modes of methyl or alkyl groups and the chelating ring.44
However, we note that the observed correlation between qRaman and Δδ/ΔT is weak, as indicated by the low correlation coefficient (R2 = 0.49), and suggests the opportunity for significant future insight. We propose three important initial hypotheses behind the weak correlation for future study. First, we propose the need to factor in the extent to which a vibration is focused on the inner coordination shell into the partition function analyses. One may surmise a ligand-only vibration should have little impact on the 59Co δ versus a Co–O-based mode, but that intuition needs quantitative testing, which could be available by local mode analyses.46 Second, we propose that couplings between the solvent cage (or bulk solvent) and individual vibrational modes also need to be investigated in detail, because these interactions may ultimately alter which modes should be weighted for temperature sensitivity. This latter point may ultimately explain the concentration dependence if aggregation affects the couplings between specific vibrations and the solvent cage. Finally, third, we propose that understanding the exact physical structure of the species in solution is important, as the diffuse reflectance suggests some small alteration of the coordination shell. Such dynamic structural changes likely affect the vibrational spectra, and how this relates to the temperature sensitivity is a key future target.
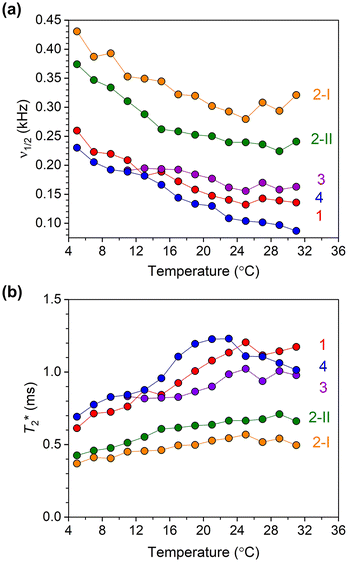 | ||
| Fig. 6 (a) 59Co NMR linewidth values for 10 mM solutions of 1–4 in CDCl3 as a function of temperature. (b) Temperature dependence of T*2 values for 1–4, calculated using 59Co NMR peak linewidths. | ||
The 59Co NMR linewidths contain information about the relaxation time T2*, the dephasing time of the nuclear spin (analogous to the coherence time, T2). The values of T2* were extracted from the temperature-dependent NMR linewidths through the relationship T2* = 1/(2πν1/2) where ν1/2 (kHz) is the linewidth (at FWHM) of the 59Co NMR peak. The temperature-dependent trends in T2* for all complexes over the 5–30 °C range are shown in Fig. 6b (see also Fig. S10, S14, S18, S21, and S24†) Complexes 1–4 all show generally increasing T2* with increasing temperature, where the temperature dependence is stronger for 1, 3 and 4 than both isomers of 2. Among all four complexes, 1 and 4 show the longest values of T2*. For both 1 and 4, the longest T2* values are found in MeOH; 1.2 and 1.6 ms for 1 and 4, respectively. While deuteration increases T2* in CDCl3 for 1, only a small effect on T2* was observed in CD2Cl2. On the other hand, an increase in T2* in 4 upon deuteration was observed. For both isomers of 2, T2* values are found to be similar. In all complexes, except 2-II and 3 where the latter is insoluble, noticeably shorter T2* values are observed in DMSO. The T2* values were also found to decrease for all four complexes as the concentration increased from 10 mM to 100 mM. We also measured the spin–spin relaxations (T2) for 1–4via Carr–Purcell–Meiboom–Gill (“CPMG”) experiments at room temperature (Fig. S26†). The T2 values are 2.38(3), 0.99(2), 1.98(3) and 3.47(4) ms for 1–4, respectively, all generally higher than the T2* values observed, but only a factor of 2. The T2* value is only determined for isomer 2-II due to limitations in the data collections for 2-I.
The T2* value of a quadrupolar nucleus like 59Co is often dictated by spin–lattice relaxation (T1), if T1 is short enough that it limits the magnitude of T2*. We measured T1 relaxation times via inversion recovery of 1–4 at room temperature (295 K) in 100 mM CDCl3 solution (Fig. S27†). The T1 values are 4.15(4), 1.23(2), 1.10(2), 2.24(3) and 4.01(4) ms for 1–4, respectively, all on the order of the T2 values obtained from CPMG and T2* from simple linewidth analyses. The effects of the T1 times are observed in the 59Co peak linewidths. Complexes 1 and 4, with the longest T1 values, have the narrowest 59Co NMR peaks, whereas 2 and 3 exhibit shorter T1 times. Hence, the linewidths here appear to follow spin–lattice relaxation times for the 59Co nuclei in 1–4.
There is additional importance of the linewidths and relaxation times in the context of the concentration dependence. Aggregation should be expected to slow down molecular rotation, potentially inducing larger linewidths through lengthening the correlation time.47 If true, then the measured T1 values would shorten, as would T2, and all spectra would increase in linewidth with the increased aggregation observed from the DLS measurements. That we do not see these trends for relaxation time measurements from 1 to 100 mM concentrations (see Table S12† for DLS results and Tables S13 and S14 for variable-concentration relaxation data) suggests that whatever the nature of the observed aggregation, it is not having conventional impacts on the 59Co NMR characteristics. Further, expecting the T1 and T2 data to follow the aggregation through correlation time variation does not acknowledge the substantial quadrupolar coupling for 59Co, which is important for spin relaxation of this nucleus.48–50 If aggregation were noticeably distorting the structure of the molecules, then these two competing systems ensure this system is far from trivial. Understanding these effects is key to sharper linewidths in future systems, and hence a key target for our future study.
We calculated the temperature resolution for 1–4 and contrasted them against values for other prominent NMR thermometer systems (Table 1). In complex 1, the highest temperature sensitivity and the narrowest peak were observed in CDCl3, which led to the ratio of 3.18, which is higher than Co(acac)3 under the same conditions that we measured 1–4 in this paper. We also note that both isomers of complex 2 show lower resolution than 1 and 4 despite the high Δδ/ΔT, owing to the relatively wide linewidths of the two isomers. Among 59Co NMR thermometers, these are the highest resolutions, eclipsing the recent spin-crossover 59Co results.20 They are also notably higher than the record temperature sensitivities for 1H and 31P. The sole measurement that eclipses our results in this manuscript is the original measurement of Co(acac)3. Again, we stress the difference in the measurement technique as an essential part of the comparison, specifically the field of measurement which is likely affecting linewidth (11.7 T vs. ca. 3.2 T in the original Levy report). The resolution here is likely limited by the field of the measurement and the resolution for 1 would likely eclipse 4 if measured under the same conditions.
| Compound |
ν
1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (ppm) a (ppm) |
(Δδ/ΔT)/ν1/2 (°C−1) |
|---|---|---|
| a From room temperature values. b From original ref. 19 by Levy et al. c From this work. d Collected in H2O at 33.3 mM concentration, 500 MHz magnet, see ref. 38. e Collected in CH2Cl2 at 400 mM, 500 MHz magnet, see ref. 20. f For 1H NMR signal, from ref. 21. g For 31P NMR signal, from ref. 22. | ||
| Co(acac)3b | 0.86 | 3.66 |
| Co(accp)3 (1)c | 1.10 | 3.18 |
| Co(bzac)3 (2)c | 2.47 | 1.37 |
| Co(tBu2-acac)3 (3)c | 1.34 | 1.22 |
| Co(acac)3 (4)c | 0.91 | 3.11 |
| K3[Co(CN)6]d | 0.40 | 2.98 |
| [Co(diNOsar)]Cl3d | 12 | 0.17 |
[(CpCo(OP(OtBu)2)3)2]Co+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e e |
128 | 1.18 |
| 1H-[tBuPNPFe-H]f | 50 | 0.28 |
| 31P-[tBu(PNP)Fe-H]g | 121 | 0.28 |
Conclusion
Tuning the number of allowed and forbidden IR and Raman-active modes in a molecule is a common exercise in inorganic and graduate level inorganic chemistry courses.51 Here we show that applying the same course-work level analyses to conventional Co(III) complexes can yield new design strategies for Δδ/ΔT. Indeed, we present two new records for the temperature sensitivities of the 59Co chemical shift in the asymmetric complexes Co(accp)3 and Co(bzac)3, the first in the over-40-year period since Co(acac)3 was initially identified as an exciting NMR thermometer.19While our study has predominantly focused on the design strategies to enhance temperature sensitivity in 59Co NMR thermometry using air-stable Co(III) complexes, it is imperative to recognize that the translation of these findings into practical applications, particularly in biological or clinical settings, requires addressing issues related to toxicity and biocompatibility. Future investigations should explore encapsulation techniques and other strategies to increase stability and to mitigate potential toxicity concerns when applying these molecular thermometers in vivo.52–55
In a similar vein, it is important to note that new molecular imaging agents do not simply appear, but follow years of fundamental studies of magnetic properties in molecules.52,56,57 It is in this context that this work should be appreciated for testing a new mechanism to increase temperature sensitivity in an 59Co nucleus by molecular design. Yet, we acknowledge that further work is still necessary. For example, the trend in qRaman with Δδ/ΔT is not a perfect correlation, implying future experiments are needed, and while the measurements here focus on high-field analyses, conventional MRI is often performed at lower fields, suggesting low-field studies are also imperative. Finally, we need to understand what mechanisms are important for governing linewidth, as this knowledge could lead to higher resolution. Two parameters, quadrupolar coupling of the I = 7/259Co nucleus and chemical shift anisotropy, are both proposed to dictate 59Co NMR linewidth.58 Studies of all of these effects will be reported in due course.
Author contributions
Ö. Ü. – methodology, investigation, formal analysis, validation, visualization, writing – original draft. S. S. – investigation, formal analysis. T. M. O – investigation, formal analysis. J. M. Z. – conceptualization, methodology, formal analysis, validation, funding acquisition, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (NSF) via a CAREER award (NSF-2047325) and Colorado State University. NMR and standard molecular characterization were performed at the Colorado State University Analytical Resources Core Facility RRID: SCR_021758, which is supported by an NIH-SIG award (1S10OD021814-01) and the CSU-CORES Program. A portion of this work was performed at the Raman Microspectroscopy Laboratory in the Department of Geological Science at the University of Colorado-Boulder. We acknowledge Eric Ellison for his experimental assistance.References
- V. Ozenne, C. Constans, P. Bour, M. D. Santin, R. Valabregue, H. Ahnine, P. Pouget, S. Lehericy, J. F. Aubry and B. Quesson, MRI Monitoring of Temperature And Displacement For Transcranial Focus Ultrasound Applications, Neuroimage, 2020, 204, 116236 CrossRef CAS PubMed.
- N. W. Lutz and M. Bernard, Contactless Thermometry by MRI and MRS: Advanced Methods for Thermotherapy and Biomaterials, iScience, 2020, 23, 101561 CrossRef CAS PubMed.
- V. Rieke and K. Butts Pauly, MRI Thermometry, J. Magn. Reson. Imaging, 2008, 27, 376–390 CrossRef PubMed.
- N. M. Rzechorzek, M. J. Thrippleton, F. M. Chappell, G. Mair, A. Ercole, M. Cabeleira, C.-T. H. R. I. S.-S. Participants, Investigators, J. Rhodes, I. Marshall and J. S. O'Neill, A Daily Temperature Rhythm In The Human Brain Predicts Survival After Brain Injury, Brain, 2022, 145, 2031–2048 CrossRef PubMed.
- L. Brateman, Chemical Shift Imaging: A Review, AJR, Am. J. Roentgenol., 1986, 146, 971–980 CrossRef CAS PubMed.
- J. Blackwell, M. J. Krasny, A. O'Brien, K. Ashkan, J. Galligan, M. Destrade and N. Colgan, Proton Resonance Frequency Shift Thermometry: A Review of Modern Clinical Practices, J. Magn. Reson. Imaging, 2022, 55, 389–403 CrossRef PubMed.
- J. Yuan, C. S. Mei, L. P. Panych, N. J. McDannold and B. Madore, Towards Fast And Accurate Temperature Mapping With Proton Resonance Frequency-Based Mr Thermometry, Quant. Imaging Med. Surg., 2012, 2, 21–32 Search PubMed.
- C. Prinz, P. R. Delgado, T. W. Eigentler, L. Starke, T. Niendorf and S. Waiczies, Toward 19F Magnetic Resonance Thermometry: Spin-Lattice And Spin-Spin-Relaxation Times And Temperature Dependence of Fluorinated Drugs At 9.4 T, MAGMA, 2019, 32, 51–61 CrossRef CAS PubMed.
- B. A. Berkowitz, J. T. Handa and C. A. Wilson, Perfluorocarbon Temperature Measurements Using 19F NMR, NMR Biomed., 1992, 5, 65–68 CrossRef CAS PubMed.
- L. D. Field, S. Sternhell and W. Veigel, A High-Temperature Thermometer For 13C NMR Spectroscopy, Org. Magn. Reson., 1984, 22, 221–223 CrossRef CAS.
- Y. Umegawa, Y. Tanaka, M. Nobuaki and M. Murata, 13C-Tmdota As Versatile Thermometer Compound For Solid-State NMR of Hydrated Lipid Bilayer Membranes, Magn. Reson. Chem., 2016, 54, 227–233 CrossRef CAS PubMed.
- F. L. Dickert and S. W. Hellmann, Chemical Shift Thermometer For Phosphorus-31 Nuclear Magnetic Resonance Measurements, Anal. Chem., 2002, 52, 996–996 CrossRef.
- R. Estrada, N. Stolowich and M. C. Yappert, Influence of Temperature On 31P NMR Chemical Shifts of Phospholipids And Their Metabolites I. In Chloroform-Methanol-Water, Anal. Biochem., 2008, 380, 41–50 CrossRef CAS PubMed.
- G. Castro, G. Wang, T. Gambino, D. Esteban-Gomez, L. Valencia, G. Angelovski, C. Platas-Iglesias and P. Perez-Lourido, Lanthanide(III) Complexes Based on an 18-Membered Macrocycle Containing Acetamide Pendants. Structural Characterization and paraCEST Properties, Inorg. Chem., 2021, 60, 1902–1914 CrossRef CAS PubMed.
- S. Zhang, C. R. Malloy and A. D. Sherry, MRI Thermometry Based on PARACEST Agents, J. Am. Chem. Soc., 2005, 127, 17572–17573 CrossRef CAS PubMed.
- A. Yamasaki, Cobalt-59 Nuclear Magnetic Resonance Spectroscopy in Coordination Chemistry, J. Coord. Chem., 1991, 24, 211–260 CrossRef CAS.
- R. Bramley, M. Brorson, A. M. Sargeson and C. E. Schaeffer, Cobalt-59 NMR Chemical Shifts of Cobalt(III) Complexes: Correlations With Parameters Calculated From Ligand-Field Spectra, J. Am. Chem. Soc., 2002, 107, 2780–2787 CrossRef.
- N. Juranić, A 59Co NMR Study of The Magnetic Shielding of The Cobalt Nucleus In Cobalt(III) Complexes, J. Chem. Phys., 1981, 74, 3690–3693 CrossRef.
- G. C. Levy, J. Terry Bailey and D. A. Wright, A Sensitive NMR Thermometer For Multinuclei FT NMR, J. Magn. Reson., 1980, 37, 353–356 CAS.
- O. Ungor, T. M. Ozvat, Z. Ni and J. M. Zadrozny, Record Chemical-Shift Temperature Sensitivity in a Series of Trinuclear Cobalt Complexes, J. Am. Chem. Soc., 2022, 144, 9132–9137 CrossRef CAS PubMed.
- J. C. Ott, H. Wadepohl, M. Enders and L. H. Gade, Taking Solution Proton NMR to Its Extreme: Prediction and Detection of a Hydride Resonance in an Intermediate-Spin Iron Complex, J. Am. Chem. Soc., 2018, 140, 17413–17417 CrossRef CAS PubMed.
- J. C. Ott, E. A. Suturina, I. Kuprov, J. Nehrkorn, A. Schnegg, M. Enders and L. H. Gade, Observability of Paramagnetic NMR Signals at over 10000 ppm Chemical Shifts, Angew. Chem., Int. Ed., 2021, 60, 22856–22864 CrossRef CAS PubMed.
- T. M. Ozvat, A. K. Rappe and J. M. Zadrozny, Isotopomeric Elucidation of the Mechanism of Temperature Sensitivity in 59Co NMR Molecular Thermometers, Inorg. Chem., 2022, 61, 778–785 CrossRef CAS PubMed.
- R. Liu, P. H. van Rooyen and J. Conradie, Geometrical Isomers of Tris(B-Diketonato)Metal(III) Complexes For M = Cr or Co: Synthesis, X-Ray Structures and DFT Study, Inorg. Chim. Acta, 2016, 447, 59–65 CrossRef CAS.
- M. A. K. Ahmed, H. Flellvåg, A. Kjekshus and P. D. C. Dietzel, Syntheses, structures, and polymorphism of β-diketonato complexes -: Co(thd), Z. Anorg. Allg. Chem., 2008, 634, 247–254 CrossRef CAS.
- G. J. Krüger and E. C. Reynhardt, New Investigation of The Structure of Trisacetylacetonatocobalt(III), Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 822–824 CrossRef.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, Continuous Symmetry Maps And Shape Classification. The Case of Six-Coordinated Metal Compounds, New J. Chem., 2002, 26, 996–1009 RSC.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape Maps and Polyhedral Interconversion Paths In Transition Metal Chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- D. W. Barnum, Electronic Absorption Spectra of Acetyl-Acetonato Complexes-I, J. Inorg. Nucl. Chem., 1961, 21, 221–237 CrossRef CAS.
- E. N. Yurchenko, V. I. Avdeev and E. A. Shugam, Ultraviolet and Visible Absorption Spectra of Complexes of Trivalent Metals With Acetylacetonate and Its Analogs, Theor. Exp. Chem., 1972, 6, 73–77 CrossRef.
- K. Kuroda, K. Yoshitani, K. Kunigita, Y. Kamiiba and K. Watanabe, Halogenation and Nitration of Some Mixed Ligand Acetylacetonato Cobalt(III) Complexes, Bull. Chem. Soc. Jpn., 1976, 49, 2445–2450 CrossRef CAS.
- J. T. Yarranton and J. K. McCusker, Ligand-Field Spectroscopy of Co(III) Complexes and the Development of a Spectrochemical Series for Low-Spin d(6) Charge-Transfer Chromophores, J. Am. Chem. Soc., 2022, 144, 12488–12500 CrossRef CAS PubMed.
- Y. Tanabe and S. Sugano, On the Absorption Spectra of Complex Ions II, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS.
- S. C. F. Au-Yeung, K. W. Kwong and R. J. Buist, Multinuclear NMR Study of The Crystal Field Strength of The Nitro Ligand And The Empirical Estimation of The Cobalt-59 NMR Chemical Shifts of Cobalt-Nitro Complexes, J. Am. Chem. Soc., 2002, 112, 7482–7488 CrossRef.
- M. Fujita, T. Fujihara, M. Kojima, Y. Yoshikawa and K. Yamasaki, Preparative Study and Characterization of the Cis-Diamminetetranitrocobaltate(III) Ion. A Missing Link in the Ammine-Nitro Cobalt(III) Series, Proc. Jpn. Soc., 1997, 73, 161–164 Search PubMed.
- B. Figgis and M. Hitchman, Ligand field theory and its applications, Wiley-VCH, New York, 2000 Search PubMed.
- M. Kanakubo, T. Uda, H. Ikeuchi and G. P. Satô, Solvent and Temperature Dependence of 59Co NMR Chemical Shifts of Tris(acetylacetonato)cobaIt(III) and Tris(dipivaloylmethanato)cobalt(III), J. Solution Chem., 1998, 27, 645–653 CrossRef CAS.
- J. A. Dean, “Lange's Handbook of Chemistry”, McGraw Hill Inc., New York, 1992 Search PubMed.
- T. M. Ozvat, M. E. Pena and J. M. Zadrozny, Influence of Ligand Encapsulation On Cobalt-59 Chemical-Shift Thermometry, Chem. Sci., 2019, 10, 6727–6734 RSC.
- K. L. Craighead and R. G. Bryant, Insignificance of Second Coordination Sphere Interactions in Cobalt-59 Nuclear Magnetic Resonance Relaxation, J. Phys. Chem., 2002, 79, 1602–1603 CrossRef.
- T. H. Martin and B. M. Fung, Outer Sphere Complex Between Trisethylenediaminecobalt(III) and Phosphate, J. Phys. Chem., 2002, 77, 637–640 CrossRef.
- P. Zhou, S. C. F. Au-Yeung and X. P. Xu, A DFT And Co Solid-State NMR Study of The Second-Sphere Interaction In Polyammonium Macrocycles Cobalt Cyanide Supercomplexes, J. Am. Chem. Soc., 1999, 121, 1030–1036 CrossRef CAS.
- K. Rose and R. G. Bryant, The Insignificance of Second Coordination Sphere Interactions in Cobalt-59 NMR Relaxation: A More Precise Assessment, J. Magn. Reson., 1979, 35, 223–226 CAS.
- H. Fakheri, S. F. Tayyari, M. M. Heravi and A. Morsali, Low Frequency Vibrational Spectra And The Nature of Metal-Oxygen Bond of Alkaline Earth Metal Acetylacetonates, J. Mol. Struct., 2017, 1150, 340–348 CrossRef CAS.
- C. J. Jameson, D. Rehder and M. Hoch, Isotope And Temperature Dependence Of Transition-Metal Shielding In Complexes Of The Type M(XY)6, J. Am. Chem. Soc., 2002, 109, 2589–2594 CrossRef.
- E. Kraka, W. Zou and Y. Tao, Decoding Chemical Information From Vibrational Spectroscopy Data: Local Vibrational Mode Theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1480 CAS.
- M. H. Levitt, Spin Dynamics, John Wiley & Sons, Inc., New York, 2nd edn, 2008 Search PubMed.
- T. M. Ozvat, S. H. Johnson, A. K. Rappé and J. M. Zadrozny, Ligand Control of 59Co Nuclear Spin Relaxation Thermometry, Magnetochemistry, 2020, 6, 58–58 CrossRef CAS PubMed.
- D. M. Doddrell, M. R. Bendall, P. C. Healy, G. Smith, C. H. L. Kennard, C. L. Raston and A. H. White, 59Co and 13C Nuclear Spin Relaxation Studies in Solutions of Symmetric, Bidentate Cobalt(III) Complexes. On the Mechanism of 59Co Spin Relaxation. Crystal Structure Determination of Tris(tropolonato)cobalt(III), Aust. J. Chem., 1979, 32, 1219–1230 CrossRef CAS.
- S. C. F. F. Au-Yeung, R. J. Buist and D. R. Eaton, Spin-Lattice Relaxation in Co Complexes of Low Symmetry, J. Magn. Reson., 1983, 55, 24–38 CAS.
- F. A. Cotton, “Chemical Applications of Group Theory”, Wiley-Interscience, New York, 3rd edn, 1990 Search PubMed.
- J. Wahsner, E. M. Gale, A. Rodriguez-Rodriguez and P. Caravan, Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed.
- F. Schilling, L. Schroder, K. K. Palaniappan, S. Zapf, D. E. Wemmer and A. Pines, MRI Thermometry Based On Encapsulated Hyperpolarized Xenon, Chem. Phys., 2010, 11, 3529–3533 CAS.
- G. H. Gao, G. H. Im, M. S. Kim, J. W. Lee, J. Yang, H. Jeon, J. H. Lee and D. S. Lee, Magnetite-Nanoparticle-Encapsulated pH-Responsive Polymeric Micelle As An MRI Probe For Detecting Acidic Pathologic Areas, Small, 2010, 6, 1201–1204 CrossRef CAS PubMed.
- Y. Yang, D. T. Schuhle, G. Dai, J. K. Alford and P. Caravan, 1H Chemical Shift Magnetic Resonance Imaging Probes With High Sensitivity For Multiplex Imaging, Contrast Media Mol. Imaging, 2012, 7, 276–279 CrossRef CAS PubMed.
- I. R. Young, Significant Events In The Development of MRI, J. Magn. Reson. Imaging, 2004, 20, 183–186 CrossRef PubMed.
- M. A. Sieber, T. Steger-Hartmann, P. Lengsfeld and H. Pietsch, Gadolinium-Based Contrast Agents And NSF: Evidence From Animal Experience, J. Magn. Reson. Imaging, 2009, 30, 1268–1276 CrossRef PubMed.
- A. Medek, V. Frydman and L. Frydman, Solid and Liquid Phase 59Co NMR Studies of Cobalamins and Their
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Derivatives, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14237–14242 CrossRef CAS PubMed.
Derivatives, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14237–14242 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental details and spectroscopic data. CCDC 2238047 for 1. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3qi01641b |
‡ qRaman values are calculated from the product of each normal mode by 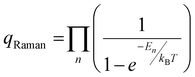 where En is the energy of the nth normal mode (cm−1), kB is Boltzmann's constant, and T is the temperature (K). where En is the energy of the nth normal mode (cm−1), kB is Boltzmann's constant, and T is the temperature (K). |
| This journal is © the Partner Organisations 2023 |