Design and synthesis of anisotropic crystals with π-conjugated rings toward giant birefringence

Abstract

Birefringent crystals play a significant role in linear optical devices due to their ability to modulate the polarization of light. Commercial birefringent crystals MgF₂, α-BaB₂O₄, CaCO₃, YVO₄, TiO₂, and LiNbO₃ have been widely used as polarization devices in the past decades. A variety of crystals have been developed to meet the requirements of large birefringence and have great potential as optical functional crystals. However, a key question is how to balance the conflict between the energy gap and birefringence. In this review, aiming to better judge the integrated properties of optical crystals, we came up with the birefringent quality factor. We also summarised our recent findings on the birefringent crystals, which contain structural units similar to [B₃O₆]³⁻ rings, from these perspectives, including crystal structure features, optical performances, and structure–property relationships. We summarised the strategy to achieve the balance between the energy gap and birefringence by adjusting the delocalized π-conjugation and the confined π-conjugation to improve the performance of birefringent crystals, which will open up a new window for the exploration of novel birefringent crystals.

---

Yunqi Zhao

Yunqi Zhao received his Bachelor's degree from Dalian University of Technology in 2021. He is currently a Master's student at the University of Chinese Academy of Sciences.

Liangmeng Zhu

Liangmeng Zhu received his Bachelor's degree in Chemical Normal Major from Wenzhou University in 2022. He is currently a Master's student at the University of Chinese Academy of Sciences.

Yanqiang Li

Yanqiang Li is pursuing PhD degree at the Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences. His PhD project focuses on nonlinear optical crystals and birefringence crystals.

Xiaojun Kuang

Xiaojun Kuang received his BSc in Chemistry from Nanchang University in 1999 and PhD in Inorganic Chemistry from Peking University in 2004. After his postdoctoral research in the University of Liverpool and University of Durham, he was appointed as an Associate Professor in the Chemistry College, Sun Yat-Sen University, in 2010 before he settled down in Guilin in 2013. His current research interests include the discovery of new oxide ion conductors, oxide and (oxy)nitride dielectrics, and their structure–property relationships.

Junhua Luo

Junhua Luo received his PhD from Fujian Institute of Research on the Structure of Matter (FJIRSM) in 2003, Chinese Academy of Science, followed by postdoctoral research at North Carolina State University and University of Florida from 2003 to 2005. From 2006 to 2009, he was funded by the Los Alamos National Laboratory at the Neutron Diffraction Center. He became Professor of chemistry at FJIRSM in 2009. His current research interests focus on development of photoelectric functional materials based on organic-inorganic hybrids.

Sangen Zhao

Sangen Zhao is a professor at Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences. He received his PhD degree from Technical Institute of Physics and Chemistry, Chinese Academy of Sciences in 2012, and then joined Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences. His current research interests are inorganic optoelectronic functional crystals, such as nonlinear optical crystals and birefringent crystals. He is a recipient of the “NSFC Excellent Young Scientists Fund in China.

---

1 Introduction

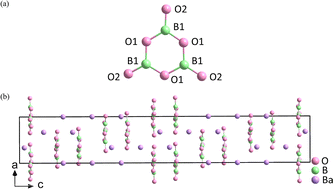
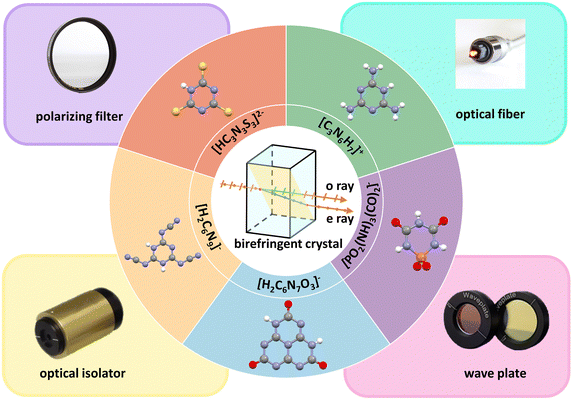
Birefringence is a linear optical property that occurs in anisotropic crystals. In anisotropic crystals, birefringence will arise when the refractive index of light changes based on the direction of light.¹ According to the difference in optical properties, crystals can be divided into two types, isotropic crystals and anisotropic crystals. In terms of symmetry, crystals with cubic symmetry belong to isotropic crystals. In consequence, they lack birefringence. In contrast, anisotropic crystals have more types of symmetry, including triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and trigonal symmetry. Therefore, they can generate birefringence. The crystals belonging to trigonal, hexagonal, and tetragonal systems are called uniaxial crystals, in which the unique optical axis coincides with the highest axis of symmetry. Birefringence can modulate polarized light in uniaxial crystals and spilt the incident light into ordinary ray (o) and extraordinary ray (e). They correspond to different refractive indices, n_o (ordinary refractive index) and n_e (extraordinary refractive index) (Fig. 1). If n_o > n_e, the crystal is called the negative uniaxial crystal. On the contrary, n_o < n_e for the positive uniaxial crystal. The birefringence can be expressed in the following equation:

Δn = |n_o – n_e|

Fig. 1 The principle of birefringence, structural units, and typical applications of commercial birefringent crystals.

In recent decades, several commercial birefringent crystals have been developed, including MgF₂,²α-BaB₂O₄ (α-BBO),^3,4 calcite (CaCO₃),⁵ YVO₄,⁶ rutile (TiO₂)⁷ and LiNbO₃.⁸ Birefringent materials benefit to obtain phase matching in the specific wavelength range of the transparency and can be used to modulate the polarization-related light propagation. Because of these excellent optical properties, birefringent crystals are used in various optical devices, such as circulators, polarizers, phase compensators, wave plates, and optical isolators.^9–15

The properties of the compound are closely associated with the structure of the microstructure group, so it is crucial to choose suitable units. In birefringent materials, planar groups containing π orbitals demonstrate better polarization anisotropy than the non-planar units.^16–19 For example, α-BBO has a large birefringence (exp. Δn = 0.12@532 nm),²⁰ and is transparent in the significant ultraviolet (UV) spectral region (λ < 400 nm). This is mainly attributed to the delocalized π-conjugated electron orbitals in the [B₃O₆]³⁻ rings (Fig. 2).^21–24 Recently, a number of birefringent crystals similar to α-BBO have been discovered, such as K₂(HC₃N₃O₃)·2H₂O (exp. 0.19@514 nm),²⁵ Rb₂(HC₃N₃O₃) (cal. 0.40@532 nm),²⁶ K₂Mg(H₂C₃N₃O₃)₄·4H₂O (cal. 0.38@800 nm),²⁷ NaRb₃(H₂C₃N₃O₃)₄·3H₂O (cal. 0.39@532 nm)²⁸ and (C₅H₆ON)⁺(H₂PO₄)⁻ (cal. 0.25@1064 nm).²⁹

Fig. 2 (a) [B₃O₆]³⁻ ring. (b) Crystal structure of α-BBO.

In order to make devices smaller, birefringent crystals should have large birefringence. From the structural perspective, π-conjugated rings are beneficial for increasing birefringence, and birefringence also depends significantly on the alignment and direction of the structural units.³⁰ The more parallel the ring, the more anisotropic is enlarged, causing larger birefringence. On the other hand, the energy gap plays a decisive role in optical crystals’ applications, and thus keeping the balance of birefringence and energy gap is also a considerable problem.

In this review, we summarised our recent efforts in exploring birefringent crystals containing π-conjugated rings. In addition, the birefringent quality factor (BQF) is used to quantify the integrated optical performance, and it can be expressed in the following equation:

BQF = E_g × Δn

Where E_g represents the energy gap in electron volt, Δn is the birefringence. The BQF is a valid measure of the overall performance of the material. The birefringent crystals with large BQF exhibit better integrated performance. They overcome the problem of birefringence and energy gap, where one property is large while the other is very small. As shown in Table 1, the birefringent crystals exhibit relatively large BQF, demonstrating that our design and synthesis of birefringent materials based on the α-BBO structural template is effective.

Table 1 Space groups and optical properties of birefringent crystals with π orbitals

Compounds	Space groups	Δn	Energy gap (eV)	BQF	Ref.
α-BaB2O4	R3̄c	0.12@532 nm	6.56	0.79@546 nm	20
(C3N6H7)2SiF6·H2O	P21/n	0.15@550 nm	4.76	0.71@550 nm	31
(C3N6H8)PbBr4	P21/c	0.32@550 nm	3.13	1.00@550 nm	32
Cs3Cl(HC3N3S3)	Pmc21	0.52@550 nm	3.34	1.74@550 nm	33
CsH2C6N9·H2O	P1̄	0.55@550 nm	4.12	2.27@550 nm	34
Ba(H2C6N7O3)2·8H2O	Fdd2	0.24@550 nm	4.10	0.98@550 nm	35
NaPO2(NH)3(CO)2	P21/c	0.28@550 nm	6.50	1.82@550 nm	36

---

2 Structure and optical properties of birefringent crystals with π orbitals

Herein, some structures like α-BBO are summarised, including (C₃N₆H₇)₂SiF₆·H₂O,³¹ MLAPbBr₄ (MLA = melamine),³² Cs₃Cl(HC₃N₃S₃),³³ CsH₂C₆N₉·H₂O,³⁴ Ba(H₂C₆N₇O₃)₂·8H₂O,³⁵ and NaPO₂(NH)₃(CO)₂.³⁶ In addition, from the perspective of the fundamental structural units, the polarizability anisotropy, and the gap from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO) of structural units are summarised in Fig. 3. The polarizability anisotropy and HOMO–LUMO gap were calculated via the Gaussian 09 package³⁷ with the hybrid B3LYP functional at 6-31G(d,p) level. After that, the calculation results were analysed by the Multiwfn 3.8 code.³⁸ The polarizability anisotropy of all structural units exceeds that of the [B₃O₆]³⁻, providing the basis for large birefringence.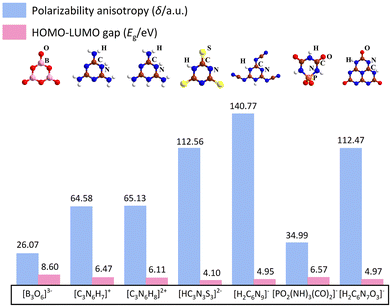

Fig. 3 Polarizability anisotropy and HOMO–LUMO gap of [B₃O₆]³⁻, [C₃N₆H₇]⁺, [C₃N₆H₈]²⁺, [HC₃N₃S₃]²⁻, [H₂C₆N₉]⁻, [PO₂(NH)₃(CO)₂]⁻, [H₂C₆N₇O₃]⁻ anion units.

(C₃N₆H₇)₂SiF₆·H₂O crystallizes in the monoclinic space group P2₁/n. The fundamental structural blocks contain a protonated melamine [C₃N₆H₇]⁺, [SiF₆]²⁻ octahedron, and the H₂O molecules. (C₃N₆H₇)₂SiF₆·H₂O combines the planar π-conjugated [C₃N₆H₇]⁺ with the highly coordinated [SiF₆]²⁻ groups. The [SiF₆]²⁻ octahedra present in the gap along the c-axis connect the quasi-two-dimensional [C₃N₆H₇]_∞ chains (Fig. 4a). In addition, the H₂O molecules with hydrogen bonds connect the adjacent [SiF₆]²⁻ octahedra (Fig. 4b). The [SiF₆]²⁻ octahedron is also connected to four [C₃N₆H₇]⁺ cations by hydrogen bonds. The parallel structure group [C₃N₆H₇]_∞ chains lead to larger birefringence due to the π-conjugated [C₃N₆H₇]⁺, which is similar to the [B₃O₆]³⁻ functional units of α-BBO, showing high anisotropy. Inside the single [C₃N₆H₇]_∞ chain, adjacent [C₃N₆H₇]⁺ cations are further linked by two N–H⋯N hydrogen bonds, resulting in the coplanar alignment (Fig. 4c). In addition, the highly symmetrical [SiF₆]²⁻ polyhedron further facilitates the aligned arrangement of each [C₃N₆H₇]_∞ chain. The Kubelka–Munk function F(R) = (1 − R)²/2R is used to calculate the absorption rate of light, where R is the reflectance.³⁹ Additionally, the experimental energy gap can be inferred by extrapolating the linear part of the rising curve to zero. The large energy gap is 4.76 eV (Fig. 4d), suggesting the (C₃N₆H₇)₂SiF₆·H₂O crystal can be used in the UV region. The birefringence of (C₃N₆H₇)₂SiF₆·H₂O is 0.15@550 nm (Fig. 4e). Thus, the BQF is 0.71@550 nm. In accordance with the crystal structure and theoretical calculation, the birefringence and energy gap of (C₃N₆H₇)₂SiF₆·H₂O should be due to the parallel aligned protonated melamine [C₃N₆H₇]⁺ groups and the highly symmetric [SiF₆]²⁻ octahedron.

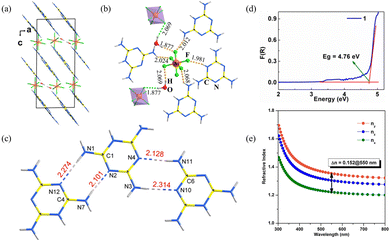Fig. 4 (a) Structure of (C₃N₆H₇)₂SiF₆·H₂O viewed along the b-axis. (b) The coordination environment of [SiF₆]²⁻ octahedra. (c) [C₃N₆H₇]_∞ chain formed by hydrogen bonds. (d) Absorption spectra. (e) Theoretically calculated refractive indices and birefringence of (C₃N₆H₇)₂SiF₆·H₂O.³¹

The MLAPbBr₄ crystallizes in the centrosymmetric monoclinic space group of P2₁/c. The crystal structure of MLAPbBr₄ is composed of melamine cations [C₃N₆H₈]²⁺ (Fig. 5a) and PbBr₆ octahedra (Fig. 5b). The structure combines the corrugated [PbBr₄]_∞ layers with the melamine cations to form a (110)-oriented perovskite framework (Fig. 5c). According to the absorption data, the energy gap of MLAPbBr₄ is about 3.13 eV, meaning the optically transparent window can achieve to the UV spectral region of 374 nm. In addition, the experimental birefringence (0.32@550 nm) was calculated according to the formula R = Δn × T.^40,41 Where R represents the optical path difference, T represents the thickness of the crystal, and Δn represents the birefringence. Hence, the BQF is 1.00@550 nm. The first-principles calculation is used to explore the potential mechanism of the large birefringence of MLAPbBr₄. As shown in Fig. 5d, theoretical birefringence is 0.29@550 nm, which is in agreement with the experimental value. The HOMO and LUMO of MLAPbBr₄ were calculated to show the origin of birefringence. Through Fig. 5e, for highly π-conjugated melamine cations, the HOMO shows an apparent anisotropy of electron densities, and the LUMO reflects highly distorted PbBr₆ octahedra. Hence, the delocalized π-conjugated melamine cations and distorted PbBr₆ octahedra coordinate to enlarge the birefringence of MLAPbBr₄.

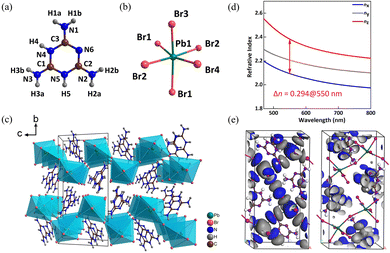Fig. 5 (a) Crystal structure of melamine cation. (b) Crystal structure of PbBr₆ octahedron. (c) Viewed along the a-axis, the crystal structure of MLAPbBr₄. (d) Theoretically calculated refractive indices and birefringence of MLAPbBr₄. (e) HOMO and LUMO of MLAPbBr₄.³² Copyright 2022, Wiley.

Cs₃Cl(HC₃N₃S₃) crystallizes in the non-centrosymmetric space group of Pmc2₁. The crystal structure of Cs₃Cl(HC₃N₃S₃) is composed of [HC₃N₃S₃]²⁻ rings (Fig. 6a), which is similar to the α-BBO, and ClCs₆ polyhedra (Fig. 6b). According to the Fig. 6c, the chains are parallel along the a axis, with the coplanar [HC₃N₃S₃]²⁻ rings occupy the interchain space. According to the UV-visible-near-infrared diffuse reflectance spectrum of Cs₃Cl(HC₃N₃S₃) powders, the absorption edge is near 371 nm with a corresponding energy gap of about 3.34 eV. The measured birefringence of Cs₃Cl(HC₃N₃S₃) is 0.52@550 nm. Thus, the BQF is 1.74@550 nm. To reveal the underlying mechanism of birefringence, first-principles calculations were calculated. As shown in Fig. 6d, the calculated Δn of Cs₃Cl(HC₃N₃S₃) is 0.60@550 nm, which is close to the measured birefringence. The HOMO and LUMO for crystal Cs₃Cl(HC₃N₃S₃) reflect the origin of birefringence (Fig. 6e and f). The HOMO is composed of the N 2p orbitals and S 3p orbitals, and the LUMO is mainly constituted by the π orbitals on the [C₃N₃] rings and the 3p orbitals of the S atoms. Therefore, from the perspective of structure–property relationships, the [HC₃N₃S₃]²⁻ structural unit is crucial to the birefringence of Cs₃Cl(HC₃N₃S₃) because of the delocalized π-conjugation. In addition, the [HC₃N₃S₃]²⁻ rings are parallel to the (100) plane, which enlarge the anisotropic. It makes a positive contribution to improving birefringence.

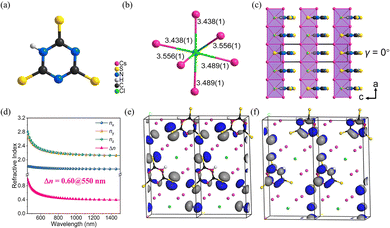Fig. 6 (a) [HC₃N₃S₃]²⁻ ring. (b) ClCs₆ polyhedron. (c) The crystal structure of Cs₃Cl(HC₃N₃S₃), (γ) is the dihedral angle between the [HC₃N₃S₃]²⁻ rings and the (100) plane. (d) Theoretically calculated refractive indices and birefringence of Cs₃Cl(HC₃N₃S₃). (e) The HOMO of Cs₃Cl(HC₃N₃S₃). (f) The LUMO of Cs₃Cl(HC₃N₃S₃). (Black, red, green, yellow, purple and white balls represent C, N, Cl, S, Cs and H atoms, respectively).³³ Copyright 2022, Wiley.

CsH₂C₆N₉·H₂O crystallizes in the centrosymmetric space group of triclinic P1̄. As the fundamental structural unit of CsH₂C₆N₉·H₂O, the [H₂C₆N₉]⁻ unit is made up of the three almost coplanar linear –(N–C≡N)– side arms and the planar π-conjugated [C₃N₃] ring (Fig. 7a). In addition, consistent with the reported protonated tricyanomelaminates, the H atoms in the [H₂C₆N₉]⁻ unit are bonded to the N atoms of the [C₃N₃] rings.^42–44 As shown in Fig. 7b, CsH₂C₆N₉·H₂O has a pseudo-two-dimensional layered structure with Cs⁺ counter cations present in the interlayer space to maintain the overall charge balance. The [H₂C₆N₉]⁻ anion units are held in place by the hydrogen bonding network, which belongs to the nearly coplanar H₂O molecules. The coplanarity of [H₂C₆N₉]⁻ anion units is an optimal arrangement for optical anisotropy and is conducive to the generation of large birefringence in CsH₂C₆N₉·H₂O, similar to the cases in α-BBO.⁴⁵ According to the UV-visible-near-infrared diffuse reflectance spectrum, CsH₂C₆N₉·H₂O has an absorption edge at about 301 nm in the UV spectral region. This represents an experimental energy gap of about 4.12 eV. The experimental birefringence of CsH₂C₆N₉·H₂O (0.55@550 nm) was measured using a polarizing microscope.⁴⁶ Hence, the BQF is 2.27@550 nm. The first-principles calculations were used to explore the microscopic origin of birefringence. According to the relationship between the wavelength and refractive index, the birefringence of CsH₂C₆N₉·H₂O is 0.52@550 nm, which agrees well with the measurement. In addition, there is a large anisotropy of refractive indices in CsH₂C₆N₉·H₂O (Fig. 7c). As shown in Fig. 7, the electron localization function (ELF)^47,48 maps of CsH₂C₆N₉·H₂O have been presented, aiming to illustrate the contribution of Cs⁺, H₂O molecules, and [H₂C₆N₉]⁻ units. In Fig. 7d, the HOMO consists mainly of N 2p orbitals. In addition, N 2p and C 2p orbitals of [H₂C₆N₉]⁻ predominate the LUMO (Fig. 7e). Especially, the π orbitals of the linear –(N–C≡N)– in the [H₂C₆N₉]⁻ and [C₃N₃] rings are parallel to one another and also parallel to the π orbitals in the adjacent [H₂C₆N₉]⁻ (Fig. 7f). Such a structural arrangement enhances microscopic anisotropy, thus increasing the birefringence. Therefore, the large birefringence of CsH₂C₆N₉·H₂O can be attributed to the delocalized π-conjugated orbitals in the [H₂C₆N₉]⁻ units.

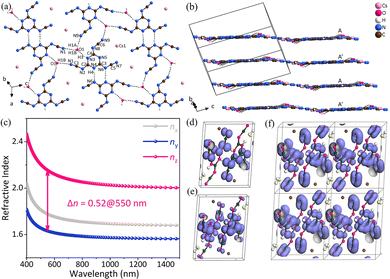Fig. 7 (a) [H₄C₆N₉O]_∞ single layer in CsH₂C₆N₉·H₂O. (b) The pseudo-two-dimensional layered structure of CsH₂C₆N₉·H₂O. (c) Theoretically calculated refractive indices and birefringence of CsH₂C₆N₉·H₂O. (d) The HOMO of CsH₂C₆N₉·H₂O. (e) The LUMO of CsH₂C₆N₉·H₂O. (f) π orbitals of (H₂C₆N₉)⁻ in CsH₂C₆N₉·H₂O, the fuchsia, yellow, brown, dark green and white spheres represent N, O, Cs, C and H atoms respectively.³⁴ Copyright 2022, Wiley.

Ba(H₂C₆N₇O₃)₂·8H₂O crystallizes in the non-centrosymmetric orthorhombic of the Fdd2 space group. The crystal structure of Ba(H₂C₆N₇O₃)₂·8H₂O consists of an independent [H₂C₆N₇O₃]⁻ anion (Fig. 8a), one Ba²⁺ cation, and four lattice H₂O molecules. In Fig. 8c, Ba(H₂C₆N₇O₃)₂·8H₂O exhibits a three-dimensional framework composed of π-conjugated [H₂C₆N₇O₃]⁻ anions, Ba²⁺ cations, and H₂O molecules. In Ba(H₂C₆N₇O₃)₂·6H₂O, each Ba²⁺ cation is shared by six H₂O molecules and two [H₂C₆N₇O₃]⁻ anions via Ba–O bonds. The UV-visible-near-infrared diffuse reflectance spectrum of Ba(H₂C₆N₇O₃)₂·8H₂O ranges from 200 nm to 1000 nm, the UV absorption edge of Ba(H₂C₆N₇O₃)₂·8H₂O is situated at λ = 302 nm, which corresponds to an energy gap of 4.10 eV. The measured birefringence of Ba(H₂C₆N₇O₃)₂·8H₂O is 0.24@550 nm. The theoretical value of birefringence is 0.22@550 nm, which agrees well with the experimental value. Hence, according to the energy gap and measured birefringence, the value of BQF is 0.98@550 nm. To investigate the cause of the large birefringence, the HOMO and LUMO patterns of Ba(H₂C₆N₇O₃)₂·8H₂O are shown in Fig. 8d and Fig. 8e. O 2p and N 2p orbitals are the main constituents of the HOMO. In comparison, the unoccupied π orbitals make up the LUMO components. In summary, due to the expanded π-conjugated delocalization in the [H₂C₆N₇O₃]⁻ building blocks, it has an enhanced birefringence.

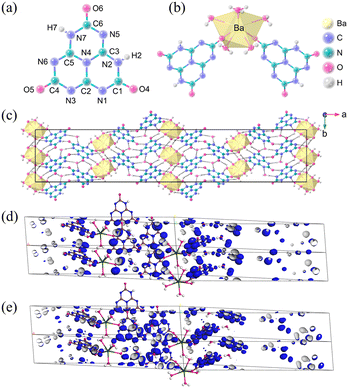Fig. 8 (a) The (H₂C₆N₇O₃)⁻ anion. (b) The coordination environment of Ba²⁺. (c) Viewed along the crystallographic c-axis, the crystal structure of Ba(H₂C₆N₇O₃)₂·8H₂O, and the yellow polyhedra represent BaO₈ polyhedra. (d) The HOMO of Ba(H₂C₆N₇O₃)₂·8H₂O. (e) The LUMO of Ba(H₂C₆N₇O₃)₂·8H₂O.³⁵ Copyright 2022, Wiley.

NaPO₂(NH)₃(CO)₂ crystallizes in the monoclinic space group P2₁/c. As shown in Fig. 9a, the crystal structure of NaPO₂(NH)₃(CO)₂ consists of six-membered rings [PO₂(NH)₃(CO)₂] formed by direct covalent bonding of two π-conjugated planar triangles [CO(NH)₂] and a non-π-conjugated tetrahedron [PO₂N₂]. The [PO₂(NH)₃(CO)₂]⁻ anions form a bond with the Na⁺ cations present in the vacancies (Fig. 9b). The UV−visible-near-infrared diffuse reflectance spectrum indicates that the energy gap is 6.50 eV. In addition, the experiment birefringence is 0.28@550 nm. Thus, the value of BQF is 1.82@550 nm. To investigate the fundamental relationship between optical performance and structure of NaPO₂(NH)₃(CO)₂, first-principles calculations were used. In Fig. 9c, NaPO₂(NH)₃(CO)₂ has a calculated birefringence of 0.28@550 nm and exhibits pronounced optical anisotropy, in general agreement with the measured value. The HOMO and LUMO were calculated to investigate further the relationship between optical properties and crystal structure at the molecular level (Fig. 9d and e). It demonstrates that the π-conjugated interactions have been partially decoupled by the PO₂(NH)₂ tetrahedron, and all of the π-conjugation is confined within the [PO₂(NH)₃(CO)₂]⁻ ring. Hence, in order to keep an effective balance between a large energy gap and large birefringence, the confined π-conjugation of [PO₂(NH)₃(CO)₂]⁻ units play a crucial role, and the integrated properties of the birefringent crystal are improved.

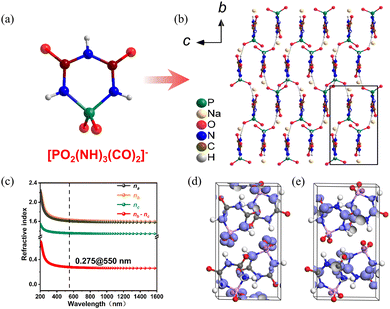Fig. 9 (a) [PO₂(NH)₃(CO)₂]⁻ anion. (b) Along the a-axis, the crystal structure of NaPO₂(NH)₃(CO)₂. (c) Theoretically calculated refractive indices and birefringence of NaPO₂(NH)₃(CO)₂. (d) The HOMO of NaPO₂(NH)₃(CO)₂. (e) The LUMO of NaPO₂(NH)₃(CO)₂.³⁶ Copyright 2022, Elsevier.

3 Conclusion

In this review, we have presented and discussed systematically the recent development of π-conjugated birefringent materials. We discussed the crystal structure, energy gap, birefringence, and the relationship between structure and property. For the birefringent materials containing π-conjugated groups, here are some perspectives and outlooks.

(1) The delocalized π-conjugated C–N rings show strong hybridization between C and N atoms and contribute significantly to the birefringence of crystals. In addition, in order to achieve an effective balance between the large energy gap and the large birefringence, confined π-conjugation plays a critical role. Confined π-conjugation can partially decouple the π-conjugated interaction, and compared with the delocalized π-conjugation, confined π-conjugated birefringent crystals have a larger energy gap. At the same time, birefringent crystals with confined π-conjugation can maintain a suitable birefringence. Since birefringence and energy gap are important factors in the application of birefringent crystals, a reasonable balance between delocalized π-conjugation and confined π-conjugation is essential to improve the integrated performance of birefringent crystals.

(2) In addition, the birefringence depends significantly on the anisotropy of the structure, while the anisotropic structure depends on the arrangement of the unit. Therefore, the internal arrangement of the structural unit should be considered. An effective strategy to enhance birefringence is to induce an ordered arrangement of the π-conjugated unit.

(3) This paper reviews the synthesis of several large BQF crystals. According to the structure–property relationship, the optical properties of birefringent crystals depend on the microscopic groups and the arrangement of the groups within the crystal. Exploring suitable microscopic groups with large polarizability anisotropy and HOMO–LUMO gap and controlling their ordered arrangement increased the BQF of the birefringent crystals.

(4) Perovskite and anti-perovskite are novel structural systems in the development of birefringent crystals. They can increase the anisotropy and thus the birefringence through the optimal arrangement of cations. This is also an important direction in the study of birefringent crystals.

(5) The structure containing H₂O will reduce the stability of the crystal. One way to improve the stability of crystals is to replace the H₂O molecule with the halogen atom.

(6) With the continuous improvement in computing power and the development of theoretical calculation theory, bottom-up synthesis strategies can also be applied to the design and synthesis of birefringent crystals. The microscopic hyperpolarizability, polarizability anisotropy, and HOMO–LUMO gap can be calculated to select suitable groups, and then the different functional units can complement each other to form highly integrated birefringent crystals. This is also useful in the design and synthesis of novel birefringent crystals.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (22122507, 22193042, 21833010, 61975207, and 21921001), the Natural Science Foundation of Fujian Province (2022J02012), the Youth Innovation Promotion Association of the Chinese Academy of Sciences (Y202069), the Fujian Institute of Innovation (FJCXY18010201) in the Chinese Academy of Sciences, the Key Research Program of Frontier Sciences of the Chinese Academy of Sciences (ZDBS-LY-SLH024), and the Ministry of Education/Guangxi Key Laboratory of Optical and Electronic Materials and Devices (20KF-11).

References

1. S. Niu, G. Joe, H. Zhao, Y. Zhou, T. Orvis, H. Huyan, J. Salman, K. Mahalingam, B. Urwin, J. Wu, Y. Liu, T. E. Tiwald, S. B. Cronin, B. M. Howe, M. Mecklenburg, R. Haiges, D. J. Singh, H. Wang, M. A. Kats and J. Ravichandran, Giant optical anisotropy in a quasi-one-dimensional crystal, Nat. Photonics, 2018, 12, 392–396.
2. M. J. Dodge, Refractive properties of magnesium fluoride, Appl. Opt., 1984, 23, 1980–1985.
3. G. Zhou, J. Xu, X. Chen, H. Zhong, S. Wang, K. Xu, P. Deng and F. Gan, Growth and spectrum of a novel birefringent α-BaB₂O₄ crystal, J. Cryst. Growth, 1998, 191, 517–519.
4. S. Wu, G. Wang, J. Xie, X. Wu, Y. Zhang and X. Lin, Growth of large birefringent α-BBO crystal, J. Cryst. Growth, 2002, 245, 84–86.
5. G. Ghosh, Dispersion-equation coefficients for the refractive index and birefringence of calcite and quartz crystals, Opt. Commun., 1999, 163, 95–102.
6. L. G. DeShazer, Improved midinfrared polarizers using yttrium vanadate, Proc. SPIE, 2002, 4481, 10–17.
7. J. R. DeVore, Refractive Indices of Rutile and Sphalerite, J. Opt. Soc. Am., 1951, 41, 416–419.
8. D. E. Zelmon, D. L. Small and D. Jundt, Infrared corrected Sellmeier coefficients for congruently grown lithium niobate and 5 mol% magnesium oxide–doped lithium niobate, J. Opt. Soc. Am. B, 1997, 14, 3319–3322.
9. L. Wu, S. Patankar, T. Morimoto, N. L. Nair, E. Thewalt, A. Little, J. G. Analytis, J. E. Moore and J. Orenstein, Giant anisotropic nonlinear optical response in transition metal monopnictide Weyl semimetals, Nat. Phys., 2017, 13, 350–355.
10. L. H. Nicholls, F. J. Rodríguez-Fortuño, M. E. Nasir, R. M. Córdova-Castro, N. Olivier, G. A. Wurtz and A. V. Zayats, Ultrafast synthesis and switching of light polarization in nonlinear anisotropic metamaterials, Nat. Photonics, 2017, 11, 628–633.
11. G. A. Ermolaev, D. V. Grudinin, Y. V. Stebunov, K. V. Voronin, V. G. Kravets, J. Duan, A. B. Mazitov, G. I. Tselikov, A. Bylinkin, D. I. Yakubovsky, S. M. Novikov, D. G. Baranov, A. Y. Nikitin, I. A. Kruglov, T. Shegai, P. Alonso-Gonzalez, A. N. Grigorenko, A. V. Arsenin, K. S. Novoselov and V. S. Volkov, Giant optical anisotropy in transition metal dichalcogenides for next-generation photonics, Nat. Commun., 2021, 12, 854.
12. E. Collett, Field Guide to Polarization, SPIE, Bellingham, 2005.
13. X. Yang, L. Ma and D. Yan, Facile synthesis of 1D organic–inorganic perovskite micro-belts with high water stability for sensing and photonic applications, Chem. Sci., 2019, 10, 4567–4572.
14. D. Yan, H. Yang, Q. Meng, H. Lin and M. Wei, Two-Component Molecular Materials of 2,5-Diphenyloxazole Exhibiting Tunable Ultraviolet/Blue Polarized Emission, Pump-enhanced Luminescence, and Mechanochromic Response, Adv. Funct. Mater., 2014, 24, 587–594.
15. S. Liu, Y. Lin and D. Yan, Hydrogen-bond organized 2D metal–organic microsheets: direct ultralong phosphorescence and color-tunable optical waveguides, Sci. Bull., 2022, 67, 2076–2084.
16. Y. Pan, S. Guo, B. Liu, H. Xue and G. Guo, Second-order nonlinear optical crystals with mixed anions, Coord. Chem. Rev., 2018, 374, 464–496.
17. Z. Zhang, Y. Wang, B. Zhang, Z. Yang and S. Pan, Polar Fluorooxoborate, NaB₄O₆F: A Promising Material for Ionic Conduction and Nonlinear Optics, Angew. Chem., Int. Ed., 2018, 57, 6577–6581.
18. F. Liang, L. Kang, P. Gong, Z. Lin and Y. Wu, Rational Design of Deep-Ultraviolet Nonlinear Optical Materials in Fluorooxoborates: Toward Optimal Planar Configuration, Chem. Mater., 2017, 29, 7098–7102.
19. Z. Du, Y. Zhou and S. Zhao, Synthesis, Crystal Structure and Birefringence Properties of Silver Cluster Compound Ag₃B₆O₁₀I, Chin. J. Appl. Chem., 2023, 40, 229–235.
20. J. Liu, X. He, J. Xu, G. Zhou, S. Zhou, G. Zhao and S. Li, The study on properties of Sr²⁺-doped α-BBO crystal, J. Cryst. Growth, 2004, 260, 486–489.
21. M. T. Anderson and K. R. Poeppelmeier, Lanthanum copper tin oxide (La₂CuSnO₆): a new perovskite-related compound with an unusual arrangement of B cations, Chem. Mater., 1991, 3, 476–482.
22. M. Azuma, S. Kaimori and M. Takano, High-Pressure Synthesis and Magnetic Properties of Layered Double Perovskites Ln₂CuMO₆ (Ln = La, Pr, Nd, and Sm; M = Sn and Zr), Chem. Mater., 1998, 10, 3124–3130.
23. X. Dong, H. Wu, Y. Shi, H. Yu, Z. Yang, B. Zhang, Z. Chen, Y. Yang, Z. Huang, S. Pan and Z. Zhou, Na₁₁B₂₁O₃₆X₂ (X = Cl, Br): Halogen Sodium Borates with a New Graphene-Like Borate Double Layer, Chem. Eur. J., 2013, 19, 7338–7341.
24. Y. Wang, S. Pan, H. Yu, X. Su, M. Zhang, F. Zhang and J. Han, Cs₄Mo₅P₂O₂₂: a first Strandberg-type POM with 1D straight chains of polymerized [Mo₅P₂O₂₃]⁶⁻ units and moderate second harmonic generation response, Chem. Commun., 2013, 49, 306–308.
25. D. Lin, M. Luo, C. Lin, F. Xu and N. Ye, KLi(HC₃N₃O₃)·2H₂O: Solvent-drop Grinding Method toward the Hydro-isocyanurate Nonlinear Optical Crystal, J. Am. Chem. Soc., 2019, 141, 3390–3394.
26. J. Lu, Y. Lian, L. Xiong, Q. Wu and L. Wu, How To Maximize Birefringence and Nonlinearity of π-Conjugated Cyanurates, J. Am. Chem. Soc., 2019, 141, 16151–16159.
27. X. Meng, F. Liang, K. Kang, J. Tang, Q. Huang, W. Yin, Z. Lin and M. Xia, A rich structural chemistry in π-conjugated hydroisocyanurates: layered structures of A₂B(H₂C₃N₃O₃)₄·nH₂O (A = K, Rb, Cs; B = Mg, Ca; n = 4, 10) with high ultraviolet transparency and strong optical anisotropy, Dalton Trans., 2019, 48, 9048–9052.
28. M. Aibibula, L. Wang and S. Huang, Rb₃Na(H₂C₃N₃O₃)₄·3H₂O with Large Birefringence, ACS Omega, 2019, 4, 22197–22202.
29. J. Lu, X. Liu, M. Zhao, X. Deng, K. Shi, Q. Wu, L. Chen and L. Wu, Discovery of NLO Semiorganic (C₅H₆ON)⁺(H₂PO₄)⁻: Dipole Moment Modulation and Superior Synergy in Solar-Blind UV Region, J. Am. Chem. Soc., 2021, 143, 3647–3654.
30. Y. Li, C. Yin, X. Yang, X. Kuang, J. Chen, L. He, Q. Ding, S. Zhao, M. Hong and J. Luo, A Nonlinear Optical Switchable Sulfate of Ultrawide Bandgap, CCS Chem., 2021, 3, 2298–2306.
31. Y. Shen, Y. Zhou, X. Xue, H. Yu, S. Zhao and J. Luo, (C₃N₆H₇)₂SiF₆·H₂O: an ultraviolet birefringent crystal exceeding the intrinsic energy gap of an organic reagent, Inorg. Chem. Front., 2022, 9, 5226–5230.
32. W. Huang, X. Zhang, Y. Li, Y. Zhou, X. Chen, X. Li, F. Wu, M. Hong, J. Luo and S. Zhao, A Hybrid Halide Perovskite Birefringent Crystal, Angew. Chem., Int. Ed., 2022, 61, e202202746.
33. M. Li, X. Zhang, Z. Xiong, Y. Li, Y. Zhou, X. Chen, Y. Song, M. Hong, J. Luo and S. Zhao, A Hybrid Antiperovskite with Strong Linear and Second-Order Nonlinear Optical Responses, Angew. Chem., Int. Ed., 2022, 61, e202211151.
34. Y. Li, X. Zhang, Y. Zhou, W. Huang, Y. Song, H. Wang, M. Li, M. Hong, J. Luo and S. Zhao, An Optically Anisotropic Crystal with Large Birefringence Arising from Cooperative π Orbitals, Angew. Chem., Int. Ed., 2022, 61, e202208811.
35. Y. Li, W. Huang, Y. Zhou, X. Song, J. Zheng, H. Wang, Y. Song, M. Li, J. Luo and S. Zhao, A High-Performance Nonlinear Optical Crystal with a Building Block Containing Expanded π-Delocalization, Angew. Chem., Int. Ed., 2023, 135, e202215145.
36. Y. Zhou, X. Zhang, M. Hong, J. Luo and S. Zhao, Achieving effective balance between bandgap and birefringence by confining π-conjugation in an optically anisotropic crystal, Sci. Bull., 2022, 67, 2276–2279.
37. M. J. Frisch, et al., Gaussian 09, Gaussian Inc., Wallingford, CT, 2009, https://www.gaussian.com/.
38. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
39. J. Tauc, Absorption edge and internal electric fields in amorphous semiconductors, Mater. Res. Bull., 1970, 5, 721–729.
40. D. T. Baran, A. M. Sorensen, T. W. Honeyman, R. Ray and M. F. Holick, 1α,25-dihydroxyvitamin D₃-induced increments in hepatocyte cytosolic calcium and lysophosphatidylinositol: Inhibition by pertussis toxin and 1β,25-dihydroxyvitamin D₃, J. Bone Miner. Res., 1990, 5, 517–524.
41. L. Cao, G. Peng, W. Liao, T. Yan, X. Long and N. Ye, A microcrystal method for the measurement of birefringence, CrystEngComm, 2020, 22, 1956–1961.
42. B. Jürgens, H. A. Höppe and W. Schnick, Synthesis, Crystal Structure and Properties of Rubidium Dihydrogentricyanomelaminate Semihydrate Rb[H₂C₆N₉]·1/2 H₂O, Z. Anorg. Allg. Chem., 2004, 630, 35–40.
43. A. Nag, B. V. Lotsch, J. Schmedtaufder Günne, O. Oeckler, P. J. Schmidt and W. Schnick, Rare-Earth Tricyanomelaminates [NH₄]Ln[HC₆N₉]₂[H₂O]₇·H₂O (Ln = La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy): Structural Investigation, Solid-State NMR Spectroscopy, and Photoluminescence, Chem. Eur. J., 2007, 13, 3512–3524.
44. A. Schwarzer, T. Saplinova and E. Kroke, Tri-s-triazines (s-heptazines)—From a “mystery molecule” to industrially relevant carbon nitride materials, Coord. Chem. Rev., 2013, 257, 2032–2062.
45. C. Chen, B. Wu, A. Jiang and G. You, A new-type ultraviolet SHG crystal β-BaB₂O₄, Sci. China, Ser. B: Chem., 1985, 28, 235–243.
46. B. E. Sørensen, A revised Michel-Lévy interference colour chart based on first-principles calculations, Eur. J. Mineral., 2012, 25, 5–10.
47. A. D. Becke and K. E. Edgecombe, A Simple Measure of Electron Localization in Atomic and Molecular Systems, J. Chem. Phys., 1990, 92, 5397–5403.
48. A. Savin, R. Nesper, S. Wengert and T. F. Fässler, ELF: The Electron Localization Function, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832.

---