Open Access Article
Open Access ArticleInvestigation of thermodynamics, and structural, dynamical, and electrical properties of polyoxometalate ionic liquid confined into carbon nanotubes during the melting process using molecular dynamics simulation†
Zahra Khalilzadeha,
Mohsen Abbaspour *ab and
Farrokhzad Mohammadi Zonoza
*ab and
Farrokhzad Mohammadi Zonoza
aDep. of Chemistry, Hakim Sabzevari University, Sabzevar, Iran. E-mail: m.abbaspour@hsu.ac.ir
bDep. of Chemistry, Faculty of Science, Ferdowsi University of Mashhad, Mashhad 9177948974, Iran
First published on 23rd December 2022
Abstract
Understanding the properties of ionic liquids confined into nano-pores is required to use ionic liquids for many applications such as electrolytes for energy storage in capacitors and solar cells. Recently, polyoxometalate ionic liquids have attracted much attention for their potential applications in electrochemistry, catalysis, and nanotechnology. In this work, we have performed MD simulations on 1-ethyl-3-methylimidazolium Keggin ([emim]3[PW12O40]) confined into armchair (20,20) CNTs to study the thermal properties and melting process. Changes in the simulated results of configurational energy of confined polyoxometallate IL indicated that the melting range of the confined polyoxometalate IL is about 650–750 K. Heat capacity at constant volume of the confined IL is about 2 (cal K−1 mol−1) which shows sharp changes around the melting range. The average number of hydrogen bonds (〈HB〉) of the confined IL is about 2.8 which also presents sharp changes around the melting range. The ion conductivity and self-diffusion coefficient of [emim]3[PW12O40] IL also present a sharp maximum of 25 (S m−1) and 6 × 10−10 (m2 s−1) at the melting point. Our results did not show a significant hysteresis in the melting process and therefore, the process is reversible. Our simulation also indicated that the confinement of the polyoxometallate IL into the CNT increases its thermal stability and melting point. Our simulations also indicated that the type of CNT configuration has a small effect on the melting point of the confined polyoxometallate IL.
1. Introduction
Ionic liquids (ILs), which remain in the liquid state at room temperatures, have some interesting properties such as nonflammability, non-volatility, low vapor pressure, electrical conductivity, thermal stability, and electrochemistry.1–4 Recently, polyoxometalate (POM) ionic liquids have attracted much attention for their potential applications in electrochemistry, catalysis, and nanotechnology.5–7 The POMs are clusters of metal cations and oxo ligands and have distinctive chemical properties.8 These inorganic compounds have several applications in materials science, catalysis, electrochemistry, and medicine.9,10 The Keggin anion, PW12O40−3, is one of the most representative POMs. In recent years, several experiments, simulations and quantum mechanics calculations have focused on this family of compounds.11 Recently, Huang et al.4 synthesized and studied a series of reversible phase transformation of POM-IL gels. They observed that the Keggin-type anion clusters decorated with long alkyl chains have a gel state at room temperature which convert into liquid state after heating-cooling process. They also showed that the thermal stability and conductivity of ammonium-based POM-ILs can be improved by decreasing the alkyl chain length. Mei et al.12 investigated the morphology of aqueous solutions of ILs with the anion Keggin and some alkyl-functionalized imidazole-typed cations using molecular dynamics (MD) simulations. They indicated that the alkyl chain length in imidazolium cation can regulate the aggregation behavior among the negative POM anions.ILs can also represent interesting applications in nano-confined systems which are different from the bulk properties.13,14 The confined ILs have also important applications in catalytic reactions, nanocomposites, lubricants, and solar cells.14–25 Previous studies reported that the thermal stability of ILs increases by confining into carbon nanotubes (CNTs).18,21 Li et al.24 studied the melting temperature of 1-ethyl-3-methylimidazolium bromide ([emim][Br]) IL confined into porous silicone oxide nanoclusters. They concluded that the confinement in the nano-pores results in the increase in the melting point. Dong et al.22 observed an ordered ion arrangement of 1-butyl-3-methylimidazolium hexafluorophosphate ([bmim][PF6]) into CNTs using MD simulation. Dou et al.13 also reported a shell-chain structure [bmim][PF6] IL into CNTs. Akbarzadeh and Abbaspour26 investigated structure and dynamics of [emim][PF6] IL into CNTs using MD simulations. They found that the diameter and chirality of the CNT have important effects on the confined IL properties. Akbarzadeh et al.27 also studied melting process of [emim][PF6] IL confined into CNTs with different sizes.
It is very hard to achieve a molecular level insight of ILs into nano-pores from experiment alone. MD simulations enable us to interpret the experimental findings and to predict the behavior of the confined system accurately.27 Understanding the properties of ionic liquids confined into nano-pores is required to use ionic liquids for many applications such as electrolytes for energy storage in capacitors and solar cells.28 Due to the important applications of polyoxometallate ILs,5–7,9,10 for the first time, we aim to study the structural and dynamical properties of 1-ethyl-3-methylimidazolium Keggin ([emim]3[PW12O40] or [emim]3[Keggin]) IL confined into armchair (20,20) CNT during the melting process. In order to do this, we have calculated and discussed the configurational energy, heat capacity at constant volume, radial distribution function, and average number of hydrogen bonds. Very small number of previous simulations investigated the electrical properties of the confined materials into CNT. Therefore, we want to examine the ion conductivity of [emim]3[Keggin] IL at the different temperatures during the melting process too.
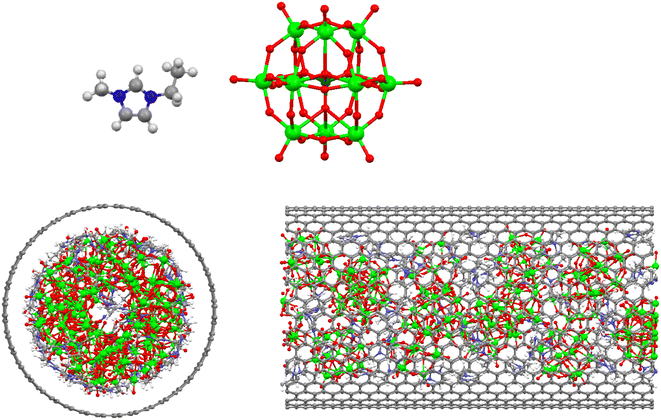
2. Simulation details
We have performed NVT molecular dynamics (MD) simulations on [emim]3[Keggin] IL confined into armchair (20,20) carbon nanotube CNT (45 cations and 15 anions according its density of 6.249 (g cm−3)) with the CNT length of 50 Å in the orthorhombic box with dimensions of 50.7 × 50.7 × 80 Å3 using the DLPOLY software.29 Shi and Sorescu also investigated the structure of a IL into armchair (20,20) CNT using MD simulations.30 To examine the effect of CNT configuration, we have also simulated [emim]3[Keggin] IL into zigzag (35,0) CNT with the same length and almost similar diameter in the same simulation box using the NVT ensemble. To investigate the confinement effect, we have also simulated the bulk IL in the simulation box with the dimensions of 40 × 40 × 40 Å3 with 225 cations and 75 anions using the NPT ensemble in the pressure of 1 atm. The snapshots of the IL confined into the armchair (20,20) CNT has been presented in Fig. 1. The Nose–Hoover thermostat was applied to all systems in order to maintain their temperature constant with a relaxation time of 0.1 ps. The equation motions have integrated using the verlet leapfrog algorithm with the integration time step of 1 fs.29 The CNT was kept in fixed positions and was filled with [emim]3[Keggin] IL corresponding to its density at 300 K. The [emim] cation was modeled using the OPLS-AA potential.31–33 The Keggin anion were modeled as a rigid particle and the all-atom force field parameters of the PW12O403− anion were taken from the work by Lopez et al.,34 which is based on the amber force field and has been extensively applied for the POM anions simulation.12,35,36The Lennard-Jones (LJ) potential was used for the IL-CNT interaction, utilizing the geometric mean for ε (the well depth of the interaction potential) and the arithmetic mean for σ (the distance at which the interaction potential is zero). The LJ parameters of the polyoxometallate IL and the CNT have been presented in Table S1 in the ESI.† The coulombic long range interactions were calculated using mesh Ewalds' method with a precision of 10−6. All interatomic interactions between the atoms in the simulation box have calculated within the cutoff distance 15 Å. The periodic boundary conditions are applied in all dimensions.
According to the previous simulations,26,27 the IL-CNT system was kept in vacuum in the center of the orthorhombic box in such a way that one side of the box (x-direction) was almost equal to the length of the CNT, and the length of the other two sides of the box was long enough to avoid any artificial effect caused by the periodic boundary conditions. The system was run long enough (30 ns) to overcome the initial configuration and reach to the equilibrium state at 300 K. Then, it was run for 6 ns (2 ns for the equilibration and 4 ns for the production runs) at every temperature. The time step for all simulation was 1 fs. The configurational energies of the system versus simulation times have been presented at the different temperatures in Fig. S1 in the ESI.† As this figure shows, the system has been reached to the equilibrium state. It can be also observed the jump in the energy in the melting range.
3. Results and discussion
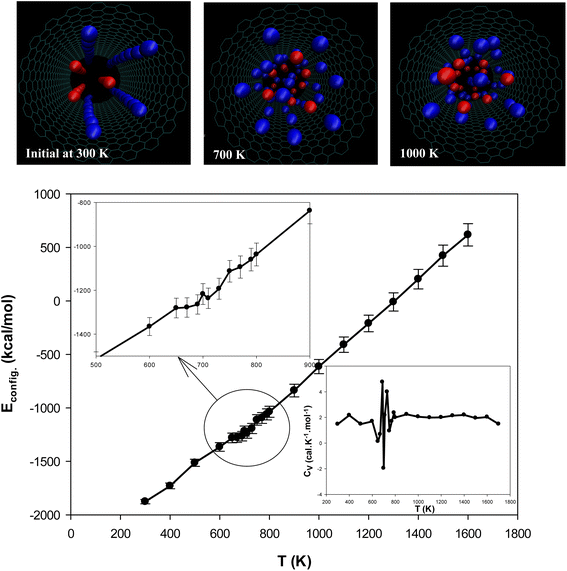
The configurational energy of [emim]3[Keggin] IL confined into (20,20) CNT has been computed at different temperatures and presented in Fig. 2. The configurational energy is the result of force field effect on the system during the MD simulation and is the sum of the various intermolecular and intramolecular energies such as van der Waals energy, coulombic energy, etc. The change in the configurational energy in the range of 650–750 K corresponds to the melting process. The snapshots of the confined IL into the CNT have been also presented in Fig. 2. These snapshots have been prepared using the center of mass of the cations and anions. According to these snapshots, the ordered arrangements of the cations and anions have been disappeared at the melting range (T = 700 K). To assure the melting range, we have also presented the heat capacity at constant volume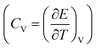 for the confined IL into the CNT in Fig. 2. The sharp peaks in the CV plot corresponds to the first-order (or pseudo first-order) melting which its range is 650–750 K (with the sharpest peak at 690 K), in according with the configurational energy results.37 At the best knowledge of the authors, there is not any experimental melting temperature for the [emim]3[Keggin] IL in the literature. However, Rajkumar and Rao38 synthesized the bulk 1-Butyl-3-methylimidazolium Keggin ([bmim]3[Keggin]) IL and reported its melting temperature at 673 K. Li et al.39 synthesized tributyltetradecylphosphonium Keggin ([TBTP]4[PW11O40]) IL and reported its melting point below 373 K. It should be also noted that the confining of IL into CNT can also increase its melting point.27 To investigate the hysteresis phenomenon in the melting process of the [emim]3[Keggin] IL into CNT, we have also simulated the cooling process and the corresponding results of CV have been presented in Fig. S2 in the ESI.† As this figure shows, there is not significant change in the melting point (650–800 K) which means that we have not a significant hysteresis in the melting process and therefore the process is reversible. This result can be due to the fact that the IL-CNT wall interactions do not change upon the melting process.
for the confined IL into the CNT in Fig. 2. The sharp peaks in the CV plot corresponds to the first-order (or pseudo first-order) melting which its range is 650–750 K (with the sharpest peak at 690 K), in according with the configurational energy results.37 At the best knowledge of the authors, there is not any experimental melting temperature for the [emim]3[Keggin] IL in the literature. However, Rajkumar and Rao38 synthesized the bulk 1-Butyl-3-methylimidazolium Keggin ([bmim]3[Keggin]) IL and reported its melting temperature at 673 K. Li et al.39 synthesized tributyltetradecylphosphonium Keggin ([TBTP]4[PW11O40]) IL and reported its melting point below 373 K. It should be also noted that the confining of IL into CNT can also increase its melting point.27 To investigate the hysteresis phenomenon in the melting process of the [emim]3[Keggin] IL into CNT, we have also simulated the cooling process and the corresponding results of CV have been presented in Fig. S2 in the ESI.† As this figure shows, there is not significant change in the melting point (650–800 K) which means that we have not a significant hysteresis in the melting process and therefore the process is reversible. This result can be due to the fact that the IL-CNT wall interactions do not change upon the melting process.
To investigate the confinement effect, we have also simulated the bulk [emim]3[Keggin] IL and the corresponding plot of the heat capacities has been presented in Fig. S3 in the ESI.† According to this figure, the melting point of the bulk IL is almost at 500–600 K. This result means that the confinement of the polyoxometallate IL into the CNT increases its thermal stability and melting point. This result is in agreement with the simulation results of Akbarzadeh et al.27 on [emim][PF 6] IL confined in CNT.
To examine the CNT configuration on the melting range of the confined [emim]3[Keggin] IL, we have also simulated the polyoxometallate IL into the zigzag (35,0) CNT and the corresponding plots of the configurational energies and heat capacities have been presented in Fig. S4 in the ESI.† According to this figure, the melting point of the IL is 700 K. In comparison with the melting range in armchair CNT (650–750 K), this result means that the there is good agreement between two configurations. In the other words, the kind of CNT configuration has small effect on the melting point of the confined polyoxometallate IL.
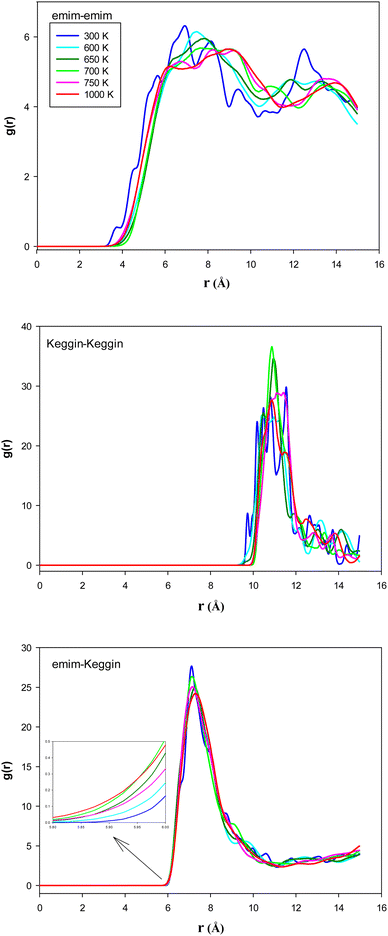
To examine the structural properties of the confined system, we have calculated the radial distribution function (RDF) using the following relation:28
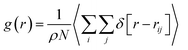 | (1) |
We have also presented the average number of hydrogen bonds (〈HB〉) in the confined [emim]3[Keggin] system at different temperatures in Fig. 4. The Keggin anion has a high negative charge and polarizes the surrounding molecules which form multiple hydrogen bonds with the external oxygens of the polyoxometalate.40 We consider the criteria for HB that if the distance between the hydrogen atom in cation and oxygen atom in anion is less than 2.67 Å, then the interaction can be recognized as HB.27,41 Fig. S7 in the ESI† shows the HBs between H atoms from emim cations and O atoms from Keggin anion (according to the final configuration of the confined IL in CNT at 500 K).
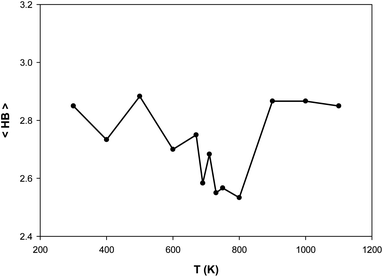 | ||
| Fig. 4 The average number of hydrogen bonds (〈HB〉) for the confined [emim]3[Keggin] IL at different temperatures. | ||
According to Fig. 4, the 〈HB〉 of the confined [emim]3[Keggin] IL is about 2.8 which is smaller than other ILs such as [emim][PF6] IL confined into CNT (〈HB〉 ≈ 7)27. This result is due to presence of less number of polyoxometallate ions into the CNT than the other ILs due to the higher density of Keggin anion. The [emim][PF6] IL has more 〈HB〉 because of the more donor (F) atoms on the anion which increases the probability of formation of HB with the cation. It is also shown in Fig. 4 that the 〈HB〉 shows small deviation with the temperature. The 〈HB〉 decreases by increasing the temperature whereas it increases by increasing the temperature after the melting range. The sudden change in 〈HB〉 is almost in agreement with the energy and RDF results but it is somewhat more (800 K) and indicates the melting range. The increasing of 〈HB〉 by increasing the temperature (after melting) is in agreement with the small shift of cation–anion RDF to the shorter distances and also by increasing of the RDF first peaks by increasing the temperature (Fig. 3). In the other words, the cations and anions get closer after melting and make more HBs between each other.
We have also computed the electrical conductivity of the confined [emim]3[Keggin] IL at different temperatures using the Nernst–Einstein relation:27,42
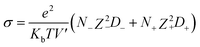 | (2) |
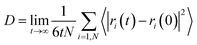 | (3) |
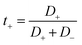 | (4) |
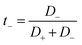 | (5) |
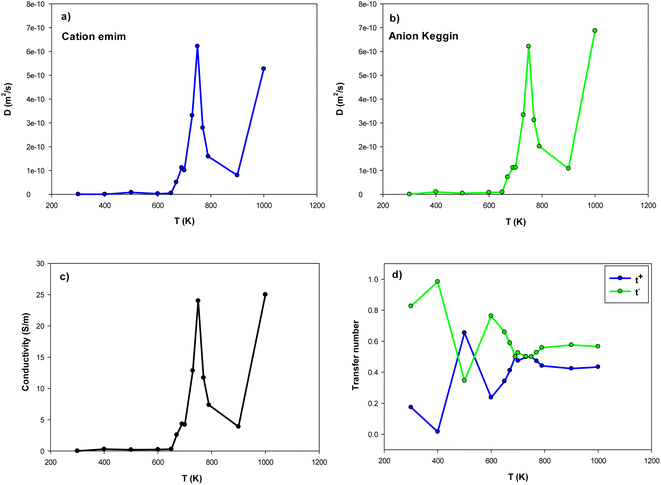 | ||
| Fig. 5 The self-diffusion, ion conductivity, and ion transference numbers for the confined [emim]3[Keggin] IL at different temperatures. | ||
Our simulated ion conductivity value of [emim]3[Keggin] IL at 300 K (0.001 (S m−1)) is almost in similar order of other ILs such as [emim][PF6] IL confined into CNT (0.004 (S m−1) in (30,0) CNT).28 However, the ion conductivity of the different ILs confined in nanopores is much less than the experimental value of the bulk IL.45 According to Fig. 5, the ion conductivity of IL represents sharp increases about the melting temperature. The sharp increase in the ion conductivity of confined [emim]3[Keggin] IL is due to the sharp increase in its self-diffusion in the melting range (Fig. 5a–c). This result is also due to the decrease of 〈HB〉 until the melting range (Fig. 4). After the melting, some oscillations can be observed in ion conductivity results which are in agreement with the 〈HB〉 results in Fig. 4. The sharp decrease of ion conductivity by increasing the temperature after the melting point is due to the sharp increase of 〈HB〉 after the melting. The sharp increase of ion conductivity after that at 1000 K is due to the sharp increase of self-diffusion coefficient by increasing the kinetic energy of the particles by more increasing of the temperature. We have also presented the MSD curves of cation and anion versus simulation time at the different temperatures in Fig. S8 in the ESI.† This figure clearly shows the sharp change in the slope of the MSD curves close to the melting range.
According to Fig. 5, the self-diffusion coefficients of cations and anions are almost similar in the melting range and beyond. Fig. 5 also represents the variation of transference number with increasing temperature. The t+ increases by increasing the temperature until the melting range. After the melting, it remains almost constant. The trend of t− is in opposite trend of t+ versus the temperature. The reason why both transference numbers remain almost constant in the melting range and after that is due to the fact that the self-diffusion of anion and cation is almost similar in theses ranges (according to eqn (4) and (5)). This is also in agreement with the 〈HB〉 results in which it remains almost constant after 900 K.
4. Conclusion
In this work, we have studied the thermal properties and melting process of confined [emim]3[Keggin] IL into (20,20) CNT. The simulated configurational energy, heat capacity at constant volume, and RDF results indicated that the melting range of the confined polyoxometalate IL is 650–750 K. Our results showed that we have not a important hysteresis in the melting process and therefore the process is reversible. This result can be due to the fact that the IL-CNT wall interactions do not change upon the melting process. Our simulation also indicated that the confinement of the polyoxometallate IL into the CNT increases its thermal stability and melting point. This result is in agreement with the previous simulation results of [emim][PF 6] IL confined in CNT. Our simulations on zigzag CNT indicated that there is good agreement between two armchair and zigzag configurations. In the other words, the kind of CNT configuration has small effect on the melting point of the confined polyoxometallate IL.The sudden change in 〈HB〉 is almost in agreement with the energy and RDF results but it is somewhat more (800 K) and indicates the melting range. The increasing of 〈HB〉 by increasing the temperature (after melting) is in agreement with the small shift of cation–anion RDF to the shorter distances. The ion conductivity of [emim]3[Keggin] IL also represents a sharp peak at the melting temperature which is due to the sharp increase in its self-diffusion because of the decrease of 〈HB〉. The t+ also increases by increasing the temperature until the melting range. After the melting, it remains almost constant. The trend of t− is in opposite trend of t+ versus the temperature. We expect that the understanding the thermal properties of [emim]3[Keggin] IL confined into nano-pore (such as the melting range, ion conductivity, etc.) help us using its potential applications in electrochemistry, catalysis, and nanotechnology.
Conflicts of interest
There are no conflicts to declare.References
- Y. Lu, K. Korf, Y. Kambe, Z. Tu and L. A. Archer, Ionic-liquid–nanoparticle hybrid electrolytes: applications in lithium metal batteries, Angew. Chem., Int. Ed., 2014, 53(2), 488–492 CrossRef CAS PubMed.
- S. Tang, G. A. Baker and H. Zhao, Ether-and alcohol-functionalized task-specific ionic liquids: attractive properties and applications, Chem. Soc. Rev., 2012, 41(10), 4030–4066 RSC.
- J. Ping, Y. Wang, Y. Ying and J. Wu, Design and synthesis of a task-specific ionic liquid as a transducer in potentiometric sensors, RSC Adv., 2013, 3(43), 19782–19784 RSC.
- T. Huang, N. Tian, Q. Wu and W. Yan, Keggin-type polyoxometalate-based ionic liquid gels, Soft Matter, 2015, 11(22), 4481–4486 RSC.
- S. Herrmann, J. T. Margraf, T. Clark and C. Streb, Thermochromic and solvatochromic properties of Lindqvist polyoxometalates, Chem. Commun., 2015, 51(71), 13702–13705 RSC.
- Q. Yin, J. M. Tan, C. Besson, Y. V. Geletii, D. G. Musaev, A. E. Kuznetsov, Z. Luo, K. I. Hardcastle and C. L. Hill, A fast soluble carbon-free molecular water oxidation catalyst based on abundant metals, Science, 2010, 328(5976), 342–345 CrossRef CAS PubMed.
- Y. Leng, J. Wang, D. Zhu, X. Ren, H. Ge and L. Shen, Heteropolyanion-based ionic liquids: reaction-induced self-separation catalysts for esterification, Angew. Chem., 2009, 121(1), 174–177 CrossRef.
- Polyoxometalate molecular science, ed. J. J. Borrás-Almenar, E. Coronado, A. Müller and M. Pope, Springer Science & Business Media, 2003, vol. 98 Search PubMed.
- C. L. Hill, Introduction: polyoxometalates multicomponent molecular vehicles to probe fundamental issues and practical problems, Chem. Rev., 1998, 98(1), 1–2 CrossRef CAS PubMed.
- Polyoxometalates: From Platonic Solids to Anti-Retroviral Activity: From Platonic Solids to Anti-Retroviral Activity, ed. M. Pope, Springer Science & Business Media, 1994, vol. 10 Search PubMed.
- X. Lopez, C. Nieto-Draghi, C. Bo, J. B. Avalos and J. M. Poblet, Polyoxometalates in solution: molecular dynamics simulations on the α-PW12O403-Keggin anion in aqueous media, J. Phys. Chem. A, 2005, 109(6), 1216–1222 CrossRef CAS PubMed.
- Y. Mei, W. Huang, Z. Yang, J. Wang and X. Yang, Ion-pairing and aggregation of ionic liquid-neutralized polyoxometalate salts in aqueous solutions, Fluid Phase Equilib., 2016, 425, 31–39 CrossRef CAS.
- Q. Dou, M. Sha, H. Fu and G. Wu, Melting transition of ionic liquid (bmim)(PF6) crystal confined in nanopores: a molecular dynamics simulation, J. Phys. Chem. C, 2011, 115(39), 18946–18951 CrossRef CAS.
- R. Singh, J. Monk and F. R. Hung, A computational study of the behavior of the ionic liquid [BMIM+][PF6−] confined inside multiwalled carbon nanotubes, J. Phys. Chem. C, 2010, 114(36), 15478–15485 CrossRef CAS.
- M. Kanakubo, Y. Hiejima, K. Minami, T. Aizawa and H. Nanjo, Melting point depression of ionic liquids confined in nanospaces, Chem. Commun., 2006,(17), 1828–1830 RSC.
- D. Kuang, S. Ito, B. Wenger, C. Klein, J. E. Moser, R. Humphry-Baker, S. M. Zakeeruddin and M. Grätzel, High molar extinction coefficient heteroleptic ruthenium complexes for thin film dye-sensitized solar cells, J. Am. Chem. Soc., 2006, 128(12), 4146–4154 CrossRef CAS PubMed.
- S. Chen, G. Wu, M. Sha and S. Huang, Transition of ionic liquid [bmim](PF6) from liquid to high-melting-point crystal when confined in multiwalled carbon nanotubes, J. Am. Chem. Soc., 2007, 129(9), 2416–2417 CrossRef CAS PubMed.
- J. Le Bideau, P. Gaveau, S. Bellayer, M. A. Neouze and A. Vioux, Effect of confinement on ionic liquids dynamics in monolithic silica ionogels: 1H NMR study, Phys. Chem. Chem. Phys., 2007, 9(40), 5419–5422 RSC.
- M. Sha, G. Wu, H. Fang, G. Zhu and Y. Liu, Liquid-to-solid phase transition of a 1, 3-dimethylimidazolium chloride ionic liquid monolayer confined between graphite walls, J. Phys. Chem. C, 2008, 112(47), 18584–18587 CrossRef CAS.
- S. Chen, K. Kobayashi, Y. Miyata, N. Imazu, T. Saito, R. Kitaura and H. Shinohara, Morphology and melting behavior of ionic liquids inside single-walled carbon nanotubes, J. Am. Chem. Soc., 2009, 131(41), 14850–14856 CrossRef CAS PubMed.
- M. Sha, G. Wu, Y. Liu, Z. Tang and H. Fang, Drastic phase transition in ionic liquid [Dmim][Cl] confined between graphite walls: new phase formation, J. Phys. Chem. C, 2009, 113(11), 4618–4622 CrossRef CAS.
- K. Dong, G. Zhou, X. Liu, X. Yao, S. Zhang and A. Lyubartsev, Structural evidence for the ordered crystallites of ionic liquid in confined carbon nanotubes, J. Phys. Chem. C, 2009, 113(23), 10013–10020 CrossRef CAS.
- H. Feng, J. Zhou and Y. Qian, Atomistic simulations of the solid-liquid transition of 1-ethyl-3-methyl imidazolium bromide ionic liquid, J. Chem. Phys., 2011, 135(14), 144501 CrossRef PubMed.
- C. Li, X. Guo, Y. He, Z. Jiang, Y. Wang, S. Chen, H. Fu, Y. Zou, S. Dai, G. Wu and H. Xu, Compression of ionic liquid when confined in porous silica nanoparticles, RSC Adv., 2013, 3(25), 9618–9621 RSC.
- G. Ori, F. Villemot, L. Viau, A. Vioux and B. Coasne, Ionic liquid confined in silica nanopores: molecular dynamics in the isobaric–isothermal ensemble, Mol. Phys., 2014, 112(9–10), 1350–1361 CrossRef CAS.
- H. Akbarzadeh and M. Abbaspour, Effects of diameter and chirality on structural and dynamical behavior of [emim][PF6] encapsulated in carbon nanotube: a molecular dynamics study, J. Mol. Liq., 2015, 212, 423–429 CrossRef CAS.
- H. Akbarzadeh, M. Abbaspour, S. Salemi and S. Abdollahzadeh, Investigation of the melting of ionic liquid [emim][PF6] confined inside carbon nanotubes using molecular dynamics simulations, RSC Adv., 2015, 5(5), 3868–3874 RSC.
- F. Taherkhani and B. Minofar, Effect of nitrogen doping on glass transition and electrical conductivity of [EMIM][PF6] ionic liquid encapsulated in a zigzag carbon nanotube, J. Phys. Chem. C, 2017, 121(29), 15493–15508 CrossRef CAS.
- W. Smith, T. R. Forester and I. T. Todorov, The DL_POLY molecular simulation package, CCLRC. Daresbury Laboratory, Daresbury, Warrington, England, 1999 Search PubMed.
- W. Shi and D. C. Sorescu, Molecular simulations of CO2 and H2 sorption into ionic liquid 1-n-hexyl-3-methylimidazolium bis (trifluoromethylsulfonyl) amide ((hmim)(Tf2N)) confined in carbon nanotubes, J. Phys. Chem. B, 2010, 114(46), 15029–15041 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. Pádua, Molecular force field for ionic liquids III: Imidazolium, pyridinium, and phosphonium cations; chloride, bromide, and dicyanamide anions, J. Phys. Chem. B, 2006, 110(39), 19586–19592 CrossRef CAS PubMed.
- S. V. Sambasivarao and O. Acevedo, Development of OPLS-AA force field parameters for 68 unique ionic liquids, J. Chem. Theory Comput., 2009, 5(4), 1038–1050 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118(45), 11225–11236 CrossRef CAS.
- X. Lopez, C. Nieto-Draghi, C. Bo, J. B. Avalos and J. M. Poblet, Polyoxometalates in solution: molecular dynamics simulations on the α-PW12O403-Keggin anion in aqueous media, J. Phys. Chem. A, 2005, 109(6), 1216–1222 CrossRef CAS PubMed.
- A. Chaumont and G. Wipff, Ion aggregation in concentrated aqueous and methanol solutions of polyoxometallates Keggin anions: the effect of counterions investigated by molecular dynamics simulations, Phys. Chem. Chem. Phys., 2008, 10(46), 6940–6953 RSC.
- A. Chaumont and G. Wipff, Polyoxometalate Keggin anions at aqueous interfaces with organic solvents, ionic liquids, and graphite: a molecular dynamics study, J. Phys. Chem. C, 2009, 113(42), 18233–18243 CrossRef CAS.
- H. Akbarzadeh, M. Abbaspour, S. Salemi and M. Abroodi, Investigation of thermal evolution of copper nanoclusters encapsulated in carbon nanotubes: a molecular dynamics study, Phys. Chem. Chem. Phys., 2015, 17(19), 12747–12759 RSC.
- T. Rajkumar and G. Ranga Rao, Investigation of hybrid molecular material prepared by ionic liquid and polyoxometalate anion, J. Chem. Sci., 2008, 120(6), 587–594 CrossRef CAS.
- Y. Li, X. Wu, Q. Wu, H. Ding and W. Yan, Reversible phase transformation ionic liquids based on ternary Keggin polyoxometalates, Ind. Eng. Chem. Res., 2014, 53(33), 12920–12926 CrossRef CAS.
- P. Miro, J. M. Poblet, J. B. Avalos and C. Bo, Towards a computational treatment of polyoxometalates in solution using QM methods and explicit solvent molecules, Can. J. Chem., 2009, 87(10), 1296–1301 CrossRef CAS.
- A. V. Bondi, van der Waals volumes and radii, J. Phys. Chem., 1964, 68(3), 441–451 CrossRef CAS.
- S. S. Sarangi, W. Zhao, F. Müller-Plathe and S. Balasubramanian, Correlation between Dynamic Heterogeneity and Local Structure in a Room-Temperature Ionic Liquid: A Molecular Dynamics Study of (bmim)(PF6), ChemPhysChem, 2010, 11(9), 2001–2010 CAS.
- D. Frenkel and B. Smit, Understanding Computer Simulation, Academic, New York, 1996, vol. 116, p. 126 Search PubMed.
- M. H. Kowsari, S. Alavi, M. Ashrafizaadeh and B. Najafi, Molecular dynamics simulation of imidazolium-based ionic liquids. I. Dynamics and diffusion coefficient, J. Chem. Phys., 2008, 129(22), 224508 CrossRef CAS PubMed.
- D. Portela, L. Segade, Y. Arosa, E. L. Lago, L. M. Varela, E. Tojo and O. Cabeza, Experimental device to measure the ionic conductivity anisotropy in liquid crystal hydrogel based in (EMIM) alkyl sulfate Ionic Liquids, Fluid Phase Equilib., 2022, 555, 113353 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra04681d |
| This journal is © The Royal Society of Chemistry 2023 |