Open Access Article
Open Access ArticleComputational insight into a mechanistic overview of water exchange kinetics and thermodynamic stabilities of bis and tris-aquated complexes of lanthanides†
Niharika Keot and
Manabendra Sarma
and
Manabendra Sarma *
*
Department of Chemistry, Indian Institute of Technology Guwahati, Assam 781039, India. E-mail: msarma@iitg.ac.in; Tel: +91 361 2582318
First published on 6th January 2023
Abstract
A thorough investigation of Ln3+ complexes with more than one inner-sphere water molecule is crucial for designing high relaxivity contrast agents (CAs) used in magnetic resonance imaging (MRI). This study accomplished a comparative stability analysis of two hexadentate (H3cbda and H3dpaa) and two heptadentate (H4peada and H3tpaa) ligands with Ln3+ ions. The higher stability of the hexadentate H3cbda and heptadentate H4peada ligands has been confirmed by the binding affinity and Gibbs free energy analysis in aqueous solution. In addition, energy decomposition analysis (EDA) reveals the higher binding affinity of the peada4− ligand than the cbda3− ligand towards Ln3+ ions due to the higher charge density of the peada4− ligand. Moreover, a mechanistic overview of water exchange kinetics has been carried out based on the strength of the metal–water bond. The strength of the metal–water bond follows the trend Gd–O47 (w) > Gd–O39 (w) > Gd–O36 (w) in the case of the tris-aquated [Gd(cbda)(H2O)3] and Gd–O43 (w) > Gd–O40 (w) for the bis-aquated [Gd(peada)(H2O)2]− complex, which was confirmed by bond length, electron density (ρ), and electron localization function (ELF) at the corresponding bond critical points. Our analysis also predicts that the activation energy barrier decreases with the decrease in bond strength; hence kex increases. The 17O and 1H hyperfine coupling constant values of all the coordinated water molecules were different, calculated by using the second-order Douglas–Kroll–Hess (DKH2) approach. Furthermore, the ionic nature of the bonding in the metal–ligand (M–L) bond was confirmed by the Quantum Theory of Atoms-In-Molecules (QTAIM) and ELF along with energy decomposition analysis (EDA). We hope that the results can be used as a basis for the design of highly efficient Gd(III)-based high relaxivity MRI contrast agents for medical applications.
1 Introduction
The chemistry of lanthanide complexes in aqueous solution has been considered one of the prominent research areas due to their fruitful implementation in diagnostics and therapy.1–5 This includes the luminescent lanthanide complexes (specifically Eu3+ and Tb3+) used in bioanalytical and optical imaging,6–8 and radioisotopes of lanthanides (177Lu) used in radioimmunotherapy.9 Indeed, Gd3+ complexes attract considerable interest since they are commonly used as contrast agents in magnetic resonance imaging (MRI).10 Though MRI has tremendous medical applications, one of the major challenges is its relatively low sensitivity.11,12 To increase the sensitivity, an additional agent called an MRI contrast agent (CA) is required, which alters the properties of nearby water protons after addition.13 The capability or sensitivity of a contrast agent is exhibited through its relaxivity (r). Relaxivity can be defined as the paramagnetic magnification of the relaxation rate of the water proton, which is directly proportional to the concentrations of the CAs used.14,15The most important MRI contrast agents are metal-based paramagnetic ions.10,16 In contrast to other metal ions, discrete Gd3+-based complexes are widely used as clinical paramagnetic contrast agents. This is because of their large number of unpaired electrons and slow electronic relaxation.17,18 However, the toxicity profile of Gd3+ ions is very high. A large or repeated dose of them causes nephrogenic systemic fibrosis (NSF) in patients with renal disorder.19 The food and drug administration (FDA) has placed restrictions on the application of Gd3+-based contrast agents (GBCs) due to the revelation of the connection between Gd3+ and NSF.20,21
The current concerns of researchers are about the safety of MRI contrast agents and designing new contrast agents with enhanced thermodynamic stability and kinetic inertness.22,23 This can be achieved by complexation of the metal ion with ligands that prevent the release of the free Gd(III) ion. Based on the toxicity profile, many research groups focus on developing a contrast agent with high relaxivity so that a lower dose can be administered.24–26 Among the various factors, water exchange of the coordinated water molecules with the bulk water is one of the important tools to be optimized for higher relaxivity of MRI CAs. Various research groups27–30 have also focused on designing CAs with more than one inner-sphere water molecule to improve relaxivity. It is well established that, indifferent to the field strength, relaxivity increases proportionally to the number of coordinated water molecules (q).31 Merbach et al.32,33 first considered the whole lanthanide series to study the water exchange rate (kex). Despite the significance of optimizing the water exchange to get an efficient MRI contrast agent, this issue is ignored in the literature. As far as the authors are aware, only limited studies have been done until now.34–37 The water exchange rate of the inner-sphere water molecules has been accelerated by factors such as increasing the overall compound negative charge and the steric hindrance surrounding the water molecules.38 Clinically approved CAs contain only a single molecule of water in the inner coordination sphere.34 The water exchange rates and structural elucidation of the most studied chelators 1,4,7,10-tetraaza-1,4,7,10-tetrakis(carboxymethyl)cyclododecane(DOTA)39,40 and diethylenetriaminepentaacetic acid (DTPA)41 have been well established. However, for q > 1 complexes, i.e. [Ln(L)(H2O)2–3]x [L = ligand, x = charge, Ln = La3+ to Lu3+], no such systematic explanation of the water exchange and structural analysis has been done so far.27,42,43 Indeed, with an increase in the number of inner-sphere water molecules, the ligand's denticity reduces, which may reduce the complexes' thermodynamic stability.34
A few Gd(III) chelates with q > 1 have been reported. One such system is the Gd(III) complex of a pyridine-containing macrocyclic ligand with two acetic acids and one methylenephosphonic arm (PCP2A),44,45 but further functionalization of this complex was found to be difficult. Another class of complexes with a higher hydration number (q > 1) is represented by tris-bidentate Gd(III)-hydroxypyridinone (HOPO) based derivatives, which are presently under strong scrutiny.46 Previously, Bretonnière et al. synthesized a ligand α,α′,α′′-nitrilotri(6-methyl-2-pyridinecarboxylic acid) (H3tpaa) containing three picolinate groups with a longitudinal relaxivity value of 13.3 mM−1 s−1 at 1.4 T and 25 °C, and the stability was observed to be low.47 In a subsequent study, they synthesized a Gd(III) complex with an octadentate N,N′-bis[(6-carboxy-2-pyridylmethyl]ethylenediamine–N,N′-diacetic acid (H4bpeada) ligand, which has two picolinate groups with a longitudinal relaxivity of 5.0 mM−1 s−1 at a magnetic field of 20 MHz and 25 °C.48 This relaxivity value is greater than for DOTA (r1 = 4.7 mM−1 s−1) and DTPA (r1 = 4.8 mM−1 s−1).49 The stability of this octadentate ligand (H4bpeda) is less than that of the ethylenediaminetetraacetic acid (H4EDTA) ligand, which is hexadentate in nature. Furthermore, the same group synthesized the ligand N,N′-bis[(6-carboxy-pyridin-2-yl)methyl]glycin (H3dpaa),50 replacing one of the picolinate groups with a carboxylate group. The ligand H3dpaa exhibits a relaxivity value of 11.93 mM−1 s−1 at 4.7 T and 25 °C, with stability higher than the H3tpaa ligand. Based on the aforementioned discussions, Phukan et al.51 synthesized a ligand H4peada with one picolinate and three carboxylate groups to obtain higher relaxivity and stability. Later, they synthesized a hexadentate ligand (H3cbda) with two picolinate and one carboxylate group to incorporate both the relaxivity and thermodynamic stability with a methyl group in the backbone of the ligand.52
On account of the above perspectives, the present computational study uncovers the thermodynamic stability and comparative binding affinities of heptadentate (peada4− and tpaa3−) and hexadentate (cbda3− and dpaa3−) ligands with Ln3+ ions in aqueous solution. Furthermore, the trend in the water exchange rate (kex) of the inner-sphere water with bulk water has been investigated, following the methodology proposed by Figueroa et al.53 Moreover, this work computationally ascertained the type of mechanism for the coordinated water molecules based on the activation parameter values. The ligands chosen in this study are shown in Scheme 1.47,50–52 In addition, the bonding interactions between the metal and ligand have been confirmed by the Quantum Theory of Atoms-In-Molecules (QTAIM) and energy decomposition analysis (EDA). This sheds light on the different binding affinity of the ligand with Ln3+ ions. Thus we believe that the thermodynamic stability and mechanistic overview of the water exchange rate kinetics provided in this study will be helpful in future ligand designing for stable lanthanide-based complexes. The last segment concludes our analyses.
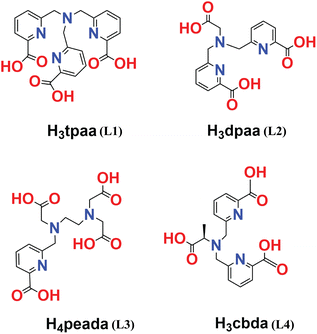 | ||
| Scheme 1 Ligands (L1 (ref. 47)), (L2 (ref. 50)), (L3 (ref. 51)) and (L4 (ref. 52)) considered in this study. | ||
2 Computational details
All the geometries of the lanthanide complexes were optimized with relativistic DFT, using the hybrid meta-GGA TPSSh functional53,54 as implemented in the Gaussian 16 program package.55 The vibrational frequency analysis has been carried out to characterize the nature of the optimized geometries as energy minima or saddle points. Additionally, we tested the performance of different density functionals (B3LYP, B3LYP-D3, and ωB97XD) for comparative purposes. The choice of the TPSSh functional is due to its better geometrical interpretation than the hybrid GGA (B3LYP) functional.53,56 Also, the long-range corrected functional (ωB97XD) does not provide a better geometrical interpretation than the hybrid meta-GGA (TPSSh) functional. Hence we used the TPSSh functional during the geometry optimization of the complexes. For the central metal atom (Ln3+), we considered both large core relativistic effective core potential (LCRECP) with its related (7s6p5d)/[5s4p3d]-GTO valence basis set,57 and small core relativistic effective core potential (SCRECP)58 with the ECP28MWB_GUESS53 basis set for comparative purposes. The standard 6-31G(d,p) and 6-31+G(d,p) (for some specific calculations) basis sets were applied for the remaining elements (H, C, N, and O). The performance of different density functionals and basis sets is discussed in detail in the dedicated sections below. At the same level of theory, the transition state geometries were located and the intrinsic reaction coordinate (IRC) paths were generated. Furthermore, to correct the activation energy barrier, we calculated the single point energy (taking the large core DFT optimized geometry) of the reactant and transition state by considering the wave function-based method, second order Møller–Plesset perturbation theory (MP2),59 with the def2-TZVP basis set for the remaining elements (H, C, N, and O).The computational investigations of lanthanide complexes using relativistic effective core potential (ECP)60–62 in conjugation with density functional theory (DFT) provide accurate results for most of the earlier reported complexes.63,64 It has been mentioned earlier that large-core (LC) calculations provide a somewhat longer bond distance than that of the small-core (SC) calculations.53 Despite its approximate nature, LCRECP is an efficient computational tool, which focuses mainly on the analysis of geometrical structures and estimation of relative energies of heavy metal-containing complexes at the DFT level.53,65,66
Moreover, to incorporate the solvent effect, the polarizable continuum model (PCM)67,68 with the integral equation formalism, i.e. the IEFPCM67 model, has been considered. To describe the accurate M–L bond and 17O hyperfine coupling constant values, we have explicitly considered the second sphere of water along with the implicit solvent model (IEFPCM).69,70 To describe the cavity of the solvent, universal force field radii71 were applied and adjusted by a factor of 1.1. Optimization was carried out by imposing nosymm constraints. Furthermore, to evaluate the Gibbs free energy values, the solvation model based on density (SMD) has been applied to incorporate the non-electrostatic contributions.72 Harmonic approximation was applied for the Gibbs free energy calculations at T = 298.15 K using five different density functionals (B3LYP, TPSSh, M06,73 B3LYP-D3, and ωB97XD).
Wave function analysis was performed by applying Bader’s Quantum Theory of Atoms-In-Molecules (QTAIM)74 to obtain the electron density (ρ), electron localization function (ELF) and Laplacian of electron density (∇2ρ) at the bond critical points (BCPs) using the Multiwfn program (version 3.8).75 Furthermore, for the extended transition state (ETS) energy decomposition analysis,76 optimized structures of the [Ln(cbda)(H2O)3]·6H2O and [Ln(peada)(H2O)2]−·4H2O complexes were considered, having been obtained from the scalar relativistic77 ZORA78,79 method, along with the SARC-ZORA80 basis set for the Ln3+ ion and the 6-31G(d,p) basis set for the rest of the elements. From these optimized structures, a single point energy decomposition analysis was performed in the ADF2021 package,81 using SARC-ZORA approximation with the TZ2P82 basis set for all the elements, and BP86 functional83–85 with no frozen core approximation. This ETS analysis has been performed for the closed shell La3+ and Lu3+ metal centres. Due to their closed shell character, spin restricted formalism was applied.
The ORCA 4.0 program86 package was used for the analysis of isotropic 17O and 1H hyperfine coupling constants, using TPSSh and the SARC2-DKH-QZVP87 basis set for the Gd3+ ion and the DKH-def2-TZVPP80 basis set for the remaining atoms.
The molecular electrostatic potential (MEP) at any point in space with position vector r and r′ for evaluating the charge distribution of the complexes can be evaluated by applying eqn (1)
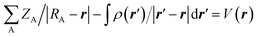 | (1) |
The M–L binding energies (BEs) were evaluated from the optimized structures of the complexes (both LC- and SC-optimized). The BEs were calculated by individually optimizing the geometries of the complexes, ligands (Scheme 1), and inner-sphere water molecules. This includes basis set superposition error (BSSE) corrections using the counterpoise method90 for the gas phase optimized structures of the complexes. The BEs of the ligands were also evaluated by doing single point energy calculations using the TPSSh functional and LCRECP (for the Gd3+ ion) along with the def2-TZVP91 basis set for the remaining elements (H, C, N, and O) to reduce the BSSE.
3 Results and discussion
3.1 Stability analysis of the Ln3+ complexes
The stability of the Ln3+ complexes in aqueous solution is an important issue for the application of Ln3+ complexes, which can be decided mainly by two factors: (i) the binding energy of the ligand to the metal ions and (ii) the solvation-free energy of the complexes and free metal ions. In the following two sections, these two factors are analyzed in detail.This is owing to the presence of the three carboxylate groups which bind more strongly to Gd3+ due to the oxyphilic nature of the Gd3+ ion.51 Also, the binding affinity of the ligand cbda3− (−166.42 kcal mol−1) is about +1.36 kcal mol−1 greater than that of the dpaa3− ligand (−165.06 kcal mol−1). This may be due to the chirality induced by the methyl group in the ligand (H3cbda) in accordance with the experimental results.52 Evaluation of BE values using two different core definitions – large core and small core pseudopotentials – (Table S2† in the ESI) regarding both sets of complexes (hexa and heptadentate) provided a similar trend in BE values. In order to justify our method, we further analyzed the BE values of the respective ligands with the Gd3+ ion by changing the basis sets (6-31+G(d,p) and def2-TZVP) and methods (B3LYP, B3LYP-D3, and ωB97XD) from the LC optimized structure. The M–L bond distances of all the complexes (Fig. 1) are presented in Tables S3–S6† in the ESI. Lastly, all the data obtained using different density functionals (TPSSh, B3LYP, B3LYP-D3, and ωB97XD) and basis sets (6-31G(d,p), 6-31+G(d,p), and def2-TZVP) along with the different core definitions (LC and SC) are reported in Table S2† of the ESI and provide similar trends towards the relative stability of the complexes.
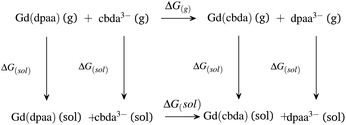 | ||
| Scheme 2 Thermodynamic cycle for explaining the comparative stabilities of [Gd(cbda)] and [Gd(dpaa)] complexes. | ||
As expected,52 the ΔG(g) and ΔG(aq) values tend to be negative on replacing the hexadentate dpaa3− ligand with the cbda3− ligand. The negative ΔG(g) and ΔG(aq) indicate the stronger binding affinity of the cbda3− ligand with the Gd3+ ion than the dpaa3− ligand, both in the gas phase and solution phase. This again confirms the influence of the methyl group in the ligand backbone for increased stability of the [Gd(cbda)] complex compared to the [Gd(dpaa)] complex. Different density functionals (B3LYP, TPSSh, M06, B3LYP-D3 and ωB97XD) and core definitions (large core and small core) provide a similar trend in the ΔG(g) and ΔG(aq) values and ligand selectivity as shown in Table S7† of the ESI.
Similarly, for the heptadentate ligand bearing [Gd(peada)]− and [Gd(tpaa)] complexes, the thermodynamic stabilities of the ligands peada4− and tpaa3− with the Gd(III) ion were analyzed (Scheme S1† in the ESI). In this case, it was found that the [Gd(peada)]− complex formation is more stable than for the [Gd(tpaa)] complex, with higher negative ΔG(g) and ΔG(aq) values (Table S7† in the ESI) as a consequence of the presence of four negative carboxylate groups compared to the tpaa3− ligand. These stability trends follow the experimental analysis of the thermodynamic stability of the complexes.51,52 The experimental ΔGexp(aq) values, as shown in Tables S7 and S8,† were estimated from the equilibrium constant values provided in the earlier literature.51,52 Furthermore, different density functionals (B3LYP, TPSSh, M06, B3LYP-D3, and ωB97XD), and basis sets (6-31G(d,p) and 6-31+G(d,p)) impart similar trends in ΔG(g) and ΔG(aq) values and ligand selectivity (Tables S7 and S8† in the ESI).
In view of the above stability analysis, we will consider the more stable heptadentate (H4peada) and hexadentate (H3cbda) ligands for further investigations.
3.2 Structural analysis
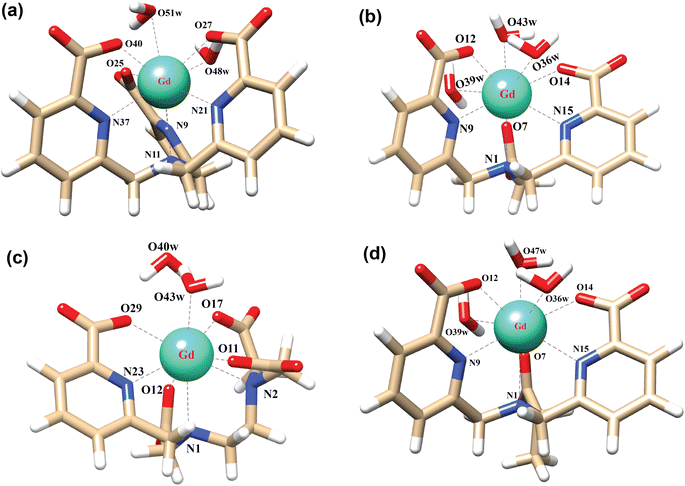
In order to explore the coordination polyhedra and bonding interactions of the ligands (peada4− and cbda3−) with lanthanide series elements we have considered the stable La3+ (4f0), Gd3+ (4f7) and Lu3+ (4f14) ions. The optimized structures of the [Ln(peada)(H2O)2]− and [Ln(cbda)(H2O)3] complexes [Ln = La, Gd, and Lu], obtained using the SC pseudopotential are shown in Fig. 2. The LC-optimized structures are provided in Fig. S1† in the ESI. To limit the drawbacks of the continuum solvation model,69,93,94 six explicit water molecules for the tris-aquated and four explicit water molecules for the bis-aquated complexes have been considered.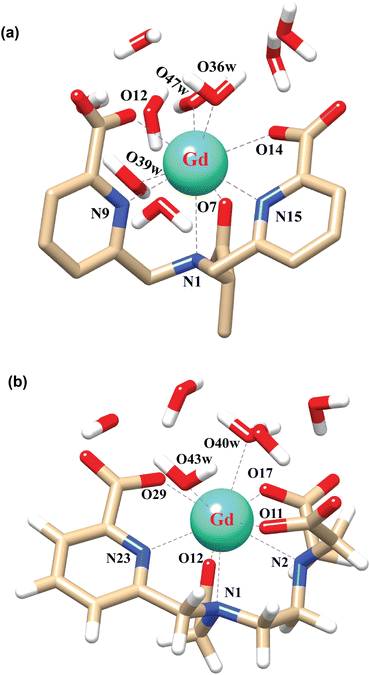 | ||
| Fig. 2 Optimized structures of the complexes (a) [Gd(cbda)(H2O)3]·6H2O, and (b) [Gd(peada)(H2O)2]−·4H2O with second sphere waters obtained using the SCRECP/TPSSh/6-31G(d,p) level of theory. | ||
The bond distances calculated using SC and LC pseudopotentials (with different density functionals) are provided in Tables S9–S12† in the ESI. According to previous investigations,53 the bond length values are longer for LCRECP than SCRECP, which is also reflected in this analysis. The bond length values are in good agreement with the previously synthesized q > 1 complex.43,95 The labilities of the three water molecules in tris-aquated [Gd(cbda)(H2O)3]·6H2O and the two water molecules in the [Gd(peada)(H2O)2]−·4H2O complex were found to be different based on the bond length analysis and the complexes are anticipated to exhibit different water exchange rates (kex).
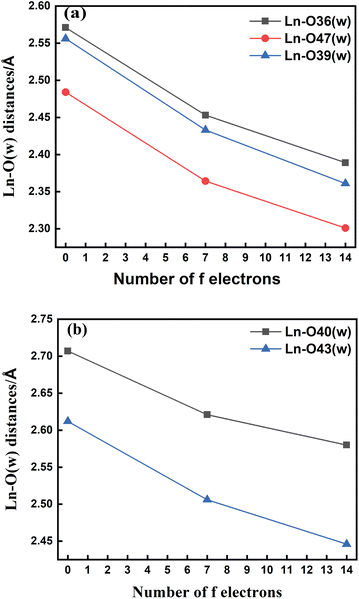
The bond length values decrease along the series as predicted as a consequence of the lanthanide contraction, as shown in Fig. 3(a) and (b). The values calculated using SCRECP decreased from La3+ to Lu3+ with some fluctuation. At first, for the tris-aquated complex the bond length values follow the trend Ln–O36 (w) > Ln–O39 (w) > Ln–O47 (w), and the fluctuations of the bond lengths were higher for Ln–O36 (w) and Ln–O39 (w) compared to Ln–O47 (w) due to the steric and pulling effects of water molecules, which reflects the weaker binding of the water molecules as shown in Fig. 3(a). In the bis-aquated complex, the bond length values follow the trend Ln–O40 (w) > Ln–O43 (w) (Fig. 3(b)).
Moreover, the average Ln–N bond length values for the tris-aquated and bis-aquated complexes decrease from 2.79 to 2.66 Å and 2.77 to 2.57 Å respectively. Whereas, the Ln–O (carboxylate) bond length only drops from 2.49 to 2.33 Å and 2.43 to 2.27 Å respectively (Tables S7–S10† in the ESI). In both bis and tris-aquated metal co-ordination polyhedra, the shortest distance is between the Ln3+ ion and the carboxylate oxygen because of the hard–hard interaction of oxygen and the Ln3+ ion according to Pearson's HSAB concept.96
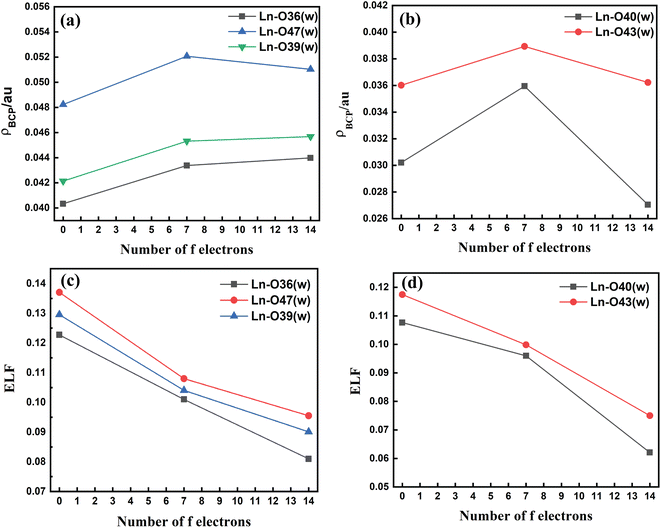
The metal–(H2O) bond strength was further confirmed by analysis of the electron density (ρBCP), the Laplacian of the electron density (∇2ρ), and the electron localization function (ELF) at the critical points of the respective bonds along the Ln3+ (Ln = La, Gd, and Lu) series as presented in Tables S11–S14† in the ESI. Our investigations show that for the tris-aquated complex the ρBCP values follow the trend Ln–O47 (w) > Ln–O39 (w) > Ln–O36 (w) as shown in Fig. 4(a). Similarly, for the bis-aquated complex the ρBCP value follows the trend Ln–O43 (w) > Ln–O40 (w) (Fig. 4(b)), opposite to that of bond length values. These ρBCP values tend to increase in the series' first half and then decrease. The decrease of the electron density indicates weaker binding of the inner-sphere water molecules.53,97 Again, the ELF values decrease along the lanthanide series as ionic radii decrease. However, the bond length becomes shorter, indicating the weaker binding of water molecules at the end of the series as shown in Fig. 4(c) and (d). This agrees well with the labile capping bond phenomenon mentioned in previous literature.97
The Ln–O (w) bond length values of the anionic [Ln(peada)(H2O)2]−·4H2O complex are longer than those of the neutral [Ln(cbda)(H2O)3]·6H2O complex, which indicates the faster kex in the anionic complex.45 Furthermore, the calculation of the electron density (ρBCP), ELF, and Laplacian of the electron density (∇2ρ) using the LC pseudopotential ensures the reliability of the SC pseudopotential for electron density calculations for q > 1 complexes.
3.3 Evaluation of water exchange kinetics
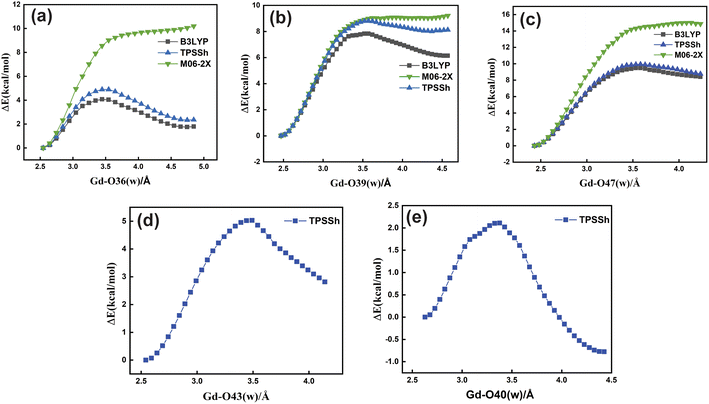
Based upon the above analysis, for the bis-aquated [Gd(peada)(H2O)2]−·4H2O complex we considered only one functional (TPSSh). An intensive assessment of other functionals was not carried out for the bis-aquated complex. In the case of the bis-aquated complex, scanning of the Gd–O40 (w) bond stabilized the eight coordinated [Gd(peada)(H2O)]−·5H2O and the scanning of Gd–O43 (w) stabilized the nine coordinated [Gd(peada)(H2O)2]−·4H2O complex, in accordance with the experimental analysis51 of the hydration equilibria, showing the co-existence of both eight and nine coordinated forms as shown in Fig. 5(d) and (e). This co-existence is due to the flexible ligand environment due to the presence of four carboxylate groups. The relaxed PES scans for both complexes obtained using the SC pseudopotential are provided in Fig. S2† in the ESI.
| Ligand | Gd–O (w) (Å) | 17O(Aiso) (MHz) | 1H (MHz) |
|---|---|---|---|
| cbda3− | Gd–O36 (w) = 2.45 | 0.5491 | 0.0227/0.0390 |
| Gd–O39 (w) = 2.43 | 0.6052 | 0.0633/0.0696 | |
| Gd–O47 (w) = 2.36 | 0.9661 | 0.0220/0.0350 | |
| peada4− | Gd–O40 (w) = 2.62 | 0.2156 | 0.0536/0.0517 |
| Gd–O43 (w) = 2.50 | 0.4724 | 0.0746/0.0102 |
| Ln–O (w)bond length | ρBCP | ELF | k298ex/106 s−1 |
|---|---|---|---|
| [Gd(cbda)(H2O)3]·6H2O | |||
| Gd–O36 (w) = 2.453 | 0.04338 | 0.101 | 22.16 |
| Gd–O39 (w) = 2.433 | 0.04532 | 0.104 | 1.4 |
| Gd–O47 (w) = 2.364 | 0.05207 | 0.108 | 0.10 |
| [Gd(peada)(H2O)2]−·4H2O | |||
| Gd–O40 (w) = 2.621 | 0.0359 | 0.0959 | 750.5 |
| Gd–O43 (w) = 2.506 | 0.03893 | 0.0998 | 56.6 |
For LCRECP,
ρBCP = 0.05941 − 0.00316![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kex kex
| (2) |
ELF = 0.13532 − 0.00503![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kex kex
| (3) |
For SCRECP,
ρBCP = 0.06440 − 0.00325![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kex kex
| (4) |
ELF = 0.12275 − 0.00296![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kex kex
| (5) |
From this analysis, we can conclude that the water exchange rate in bis and tris-aquated complexes is mainly related to the strength of the Gd–O (w) bond to reach the eight coordinated transition state (TS). The relatively high water exchange rate of the [Gd(peada)(H2O)2]−·4H2O complex is due to the overall negative charge of the complex, as anionic complexes exhibit a faster kex than neutral complexes.45 Among the two water molecules, Gd–O40 (w) with a bond length of 2.62 Å shows a very high kex, which may be related to the hydration equilibrium between the mono and bis-aquated forms and the flexible coordination sphere surrounding the Gd3+ ion.
| Methods | [Gd(cbda)(H2O)3]·6H2O | [Gd(peada)(H2O)2]−·4H2O | ||||
|---|---|---|---|---|---|---|
| Gd–O36 (w) | Gd–O39 (w) | Gd–O47 (w) | Gd–O40 (w) | Gd–O43 (w) | ||
| TPSSh | ΔEa‡ (kcal mol−1) | 4.93 | 8.90 | 9.95 | 2.10 | 5.02 |
| rGd–O/Å | 2.53 | 2.46 | 2.42 | 2.63 | 2.54 | |
| rGd–O(TS)/Å | 3.48 | 3.37 | 3.55 | 3.35 | 3.45 | |
| ΔH‡ (kcal mol−1) | 4.26 | 8.31 | 9.25 | 1.34 | 4.32 | |
| ΔG‡ (kcal mol−1) | 3.95 | 7.70 | 8.40 | 1.25 | 3.57 | |
| ΔS‡ (J mol−1 K−1) | 4.35 | 9.20 | 11.84 | 1.37 | 10.46 | |
| MP2 | ΔEa‡ (kcal mol−1) | 4.24 | 8.67 | 8.80 | 1.43 | 4.54 |
Moreover, we observe that the activation free energy (ΔG‡) values increase with a decrease in the bond length for both complexes (Table 3). The analysis of the activation enthalpies (ΔH‡) provides a shred of additional evidence for faster water exchange in Gd–O36 (w) followed by Gd–O39 (w) and Gd–O47 (w) in the tris-aquated complex (Table 3). Further, for the bis-aquated complex, the ΔH‡ value increases drastically from Gd–O40 (w) to Gd–O43 (w). In addition, the positive activation entropies (ΔS‡) (Table 3) indicate a dissociative type of mechanism.36,105,106 Further, to confirm the nature of the mechanism, we have performed intrinsic reaction coordinate (IRC) calculations (Fig. S5† in the ESI), ensuring the dissociative nature of the mechanism.
We tested both large core (4f, in core) and small core pseudopotentials and found that activation parameter values are sensitive to the choice of the core definitions. But both SCRECP and LCRECP provide a similar trend in the activation parameter values except in Gd–O40 (w) (Table S16† in the ESI). The unexpectedly high water exchange rate (kex) in Gd–O40 (w) is due to the very low ΔH‡ value, corresponding to the weaker metal and water molecule interaction. Moreover, we have performed single point energy calculations using the MP2 method for a comparative purpose. The DFT (TPSSh) and MP2 methods exhibit quite similar values of activation energies (Table 3).
3.4 Bonding nature of the complexes
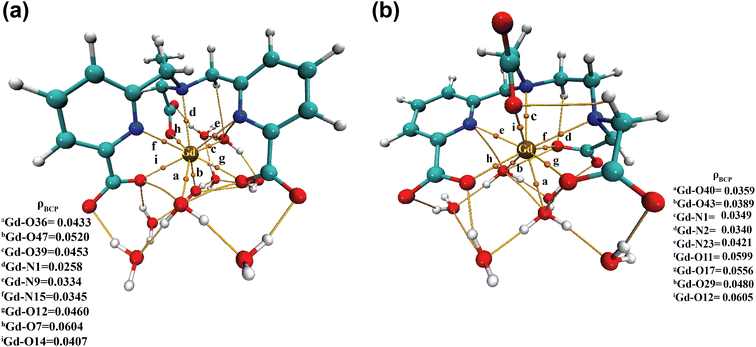 | ||
| Fig. 6 Electron density (ρ) values at the bond critical points (BCPs) of (a) [Gd(cbda)(H2O)3]·6H2O and (b) [Gd(peada)(H2O)2]−·4H2O complexes. | ||
Moreover, to assess the bonding interaction between the metal and the ligand a useful quantum mechanical method, i.e. the electron localization function (ELF), was employed. ELF is a simple and useful descriptor of the topological analysis of chemical bonds based on Pauli's repulsion effect. Here, the implementation of ELF based on Pauli's repulsion was investigated. In the ELF color-filled map surface (Fig. 7) the region between the metal (Gd3+) and the oxygen or nitrogen atoms of the ligands is considered. The color scale is from 0 (blue) to 1 (red) as shown in Fig. 7. According to Becke and Edgecombe,107 an ELF value close to 1 (colored red in Fig. 7) indicates the highest Pauli's repulsion zone. While a value close to 0 indicates the minimum Pauli's repulsion zone which is colored blue in the ELF color-filled map (Fig. 7). The highest Pauli's repulsion zone corresponds to the localization of electrons, indicating covalent bonding, but electrons are delocalized in the lowest Pauli's repulsion area. Subsequently in our analysis the ELF values are close to 0 (Tables S11–S14† in the ESI), exhibiting clearly the ionic nature of the M–L bond. Therefore, both atoms-in-molecules (AIM) and ELF results indicate the presence of ionic bonding.
| ΔEint = ΔVelst + ΔEPauli + ΔEoi | (6) |
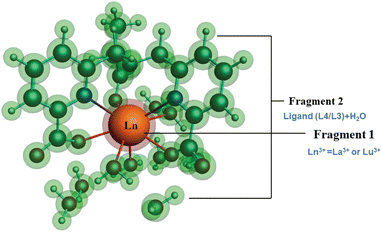 | ||
| Fig. 8 Schematic representation of different fragmentation modes of the [Ln(cbda)(H2O)3]·6H2O and [Ln(peada)(H2O)2]−·4H2O complexes (Ln = La3+ and Lu3+). | ||
The detailed physical significance of the above terms has been described by Bickelhaupt and Baerends.108 The data for the EDA analysis are presented in Table S18† in the ESI. We observed (Table S18†) that the attractive interaction within the M–L complex is derived from the ΔEoi and ΔEelst terms. Moreover, in ionic bonding, ΔEoi is less than ΔEelst but the opposite is true for covalent bonds. In this study, the interaction of the ligand (cbda3− and peada4−) with lanthanides (La3+, Lu3+) was evaluated to figure out the strength and the changes in the M–L bonding in the series. In particular, the data presented in Table S18† reflects the following salient features:
(I) A relationship can be derived between the metal complex stability in terms of interaction energy (ΔEint) and the f-electrons. As depicted in Table S18† in the ESI, the ΔEint value of the Lu–ligand (a fully occupied f-shell) complex is higher than that of the La–ligand complex (an empty f-shell).
(II) The electrostatic contribution is about two to three times larger in magnitude than the covalent contribution in f0 and f14 systems, implying that M–L bonding is electrostatic in nature rather than covalent.
(III) Again, as the charge character of the ligand increases from cbda3− to peada4−, the electrostatic contribution of the [Ln(peada)]− complex is larger compared to the [Ln(cbda)] complex. The percentage of electrostatic contribution in the [Ln(peada)]− complex is also greater than that in the [Ln(cbda)] complex.
(IV) The percentage of electrostatic contribution decreases from La (f0) to the Lu (f14) system, i.e., the covalent contribution is somewhat larger in the Lu (f14) system.
(V) The Pauli (ΔEPauli) and orbital ΔEoi contributions do not change markedly upon changing the ligand charges, as they fluctuate only within a few hundred kilojoules per mole.
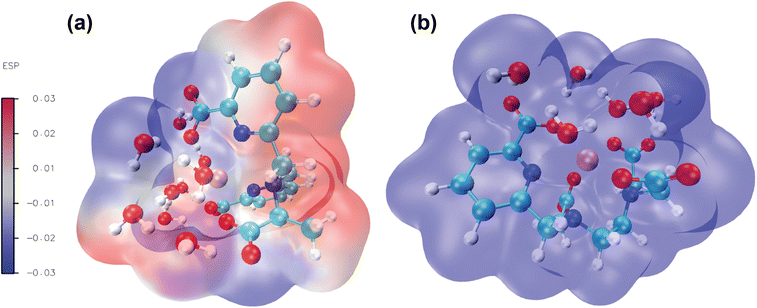
3.5 Analysis of molecular electrostatic potential (MEP)
Molecular electrostatic potential analysis has been carried out to understand the charge distribution within the respective molecules based on their ligand's denticity (hexadentate or heptadentate). This helps evaluate the different interactive behaviour, reactivity and structure of the molecules.109 As noted earlier,92 different colors of the molecular surface indicate different interactive areas. On account of this, we have investigated the MEP of the [Gd(cbda)(H2O)3] and [Gd(peada)(H2O)2]− complexes as shown in Fig. 9(a) and (b). The molecular surface of the complexes is divided into two regions: hydrophilic (blue) and hydrophobic (red). The blue color of the [Gd(peada)(H2O)2]− complex indicates a hydrophilic area and a more negative electrostatic potential. This is due to a large number of carboxylic groups (four) pointing in the same direction and the overall negative charge of the anionic complex compared to the neutral complex.In the neutral [Gd(cbda)(H2O)3] complex, carboxylate groups (three) are present and attached at different sides of the complex.
4 Conclusions
In summary, the stability of lanthanide complexes fluctuates with the nature of the ligand, and its environment. First, a comparison of the coordination properties and the thermodynamic stability of hexadentate (cbda3− and dpaa3−) and heptadentate (peada4− and tpaa3−) ligands with the Gd3+ ion was carried out in aqueous solution. This stability analysis allows rationalizing that the hexadentate cbda3− ligand forms a reasonably stable complex with the Gd3+ ion compared to the dpaa3− ligand. The presence of a methyl group in the ligand backbone causes a slight increase in the selectivity of this ligand. Likewise, the presence of a large number of carboxylate groups in the peada4− ligand causes an increased selectivity of this ligand compared with tpaa3− towards the Gd3+ ion. A detailed structural analysis has been carried out for the more stable bis-aquated [Gd(peada)(H2O)2]−·4H2O and tris-aquated [Gd(cbda)(H2O)3]·6H2O complexes at the molecular level. The work also established that the complex [Gd(cbda)(H2O)3]·6H2O possesses a stable hydration state of three. In contrast, for the [Gd(peada)(H2O)2]−·4H2O complex, a hydration equilibrium exists between the mono and bis-aquated forms.The kinetic study interpretation by analyzing the water exchange rate of the inner-sphere water molecules reveals that water molecules exhibit different kex rates depending on the ligand environment. The increased water exchange rate is related to the weaker Ln–O(w) bond length, low electron density, and low ELF value. Moreover, from the mechanistic perspective, the dissociative nature of the water exchange mechanism was observed for the exchange of coordinated water molecules with bulk water. However, we have established that for the bis-aquated complex, one coordinated water exhibits an unexpectedly fast kex rate (k298ex = 750 × 106 s−1). This is due to the existence of hydration equilibria and a flexible ligand environment.
Additionally, this study confirms that the M–L bonding interaction is purely ionic. The percentage of electrostatic contribution increases with the increased charge of the ligand and decreases from La (f0) to Lu (f14) systems. The interaction energy between the metal and ligand was found to increase in the order [La(cbda)(H2O)3] < [Lu(cbda)(H2O)3] < [La(peada)(H2O)2]− < [Lu(peada)(H2O)2]−. Thus we believe that these findings will be helpful for designing lanthanide-based complexes with higher hydration number and stability. This lights the way for less toxic MRI contrast agents with higher relaxivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the PARAM-ISHAN super-computing facilities for providing high performance computations and the Department of Chemistry, IIT Guwahati for infrastructure facilities. NK acknowledges the Council of Scientific and Industrial Research (CSIR), India for the fellowship and the financial support, through the registration number 09/731(0167)/2019-EMR-I.Notes and references
- D. Parker and J. G. Williams, J. Chem. Soc., Dalton Trans., 1996, 3613–3628 RSC.
- D. Parker, R. S. Dickins, H. Puschmann, C. Crossland and J. A. Howard, Chem. Rev., 2002, 102, 1977–2010 CrossRef CAS PubMed.
- T. Cheisson and E. J. Schelter, Science, 2019, 363, 489–493 CrossRef CAS PubMed.
- E. Aluicio-Sarduy, N. A. Thiele, K. E. Martin, B. A. Vaughn, J. Devaraj, A. P. Olson, T. E. Barnhart, J. J. Wilson, E. Boros and J. W. Engle, Chem. - Eur. J., 2020, 26, 1238–1242 CrossRef CAS PubMed.
- N. M. Shavaleev, S. V. Eliseeva, R. Scopelliti and J.-C. G. Bünzli, Chem. - Eur. J., 2009, 15, 10790–10802 CrossRef CAS PubMed.
- G. R. Motson, J. S. Fleming and S. Brooker, Adv. Inorg. Chem., 2004, 55, 361–432 CrossRef CAS.
- J.-C. G. Bunzli, Chem. Rev., 2010, 110, 2729–2755 CrossRef CAS PubMed.
- A. M. Nonat and L. J. Charbonnière, Coord. Chem. Rev., 2020, 409, 213192–213207 CrossRef CAS.
- D. Carpanese, G. Ferro-Flores, B. Ocampo-Garcia, C. Santos-Cuevas, N. Salvarese, M. Figini, G. Fracasso, L. De Nardo, C. Bolzati and A. Rosato, et al., Sci. Rep., 2020, 10, 1–10 CrossRef PubMed.
- Y.-D. Xiao, R. Paudel, J. Liu, C. Ma, Z.-S. Zhang and S.-K. Zhou, Int. J. Mol. Med., 2016, 38, 1319–1326 CrossRef CAS PubMed.
- A. Webb, Anal. Chem., 2012, 84, 9–16 CrossRef CAS.
- R. D. Alvares, D. A. Szulc and H.-L. M. Cheng, Sci. Rep., 2017, 7, 1–9 CrossRef CAS PubMed.
- P. Caravan, Chem. Soc. Rev., 2006, 35, 512–523 RSC.
- P. Marzola, F. Osculati and A. Sbarbati, Eur. J. Radiol., 2003, 48, 165–170 CrossRef PubMed.
- P. Caravan, C. T. Farrar, L. Frullano and R. Uppal, Contrast Media Mol. Imaging, 2009, 4, 89–100 CrossRef CAS PubMed.
- D. Pan, A. H. Schmieder, S. A. Wickline and G. M. Lanza, Tetrahedron, 2011, 67, 8431–8444 CrossRef CAS PubMed.
- S. Aime, M. Botta, M. Fasano and E. Terreno, Chem. Soc. Rev., 1998, 27, 19–29 RSC.
- J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed.
- S. A. Woolen, P. R. Shankar, J. J. Gagnier, M. P. MacEachern, L. Singer and M. S. Davenport, JAMA Intern. Med., 2020, 180, 223–230 CrossRef CAS PubMed.
- D. Levine, R. J. McDonald and H. Y. Kressel, JAMA, J. Am. Med. Assoc., 2018, 320, 1853–1854 CrossRef PubMed.
- J. S. McDonald and R. J. McDonald, Magn. Reson. Imaging Clin. N. Am., 2020, 28, 497–507 CrossRef PubMed.
- M. Port, J.-M. Idée, C. Medina, C. Robic, M. Sabatou and C. Corot, BioMetals, 2008, 21, 469–490 CrossRef CAS PubMed.
- A. Rodriguez-Rodriguez, M. Regueiro-Figueroa, D. Esteban-Gomez, R. Tripier, G. Tircso, F. K. Kalman, A. C. Benyei, I. Toth, A. d. Blas and T. Rodriguez-Blas, et al., Inorg. Chem., 2016, 55, 2227–2239 CrossRef CAS PubMed.
- B. Zhang, L. Cheng, B. Duan, W. Tang, Y. Yuan, Y. Ding and A. Hu, Dalton Trans., 2019, 48, 1693–1699 RSC.
- H. U. Rashid, M. A. U. Martines, J. Jorge, P. M. de Moraes, M. N. Umar, K. Khan and H. U. Rehman, Bioorg. Med. Chem., 2016, 24, 5663–5684 CrossRef CAS PubMed.
- P. D. Garimella, A. Datta, D. W. Romanini, K. N. Raymond and M. B. Francis, J. Am. Chem. Soc., 2011, 133, 14704–14709 CrossRef CAS PubMed.
- S. Aime, L. Calabi, C. Cavallotti, E. Gianolio, G. B. Giovenzana, P. Losi, A. Maiocchi, G. Palmisano and M. Sisti, Inorg. Chem., 2004, 43, 7588–7590 CrossRef CAS PubMed.
- N. Graeppi, D. H. Powell, G. Laurenczy, L. Zékány and A. Merbach, Inorg. Chim. Acta, 1995, 235, 311–326 CrossRef CAS.
- R. Negri, F. Carniato, M. Botta, G. B. Giovenzana and L. Tei, ChemPlusChem, 2016, 81, 235–241 CrossRef CAS PubMed.
- E. M. Gale, N. Kenton and P. Caravan, MedChemComm, 2013, 49, 8060–8062 CAS.
- A. Varga-Szemes, P. Kiss, A. Rab, P. Suranyi, Z. Lenkey, T. Simor, R. G. Bryant and G. A. Elgavish, PLoS One, 2016, 11, e0149260 CrossRef PubMed.
- C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1988, 27, 1973–1979 CrossRef CAS.
- C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1989, 28, 2699–2703 CrossRef CAS.
- S. Karimi and L. Helm, Inorg. Chem., 2016, 55, 4555–4563 CrossRef CAS PubMed.
- Z. Baranyai, D. D. Castelli, C. Platas-Iglesias, D. Esteban-Gomez, A. Bényei, L. Tei and M. Botta, Inorg. Chem. Front., 2020, 7, 795–803 RSC.
- L. Leone, D. Esteban-Gómez, C. Platas-Iglesias, M. Milanesio and L. Tei, MedChemComm, 2019, 55, 513–516 CAS.
- B. Phukan, K. P. Malikidogo, C. S. Bonnet, É. Tóth, S. Mondal and C. Mukherjee, ChemistrySelect, 2018, 3, 7668–7673 CrossRef CAS.
- S. Laus, R. Ruloff, É. Tóth and A. E. Merbach, Chem. - Eur. J., 2003, 9, 3555–3566 CrossRef CAS PubMed.
- P. Hermann, J. Kotek, V. Kubíček and I. Lukeš, Dalton Trans., 2008, 3027–3047 RSC.
- S. Aime, M. Botta, M. Fasano, M. P. M. Marques, C. F. Geraldes, D. Pubanz and A. E. Merbach, Inorg. Chem., 1997, 36, 2059–2068 CrossRef CAS PubMed.
- S. Laurent, L. V. Elst and R. N. Muller, Contrast Media Mol. Imaging, 2006, 1, 128–137 CrossRef CAS PubMed.
- M. K. Thompson, M. Botta, G. Nicolle, L. Helm, S. Aime, A. E. Merbach and K. N. Raymond, J. Am. Chem. Soc., 2003, 125, 14274–14275 CrossRef CAS PubMed.
- Z. Baranyai, M. Botta, M. Fekete, G. B. Giovenzana, R. Negri, L. Tei and C. Platas-Iglesias, Chem. - Eur. J., 2012, 18, 7680–7685 CrossRef CAS PubMed.
- S. Aime, M. Botta, L. Frullano, S. Geninatti Crich, G. Giovenzana, R. Pagliarin, G. Palmisano, F. R. Sirtori and M. Sisti, J. Med. Chem., 2000, 43, 4017–4024 CrossRef CAS PubMed.
- P. Caravan, D. Esteban-Gómez, A. Rodríguez-Rodríguez and C. Platas-Iglesias, Dalton Trans., 2019, 48, 11161–11180 RSC.
- A. Datta and K. N. Raymond, Acc. Chem. Res., 2009, 42, 938–947 CrossRef CAS PubMed.
- Y. Bretonnière, M. Mazzanti, J. Pécaut, F. A. Dunand and A. E. Merbach, MedChemComm, 2001, 621–622 Search PubMed.
- N. Chatterton, C. Gateau, M. Mazzanti, J. Pécaut, A. Borel, L. Helm and A. Merbach, Dalton Trans., 2005, 1129–1135 RSC.
- J. Peters, E. Zitha-Bovens, D. Corsi and C. Geraldes, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, John Wiley & Sons, 2001, p. 67 Search PubMed.
- A. Nonat, P. H. Fries, J. Pécaut and M. Mazzanti, Chem. - Eur. J., 2007, 13, 8489–8506 CrossRef CAS PubMed.
- B. Phukan, C. Mukherjee and R. Varshney, Dalton Trans., 2018, 47, 135–142 RSC.
- M. Khannam, S. K. Sahoo and C. Mukherjee, Eur. J. Inorg. Chem., 2019, 2019, 2518–2523 CrossRef CAS.
- M. Regueiro-Figueroa and C. Platas-Iglesias, J. Phys. Chem. A, 2015, 119, 6436–6445 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian – 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- A. Roca-Sabio, M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Comput. Theor. Chem., 2012, 999, 93–104 CrossRef CAS.
- M. Dolg and H. Stoll, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1989, 90, 1730–1734 CrossRef CAS.
- A. Grüneis, M. Marsman and G. Kresse, J. Chem. Phys., 2010, 133, 074107 CrossRef PubMed.
- M. Dolg and X. Cao, Chem. Rev., 2012, 112, 403–480 CrossRef CAS PubMed.
- M. Dolg and H. Stoll, Theor. Chim. Acta, 1989, 75, 369–387 CrossRef CAS.
- A. Weigand, X. Cao, J. Yang and M. Dolg, Theor. Chem. Acc., 2010, 126, 117–127 Search PubMed.
- U. Cosentino, A. Villa, D. Pitea, G. Moro, V. Barone and A. Maiocchi, J. Am. Chem. Soc., 2002, 124, 4901–4909 CrossRef CAS.
- R. O. Freire, G. B. Rocha and A. M. Simas, J. Mol. Model., 2006, 12, 373–389 CrossRef CAS.
- L. Maron and O. Eisenstein, J. Phys. Chem. A, 2000, 104, 7140–7143 CrossRef CAS.
- D. Guillaumont, J. Phys. Chem. A, 2004, 108, 6893–6900 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- D. Esteban-Gómez, A. De Blas, T. Rodríguez-Blas, L. Helm and C. Platas-Iglesias, ChemPhysChem, 2012, 13, 3640–3650 CrossRef PubMed.
- A. Zawada, R. W. Gora, M. M. Mikołajczyk and W. Bartkowiak, J. Phys. Chem. A, 2012, 116, 4409–4416 CrossRef CAS.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- C. F. Matta and R. J. Boyd, The quantum theory of atoms in molecules: from solid state to DNA and drug design, 2007 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- C. Van Wüllen, J. Comput. Chem., 1999, 20, 51–62 CrossRef.
- E. v. Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef.
- E. van Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2009, 5, 2229–2238 CrossRef CAS PubMed.
- G. t. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B, 1986, 33, 8822 CrossRef PubMed.
- X. Yang, C. P. Burns, M. Nippe and M. B. Hall, Inorg. Chem., 2021, 60, 9394–9401 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- D. Aravena, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2016, 12, 1148–1156 CrossRef CAS PubMed.
- S. R. Gadre and R. N. Shirsat, Electrostatics of atoms and molecules, Universities Press, 2000 Search PubMed.
- P. V. Bijina and C. H. Suresh, J. Chem. Sci., 2016, 128, 1677–1686 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- R. Gulde, P. Pollak and F. Weigend, J. Chem. Theory Comput., 2012, 8, 4062–4068 CrossRef CAS PubMed.
- M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Chem. - Eur. J., 2014, 20, 3974–3981 CrossRef CAS PubMed.
- D. Esteban-Gómez, C. Cassino, M. Botta and C. Platas-Iglesias, RSC Adv., 2014, 4, 7094–7103 RSC.
- V. Patinec, G. A. Rolla, M. Botta, R. Tripier, D. Esteban-Gómez and C. Platas-Iglesias, Inorg. Chem., 2013, 52, 11173–11184 CrossRef CAS PubMed.
- A. M. Nonat, C. Gateau, P. H. Fries, L. Helm and M. Mazzanti, Eur. J. Inorg. Chem., 2012, 2012, 2049–2061 CrossRef CAS.
- P. W. Ayers, R. G. Parr and R. G. Pearson, J. Chem. Phys., 2006, 124, 194107–194116 CrossRef PubMed.
- J. Zhang and M. Dolg, J. Phys. Chem. A, 2015, 119, 774–780 CrossRef CAS PubMed.
- K. Pota, Z. Garda, F. K. Kálmán, J. L. Barriada, D. Esteban-Gómez, C. Platas-Iglesias, I. Tóth, E. Brücher and G. Tircsó, New J. Chem., 2018, 42, 8001–8011 RSC.
- O. V. Yazyev, L. Helm, V. G. Malkin and O. L. Malkina, J. Phys. Chem. A, 2005, 109, 10997–11005 CrossRef CAS PubMed.
- O. V. Yazyev and L. Helm, Eur. J. Inorg. Chem., 2008, 2008, 201–211 CrossRef.
- R. Pollet, N. N. Nair and D. Marx, Inorg. Chem., 2011, 50, 4791–4797 CrossRef CAS PubMed.
- G. I. Csonka, J. P. Perdew and A. Ruzsinszky, J. Chem. Theory Comput., 2010, 6, 3688–3703 CrossRef CAS.
- X. Jin, Z. Qian, B. Lu and S. Bi, Dalton Trans., 2011, 40, 567–572 RSC.
- A. S. Merbach, L. Helm and E. Toth, The chemistry of contrast agents in medical magnetic resonance imaging, John Wiley & Sons, 2013 Search PubMed.
- R. Pujales-Paradela, F. Carniato, D. Esteban-Gómez, M. Botta and C. Platas-Iglesias, Dalton Trans., 2019, 48, 3962–3972 RSC.
- L. Leone, S. Camorali, A. Freire-García, C. Platas-Iglesias, D. E. Gomez and L. Tei, Dalton Trans., 2021, 50, 5506–5518 RSC.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 1–86 CAS.
- E. M. Lopez-Vidal, M. Regueiro-Figueroa, M. D. García, C. Platas-Iglesias, C. Peinador and J. M. Quintela, Inorg. Chem., 2012, 51, 4429–4431 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Bond length and binding energy values, optimized geometries of the complexes, relaxed potential energy surface scan, intrinsic reaction coordinate, electron density, ELF and Laplacian values, and Cartesian coordinates of the complexes. See DOI: https://doi.org/10.1039/d2ra05810c |
| This journal is © The Royal Society of Chemistry 2023 |