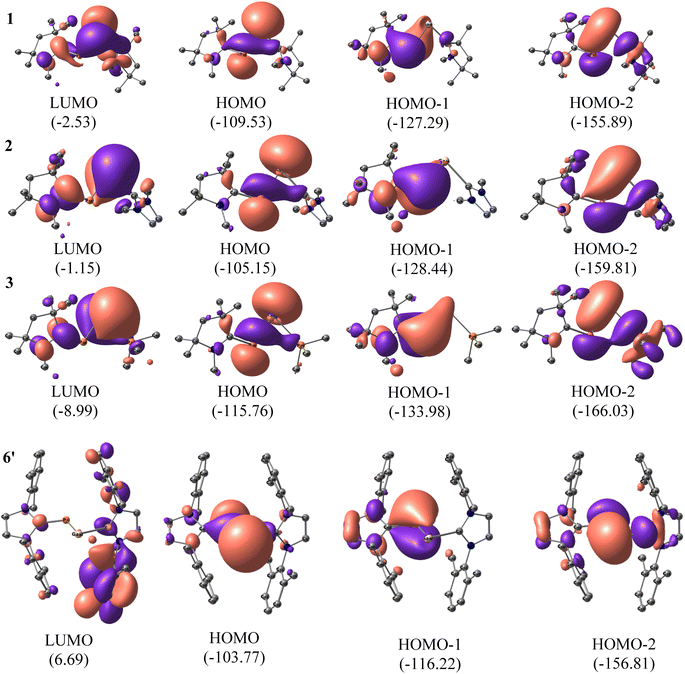Open Access Article
Open Access ArticleStabilisation and reactivity studies of donor-base ligand-supported gallium-phosphides with stronger binding energy: a theoretical approach†
Maria Francis and
Sudipta Roy
and
Sudipta Roy *
*
Department of Chemistry, Indian Institute of Science Education and Research (IISER) Tirupati, Tirupati 517507, India. E-mail: roy.sudipta@iisertirupati.ac.in
First published on 8th March 2023
Abstract
Gallium phosphide is a three-dimensional polymeric material of the hetero-diatomic GaP unit, which has a wurtzite type structure, and captivating application as a light emitting diode (LED). As a result, there is a constant search for suitable precursors to synthesise GaP-based materials. However, the corresponding monomeric species is exotic in nature due to the expected Ga![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P multiple bond. Herein, we report on the theoretical studies of stability, chemical bonding, and reactivity of the monomeric gallium phosphides with two donor base ligands having tuneable binding energies. We have performed detailed investigations using density functional theory at three different levels (BP86/def2-TZVPP, B3LYP/def2-TZVPP, M06-2X/def2-TZVPP), QTAIM and EDA-NOCV (BP86-D3(BJ)/TZ2P, M06-2X/TZ2P) to analyse various ligand-stabilised GaP monomers, which revealed the synthetic viability of such species in the presence of stable singlet carbenes, e.g., cAAC, and NHC as ligands [cAAC = cyclic alkyl(amino) carbene, NHC = N-heterocyclic carbene] due to the larger bond dissociation energy compared to a phosphine ligand (PMe3). The calculated bond dissociation energies between a pair of ligands and the monomeric GaP unit are found to be in the range of 87 to 137 kcal mol−1, predicting their possible syntheses in the laboratory. Further, the reactivity of such species with metal carbonyls [Fe(CO)4, and Ni(CO)3] have been theoretically investigated.
P multiple bond. Herein, we report on the theoretical studies of stability, chemical bonding, and reactivity of the monomeric gallium phosphides with two donor base ligands having tuneable binding energies. We have performed detailed investigations using density functional theory at three different levels (BP86/def2-TZVPP, B3LYP/def2-TZVPP, M06-2X/def2-TZVPP), QTAIM and EDA-NOCV (BP86-D3(BJ)/TZ2P, M06-2X/TZ2P) to analyse various ligand-stabilised GaP monomers, which revealed the synthetic viability of such species in the presence of stable singlet carbenes, e.g., cAAC, and NHC as ligands [cAAC = cyclic alkyl(amino) carbene, NHC = N-heterocyclic carbene] due to the larger bond dissociation energy compared to a phosphine ligand (PMe3). The calculated bond dissociation energies between a pair of ligands and the monomeric GaP unit are found to be in the range of 87 to 137 kcal mol−1, predicting their possible syntheses in the laboratory. Further, the reactivity of such species with metal carbonyls [Fe(CO)4, and Ni(CO)3] have been theoretically investigated.
Introduction
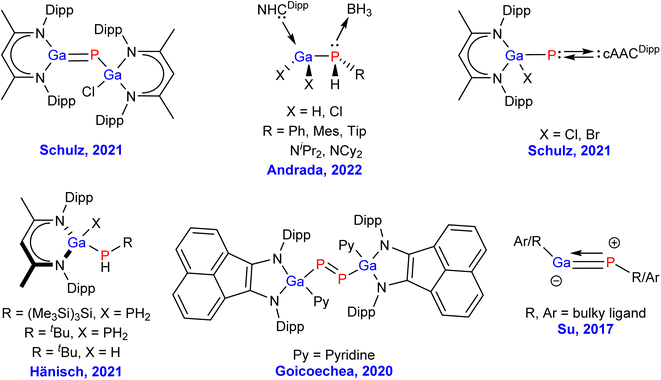
Gallium phosphide (GaP) is widely used in semiconductor containing devices, like long-wavelength detectors and semiconductor lasers, light emitting diodes (LEDs), and as a host material for diluted magnetic semiconductors, because of its low cost, excellent optical properties, and good performance.1–10 Due to its extensive use in electroluminescent devices, gallium phosphide (GaP), having an indirect band gap with a zinc blende (ZnS) structure (wurtzite/w-BN), is one of the very important group III–V semiconductors with the highest industrial importance, and used in MOCVD (MOCVD = metal organic chemical vapour deposition) processes.11–14 By virtue of the 2.26 eV band gap, GaP emits at 555 nm, which makes it not just a semiconducting material, but also a green light emitting LED. The advantageous spectral range of GaP is found to be between 570 nm to 11 μm.15 Moreover, GaP has the highest refractive index of 3.1 in the visible region. This helps to remove a few challenges in designing optical elements, and fast lens. Another crucial property of GaP is the mechanical durability, and chemical resistivity compared to other materials in the same family, leading to useful optical materials that are subjected to mechanical stress, extreme weather, or abrasive dust.16–19 Although, GaP is a polymeric material in the solid-state,15 from the view point of main group chemists we were curious about the chemical bonding, and stability of the corresponding monomeric species, since such combination of heavier elements might lead to an exotic bonding scenario due to the poor overlap of their respective diffused valence orbitals.20 The presence of internal nodes in the more diffused valence orbitals make the heavier main group elements unusual when compared to their lighter analgues.20 The Pauli repulsion energy, and the London dispersion forces play a crucial role in their chemical bonding for possible isolation in the laboratory. In the recent times, the chemistry of molecules having bonds between group 13, and 15 atoms has drawn extensive attention. However, due to the immense synthetic challenges to stabilize such species, there are only a few experimental reports on GaP single and multiple bonded compounds.21–28 The representative Ga–P containing species, which have been isolated in the laboratory by various research groups are shown in Fig. 1. More than two decades ago, Hoffmann et al. have theoretically studied GaP multiple bonds showing Ga![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P triple bond possessing the bond dissociation energy of 101 kcal mol−1 at MP2/6-311++G(d,p) level of theory, while the corresponding values of GaP single and double bonds were found to be 62, and 89 kcal mol−1, respectively.28b Very recently, Schulz group has synthesized gallophosphene L(Cl)GaPGaL (L = HC[C-(Me)N(2,6-iPr2C6H3)]2), which can be used for heteroallyl cation generation, CO2 storage, and C(sp3)–H bond activation.22 The same group has isolated cAACDipp = P–Ga(Cl)L species (Fig. 1, top right).27 Ming–Der Su and co-workers have theoretically predicted the triply bonded Ga
P triple bond possessing the bond dissociation energy of 101 kcal mol−1 at MP2/6-311++G(d,p) level of theory, while the corresponding values of GaP single and double bonds were found to be 62, and 89 kcal mol−1, respectively.28b Very recently, Schulz group has synthesized gallophosphene L(Cl)GaPGaL (L = HC[C-(Me)N(2,6-iPr2C6H3)]2), which can be used for heteroallyl cation generation, CO2 storage, and C(sp3)–H bond activation.22 The same group has isolated cAACDipp = P–Ga(Cl)L species (Fig. 1, top right).27 Ming–Der Su and co-workers have theoretically predicted the triply bonded Ga![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P species using covalently bonded sterically bulky ligands (Fig. 1).29 However, the GaP moiety, stabilised by neutral, donor base ligands, such as, carbenes and phosphines could not be isolated in the laboratory so far.
P species using covalently bonded sterically bulky ligands (Fig. 1).29 However, the GaP moiety, stabilised by neutral, donor base ligands, such as, carbenes and phosphines could not be isolated in the laboratory so far.
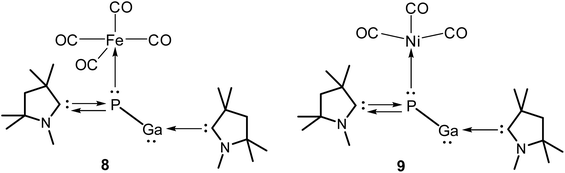
Herein, we report on the detailed theoretical studies on stability, chemical bonding, and reactivity of two donor base ligands-supported monomeric gallium phosphides with general formula (L)GaP(L′) [L,L′ = neutral donor base ligand, e.g., carbene and phosphine; L,L′ = cAACMe (1); L = cAACMe, L′ = NHCMe (2); L = cAACMe, L′ = PMe3 (3); L = NHCMe, L′ = cAACMe (4); L = NHCMe, L′ = PMe3 (5); L,L′ = NHCMe (6); L,L′ = NHCDMP (DMP = 2,6-dimethylphenyl) (6′); L,L′ = PMe3 (7)] (Scheme 1) by using density functional theory (DFT) at three different levels (BP86/def2-TZVPP, B3LYP/def2-TZVPP, and M06-2X/def2-TZVPP), QTAIM, and energy decomposition analysis coupled with natural orbital for chemical valence (EDA-NOCV) (at BP86-D3(BJ)/TZ2P, and M06-2X/TZ2P) methods to demonstrate the synthetic viability of such species.30 These species, once isolated in the laboratory with neutral ligands, and sizeable bond dissociation energies, could be the promising precursors for GaP-based materials. Furthermore, we have studied the stability, and bonding of the corresponding metal carbonyl complexes of compound 1 with general formula (cAAC)2GaP-MCOn [M = Fe; n = 4 (8), M = Ni; n = 3 (9)].
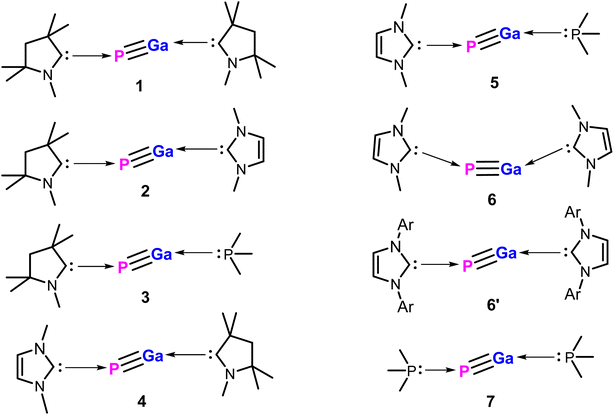 | ||
| Scheme 1 Apparent structures of compounds 1–7 containing a pair of donor base ligands. Ar = 2,6-Dimethylphenyl. | ||
Very often, the EDA-NOCV method has been proven to be a significant tool for predicting the stability, and synthetic viability of exotic species.31 In this context, it is worth mentioning that recently, our group has reported the successful syntheses of carbene-supported phosphinidene-chloroterylenes31a following our previous theoretical prediction of such elusive species.32
The role played by the ligands employed in stabilizing such exotic species are often found to be pivotal. These elusive species have been stabilised with success either by donor-base ligands or by sterically bulky ligands. Superior candidates for stabilizing these transient molecules are in general, the donor ligands, like phosphines, NHCs (N-heterocyclic carbenes), and cAACs (cyclic alkyl(amino) carbenes).33 During the past two decades, using carbenes as ligands have had a tremendous impact on synthetic accomplishments of various apparently elusive species.33–35 A significant number of these carbene containing species are now used for various applications in material chemistry, catalysis, etc.36
Computational methods
The geometry optimisations and frequency calculations of compounds 1–7 with general formula L-PGa-L′ [L,L′ = cAACMe (1); L = cAACMe, L′ = NHCMe (2); L = cAACMe, L′ = PMe3 (3); L = NHCMe, L′ = cAACMe (4); L = NHCMe, L′ = PMe3 (5); L,L′ = NHCMe (6); L,L′ = NHCDMP (DMP = 2,6-dimethylphenyl) (6′); L,L′ = PMe3 (7)] and 8–9 with general formula (cAAC)2GaP-MCOn [M = Fe; n = 4 (8), M = Ni; n = 3 (9)] were performed at BP86/def2-TZVPP,37 B3LYP/def2-TZVPP37a,38 (hybrid functional), and M06-2X/def2-TZVPP (meta-hybrid functional)39 levels using Gaussian 16.40 BP86 (ref. 37) is composed of generalized gradient approximation (GGA) functional with Becke 1988![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37a exchange functional, and Perdew 86
37a exchange functional, and Perdew 86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37b correlation functional. BP86, and B3LYP37a,38 consist of Becke function in common with P86 correlation functional and 3LYP (Lee–Yang–Parr) exchange-correlation function, respectively. B3LYP is a hybrid functional, which is typically faster than the majority of Post–Hartree–Fock approaches and produces comparable outcomes. It covers Hartree–Fock exchange, local exchange, gradient exchange correction, local correlation, and gradient correlation correction involving different mixing parameters:
37b correlation functional. BP86, and B3LYP37a,38 consist of Becke function in common with P86 correlation functional and 3LYP (Lee–Yang–Parr) exchange-correlation function, respectively. B3LYP is a hybrid functional, which is typically faster than the majority of Post–Hartree–Fock approaches and produces comparable outcomes. It covers Hartree–Fock exchange, local exchange, gradient exchange correction, local correlation, and gradient correlation correction involving different mixing parameters:| EXC = 0.2 × EX(HF) + 0.8 × EX(LSDA) + 0.72 × DEX(B88) + 0.81 × EC(LYP) + 0.19 × EC(VWN) | (1) |
HF = Hartree–Hock, LSDA = Local Spin Density Approximation, EX(B88) = Becke exchange functional, VWN = Vosko, Wilk, and Nusair 1980 correlation functional, EC(LYP) = Lee–Yang–Parr exchange-correlation function. M06-2X39 is a functional with double the amount of the nonlocal exchange 2×, parameterized exclusively for main group elements. It is a combination of four meta-GGA, and hybrid meta-GGA functionals with 54% HF exchange, which are constructed by empirically fitting their parameters and constrained to a uniform electron gas. It is highly parameterized with approximate exchange-correlation energy functionals. M06-2X functional is quite useful for the kinetics, thermochemistry, noncovalent interactions, electronic excitation energies to valence, and Rydberg states for main-group compounds.
All of our calculations were performed including dispersion corrections. The absence of imaginary frequency indicated that the optimised molecules are at the minima of the potential energy surfaces. The Wiberg bond indices (WBI),41 occupation numbers (ON), partial charges (q) on the atoms, and natural bond orbitals have all been evaluated using the NBO 6.0 programme on the above mentioned three levels.42 Wavefunction generation were performed using the BP86/def2-TZVPP and M06-2X/def2-TZVPP levels of theory and basis set. Laplacian of electron density were generated using AIMALL software package.43 Using the ADF 2020.102 software package, energy decomposition analysis (EDA)30b coupled with natural orbitals for the chemical valence (NOCV)30c,d computations were carried out on pre-optimised geometries at the BP86-D3(BJ)/def2-TZVPP level. EDA-NOCV were carried out for selected molecules in M06-2X/def2-TZV2P including Grimme dispersion. The EDA-NOCV approach entails the decomposition of the intrinsic interaction energy (ΔEint) between the two fragments into the following four energy components:
| ΔEint = ΔEelstat + ΔEPauli + ΔEorb + ΔEdisp | (2) |
The interaction energy, ΔEint, is the actual energy change that occurs when the geometrically deformed fragments unite to form the overall complex. The term ΔEelstat, usually attractive, refers to the classical electrostatic interaction between the unperturbed charge distributions of the fragments in the geometry. The Pauli-repulsion, ΔEPauli, between these fragments consists of destabilising interactions between occupied orbitals and is responsible for steric repulsion. The orbital interaction, ΔEorb, between these fragments account for bond pair formation, charge transfer (empty/occupied orbital mixing between different fragments), and polarisation (empty/occupied orbital mixing on one fragment due to the presence of another fragment). Finally, the ΔEdisp term considers the attractive dispersion interactions.
The NOCV approach identifies the orbitals of the components A and B that contribute the most to the formation of the bond A–B. Deformation density (Δρ(r)) can be defined as the between the densities of the fragments before and after bond formation which can be expressed as
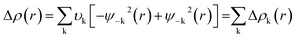 | (3) |
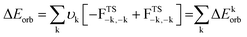 | (4) |
The terms FTS−k,−k and FTS−k,−k are diagonal transition-state (TS) Kohn–Sham matrix elements corresponding to NOCVs with the eigenvalues – υk and υk, respectively.
Method validation
We performed our studies in pure GGA (BP86),44 hybrid GGA (B3LYP), and meta-GGA (M06-2X) functionals. The structural parameters of equilibrium geometries for compounds 1–7 were found to be slightly different in three level of theories (see ESI†). The singlet-triplet energy gaps of 1–7 with M06-2X functional were found to be in between to those values calculated with B3LYP, and M06-2X functionals. The bond dissociation energies (BDE) of 1–6′ were found to be close to each other with M06-2X, and B3LYP functionals. However, the lowest BDE values were obtained with M06-2X functional.Results and discussion
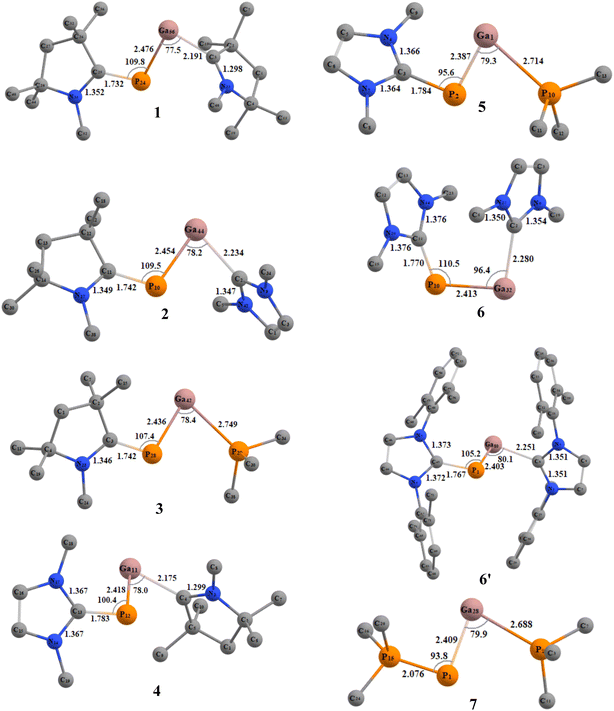
We initiated our studies with structural optimizations of all the proposed molecules, 1–7 at BP86/def2-TZVPP,37 B3LYP/def2-TZVPP,37a,38 and M06-2X/def2-TZV2P39 levels of theory in both singlet and triplet states. For all molecules (1–7), it was found that the singlet states are lower in energy compared to the triplet states by 12.09–35.33 kcal mol−1 (Table S1†), and thus the singlet states are considered to be the ground states for 1–7 (Fig. 2). The absence of imaginary frequencies promises the minima on the potential energy surface in each case.The PGa moiety in compounds 1, 6, and 7 is flanked by cAAC (cyclic alkyl(amino) carbene), NHC (N-heterocyclic carbene), and PMe3 ligands; whereas in the remaining compounds, the ligands at P atom are either cAAC (2, 3) or NHC (4, 5), and at Ga there are different types of donor ligands, such as, cAAC, NHC and PMe3. The extent of σ-donation and π-backdonation properties of the ligands employed in this study decide the final bonding of the compounds 1–7. The optimised geometries shown in Fig. 2 shows that in all the compound except 6, the ligands are arranged in trans fashion with respect to the PGa moiety, whereas in 6, the ligands are arranged in a cis manner. The unusual cis geometry of compound 6 insisted us to change the N-substitution of the NHC ligand to a bulkier group, viz., the 2,6-dimethyl phenyl (DMP) group (6′). The profound effect of the bulkier groups at N atoms of NHC was reflected in the changed orientation of the ligands from cis to a more favoured trans geometry. The energy difference between the singlet and triplet states of 6′ was found to be 26.07 kcal mol−1 (at BP86-D3(BJ)/def2-TZVPP), which is 1.31 kcal mol−1 higher than 6. For compounds 1–7, the calculated bond parameters at three different levels were found to be comparable (Tables S5 and S6†). The calculated CcAAC–P bond length (at BP86-D3(BJ)/def2-TZVPP) was found to be approximately the same as 1.75 Å, when the P bonded ligand was cAAC (1.732, 1.742, and 1.742 Å, respectively for the compounds 1, 2, and 3), which are in well agreement with the laboratory isolated chlorophosphinidene (cAAC)P–Cl (1.7513 (15) Å),45 and the related computationally studied molecules.30 The calculated CcAAC–P bond lengths were found to be similar when calculated at B3LYP/def2-TZVPP, and M06-2X/def2-TZVPP levels (Table S5†). When the P bonded ligand changes from cAAC to NHC (in 4–6), a significant elongation was observed in the CNHC–P bond lengths (1.783–1.784 Å in compounds 4–5, and 1.770 (1.767) Å in compound 6 (6′)) (Table S5†), which is longer than the CNHC–P bond found in the isolated NHC-stabilized diphosphorous (1.7504 (17), 1.754 (3) Å).47 However, the CNHC–P bond length falls in between a C–P single bond (1.839 (5) Å),46 and double bonds of non-conjugated phosphaalkenes (1.65–1.67 Å).47 The CNHC–P bond length in 6′ with bulkier NHCs remained almost unchanged, but slight shortening of the bond length of P–Ga (0.01 Å), and Ga–CNHC (0.029 Å) were observed when compared to the same in compound 6 with smaller substitutions at the N atoms. Similarly, there was also reduction of bond angles observed at P and Ga centres. The CNHC–P–Ga and P–Ga–CNHC bond angles were found to be 105.2° and 80.1°, respectively (at M06-2X/def2-TZVPP). The Ga–CcAAC bond lengths in compounds 1, and 4 were found to be 2.191, and 2.175 Å, respectively, which are considerably longer than the same observed in the isolated cAAC-stabilised Ga radicals based on amidinate scaffolds (1.9342 (17) Å).48 The EDA-NOCV studies conducted on CcAAC–Ga bond by the authors48 on the cAAC stabilised Ga radicals based on amidinate scaffolds suggests that the bond between Ga and the cAAC is covalent, and not a coordinate bond. From this, we may suggest that the CcAAC–Ga bond might not be a covalent bond, because it is slightly elongated than the experimentally observed CcAAC–Ga bond in the cAAC-stabilised Ga radicals.49 When the Ga-bonded ligand is NHC, the bond length is 2.234, and 2.280 Å for 2, and 6 admitting with NHC-stabilised Ga–P compounds, like the monomeric [(IMes)GaEt2P(H)SitBuPh2] (2.1254 (7) Å),49 but shorter than the NHC-stabilised silylphosphogallanes (2.059 (2), 2.077 (3)–2.087 (3) Å).50 The bond length of P–Ga in 6 is found to be approximately 2.40 Å (Fig. 2). The group of Ming-Der Su theoretically studied the stability of the GaP moiety using various ligands, such as, F, OH, H, CH3, SiH3, SiMe(SitBut3)2, SiiPrDis2, Tbt (C6H2-2,4,6-{CH(SiMe3)2}3), and Ar* (C6H3-2,6-(C6H2-2,4,6-iPr3)2).29 Their theoretical observations proved that the triply bonded Ga![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) P could be effectively stabilised by employing bulkier, and stronger donating ligands. The observed triple bond length was in the range of 2.146–2.183 Å,29 while the GaP bond distances for a single and triple bonds are 2.328 and 2.067 Å, respectively, at MP2/6-311++G(d,p) level of theory.28b However, in our studies, when we tried stabilising the GaP moiety using carbenes, we could see considerable elongation of the bond length, which is conceding in the range of Ga–P single bond. The GaP bond length observed in the NHC-stabilised silylphosphogallanes is slightly shorter than the theoretically observed bond lengths (2.365 (6)–2.366 (6) Å, and 2.372 (1)–2.373 (1) Å).50 When the Ga-bonded ligand is PMe3, the bond between is found to be significantly higher than the GaP moiety. In compounds 3/5 the Ga–PPMe3 bond lengths are 2.749/2.714 Å. These bond lengths typically fall in the range of GaP adducts (2.582 and 2.720 Å).51 We have calculated the bond dissociation energies (BDE) for the P–Ga bond at three different levels of theory (BP86/def2-TZVPP, B3LYP/def2-TZVPP, and M06-2X/def2-TZVPP). The highest BDE is overserved for compound 1 (125.38 kcal mol−1 (with M06-2X), 137.09 kcal mol−1 (with BP86), and 128.86 kcal mol−1 (with B3LPY). The least BDE is observed for the compound 7 (87.644 kcal mol−1 (with M06-2X), 93.96 kcal mol−1 (with BP86), 89.44 kcal mol−1 (with B3LPY). When P bonded ligand is cAAC (1–3), the BDE increases in the order 3 < 2 < 1. When P bonded ligand is NHC (4–6), the BDE increases in the order 5 < 6 < 4. Both the trends mentioned above concludes that when the ligand on Ga is cAAC, highest bonding energy is observed. The second highest BDE is observed when the ligand is NHC, and the least when the ligand is PMe3. When Ga is bonded to cAAC (1, 4) the highest BDE was observed for 1 (P bonded ligand is cAAC), and when Ga bonded ligand is NHC (2, 6) the highest BDE was observed for 2 (P bonded ligand is cAAC). In all the cases we observed the same trend. It follows the same trend as the electron donating and accepting nature of the ligands (cAAC > NHC > PMe3). The σ-donating
and π-accepting nature of cAAC ligands make the bond stronger, and thus the highest BDE is observed. The calculations performed at BP86 were highest compared to M06-2X, and B3LYP. The BDE computed at M06-2X, and B3LYP were found to be comparable for all the proposed molecules (Table S2†).
P could be effectively stabilised by employing bulkier, and stronger donating ligands. The observed triple bond length was in the range of 2.146–2.183 Å,29 while the GaP bond distances for a single and triple bonds are 2.328 and 2.067 Å, respectively, at MP2/6-311++G(d,p) level of theory.28b However, in our studies, when we tried stabilising the GaP moiety using carbenes, we could see considerable elongation of the bond length, which is conceding in the range of Ga–P single bond. The GaP bond length observed in the NHC-stabilised silylphosphogallanes is slightly shorter than the theoretically observed bond lengths (2.365 (6)–2.366 (6) Å, and 2.372 (1)–2.373 (1) Å).50 When the Ga-bonded ligand is PMe3, the bond between is found to be significantly higher than the GaP moiety. In compounds 3/5 the Ga–PPMe3 bond lengths are 2.749/2.714 Å. These bond lengths typically fall in the range of GaP adducts (2.582 and 2.720 Å).51 We have calculated the bond dissociation energies (BDE) for the P–Ga bond at three different levels of theory (BP86/def2-TZVPP, B3LYP/def2-TZVPP, and M06-2X/def2-TZVPP). The highest BDE is overserved for compound 1 (125.38 kcal mol−1 (with M06-2X), 137.09 kcal mol−1 (with BP86), and 128.86 kcal mol−1 (with B3LPY). The least BDE is observed for the compound 7 (87.644 kcal mol−1 (with M06-2X), 93.96 kcal mol−1 (with BP86), 89.44 kcal mol−1 (with B3LPY). When P bonded ligand is cAAC (1–3), the BDE increases in the order 3 < 2 < 1. When P bonded ligand is NHC (4–6), the BDE increases in the order 5 < 6 < 4. Both the trends mentioned above concludes that when the ligand on Ga is cAAC, highest bonding energy is observed. The second highest BDE is observed when the ligand is NHC, and the least when the ligand is PMe3. When Ga is bonded to cAAC (1, 4) the highest BDE was observed for 1 (P bonded ligand is cAAC), and when Ga bonded ligand is NHC (2, 6) the highest BDE was observed for 2 (P bonded ligand is cAAC). In all the cases we observed the same trend. It follows the same trend as the electron donating and accepting nature of the ligands (cAAC > NHC > PMe3). The σ-donating
and π-accepting nature of cAAC ligands make the bond stronger, and thus the highest BDE is observed. The calculations performed at BP86 were highest compared to M06-2X, and B3LYP. The BDE computed at M06-2X, and B3LYP were found to be comparable for all the proposed molecules (Table S2†).
To understand the electronic structures of compounds 1–7, we performed natural bond orbital (NBO) analyses42 on the optimised coordinates at BP86-D3(BJ)/def2-TZVPP, B3LYP/def2-TZVPP, and M06-2X/def2-TZVPP levels of theory (Fig. 3 and S2†). The comparative results are included in the Fig. S2, and Tables 1, S23, S24.† When the P-bonded ligand is cAAC, the CcAAC–P bond is having two occupancies, the first one polarized towards CcAAC (∼66%), and the other is polarized towards P (∼60%). We could observe only one occupancy on the Ga side, which is polarized towards ligand (86–87%). This could be due to the larger size and more diffused orbitals, and internal nodes of Ga. The Wiberg bond index (WBI) of compounds 1–3 clearly indicates the bond between CcAAC–P is double bond (1.47). WBI observed for the bond between Ga–P of GaP moiety (0.81–0.93), and the values predict a single bond between Ga and P (Table 1). The WBI decreases for the bond between Ga–L, when the ligand changes from cAAC, NHC, and PMe3 irrespective of the ligands bonded to P. The same trend is followed by the ligand's π-accepting property. The HOMOs of compounds 1–7 are the lone pairs of electrons on P, and Ga, mixing with the σ-electron pair of Ga–P bond. The HOMO−1 is essentially the cAAC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P π bond, which is in conjugation with the lone pair of the electron of Ga-atom. The HOMO−2 contains the lone pair on P atom, and the overlap of orbitals with the adjacent Ga atom having some interaction with σ-orbital of Ga–L′ (Fig. 3). The P-atom possesses a negative charge, while the Ga-atom of compounds 1–7 are positively charged as expected from their electronegativity values (see Table 1).
P π bond, which is in conjugation with the lone pair of the electron of Ga-atom. The HOMO−2 contains the lone pair on P atom, and the overlap of orbitals with the adjacent Ga atom having some interaction with σ-orbital of Ga–L′ (Fig. 3). The P-atom possesses a negative charge, while the Ga-atom of compounds 1–7 are positively charged as expected from their electronegativity values (see Table 1).
| Compound | Bond | ON | Polarization and hybridization (%) | WBI | q | ||
|---|---|---|---|---|---|---|---|
| P | Ga | ||||||
| 1 | C25–P24 | 1.97 | P: 34.0 s(19.0), p(80.2) | C: 66.0 s(39.7), p(60.0) | 1.47 | −0.27 | 0.34 |
| 1.87 | P: 60.4 s(0.1), p(99.5) | C: 39.6 s(0.0), p(99.8) | |||||
| P24–Ga56 | 1.80 | P: 76.1 s(15.4), p(84.0) | Ga: 23.9 s(10.6), p(89.1) | 0.81 | |||
| Ga56–C3 | 1.91 | C: 86.1 s(39.6), p(60.3) | Ga: 13.9 s(8.3), p(91.3) | 0.69 | |||
| 2 | P10–C11 | 1.86 | P: 60.3 s(0.1), p(99.5) | C: 39.7 s(0.0), p(99.8) | 1.47 | −0.33 | 0.22 |
| 1.97 | P: 34.0 s(19.7), p(79.6) | C: 66.0 s(39.9), p(59.7) | |||||
| P10–Ga44 | 1.86 | P: 77.1% s(15.7), p(83.7) | Ga: 22.9% s(8.5), p(91.1) | 0.83 | |||
| Ga44–C2 | 1.92 | C: 86.4% s(41.8), p(58.2) | Ga: 13.6% s(5.33), p(94.1) | 0.52 | |||
| 3 | P28–C3 | 1.97 | P: 34.5 s(20.5), p(78.8) | C:65.5 s(39.8), p(59.9) | 1.47 | −0.40 | 0.21 |
| 1.86 | P: 60.8 s(0.0), p(99.5) | C: 39.2 s(0.0), p(99.8) | |||||
| P28–Ga42 | 1.89 | P: 78.6 s(14.8), p(84.7) | Ga: 21.4 S(7.2), p(92.6) | 0.84 | |||
| Ga42–P29 | 1.90 | P: 87.8 s(30.0), p(69.9) | Ga: 12.2 S(2.6), p(96.9) | 0.41 | |||
| 4 | P12–C13 | 1.97 | P: 32.4 s(14.8), p(84.3) | C: 67.6 s(43.6), p(56.1) | 1.22 | −0.44 | 0.28 |
| P12–Ga11 | 1.80 | P: 82.7 s(10.8), p(88.7) | Ga: 17.3 s(5.1), p(94.4) | 0.89 | |||
| Ga11–C4 | 1.90 | C: 86.0 s(39.4), p(60.5) | Ga: 14.0 s(8.0), p(91.4) | 0.66 | |||
| 5 | P2–C3 | 1.97 | P: 32.9 s(15.5), p(83.6) | C: 67.1 s(43.6), p(56.1) | 1.23 | −0.54 | 0.17 |
| P2–Ga1 | 1.85 | P: 84.8 s(3.6), p(69.6) | Ga: 15.2 s(2.0), p(97.6) | 0.94 | |||
| Ga1–P10 | 1.90 | P: 87.9 s(30.4), p(69.6) | Ga: 12.1 s(2.8), p(96.7) | 0.42 | |||
| 6 | C11–P10 | 1.97 | P: 32.5 s(15.9), p(83.3) | C: 67.5 s(44.5), p(55.2) | 1.28 | −0.41 | 0.23 |
| P10–Ga32 | 1.81 | P: 85.2 s(3.2), p(96.3) | Ga: 14.8 s(2.0), p(97.5) | 0.93 | |||
| Ga32–C2 | 1.93 | C: 87.2 s(41.6), p(58.4) | Ga: 12.8 s(5.2), p(94.4) | 0.48 | |||
| 7 | P15–P1 | 1.97 | P15: 59.1 s(32.2), p(67.23) | P1: 40.9 s(13.4), p(85.4) | 1.26 | −0.82 | 0.16 |
| P1–Ga28 | 1.85 | P: 79.2 s(13.1), p(85.9) | Ga: 20.8 s(7.5), p(92.4) | 0.92 | |||
| Ga28–P2 | 1.91 | Ga: 13.1 s(3.4), p(96.2) | P: 86.9 s(30.5), p(69.5) | 0.45 | |||
R. F. W. Bader and his team created the quantum theory of atoms in molecules (QTAIM), which is based on quantum observables like the electron density ρ(r), and second derivative of energy densities ∇2ρ(r).52 The optimised geometries of compounds 1–7 were used to compute the wavefunctions for the QTAIM analyses at the BP86/def2-TZVPP level of theory. It is observed that the bonds between L–P (0.161–0.129 a.u.), and Ga–L′ (0.201–0.138 a.u.) is having greater ∇2ρ(r), when the L and L′ are cAAC and NHC. But when L′ is PMe3, it is observed that the Laplacian of electron density decreases, and it is very close to zero (0.032–0.040 a.u.). This reveals the better closed shell interaction when the ligands are carbenes. In the similar way, the values are close to zero (0.033–0.043 a.u.) for bonds between P and Ga of PGa moiety, implying a weaker closed shell interation. The ρ(r) is observed for L–P is significantly higher compared to P–Ga and Ga–L′ bond. The bond's nature is measured by its ellipticity, ε. In the situation of single and triple bonds, where the bond is cylindrically symmetrical, ε is near to zero. Due to the asymmetrical distribution of electron density, perpendicular to the bond path, for a double bond, it is greater than zero. Ellipticity is observed the highest when the P bonded ligand is cAAC. The ligand cAAC being a good σ-donor and π-acceptor, this bond may have a partial double bond character.
We conducted energy decomposition analysis coupled with natural orbital for chemical valence (EDA-NOCV) at BP86-D3(BJ)/TZ2P and M06-2X/TZ2P level of theories to arrive at the best bonding description. EDA part was developed independently by Morokuma30a and by Ziegler and Rauk30b. Several decades later, NOCV analyses was introduced by M. Mitoraj, A. Michalak. The bonding scenarios have remained the same although the numerical values with BP86 and M06-2X functionals have varied slightly by 2–3% (Tables 2, 3 and Scheme 2) except compound 7. The ΔEint of the species shown Tables 2 and 3 with two different functionals differ nearly by 20 kcal mol−1. The values are smaller in M06-2X functionals. Frenking et al. have faced a similar problem with GGA functionals (BP86) with L2E systems [E = BH, C, N+; L = donor base ligands]. The authors have finally have shown that meta-GGA [M05-2X] are suitable for calculations of bond dissociation energies of those species.46 The differences between these functionals have been discussed in the computational method.
| Energy | Interaction | [(cAAC)2] (S) + [P–Ga] (S) | [(cAAC) (NHC)] (S) + [P–Ga] (S) | [(NHC) (cAAC)] (S) + [P–Ga] (S) | [(NHC) (PMe3)] (S) + [P–Ga] (S) | [(NHC)2] (S) + [P–Ga] (S) |
|---|---|---|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction ΔEdisp + ΔEelstat + ΔEorb.b The values in parentheses show the contribution to the total orbital interaction ΔEorb. | ||||||
| Compound | 1 | 2 | 4 | 5 | 6 | |
| ΔEint | −161.1 | −163.2 | −141.4 | −125.5 | −130.6 | |
| ΔEPauli | 528.0 | 545.7 | 413.0 | 368.5 | 448.1 | |
| ΔEdispa | −19.3 (2.8%) | −17.5 (2.5%) | −18.4 (3.3%) | −16.1 (3.3%) | −14.1 (2.4%) | |
| ΔEelstata | −345.1 (50.1%) | −344.2 (48.6%) | −283.6 (51.2%) | −248.5 (50.3) | −285.2 (49.3%) | |
| ΔEorba | −324.7 (47.1%) | −347.2 (48.9%) | −252.5 (45.5%) | −229.5 (46.4%) | −279.3 (48.3%) | |
| ΔEorb(1)b | L → P–Ga ← L′ σ donation | −174.5 (53.7%) | −214.1 (61.7%) | −139.3 (55.2%) | −139.2 (60.6%) | −158.7 (56.8%) |
| ΔEorb(2)b | L → P–Ga ← L′ σ donation | −24.4 (7.5) | −69.4 (20.0%) | −33.7 (13.4%) | 23.9 (10.4%) | −31.8 (11.4%) |
| ΔEorb(3)b | L ← P–Ga → L′ π backdonation | −58.8 (18.1) | −27.4 (7.9%) | −44.3 (17.5%) | 33.5 (14.6%) | −50.5 (18.1%) |
| ΔEorb(4)b | L ← P–Ga → L′ π backdonation | −43.4 (13.4) | −15.2 (4.4%) | 13.3 (5.8%) | −21.2 (7.6%) | |
| ΔEorb(rest) | −36.3 (10.4%) | −35.2 (13.9%) | 19.6 (8.6%) | −17.1 (6.1%) | ||
 | ||
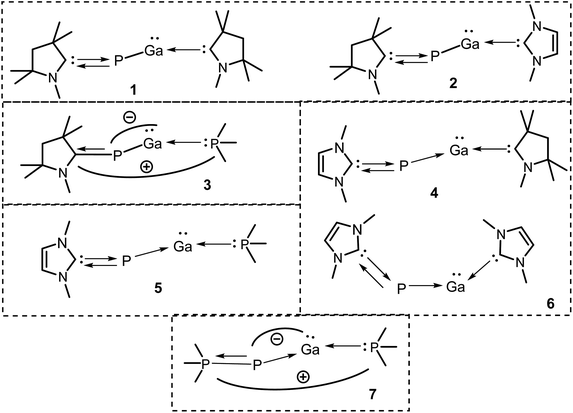
| Scheme 2 Possible bonding scenarios of compounds 1–7 (also see Table S12†). (a) [L,L′] and [PGa] in neutral electronic singlet states forming a dative bond; (b) [L,L′] and [PGa] in neutral electronic quintet states forming four electron sharing/covalent bonds; (c) doubly charged [L,L′]2+ and [PGa]2− fragments in triplet states forming σ electron sharing and π dative bonds; (d) singly charged [L,L′]+ and [PAl]− fragments in doublet states forming both electron sharing and dative bonds. | ||
| Energy | Interaction | [(cAAC)2] (S) + [P–Ga] (S) | [(cAAC) (NHC)] (S) + [P–Ga] (S) | [(NHC) (cAAC)] (S) + [P–Ga] (S) | [(PMe3)2] (S) + [P–Ga] (S) |
|---|---|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction ΔEdisp + ΔEelstat + ΔEorb.b The values in parentheses show the contribution to the total orbital interaction ΔEorb. | |||||
| Species | 1 | 2 | 4 | 7 | |
| ΔEint | −140.1 | −136.3 | −125.3 | −96.9 | |
| ΔEPauli | 553.9 | 508.3 | 401.1 | 291.3 | |
| ΔEdispa | −0.38 (0.1%) | −0.27 (0.04%) | −0.3 (0.05%) | −0.14 (0.03%) | |
| ΔEelstata | −360.5 (52%) | −331.3 (51.4%) | −292.1 (55.5%) | −195.7 (50.4%) | |
| ΔEorba | −333.1 (48%) | −312.9 (48.5%) | −234.0 (44.45%) | −192.4 (49.6%) | |
| ΔEorb(1)b | L → P–Ga ← L′ σ donation | −215.5 (64.7%) | −203.6 (65.1%) | −134.1 (57.3%) | −126.8 (65.9%) |
| ΔEorb(2)b | L → P–Ga ← L′ σ donation | −37.6 (11.3%) | −28.5 (9.1%) | −44.0 (18.8%) | 29.3 (15.3%) |
| ΔEorb(3)b | L ← P–Ga → L′ π backdonation | −49.6 (14.9%) | −53.4 (17.1%) | −27.7 (11.8%) | 18.8 (9.8%) |
| ΔEorb(4)b | L ← P–Ga → L′ π backdonation | −16.3 (4.9%) | −14.1 (6.0%) | 13.1 (6.8%) | |
| ΔEorb(rest) | −14.1 (4.2%) | −27.4 (8.7%) | −14.1 (6.0%) | 4.4 (2.2%) | |
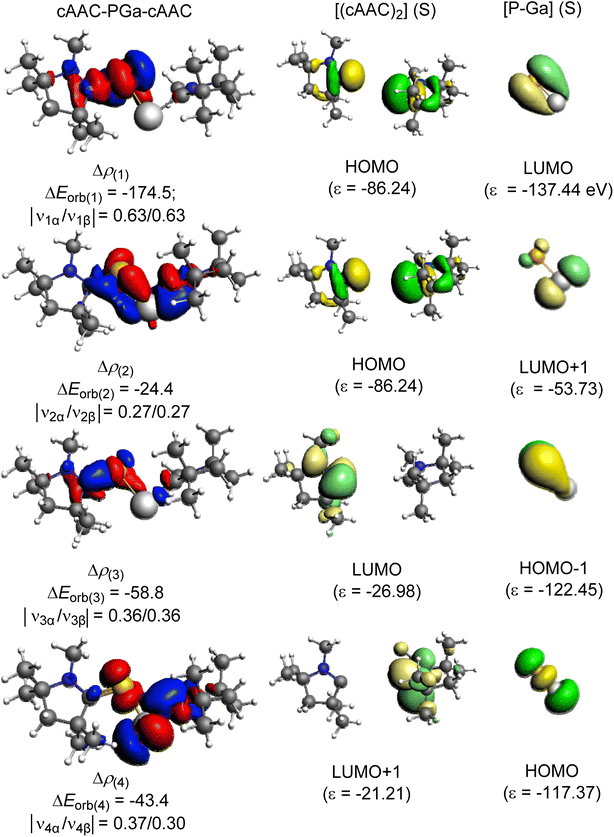
Each species was split into two fragments containing ligands [(L)(L′)] and the central PGa diatom in different spin and charged states. We have considered four different types of bonding interactions between the ligand pairs and PGa for the present studies. The first bonding possibility (Scheme 2a) is the interaction of neutral [(L)(L′)] and PGa fragments forming covalent dative bonds (single headed arrows) in their excited singlet states. The second bonding scenario (Scheme 2b) is the interaction of neutral [(L)(L′)] and PGa fragments forming four covalent electron sharing σ-bonds (double headed arrows) in their quintet states. The third bonding possibility (Scheme 2c) is the interaction of these fragments between doubly positive charged ligand and doubly negative charged PGa in their triplet electronic states (T), forming two electron sharing σ-bonds and two covalent π-dative bonds. The forth one (Scheme 2d) is the interaction of these fragments between singly positive charged ligand and singly negative charged PGa in their doublet electronic states (D), forming one electron sharing σ-bonds and three covalent dative π-bonds. The summary of the bonding scenarios of 1–7 is shown in Scheme 2. Species 1, 2, 4–6 possess all four dative bonds (bonding scenario (a), Scheme 2) while 3 and 7 prefer bonding scenario (d) of Scheme 2 ([L,L′]+ [PGa]−).
EDA-NOCV results predicted the formation of dative bonds between ligands and the central PGa fragment. Out of the attractive energies, the electrostatic contribution (ΔEelstat = 48.6–51.2%) is slightly more significant than the orbital contribution (ΔEorb = 45.5–48.9%) (Table 2). The remaining contribution to the attractive force is contributed by dispersion energy which is small (ΔEdisp = 2.4–3.3%).
The pairwise breakdown of total orbital interactions (ΔEorb) sheds more light on the nature of the bond. For compounds 1, 2, 5, and 6, the calculations show four relevant orbital contributions (ΔEorb(1–4)), whereas, for compounds 3, 4, and 7 the calculation predicted three significant orbital contributions (ΔEorb(1–3)). The first and the major orbital (ΔEorb(1)) contribution (53.7–61.7%) of the compounds 1, 2, 4, 5, and 6 involve the σ-donation from the filled orbital of [L,L′] to the vacant orbital of [PGa] fragment. The σ-donation happens from HOMO of [L,L′] fragment to LUMO of [PGa] in compounds 1, 2, and 5 and HOMO−1 of [L,L′] fragment to LUMO of [PGa] fragment in compounds 4, and 6. The second orbital contribution (ΔEorb(2)) describes another σ-donation, which is relatively weaker (7.5–20.0%) than the latter one. The third and fourth orbital contribution occurs due to the backdonation from [PGa] fragment to the [L,L′] fragment. In compound 1, ΔEorb(3) (18.1%) is due to the backdonation from LUMO of [PGa] to the HOMO−1 of [(cAAC)2] and ΔEorb(4) (13.4%) is due to the backdonation from LUMO+1 of [PGa] to the HOMO of [(cAAC)2]. The contribution due to π-backdonation decreases considerably when the Ga-bonded ligand is NHC (2). ΔEorb(3) and ΔEorb(4) contributes 7.9 and 4.4%, and is due to the π-backdonation from HOMO of [PGa] to LUMO+3 of [(cAAC) (NHC)]. Only one orbital contribution, ΔEorb(3), corresponding to π-backdonation is observed in 4, which is due to the π-backdonation from HOMO−1 of [PGa] to LUMO+1 of [(cAAC) (NHC)]. In compound 5 and 6, ΔEorb(3) contributes 14.6% and 18.1% to the total orbital contribution. π-backdonation happens from HOMO of [PGa] to LUMO of [(NHC) (PMe3)] in 5, and from HOMO of [PGa] to LUMO+2 of [(NHC)2] in 6. ΔEorb(4) corresponds to a minor π backdonation (5.8% (5) and 7.6% (6)) from [PGa] to the ligand fragments. From the deformation plots (Fig. 4, 5, S12 and S19 in the ESI†), it is evident that the π-backdonation is more prominent from P to L (7.9–18.1%) rather than from Ga to L′ in 6.
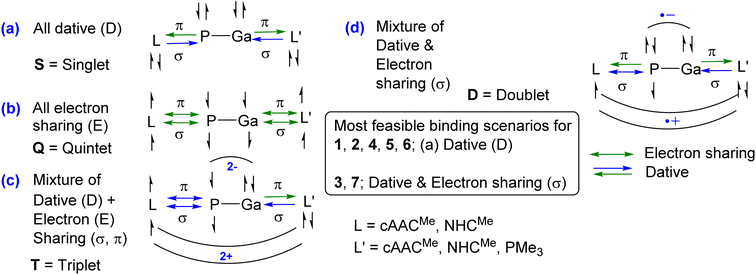
The unusual cis-geometry of compound 6 led to the N substitution being changed trans due to the bulkier groups on the N-atoms of NHC ligands of 6′. One NHC ligand in 6, which is formatting a dative bond with the Ga-atom, is expected to be electron deficient (δ+), while in comparison, the other NHC ligand slightly electron rich (δ−) (due to π-backdonation from P-atom to CNHC atom) leading to a dipolar π-stacking interaction between two five membered imidazole rings with a short CNHC–CNHC bond distance of 3.097 Å (Fig. 5, right). The same is visible deformation densities (red and blue regions of two NHC C-atoms) of 6 (Fig. 5, left). This weak stabilisation interaction is overcome by the steric hindrance posed by the bulky groups on the N-atoms of the two NHC ligands leading to a trans geometry of 6′ (Fig. 2). For the compounds 3, and 7 the best bonding possibility predicted by EDA-NOCV is the formation of both σ-electron sharing and dative bonds from the interaction of the singly charged doublet species of [L,L′]+ and [PGa]−. The contribution of electrostatic interaction energy (50.0%) between [L,L′] and [PGa]+ is slightly higher than the orbital contribution (47.8%) towards the total attractive forces in compound 3, whereas, these energies contribute equally in compound 7 (ΔEelstat = 48.6%; ΔEorb = 48.9%). The stabilisation due to dispersion energy (2.1% (3); 2.5% (7)) is small compared to the later energies discussed above. ΔEorb can be further divided into three different pairwise interaction. The electron sharing bond formation between the ligand fragment and PGa is well described in (ΔEorb(1)) and this is the major contribution (67.3% (3); 66.0% (7) Table S13†) to the total orbital interaction.
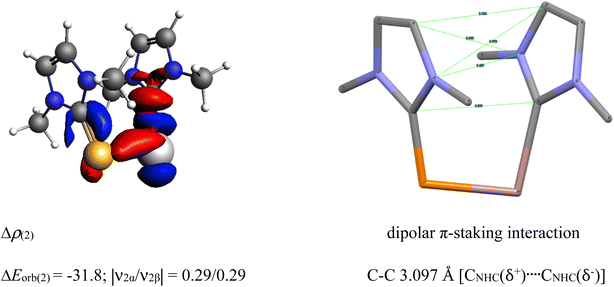 | ||
| Fig. 5 Selected deformation densities (left) and corresponding dipolar π-stacking interaction (right) of 6 with a short C–C bond distance of 3.097 Å [CNHC(δ+)…CNHC(δ−)]. | ||
Δρ(2) dipolar π-stacking interaction
| ΔEorb(2) = −31.8; |ν2α/ν2β| = 0.29/0.29 C–C 3.097 Å [CNHC(δ+)…CNHC(δ−)] |
The dative out-of-phase σ-donation from HOMO of [L,L′]+ to [PGa]− in compound 3 and HOMO of [L,L′]+ to LUMO of [PGa]− in compound 7 is the second orbital term, ΔEorb(2) (Fig. S10 and S13†). The most minuscule contribution (10.3% (3); 6.7% (7)) to the ΔEorb is the π-backdonation from [PGa]− to [L,L′]+, which is depicted in ΔEorb(3). π-backdonation is observed from HOMO−1 of [PGa]− to LUMO+20 of [L,L′]+ and HOMO−1 of [PGa]− to LUMO+4 of [L,L′]+ in 3 and 7, respectively.
Next, we tried to explore whether (cAAC)2PGa (1) can act as a ligand for the stabilisation of unsaturated metal-carbonyls having the general formulae (cAAC)2PGa-M(CO)n [M = Fe (8), n = 4; Ni (9), n = 3] (Fig. 6, see ESI†). The optimized geometries of 8–9 have been displayed in Fig. 7.
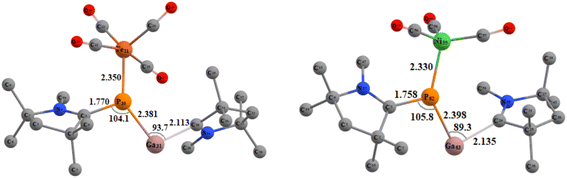 | ||
| Fig. 7 Optimized geometries of compound 8 (left) and 9 (right) in singlet ground state at BP86-D3(BJ)/def2-TZVPP level of theory. | ||
The further theoretical analyses revealed that (cAAC)2PGa-Fe(CO)4 (8) may be stable and hence it may be isolated in the laboratory (see ESI†). The P–Fe bond of 8 is mostly stabilised by strong σ-donation from 8 having six times weaker π-backdonation from Fe(CO)4 to backbone of 1 (see Table 4). The corresponding dissociation energy is 35.69 kcal mol−1 1 likely to form a week bond with the nickel–carbonyl.
| Energy | Interaction | (cAAC)2PGa (S) + Fe(CO)4 (S) | (cAAC)2PGa (S) + Ni(CO)3 (S) |
|---|---|---|---|
| a The values in the parentheses show the contribution to the total attractive interaction ΔEdisp + ΔEelstat + ΔEorb.b The values in parentheses show the contribution to the total orbital interaction ΔEorb. | |||
| Complex | 8 | 9 | |
| ΔEint | −43.9 | −30.0 | |
| ΔEPauli | 88.2 | 64.6 | |
| ΔEdispa | −1.7 (1.1%) | −1.5 (1.4%) | |
| ΔEelstata | −84.3 (56.7%) | −64.6 (59.6%) | |
| ΔEorba | −62.6 (42.1%) | −42.3 (39.0%) | |
| ΔEorb(1)b | (cAAC)2GaP → M(CO)n σ-donation | −42.3 (66.6%) | −29.4 (69.5%) |
| ΔEorb(2)b | (cAAC)2GaP ← M(CO)n π-backdonation | −5.8 (9.3%) | −3.5 (8.3%) |
| ΔEorb(rest) | −14.5 (23.1%) | −9.4 (22.2%) | |
Conclusion
In conclusion, the stability and bonding of monomeric GaP with donor base ligands have been studied with three different functionals [GGA, BP86; hybrid, B3LYP; GGA and meta-GGA, M06-2X]. We will prefer M06-2X functional over other two functionals. A similar problem previously faced by Frenking et al. They have shown that M06 functional is more suitable providing support with additional calculations with CCSD(T)/MP2 level of theory which are believed to be the gold standard. Using various donor-base ligands, including cAAC, NHC, and PMe3, we have examined the structure and bonding of gallium phosphide. Due to the better σ-donation and π-acceptance properties of cAAC, it is observed that the bond between cAAC and P (1–3) has a partial double bond character. The larger and diffused orbitals of Ga and the poor π-acceptance of the donor-base ligands, NHC and PMe3 made the Ga–L′ bond weaker. EDA-NOCV studies predicted the best bonding between ligand fragments and PGa moiety is dative due to the interaction of neutral singlet fragments. For the compounds 1–2, and 4–6. Whereas, for 3, and 7 the best bonding scenario was when the singly charged doublet [L,L′]+ and [PGa]− fragments interacted to form electron sharing and dative bonds (Scheme 3). EDA-NOCV studies conducted on P–Ga bond suggested that 1 and 2 will be electron sharing between the interaction of neutral doublet fragments of [LP] and [GaL']. The bond between P–Ga is dative for 3–7 happening due to the interaction of singly charged singlet fragments of [LP]− and [GaL']−. The bond dissociation energies (−120 to −125 kcal mol−1 with M06-2X functional) of [L,L′] and GaP pair are significantly high for 1 [L = cAAC, L′ = cAAC] and 2 [L = cAAC, L′ = NHC] suggesting that they may be possible to experimentally isolate in the laboratory. Further calculations have showed that cAAC stabilised PGa compound can form stable complex with iron-carbonyl.Conflicts of interest
The authors do not have any conflict of interest.Acknowledgements
SR gratefully acknowledges SERB, New Delhi for the Power grant (SPG/2021/003237). MF thanks CSIR for the SRF.References
- Z.-C. Zhang and D.-L. Cui, Chin. J. Chem., 2005, 23, 1213–1217 CrossRef CAS.
- A. Höglund, C. W. M. Castleton and S. Mirbt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195213–195216 CrossRef.
- J. Mašek, J. Kudrnovský, F. Máca, J. Sinova, A. H. MacDonald, R. P. Campion, B. L. Gallagher and T. Jungwirth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 045202–045207 CrossRef.
- C. Çelebi, P. M. Koenraad, A. Yu. Silov, W. Van Roy, A. M. Monakhov, J.-M. Tang and M. E. Flatté, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075328–075335 CrossRef.
- P. Karamanis, C. Pouchan and J. Leszczynski, J. Phys. Chem. A, 2008, 112, 13662–13671 CrossRef CAS PubMed.
- Z.-C. Zhang and B.-P. Wang, Part. Part. Syst. Charact., 2009, 26, 53–57 CrossRef CAS.
- A. Y. Timoshkin and H. F. Schaefer, J. Phys. Chem. A, 2010, 114, 516–525 CrossRef CAS PubMed.
- F. Cheng, K. George, A. L. Hector, M. Jura, A. Kroner, W. Levason, J. Nesbitt, G. Reid, D. C. Smith and J. W. Wilson, Chem. Mater., 2011, 23, 5217–5222 CrossRef CAS.
- O. Romanyuk, T. Hannappel and F. Grosse, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115312–115320 CrossRef.
- C. Lacroix, S. Lambert-Milot, R. A. Masut, P. Desjardins and D. Ménard, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024412–024422 CrossRef.
- J. R. Chelikowsky and M. L. Cohen, Phys. Rev. B: Solid State, 1973, 14, 556–582 CrossRef.
- R. L. Wells and W. L. Gladfelter, J. Cluster Sci., 1997, 8, 217–238 CrossRef CAS.
- S. Schulz, Adv. Organomet. Chem., 2003, 49, 225–317 CrossRef CAS.
- M. A. Malik, M. Afzaal and P. O′Brien, Chem. Rev., 2010, 110, 4417–4446 CrossRef CAS PubMed.
- (a) F. P. Miller, A. F. Vandome and J. McBrewster, Gallium Arsenide Phosphide, Alphascript, Publishing, India, 2010 Search PubMed; (b) P. B. Hart, Gallium Phosphide, in Electronics Design Materials, ed. W. F. Waller, Macmillan Engineering Evaluations, Palgrave Macmillan, London, 1971 Search PubMed; (c) F. P. Miller, A. F. Vandome and J. McBrewster, Aluminium Gallium Phosphide, Alphascript Publishing, India, 2010 Search PubMed; (d) S. Singh and P. Srivastava, Appl. Nanosci., 2012, 3, 89–94 CrossRef; (e) T. Zhang, Y. Qian, H. Gao, Z.-C. Huang-Fu, J. B. Brown and Y. Rao, J. Phys. Chem. C, 2022, 126, 6761–6772 CrossRef CAS.
- E. D. Palik, Handbook of Optical Constants of Solids, Elsevier, Burlington, 1985 Search PubMed.
- E. D. Palik, Handbook of Optical Constants of Solids, Burlington Elsevier Science & Technology Ann Arbor, Michigan Proquest, 1991, vol. 2 Search PubMed.
- M. J. Weber, Handbook of Optical Materials, Crc Press, Boca Raton, 2003 Search PubMed.
- J. Václavík and D. Vápenka, in EPJ Web of Conferences, 2013, 48, p. 0028 Search PubMed.
- W. E. Dasent, Nonexistent Compounds: Compounds of Low Stability, Dekker, New York, 1966 Search PubMed.
- D. W. N. Wilson, J. Feld and J. M. Goicoechea, Angew. Chem., Int. Ed., 2020, 59, 20914–20918 CrossRef CAS PubMed.
- M. K. Sharma, C. Wölper, G. Haberhauer and S. Schulz, Angew. Chem., Int. Ed., 2021, 60, 6784–6790 CrossRef CAS.
- D. W. N. Wilson, W. K. Myers and J. M. Goicoechea, Dalton Trans., 2020, 49, 15249–15255 RSC.
- J. Feld, D. W. N. Wilson and J. M. Goicoechea, Angew. Chem., Int. Ed., 2021, 60, 22057–22061 CrossRef CAS PubMed.
- M. K. Sharma, C. Wölper, G. Haberhauer and S. Schulz, Angew. Chem., Int. Ed., 2021, 60, 21784–21788 CrossRef CAS.
- J. Krüger, C. Wölper and S. Schulz, Angew. Chem., Int. Ed., 2020, 60, 3572–3575 CrossRef.
- B. Li, C. Wölper, G. Haberhauer and S. Schulz, Angew. Chem., Int. Ed., 2020, 60, 1986–1991 CrossRef PubMed.
- (a) T. I. Demirer, B. Morgenstern and D. M. Andrada, Eur. J. Inorg. Chem., 2022 DOI:10.1002/ejic.202200477; (b) T. J. Dudley, W. W. Brown and M. R. Hoffmann, J. Phys. Chem. A, 1999, 103, 5152–5160 CrossRef CAS.
- J.-S. Lu, M.-C. Yang and M.-D. Su, J. Phys. Chem. A, 2017, 121, 6630–6637 CrossRef CAS.
- (a) K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS; (b) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS; (c) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580 CrossRef CAS; (d) M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681–687 CrossRef CAS PubMed; (e) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- (a) G. Deng, S. Pan, G. Wang, L. Zhao, M. Zhou and G. Frenking, Angew. Chem., 2020, 132, 10690–10696 CrossRef; (b) D. M. Andrada and G. Frenking, Angew. Chem., Int. Ed., 2015, 54, 12319–12324 CrossRef CAS PubMed; (c) S. K. Kushvaha, S. M. N. V. T. Gorantla and K. C. Mondal, J. Phys. Chem. A, 2022, 126, 845–858 CrossRef CAS; (d) M. Hermann, C. Goedecke, C. Jones and G. Frenking, Organometallics, 2013, 32, 6666–6673 CrossRef CAS; (e) S. M. N. V. T. Gorantla, S. Pan, K. C. Mondal and G. Frenking, Chem. – Eur. J., 2020, 26, 14211–14220 CrossRef CAS PubMed; (f) L.-H. Mou, Y. Li, Z.-Y. Li, Q.-Y. Liu, H. Chen and S.-G. He, J. Am. Chem. Soc., 2021, 143, 19224–19231 CrossRef CAS PubMed; (g) L. Bondì, A. L. Garden, P. Jerabek, F. Totti and S. Brooker, Chem. – Eur. J., 2020, 26, 13677–13685 CrossRef PubMed; (h) S. M. N. V. T. Gorantla and K. C. Mondal, Eur. J. Inorg. Chem., 2021, 2021, 960–968 CrossRef CAS; (i) F. S. S. Schneider, G. F. Caramori, R. L. T. Parreira, V. Lippolis, M. Arca and G. Ciancaleoni, Eur. J. Inorg. Chem., 2018, 2018, 1007–1015 CrossRef CAS; (j) I. Rodstein, L. Kelling, J. Löffler, T. Scherpf, A. Sarbajna, D. M. Andrada and V. H. Gessner, Chem. Sci., 2022, 13, 13552–13562 RSC; (k) S. M. N. V. T. Gorantla, M. Francis, S. Roy and K. C. Mondal, RSC Adv., 2021, 11, 6586–6603 RSC.
- E. Nag, M. Francis, S. Battuluri, B. B. Sinu and S. Roy, Chem. – Eur. J., 2022, e202201242 CAS.
- (a) S. Roy, K. C. Mondal and H. W. Roesky, Acc. Chem. Res., 2016, 49, 357–369 CrossRef CAS PubMed; (b) K. C. Mondal, S. Roy and H. W. Roesky, Chem. Soc. Rev., 2016, 45, 1080–1111 RSC; (c) H. Braunschweig, R. D. Dewhurst and V. H. Gessner, Chem. Soc. Rev., 2013, 42, 3197–3208 RSC; (d) M.-A. Légaré, C. Pranckevicius and H. Braunschweig, Chem. Rev., 2019, 119, 8231–8261 CrossRef PubMed; (e) M. Melaimi, R. Jazzar, M. Soleilhavoup and G. Bertrand, Angew. Chem., Int. Ed., 2017, 56, 10046–10068 CrossRef CAS PubMed.
- R. Kinjo, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2010, 49, 5930–5933 CrossRef CAS PubMed.
- V. Lavallo, Y. Canac, C. Präsang, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2005, 44, 5705–5709 CrossRef CAS PubMed.
- D. Pichon, M. Soleilhavoup, J. Morvan, G. P. Junor, T. Vives, C. Crévisy, V. Lavallo, J.-M. Campagne, M. Mauduit, R. Jazzar and G. Bertrand, Chem. Sci., 2019, 10, 7807–7811 RSC.
- (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- M. J. Frisch, et al., Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- (a) F. Weinhold and C. Landis, Valency and Bonding, A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, Cambridge, 2005 Search PubMed; (b) C. R. Landis and F. Weinhold, The NBO View of Chemical Bonding, The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley, 2014, pp. 91–120 Search PubMed; (c) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- T. A. Keith, AIMAll (Version 10.05.04), 2010, https://aim.tkgristmill.com Search PubMed.
- M. A. Celik, R. Sure, S. Klein, R. Kinjo, G. Bertrand and G. Frenking, Chem. – Eur. J., 2012, 18, 5676–5692 CrossRef CAS PubMed.
- S. Roy, K. C. Mondal, S. Kundu, B. Li, C. J. Schürmann, S. Dutta, D. Koley, R. Herbst-Irmer, D. Stalke and H. W. Roesky, Chem. – Eur. J., 2017, 23, 12153–12157 CrossRef CAS PubMed.
- Y. Wang, Y. Xie, P. Wei, R. B. King, H. F. Schaefer, P. v. R. Schleyer and G. H. Robinson, J. Am. Chem. Soc., 2008, 130, 14970–14971 CrossRef CAS PubMed.
- L. Weber, Eur. J. Inorg. Chem., 2000, 2000, 2425–2441 CrossRef.
- M. M. Siddiqui, S. Banerjee, S. Bose, S. K. Sarkar, S. K. Gupta, J. Kretsch, N. Graw, R. Herbst-Irmer, D. Stalke, S. Dutta, D. Koley and H. W. Roesky, Inorg. Chem., 2020, 59, 11253–11258 CrossRef CAS PubMed.
- M. Kapitein and C. von Hänisch, Eur. J. Inorg. Chem., 2015, 2015, 837–844 CrossRef CAS.
- M. Kapitein, M. Balmer, L. Niemeier and C. von Hänisch, Dalton Trans., 2016, 45, 6275–6281 RSC.
- A. Kuczkowski, S. Schulz and M. Nieger, Appl. Organomet. Chem., 2004, 18, 244–251 CrossRef CAS.
- (a) R. F. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Pr, Oxford, 1990 Search PubMed; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS; (c) R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS; (d) C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley-Vch, Weinheim, 2007 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06001a |
| This journal is © The Royal Society of Chemistry 2023 |