Impact of counteranions on N-heterocyclic carbene gold(I)-catalyzed cyclization of propargylic amide

Abstract

N-Heterocyclic carbene (NHC) Au(I)-catalyzed organic synthesis has recently been receiving increasing attention, especially with the activation of alkynes. In contrast, counteranions, being widely problematic in Au(I)-catalyzed transformations, are commonly considered as innocent partners and are not respectably included in a computational model. Herein, we report density functional theory (DFT) investigations of the Au(I)-catalyzed cyclization of propargylic amides to exploit the mechanistic effect of several counteranions to shed some light for further future developments. Among the counteranions used in this study, NTf₂⁻, ClO₄⁻, TsO⁻, TFA⁻, TfO⁻, MsO⁻, and SbF₆⁻, both the cyclization and protodeauration step favor the 5-exo-dig product over the 6-endo-dig product when the alkyne moiety is terminated with hydrogen. These anions reveal a crucial influence on the energy profile through lowering the barriers of the reaction. Mechanistically, the results obtained from all counteranions show that the protodeauration is slower than the cyclization. By using an energetic span model, the results clearly indicate that the rate-determining state is the protodeauration step for all counteranions, and thus protodeauration is the turnover-limiting step. The turnover frequency (TOF) results for the formation of the 5-exo-dig product show cyclization reactivity in the order of MsO⁻ > TFA⁻ > ClO₄⁻ > NTf₂⁻ > TfO⁻ > TsO⁻ ≫ SbF₆⁻, whereas an order of TFA⁻ > MsO⁻ > NTf₂⁻ > TfO⁻ ≈ ClO₄⁻ > SbF₆⁻ ⋙ TsO⁻ is calculated for the protodeauration, suggesting that SbF₆⁻ and TsO⁻ are disfavored due to their slow protodeauration. In this regard, and for the 6-endo-dig pathway, our conclusions demonstrate an order of TfO⁻ > TFA⁻ > MsO⁻ > NTf₂⁻ > ClO₄⁻ > TsO⁻ ⋙ SbF₆⁻ for the cyclization and TFA⁻ > TsO⁻ > MsO⁻ > TfO⁻ > NTf₂⁻ > ClO₄⁻ ⋙ SbF₆⁻ for the protodeauration, advocating that the anions SbF₆⁻, NTf₂⁻ and ClO₄⁻ are unlikely partners for the 6-endo-dig pathway because of their slow protodeauration. Finally, the findings here advise that any engineering of the counteranion to increase the efficiency of catalytic system would be more effective on the protodeauration step rather than the cyclization step.

---

Introduction

Gold(I) catalysis has been become an important synthetic methodology,^1–5 and N-heterocyclic carbene (NHC)–gold(I) complexes have been shown to be an elegant combination^6–13 for activation of alkynes or alkenes to access a plethora of organic transformations.^14–21 Gold(I) catalysis always requires optimization of the counteranions.²² For example, among the diverse range of counteranions, halides (Cl⁻, Br⁻, and I⁻), oxygen-based (OTs⁻, OMs⁻, OTf⁻, TFA⁻, ClO₄⁻), nitrogen-based (NTf₂⁻), carbon-based (CN⁻ and CTf₃⁻), boron-based (BF₄⁻ and B(C₆F₅)₄⁻), and fluorinated (SbF₆⁻ and PF₆⁻) counteranions have been employed extensively.²³ However, OTf⁻, SbF₆⁻, and NTf₂⁻ are the most commonly used counteranions in gold-catalyzed transformations owing to their high stability and low price.^23–25 Mechanistically, Au(I) catalysis in general involves association/dissociation of the counteranions from the cationic gold center, but this process is affected by the polarity of the solvents. On one hand, low dielectric constant solvents make the gold catalyst exist as a contact ion pair,^26–29 accordingly playing an essential role in the reaction pathway.³⁰ On the other hand, a dissociated ion pair due to the solvation around the ion may exist in the presence of high dielectric constant solvents, resulting in a negligible impact on the catalytic mechanism pathway.^26,31 In this regard, it has been reported that the presence of peculiar functional groups in the solvent regulates and impacts the gold catalysis steps, i.e., the nucleophilic attack, protodeauration steps, or coordination with the cationic gold center rather than π-coordination of Au(I) with the alkyne/alkene substrate.^32–35 Additionally, the effect of counteranions on gold affinity is important since a high affinity for gold with its counteranion implies a high energy barrier to overcome, thus preventing the coordination with the alkyne moiety and therefore impeding the fluency of the catalytic cycle.³⁶ Besides the affinity, another important factor is the proton transfer in a reaction. Here, the counteranions are more likely to be hydrogen-bond acceptors with that proton, so affecting the overall rate of the reaction and consequently enhancing the nucleophilicity of the attacking nucleophile, however it may have a high affinity for gold and thus shut down the catalytic cycle.³⁷ Moreover, the stability of gold catalysts has been also reported to be affected by their counterions.^35,38 Therefore, counteranion selection is very important and the overall effectiveness will be delicately determined by the affinity, hydrogen bonding basicity and stability of the gold catalyst; however, the understanding of counteranions is still unclear. Understanding the total role of these counteranions in a reaction will allow further industrial optimization and then minimize harsh conditions and costs accordingly. We were recently interested in understanding the effect of expanded-ring N-heterocyclic carbenes on the Au(I)-catalyzed cyclization of propargylic amides by means of density functional theory (DFT) simulations.³⁹ Our results showed that the corresponding catalytic cycle is composed of four main steps, shown in Fig. 1, namely complexation, cyclization, deprotonation and protonation/protodeauration. These steps are greatly facilitated by the counteranion NTf₂⁻ in which the reaction becomes highly disfavored when NTf₂⁻ is absent. We indicated that the counteranion is required to increase the nucleophilicity of the carbonyl group. Although the proton transfer enabled by NTf₂⁻ anion was seen to be moderately slower than that by product 2, once the product 2 is formed, the autocatalyzed 2-assisted proton transfer will dominate the reaction. Recent work reported by Hammond and Xu on the cyclization of propargylic amides with JohnPhos–Au–X (X = counteranions) allowed them to rationalize the kinetic effects of counterions, where high hydrogen-bond basicity, like with OTf⁻, assists the proton transfer to accelerate the reaction.⁴⁰ Since each counteranion behaves differently, our debate is focused on the kinetic impact of each anion on cyclization and protodeauration, and therefore how counteranions affect these steps. More specifically, can counteranions turn the mode of cyclization from 5-exo-dig to 6-endo-dig in the gold-catalyzed reaction of propargylic amide? Broadly, can these anions change the rate-determining step for the reaction shown in Fig. 1? Herein we report the effect of various counteranions on the NHC Au(I)-catalyzed cyclization and protodeauration steps of propargylic amide based on our recent DFT-calculated mechanism to obtain deeper insights into this important transformation from a molecular perspective to establish an index of reactivity in gold catalysis.³⁹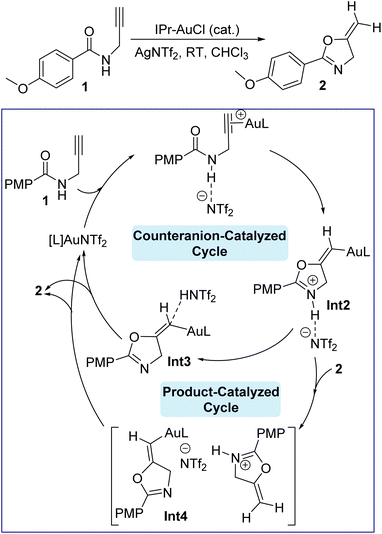

Fig. 1 Gold-catalyzed cyclization of propargylic amides 1 via 5-exo-dig cyclization, showing our recently computed catalytic cycle when the counteranion is NTf₂⁻ and the NHC ligand (L) is IPr.

Results and discussion

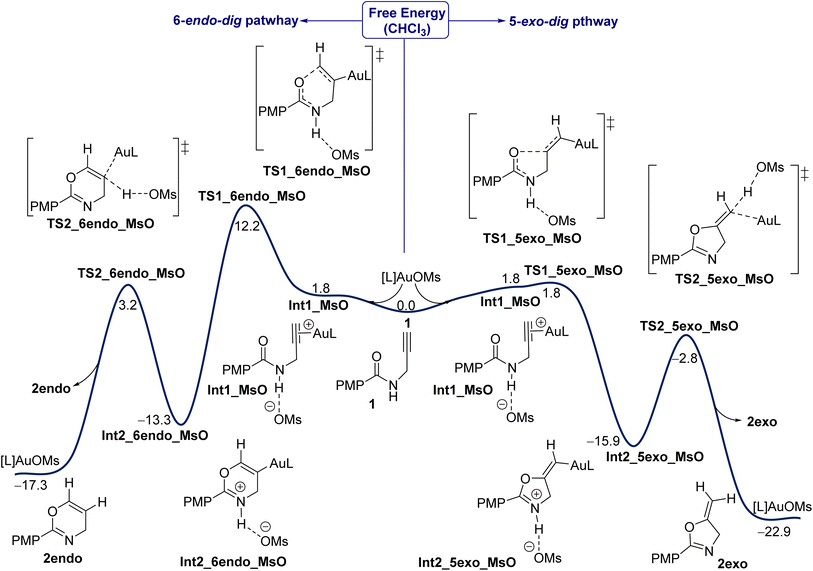
In this work, IPr is used as the model ligand and all our investigations are calculated at the SMD(CHCl₃)-PBE0-D3BJ/def2-TZVP,6-311+G(d,p) level of theory based on solvated optimization calculated at the SMD(CHCl₃)-PBE0-D3BJ/SDD,6-31G(d) level of theory (see computational details). Under the experimental conditions shown in Fig. 1, the presence of IPrAuCl with AgNTf₂ leads to salt metathesis to give IPrAuNTf₂ as an active catalyst. In this aspect, the presence of positively charged IPrAu⁺ as a “naked” counterion, without its negative part NTf₂⁻, is unlikely due to its tight binding to the key intermediates and transition states (TSs) through both hydrogen bonding and direct Au–counterion interaction.³⁹ Some previous computational studies have indicated a small impact from the anion SbF₆⁻ on calculations of Au(I)-catalyzed pathways.^41–43 Initially, the energy profile for one of the selected counteranions, MsO⁻, is considered for both the exo and endo pathways. Fig. 2 shows the energy profile for the Au(I)-catalyzed 5-exo-dig and 6-endo-dig cyclization of propargylic amides 1 when the counteranion is MsO⁻ and L is IPr. The reaction is initiated by coordination of the Au center to the alkyne moiety whereas the counteranion interacts with the amide site in a slightly endergonic step (1.8 kcal mol⁻¹), giving intermediate Int1_MsO. We showed in our previous work that the deprotonation of the amide site by the counteranion is highly disfavored, instead strong hydrogen bonding between the counteranion (MsO⁻) and the amide group drives the cyclization step.³⁹ The cyclization step, with the counteranion MsO⁻ involved, proceeds through transition states (TSs) TS1_5exo_MsO or TS1_6endo_MsO to give either the exo or endo product, respectively. Our results here show that there is a substantial regioselectivity preference for the exo product. The exo cyclization through TS TS1_5exo_MsO is approximately barrierless as an exergonic step of 15.9 kcal mol⁻¹ (Int1_5exo_MsO). Then, a deprotonation/protodeauration process has to occur to furnish the product and propagate the catalytic cycle. Based on our previous observations,³⁹ the deprotonation of the amide site and protodeauration by the counteranion could smoothly move inside the solvation shell without a need for the full dissociation to the discrete species. Thus, the protodeauration proceeds through TS TS2_5exo_MsO with a barrier of 13.1 kcal mol⁻¹ as a moderately exergonic step (ΔG_r = −7 kcal mol⁻¹) to furnish the exo product 2exo and regenerate the catalyst IPrAuOMs to propagate the iterative cycle. Based on these results we will turn our attention to the impact of other counteranions (see below).

Fig. 2 The Gibbs free energy profile (in kcal mol⁻¹) for the Au(I)-catalyzed 5-exo-dig (right) and 6-endo-dig (left) cyclization of propargylic amides 1 when the counteranion is MsO⁻ and L is IPr. The results are calculated at the SMD(CHCl₃)-PBE0-D3BJ/def2-TZVP,6-311+G(d,p)//SMD(CHCl₃)-PBE0-D3BJ/SDD,6-31G(d) level of theory at 298.15 K.

Impact of counteranions on mechanistic pathway

The strong binding of the counteranion to the Au center in the in situ generated reactive catalyst, the key role in the cyclization and protodeauration steps, and the strong Au–counteranion interaction in various key species prompted us to investigate the effects of various counteranions on the overall barrier and regioselectivity. Generally, the roles of the counteranions are not well understood and are often neglected in computational studies, especially when an organometallic species is present or any of the reagents is ionic. However, recent studies showed that counterions influence organometallic transformations.^36,44–50 Based on the energy profile shown in Fig. 2, seven counteranions were examined for both 5-exo and 6-endo pathways, namely NTf₂⁻, ClO₄⁻, TsO⁻, CF₃COO⁻ (TFA⁻), TfO⁻, MsO⁻, and SbF₆⁻ (Fig. 3). These anions were involved in all of the steps of the reaction pathway: coordination to the alkyne moiety, cyclization, and protodeauration. Although no experimental data are available for their basicity in unified measurement conditions, our calculation shows that their basicity follows the order of TFA⁻ > TsO⁻ > MsO⁻ > NTf₂⁻ > TfO⁻ > ClO₄⁻ ⋙ SbF₆⁻ in chloroform, whereas their Au affinity follows the order of TFA⁻ > NTf₂⁻ > MsO⁻ > TsO⁻ > ClO₄⁻ ≈ TfO⁻ ≫ SbF₆⁻ (Table ESI1†). According to the calculated energies, the complexation of the Au center to the alkyne moiety in 1 has different thermodynamic stabilities for all counteranions and ranges from ∼−18 to ∼+5 kcal mol⁻¹ (Fig. 3). On one hand, among all selected anions, anion SbF₆⁻ shows the best π-coordination of −18.1 kcal mol⁻¹ due to its lowest basicity and consequently providing the highest gold affinity (Table ESI1†). On the other hand, an endergonic complexation of +5.6 kcal mol⁻¹ was accounted for NTf₂⁻. Moreover, the anions MsO⁻ and TFA⁻ exhibit slightly endergonic complexation of +1.8 and +2.1 kcal mol⁻¹, respectively. Among these anions, the TsO⁻ and TfO⁻ display moderate exergonic complexation of −3.6 and −4.9 kcal mol⁻¹, respectively.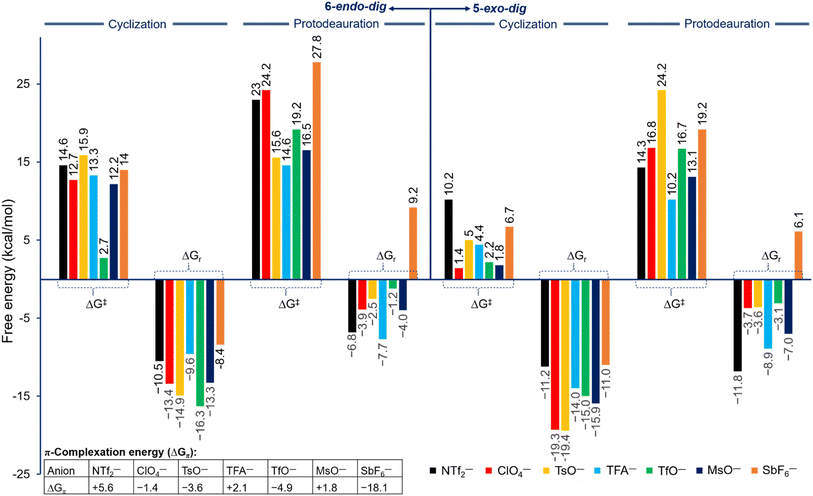

Fig. 3 Free energy of barrier (ΔG^‡) and reaction (ΔG_r) for the cyclization and protodeauration steps for propargylic amide 1 with different counteranions along the 5-exo-dig (right) and 6-endo-dig (left) pathways at 298.15 K according to Fig. 2. ΔG_π is the π-complexation energy of the Au center to the alkyne moiety on propargylic amide 1.

Based on their behavior, these anions have different effects on the reaction pathway and the energetic impact on each step is clearly pronounced, however the regioselectivity is not changed. The relative free energies of reaction and barriers along the three steps were examined and are shown in Fig. 3 for both 5-exo-dig and 6-endo-dig cyclization. A correlation between the calculated basicity and affinity of each anion with the calculated barriers for the cyclization and protodeauration is absent. In this regard, the recent work has also reached the same conclusions, in which every counteranion behaves differently, leading to a lack of a perspicuous relationship. The hydrogen bonding, basicity, and affinity/coordination to Au all affect the reactivity of gold catalysts.^36,40,46,51 Therefore, the need for a new parameter that determines the strength and behavior of each anion in an informative index is necessary to understand their reactivity in cationic gold catalysis.

Overall, for all anions the regioselectivity for 5-exo-dig cyclization is substantially preferred over 6-endo-dig cyclization, except for TfO⁻ in which the regioselectivity for TfO⁻ is 0.5 kcal mol⁻¹ (Fig. 3). Moreover, for all anions the computed free energy of barrier and reaction for cyclization and protodeauration tend to be preferred for the 5-exo-dig over 6-endo-dig pathways. This result clearly agrees with the experimental observations in which the anion does not change the outcome of the reaction when the alkyne moiety is terminated with hydrogen rather than other electronic groups.⁵² In a detailed description of each anion's effect, the four anions TFA⁻, MsO⁻, NTf₂⁻, and ClO₄⁻ exhibit a favorable forward reaction despite each one of them having a different impact on the energy barrier and reaction. In particular, the anions TFA⁻, MsO⁻, and ClO₄⁻ have relatively lower energy barriers in terms of cyclization and protodeauration than NTf₂⁻. Interestingly, although the cyclization step with the anions TsO⁻ and SbF₆⁻ proceeds smoothly and quickly, the protodeauration step is disfavored. The energy barrier for the protodeauration step for TsO⁻ is very slow at 24.2 kcal mol⁻¹, so the backward reaction of the cyclization step is a significant competing pathway. In the case of SbF₆⁻, the backward reaction (ΔG^‡ = 17.7 kcal mol⁻¹) is preferred over the protodeauration step (ΔG^‡ = 19.2 kcal mol⁻¹). Furthermore, notable competition between the forward and backward direction is seen in the case of TfO⁻, where the protodeauration requires 16.7 kcal mol⁻¹ to release the product whereas the backward cyclization step needs 17.2 kcal mol⁻¹.

Furthermore, in order to answer our main concern about determining the rate-limiting step/state for these anions in cyclization and protodeauration, the calculated free energy barriers shown in Fig. 3 for the catalytic cycle shown in Fig. 1 do not provide a straightforward and informative answer. Thus, to solve this issue and prove that all of the counteranions used in this study do not change the rate-limiting state, we turn our attention to the energetic span model as a more informative approach than the classical free energy profile.

By using the energetic span model, the catalytic efficiency and turnover frequency (TOF) of each anion in our theoretically obtained free energy profile have been considered for all counteranions through calculating the apparent free energy of activation, allowing us to determine whether the rate-determining state (RDS) is cyclization or protodeauration. This model examines the compatibility of the resulting overall barrier with the experimental conditions and establishes the step that is a RDS in a catalytic system.^53,54 We recently used this model for determining the turnover-limiting state in the homogenously Os-catalyzed dihydroxylation of alkene and successfully predicted it to be the reoxidation step rather than hydrolysis.⁵⁵

This model requires two fundamental terms: the TOF-determining transition state (TDTS) and the TOF-determining intermediate (TDI). The calculated catalytic cycle presented in Fig. 2 shows two states of TDTS, the cyclization (TDTS1, TS1) as the energetic span 1 (δE1) and protodeauration (TDTS2, TS2) as the energetic span 2 (δE2) steps. The calculated energetic span and their TOFs for both cyclization and protodeauration steps along 5-exo-dig and 6-endo-dig pathways are shown in Table 1. According to the calculated results, we can clearly see that the RDS is the protodeauration step rather than the cyclization step for all counteranions, so protodeauration is the turnover-limiting state and changing the counteranion would not change the nature of the RDS.

Table 1 Calculated apparent free energy of activation (in kcal mol⁻¹) and turnover frequency (TOF, in h⁻¹) for 5-exo-dig and 6-endo-dig cyclization and the corresponding protodeauration step with different counteranions

5-exo-dig pathway					6-endo-dig pathway
Anion	δE1	TOF1	δE2	TOF2	δE1	TOF1	δE2	TOF2
NTf2^−	−1.6	3.3 × 10^17	14.3	7.4 × 10^5	7.8	4.3 × 10^10	23	3.1 × 10^−1
ClO4^−	−2.3	1.1 × 10^18	16.8	1.1 × 10^4	8.8	7.9 × 10^9	24.2	4.0 × 10^−2
TsO^−	1.4	2.1 × 10^15	24.2	4.1 × 10^−2	13.4	3.4 × 10^6	15.6	8.2 × 10^4
TFA^−	−4.5	4.5 × 10^19	10.2	7.5 × 10^8	5.6	1.8 × 10^12	14.6	4.4 × 10^5
TfO^−	−0.9	1.0 × 10^17	16.7	1.3 × 10^4	1.5	1.8 × 10^15	19.2	1.9 × 10^2
MsO^−	−5.2	1.5 × 10^20	13.1	5.6 × 10^6	8.2	2.2 × 10^10	16.5	1.8 × 10^4
SbF6^−	12.8	9.3 × 10^6	19.2	1.9 × 10^2	23.2	2.2 × 10^−1	27.8	9.4 × 10^−5

---

In comparison between the TOF for 5-exo-dig pathway, the TOF1 for cyclization follows the order of MsO⁻ > TFA⁻ > ClO₄⁻ > NTf₂⁻ > TfO⁻ > TsO⁻ ≫ SbF₆⁻ whereas for protodeauration (TOF2) the trend has the order of TFA⁻ > MsO⁻ > NTf₂⁻ > TfO⁻ ≈ ClO₄⁻ > SbF₆⁻ ⋙ TsO⁻. Although a considerable gap in TOF between SbF₆⁻ (TOF = 9.3 × 10⁶ h⁻¹) and other anions (ranged between ∼1 × 10²⁰ h⁻¹ to ∼2 × 10¹⁵ h⁻¹) is seen, this would suggest that all the anions can facilitate the cyclization, but an attention must be given to the protodeauration step prior choosing a counteranion. For instance, protodeauration with the anion TsO⁻ (TOF = 4.1 × 10⁻² h⁻¹) is disfavored. Similarly, the anion SbF₆⁻ (TOF = 1.9 × 10² h⁻¹) would be also excluded in comparison with other anions. For the 6-endo-dig pathway, the TOF1 cyclization has an order of TfO⁻ > TFA⁻ > MsO⁻ > NTf₂⁻ > ClO₄⁻ > TsO⁻ ⋙ SbF₆⁻ whereas for the protodeauration (TOF2) the order of reactivity is TFA⁻ > TsO⁻ > MsO⁻ > TfO⁻ > NTf₂⁻ > ClO₄⁻ ⋙ SbF₆⁻. The general trend suggests that the anions SbF₆⁻, NTf₂⁻ and ClO₄⁻ are not preferred. In particular, SbF₆⁻ (TOF = 2.2 × 10⁻¹ h⁻¹) is unsuitable for cyclization and highly unlikely for protodeauration (TOF = 9.4 × 10⁻⁵ h⁻¹). In addition, although the anions NTf₂⁻ and ClO₄⁻ have fast TOF of 4.3 × 10¹⁰ h⁻¹ and 7.9 × 10⁹ h⁻¹, respectively, in the cyclization step, their protodeauration is very slow at 3.1 × 10⁻¹ h⁻¹ and 4.0 × 10⁻² h⁻¹, respectively. In summary, this approach provides us with a good understanding of the turnover-limiting state and proposes an index of preferred and unpreferred anions that can be used in synthetic applications under gold catalysis.

Conclusions

In summary, the effect of counteranions on the mechanism and regioselectivity of the Au(I)-promoted propargylic amide cyclization reaction was studied computationally using DFT simulations. Seven counteranions were examined in this reaction to understand their impact on the reactivity. In this scheme, both the cyclization and protodeauration step favor the 5-exo-dig product over 6-endo-dig formation when the alkyne moiety is terminated with hydrogen rather than other substituents for all counteranions used in this study. We have previously shown that a counteranion such as NTf₂⁻ has a crucial influence on the energy profile since it binds tightly to the key intermediates and TSs through both hydrogen bonding and direct Au–counterion interaction.³⁹ In this work, other counteranions used in gold catalysis, such as ClO₄⁻, TsO⁻, TFA⁻, TfO⁻, MsO⁻, and SbF₆⁻, have confirmed our previous findings that these partners lower the barriers of reaction and, more importantly, facilitate the protodeauration step. Regarding the energetic impact, the counteranions have shown different effects on all steps of the reaction, π-coordination, cyclization and protodeauration. However, changing the type of counteranion did not change the rate-determining step, namely the protodeauration step. The energetic span model was used to calculate the TOF for each counteranion, and the results clearly indicated that the RDS is the protodeauration step for all counteranions, and thus protodeauration is the turnover-limiting state. According to this model, an index of preferred and unpreferred anions was proposed. According to the calculated TOF for the 5-exo-dig pathway, the results suggest that SbF₆⁻ and TsO⁻ are not preferred due to their slow protodeauration. In this regard, the reactivity of cyclization was seen to follow the order of MsO⁻ > TFA⁻ > ClO₄⁻ > NTf₂⁻ > TfO⁻ > TsO⁻ ≫ SbF₆⁻ whereas an order of TFA⁻ > MsO⁻ > NTf₂⁻ > TfO⁻ ≈ ClO₄⁻ > SbF₆⁻ ⋙ TsO⁻ was calculated for protodeauration step. For the 6-endo-dig pathway, our calculations advised that the SbF₆⁻, NTf₂⁻ and ClO₄⁻ are undesired anions due to their slow protodeauration. Also, according to the TOF results on the 6-endo-dig pathway the reactivity of cyclization showed an order of TfO⁻ > TFA⁻ > MsO⁻ > NTf₂⁻ > ClO₄⁻ > TsO⁻ ⋙ SbF₆⁻ whereas on the protodeauration follows the order of TFA⁻ > TsO⁻ > MsO⁻ > TfO⁻ > NTf₂⁻ > ClO₄⁻ ⋙ SbF₆⁻. Finally, and based on our computed results, we propose that engineering of the counteranion, especially for the protodeauration step, can provide a catalytic system with higher reactivity and selectivity. For example, with weakly basic counteranions, the rate is limited by the protodeauration of the cyclized intermediate Int2, and extra acid/base additives might improve the rate. Further engineering of the shape of the counteranion to tune the Au–counteranion interaction and finally tune the energy profile is also a possible approach to improve both reactivity and selectivity in gold catalysis.

Computational details

All calculations were performed using Gaussian 16 program⁵⁶ with default integration grid settings. For geometry optimization, the hybrid functional PBE0 was used with the SDD⁵⁷ pseudopotential basis set for Au and the 6-31G(d)^58,59 basis set for other atoms, in combination with Grimme's D3BJ dispersion⁶⁰ correction during geometry optimization. The solvent effect of chloroform was included via the SMD implicit solvation model in the optimization calculations using chloroform as a medium solvent.⁶¹ All minimums and TSs were verified by frequency calculation. Furthermore, single point energy calculations were done with the def2-TZVP⁶² basis set for Au and 6-311+G(d,p)^63,64 for other atoms with SMD solvation/CHCl₃. Gibbs free energies were obtained through thermochemical corrections derived from vibrational frequencies at 298.15 K using unscaled frequencies under Grimme's quasi-RRHO treatment⁶⁵ at the (SMD/CHCl₃)-PBE0-D3BJ/6-31G(d)/SDD level, and single point energies at the (SMD/CHCl₃)-PBE0-D3BJ/6-311+G(d,p),def2-TZVP level of theory.

Author contributions

The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

A. A. H. acknowledges the University of Southampton School of Chemistry for providing the scientific visiting (2717441/EB00-VISIT). H. S. A. thanks IT services at the University of Manchester for providing the Computational Shared Facility. Mr Yumiao Ma is acknowledged for his early calculations on this project.

References

1. W. Zi and F. Dean Toste, Chem. Soc. Rev., 2016, 45, 4567.
2. V. K. Y. Lo, A. O. Y. Chan and C. M. Che, Org. Biomol. Chem., 2015, 13, 6667.
3. H. C. Shen, Tetrahedron, 2008, 64, 3885.
4. H. C. Shen, Tetrahedron, 2008, 64, 7847.
5. A. Collado, D. J. Nelson and S. P. Nolan, Chem. Rev., 2021, 121, 8559–8612.
6. A. S. K. Hashmi, T. Hengst, C. Lothschütz and F. Rominger, Adv. Synth. Catal., 2010, 352, 1315–1337.
7. A. S. K. Hashmi, C. Lothschütz, C. Böhling, T. Hengst, C. Hubbert and F. Rominger, Adv. Synth. Catal., 2010, 352, 3001–3012.
8. A. S. K. Hashmi, C. Lothschütz, C. Böhling and F. Rominger, Organometallics, 2011, 30, 2411–2417.
9. A. S. K. Hashmi, C. Lothschütz, K. Graf, T. Häffner, A. Schuster and F. Rominger, Adv. Synth. Catal., 2011, 353, 1407–1412.
10. M. J. Spallek, D. Riedel, F. Rominger, A. S. K. Hashmi and O. Trapp, Organometallics, 2012, 31, 1127–1132.
11. A. S. K. Hashmi, D. Riedel, M. Rudolph, F. Rominger and T. Oeser, Eur. J. Chem., 2012, 18, 3827–3830.
12. D. Riedel, T. Wurm, K. Graf, M. Rudolph, F. Rominger and A. S. K. Hashmi, Adv. Synth. Catal., 2015, 357, 1515–1523.
13. T. Wurm, F. Mulks, C. R. N. Böhling, D. Riedel, P. Zargaran, M. Rudolph, F. Rominger and A. S. K. Hashmi, Organometallics, 2016, 35, 1070–1078.
14. Z. Zheng, X. Ma, X. Cheng, K. Zhao, K. Gutman, T. Li and L. Zhang, Chem. Rev., 2021, 121, 8979–9038.
15. C. M. Hendrich, K. Sekine, T. Koshikawa, K. Tanaka and A. S. K. Hashmi, Chem. Rev., 2020, 121, 9113–9163.
16. R. Dorel and A. M. Echavarren, Chem. Rev., 2015, 115, 9028–9072.
17. A. S. K. Hashmi, Angew. Chem., Int. Ed., 2010, 49, 5232–5241.
18. M. C. Blanco Jaimes, C. R. N. Böhling, J. M. Serrano-Becerra and A. S. K. Hashmi, Angew. Chem., Int. Ed., 2013, 52, 7963–7966.
19. J. C. Y. Lin, R. T. W. Huang, C. S. Lee, A. Bhattacharyya, W. S. Hwang and I. J. B. Lin, Chem. Rev., 2009, 109, 3561–3598.
20. N. Marion and S. P. Nolan, Chem. Soc. Rev., 2008, 37, 1776–1782.
21. P. Fernández-Canelas, P. Barrio and J. M. González, Tetrahedron Lett., 2022, 99, 153857.
22. Z. Lu, T. Li, S. R. Mudshinge, B. Xu and G. B. Hammond, Chem. Rev., 2021, 121, 8452–8477.
23. X. Zeng, S. Liu and B. Xu, RSC Adv., 2016, 6, 77830–77833.
24. C. Nieto-Oberhuber, S. Lopez, M. P. Munoz, D. J. Cardenas, E. Bunuel, C. Nevado and A. M. Echavarren, Angew. Chem., Int. Ed., 2005, 44, 6146–6148.
25. C. Nieto-Oberhuber, M. P. Munoz, S. Lopez, E. Jimenez-Nuner, C. Nevado, E. Herrero-Gomez, M. Raducan and A. M. Echavarren, Chem. –Eur. J., 2006, 12, 1677–1693.
26. A. Macchioni, Chem. Rev., 2005, 105, 2039–2073.
27. D. Zuccaccia, L. Belpassi, F. Tarantelli and A. Macchioni, J. Am. Chem. Soc., 2009, 131, 3170.
28. J. Bucher, T. Wurm, K. S. Nalivela, M. Rudolph, F. Rominger and A. S. K. Hashmi, Angew. Chem., Int. Ed., 2014, 53, 3854–3858.
29. L. N. D. Comprido, J. Klein, G. Knizia, J. Kastner and A. S. K. Hashmi, Chem. –Eur. J., 2016, 22, 2892–2895.
30. M. Trinchillo, P. Belanzoni, L. Belpassi, L. Biasiolo, V. Busico, A. D'Arnora, L. D'Amore, A. Del Zotto, F. Tarantelli, A. Tuzi and D. Zuccaccia, Organometallics, 2016, 35, 641–654.
31. Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621.
32. A. Zhdanko and M. E. Maier, Chem. –Eur. J., 2014, 20, 1918–1930.
33. W. B. Wang, M. Kumar, G. B. Hammond and B. Xu, Org. Lett., 2014, 16, 636–639.
34. M. Gatto, W. Baratta, P. Belanzoni, L. Belpassi, A. Del Zotto, F. Tarantelli and D. Zuccaccia, Green Chem., 2018, 20, 2125–2134.
35. M. Kumar, J. Jasinski, G. B. Hammond and B. Xu, Eur. J. Chem., 2014, 20, 3113–3119.
36. G. Ciancaleoni, L. Belpassi, D. Zuccaccia, F. Tarantelli and P. Belanzoni, ACS Catal., 2015, 5, 803–814.
37. B. Yuan, R. He, W. Shen and M. Li, Eur. J. Org. Chem., 2017, 2017, 3947–3956.
38. N. Mezailles, L. Ricard and F. Gagosz, Org. Lett., 2005, 7, 4133–4136.
39. Y. Ma, H. S. Ali and A. A. Hussein, Catal. Sci. Technol., 2021, 12, 674–685.
40. Z. Lu, J. Han, O. E. Okoromoba, N. Shimizu, H. Amii, C. F. Tormena, G. B. Hammond and B. Xu, Org. Lett., 2017, 19, 5848–5851.
41. A. A. Hussein and H. S. Ali, J. Org. Chem., 2020, 85, 12682–12691.
42. Y. Duan, Y. Liu, S. Bi, B. Ling, Y.-Y. Jiang and P. Liu, J. Org. Chem., 2016, 81, 9381–9388.
43. B. Alcaide, P. Almendros, I. Fernández, R. Martín-Montero, F. Martínez-Peña, M. P. Ruiz and M. R. Torres, ACS Catal., 2015, 5, 4842–4845.
44. O. Seppänen, S. Aikonen, M. Muuronen, C. Alamillo-Ferrer, J. Burés and J. Helaja, Chem. Commun., 2020, 56, 14697–14700.
45. B. Yuan, R. He, X. Guo, W. Shen, F. Zhang, Y. Xu and M. Li, New J. Chem., 2018, 42, 15618–15628.
46. M. Jia and M. Bandini, ACS Catal., 2015, 5, 1638–1652.
47. M. Jiménez-Tenorio, M. C. Puerta, P. Valerga, M. A. Ortuño, G. Ujaque and A. Lledós, Inorg. Chem., 2013, 52, 8919–8932.
48. E. Clot, Eur. J. Inorg. Chem., 2009, 2009, 2319–2328.
49. A. Macchioni, Chem. Rev., 2005, 105, 2039–2074.
50. R. G. Epton, W. P. Unsworth and J. M. Lynam, Isr. J. Chem., 2022, e202200033.
51. A. Zhdanko and M. E. Maier, ACS Catal., 2014, 4, 2770–2775.
52. A. S. K. Hashmi, A. M. Schuster, M. Schmuck and F. Rominger, Eur. J. Org. Chem., 2011, 2011, 4595–4602.
53. S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110.
54. S. Kozuch, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 795–815.
55. A. A. Hussein, Y. Ma and G. A. I. Moustafa, Catal. Sci. Technol., 2022, 12, 880–893.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
57. P. Schwerdtfeger, M. Dolg, W. H. E. Schwarz, G. A. Bowmaker and P. D. W. Boyd, J. Chem. Phys., 1989, 91, 1762–1774.
58. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
59. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
60. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
61. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
62. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
63. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
64. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
65. S. Grimme, Eur. J. Chem., 2012, 18, 9955–9964.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06210k

---