Crystal structures, phase transitions, and nuclear magnetic resonance of organic–inorganic hybrid [NH₂(CH₃)₂]₂ZnBr₄ crystals

Abstract

Organic–inorganic hybrid [NH₂(CH₃)₂]₂ZnBr₄ crystals were grown via slow evaporation, and their monoclinic structure was determined using single-crystal X-ray diffraction (XRD). The two phase transition temperatures at 401 K (T_C1) and 436 K (T_C2) were defined using differential scanning calorimetry and powder XRD. In the nuclear magnetic resonance spectra, a small change was observed in the ¹H chemical shifts for NH₂, ¹³C chemical shifts for CH₃, and ¹⁴N resonance frequency for NH₂ near T_C1. ¹H spin-lattice relaxation times T_1ρ and ¹³C T_1ρ for NH₂ and CH₃, respectively, rapidly decreased near T_C1, suggesting that energy was easily transferred. NH₂ in the [NH₂(CH₃)₂]⁺ cation was significantly influenced by the surrounding environments of ¹H and ¹⁴N, indicating a change in the N–H⋯Br hydrogen bond with the coordination geometry of the ZnBr₄ anion. These fundamental properties open efficient avenues for the development of organic–inorganic hybrids, thus qualifying them for practical applications.

---

1. Introduction

Interest in organic–inorganic hybrid compounds has been primarily associated with their various applications, such as in sensors, fuel and solar cells, light-emitting diodes, and light-emitting transistors.^1–4 Furthermore, the important applications for materials with organic–inorganic hybrid perovskite are also as ferroelectrics, dielectric switches, and optical switches.^5–12 CH₃NH₃PbX₃ (X = Cl⁻, Br⁻, I⁻) thin-film photovoltaic devices have been used as solar cells,^13–18 but these materials readily decompose in humid air and are toxic because of the presence of Pb. Thus, it is necessary to develop lead-free hybrid perovskite solar cells. Two-dimensional compounds of [NH₃(CH₂)_nNH₃]MX₄ (n = 1, 2, 3, …; M = Mn²⁺, Co²⁺, Cu²⁺, Zn²⁺, Cd²⁺, Pb²⁺, X = Cl⁻, Br⁻, I⁻) and [(C_nH_2n+1NH₃)]₂MX₄ are examples of organic–inorganic hybrids that have recently attracted considerable attention.^19–26 In addition, the dimethylammonium tetrabromozincate(II), [NH₂(CH₃)₂]₂ZnBr₄, crystal is a member of the [NH₂(CH₃)₂]₂MX₄ family, which belongs to a group of A₂MX₄ types, where A⁺ is a univalent cation, M²⁺ is a divalent transition metal, and X is a halogen.^27–36 These crystals undergo several structural phase transitions, often associated with the ordering of hydrogen bonds and related changes in the molecular dynamics of the [NH₂(CH₃)₂]⁺ ions. The individual MX₄ tetrahedral anions in these materials are completely isolated and surrounded by organic [NH₂(CH₃)₂]⁺ cations. These substances are expected to act as potential proton conductors via hydrogen bonds. The structure of [NH₂(CH₃)₂]₂ZnBr₄, at 291 K is monoclinic with space group P2₁/c, and its lattice parameters are a = 8.706 Å, b = 11.956 Å, c = 16.289 Å, β = 121.84°, and Z = 4.³⁷ At 150 K, the structure is monoclinic, similar to that at 300 K; however, the space group and lattice constants are P2₁/n and a = 8.5512 Å, b = 11.825 Å, c = 13.499 Å, β = 90.358°, and Z = 4.³⁸ In the molecular unit, the ZnBr₄ anions are connected to the organic [NH₂(CH₃)₂]⁺ cations through N–H⋯Br hydrogen bonds.

With reference to previous reports on [NH₂(CH₃)₂]₂ZnBr₄, Ishihara et al.³⁷ investigated ⁸¹Br nuclear quadrupole resonance (NQR) frequencies with varying temperature. Four NQR resonance signals to the four Br atoms in the ZnBr₄ tetrahedron were obtained; their NQR peaks disappeared at temperatures above 355 K, and no evidence of a phase transition was observed between 77 and 350 K. In addition, the phase transition temperatures measured using differential scanning calorimetry (DSC) were 401 and 435 K, and the melting temperature was reported to be 459 K by Horiuchi et al.³⁹ Mahfoudh et al.³⁸ reported considerably small endothermic peaks at 281, 340, and 377 K and a large endothermic peak at 408 K between 250 and 420 K. Their conductive and dielectric properties were reported to be functions of temperature. Subsequently, Mahfoudh et al.⁴⁰ investigated the optical and dielectric properties of [NH₂(CH₃)₂]₂ZnBr₄. Although the structure, NQR spectrum, and phase transition temperatures have been reported, the thermodynamic stability and molecular dynamics based on varying temperature have not been widely evaluated.

In this study, we aimed to grow [NH₂(CH₃)₂]₂ZnBr₄, which is possibly a proton conductor owing to the availability of hydrogen bonds. The crystal structures and phase transition temperatures of [NH₂(CH₃)₂]₂ZnBr₄ were determined using single-crystal X-ray diffraction (XRD), powder XRD, DSC, and differential thermal analysis (DTA). Thermogravimetry analysis (TGA) was performed to better understand the thermal properties of the samples. In addition, nuclear magnetic resonance (NMR) chemical shifts for ¹H, ¹³C, and ¹⁴N were investigated to understand the coordination geometry and molecular dynamics of the organic [NH₂(CH₃)₂]⁺ cation near the phase transition temperature T_C. In addition, to elucidate the molecular motion and energy transfer, the spin-lattice relaxation time, T_1ρ, for ¹H and ¹³C were measured and investigated according to the temperature change. Herein, changes in the coordination geometry according to changes in temperature are explained by the changes in the N–H⋯Br hydrogen bonds between the [NH₂(CH₃)₂]⁺ cations and ZnBr₄ anions. Investigating the physicochemical properties of the phase transition mechanism can help expand the application scope of [NH₂(CH₃)₂]₂ZnBr₄ crystals.

2. Experimental

[NH₂(CH₃)₂]₂ZnBr₄ single crystals were grown via slow evaporation in a thermostat at 300 K using an aqueous solution containing NH(CH₃)₂·HBr (Aldrich, USA) and ZnBr₂ (99.99%, Aldrich, USA) of 2 : 1. To obtain a homogeneous solution, the solution was stirred and heated and then filtered through a filter. Thereafter, colourless single crystals grew after a few weeks.

The lattice parameters of the [NH₂(CH₃)₂]₂ZnBr₄ crystal at 150 and 300 K were determined by single-crystal XRD at the Korea Basic Science Institute (KBSI) Seoul Western Center. A colourless crystal was mounted on a Bruker D8 Venture PHOTON III M14 diffractometer with a Mo-Kα radiation source and a nitrogen cold stream (223 K). Data was collected and integrated using SMART APEX3 (Bruker, 2016) and SAINT (Bruker, 2016). The absorption was corrected using the multiscan method implemented in SADABS. The structure was solved using direct methods and refined by full-matrix least-squares on F2 using SHELXTL.⁴¹ All non-hydrogen atoms were refined anisotropically and hydrogen atoms were added to their geometrically ideal positions. The powder XRD patterns were measured at several temperatures using an XRD system with a Mo-Kα radiation source.

DSC measurements were performed on the powder using a DSC 25 apparatus (TA Instruments, USA) at a heating rate of 10 K min⁻¹ under a nitrogen gas atmosphere. A sample weighing 4.5 mg was used for temperature measurements between 200 and 570 K.

TGA and DTA experiments were conducted using a thermo-gravimetric analyser (TA Instruments, USA) at the same heating rate as that used for DSC from 300 to 873 K under nitrogen gas. Optical observations were performed using a Carl Zeiss microscope equipped with a Linkam THM-600 heating stage.

Magic-angle spinning (MAS) NMR chemical shifts and spin-lattice relaxation time T_1ρ of the [NH₂(CH₃)₂]₂ZnBr₄ crystal were measured using a Bruker 400 MHz Avance II+ NMR spectrometer (Bruker, Germany) at KBSI. The Larmor frequency for the ¹H MAS NMR experiment was ω_o/2π = 400.13 MHz, and that for ¹³C MAS NMR was ω_o/2π = 100.61 MHz. To minimise spinning sidebands, the MAS speeds for ¹H and ¹³C were measured at 10 kHz. Tetramethylsilane (TMS) and NH₄NO₃ were used as standard materials for accurate NMR chemical shift measurements. T_1ρ values were obtained using a π/2−τ pulse, followed by a spin-lock pulse of duration τ, and the π/2 pulse widths for ¹H and ¹³C were measured using a previously published method.³⁸ NMR experiments were not feasible at higher temperatures because of the limitations of the instrument.

3. Results and discussion

3.1. Crystal structure and phase transition

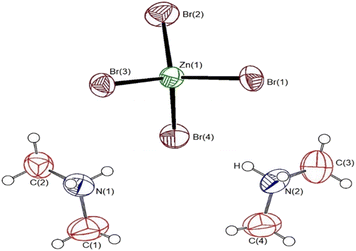
Single-crystal XRD results for the [NH₂(CH₃)₂]₂ZnBr₄ crystals were obtained at 150 and 300 K. The crystal structure at the two temperatures were grown to a monoclinic structure with space group P2₁/n. The lattice constants at 150 K are a = 8.6262 Å, b = 11.9760 Å, c = 13.6877 Å, β = 90.3690°, and Z = 4, and those at 300 K are a = 8.7140 Å, b = 11.9709 Å, c = 13.8563 Å, β = 90.513°, and Z = 4. At both temperatures, the structures, space groups, and lattice constants are almost identical. The results at 150 and 300 K in our study are consistent with those obtained at 150 K by Mahfoudh et al.,⁴⁰ but slightly different from those obtained at 300 K by Ishihara et al.³⁷ Table 1 shows the XRD data of the [NH₂(CH₃)₂]₂ZnBr₄ crystal at 150 and 300 K; the atomic numbering and thermal ellipsoids for each atom are shown in Fig. 1. The Zn atom is coordinated by four Br atoms, forming a nearly regular tetrahedron of ZnBr₄. The hydrogen atoms of each formula unit form N–H⋯Br hydrogen bonds. Here, the length of N–H is 0.89 Å, and that of H⋯Br is in the range of 2.5–3.1 Å, which is consistent with previously reported results.^37,38 The detailed crystallographic parameters at 150 and 300 K are presented in the ESI.†

Table 1 Crystal data and structure refinement for [NH₂(CH₃)₂]₂ZnBr₄ at 150 and 300 K (the complete data are available in the CIF files)

Chemical formula	C4H16N2ZnBr4	C4H16N2ZnBr4
Weight	477.20	477.20
Crystal system	Monoclinic	Monoclinic
Space group	P21/n	P21/n
T (K)	150	300
a (Å)	8.6262 (3)	8.7140 (11)
b (Å)	11.9760 (4)	11.9709 (12)
c (Å)	13.6877 (5)	13.8563 (16)
β (°)	90.3690 (10)	90.513 (4)
Z	4	4
V (Å^3)	1414.01	1445.4
Radiation type	Mo-Kα	Mo-Kα
Wavelength (Å)	0.71073	0.71073
Reflections collected	26 223	31 613
Independent reflections	3503 (Rint = 0.0559)	3610 (Rint = 0.0576)
Goodness-of-fit on F^2	1.048	1.025
Final R indices [I > 2sigma(I)]	R1 = 0.0214, wR2 = 0.0455	R1 = 0.0312, wR2 = 0.0685
R indices (all data)	R1 = 0.0268, wR2 = 0.0471	R1 = 0.0444, wR2 = 0.0738

---

Fig. 1 Thermal ellipsoid plot (50% probability) for the [NH₂(CH₃)₂]₂ ZnBr₄ structure at 300 K.

DSC curves were obtained for the [NH₂(CH₃)₂]₂ZnBr₄ crystals at heating and cooling rates of 10 K min⁻¹. In terms of heating, three strong endothermic peaks are observed at 401, 436, and 459 K (Fig. 2). This result is consistent with the DSC data reported by Horiuchi et al.³⁹ The transition enthalpies (ΔH) obtained from the peak area for 401 and 436 K are 9.79 and 6.64 kJ mol⁻¹, respectively, whereas that for 459 K is 13.79 kJ mol⁻¹, which is determined using the same method. Furthermore, exothermic peaks attributed to cooling are observed at 313, 361, 386, and 421 K, and the resulting entropies are 0.74, 3.56, 2.21, and 13.07 kJ mol⁻¹, respectively. The phase transition during heating and cooling is irreversible.

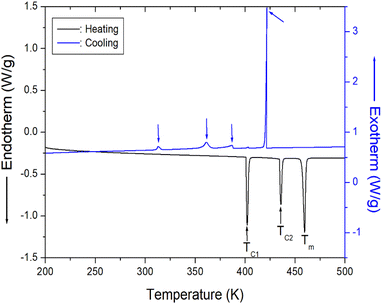Fig. 2 Differential scanning calorimetry curve of [NH₂(CH₃)₂]₂ZnBr₄ crystal measured at heating and cooling speed of 10 K min⁻¹.

To further interpret the three endothermic peaks, the powder XRD patterns of [NH₂(CH₃)₂]₂ZnBr₄ were measured at increasing temperatures. The results in the measuring range (2θ) of 5–60° are depicted in Fig. 3. The XRD powder patterns below 390 K (green) are slightly different from that recorded at 420 K (red); this difference is ascribed to T_C1 (401 K), exhibiting a clear change in structure.

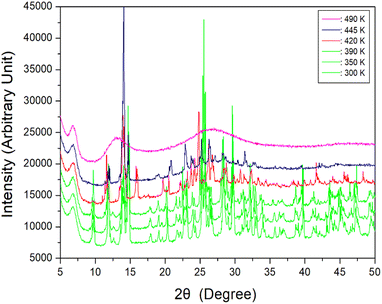Fig. 3 Powder X-ray diffraction patterns of [NH₂(CH₃)₂]₂ZnBr₄ at 300, 350, 390, 420, 445, and 490 K.

Furthermore, the XRD pattern recorded at 420 K is different from that recorded at 445 K, which is attributed to T_C2 (436 K). Finally, when the temperature is increased to 490 K, the powder pattern exhibits a completely different appearance, specifically, a non-crystalline form. The appearance of a single crystal is observed as a final check using an optical polarizing microscope. The crystal exhibits colourless transparency without significant change until the temperature is increased from 300 to 450 K. Finally, the surface of the single crystal begins to melt at approximately 460 K. The phase transition and melting temperatures shown in the powder XRD results are in reasonable agreement with the endothermic peaks in the DSC curves. From the DSC, XRD, and polarising microscopy experiments, the phase transition and melting temperatures are defined as T_C1 = 401 K, T_C2 = 436 K, and T_m = 459 K, respectively. Based on the results of DSC, single-crystal XRD, and powder XRD experiments, the structure does not change at 281, 340, and 377 K. Therefore, phase transitions apparently do not occur at the three previously reported temperatures. More comprehensively, the difference in this result is presumably attributed to measurements performed under heating rate of 5 and 10 K min⁻¹ during the DSC experiment. Moreover, a slight difference is considered to have occurred owing to the different basic reagents required for crystal growth.

3.2. Thermal properties

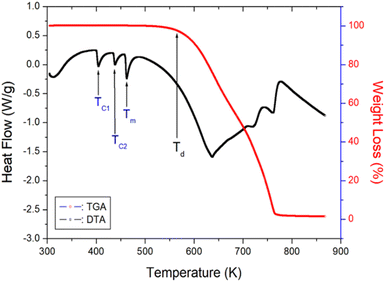
The TGA and DTA results obtained at a heating rate of 10 K min⁻¹ are shown in Fig. 4. As the temperature is increased, the molecular weight of the [NH₂(CH₃)₂]₂ZnBr₄ crystals remains almost constant up to 550 K. The initial molecular weight loss is 2% at 560 K, and this temperature is defined as the partial thermal decomposition temperature, T_d. The molecular weight decreases sharply in the temperature range from 600 to 750 K, with a corresponding weight loss of 80% near 750 K, which is attributed to organic decomposition. Approximately 98% of the residual molecular weight is lost. Furthermore, the three endothermic peaks at 401, 436, and 459 K, shown in the DSC curve, are confirmed in the DTA curve.

Fig. 4 Thermogravimetric analysis and differential thermal analysis curves of [NH₂(CH₃)₂]₂ZnBr₄.

3.3. ¹H and ¹³C NMR chemical shifts and spin-lattice relaxation times

The ¹H NMR chemical shifts according to temperature change are shown in Fig. 5, and the two ¹H signals attributed to NH₂ and CH₃ in the cation structure are expressed in different colours. At 300 K, the ¹H chemical shift for NH₂ was recorded at 7.84 ppm, and that for CH₃ was obtained at 2.93 ppm. The ¹H chemical shifts for CH₃ are nearly independent of temperature, whereas those for NH₂ move in a slightly negative direction with increasing temperature. The surrounding environment of ¹H in NH₂ continuously changes with temperature, without an abrupt change near the phase transition temperature T_C1.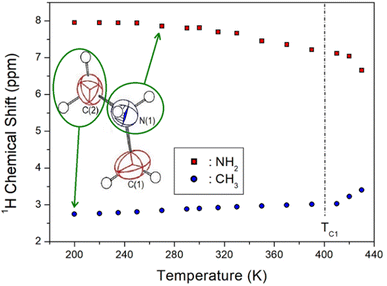

Fig. 5 ¹H nuclear magnetic resonance chemical shifts of NH₂ and CH₃ in [NH₂(CH₃)₂]₂ZnBr₄ based on the temperature change.

The ¹³C chemical shifts in the MAS NMR spectra of [NH₂(CH₃)₂]₂ZnBr₄ with increasing temperature are shown in Fig. 6. The ¹³C chemical shift for TMS as the standard reference at 300 K is recorded at 38.3 ppm, and this value is set to 0 ppm. Only the ¹³C resonance line is recorded as one type of ¹³C for the methyl carbons in the cation (inset of Fig. 6). The ¹³C chemical shifts change more rapidly with temperature that those of ¹H. At 300 K, the ¹³C chemical shift is recorded at 37.14 ppm, whereas that at 410 K above T_C1 is discontinuously shifted to 39.12 ppm. In addition, at 430 K, which is close to T_C2, the NMR spectrum is separated into two resonance lines, showing chemical shifts of 39.36 and 38.28 ppm. The spectra below and above the phase transition temperature T_C1 are depicted in blue and red, respectively. The chemical shifts of ¹³C close to ¹⁴N considerably change near T_C1, which implies that the environments surrounding ¹³C change. The full-width at half-maximum for ¹³C NMR spectra with respect to the temperature is shown in the inset of Fig. 6. The width of the resonance line is approximately 0.61 ppm at 300 K. As the temperature increases, the line width decreases rapidly, and that above T_C1 is broadened again. The line width decreases with increasing temperature owing to internal molecular motion.

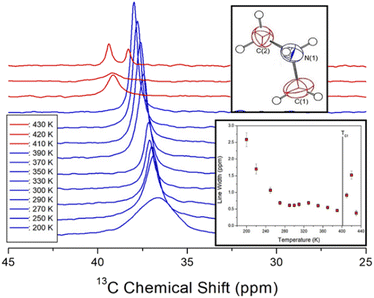Fig. 6 In situ ¹³C NMR spectra in [NH₂(CH₃)₂]₂ZnBr₄ for different temperatures (inset: change in line width for ¹³C in [NH₂(CH₃)₂]₂ZnBr₄ with changing temperature).

The ¹H and ¹³C MAS NMR spectra were measured by changing the delay time at each temperature, and the plots of changes in intensity versus delay time were expressed as single-exponential functions. As shown in eqn (1), the reciprocal of the slope of the graph can be characterised as the spin-lattice relaxation time T_1ρ.^42–44

I(τ) = I(0) exp(−τ/T_1ρ) (1)

where I(τ) and I(0) are the signal intensities of the protons and carbons at times τ and τ = 0, respectively. Decay curves for various delay times are measured, and their recovery traces exhibit different slopes at several temperatures. The ¹H T_1ρ values are determined using eqn (1) for NH₂ and CH₃, and the ¹H T_1ρ results as a function of 1000/temperature are shown in Fig. 7. The decay curves for carbon are also described by a single-exponential function to obtain ¹³C T_1ρ values. ¹H and ¹³C T_1ρ were measured with a spin-lock field of 73.53 kHz using the spin-locking pulse sequence method. From these results, the ¹³C T_1ρ values are obtained for methyl carbons as a function of 1000/temperature (Fig. 7).

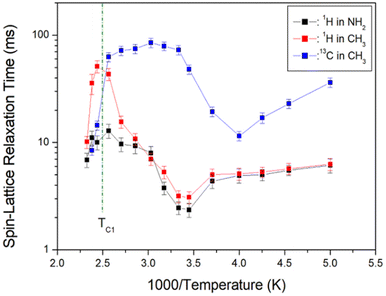Fig. 7 ¹H and ¹³C NMR spin-lattice relaxation times T_1ρ in [NH₂(CH₃)₂]₂ZnBr₄ as functions of inverse temperature.

The ¹H T_1ρ values are strongly dependent on the temperature change; ¹H T_1ρ of CH₃ above T_C1 exhibits longer values than that of NH₂. An abruptly short value is observed above T_C1, and energy transfer is facilitated with abruptly short T_1ρ values. ¹H T_1ρ values for NH₂ and CH₃ decrease slightly with increasing temperature and increase again above 290 K. Below T_C1, the ¹H T_1ρ values for CH₃ demonstrate a similar trend to that of the ¹H values for NH₂. In addition, the ¹³C T_1ρ values decrease with increasing temperature, similar to ¹H T_1ρ, and again increase above 250 K. At temperatures below T_C1, ¹³C T_1ρ values are approximately 10 times longer than ¹H T_1ρ. At temperatures below T_C1, the T_1ρ values of ¹H and ¹³C are minimum at 290 and 250 K, respectively, indicating molecular motion according to the Bloembergen–Purcell–Pound (BPP) theory. The T_1ρ minimum is related to the re-orientational motion of NH₂ and CH₃ ions. The experimental value of T_1ρ is expressed as the correlation time τ_C by the BPP theory, according to which T_1ρ for molecular motion is given by:^34,35

(1/T_1ρ) = C (γ_H²γ_C²ħ²/r⁶){4τ_C/[1 + ω₁²τ_C²] + τ_C/[1 + (ω_C − ω_H)²τ_C²] + 3τ_C/[1 + ω_C²τ_C²] + 6τ_C/[1 + (ω_C + ω_H)²τ_C²] + 6τ_C/[1 + ω_H²τ_C²]} (2)

where C is a constant; γ_H and γ_C are the gyromagnetic ratios for protons and carbon, respectively; r is the distance of the H–C internucleus; ω₁ is the spin-lock field; ω_C and ω_H are the Larmor frequencies for carbon and protons, respectively. The data were analysed assuming that T_1ρ was the minimum when ω_Cτ_C = 1, and the relationship between T_1ρ and ω₁ was applicable. As the T_1ρ curves have a minimum value, coefficient C can be obtained using eqn (2). Using C, τ_C is calculated as a function of temperature. The local field fluctuation, according to the BPP theory, is attributed to the thermal motion of protons and carbons, which are activated by thermal energy. 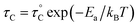The correlation time τ_C of a motion follows Arrhenius behaviour, , where 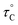is the pre-correlation time, E_a is the activation energy of the molecular motions, and k_B is the Boltzmann constant.³⁶ The activation energy E_a depends on the molecular dynamics. To determine the molecular dynamics, τ_C is plotted against 1000/T on a logarithmic scale as shown in Fig. 8. The obtained values of E_a are 37.19 ± 1.66 kJ mol⁻¹ for ¹H in NH₂, 31.87 ± 1.50 kJ mol⁻¹ for ¹H in CH₃, and 21.67 ± 3.82 kJ mol⁻¹ for ¹³C in CH₃.

Fig. 8 Activation energies with correlation times for ¹H and ¹³C in [NH₂(CH₃)₂]₂ZnBr₄ as functions of inverse temperature.

3.4. Static ¹⁴N resonance frequency

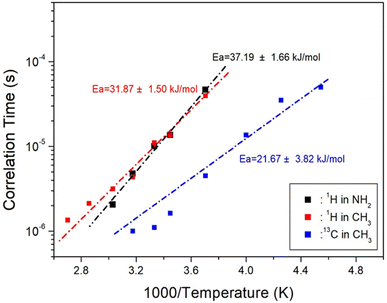
The static NMR spectra of ¹⁴N at the centre of the cation in the [NH₂(CH₃)₂]₂ZnBr₄ single crystal are shown in Fig. 9. Spectra in the temperature range of 200–420 K are obtained, and the direction of the applied magnetic field is measured with reference to the arbitrary direction of the single crystal. ¹⁴N has a spin number of 1,⁴⁴ and two resonance signals are expected from the quadrupole interaction. The ¹⁴N resonance frequency is extremely low at 28.90 MHz, and a resonance signal is not easily obtained by wiggling the baseline (inset of Fig. 9). Owing to the low intensity and the relatively broad line width, the signals are not easily distinguished. The resonance frequencies of the ¹⁴N NMR spectra are shown in Fig. 9 at several temperatures. Pairs for ¹⁴N are indicated by symbols of the same colour.

Fig. 9 Temperature dependence of ¹⁴N resonance frequency in the [NH₂(CH₃)₂]₂ZnBr₄ crystal (inset: in situ ¹⁴N NMR spectra of [NH₂(CH₃)₂]₂ZnBr₄ as a function of temperature).

The separation of two resonance lines increase slightly with increasing temperature. However, the ¹⁴N NMR spectra disappear at temperatures near T_C1 because of the re-orientational motion of ZnBr₄ tetrahedra and/or the thermal motion of the [NH₂(CH₃)₂]⁺ cations. The continuous variation in the ¹⁴N resonance frequency with changing temperature indicates a change in the coordination geometry of the environment around N.⁴⁵

4. Conclusions

The crystal structure, phase transition, thermal stability, and molecular dynamics of [NH₂(CH₃)₂]₂ZnBr₄ crystals were investigated using XRD, DSC, TGA, and NMR. T_C values obtained from the DSC and XRD results were only 401 and 436 K, respectively, and single-crystal XRD results indicated that no phase transition occurred between 150 and 300 K. The peak at 459 K, as observed in the DSC experiment, was confirmed to be the melting temperature. The thermal stability was considerably high, with a thermal decomposition temperature of ∼560 K. In the NMR spectra, changes were observed in the ¹H and ¹⁴N chemical shifts for NH₂ and in the ¹³C chemical shifts near T_C1, indicating changing structural environments. The environments of ¹H, ¹³C, and ¹⁴N located near NH₂ in the [NH₂(CH₃)₂]⁺ cation significantly influenced it, thus indicating a change in the N–H⋯Br hydrogen bond with the coordination geometry of the ZnBr₄ anion. The ¹H T_1ρ and ¹³C T_1ρ values decreased rapidly near T_C1, suggesting that energy transfer was facilitated. The increased variations in the ¹H NMR chemical shift and T_1ρ of NH₂ in the cation with changes in temperature relative to those of CH₃ caused the significant change in the N–H⋯Br hydrogen bonding between the Br around Zn and H of NH₂. These fundamental properties open efficient avenues for the development of organic–inorganic hybrids, thus qualifying them for practical applications.

Author contributions

A. R. Lim performed NMR and X-ray experiments, and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Basic Science Research Program of the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science, and Technology (2018R1D1A1B07041593 and 2016R1A6A1A03012069).

References

1. Y.-F. Gao, T. Zhang, W.-Y. Zhang, Q. Ye and F. Da-Wei, J. Mater. Chem. C, 2019, 7, 9840.
2. Z.-X. Yu, P.-P. Zhang, W.-Y. Shi, Q. Y. Zhang and D.-W. Fu, J. Phys. Chem. C, 2019, 123, 28385.
3. M. Mathlouthi, A. Valkonen, M. Rzaigui and W. Smirani, Phase Transitions, 2017, 90, 399.
4. X.-N. Hua, J.-X. Gao, T. Zhang, X.-G. Chen, D.-S. Sun, Y.-Z. Zhang and W.-Q. Liao, J. Phys. Chem. C, 2019, 123, 21161.
5. Z.-X. Wang, Y. Zhang, Y.-Y. Tang, P.-F. Li and R.-G. Xiong, J. Am. Chem. Soc., 2019, 141, 4372.
6. Z.-X. Wang, H. Zhang, F. Wang, H. Cheng, W.-H. He, Y.-H. Liu, X.-Q. Huang and P.-F. Li, J. Am. Chem. Soc., 2020, 142, 12857.
7. Y.-L. Zeng, X.-Q. Huang, C.-R. Huang, H. Zhang, F. Wang and Z.-X. Wang, Angew. Chem., Int. Ed., 2021, 60, 10730.
8. X.-G. Chen, X.-J. Song, Z.-X. Zhang, P.-F. Li, J.-Z. Ge, Y.-Y. Tang, J.-X. Gao, W.-Y. Zhang, D.-W. Fu, Y.-M. You and R.-G. Xiong, J. Am. Chem. Soc., 2020, 142, 1077.
9. M. Maczka, J. K. Zareba, A. Gagor, D. Stefanska, M. Ptak, K. Roleder, D. Kajewski, A. Soszynski, K. Fedoruk and A. Sieradzki, Chem. Mater., 2021, 33, 2331.
10. M. Maczka, M. Ptak, A. Gagor, D. Stefanska, J. K. Zareba and A. Sieradzki, Chem. Mater., 2020, 32, 1667.
11. K. Han, X. Ye, B. Li, Z. Wei, J. Wei, P. Wang and H. Cai, Inorg. Chem., 2022, 61, 11859.
12. H. Zhang, Y.-H. Tan, Y.-Z. Tang, X.-W. Fan, X.-L. Peng, R.-R. Han, Y.-K. Li and F.-X. Wang, Inorg. Chem., 2022, 61, 10454.
13. O. Knop, R. E. Wasylishen, M. A. White, T. S. Cameron and M. J. M. Van Oort, Can. J. Chem., 1990, 68, 412.
14. Q. Chen, N. D. Marco, Y. Yang, T.-B. Song, C.-C. Chen, H. Zhao, Z. Hong, H. Zhou and Y. Yang, Nano Today, 2015, 10, 5.
15. I. M. Hermes, S. A. Bretschneider, V. W. Bergmann, D. Klasen, J. Mars, W. Tremel, F. Laquai, H.-J. Butt, M. Mezger, R. Berger, B. J. Rodriguez and S. A. L. Weber, J. Phys. Chem., 2016, 120, 5724.
16. E. Strelcov, Q. Dong, T. Li, J. Chae, Y. Shao, Y. Deng, A. Gruverman and J. Huang, Sci. Adv., 2017, 3, e1602165.
17. S. K. Abdel-Aal, A. S. Abdel-Rahman, G. G. Kocher-Oberlehner, A. Ionov and R. Mozhchil, Acta Crystallogr., Sect. A: Found. Adv., 2017, 70, C1116.
18. Y. Liu, L. Collins, R. Proksch, S. Kim, B. R. Watson, B. Doughty, T. R. Calhoun, M. Ahmadi, A. V. Ievlev, S. Jesse, S. T. Retterer, A. Belianinov, K. Xiao, J. Huang, B. G. Sumpter, V. Kalinin, B. Hu and O. S. Ovchinnikova, Nat. Mater., 2018, 17, 1013.
19. S. Gonzalez-Carrero, R. E. Galian and J. Perez-Prieto, Part. Part. Syst. Charact., 2015, 32, 709.
20. B. Staskiewicz, O. Czupinski and Z. Czapla, J. Mol. Struct., 2014, 1074, 723.
21. B. Staskiewicz, I. Turowska-Tyrk, J. Baran, C. Gorecki and Z. Czapla, J. Phys. Chem. Solids, 2014, 75, 1305.
22. Z. Czapla, J. Przesławski, M. Crofton, J. Janczak, O. Czupinski, A. Ingram and M. Kostrzewa, Phase Transitions, 2017, 90, 637.
23. S. K. Abdel-Aal, G. Kocher-Oberlehner, A. Ionov and R. N. Mozhchil, Appl. Phys. A, 2017, 123, 531.
24. Y. Wei, P. Audebert, L. Galmiche, J. S. Lauret and E. Deleporte, Materials, 2014, 7, 4789.
25. S. Ahmad, C. Hanmandlu, P. K. Kanaujia and G. V. Prakash, Opt. Mater. Express, 2014, 4, 1313.
26. S. K. Abdel-Aal and A. S. Abdel-Rahman, J. Cryst. Growth, 2017, 457, 282.
27. G. Vlokh, V. B. Kapustyanyk, I. I. Polovinko, S. A. Sveleba, V. M. Varikash and Z. A. Bobrova, Appl. Spectrosc., 1990, 52, 527.
28. V. I. Torgashev, Yu. I. Yuzyuk, L. M. Rabkin, Yu. I. Durnev and Z. A. Bobrova, Phys. Status Solidi B, 1991, 168, 317.
29. I. I. Polovinko, S. A. Sveleba, V. Kapustianyk and V. S. Zhmurko, Phys. Status Solidi A, 1992, 131, 13.
30. V. B. Kapustianik, I. I. Polovinko, S. A. Sveleba, O. G. Vlokh, Z. A. Bobrova and V. M. Varikash, Phys. Status Solidi A, 1992, 133, 45.
31. V. Dzhala, V. Kapustianik, I. Kityk, I. Polovinko and S. Sveleba, Ferroelectrics, 1994, 152, 273.
32. V. B. Kapustianik, H. Kabelka, H. Warhanek and A. Fuith, Phys. Status Solidi A, 1996, 155, 95.
33. V. B. Kapustyanyk, Appl. Spectrosc., 1998, 65, 427.
34. N. H. Kim, J. H. Choi and A. R. Lim, Solid State Sci., 2014, 38, 103.
35. A. R. Lim and Y. Paik, Solid State Sci., 2017, 65, 61.
36. N. Mahfoudh, K. Karoui, M. Gargouri and A. BenRhaiem, Appl. Organomet. Chem., 2020, 34, e5404.
37. H. Ishihara, S.-q. Dou, K. Horiuchi, V. G. Krishnan, H. Paulus, H. Fuess and A. Weiss, Z. Naurforsch. A, 1996, 51, 1027.
38. N. Mahfoudh, K. Karoui, F. Jomni and A. B. Rhaiem, Appl. Organomet. Chem., 2020, 34, e5656.
39. K. Horiuchi, H. Ishihara and H. Terao, J. Phys.: Condens. Matter, 2000, 12, 4799.
40. N. Mahfoudh, K. Karoui and K. BenRhaiem, RSC Adv., 2021, 11, 24526.
41. M. Y. Choi, S. J. Lee, H. Ju and A. R. Lim, RSC Adv., 2022, 12, 20679.
42. A. R. Lim, Sci. Rep., 2020, 10, 20853.
43. A. Abragam, The Principles of Nuclear Magnetism, Oxford Univ. Press, 1961.
44. J. L. Koenig, Spectroscopy of Polymers, Elsevier, New York, 1999.
45. S. H. Kim and A. R. Lim, Solid State Sci., 2022, 131, 106927.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra06697a

---