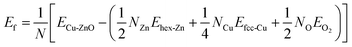Experimental and ab initio studies on the structural, magnetic, photocatalytic, and antibacterial properties of Cu-doped ZnO nanoparticles

Abstract

Copper-doped ZnO nanoparticles with a dopant concentration varying from 1–7 mol% were synthesized and their structural, magnetic, and photocatalytic properties were studied using XRD, TEM, SQUID magnetometry, EPR, UV-vis spectroscopy, and first-principles methods within the framework of density functional theory (DFT). Structural analysis indicated highly crystalline Cu-doped ZnO nanoparticles with a hexagonal wurtzite structure, irrespective of the dopant concentration. EDX and EPR studies indicated the incorporation of doped Cu²⁺ ions in the host ZnO lattice. The photocatalytic activities of the Cu-doped ZnO nanoparticles investigated through the degradation of methylene blue demonstrated an enhancement in photocatalytic activity as the degradation rate changed from 9.89 × 10⁻⁴ M min⁻¹ to 4.98 × 10⁻² M min⁻¹. By the first-principles method, our results indicated that the Cu(3d) orbital was strongly hybridized with the O(2p) state below the valence band maximum (VBM) due to covalent bonding, and the ground states of the Cu-doped ZnO is favorable for the ferromagnetic state by the asymmetry of majority and minority states due to the presence of unpaired electron.

---

1 Introduction

ZnO is definitely one of the most interesting oxides for industrial applications.^1,2 It is used for instance as an additive in rubbers, plastics, glass, cement, paints, adhesives, sealants, pigments, food, batteries, ceramics, and fire retardants, just to name a few. It is also extensively used in sensors to monitor or to trap, for instance the presence of H₂S.³ As a transparent semiconductor with a wide band gap of 3.37 eV,⁴ ZnO is also utilized in transparent electrodes and liquid crystal displays, energy-saving or heat-protecting windows.^5,6 Zinc oxide, especially on a nanometric scale, is cost-effective and environmentally friendly with potentially high photocatalytic properties.^7,8 It has been shown that the photocatalytic activity of ZnO strongly depends on the size and morphology of the nanoparticles. For instance, Yao Guo et al. have shown that tetrapods can exhibit degradation of dyes five times better than spherical nanoparticles.⁸ Yet, its broader bandgap compared to TiO₂ makes ZnO less appealing for photocatalytic applications.^9–12 To circumvent this problem, researchers have doped ZnO with different metals such as Cr, Sm, Co, Cu, or Ag to improve the photocatalytic activity.^13,14 Among the promising dopants, Cu is preferred due to its advanced attributes such as low toxicity and abundance. Its band gap (3.37 eV) can indeed be tuned by Cu⁺ and/or Cu²⁺ substitutions.¹⁵

Doping with Cu not only enhances the photocatalytic properties of ZnO nanoparticles by lowering its band gap¹⁶ but also affects the magnetic properties of the nanoparticles by combining electronic charges with spins.¹⁷

The origin of ferromagnetism (FM) in Cu-doped ZnO is unclear. A mechanism, such as a double exchange or super-exchange interaction has been proposed. Ali et al. indicated that the carriers are highly localized at intrinsic defect sites in Cu-doped ZnO. They concluded that the Rudermann–Kittel–Kausya–Yosida (RKKY) model for ferromagnetism is not the origin of ferromagnetism in Cu-doped ZnO.¹⁸ However, Nayek et al. have shown that the origin of magnetic ordering for ferromagnetism in Cu-doped ZnO follows the indirect exchange mechanism of the RKKY model.¹⁹ Wang et al. have experimentally shown that the Cu ions can enhance the long-range ferromagnetic ordering at an ultralow concentration via the indirect double exchange mechanism, but antiferromagnetic “Cu⁺–V₀–Cu²⁺” coupling may also be generated, as a super-exchange mechanism, even at a very low Cu-doping concentration.²⁰

One of the key objectives of this work was to determine quantitively the amount of Cu inserted into the ZnO host matrix. Some researchers have noticed that the hexacoordinated ionic radius of Cu²⁺ (0.73 Å) is slightly smaller than the one of Zn²⁺ (0.74 Å), they have argued that this could solve the determination of the copper content by scrutinizing its effect on the lattice parameters that should decrease upon doping with Cu.^21,22 Note here that Zn in wurtzite is fourfold coordinated so that ionic radii should be taken as 0.6 Å for Zn and 0.57 Å for copper, thus provoking an even stronger effect. Yet a rapid survey of the literature clearly contradicts this statement. For instance, Ma et al.²³ showed that copper favors an increase in the lattice parameters going from a = 3.249 Å and c = 5.206 Å for pure ZnO to a = 3.272 Å, c = 5.284 Å for x = 0.0417 in Zn_1−xCu_xO. A similar effect was found in the study by M. Mukhtar et al.²⁴ who used EDX to monitor the content of Cu in their samples using the K-alpha lines of copper and zinc. On the opposite, S. Singhal et al.²⁵ evidenced that the a and c lattice parameters decrease for x varying from 0 to 0.15 (a = 3.248 Å, c = 5.023 Å at x = 0.15). Of course, at low concentrations, EDX is not very quantitative, and it is therefore important to probe in a quantitative manner the content of copper by a more reliable technique.

Techniques such as XPS and XANES at synchrotron facilities are of great interest but XPS probes only the surface, while XANES generally needs the use of a synchrotron. Among the reliable ways to determine copper content at laboratory facilities, the value of x for copper in Zn_1−xCu_xO can be legitimately determined using EPR based on the paramagnetic behavior of Cu²⁺ ions.

We used EPR to detect the amount of the doped Cu and investigated the relationship between the doping amount and the photocatalytic performance for Cu-doped ZnO. We also attempted to gain insight into the correlation between the electronic structure and magnetic properties of the copper-doped ZnO nanoparticles, experimentally, using XRD and SQUID magnetometry as well as the first principle method based on the density functional theory.

2 Materials and methods

2.1 Synthesis of Cu-doped ZnO nanoparticles

Zinc(II) acetate ((CH₃CO₂)₂Zn), copper(II) acetate (Cu (CO₂CH₃)₂), and benzyl alcohol (C₆H₅CH₂OH) were purchased from Sigma Aldrich and used without further purification.

Cu-doped ZnO nanoparticles were obtained using the solvothermal synthesis of the 5.45 mmol of zinc acetate, X equivalent (X = 1, 3, 5, and 7 mol%) of copper acetate in 83.22 mmol of benzyl alcohol. The reaction mixture was inserted into a Teflon cup with an internal volume of 23 mL. Then, the cup was slipped into a steel autoclave, which was placed into an oven at 210 °C for 24 h. The resulting suspension was separated from its stock solution by centrifugation for 15 min at 15 000 rpm. The precipitates were washed with ethanol several times and then dried at 60 °C. In the end, a gray powder was obtained.

2.2 Characterization techniques and equipment

X-ray diffraction experiments were carried out using an Empyrean diffractometer (Panalytical) equipped with a copper anode. The CuKα radiation was selected by a monochromator and the measurements were carried out at room temperature using an accelerating voltage and a current of 40 kV and 30 mA, respectively. We used the standard formula for the hexagonal crystal system²⁶ to obtain the lattice constants a and c from X-ray measurements. The TEM study (SAED and HRTEM) was performed using a JEOL 2010 electron microscope, operating at 200 kV. EPR measurements were performed at a 9.4 GHz frequency using an X-band Bruker EMX spectrometer equipped with a continuous nitrogen flow cryostat. The spectrometer was operated at a modulation frequency of 100 kHz and a microwave power of 20 mW. The studied sample was sealed directly into glass tubes (with a mass of approximately 10 mg). The concentration of the paramagnetic species was evaluated based on the use of a reference sample of CuSO₄ × 5H₂O with calibrated content of the unpaired spins from Cu²⁺. Magnetic properties were measured using the SQUID S700× magnetometer from 5 K to 300 K. The UV-vis absorption spectra were recorded using a UV-vis spectrometer (Agilent technologies Carry 60) with a 150 W Xe light source.

2.3 Photocatalytic activity of Cu-doped ZnO nanoparticles

In a typical process, 20 mL of 6.5 μM methylene blue (MB) solution was used as a contamination test with a 150 W Xe light source. First, the initial absorbance of the dye was measured, and then 10 mg of nanoparticle was added to the dye solution. Then, the reaction mixture was continuously stirred for 30 minutes in the dark to measure the absorption–desorption balance of the catalyst and MB solution. After the irradiation period, the nanoparticles were precipitated by centrifugation and 1.5 mL of the dye solution was placed in a cuvette to measure the spectrum of the dye. This method was used for each spectrum. To study the photodegradation of the dye, the reaction mixture vessel was placed under the light source. The absorption spectrum was measured every 10 minutes.

2.4 Antibacterial activity of undoped and Cu-doped ZnO nanoparticles

Gram-negative Escherichia coli (E. coli), Gram-positive Staphylococcus aureus (S. aureus), Mueller–Hinton broth (Difco), nutrient broth (Difco), nutrient agar (Sigma Aldrich), sodium chloride (Sigma Aldrich), and deionized water were used without further purification. All Petri dishes, solutions, and media were sterilized in an autoclave at 121 °C for 90 min before the experiments. The Mueller–Hinton broth dilution method was used to examine the antibacterial activity of ZnO nanoparticles across Gram-negative and Gram-strains of the positive bacteria. 100 mg of nanoparticles were weighed and dispersed in sterilized water and diluted with saline water. Nutrient broth and nutrient agar were used as the sources of culture. The bacterial cell density was estimated by optical density at 600 nm (OD₆₀₀) wavelength. The liquid cultures having OD value 0.1 for E. coli corresponded to a bacterial concentration of 1 × 10⁸ CFU mL⁻¹ and 0.08 for S. aureus (3.7 × 10⁷ CFU mL⁻¹) in liquid cultures. Equivalent concentrated bacteria solutions were poured into glass tubes containing 2 mL of the medium. Negative and positive control-labeled tubes contained only inoculated broth. The other tubes contained solutions of undoped and Cu-doped ZnO nanoparticles. All the tubes were then incubated at 37 °C for 24 h. After incubation, the tubes were checked for the visible growth (turbidity) of bacteria. The labeled tubes were containing 2 × 10⁻⁷ g μL⁻¹ of nanoparticles except for the positive control. Each control and all tubes were diluted with saline water, then dropped and spread onto the NA Petri dish. After 24 h of incubation, the antibacterial activities of the as-synthesized nanoparticles were determined by counting the number of viable (visible) bacteria colonies and expressed as a percentage.

2.5 Computational details

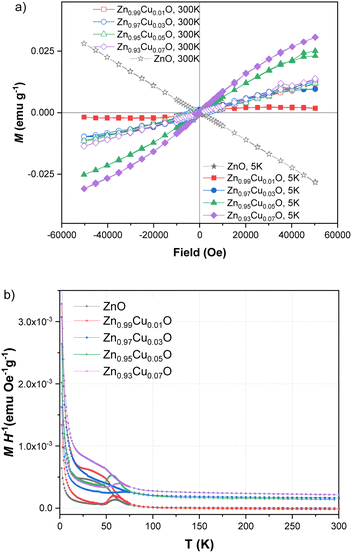
We carried out the spin-polarized density functional calculations based on the plane wave (PW) and projector augmented wave (PAW) methods²⁷ using the generalized gradient approximation (GGA) by Perdew and Wang (PBE),²⁸ as implemented in the QUANTUM ESPRESSO package^29–31 within the framework of DFT.^32,33 The following electronic states are treated as valence: Cu(3d¹⁰4s¹), Zn(3d¹⁰4s²) and O(2s²2p⁴) for atoms. The interactions between the ions and valence electrons were expressed as the pseudopotential created by Dal Corso.³⁴ The wave functions and the charge densities are expressed as plane waves up to a kinetic energy cutoff of 60 and 300 Ry, respectively. We performed calculations on the hexagonal wurtzite ZnO unit cell and ZnO (3 × 3 × 2) supercell, including the 36 Zn and 36 O atoms. The summation of the charge densities for the hexagonal ZnO unit cell and ZnO supercell was performed using the special k-points generated by the 8 × 8 × 6 and 4 × 4 × 4 Monkhorst–Pack meshes, respectively.³⁵ We used the tetrahedral method³⁶ to evaluate the electronic density of the state (DOS). For the self-consistent field (SCF) iterations, the total energy convergence was 10⁻⁵ eV. The occupation numbers of electrons are expressed as a Gaussian distribution function with an electronic temperature of kT = 0.02 Ry. To express the strongly correlated effect of electrons in the Cu(3d) and Zn(3d) states, we chose U = 3.5 and 8.5 eV, respectively, using the simplified rotational-invariant formulation based on the linear response method.^37,38 The numerical error in the magnetic energy gain was 3 meV. The ionic positions were relaxed at the fixed lattice parameters until the residual forces were less than 0.05 eV Å⁻¹.

The formation energy of the Cu-doped bulk ZnO system was determined as:

where E_Cu-ZnO, E_hex-Zn, E_fcc-Cu and E_O2 are the ground state energies of Cu-doped bulk ZnO, hexagonal bulk Zn, fcc bulk Cu and oxygen molecule, respectively. HereN is the number of the total atoms and N_Zn, N_Cu and N_O are the numbers of Zn, Cu and O atoms, respectively.

3 Results and discussion

3.1 Synthesis and structural analysis

Solvothermal synthesis of ZnO nanoparticles using different types of precursor reaction conditions is well documented.^39,40 However, when doped with a copper precursor, the reaction mechanism is complicated. Copper-doped ZnO nanoparticles were synthesized following the nonhydrolytic organic phase method, as previously reported,⁴¹ but with a modification. In this work, ZnO nanoparticles doped with copper at concentrations ranging from 1–7 mol% were obtained by adding copper acetate to the reaction medium of zinc acetate in benzyl alcohol before heating at 210 °C. During the reaction, the formation of Cu-doped ZnO nanoparticles occurred simultaneously with the reduction reaction of the copper precursor with benzyl alcohol. As a representative example shown in Fig. 1A(a–c), the XRD profiles of 7 mol% Cu-doped ZnO nanoparticles were compared with undoped ZnO nanoparticles. The relative intensity and peak positions of the doped and undoped ZnO nanoparticles match well with the hexagonal wurtzite structure with the space group of P6₃mc (#186), (a = 3.249 Å, c = 5.206 Å) of ZnO (JCPDS 36-1451).

Fig. 1 (A) XRD patterns of undoped ZnO (a), Zn_0.93Cu_0.07O nanoparticles before wash (b); and after wash (c), Zn_0.95Cu_0.05O nanoparticles (d), Zn_0.97Cu_0.03O nanoparticles (e) and Zn_0.99Cu_0.01 nanoparticles (f). (B) magnified pattern of undoped ZnO (a), Zn_0.99Cu_0.01 nanoparticles (b), Zn_0.97Cu_0.03O nanoparticles (c), Zn_0.95Cu_0.05O nanoparticles (d) and Zn_0.93Cu_0.07O nanoparticles (e).

However, irrespective of the doping concentration, there are additional peaks at 43.35° and 40.49° for the Cu-doped ZnO nanoparticles, corresponding to 111 and 200 peaks of elemental copper (JCPDS 04-0836) as a secondary phase. This impurity phase was formed from the side reduction reaction of copper acetate with benzyl alcohol, which is a well-known reducing agent for some metals.⁴² On the other hand, it also highlighted the low solubility of copper in ZnO. The impurity elemental copper was completely removed by washing the as-synthesized nanoparticles with a 10% ammonia solution to generate the copper ammonia complex.

As shown in Fig. 1A(c–f), the disappearance of the peaks at 43.35° and 40.49° corresponding to the copper phase for the Cu-doped ZnO nanoparticles confirmed that we successfully removed the secondary phase. These washed samples were used for further studies. The lattice parameters calculated from the 100 and 002 Bragg peaks of the XRD patterns are shown in Table 1. With the increase in the dopant concentration, the diffraction peaks shift to lower angles (higher d value) and the broadening of the diffraction peaks was also observed in comparison to ZnO nanoparticles. This suggested internal strain due to the difference in the ionic radii of Cu and Zn ions. This is the signature, that dopant ions were incorporated into the lattice in agreement with previous reports.²⁴

Table 1 Lattice parameters of ZnO and Cu-doped ZnO nanoparticles

Sample	2θ	FWHM	d	a = b (Å)	c/a
ZnO	31.74	0.2327	2.817	3.254	1.601
	34.39	0.2277	2.606
Zn0.99Cu0.01O	31.69	0.2813	2.821	3.257	1.601
	34.35	0.2764	2.609
Zn0.97Cu0.03O	31.58	0.2826	2.830	3.268	1.601
	34.23	0.278	2.617
Zn0.95Cu0.05O	31.56	0.3102	2.832	3.271	1.601
	34.21	0.2986	2.619
Zn0.93Cu0.07O	31.57	0.2825	2.831	3.269	1.601
	34.23	0.278	2.617

---

Copper doping was also confirmed by EDS elemental mapping analysis. Fig. 2 shows TEM images of the undoped ZnO and 3 mol% Cu-doped ZnO nanoparticles with the electron diffraction pattern in the inset and HR-STEM images. This indicates that the Cu dopant was evenly distributed within the particles and the polydispersed morphology of the synthesized nanoparticles with a particle size of about 60–70 nm. The atomic planes 100, 002, and 101 were identified from scattering images of the electron diffraction patterns. These results are consistent with the measurements made using X-ray diffraction.

Fig. 2 HR-STEM images of undoped ZnO (a) and Zn_0.97Cu_0.03O nanoparticles (b). The inset shows diffraction pattern (A), HAADF image (B), and elemental mapping (C–E) of the ZnO and Zn_0.97Cu_0.03O nanoparticles, respectively.

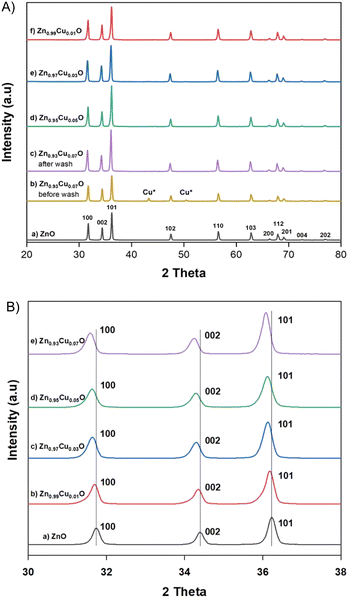
EPR spectroscopy was used to detect the unpaired electrons localized on defined paramagnetic species (atoms, molecules), which are intrinsically present in the material or introduced by chemical doping, or under high energy irradiation.

The high sensitivity of the technique allows the detection and evaluation of concentrations as low as 10⁻⁸ moles. In Fig. 3, the recorded EPR spectra of Cu-doped ZnO nanoparticles at room temperature (300 K) and low temperature (140 K) are shown to improve the resolution of the signal details. Excluding the small signal from a reference sample with a g-factor at 2.0023, the typical EPR spectrum of ZnO nanoparticles is composed of three contributions associated with characteristic spectral parameters, namely, the Landé factor (g), which is indicative of the nature of the involved paramagnetic species. The line at a g-factor of 1.989 is associated with surface defects related to the charged oxygen vacancies. Such defects are reported in nanostructured ZnO with a high specific surface.⁴³ The second EPR signal with the g-factor at 1.96 was frequently reported in the ZnO structure. Its origin consists of intrinsic defects such as oxygen vacancies and interstitial zinc with the features of shallow donors.⁴⁴

Fig. 3 EPR spectra of undoped ZnO and 1–7 mol% Cu-doped ZnO nanoparticles.

The third EPR contribution occurs from the doping Cu²⁺ ions and gives rise to an anisotropic signal with the main components of the g-tensor g_x = 2.10 ± 0.005, g_y = 2.05 ± 0.005 and g_z = 2.34 ± 0.01. The hyperfine coupling constants were evaluated as A_x(MHz) = 69 ± 10, A_y(MHz) = 38 ± 10, and A_z(MHz) = 133 ± 10.

The large uncertainty range for both the Landé g-tensor and hyperfine A-tensor was induced by the broad resonance lines and the hyperfine coupling was difficult to extract from the line broadening. Anyway, the anisotropy of the Cu²⁺ EPR spectrum was clearly involved and then indicated the incorporation of Cu²⁺ doping ions into the host ZnO lattice. Comparing the EPR spectra as a function of the Cu doping concentration (Fig. 3), we may underline the correlation between the increase of the Cu doping ratio and the decrease of the intrinsic defects involved with the ZnO lattice in both bulk and surface as well (V₀, Zn_i).

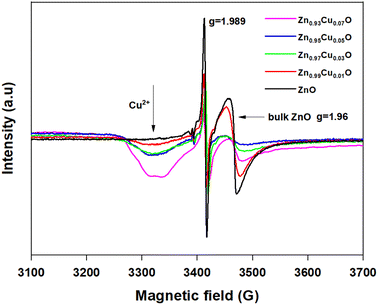
As also reported in previous work on copper-doped metal oxides, the incorporation and stabilization of Cu²⁺ ions in the host lattice acts on the electronic active defects notably the oxygen vacancies.⁴⁵ For doped samples, the real content of Cu²⁺ ions incorporated in the lattice can be estimated from the EPR signal. Indeed, by using a reference sample as copper sulfate pentahydrate CuSO₄ × 5H₂O, the copper ion Cu²⁺ with an electronic spin s = 1/2 gave rise to an EPR signal with a double integrated intensity proportional to the concentration of Cu²⁺. Simple estimation of the content of Cu²⁺ ions in one gram of CuSO₄ × 5H₂O leads to N_Cu = 2.4 × 10²¹ spin per g. Therefore, by using a suitable normalization of the EPR signals of the reference sample and the Cu-doped ZnO, the content of Cu ions in ZnO samples can be quantitatively evaluated. It is worth noting that the normalization of the EPR spectra was performed taking into account the amplification of the EPR signal, the microwave power, and the mass of the used samples. Thus, the comparative double-integrated intensity of the EPR signals leads to the Cu contents in ZnO samples, as summarized in Table 2. Cu²⁺ concentrations were found to vary from 2.09 × 10¹⁶ up to 16.29 × 10¹⁶ ions per gram with an increase in doping from 1–7 mol%. The correlation is clearly shown between the doping concentration and the content of paramagnetic Cu²⁺ ions inferred from their unpaired spin concentrations. This result confirms the incorporation of Cu²⁺ and their good dispersion within the ZnO lattice. From the evolution of the EPR signals at g = 1.96 related to the oxygen vacancies or interstitial Zn, we noticed a drastic reduction in the concentration of such bulk defects. This effect is less important for the surface defect, which showed a limited reduction of the integrated intensity with increased concentrations of Cu²⁺ doping. As stated and also from the anisotropy of the g-tensor of Cu²⁺, such behavior suggests the preferential incorporation of the doping ions into the crystalline sites preferentially within the bulk instead of locating on the surfaces of the nanoparticles. Magnetic properties of the Cu-doped ZnO nanoparticles measured using a SQUID magnetometer show how the Cu concentration changes the magnetic behaviour. Magnetizations versus field curves for the different Cu concentrations of the synthesized nanoparticles are shown in Fig. 4(a). The undoped ZnO nanoparticles clearly show the diamagnetic behaviour of a linear curve with a negative slope at room temperature, as does bulk ZnO, in good agreement with previous reports.⁹ For Cu-doped ZnO nanoparticles, diamagnetic background due to the undoped ZnO nanoparticles were subtracted to clarify the magnetic contribution of the doped copper. As shown in Fig. 4(a), the ZnO nanoparticles doped with Cu showed closed hysteresis with unsaturated magnetization at both 300 K and 5 K, suggesting the absence of ferromagnetic domains. It can be seen from the temperature-dependent magnetization, Fig. 4(b), a bifurcation between FC and ZFC and a cusp at ZFC was observed at temperatures below 75 K for all the samples. This result, together with non-hysteresis magnetization confirmed a magnetically-disordered or spin glass state for the Cu-doped ZnO nanoparticles. This result, together with the non-hysteresis magnetization confirmed the magnetically-disordered or spin glass state for the Cu-doped ZnO nanoparticles. An increase in the magnetization with the increase in Cu doping concentration indicates that Cu²⁺ ions enhance the magnetic properties of the Cu-doped ZnO nanoparticles. It indeed shows that Cu atoms could strongly affect the magnetic properties of the Cu-doped ZnO nanoparticles.

Table 2 Spin concentration of copper ions in the 1–7 mol% Cu doped ZnO nanoparticles

Sample	Intensity arb. units	Spin per g
Zn0.99Cu0.01O	0.14 × 10^6	2.09 × 10^16
Zn0.97Cu0.03O	0.32 × 10^6	4.78 × 10^16
Zn0.95Cu0.05O	0.48 × 10^6	7.17 × 10^16
Zn0.93Cu0.07O	1.09 × 10^6	16.29 × 10^16

---

Fig. 4 Field-dependent magnetization curves of undoped ZnO and ZnO nanoparticles doped with various concentrations of Cu from 1–7 mol% at 5 K and 300 K (a). Zero field-cooled and field-cooled magnetization curves of undoped ZnO and ZnO nanoparticles doped with various concentrations of Cu from 1–7 mol% (b).

3.2 Photocatalytic activity

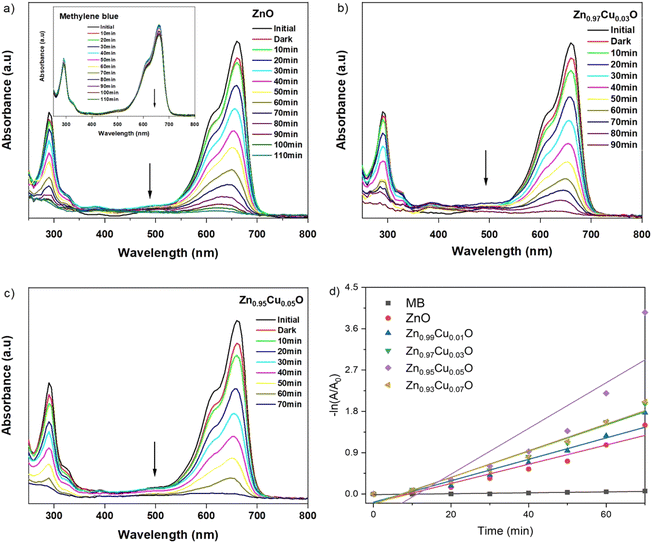
UV-vis spectroscopy was used to characterize the optical absorption properties of the undoped and Cu-doped ZnO nanoparticles. Absorption spectra of ZnO and Cu-doped ZnO nanoparticles are shown in Fig. 5. As shown, the characteristic absorption peak of ZnO nanoparticles was observed to be shifted to the red side of the spectrum upon the addition of Cu. This indicates the narrowing of the band gap between valence and conduction levels of ZnO due to the appearance of the intermediate energy level of copper between them. The band gap energy of the as-synthesized nanoparticles was obtained from the absorption spectra and for undoped ZnO nanoparticles, it was found to be 3.32 eV, which is characteristic of the wurtzite structure of ZnO. With the increasing concentration of Cu, the band gap energy was reduced continuously and the lowest value was found to be 3.28 eV for ZnO nanoparticles doped with 5 mol% of copper. In order to compare the catalytic activity of the as-synthesized nanoparticles, the exposure time-dependent absorption spectra of MB were recorded in the absence and presence of nanoparticles (Fig. 6). The inset in Fig. 6(a) shows UV-vis absorption spectra in the range of 250 to 800 nm of MB for 110 min without nanoparticles. Spectra clearly showed that no significant change was observed in the absorbance of the characteristic peak of MB dye at around 670 nm, which indicated that a photo-induced degradation process did not occur. In comparison, the existence of the ZnO nanoparticles significantly enhanced the degradation rate of MB dye, and the characteristic peak in the absorption spectra completely disappeared within 110 minutes. Time-dependent absorption spectra of MB dye in the presence of undoped and doped ZnO with 3 mol% and 5 mol% of Cu concentrations are shown in Fig. 6(a)–(c), respectively. The rate of the MB degradation process was determined from the absorption spectra by using first-order reaction kinetics and the data are summarized in Table 3. These results revealed that Cu doping increases the efficiency of photocatalytic degradation compared with that of undoped samples. For all concentrations studied in this work, the optimal doping concentration for the maximum degradation of MB was 5 mol%. In the range of 1–5 mol% doping concentration, interstitial Cu atoms may decrease the band gap energy leading to enhancement of the photocatalytic activity of ZnO NPs. But at 7 mol%, the number of substitutional Cu atoms began to dominate over the interstitials and caused the band gap energy to increase back slightly. Also, the substitutional Cu atoms may play the main role in the recombination of electrons and holes due to the shortening of the distance between neighbor Cu sites at the highest concentration. Therefore, we concluded that these factors might be the reasons that lead to a decrease in photocatalytic activity at 7 mol% doping. During the exposure, pairs of electron (e⁻) holes (h⁺) were generated on the surface of the zinc oxide. Molecules of dissolved oxygen (O₂) react with electrons (e⁻) to generate hydroxyl radicals (˙OH) and superoxide radical anions (O₂˙⁻). Thus, holes and other radicals effectively decompose dyes.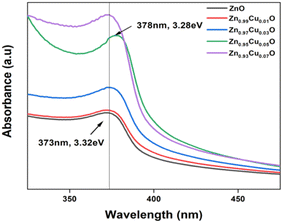

Fig. 5 UV-vis absorption spectra of undoped ZnO and ZnO nanoparticles with a varying dopant concentrations of Cu from 1–7 mol%.

Fig. 6 Time-dependent UV-vis absorption spectra for the degradation of MB dye (inset) in the presence of undoped ZnO (a), 3 mol% Cu-doped (b), and 5 mol% Cu-doped ZnO nanoparticles (c). Kinetic study of the degradation of MB in the presence of undoped ZnO and ZnO nanoparticles doped with various concentrations of Cu from 1–7 mol% (d).

Table 3 Reaction rate comparisons of the undoped ZnO and 1–7 mol% Cu-doped ZnO nanoparticles with MB

Sample	Rate (M min^−1)
MB	9.89 × 10^−4
ZnO	2.09 × 10^−2
Zn0.99Cu0.01O	2.33 × 10^−2
Zn0.97Cu0.03O	2.85 × 10^−2
Zn0.95Cu0.05O	4.98 × 10^−2
Zn0.93Cu0.07O	2.9 × 10^−2

---

3.3 Antibacterial activity

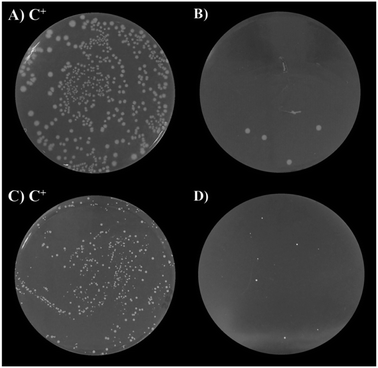
The antibacterial activity of undoped and Cu-doped ZnO nanoparticles was tested with two kinds of pathogenic bacteria, including Gram-positive and Gram-negative types. As shown in Fig. 7, after the incubation, 91.3–98.9% of E. Coli colony and 67.2–97.4% of the S. Aureus colony were inhibited by ZnO and Cu-doped ZnO nanoparticles (Fig. S1 and S2†). This clearly shows that both bacteria colonies were inhibited by the as-synthesized nanoparticles. Table 4 shows the viable colony number comparison between E. Coli and S. Aureus after the incubation. The bactericidal growth property was found to be dopant concentration-dependent and ZnO nanoparticles with 7 mol% Cu dopants showed the maximum inhibition against bacterial growth. Upon increasing the dopant concentration, the antibacterial activity was also increased. It is clear that doping of Cu in ZnO nanoparticles enhances the antibacterial activity of ZnO nanoparticles. Several mechanisms have been developed to explain the antibacterial activity of ZnO nanoparticles but the mechanism is not obviously recognized, such as the release of Zn²⁺ ions, reactive oxygen species (ROS),⁴⁶ and electrostatic interactions.⁴⁷ Padmavathy et al. have shown that the release of ROS from the transfer of electrons from VB to CB of ZnO nanoparticles causes oxidative stress by preventing bacterial growth leading to cell death. Based on the experiments, Heinlaan et al. have concluded that the direct contact area between the bacterial cell and nanoparticles where the cell membrane is damaged or disorganized could be a more significant factor.⁴⁸ Accordingly, the bacterial killing capacity is increased with increasing doping concentration and in this case, 7 mol% Cu-doped ZnO nanoparticles showed maximum prevention because Cu-doped ZnO nanoparticles released more ROS. Also, nanoparticles have the ability to adhere to the cell wall of both Gram-negative and Gram-positive bacteria, thereby causing their destruction and cell death.

Fig. 7 Antibacterial activity of Cu-doped ZnO nanoparticles. Positive control of E. coli (A), 7 mol% Cu-doped ZnO against E. coli (B), positive control of S. aureus (C), and 7 mol% Cu-doped ZnO against S. aureus (D), respectively.

Table 4 Antibacterial activity of the undoped and Cu-doped ZnO nanoparticles

Sample	Antibacterial activity (%)
	E. coli	S. Aureus
ZnO	91.3	67.2
Zn0.99Cu0.01O	94.8	71.2
Zn0.97Cu0.03O	95.1	93.4
Zn0.95Cu0.05O	98.1	94.4
Zn0.93Cu0.07O	98.9	97.4

---

3.4 The results of Ab initio calculation

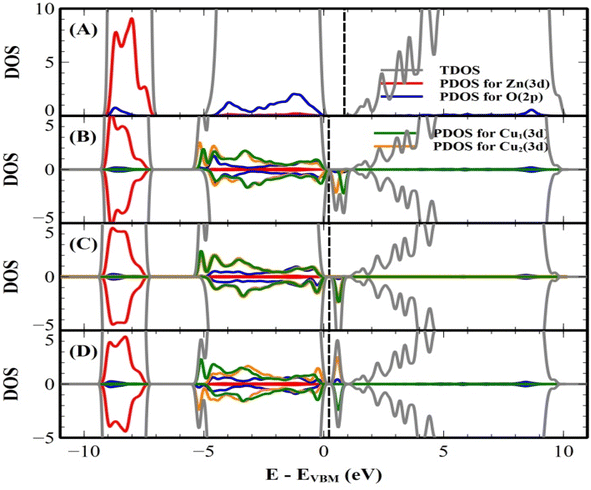
We first predict the lattice parameters, formation energy, and band gap of the undoped (pure) bulk ZnO crystal using both the PAW and PW methods. The main results of undoped and 1–7 mol% Cu-doped ZnO crystals are shown in Table 5. Our predicted lattice parameter a and the ratio of c/a are found to be 3.287 Å (3.291 Å) and 1.611 (1.600) by the PAW (PW) method, respectively. These results agree with the experimental values of the crystal structure, in which the error of the lattice parameter a are 1.01% and 1.14%, by the PAW and PW methods, respectively (see Table 1). The formation energies are found to be −7.0551 and −7.0595 eV per atom, by the PAW and PW methods, respectively. For the PAW method, the total and projected density of states (DOS) of the PAW method are shown in Fig. 9(A). The DOS of the PW method is similar to that of the PAW method. The band gap of undoped bulk ZnO crystal was found to be 1.72 and 1.74 eV using the PAW and PW methods, respectively. These values are lower than our experimental value of 3.32 eV. However, this value agrees with the other theoretical predicted values of the bulk ZnO crystal.^38,49 When we consider the Cu doping into bulk ZnO, we tested both the interstitial and substitutional Cu doping cases in both the PAW and PW methods. For the interstitial Cu doping case, our results indicated that the non-magnetic (NM) and the substitutional Cu doping changes the magnetic states of our system. When we considered the substitutional Cu-doped ZnO crystals, we calculated the three different configurations of the two Cu ions (5.88 at%), which are short, medium, and long distances of 2.99 (3.00), 5.73 (5.67), and 7.67 (7.78) Å, by the PAW (PW) method, respectively. We predicted the formation energy of three different configurations of two Cu ions, and the most stable configuration was found to be the short distance of two Cu ions in both the PAW and PW methods.

Table 5 The predicted lattice parameters (a and c/a), distance (d_Cu–Cu) between the two Cu ions, formation energy (E_f), magnetic energy gain (ΔE = E_AFM/SG − E_FM) between the antiferromagnetic (AFM)/spin glass (SG) and ferromagnetic (FM) states, spin state, magnetic moments (m) of magnetic ions and total magnetization (M_tot) for undoped (pure) and Cu-doped ZnO using the PAW and PW methods with the GGA + U approach

	Projected augmented wave (PAW) method				Plane wave (PW) method
	Pure ZnO	Cu-doped ZnO			Pure ZnO	Cu-doped ZnO
		Short	Medium	Long		Short	Medium	Long
a (Å)	3.287	3.283	3.274	3.282	3.291	3.283	3.284	3.284
c/a	1.611	1.614	1.617	1.613	1.600	1.614	1.612	1.614
dCu–Cu (Å)	—	2.991	5.730	7.671	—	2.996	5.669	7.780
Ef (eV per atom)	−7.0551	−7.0386	−7.0381	−7.0379	−7.0595	−7.0407	−7.0375	−7.0375
ΔE, (meV per cell)	—	0.608	2.532	−1.213	—	0.999	0.269	0.351
Spin state	NM	FM	FM	SG	NM	FM	FM	FM
m(Cu1) (μB per atom)	—	0.608	0.616	0.619	—	0.379	0.653	0.454
m(Cu2) (μB per atom)	—	0.588	0.618	−0.633	—	0.409	0.306	0.515
Mtot (μB per cell)	—	2.00	1.99	0.01	—	1.95	1.96	1.96

---

Fig. 8 The total and orbital projected DOS (in the unit of state/eV per atom) of (A) undoped, (B) short, (C) medium, and (D) long distances of two Cu ions for Cu-doped bulk ZnO crystal by the PAW method. The vertical dashed line is the Fermi level.

Fig. 9 The spin densities (Δρ↑↓ = ρ↑ − ρ↓) of (A) short, (B) medium and (C) long distances of two Cu ions for Cu doped bulk ZnO crystal. Here the grey, red and orange balls are Zn, O and Cu atoms, respectively. The isosurface with isovalue of 0.001 is yellow colour (created using the XCrySDen software).

Our results are shown to be the FM state at the short (2.99 Å) and medium (5.73 Å) distances of the two Cu ions, and the spin glass (SG) state is at the long (7.67 Å) distance of the two Cu ions by the PAW method. But the FM state is favorable at all the distances of two Cu ions by the PW method. The main results are shown in Table 5. For the PAW method, the total and orbital projected DOS are shown in Fig. 8 (B) and (C). These results show that the Cu(3d) orbital is strongly hybridized with the O(2p) state due to the Cu–O covalent bonding.

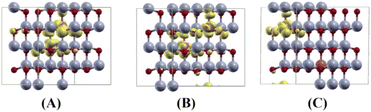
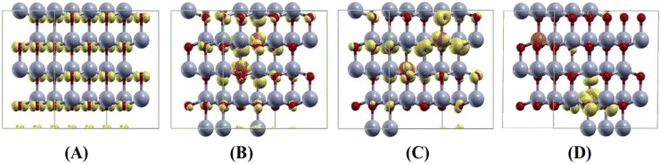
For the short distance of two Cu ions, the band gaps of majority and minority states are found to be 2.18 and 2.08 eV, (See Fig. 8(B)). As the Fermi level shifts to the VBM side, the two holes on the Cu ions create two localized defect levels via a double exchange mechanism, with magnetic energy gain ΔE = 0.608 meV per cell due to the presence of the unpaired electrons.³⁸ For the medium distance of the two Cu ions, the FM state is favorable, with magnetic energy gain ΔE = 2.532 meV per cell, and the localized two defect levels are overlapped on the minority state (See Fig. 8(C)). The band gaps of the majority and minority states were found to be 2.22 and 2.12 eV, respectively. For the short and medium distances of two Cu ions, the total magnetizations were found to be 2.00 and 1.99 μ_B per cell, respectively. The magnetic moments of the magnetic ions are shown in Table 5. The localized empty t_2g states overlapped on the minority state within the band gap, via the double exchange mechanism. For the long distance of the two Cu ions, the SG state is favorable, and the magnetic energy gain ΔE = −1.213 meV per cell, by the PAW method due to the asymmetry of hybridization for O(2p) and Cu(3d) states. The band gaps of the majority and minority states are found to be 2.10 and 2.12 eV, respectively (See Fig. 8(D)). But the FM state is favorable by the PW method. This corresponds to a low concentration of Cu ions. The spin densities of the short, medium and long distances of two Cu ions are shown in Fig. 9 (A)–(C), respectively. It is shown that the induced magnetization creates the O ions around the two magnetic Cu ions. For the undoped ZnO, the photocatalytic activity is going from the delocalized O(2p) state below the valence band maximum (VBM). The isosurface of the HOMO level of the undoped ZnO is shown in Fig. 10(A), and the HOMO level is delocalized on the O²⁻ ions. For the Cu-doped ZnO, the O(2p) and Cu(3d) states are hybridized below the VBM. The HOMO level is localized on the Cu²⁺ ions and it creates the bound magnetic polarons (BMPs) in diluted magnetic semiconductors.¹⁸ The photocatalytic activity creates recombination centers from the localized t_2g levels due to BMPs. We show that the main contribution created by the two magnetic Cu ions and the isosurface of the HOMO level of FM states is distributed through O atoms. (See Fig. 10 (B)–(D)).

Fig. 10 The isosurfaces of the HOMO level of (A) undoped, (B) short, (C) medium, and (D) long distances of two Cu ions for the Cu-doped bulk ZnO crystal. Here the grey, red and orange balls are Zn, O, and Cu atoms, respectively. The isosurface with an isovalue of 0.001 is yellow color (created using the XCrySDen software).

4 Conclusions

Highly crystalline Cu-doped ZnO nanoparticles with a mean diameter of 60–70 nm were synthesized by the surfactant-free organic phase method. The presence of the doped Cu in the ZnO nanoparticles was confirmed qualitatively by XRD and EDX and quantitatively by EPR. The magnetic and antibacterial activity of ZnO nanoparticles was observed to be enhanced by increasing the doping concentration in the range of 1–7 mol%. The photocatalytic performance was clearly enhanced as the dopant Cu concentration increased from 1 to 5 mol%. At 7 mol%, the band gap energy increased back slightly due to the number of substitutional Cu atoms that began to dominate over the interstitials. These substitutional Cu atoms may play the main role in the recombination of electrons and holes due to the shortening of the distance between neighbouring Cu sites at the highest concentration. As such, we conclude that the increase in band gap energy and the number of recombination centres lead to a decrease in the photocatalytic activity at a 7 mol% doping concentration. An experimental result was validated theoretically by performing DFT calculations. Our predicted value of the lattice parameters agrees with our experimental values of the crystal structure, in which the errors of the lattice parameter a are 1.14% and 1.01% by the PW and PAW methods, respectively. Our magnetism results show that the hole-mediated ferromagnetism of the Cu-doped ZnO is created by the double exchange mechanism, as created by localized empty holes on the localized t_2g state of Cu ions due to the bound magnetic polarons. These results agree with our experimental results.

Author contributions

All authors have given approval for the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to gratefully thank the Erasmus+ program of the European Union for financial support to study a Joint Thesis between Le Mans University and the National University of Mongolia. We thank the “Asian Research Center” projects #P2016-1255 and #P2018-3573. NT. would like to acknowledge support from the International Centre for Theoretical Physics (ICTP) through the Associates Programme (2021–2022).

References

1. S. Briefs and I. N. Environmental, Emerging Trends of Nanotechnology in Environment and Sustainability, 2018.
2. S. Jadoun, R. Arif, N. K. Jangid and R. K. Meena, Environ. Chem. Lett., 2021, 19, 355–374.
3. I. I. Novochinskii, C. Song, X. Ma, X. Liu, L. Shore, J. Lampert and R. J. Farrauto, Energy Fuels, 2004, 18, 576–583.
4. S. Baruah and J. Dutta, Sci. Technol. Adv. Mater., 2009, 10, 013001.
5. A. Kolodziejczak-Radzimska and T. Jesionowski, Materials, 2014, 7, 2833–2881.
6. B.-Y. Oh, M.-C. Jeong, T.-H. Moon, W. Lee and J.-M. Myoung, J. Appl. Phys., 2006, 99, 124505.
7. D. Chu, Y. Masuda, T. Ohji and K. Kato, Langmuir, 2010, 26, 2811–2815.
8. M. Y. Guo, A. M. C. Ng, F. Liu, A. B. Djuriŝić, W. K. Chan, H. Su and K. S. Wong, J. Phys. Chem. C, 2011, 115, 11095–11101.
9. F. Wang, M. Hao, W. Liu, P. Yan, B. Fang, S. Li, J. Liang, M. Zhu and L. Cui, Nano Mater. Sci., 2021, 3, 205–212.
10. P. Shandilya, A. Guleria and B. Fang, J. Environ. Chem. Eng., 2021, 9, 106461.
11. P. Shandilya, S. Sambyal, R. Sharma, P. Mandyal and B. Fang, J. Hazard. Mater., 2022, 428, 128218.
12. D. Wang, J. Bai, M. Hao, J. Liang, B. Fang, Y. Wang, K. Cui and F. Wang, CrystEngComm, 2022, 24, 6498–6504.
13. J. R. Torres-Hernández, E. Ramírez-Morales, L. Rojas-Blanco, J. Pantoja-Enriquez, G. Oskam, F. Paraguay-Delgado, B. Escobar-Morales, M. Acosta-Alejandro, L. L. Díaz-Flores and G. Pérez-Hernández, Mater. Sci. Semicond. Process., 2015, 37, 87–92.
14. K. V. Karthik, A. V. Raghu, K. R. Reddy, R. Ravishankar, M. Sangeeta, N. P. Shetti and C. V. Reddy, Chemosphere, 2022, 287, 132081.
15. W. Phoohinkong, T. Foophow and W. Pecharapa, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2017, 8, 035003.
16. M. Sajjad, I. Ullah, M. I. Khan, J. Khan, M. Y. Khan and M. T. Qureshi, Results Phys., 2018, 9, 1301–1309.
17. M. Zhu, Z. Zhang, M. Zhong, M. Tariq, Y. Li, W. Li, H. Jin, K. Skotnicova and Y. Li, Ceram. Int., 2017, 43, 3166–3170.
18. N. Ali, B. Singh, Z. A. Khan, A. R. Vijaya, K. Tarafder and S. Ghosh, Sci. Rep., 2019, 9, 3–9.
19. A. K. Nayek, H. Luitel, B. Haldar, D. Sanyal and M. Chakrabarti, Comput. Condens. Matter, 2020, 23, e00455.
20. Z. Wang, W. Xiao, M. Tian, N. Qin, H. Shi, X. Zhang, W. Zha, J. Tao and J. Tian, Nanomaterials, 2020, 10, 1–11.
21. S. Muthukumaran and R. Gopalakrishnan, Opt. Mater., 2012, 34, 1946–1953.
22. I. Ben Elkamel, N. Hamdaoui, A. Mezni, R. Ajjel and L. Beji, J. Mater. Sci.: Mater. Electron., 2019, 30, 9444–9454.
23. Z. Ma, F. Ren, X. Ming, Y. Long and A. A. Volinsky, Materials, 2019, 12, 196.
24. M. Mukhtar, L. Munisa and R. Saleh, Mater. Sci. Appl., 2012, 03, 543–551.
25. S. Singhal, J. Kaur, T. Namgyal and R. Sharma, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 407, 1223–1226.
26. M. Frentrup, N. Hatui, T. Wernicke, J. Stellmach, A. Bhattacharya and M. Kneissl, J. Appl. Phys., 2013, 114, 213509.
27. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
29. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
30. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. Distasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-De-La-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
31. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. De Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
32. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136(3B), 864–871.
33. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140(4A), 1133–1138.
34. A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350.
35. K. Hu, M. Wu, S. Hinokuma, T. Ohto, M. Wakisaka, J. I. Fujita and Y. Ito, J. Mater. Chem. A, 2019, 7, 2156–2164.
36. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(23), 16223–16234.
37. M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 1–16.
38. N. Tsogbadrakh, E. A. Choi, W. J. Lee and K. J. Chang, Curr. Appl. Phys., 2011, 11, 236–240.
39. S. K. N. Ayudhya, P. Tonto, O. Mekasuwandumrong, V. Pavarajarn and P. Praserthdam, Cryst. Growth Des., 2006, 6, 2446–2450.
40. M. Zare, K. Namratha, K. Byrappa, D. M. Surendra, S. Yallappa and B. Hungund, J. Mater. Sci. Technol., 2018, 34, 1035–1043.
41. N. Pinna and M. Niederberger, Angew. Chem., Int. Ed., 2008, 47, 5292–5304.
42. M. Niederberger and G. Garnweitner, Chem.–Eur. J., 2006, 12, 7282–7302.
43. C. T. Altaf, O. Coskun, A. Kumtepe, A. M. Rostas and I. Iatsunskyi, Sci. Rep., 2022, 1–15.
44. Q. Sun, T. Tian, L. Zheng, Z. Man, G. Li, M. Barré, J. Dittmer, A. Bulou and A. H. Kassiba, J. Eur. Ceram. Soc., 2019, 39, 3070–3076.
45. V. I. Merupo, S. Velumani, K. Ordon, N. Errien, J. Szade and A. H. Kassiba, CrystEngComm, 2015, 17, 3366–3375.
46. A. Sirelkhatim, S. Mahmud, A. Seeni, N. H. M. Kaus, L. C. Ann, S. K. M. Bakhori, H. Hasan and D. Mohamad, Nano-Micro Lett., 2015, 7, 219–242.
47. R. Brayner, R. Ferrari-Iliou, N. Brivois, S. Djediat, M. F. Benedetti and F. Fiévet, Nano Lett., 2006, 6, 866–870.
48. M. Heinlaan, A. Ivask, I. Blinova, H. C. Dubourguier and A. Kahru, Chemosphere, 2008, 71, 1308–1316.
49. L. M. Huang, A. L. Rosa and R. Ahuja, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 1–6.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra07204a

---