 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Refined definition of the critical micelle concentration and application to alkyl maltosides used in membrane protein research†
Adrian Bothea,
Athina Zouni a and
Frank Müh
a and
Frank Müh *b
*b
aInstitut für Biologie, Humboldt Universität zu Berlin, Leonor-Michaelis-Haus, Philippstrasse 13, D-10095 Berlin, Germany
bInstitut für Theoretische Physik, Johannes Kepler Universität Linz, Altenberger Strasse 69, A-4040 Linz, Austria. E-mail: frank.mueh@jku.at
First published on 22nd March 2023
Abstract
The critical micelle concentration (CMC) of nonionic detergents is defined as the breaking point in the monomer concentration as a function of the total detergent concentration, identified by setting the third derivate of this function to zero. Combined with a mass action model for micelle formation, this definition yields analytic formulae for the concentration ratio of monomers to total detergent at the CMC and the relationship between the CMC and the free energy of micellization gmic. The theoretical breaking point is shown to coincide with the breaking point of the experimental titration curve, if the fluorescence enhancement of 8-anilino-1-naphthalene-sulfonic acid (ANS) or a similar probe dye is used to monitor micelle formation. Application to a series of n-alkyl-β-D-maltosides with the number of carbon atoms in the alkyl chain ranging from 8 to 12 demonstrates the good performance of a molecular thermodynamic model, in which the free energy of micellization is given by gmic = σΦ + gpack + gst. In this model, σ is a fit parameter with the dimension of surface tension, Φ represents the change in area of hydrophobic molecular surfaces in contact with the aqueous phase, and gpack and gst are contributions, respectively, from alkyl chain packing in the micelle interior and steric repulsion of detergent head groups. The analysis of experimental data from different sources shows that varying experimental conditions such as co-solutes in the aqueous phase can be accounted for by adapting only σ, if the co-solutes do not bind to the detergent to an appreciable extent. The model is considered a good compromise between theory and practicability to be applied in the context of in vitro investigations of membrane proteins.
1 Introduction
Detergents (or surfactants) are amphiphilic substances with major contributions to many aspects of modern life and play an essential role in scientific applications such as membrane protein research.1–3 Detergent molecules consist of a hydrophilic (polar) segment and a hydrophobic part, covalently joined together.4 The hydrophobic section is often made up of a hydrocarbon chain, i. e. an n-alkyl group. In an aqueous phase, detergents tend to form globular aggregates termed micelles, where the hydrophobic parts of individual detergent molecules are located in the center of the aggregate and shielded from the surrounding water by the polar groups at the surface of the micelle. Mild uncharged detergents like alkyl maltosides can be used to extract membrane proteins from native biological membranes and solubilize them in an aqueous environment by binding of detergent molecules to hydrophobic domains and formation of a detergent belt surrounding those parts of the protein.5 The protein plus detergent belt is referred to as the protein-detergent complex (PDC), and it is soluble in water due to its polar exterior. Only after such solubilization with detergents are membrane proteins accessible with structural biology methods such as cryo-electron microscopy (cryo-EM)1 or X-ray diffraction (XRD).2 The structure determination in turn is crucial to the functional understanding of proteins and enzymes. A plethora of essential proteins is embedded into membranes, which is why detergents are indispensable to the study of many fundamental biological processes such as respiration and photosynthesis.However, the use of detergents poses additional challenges to these methods. In cryo-EM, the presence of free detergent micelles along with PDCs affects the classification of projections, if the micelles are similar to the PDC in size and shape or due to interactions between both types of particles.1 For XRD, the growth of protein crystals is a necessary prerequisite, and finding suitable crystallizing conditions is challenging.6 When crystallizing intrinsic membrane proteins, special attention has to be paid to the detergent belt, its stability and possible interactions between the detergent and the buffer components (e.g., precipitants, additives), because the detergent may interfere with attractive intermolecular forces that hold proteins together within the crystal lattice, or the detergent belt may be destabilized by components of the buffer. In the particular case of photosystem II of oxygenic photosynthesis, various types of crystals with different quality are obtained depending on detergent type and concentration.6,7 Accordingly, much effort was put recently into the characterization of the detergent belt in PDCs employing small-angle scattering methods.8–10 A detailed characterization of the detergent's self-aggregation behavior is clearly beneficial to understanding the outcomes of those experiments as well as the growth of membrane protein crystals.
The behavior of detergents in aqueous solutions is mainly governed by interactions between the detergent molecule and the solvent (water), as well as among detergent molecules. These interactions are a direct function of the detergent's molecular structure, which in a molecular thermodynamic model can be linked to the free energy difference between the detergent monomer and the micelle.3,11–16 A quantity of particular interest is the critical micelle concentration (CMC), which is the total detergent concentration that must be exceeded for micellar structures to be formed in the solution11–14 and for hydrophobic substances or membrane proteins to be solubilized.17
In our earlier work,3 we investigated the influence of poly(ethylene glycol) (PEG), a common precipitant used to induce protein crystallization, on the CMC of alkyl maltosides in order to better understand the detergent behavior under the conditions of membrane protein crystallization. The CMC was measured by employing fluorescence techniques involving the dye 8-anilino-1-naphthalene-sulfonic acid (ANS), which is known to increase its fluorescence intensity upon binding to micelles.18,19 The micelle formation was modelled with molecular thermodynamics,14 which was modified to explore the role of surface tension in the description of hydrophobic molecular surfaces in contact with water. Although data exist for PEG types of different molecular weight, the original analysis3 was restricted to PEG2000. In the course of analyzing the remaining data, we realized that there is room for improvement of the molecular thermodynamic model for the micelle formation of alkyl maltosides even in the absence of PEG. In particular, the modelling of the micellization free energy in terms of hydrophobic molecular surfaces and an associated surface tension required more care in a biophysical context, where the aqueous solutions contain additives like salts and buffer. Eventually, the modelling reached a status, where it became necessary to reconsider the definition of the CMC in the context of its experimental determination by using fluorescence probes. The resulting values for the surface tension were confronted with literature data, which ultimately led to an analysis of the underlying thermodynamics and common approximations to uncover systematic errors.
The goal of the present paper is to describe the improvement of the model of micelle formation for alkyl maltosides alongside a fundamental discussion of the underlying thermodynamics and a refined definition of the CMC motivated by the classical work of Philipps.20 This analysis will set the stage for future work to apply the modelling philosophy to analyze the influence of PEG and to describe the formation of PDCs in detergent solutions.
2 Theoretical basis and computational methods
2.1 Thermodynamics of micelle formation
The Gibbs free energy G of a composite system consisting of Nj particles of type j with chemical potential μj is given by the Euler equation:21,22
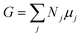 | (1) |
To describe an aqueous solution with Nwat water molecules containing besides Ndet detergent molecules a total of Ncos molecules of co-solutes, we model G as consisting of two parts:23–26
| G = Gf + Gmix | (2) |
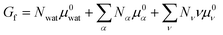 | (3) |
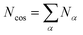 | (4) |
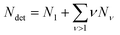 | (5) |
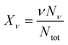 | (6) |
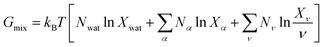 | (7) |
To find the size distribution of micelles at equilibrium, we have to determine the minimum of G with respect to a variation of the numbers Nν subject to the constraint stated in eqn (5). We apply the method of Lagrange multipliers by defining a function
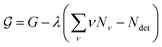 | (8) |
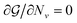 for all ν. This procedure yields the equilibrium condition
for all ν. This procedure yields the equilibrium condition
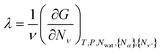 | (9) |
From eqn (9), we can identify λ as the chemical potential of detergent monomers μ1, which has to be equal to the chemical potential of detergent molecules in micelles of size ν. The resulting equation11
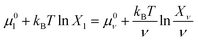 | (10) |
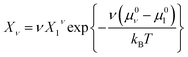 | (11) |
Note that this size distribution function assumes ideal mixing and is restricted to dilute solutions where interactions between micelles can be ignored.11,26
At this point, we make the simplifying assumption that the micellar size distribution is sufficiently narrow, so that it is adequate to consider only one type of micelle with a fixed aggregation number ν = m. We expect this to be a good approximation for alkyl maltosides at concentrations well above the CMC.3,29,30 (The validity of this assumption in the vicinity of the CMC is further discussed in Section 4.2.) For this particular aggregation number, we introduce the abbreviation
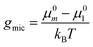 | (12) |
Xmic ≡ Xm = mX1m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−mgmic e−mgmic
| (13) |
Eqn (13) can be used to define a critical monomer concentration (X1)crit that is usually taken as the CMC following an argumentation given by Israelachvili:11 Since Xm is a mole fraction, it can never exceed unity. Consequently, the monomer mole fraction X1 must not exceed some critical value that is given by:
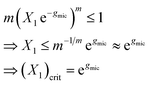 | (14) |
Note that m−1/m → 1 for sufficiently large m. In eqn (14), (X1)crit is the critical mole fraction of detergent monomers. However, since it is assumed that there is no significant amount of micelles present below (X1)crit, it is usually identified with the total mole fraction of detergent and employed as an approximation for the CMC.11–13 In the present work, we use a refined definition of the CMC (see Section 2.2) in order to better describe experimental data. Irrespectively, the relationship between the CMC and the total mole fraction of detergent at the CMC, XCMC, is given by
| CMC = ctotXCMC | (15) |
2.2 Refined definition of the critical micelle concentration
For the sake of simplifying the notation, we introduce the following abbreviations: the total mole fraction of detergent is x: = Ndet/N, the mole fraction of detergent monomers is y: = X1, and the mole fraction of detergent in micelles (with aggregation number m) is z: = Xmic = mym![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−mgmic. Then, the mass balance of detergent is given by x = y + z. To determine the CMC experimentally, a suitable observable ϕ (e.g., the fluorescence intensity of ANS) is monitored as a function of x. Usually, ϕ(x) exhibits a sharp breaking point that can be used to read off the CMC (see Fig. 1 for a representative titration curve). For a better definition of the breaking point, Phillips proposed the condition20
e−mgmic. Then, the mass balance of detergent is given by x = y + z. To determine the CMC experimentally, a suitable observable ϕ (e.g., the fluorescence intensity of ANS) is monitored as a function of x. Usually, ϕ(x) exhibits a sharp breaking point that can be used to read off the CMC (see Fig. 1 for a representative titration curve). For a better definition of the breaking point, Phillips proposed the condition20
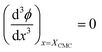 | (16) |
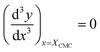 | (17) |
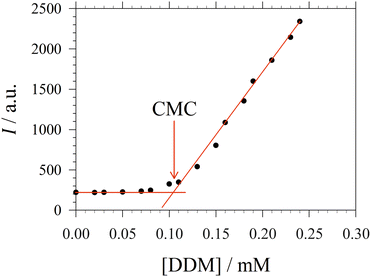 | ||
| Fig. 1 Representative titration curve of the ANS fluorescence intensity I versus the total detergent concentration of DDM (dodecyl maltoside) in 100 mM PIPES (pH 7.0) and 5 mM CaCl2 (same experimental data as in Fig. 1 of ref. 3). The straight lines illustrate the graphical procedure to determine the CMC. Figure made with SigmaPlot 13 (© 2014 Systat Software Inc.). | ||
In the following, a prime indicates a derivative with respect to x, while a dot denotes a derivative with respect to y. Then, in order to exploit the y-condition, we define the function f(x,y) = x − y − z(y) = 0 and obtain from implicit differentiation:
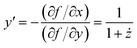 | (18) |
From eqn (18), we obtain the second and third derivative with respect to x and finally find that eqn (17) implies
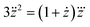 | (19) |
We note that it follows from the mass balance of detergent that z′ = 1 − y′, z′′ = −y′′, and z′′′ = −y′′′, so that the y-condition can also be expressed as z′′′ = 0, i.e., in terms of a breaking point in the concentration of detergent in micelles as a function of total detergent concentration.
Combining eqn (19) with eqn (13), we find that
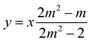 | (20) |
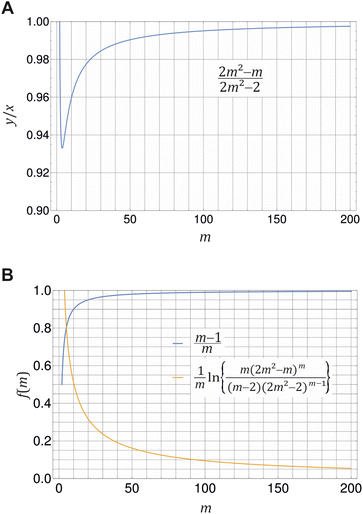 | ||
Fig. 2 Illustration of eqn (20) (A) and (21) (B) for different values of m ≥ 2. (A) Ratio of monomer to total detergent concentration (y/x) at the breaking point as a function of aggregation number m according to eqn (20). (B) The prefactor of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XCMC and the second term in eqn (21) as a function of m. Plots made with Mathematica 11.2 (© 1988–2017 Wolfram Research). XCMC and the second term in eqn (21) as a function of m. Plots made with Mathematica 11.2 (© 1988–2017 Wolfram Research). | ||
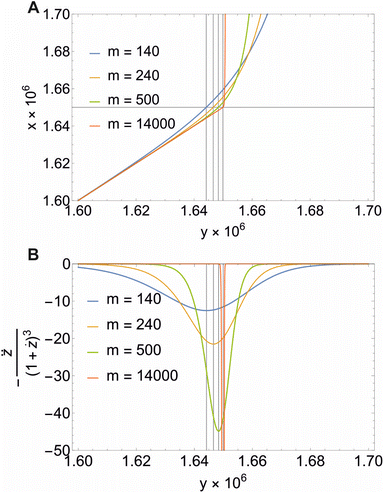 | ||
Fig. 3 Illustration of eqn (22) (A) and the second derivative 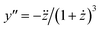 (B) for different values of m and XCMC = 1.65 × 10−6 (DDM). Note that all concentrations are in mole fraction units. The horizontal line in A indicates the value of XCMC. The vertical lines in (A) and (B) are the corresponding values for y at the breaking point according to eqn (20). Figure made with Mathematica 11.2 (© 1988–2017 Wolfram Research). (B) for different values of m and XCMC = 1.65 × 10−6 (DDM). Note that all concentrations are in mole fraction units. The horizontal line in A indicates the value of XCMC. The vertical lines in (A) and (B) are the corresponding values for y at the breaking point according to eqn (20). Figure made with Mathematica 11.2 (© 1988–2017 Wolfram Research). | ||
If we define x at the breaking point as XCMC, we can relate the CMC to the free energy of micellization according to
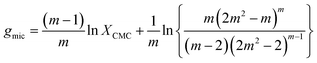 | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XCMC. It is instructive to see, how the corrections to the latter approximation change with m (Fig. 2B). The prefactor of ln
XCMC. It is instructive to see, how the corrections to the latter approximation change with m (Fig. 2B). The prefactor of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XCMC in eqn (21) approaches unity quite fast, so that it is of minor importance for aggregation numbers around 100. However, in the same range of aggregation numbers, the additional second term in eqn (21) is still in the order of 0.1 and not necessarily negligible.
XCMC in eqn (21) approaches unity quite fast, so that it is of minor importance for aggregation numbers around 100. However, in the same range of aggregation numbers, the additional second term in eqn (21) is still in the order of 0.1 and not necessarily negligible.
The mass balance for the detergent now reads
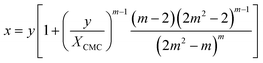 | (22) |
Illustrative theoretical titration curves are shown in Fig. 3A. Note that these curves are inverted, i.e., shown is x(y) for XCMC = 1.65 × 10−6 (corresponding to DDM) and aggregation numbers of 140 (the real one for DDM) as well as 240, 500, and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. It can be seen that the curves become sharper and the monomer concentration above the breaking point becomes smaller with increasing m (keeping XCMC constant). The largest value of m is intended to approximate the limit m → ∞ that reflects the traditional definition of the CMC. Apparently, in this limit, the monomer concentration above the CMC is underestimated.
000. It can be seen that the curves become sharper and the monomer concentration above the breaking point becomes smaller with increasing m (keeping XCMC constant). The largest value of m is intended to approximate the limit m → ∞ that reflects the traditional definition of the CMC. Apparently, in this limit, the monomer concentration above the CMC is underestimated.
It is not so obvious from the curves in Fig. 3A that the breaking point is indeed at XCMC = 1.65 × 10−6 (except, possibly, for m = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). To check the consistency of the formalism, we computed the second derivative
000). To check the consistency of the formalism, we computed the second derivative 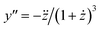 , which is an intermediate step in the derivation of eqn (19). This function should exhibit a minimum for the value of y at the breaking point, which is related to x = XCMC via eqn (20). As can be seen from Fig. 3B, this is indeed the case. However, the curve for m = 14
, which is an intermediate step in the derivation of eqn (19). This function should exhibit a minimum for the value of y at the breaking point, which is related to x = XCMC via eqn (20). As can be seen from Fig. 3B, this is indeed the case. However, the curve for m = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 is not completely shown in Fig. 3B. It has a sharp minimum close to y = XCMC = 1.65 × 10−6 as expected in the limit m → ∞.
000 is not completely shown in Fig. 3B. It has a sharp minimum close to y = XCMC = 1.65 × 10−6 as expected in the limit m → ∞.
It should be noted that eqn (18)–(22) are, to the best of our knowledge, new results that have not been published before.
2.3 Experimental reference data and interpretation of titration curves
A significant increase in the fluorescence intensity I above the CMC is known for the indicator dye ANS.18,19 In this case, the CMC is defined as the total detergent concentration at which the slope of the fluorescence intensity abruptly increases (see Fig. 1). This definition corresponds to the ϕ-condition with ϕ = I. In the following, we show that in this particular case, the ϕ-condition coincides with the y-condition.We make the simplifying assumption that at most one ANS molecule binds to a micelle and neglect binding of ANS to detergent monomers. Then, the association of ANS with micelles can be characterized by the equilibrium constant
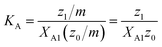 | (23) |
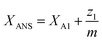 | (24) |
Let us denote by I1 the fluorescence intensity of one mole of ANS in an aqueous environment and by Imic that of ANS bound to a micelle. Then, the total fluorescence intensity is
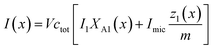 | (25) |
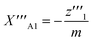 | (26) |
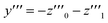 | (27) |
One solution for y′′′ = 0 under these conditions is 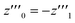 , which is, however, unphysical as it implies an unrealistically different behavior of micelles with and without ANS. A more realistic assumption is that the aggregation of m detergent molecules into one micelle is not significantly affected by one ANS molecule. Then, z0 and z1 should show the same dependence on x, which is the same as that of z in the absence of ANS. Hence, the y-condition implies
, which is, however, unphysical as it implies an unrealistically different behavior of micelles with and without ANS. A more realistic assumption is that the aggregation of m detergent molecules into one micelle is not significantly affected by one ANS molecule. Then, z0 and z1 should show the same dependence on x, which is the same as that of z in the absence of ANS. Hence, the y-condition implies 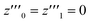 , and it follows from eqn (26) and (25) that
, and it follows from eqn (26) and (25) that
| y′′′ = 0 ⇒ I′′′ = 0 | (28) |
The last equation means that the breaking point of the experimental curve I(x) and the theoretical curve y(x) are the same, rendering the ANS fluorescence an ideal tool to determine the CMC based on the definition given in Section 2.2.
The focus of the present work is on n-alkyl-β-D-maltosides CnG2, where “G2” stands for the maltose head group and “Cn” for an n-alkyl chain with n carbon atoms. (Note that the “n” in “n-alkyl” stands for “normal”.) For convenience, the three detergents with n = 10, 11, 12 will also be referred to by their more common names DM (decyl maltoside), UDM (undecyl maltoside) and DDM (dodecyl maltoside), respectively. Our own experimental data concerning the CMC of these three detergents, which are re-analyzed here, were obtained by D. DiFiore in the course of our earlier work,3 measuring the fluorescence enhancement of ANS at a final concentration of 10 μM in buffered aqueous solutions containing 100 mM piperazine-1,4-bis-(2-ethanesulfonic acid) (PIPES), adjusted to pH = 7.0 with NaOH, and 5 mM CaCl2. The fluorescence spectra were taken with a Horiba Jobin Yvon FluoroMax-2 spectrometer. For comparison, additional experimentally determined values of the CMC and the aggregation number for alkyl maltosides with chain length n = 8–13 were taken from the literature.29,30,32–45
2.4 Molecular thermodynamic model of micelle formation
In the traditional molecular thermodynamic (TMT) modelling approach,14 the micellization free energy gmic is decomposed into several additive contributions:| gmic = gtr + gint + gpack + gst | (29) |
This decomposition is based on a thought process (thermodynamic cycle), in which the process of assembly of detergent molecules into a micelle is formally split into steps such as the detachment of head groups from the alkyl tails, aggregation of alkyl tails, reattachment of head groups to the alkyl tails etc.46–48 The transfer term gtr reflects the free energy change of transferring the alkyl tail from an aqueous environment into a liquid hydrocarbon phase representing the hydrophobic core of the micelle and is calculated on the basis of experimental transfer free energies, Δμ0tr, in the TMT approach.14 The linear dependence of gtr on n, the number of carbon atoms in the alkyl chain, largely determines the well-known exponential dependence of the CMC on n.
The interfacial term gint refers to the creation of a hydrocarbon–water interface due to the formation of the micellar core and is traditionally modelled as14
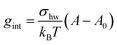 | (30) |
The packing term gpack is necessary to model the energetic and entropic consequences of a different conformational distribution of the alkyl chains in the micellar core compared to a pure liquid hydrocarbon phase and is computed here in the same way as in our earlier work:3
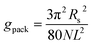 | (31) |
The meaning of the quantities occurring in eqn (31) and its applicability to the micelles of alkyl maltosides are discussed in Section 4.4.
Finally, the term gst describes the steric repulsion of the head groups moving on the surface of the micellar core and is modelled by assuming a hard core repulsion interaction according to14
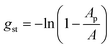 | (32) |
In our earlier work,3 the modelling of gtr had been altered in favor of a surface-based description. The assembly of detergent molecules implies that the area S of the hydrophobic surface of the alkyl tail is no longer in contact with water in the micelle except for the small part that contributes to the area A − A0 of the micellar core that is not shielded by the head groups; cf. eqn (30). Thus, it is possible to understand the transfer and interfacial terms jointly as the contribution to gmic that is due to a change of the effective molecular surface of hydrocarbons exposed to water. In this approach, gtr is supposed to be proportional to the surface area S according to:
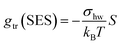 | (33) |
Indeed, there is a linear correlation of the SES values for alkanes with the transfer free energies;52 however, these values for the transfer free energies are different from those that are used in the traditional approach (as discussed below). Therefore, a correction factor α = 0.71 had to be introduced in the previous treatment.3 Taken together, the transfer and interfacial terms now become
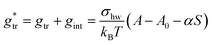 | (34) |
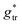 , in which the correction factor α is unnecessary, an effective interfacial tension σ is used that depends on the presence of co-solutes in the aqueous phase, and the SES of the alkyl tail is computed differently (termed S*, see Section 2.7):
, in which the correction factor α is unnecessary, an effective interfacial tension σ is used that depends on the presence of co-solutes in the aqueous phase, and the SES of the alkyl tail is computed differently (termed S*, see Section 2.7):
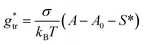 | (35) |
2.5 Structural model of micelles
As in our previous work,3 we do not aim here at a prediction of aggregation numbers, but rather use constraints from experiments to model the various contributions to gmic. Accordingly, we use the same geometric model3 that is motivated by small angle X-ray scattering (SAXS) and small angle neutron scattering (SANS) data.29,44,45 These data suggest29 that the micellar core is an oblate spheroid with minor radius a and major radius b, and the shell of detergent head groups has a thickness of 6.15 ± 0.15 Å. The experimentally determined values of a and b for DM and DDM are listed in Table 1 together with the eccentricity (or ellipticity)
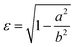 | (36) |
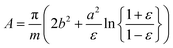 | (37) |
| n | 10 | 11 | 12 |
| N | 3.0566 | 3.3333 | 3.6111 |
| a/Å | 12.25 | 13.15 | 14.05 |
| b/Å | 23.50 | 26.13 | 28.75 |
| ε | 0.853 | 0.864 | 0.873 |
| Rs/Å | 18.91 | 20.78 | 22.65 |
| gpack | 2.05 | 2.27 | 2.49 |
| A/Å2 | 57.30 | 56.00 | 50.75 |
| S*/Å2 | 207.6 | 226.7 | 245.7 |
| Φ/(N m−1)−1 | −420.48 | −470.55 | −530.07 |
| gst | 1.20 | 1.25 | 1.55 |
| m | 85 | 106 | 140 |
| gmic(exp;m) | −10.41 | −11.67 | −13.15 |
| gmic(exp;∞) | −10.65 | −11.88 | −13.32 |
| CMC(calc;m)/mM | 1.35 | 0.36 | 0.091 |
| CMC(calc;∞)/mM | 1.44 | 0.37 | 0.087 |
| CMC(exp)/mM | 1.30 ± 0.07 | 0.38 ± 0.02 | 0.090 ± 0.005 |
2.6 Determination of total molarity
In order to connect the micellization free energy gmic and the CMC via eqn (15) and (21), the total molarity ctot of the buffer is needed. Knowing the density ρ of the solution as well as the molar concentrations c and molar masses M of buffer components (buffer, PIP; CaCl2, CaC) the total molarity can be calculated from
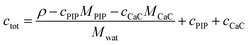 | (38) |
2.7 Determination of solvent excluded surface area
Previously, the surface area of alkyl tails within maltoside detergents was calculated from group contributions inferred from surface areas of short alkanes (n ≤ 10). However, it is expected that within the detergent molecule, the alkane is partly shielded from the surrounding water by the maltose head group. Therefore, the surface of the explicit alkyl chain within a detergent molecule was determined with the following approach: three-dimensional models were built for maltose, alkanes (n ≤ 12) and alkyl maltosides (n ≤ 12) in Avogadro,53 and the geometry was corrected with the built-in molecular mechanics function. Based on the Cartesian coordinates, the SES areas were determined using the MSMS program54 with the default probe radius of 1.4 Å and the atomic radii for each atom (1.20 Å for H, 1.74 Å for C, 1.40 Å for O; according to the atmtypenumbers library). Finally, the surface area of the alkyl tail was calculated using the following linear relations (see ESI, Fig. 7†):
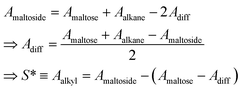 | (39) |
Group contributions S(CH3) and S(CH3) were obtained from a fit of S* as a function of n − 1, yielding S(CH3) = 36.27 Å2 and S(CH3) = 19.04 Å2.
3 Results
3.1 Definition of the critical micelle concentration
In the following, we investigate the question of whether the relationship between the CMC (that is XCMC) and the micellization free energy gmic (in units of kBT) should be described by the traditional approach represented by eqn (14) (where (X1)crit is the traditional “CMC”) or by our new eqn (21). We first compute XCMC from experimental data based on eqn (15) and the graphical extrapolation procedure indicated in Fig. 1 (thereby using the ϕ-condition). The experimental values for the CMC, CMC(exp), have been determined previously.3 Then, we connect XCMC with gmic according to the two different definitions of the CMC, where gmic is modelled according to Sections 2.4 and 2.5; specifically
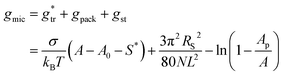 | (40) |
All parameters in eqn (40) can be determined from molecular thermodynamic modelling except for σ (see Table 1). Since σ depends in a complicated way on the co-solutes, it is more convenient to treat it as a fit parameter as discussed further below. To this end, we compute the quantity
| Γ: = gmic(exp;m) − (gpack + gst) | (41) |
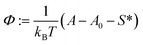 | (42) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XCMC.
XCMC.
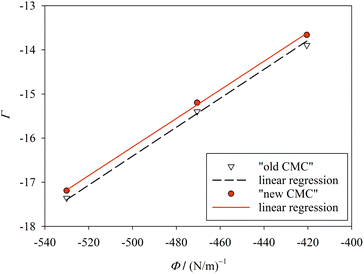 | ||
| Fig. 4 Plot of Γ (eqn (41)) against Φ (eqn (42)) for finite m (Table 1; “new CMC”) and for m → ∞ (“old CMC”). The slope of the line yields the surface tension σ. The fitting results are σ = 32.4 ± 0.055 mN m−1 (R2 = 0.9993) for “new CMC” and σ = 32.8 ± 0.095 mN m−1 (R2 = 0.9980) for “old CMC”. Figure made with SigmaPlot 13 (© 2014 Systat Software Inc.). | ||
When treating σ as a fit parameter, it becomes a system and model dependent quantity. Accordingly, different values of σ are obtained when using different definitions of the CMC despite the same molecular thermodynamic model underlying the analysis (Fig. 4). The quality of the linear fit based on the new definition of the CMC is somewhat higher than that based on the old definition, but the improvement seems to be minor. However, the CMC depends exponentially on gmic. To see the improvement in predicting the CMC, we recalculate the CMC in molarity units using the fitted values of σ based on
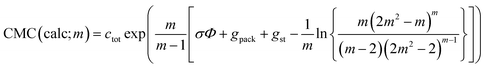 | (43) |
CMC(calc;∞) = ctot![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σΦ + gpack + gst) exp(σΦ + gpack + gst)
| (44) |
In contrast to ref. 3, where we estimated the consequences of errors in the experimentally determined quantities m, a, and b, no such errors are considered in the present work (Table 1). The reason is that we found the tedious evaluation of error propagation to be of limited use. In our view, what ultimately counts is the difference between calculated and experimental CMC values, where the error margins of the latter (given in Table 1) are relevant. It can be seen that redefining the CMC (and using a correspondingly changed value for σ) causes the calculated CMC values for all three detergents to lie within the boundaries set by experimental uncertainties. This accuracy is achieved in none of the models based on the traditional definition of the CMC (with one exception; see below and ESI, Table 2†).
For completeness, it should be noted that the TMT approach, in which gtr is treated separately from gint using experimental transfer free energies, can also lead to a very good agreement between calculated and experimental CMC values with the “old” definition of the CMC. If we use σhw = 32.7 mN m−1, the re-defined geometry for UDM micelles (see Section 3.3), and eqn (14), all calculated CMC values agree within the experimental error margins with the measured values (see model 7 in ESI, Table 2†). The rms deviation even decreases to 0.01 mM. In this case, however, using eqn (21) instead of (14) does not yield better results (see model 7a).
3.2 Surface-based modelling of the micellization free energy
In this section we describe what led us to treat σ as a fit parameter. For a macroscopic interface (e.g. the surface of an oil droplet in water), it is known that the interfacial tension depends on the curvature of the surface.55 Accordingly, it has been suggested that such a dependence also exists for a microscopic interface such as the molecular surface of an alkane.56 The value of σhw = 50.0 mN m−1 (equivalent to ≈72 cal mol−1 Å−2) used in ref. 3 (cp. models 1 and 2 in ESI, Table 3†) corresponds to the interfacial tension of a planar macroscopic hydrocarbon-water interface. Based on their analysis of alkane transfer into water, Sharp et al.56 suggested a smaller value of 32.7 mN m−1 (equivalent to ≈47 cal mol−1 Å−2) to be used in conjunction with the SAS of the alkane molecules, which they ascribed to the curvature of the SAS. When we used this value for σhw in eqn (30) for gint (together with the traditional modelling of gtr), we found a remarkable improvement in predicting the CMC (see model 4 in ESI, Tables 2 and 3†). Note that in this model, it is only the curvature of the surface of the micellar core that matters.The next question was, whether the SES approach, in which gtr and gint are treated jointly using the solvent-excluded surface as in eqn (34), could also be improved. We first checked the influence of the revised surface areas S* (see Table 1; group contributions S(CH3) and S(CH3) listed in ESI, Table 3†) as described in Section 2.7. However, with α = 0.71, the rms deviation of model 3 practically doubled compared to model 2 (ESI, Table 2,† σhw = 50.0 mN m−1). One interpretation of the factor α is that it effectively reduced the surface tension used in gtr(SES) to a value of ασhw = 35.5 mN m−1. This could make sense, since the curvature of the surface of the alkyl tail is larger than that of the micellar core, so that α could be understood as a curvature correction. The problem with this interpretation, however, is that the surface of the micellar core is different from that of an oil droplet, because it is decorated with maltose head groups (see, e.g., the MD simulations by Stephenson et al.57). In view of the way, such a surface interacts with water molecules, it is not clear, whether a curvature correction is reasonable in the framework of the simple model represented by eqn (30).
Another problem is that curvature corrections are discussed for the SAS rather than for the SES.56 Note that in our model, both the molecular surface of the alkyl tail S and the surface of the micellar core S (see eqn (37)) are to be understood as Connolly surfaces (SES). Simulations suggest that for the SES, curvature corrections are actually not necessary, at least at room temperature.58,59 This line of reasoning led to model 5, which employs eqn (35) with σ = 32.7 mN m−1 and α = 1, but does not improve the rmsd between computed and measured CMCs compared to models 2 and 4 (ESI, Tables 2 and 3†).
In another attempt to unify the description of contributions to gmic originating from the hydrophobic effect, we assumed
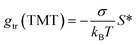 | (45) |
Although suitable values for σ to be used in eqn (35) are apparently very similar to the “microscopic” surface tension suggested by Sharp et al.,56 identifying σ with this surface tension is actually not justified. Like the transfer free energies, the value of σ deduced by Sharp et al.56 refers to the transfer of alkanes from pure water into a hydrocarbon phase. It is well known that co-solutes in the aqueous phase affect the transfer free energies, so that an effect of co-solutes on σ might be expected. Thus, we finally decided to use σ as a fit parameter in the procedure described in Section 3.1 to have a model at hand that is flexible enough to account for realistic buffer conditions in a biophysical context. This flexibility also allowed us to account for a refined definition of the CMC.
3.3 Improved micelle geometry for undecyl maltoside
In our earlier work,3 we used m = 110 as the aggregation number of UDM micelles. This value roughly corresponds to a linear relationship between m and the alkyl chain length n in accordance with claims in the literature.40 However, when values for m from several sources are considered,29,40–43 they together suggest an exponential dependence of m on n (see ESI, Fig. 8, Table 4†):
m = 5.4276![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e0.2699n e0.2699n
| (46) |
For DM, UDM, and DDM, this equation predicts aggregation numbers of 80.5, 105.7 and 137.7, respectively, in good agreement with the experimental values found by Lipfert et al.29 for DM and DDM that we already used for the molecular thermodynamic modelling. Based on these findings, we adopted the value m = 106 in our refined modelling of UDM (cf. Table 1).
Experimental SAXS data provide values for a and b of oblate spheroidal micelles of octyl maltoside (OM), DM, and DDM.40 The lengths of both axes seem to be correlated to the alkyl chain length in an almost perfectly linear way (see ESI, Fig. 9†), which allows determining these parameters for UDM by linear interpolation as listed in Table 1.
3.4 Application to other alkyl maltosides
In order to further test our method, we searched the literature for published values of the CMC of alkyl maltosides.32–39 However, since we require the CMC to be measured by a fluorescence technique, which is compatible with the y-condition, only the data by Alpes et al.32 (with one data point taken over from De Grip and Bovee-Geurts34) could be analyzed. Alpes et al.32 determined the CMC of OM, nonyl maltoside (NM), and DM in 150 mM KCl by using the dye 1,6-diphenyl-1,3,5-hexatriene (while De Grip and Bovee-Geurts34 used ANS for DDM under similar conditions). These data can be described well by our model (Fig. 5, ESI, Table 5†), with the new definition of the CMC performing slightly better than the old definition. The values for σ are smaller than those from our data (cp. Fig. 4), which can be traced back to the differences in solution conditions, and the value for the new definition of the CMC is consistently smaller than that for the old definition.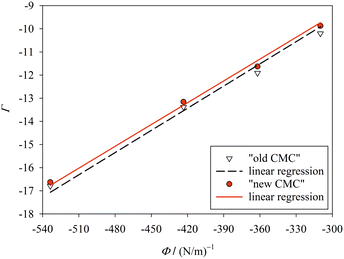 | ||
| Fig. 5 Same as in Fig. 4, but for the experimental CMC data of Alpes et al.32 The fitting results are σ = 31.4 ± 0.2 mN m−1 (R2 = 0.9950) for “new CMC” and σ = 32.0 ± 0.4 mN m−1 (R2 = 0.9873) for “old CMC”. Figure made with SigmaPlot 13 (© 2014 Systat Software Inc.). | ||
To summarize, we show in Fig. 6 the correlation between computed CMC values according to both definitions of the CMC and the experimental CMC values from both data sets in a log–log plot. The molecular thermodynamic model based on eqn (40) yields a very good description of the CMC of alkyl maltosides. For almost all data points, the new definition of the CMC results in a better description of the experiments than the old definition as can also be seen from the relative deviations [CMC(calc) − CMC(exp)]/CMC(exp) (see ESI, Fig. 10†). Although the refined definition of the CMC results only in relatively slight improvements, we consider it relevant to employ a definition of the CMC that is consistent with the experimental procedure in order to reliably evaluate the molecular thermodynamic model.
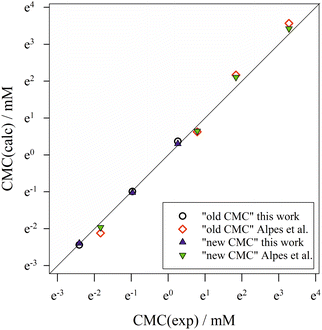 | ||
| Fig. 6 Correlation of calculated CMC values according to the “old” and “new” definitions of the CMC with experimental CMC values from both data sets (this work and Alpes et al.32). The symbol size represents the estimated experimental error, while the straight diagonal line represents perfect correlation. Figure made with SigmaPlot 13 (© 2014 Systat Software Inc.). | ||
4 Discussion
4.1 A new angle on the critical micelle concentration
What we here call the “new” definition of the CMC to have a handy notion, in fact, dates back to the 1955 paper by Phillips,20 who introduced the idea of taking the third derivative of a quantity as a function of the total detergent concentration to define the CMC. So what is actually new in our treatment?First of all, Philips’ idea appears to have only a relatively minor impact on detergent research as the overwhelming majority of works in the field relies on the “old” definition in the spirit of eqn (14) as nicely explained by Israelachvili11 (see also the seminal work by Nagarajan and Ruckenstein14). A rare example of a direct implementation of Phillips’ approach is the work by Garcia-Mateos et al.,61 who investigated conductivity data of ionic detergents. In the sequel, the method was further developed mostly for this kind of data.62–64
Secondly, in Phillips’ approach, it is rigorously assumed that the measured quantity ϕ is “ideal” in the sense that the breaking point in the ϕ(x) curve directly reflects the molecular behaviour. This assumption can be made more precise by writing for the measured observable
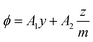 | (47) |
Thirdly, Phillips applied his method to ionic detergents bearing an effective charge and interacting with counter ions.20 Interestingly, he arrived at a different formula for the ratio of monomer to total detergent concentration at the breaking point (see his eqn (8b)) and for the relationship between micellization free energy and CMC (see his eqn (12)). We have to conclude that our results are not general, but only apply to nonionic or zwitterionic detergents, where no counter ions have to be taken into account. Since under the constraint that eqn (47) holds, our method is equivalent to that of Phillips, it might be possible to arrive at his equations without recourse to a specific “ideal” experimental quantity. This possibility remains to be investigated.
Fourthly, it is noteworthy that many works even when employing Phillips’ idea, assume that the micelle concentration is practically zero below and even at the CMC. By combining eqn (15) and (20) with the mass balance of the detergent, we obtain for the micelle concentration [micelle] at the CMC:
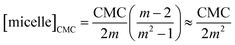 | (48) |
It is easy to see from this equation that [micelle]CMC is at least four orders of magnitude smaller than the CMC and, indeed, goes to zero for m → ∞. Thus, neglecting the micelle concentration at (and below) the CMC seems justified. However, the concentration of detergent bound to micelles scales with CMC/2m and thus is only two orders of magnitude smaller than the CMC. It should be stressed that the definition of the CMC to be employed is actually not a matter of taste: if the fluorescence technique is used, the detergent concentration at the breaking point of the titration curve is taken as the CMC. Then, according to our analysis, depending on the aggregation number m, 0.3 to 1.0% of detergent is bound to micelles at the CMC. For example, for n = 8, this amounts to about 0.3 mM, whereas for n = 12, it is only 0.3–0.6 μM depending on the solution conditions.
Fifthly, it is also usually assumed that the monomer concentration equals the CMC above the CMC. This, too, is an approximation: If 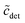 is the total detergent concentration divided by the CMC and
is the total detergent concentration divided by the CMC and 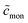 the monomer concentration divided by the CMC, it follows from eqn (22) that
the monomer concentration divided by the CMC, it follows from eqn (22) that
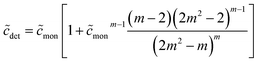 | (49) |
From eqn (49), we can estimate 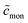 equals 1.143, 1.084, and 1.054, respectively, for OM, DM, and DDM, if
equals 1.143, 1.084, and 1.054, respectively, for OM, DM, and DDM, if 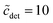 . Thus, depending on n (and hence m), the monomer concentration is between 5 and 14% above the CMC, if the total detergent concentration is ten times the CMC.
. Thus, depending on n (and hence m), the monomer concentration is between 5 and 14% above the CMC, if the total detergent concentration is ten times the CMC.
4.2 Simplifying assumptions
Despite the good performance of our model, it should be kept in mind that it relies on a number of approximations, which may require a critical analysis in future refinements. We shall briefly discuss only two of these approximations. One is the use of the ideal solution model for the entropy of mixing. This model ignores the differences in the sizes of the various species present in the solution. Nagarajan26 investigated the performance of various entropy models in predicting the CMC and other detergent properties in a molecular thermodynamic framework. We note that in this particular work, Nagarajan practically uses the y-condition by defining the CMC as “the total surfactant concentration at which a sharp transition is observed in a plot of the total surfactant concentration versus the singly dispersed surfactant concentration”,26 corresponding to our x(y) curves (cf. Fig. 3A). The main conclusion from Nagarajan's analysis is that the ideal solution model, while failing in the prediction of the solution phase behavior, provides a good prediction of the CMC.Size differences between molecular species in the solution are also central to the analysis of transfer free energies by Sharp et al.56 that led to a revision of the “microscopic” surface tension. It can be assumed that molecular volume effects are as important for the micellization free energy as they are for partition coefficients. It is then somewhat surprising that the neglect of these volume effects in our treatment yields effective surface tensions that are similar to the value inferred by Sharp et al.56 We will come back to this problem in Section 4.3.
The second important approximation is the assumption of a fixed aggregation number m, which corresponds to using a mass action model of micelle formation (cf. ESI Text S2, eqn (S5)†). We note that this assumption was not made by Nagarajan,26 but is inherent to all the methods discussed above in Section 4.1. In general, the micellar size distribution (see eqn (11)) can have a complex dependence on the total detergent concentration, which is determined by the standard chemical potential difference μ0ν − μ01. In this respect, important cornerstones regarding DDM are provided by the seminal work of Warr et al.,30 who demonstrated some peculiar properties of sugar surfactants. Aqueous disaccharide surfactant systems show a strikingly simple phase diagram with an isotropic micellar solution extending to very high total surfactant concentrations (>40 wt% in the case of DDM). The micelle size distribution is relatively insensitive to temperature. It is concluded from viscosity measurements that there is no change in micelle size with increasing concentration. However, the picture emerging from fluorescence quenching experiments to determine the aggregation number appears to be somewhat more complicated. Warr et al.30 determined the (mean) aggregation number of DDM to be 111 ± 10 for 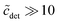 . In the region
. In the region 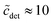 , it is only between 90 and 100, and at smaller detergent concentrations, it even drops below 80. At the same time, the aggregation number distribution shows a fairly concentration-independent rms deviation of about 40 and practically no skewness. The value of the rms deviation is considered too high for the micelles to be spherical. These data are in reasonable agreement with those of Lipfert et al.,29 if one takes into account that in the SAXS experiments, the aggregation number is somewhat higher (140 ± 10) and its determination is obscured by intermicellar repulsion at higher concentrations. The lowest concentration investigated by Lipfert et al.29 is in fact
, it is only between 90 and 100, and at smaller detergent concentrations, it even drops below 80. At the same time, the aggregation number distribution shows a fairly concentration-independent rms deviation of about 40 and practically no skewness. The value of the rms deviation is considered too high for the micelles to be spherical. These data are in reasonable agreement with those of Lipfert et al.,29 if one takes into account that in the SAXS experiments, the aggregation number is somewhat higher (140 ± 10) and its determination is obscured by intermicellar repulsion at higher concentrations. The lowest concentration investigated by Lipfert et al.29 is in fact 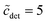 (for DDM), and aggregation numbers are extrapolated to zero concentration (which are the values that we are using in our modeling). Since detergent concentrations applied in membrane protein research are typically below ten times the CMC, the question of a possible dependence of the sizes of micelles (and eventually the sizes of detergent belts in PDCs8–10) in this region is of interest (cf. the discussion in ref. 3). Unfortunately, this concentration range is hardly resolved in experiments that determine the aggregation number. At least, the data by Warr et al.30 point to the possibility that the aggregation numbers of alkyl maltosides, while being fairly constant at higher concentrations, may be somewhat smaller in the vicinity of the CMC. This problem will have to be taken into account in future refinements of the model. Meanwhile, the mass action model, although not able to resolve the size variation issue, may still serve as a valuable tool to study the influence of various factors on the CMC.
(for DDM), and aggregation numbers are extrapolated to zero concentration (which are the values that we are using in our modeling). Since detergent concentrations applied in membrane protein research are typically below ten times the CMC, the question of a possible dependence of the sizes of micelles (and eventually the sizes of detergent belts in PDCs8–10) in this region is of interest (cf. the discussion in ref. 3). Unfortunately, this concentration range is hardly resolved in experiments that determine the aggregation number. At least, the data by Warr et al.30 point to the possibility that the aggregation numbers of alkyl maltosides, while being fairly constant at higher concentrations, may be somewhat smaller in the vicinity of the CMC. This problem will have to be taken into account in future refinements of the model. Meanwhile, the mass action model, although not able to resolve the size variation issue, may still serve as a valuable tool to study the influence of various factors on the CMC.
4.3 Understanding the microscopic surface tension
How to interpret the parameter σ in eqn (40)? It clearly has the dimension of a surface tension as it originates from a surface-based description of the free energy change due to the transfer of hydrophobic parts of the detergent molecule from water into the micelle. However, when determined by a fit as shown in Fig. 4, it is also affected by limitations of the molecular thermodynamic model that are not related to molecular surfaces. The quantity Γ not only contains the experimental error of the CMC, but also deficiencies of modeling gpack and gst (cf. eqn (41)). Furthermore, it depends on the way the CMC is defined. Thus, a physical interpretation of σ seems difficult.If we interpret σ as a surface tension, we may ask what the meaning is of a surface tension at the molecular scale. In our study, we made two interesting observations: (i) the values of σ obtained by the fit are very close to the “microscopic” surface tension determined by Sharp et al.56 (ii) the CMC is very sensitive to the value of σ. The latter point can best be seen from a comparison of the cases n = 10 (DM) and n = 12 (DDM) in our data set and that of Alpes et al.32 (see the data points in the lower left corner and in the center of Fig. 6). For example, Alpes et al.32 (or actually De Grip and Bovee-Geurts34) obtain a CMC of 0.16 mM for DDM, whereas we obtain 0.09 mM under our buffer conditions.3 Both values can be reconciled by changing only σ. Although there are slight differences in the temperature and the total molarity, all other parameters entering gmic except for σ are the same including those entering gpack and gst as well as A, A0, and S* (cf. Table 1 and ESI Table 5†).
Why is σ similar to the microscopic surface tension determined by Sharp et al.?56 Note that we employ the SES rather than the SAS used by Sharp et al. Based on the surface increment of a methylene group, which is 19.04 Å2 in our SES calculation (see Section 2.7 and ESI Table 3†) and ≈ 29 Å2 for the SAS,56 one can estimate that the SAS is larger than the SES by a factor of approximately 1.5. Thus, if we had used the SAS, we would have obtained a value of σ = (32.4/1.5) mN m−1 = 21.6 mN m−1 from the fit. It follows that our value of σ is actually too small.
A possible reason for confusion is that the increase of the surface tension due to considering molecular volume effects in the analysis of transfer free energies by Sharp et al.56 is by a factor of 32.5/21.5 ≈ 1.5, which accidently is the same as the SAS/SES ratio. (It may add to the confusion that the conversion factor from cal mol−1 Å−2 to mN m−1 is also ≈ 1.5.) Thus, using the SES instead of the SAS compensates for neglecting molecular volume effects in the entropy of mixing. Indeed, if the transfer free energies of alkanes are corrected for volume effects and correlated with the SES, a value of σ = 47.9 mN m−1 is obtained.52 It is remarkable that the latter value is very close to the surface tension of a macroscopic alkane–water interface.3
It follows that the ideal solution model for the entropy of mixing as represented by eqn (7) could be the cause of a systematic error that results in values of the effective surface tension σ in eqn (40) that are too low by a factor of about 2/3. To further investigate this problem and to learn more about the effects of co-solutes on σ, we drafted a non-ideal solution model (see ESI Text S3†). In this model, molecular volume effects are taken into account following the work of Hildebrand,65 while the interaction of detergent with one type of co-solute is described in a mean field approach akin to the Bragg-Williams approximation.66 The equilibrium constant of the mass action model then becomes
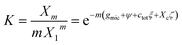 | (50) |
To take non-ideality into account in the analysis of experimental CMCs, we can define Γ and Φ as in eqn (41) and (42), respectively, and compute gmic(exp;m) from experimental data on the basis of eqn (21) and (15). Then, we have to find σ by fitting
| Γ − ψ − ctotξ − Xcζ = σΦ | (51) |
Further quantification of ξ and ζ is very challenging and clearly beyond the scope of the present paper. Therefore, in the absence of a reliable model for the non-ideality of the solution, we can specify co-solute effects in our model with a fitted, solution-dependent σ in a kind of semi-empirical way. Is it possible to describe the effects of all types of co-solutes in this way? The answer is decisively no. Our model rests on experimental information about the size and geometry of the micelles. In implementing this information, we make the tacit assumption that the co-solutes do not alter these micellar properties. However, this assumption is not always tenable. For example, small amphiphilic molecules like heptane-1,2,3-triol are known to decrease micelles67,68 and are employed in membrane protein crystallization with the goal to downsize the detergent belt in the PDC.69,70 Similar effects can be expected for glycerol.71,72 In such cases, where a co-solute tends to enter the micelles to an appreciable extent, the model for gmic would have to be modified to directly contain a term depending on the concentration of the co-solute. However, even macromolecular co-solutes, which do not enter the micelles, can attach to either detergent monomers or micelles. In those cases, it would likewise be necessary to modify the equation for gmic. Problems of this type will be discussed in a forthcoming publication dealing with PEG.
4.4 Modelling the packing free energy
The analytical expression for the packing free energy in eqn (31) was introduced by Nagarajan and Ruckenstein14 based on the theoretical work by Semenov, who formulated an analytical expression for the deformation free energy of block-copolymers within spherical microdomains.73 Nagarajan and Ruckenstein defined the alkyl chain to be composed of N segments with the length L = 4.6 Å, following the lattice definition used by Dill and Flory in their description of the micellar core.74 The number of segments N is defined as N = (n + 1)/3.6, where 3.6 is the number of methylene groups per lattice site. Rs in eqn (31) is the radius of the aggregate assumed to be spherical. For the present modelling of ellipsoidal micelles, Rs was defined as the radius of a sphere with the same volume as the micellar core:3 Rs = (ab2)1/3.Interestingly, despite the non-spherical micelle shape, using eqn (31) results in a model that predicts the CMC very well. In order to understand why this might be the case, it is interesting to examine a proposed correction for ellipsoidal micelles. Iyer and Blankschtein used a statistical-mechanical model to compute the packing free energy for prolate and oblate ellipsoidal geometries.25 In contrast to spheres, cylinders, and bilayers, the computationally expensive determination of the packing free energy for ellipsoids cannot be condensed into an analytical expression. Therefore, a direct application of their method to the micelles of alkyl maltosides was not feasible within the scope of the present paper.
However, the results from Iyer and Blankschtein25 indicate that the micelle shape has a significant impact on gpack only for small micelles. For large oblate spheroidal micelles with a minor axis a = 0.95lc (where lc is the maximum extension of the alkyl chain), the value of gpack only changed by less than 5% for a ratio b/a = 2 compared to a sphere (b/a = 1), which was attributed to the lower curvature of large micelles and the correspondingly lower conformational constraints. For the alkyl maltosides studied in the present work, b/a ≈ 2 and a ≈ 0.88lc, which is similar to the above values. Moreover, the micelles of alkyl maltosides are even larger than those investigated by Iyer and Blankschtein, which could imply that the movement of alkyl chains is even less constrained and correspondingly, the effect of curvature on the value of gpack becomes negligible. This, in turn would explain why eqn (31) allows predicting the CMC well, although it strictly applies only to spheres.
5 Conclusions and outlook
A precise definition of the CMC is possible by setting to zero the third derivative of the concentration of detergent monomers as a function of the total detergent concentration. When combined with a mass action model for micelle formation (without counter ions), this definition results in controllable analytic formulae for the concentration ratio of monomers to total detergent at the CMC and the relationship between the CMC and the free energy of micellization. These equations differ from those obtained earlier by Phillips20 for ionic detergents and do not require the assumption of an ideal measurable quantity obeying eqn (47). The fluorescence enhancement of ANS (and similar probe dyes) is a suitable observable, for which the breaking point in the experimental titration curve coincides with the breaking point in the theoretical curve, thus allowing for a direct determination of the CMC according to the above definition.When applied to a series of n-alkyl-β-D-maltosides CnG2 with alkyl chain lengths n ranging from 8 to 12, the more precise definition of the CMC allows for demonstrating the good performance of a molecular thermodynamic model, in which the free energy of micellization is given by eqn (40). In this model, σ is a fit parameter with the dimension of a surface tension, which represents those parts of the micellization free energy that are due to a change in the area of hydrophobic molecular surfaces in contact with the aqueous phase. All other parameters of the model are inferred from a consideration of the micelle geometries based on independent experimental data and molecular structure. It turns out that different experimental conditions due to co-solutes that do neither attach to detergent monomers nor to micelles to a significant extent can be accounted for by adapting only σ. However, the relation of σ to macroscopic surface tension concepts remains unclear.
The present work sets the stage for future applications of the theoretical approach in biophysics and biochemistry, but also in the more general field of detergency, where it is still an unsolved problem to reconcile CMC data from different experimental methods. Our contribution provides a first step in this direction by demonstrating the way to link theory and experiment for the case of one particular experimental method. Applications to other methods and other types of detergents (e.g., surface tension measurements and gemini surfactants75) will follow. The model will also be applied to problems in the context of membrane protein research such as the influence of PEG on the CMC or the formation of PDCs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dörte DiFiore for performing titration experiments. This research was funded in part F. M. is supported by the Austrian Science Fund (FWF) in conjunction with the district of Upper Austria (project P 33154-B). For the purpose of open access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. F. M. is further supported by the JKU Linz through the Linz Institute of Technology (grant LIT-2019-8-SEE-120). A. Z. acknowledges support by Germany's Excellence Strategy Project EXC 2008/1-390540038 coordinated by TU Berlin and by the German Research Foundation (DFG) via the Collaborative Research Center SFB1078 (Humboldt Universität zu Berlin), TP A5.References
- N. Thonghin, V. Kargas, J. Clews and R. C. Ford, Methods, 2018, 147, 176–186 CrossRef CAS PubMed.
- G. G. Privé, Methods, 2007, 41, 388–397 CrossRef PubMed.
- F. Müh, D. DiFiore and A. Zouni, Phys. Chem. Chem. Phys., 2015, 17, 11678–11691 RSC.
- A. Sorrenti, O. Illa and R. M. Ortuno, Chem. Soc. Rev., 2013, 42, 8200–8219 RSC.
- M. Ceccarelli and M. Marchi, J. Phys. Chem. B, 2003, 107, 1423–1431 CrossRef CAS.
- J. Kern, F. Müh and A. Zouni, in Metabolism, Structure and Function of Plant Tetrapyrroles: Control Mechanisms of Chlorophyll Biosynthesis and Analysis of Chlorophyll-Binding Proteins, ed. B. Grimm, Elsevier, London, 2019, ch. 2, pp. 33–67 Search PubMed.
- J. Hellmich, M. Bommer, A. Burkhardt, M. Ibrahim, J. Kern, A. Meents, F. Müh, H. Dobbek and A. Zouni, Structure, 2014, 22, 1607–1615 CrossRef CAS PubMed.
- M. Golub, R. Hussein, M. Ibrahim, M. Hecht, D. C. F. Wieland, A. Martel, B. Machado, A. Zouni and J. Pieper, J. Phys. Chem. B, 2020, 124, 8583–8592 CrossRef CAS PubMed.
- M. Golub, A. Kölsch, A. Feoktystov, A. Zouni and J. Pieper, Crystals, 2021, 11, 203 CrossRef CAS.
- M. Golub, J. Gatcke, S. Subramanian, A. Kölsch, T. Darwish, J. K. Howard, A. Feoktystov, O. Matsarskaia, A. Martel, L. Porcar, A. Zouni and J. Pieper, J. Phys. Chem. B, 2022, 126, 2824–2833 CrossRef CAS PubMed.
- J. N. Israelachvilli, Intermolecular and Surface Forces, Academic Press, Elsevier, Amsterdam, 2011 Search PubMed.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- H. Wennerström and B. Lindman, Phys. Rep., 1979, 52, 1–86 CrossRef.
- R. Nagarajan and E. Ruckenstein, Langmuir, 1991, 7, 2934–2969 CrossRef CAS.
- T. Chakraborty and S. Ghosh, J. Surfactants Deterg., 2008, 11, 323–334 CrossRef CAS.
- A. Dey, R. Banik and S. Ghosh, J. Surfactants Deterg., 2021, 24, 459–472 CrossRef CAS.
- F. Müh and A. Zouni, Biochim. Biophys. Acta, 2008, 1778, 2298–2307 CrossRef PubMed.
- E. De Vendittis, G. Palumbo, G. Parlato and V. Bocchini, Anal. Biochem., 1981, 115, 278–286 CrossRef CAS PubMed.
- E. B. Abuin, E. A. Lissi, A. Aspée, F. D. Gonzalez and J. M. Varas, J. Colloid Interface Sci., 1997, 186, 332–338 CrossRef CAS PubMed.
- J. N. Phillips, Trans. Faraday Soc., 1955, 51, 561–569 RSC.
- H. B. Callen, Thermodynamics and an Introduction to Thermostatistics, Wiley, New York, 1985 Search PubMed.
- M. E. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, Oxford University Press, New York, 2010 Search PubMed.
- D. Blankschtein, G. M. Thurston and G. B. Benedek, Phys. Rev. Lett., 1985, 54, 955–958 CrossRef CAS PubMed.
- S. Puvvada and D. Blankschtein, J. Chem. Phys., 1990, 92, 3710–3724 CrossRef CAS.
- J. Iyer and D. Blankschtein, J. Phys. Chem. B, 2012, 116, 6443–6454 CrossRef CAS PubMed.
- R. Nagarajan, Colloids Surf., A, 1993, 71, 39–64 CrossRef.
- J. B. Ott and J. Boerio-Goates, Chemical Thermodynamics - Principles and Applications, Academic Press, San Diego, USA, 2000 Search PubMed.
- W. J. Moore, Physical Chemistry, Longmans, London, 1962 Search PubMed.
- J. Lipfert, L. Columbus, V. B. Chu, S. A. Lesley and S. Doniach, J. Phys. Chem. B, 2007, 111, 12427–12438 CrossRef CAS PubMed.
- G. G. Warr, C. J. Drummond, F. Grieser, B. W. Ninham and D. F. Evans, J. Phys. Chem., 1986, 90, 4581–4586 CrossRef CAS.
- W. Al-Soufi, L. Pineiro and M. Novo, J. Colloid Interface Sci., 2012, 370, 102–110 CrossRef CAS PubMed.
- H. Alpes, K. Allmann, H. Plattner, J. Reichert, R. Riek and S. Schulz, Biochim. Biophys. Acta, 1986, 862, 294–302 CrossRef CAS.
- A. D. Tsamaloukas, A. Beck and H. Heerklotz, Langmuir, 2009, 25, 4393–4401 CrossRef CAS PubMed.
- W. J. De Grip and P. H. M. Bovee-Geurts, Chem. Phys. Lipids, 1979, 23, 321–335 CrossRef CAS.
- M. Aoudia and R. Zana, J. Colloid Interface Sci., 1998, 206, 158–167 CrossRef CAS PubMed.
- P. Liljekvist and B. Kronberg, J. Colloid Interface Sci., 2000, 222, 159–164 CrossRef CAS PubMed.
- L. Zhang, P. Somasundaran and C. Maltesh, Langmuir, 1996, 12, 2371–2373 CrossRef CAS.
- C. J. Drummond, G. G. Warr, F. Grieser, B. W. Ninham and D. F. Evans, J. Phys. Chem., 1985, 89, 2103–2109 CrossRef CAS.
- R. Aveyard, B. P. Binks, J. Chen, J. Esquena, P. D. I. Fletcher, R. Buscall and S. Davies, Langmuir, 1998, 14, 4699–4709 CrossRef CAS.
- R. C. Oliver, J. Lipfert, D. A. Fox, R. H. Lo, S. Doniach and L. Columbus, Plos One, 2013, 8, e62488 CrossRef CAS PubMed.
- E. R. S. Kunji, M. Harding, P. J. G. Butler and P. Akamine, Methods, 2008, 46, 62–72 CrossRef CAS PubMed.
- P. J. Tummino and A. Gafni, Biophys. J., 1993, 64, 1580–1587 CrossRef CAS PubMed.
- T. Jumpertz, B. Tschapek, N. Infed, S. H. J. Smits, R. Ernst and L. Schmitt, Anal. Biochem., 2011, 408, 64–70 CrossRef CAS PubMed.
- C. Cecutti, B. Focher, B. Perly and T. Zemb, Langmuir, 1991, 7, 2580–2585 CrossRef CAS.
- C. Dupuy, X. Auvray and C. Petipas, Langmuir, 1997, 13, 3965–3967 CrossRef CAS.
- S. Puvvada and D. Blankschtein, J. Phys. Chem., 1992, 96, 5579–5592 CrossRef CAS.
- Y. J. Nikas and D. Blankschtein, Langmuir, 1994, 10, 3512–3528 CrossRef CAS.
- L. Maibaum, A. R. Dinner and D. Chandler, J. Phys. Chem. B, 2004, 108, 6778–6781 CrossRef CAS.
- R. Nagarajan, Adv. Colloid Interface Sci., 1986, 26, 205–264 CrossRef CAS.
- M. L. Connolly, J. Appl. Crystallogr., 1983, 16, 548–558 CrossRef CAS.
- F. M. Richards, Annu. Rev. Biophys. Bioeng., 1977, 6, 151–176 CrossRef CAS PubMed.
- I. Tunón, E. Silla and J. L. Pascual-Ahuir, Protein Eng., 1992, 5, 715–716 CrossRef PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- M. F. Sanner, A. J. Olson and J. C. Spehner, Biopolymers, 1996, 38, 305–320 CrossRef CAS PubMed.
- R. C. Tolman, J. Chem. Phys., 1949, 17, 333–337 CrossRef CAS.
- K. A. Sharp, A. Nicholls, R. F. Fine and B. Honig, Science, 1991, 252, 106–109 CrossRef CAS PubMed.
- B. C. Stephenson, A. Goldsipe, K. J. Beers and D. Blankschtein, J. Phys. Chem. B, 2007, 111, 1045–1062 CrossRef CAS PubMed.
- H. S. Ashbaugh and M. E. Paulaitis, J. Am. Chem. Soc., 2001, 123, 10721–10728 CrossRef CAS PubMed.
- H. S. Ashbaugh and L. R. Pratt, Rev. Mod. Phys., 2006, 78, 159–178 CrossRef CAS.
- A. Bothe, Master thesis, Humboldt Universität zu Berlin, 2021 Search PubMed.
- I. Garcia-Mateos, M. M. Velazquez and L. J. Rodriguez, Langmuir, 1990, 6, 1078–1083 CrossRef CAS.
- P. C. Shanks and E. I. Franses, J. Phys. Chem., 1992, 96, 1794–1805 CrossRef CAS.
- M. Perez-Rodriguez, G. Prieto, C. Rega, L. M. Varela, F. Sarmiento and V. Mosquera, Langmuir, 1998, 14, 4422–4426 CrossRef CAS.
- P. Carpena, J. Aguiar, P. Bernaola-Galvan and C. C. Ruiz, Langmuir, 2002, 18, 6054–6058 CrossRef CAS.
- J. H. Hildebrand, J. Chem. Phys., 1947, 15, 225–228 CrossRef CAS.
- K. A. Dill and S. Bromberg, Molecular Driving Forces, Garland Science, London, New York, 2 edn, 2011 Search PubMed.
- P. A. Timmins, J. Hauk, T. Wacker and W. Welte, FEBS Lett., 1991, 280, 115–120 CrossRef CAS PubMed.
- P. Gast, P. Hemelrijk and A. J. Hoff, FEBS Lett., 1994, 337, 39–42 CrossRef CAS PubMed.
- H. Michel, Trends Biochem. Sci., 1983, 8, 56–59 CrossRef CAS.
- C. Ostermeier and H. Michel, Curr. Opin. Struct. Biol., 1997, 7, 697–701 CrossRef CAS PubMed.
- L. Cantu, M. Corti, V. Degiorgio, H. Hoffmann and W. Ulbricht, J. Colloid Interface Sci., 1987, 116, 384–389 CrossRef CAS.
- G. D'Errico, D. Ciccarelli and O. Ortona, J. Colloid Interface Sci., 2005, 286, 747–754 CrossRef PubMed.
- A. N. Semenov, Sov. Phys. JETP, 1985, 61, 733–742 Search PubMed.
- K. A. Dill and P. J. Flory, Proc. Natl. Acad. Sci. U. S. A., 1981, 78, 676–680 CrossRef CAS PubMed.
- S. Ghosh and T. Chakraborty, J. Phys. Chem. B, 2007, 111, 8080–8088 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables 2–6, Fig. 7–10, modelling of the steric free energy, alternative derivation of eqn (20), draft of a non-ideal solution model. See DOI: https://doi.org/10.1039/d2ra07440k |
| This journal is © The Royal Society of Chemistry 2023 |
