Bond-bending isomerism and metallophilicity in metal–halogen anions (Cu,Ag,Au)₂X₃⁻, X = F, Cl, Br, I, At

Abstract

In the framework of DFT (ABINIT package), we have performed atomic relaxations on the (Cu,Ag,Au)₂X₃⁻, X = F, Cl, Br, I, At anion series. Opposite to linear (MX₂)⁻ anions, all (M₂X₃)⁻ systems are triangular (C_2v symmetry). According to the system, we classified these anions in three categories according to the relative strength of electronegativity, chemical hardness, metallophilicity and van der Waals interaction. We found two bond-bending isomers: (Au₂I₃)⁻ and (Au₂At₃)⁻.

---

I Introduction

From its origins, over the years the concept of isomerism has been considerably extended, so that a variety of different types is presently recognized, including structural, geometrical, optical, and conformational isomerism. The existence of isomers requires both a double minimum on a potential energy surface and a significant barrier between the two minima (≥30 kcal mol⁻¹). For lower energy differences, the term conformers may be preferred but refers to the same phenomenon.

Among the different types of isomerism, the term “distortional isomerism” was proposed by Chatt,¹ in 1970 to characterize metallic complexes that differ only by the length of one or several bonds. Typical systems were mer-MoOCl₂(PEt₂Ph)₃ and related phosphine compounds, which present two isomers, one green and one blue. Although the molybdenum coordination and environment were similar in both isomers, an important difference was first observed for the lengths of the Mo–O bonds (blue: 1.676 Å, green: 1.803 Å (ref. 2 and 3)) and suggested the origin of the phenomenon.

Two years later, the concept was investigated theoretically by Hoffmann and coworkers^4,5 and thereby named the phenomenon “bond-stretch isomerism” (BSI). They showed on series of hypothetical molecules of the type (CH₄)⁵⁺ and (CH)₄CO that a double minimum may be obtained on the potential energy surface of a molecule because of the crossing of energy levels. A large variety of investigations followed in order to identify the BSI in the solid phase and in transition metal chemistry.⁶

Later the BSI hypothesis was ruled out for mer-MoOCl₂(PEt₂Ph)₃ and the concept of BSI was questioned.^6–8 In spite of thorough investigations, the most debated issue of bond-stretch isomerism has remained elusive up to now in transition metal chemistry.⁹ Although a number of systems have been suspected to be BSI and investigated,¹⁰ the number of compounds, which demonstrate this isomerism, is very limited but undoubtedly observed.^11,12 As some systems differs in their magnetic states, Hoffmann and Parkin distinguished “bond-stretch” isomerism, where both isomers, lie on the same energy surface, from “spin-state” isomerism where a change of multiplicity occurs.¹³

More recently, giving up controversies, Li et al.¹⁴ investigated the possible relationship between bond-isomerism and the competition between covalent bonding and aurophilic interactions in the gaseous complex (Au₂I₃)⁻. This cluster (Au₂I₃)⁻ is found to form a triangle (C_2v) geometry and exhibits two near-degenerate isomers that differ only by the bending angle <Au–I–Au>. Similar to BSI, they introduced the new term of “bond-bending isomerism” (BBI). The two isomers, shown in Fig. 1, are separated by a small barrier (1.78 kJ mol⁻¹) and the obtuse isomer being slightly more stable (obtuse <Au–I–Au> = 100.7°, acute <Au–I–Au> = 72.0°).

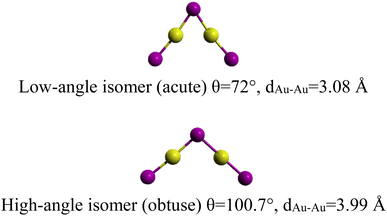Fig. 1 The two (Au₂I₃)⁻ bond-bending isomers.¹⁴

The two bond-bending isomers for gaseous (Au₂I₃)⁻ are the result of the competition between Au–I covalent bonding and Au–Au aurophilic interactions. Similar effects were observed in the (Au_nCl_n+1)⁻, 2 ≤ n ≤ 7 zigzag series with an increasing aurophilic interaction with the number of Au atoms and a progressive stabilization for large-sized cluster anions.¹⁵ Belonging to the same family, some copper related anions as (Cu₂Cl₃)⁻ were also observed and studied in ionic liquids as butyl-3-methylimidazolium ([BMIM]⁺ [Cu₂Cl₃]⁻).^16,17

All these anions belong to a vast category of small clusters formed by the association of a noble metal and a halogen.^18,19 More recently, another kind of bond-bending isomerism was found in hexaphenyl carbo diphosphorane with two isomers only differing by the angle <P–C–P>.²⁰

Besides strong chemical bondings, weaker interactions act in chemical systems. Among them, Schmidbaur first described the aurophilic interaction in peculiar gold-containing compounds and clusters.²¹ This interaction binds two gold atoms with a bonding intermediate between conventional covalent/ionic and van der Waals interactions and reflects the tendency of the low-coordinate compounds of Au(I) to associate into dimers, oligomers or uni- and multidimensional polymers.^21,22 This interaction may be considered as a “super van der Waals bonding”. Pyykkö and co-workers theoretically investigated the aurophilic interactions between closed shell Au(I) cationic centers over the past years.²³ Although weaker, this interaction is also observed in other noble-metal systems as silver (argentophilic effect) and copper (cuprophilic effect). This interaction is generalized as metalophilic interaction.

Due to the theoretical ambiguity surrounding BSI and BBI, in order to improve the understanding of the competition between metalophilicity and ionocovalency in clusters (Cu,Ag,Au)₂X₃⁻, we performed quantum simulations within the density functional theory (DFT). The two effects are decomposed: the metalophilic character is modify by the substitution of gold for silver and copper and the ionocovalency is varying by studying the whole halogen series form fluorine to astatine. Beside the theoretical interest in chemistry, this family of anions plays an important role in the field of supramolecular chemistry and catalysis. In research of medical artefacts, the astatine systems are also more and more investigated.

II Theoretical approach

We performed structural optimization of the clusters (Cu,Ag,Au)₂X₃⁻, X = F, Cl, Br, I, At in DFT starting from the Li et al. structure and using periodic boundary conditions as implemented in the ABINIT package in the projector augmented wave formalism (PAW).²⁴ The first-principles total energy calculations were performed using the Generalized Gradient Approximation Density Functional of Perdew, Burke and Ernzerhof (GGA-PBE).²⁵ Scalar relativistic effects are taken into account and spin–orbit coupling (SOC) added together with the dispersion correction term (van der Waals – VdW), which is included according to the formalism of Grimme for accurate calculations in DFT (DFT-D3).²⁶ These different effects are mandatory in order to characterize noble metals and metalophilicity.

As ABINIT is a periodic DFT code, the simulation of an isolated system, needs large, essentially empty DFT mesh (simulation cell) to effectively isolate the system from its periodic images. Classically, each system is placed at the center of a large cubic simulation box and the periodic cell must be made large enough to damp out interactions of the system with its periodic images. As total energy may converge slowly with the cell size, we checked the influence of the size by calculating the total energy versus the cell parameter. In all the calculations, we have used boxes of dimensions 20 × 20 × 20 ų with at least 15 Å of vacuum space between adjacent replicas in each direction. Moreover, we corrected the total energies (first order corrections) for electrostatic interactions between charges anions. The Brillouin zone was sampled with the Γ point only. For each system, we performed a full atomic relaxation and a set of relaxations in which the metal–metal bond-length was fixed to a given value; all other atoms were free to relax. It allows the calculation of potential energy surfaces (energy versus the <M–X–M> angle).

The pseudopotentials of copper, silver, gold, and halogens have been generated for the PBE exchange-correlation functional using the ATOMPAW code.²⁷ The plane-wave expansion of the Bloch functions was truncated at an energy cutoff of 816 eV and the self-consistent convergence was set to 10⁻⁸ Ha, forces were converged to 0.02 Ha bohr⁻¹ for the atomic relaxations, in order to ensure fully converged forces for all systems.

We checked on (Au₂I₃)⁻ the relevance of PBE functional by performing some calculations in the framework of the more cumbersome HSE06 hybrid functional. We obtained similar results, i.e. a double-well potential energy surface. We also compared our results with SCS-MP2 and CCSD(T) calculations of Li et al.¹⁴ with an identical energy curve and the same conclusion. These additional calculations and checking suggest that the GGA-PBE including SOC and dispersion effects is perfectly able to describe the structures and properties of the clusters.

III Gold clusters (Au₂X₃)⁻, X = F, Cl, Br, I, At clusters

Opposite to the linear (Na₂X₃)⁻,²⁸ and (AuX₂)⁻ clusters, all the (Au₂X₃)⁻ anions adopt a triangular C_2v configuration. For instance, the energy calculated for (Au₂I₃)⁻ in the linear configuration is high, around +53 kJ mol⁻¹ above the energy obtained in the obtuse triangular configuration. This fact implies an aurophilic contribution between gold atoms together the ionocovalent interaction between Au⁺ cation and X⁻ anion.

We present the potential energy surfaces (energy versus the <Au–X–Au> bond-bending angle) on Fig. 2.

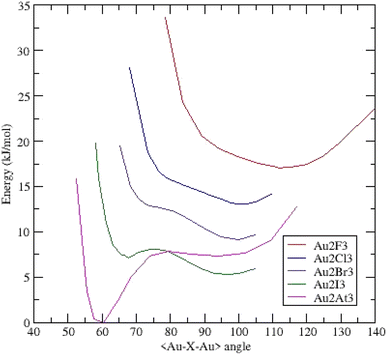Fig. 2 Potential energy surfaces (energy versus <Au–X–Au> bond bending angle) for (Au₂X₃)⁻ clusters – each curve is shifted by 0.002 Ha (5.24 kJ mol⁻¹).

The (Au₂F₃)⁻ cluster evidences a broad dissymmetric curve with one minimum at an obtuse bond-bending angle of 105.66°. No other minimum is present but the gold–gold interaction is responsible for the shape at low angles. Substituting F by Cl reveals a more dissymmetric curve toward low angles and a minimum at an obtuse angle of 99.96°. The related (Au₂Br₃)⁻ curve evidenced one minimum around 100.00° and a pronounced shoulder around 77.00°. For (Au₂I₃)⁻ cluster, the shoulder becomes deeper and a second minimum appears at an acute angle of 67.87° together with the deepest minimum at 97.17°. This asymmetrical two-well potential curve is the same as those already published by Li et al.¹⁴ The energy difference between the two minima is 1.88 kJ mol⁻¹ (1.78 kJ mol⁻¹ in ref. 14). This system is then a BBI with two isomers; an aurophilic bond between the two Au atoms characterizes the low-angle isomer. The last complex (Au₂At₃)⁻ presents a deep well at an acute angle of around 60.50° and a weaker one at 91.91° separated by 7.35 kJ mol⁻¹. Similarly, to (Au₂I₃)⁻, the (Au₂At₃)⁻ cluster evidences two BBIs, but the magnitude of the two energetic minima is inverted. The geometrical parameters of the different clusters are summarized in ESI (Table I).†

On the basis of an harmonic model, it's possible to estimate the lifetime of the aurophilic state at 298 K. Compared to (Au₂I₃)⁻, the string constant is twice as strong and the potential wells deeper in (Au₂At₃)⁻. It results a lifetime about fifteen longer for the aurophilic state in the astatine system. Then it would be experimentally possible to observe this cluster at ambient temperature.

For these two BBI, according to the Poincaré–Hof's relationship, a Bader analysis on both acute systems evidenced six critical points: four bond critical points (BCP) which correspond to the four gold–halogen chemical bonds, one BCP for the aurophilic Au–Au bond and one ring critical point (RCP) located at the center of the Au–X–Au triangle. For the aurophilic BCP, the main Bader descriptors are reported in ESI (Table II†) such as the electron density ρ(r_c) and Laplacian ∇²ρ(r_c), which is the sum of the three curvatures of the electron density Hessian matrix, λ₁, λ₂ and λ₃. Negative values of λ₁ and λ₂ and positive λ₃ indisputably characterize the existence of a chemical bond between the two gold atoms. The density at the BCP is weak, the local energy density H(r_c) is negative and the Laplacian is positive. The chemical bonding characterized by such descriptors is referred as “intermediate” bond.²⁹ This indicates that the Au–Au bond is mainly weak (closed-shell) and partially covalent (shared-shell), which is indeed the signature of an aurophilic bond. Going from iodine to astatine, the density ρ(r_c) increases and H(r_c) grows larger as the interaction become stronger. This result is consistent with the deeper wells observed in the potential energy surface of (Au₂At₃)⁻ compared to (Au₂At₃)⁻.

To summarize, going from fluorine to astatine, the position of the obtuse bond bending angle minimum decreases from 105.66° to 91.91° and another minimum appears at an acute angle. The (Au₂X₃)⁻, X = F, Cl, Br, I, At clusters evolve from a monomer dominated by gold–halogen interactions in (Au₂F₃)⁻ to two bond-bending isomers for (Au₂I₃)⁻and (Au₂At₃)⁻. In this last case, the aurophilic interaction is predominant on the ionocovalent one.

IV Silver clusters (Ag₂X₃)⁻, X = F, Cl, Br, I, At clusters

Similar to the gold clusters, the (Ag₂X₃)⁻ anions are triangular and belong to the C_2v symmetry.

Fig. 3 presents the potential energy surfaces of the clusters. The (Ag₂F₃)⁻ cluster exhibits a behavior very similar to its gold homologue i.e. one minimum at an obtuse bond bending angle of 115.69° and a dissymmetric energy profile. For the (Ag₂Cl₃)⁻ cluster, the curve is broad and very flat upon a magnitude of around twenty degrees with a small hollow at 92.14°. The two possible minima are quasi-degenerated into energy; both argentophilic and ionocovalent contributions to the energy seem equivalent. Substituting Cl for Br leads to the formation of a shoulder at low angles with a shallow minimum (75.14°). The last systems (Ag₂I₃)⁻ and (Ag₂At₃)⁻ clusters exhibit a deep minimum at respectively 67.77° and 61.94°.

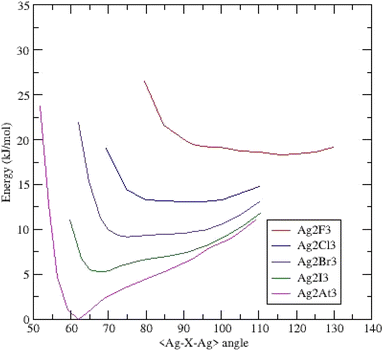Fig. 3 Potential energy surfaces (energy versus <Ag–X–Ag> bond bending angle) for (Ag₂X₃)⁻ clusters – each curve is shifted by 0.002 Ha (5.24 kJ mol⁻¹).

Focusing on this last cluster, the Bader analysis (ESI Table II†) points out similar descriptors as those of its homologue (Au₂At₃)⁻. The density ρ(r_c) and energy H(r_c) are both slightly weaker involving a weaker Ag–Ag interaction.

In this silver series, no cluster evidences two well-separated minima as in the gold homologues.

The geometrical parameters are summarized in ESI (Table III†).

V Copper clusters (Cu₂X₃)⁻, X = F, Cl, Br, I, At clusters

Once again, the (Cu₂X₃)⁻ anions are triangular and belong to the same C_2v symmetry. All the systems present a unique deep minimum at an acute bond-bending angle. As expected, the Cu–Cu distances are shorter than the Au–Au and Ag–Ag ones (ESI Table IV†). These distances are shorter or equal than those measured in hexanuclear copper(I) carboxylates (2.7044 Å < d_Cu–Cu < 2.8259 Å)³⁰ showing stronger interactions. The (Cu₂At₃)⁻ anion exhibits the shortest and strongest bond: d_Cu–Cu = 2.197 Å (Fig. 4).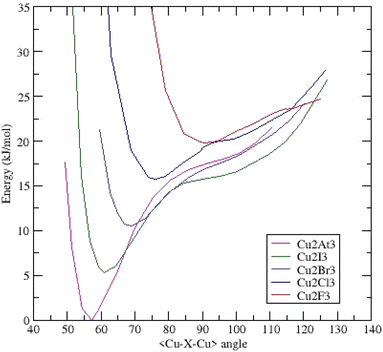

Fig. 4 Potential energy surfaces (energy versus <Cu–X–Cu> bond bending angle) for (Cu₂X₃)⁻ clusters – each curve is shifted by 0.002 Ha (5.24 kJ mol⁻¹).

VI Discussion

The general shape of the potential energy surfaces rests on the competition of two phenomena: the metal–halogen ionocovalent bonding and the metal–metal interaction (metalophilicity).

For a given metal, the resulting configuration of a cluster depends on the strength of the metal–halogen interaction. According to the Pearson's classification for Lewis acids and bases,³¹ the three cations Au⁺, Ag⁺ and Cu⁺ are soft acids, F⁻ and Cl⁻ are hard bases, I⁻ is soft and Br⁻ is borderline. Although At⁻ is not well defined it may be considered as a soft base in this case. Along the halogen column, the electronegativity decreases from fluorine (3.98 – Pauling's scale) to iodine (2.66) and probably astatine. The absolute hardness follows the same evolution and steadily decreases from F⁻ (η = 7 eV) to I⁻ (η = 3.7 eV).³² The electronegativity and hardness of astatine are unknown and assumed to be close to that of iodine. The shape of the potential energy surfaces calculated for (M₂X₃)⁻ clusters depends on the variation of these two properties along the halogen series. The softness of the ligand is significant for the aurophilic interaction. As previously stated in ref. 15 and 33 the softness of the ligand is significant for the aurophilic attraction, this attraction gets stronger as the ligand goes from hard (Cl) to soft (I). More generally the metallophilic attraction gets stronger from F to At.

For the (M₂F₃)⁻ clusters, the metalophilic attraction is weak; the strength of the metal-fluoride bond is high and predominates on the metallophilic interaction. Then, the cluster only presents one minimum at an obtuse angle; the potential curve is dissymmetric due to a slight contribution of metalophilicity. Opposite, for the (M₂At₃)⁻ clusters, the metallophilic attraction is strong, the metal–astatine bond strength is weak and the metalophilic effect could dominate leading to a deep well at an acute angle. Between these two utmost anions, for (M₂Cl₃)⁻, (M₂Br₃)⁻ and (M₂I₃)⁻ the relative strength of both interactions evolves and the magnitude of the two minima or shoulders are more or less marked.

Going on from gold to silver, the strength of the silver–halogen interaction decreases due to the decrease of relativistic effects present in gold. It is known that a maximum of relativistic effects has been identified in gold³⁴ leading to significant effects on the bonding properties. Although heavier than silver, atomic radii of both metals are close due to the relativistic contraction of the valence 6s and 6p orbitals of gold. When gold bonding with a ligand is involved, the bond length contraction pulls in the Au⁺–L single bond length to length similar or less than that of the corresponding Ag⁺–L bonds. Simultaneously the bond is strengthened.^33,35 Moreover, gold (η = 5.7 eV) is softer than silver (η = 6.9 eV). These effects are observed in the (M₂X₃)⁻ clusters (Tables 1 and 2 ESI†) where all the gold–halogen distances are shorter than the silver–halogen ones. The differences increases along the halogen series.

Due to different polarizabilities (Au: 5.8 ų, Ag: 7.2 ų), the van der Waals contribution to the Ag–Ag interaction is stronger than the Au–Au one. For instance, at the minimum acute angle, the van der Waals contribution to the total energy is −0.00383 Ha in the (Au₂I₃)⁻ cluster and −0.00412 Ha in the (Ag₂I₃)⁻ cluster, respectively.

Comparing silver to gold clusters, the ionocovalent M–X bond-strength and the metalophilicity effects are weaker in silver anions but the van der Waals contribution between silver cations is stronger. It results that most of silver anions (Ag₂X₃)⁻ are dominated by the argentophilic interactions with clusters presenting an acute <Ag–X–Ag> bond-bending angle.

Going on to copper clusters, the copper–halogen bond is strengthened compared to both Ag and Au halogen bonds, as the electronegativity difference is larger. For the three cations, the copper ionic radii is the smallest (Cu⁺: 0.46 Å; CN = 2 (ref. 36)). It results that the copper–halogen bond length is short (cf. Table III in ESI†) and the distance Cu–Cu in the triangular structure is shorter than the Ag–Ag and Au–Au ones. The van der Waals contribution to the bond is intermediate between Au and Ag (polarizability; Cu: 6.1 ų). Although the cuprophilic effect is weaker than argentophilic and aurophilic ones, its strength is important enough to stabilize a C_2v symmetry of the clusters rather than a linear configuration. It also allows the presence of a deep well at an acute angle.

For the three systems, we report the main bond lengths and <X–M–X> angles versus atomic number on Fig. 5.

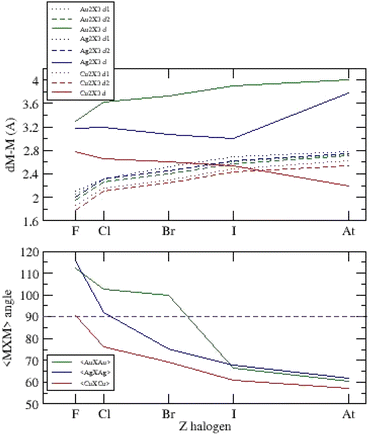Fig. 5 Bond lengths and <X–M–X> angles versus atomic number Z for (Cu,Ag,Au)₂X⁻₃, X = F, Cl, Br, I, At.

The metal–halogen bond lengths are of the same order of magnitude for the three-anion families with d_Au–Au > d_Ag–Ag > d_Cu–Cu, and evolve with atomic number according to the electronic nature of the respective ions (electronegativity and hardness). We observe the main differences on metal–metal distances depending on the metallophilic and van der Waals interactions. The <X–M–X> angles decrease with Z with a jump between obtuse and acute ground state configurations. All these distances move towards similar values for astatine systems.

Two simple conditions are necessary for the existence of a metalophilic interaction:³⁷ the distance between metal atoms must not exceed the sum of van der Waals radii (Au: 1.66 Å, Ag: 1.72 Å, Cu: 1.40 Å) and cannot be shorter than the sum of atomic radii (Au: 1.36 Å, Ag: 1.44 Å, Cu: 1.32 Å). Then, metalophilicity can exist if:

2.72 Å < d_Au–Au < 3.32 Å

2.88 Å < d_Ag–Ag < 3.44 Å

2.64 Å < d_Cu–Cu < 2.80 Å

All acute systems (Fig. 5, Tables ESI-I, II and III†) confirm these two conditions.

VII Conclusion

In the framework of DFT (ABINIT package), we have performed atomic relaxations on the (Cu,Ag,Au)₂X₃⁻, X = F, Cl, Br, I, At series. The relative strength of (i) the metal–halogen ionocovalent interaction, (ii) the metalophillic effect and (iii) the amplitude of the metal–metal van der Waals interaction governs the geometry of these anions. Opposite to linear (MX₂)⁻ anions, which do not present any metalophillic attraction, all (M₂X₃)⁻ systems are triangular (C_2v symmetry). According to the metal and halogen atom, the <M–X–M> equilibrium angle is different and we can sort three kind of systems:

(1) The angle is obtuse – one monomer:

(Au₂F₃)⁻, (Au₂Cl₃)⁻, (Au₂Br₃)⁻, (Au₂I₃)⁻; (Ag₂F₃)⁻, (Ag₂Cl₃)⁻; (Cu₂F₃)⁻;

(2) The angle is acute – one monomer:

(Au₂At₃)⁻; (Ag₂Br₃)⁻, (Ag₂I₃)⁻, (Ag₂At₃)⁻; (Cu₂Cl₃)⁻, (Cu₂Br₃)⁻, (Cu₂I₃)⁻, (Cu₂At₃)⁻;

(3) Two angles (obtuse and acute) – two bond-bending isomers – BBI:

(Au₂I₃)⁻ and (Au₂At₃)⁻

Our set of calculations did not allow finding bond-bending isomerism in silver and copper anions. The phenomenon only occurs in two gold anions (Au₂I₃)⁻ and (Au₂At₃)⁻, the first one has been already observed¹⁴ and we evidenced a new system (Au₂At₃)⁻. The amplitude of energy minima are reversed between the two anions: (Au₂I₃)⁻ ground state is an obtuse triangle (<Au–I–Au> = 97.17°) and (Au₂At₃)⁻ ground state is an acute triangle (<Au–I–Au> = 60.50°). The respective energy difference between isomers are 1.88 kJ mol⁻¹ and 7.35 kJ mol⁻¹. The Bader analysis confirms our hypotheses on metalophilic interactions.

Conflicts of interest

There are no conflicts of interest to declare.

References

1. A. V. Butcher and J. Chatt, J. Chem. Soc. A, 1970, 2652–2656.
2. J. Chatt, L. Manojlovic-Muir and K. W. Muir, J. Chem. Soc. D, 1971, 655–656.
3. J. Chatt, L. Manojlovic-Muir and K. W. Muir, J. Chem. Soc. A, 1971, 2796–2800.
4. W. D. Stohrer and R. Hoffmann, J. Am. Chem. Soc., 1972, 94, 449–786.
5. Y. Jean, A. Lledos, J. K. Burdett and R. Hoffmann, J. Am. Chem. Soc., 1988, 110, 4506–4516.
6. G. Parkin, Acc. Chem. Res., 1992, 25, 455–460.
7. G. Parkin, Chem. Rev., 1993, 93, 887–911.
8. J. M. Mayer, Angew. Chem., 1992, 102, 293.
9. J. A. Labinger, C. R. Chim., 2002, 5(4), 235–244.
10. M. Homray, S. Mondal, A. Misra and P. K. Chattarai, Phys. Chem. Chem. Phys., 2019, 21, 7996–8003.
11. B. Molina, L. Alexandrova, R. Lelagadec, L. E. Sansores, D. Rios-Jara, F. Espinosa-Magana and R. Salcedo, Molecules, 2011, 17(1), 34–35.
12. M. M. Rohmer and M. Bénard, Chem. Soc. Rev., 2001, 30, 340–354.
13. G. Parkin and R. Hoffmann, Angew. Chem., 1994, 106, 1530.
14. W. L. Li, H. T. Liu, T. Jian, G. V. Lopez, Z. A. Piazza, D. L. Huang, T. T. Chen, J. Su, P. Yang, X. Chen, L. S. Wang and J. Li, Chem. Sci., 2016, 7, 475–480.
15. Y. Ma, S. Bian, Y. Shi, X. Fan and X. Kong, ACS Omega, 2019, 4, 650–654.
16. R. Lü, H. Tangbo and Z. Cao, J. Nat. Gas Chem., 2017, 16, 70–77.
17. R. Lü, D. Liu, Y. Lu and S. Wang, J. Saudi Chem. Soc., 2016, 20, 303–306.
18. W. M. Li, Y. Li, C. Q. Xu, X. B. Wang, E. Vorpagel and J. Li, Inorg. Chem., 2015, 54, 11157–11167.
19. C. Q. Xu, X. G. Xiong, W. L. Li and J. Li, Eur. J. Inorg. Chem., 2016, 1395–1404.
20. S. Böttger, M. Gruber, J. Eike, J. E. Münzer, G. M. Bernard, N.-J. H. Kneusels, C. Poggel, M. Klein, F. Hampel, B. Neumüller, J. Sundermeyer, V. K. Michaelis, R. Tonner, R. R. Tykwinski and I. Kuzu, Inorg. Chem., 2020, 59, 12054–12064.
21. H. Schmidbaur, Gold Bull., 1990, 23, 11.
22. G. Jones, Gold Bull., 1983, 14, 102.
23. P. Pyykkö, Angew. Chem., 2004, 43, 4412–4456; P. Pyykkö, Inorg. Chim. Acta, 2004, 358, 4113–4130; P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967–1997; P. Pyykkö, Chem. Rev., 1997, 97, 597–636.
24. X. Gonze, F. Jollet, F. Abreu Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J.-M. Beuken, J. Bieder, A. Bokhanchuk, E. Bousquet, F. Bruneval, D. Caliste, M. Côté, F. Dahm, F. Da Pieve, M. Delaveau, M. Di Gennaro, B. Dorado, C. Espejo, G. Geneste, L. Genovese, A. Gerossier, M. Giantomassi, Y. Gillet, D. R. Hamann, L. He, G. Jomard, J. Laflamme Janssen, S. Le Roux, A. Levitt, A. Lherbier, F. Liu, I. Lukačević, A. Martin, C. Martins, M. J. T. Oliveira, S. Poncé, Y. Pouillon, T. Rangel, G.-M. Rignanese, A. H. Romero, B. Rousseau, O. Rubel, A. A. Shukri, M. Stankovski, M. Torrent, M. J. Van Setten, B. Van Troeye, M. J. Verstraete, D. Waroquiers, J. Wiktor, B. Xu, A. Zhou and J. W. Zwanziger, Comput. Phys. Commun., 2016, 205, 106–131.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
26. S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132(15), 154104.
27. N. A. W. Holzwarth, A. R. Tackett and G. E. A. Matthews, Comput. Phys. Commun., 2001, 135(3), 329–347.
28. T. P. Pogrebnaya, A. M. Pogrebnoi and L. S. Kudin, J. Struct. Chem., 2007, 48(6), 987–995.
29. W. Nakanishi, S. Hayashi and K. Narahare, J. Phys. Chem. A, 2008, 112, 13593–13599.
30. Y. Sevryugina, A. Y. Rogachev and M. A. Petrukina, Inorg. Chem., 2007, 46, 7870–7879.
31. R. G. Pearson, J. Am. Chem. Soc., 1963, 85(22), 3533–3539.
32. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
33. P. Pyykkö, Chem. Rev., 1988, 88, 563.
34. P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
35. P. Descaux and P. Pyykkö, Chem. Phys. Lett., 1976, 39(2), 300–303.
36. R. D. Shannon and C. T. Prewitt, Acta Crystallogr., 1961, 25, 925.
37. R. A. Evarestov, A. I. Panin and Y. S. Tverjanovich, J. Comput. Chem., 2021, 42, 242–247.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra07457e

---