Temperature switch of electrochemical Seebeck coefficient of Fe²⁺/Fe³⁺ via formation of [FeCl₄]²⁻/[FeCl₄]⁻

Abstract

The electrochemical Seebeck coefficient (α = dV/dT; V and T are the redox potential and temperature, respectively) is important parameter for thermoelectric conversion. Here, we found that α of Fe²⁺/Fe³⁺ in dimethyl sulfoxide (DMSO) with small amount of 19 M LiCl aqueous solution exhibits a crossover behavior from 1.4 mV K⁻¹ (20 °C ≤ T ≤ 40 °C) to ≈0 mV K⁻¹ (50 °C ≤ T ≤ 80 °C). The molar absorption (ε) spectra revealed that the crossover is ascribed to the transformation of the dominant Fe³⁺ complex from [FeL₆]³⁺ (L is solvent molecule) to [FeCl₄]⁻.

---

1 Introduction

Electrochemical Seebeck coefficient (α = dV/dT, V and T are the redox potential and temperature, respectively) is significant parameter for energy harvesting device, such as liquid thermoelectric conversion cell (LTE).^1–7 In this sense, the deep understanding of α in solute–solvent system is scientifically and technologically important. α(V) is equivalent to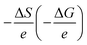 , where ΔS (ΔG) and e are the variation in the entropy (Gibbs free energy) and elementary charge (≥0), respectively. Then, the complex state of redox pair significantly influences α as well as V. For example, the V value of Fe²⁺/Fe³⁺ in methanol (MeOH) significantly decreases by 200 mV when the Fe complex state changes from [FeL₆]²⁺/[FeL₆]³⁺ (L is solvent molecule) to [FeCl₄]²⁻/[FeCl₄]⁻.⁸ In addition, the α value of Fe²⁺/Fe³⁺ significantly depends on the solvent and ranges from 0.14 mV K⁻¹ in glycerine to 3.60 mV K⁻¹ in acetone.⁹ Addition of water alters the α value of [Fe(CN)₆]⁴⁻/[Fe(CN)₆]³⁻ in organic solvent.¹⁰ In a technological point of view, temperature switch of the electrochemically-active redox pair is important because it not only can control of the α value but also change the V value discontinuously. The discontinuous change in V causes a substantially large α to realize a high performance LTE.

The Fe ion in solution is usually octahedrally coordinated by six Ls forming [FeL₆]²⁺ and/or [FeL₆]³⁺. Inada et al.¹¹ reported that Fe²⁺ is coordinated by six Ls in aqueous, MeOH, ethanol (EtOH), dimethyl sulfoxide (DMSO) solutions. Inoue et al.¹² reported that Fe³⁺ is also coordinated by six Ls in many organic solutions in which Fe(ClO₄)₃ is dissolved. Importantly, Fe³⁺ in many organic solutions forms [FeCl₄]⁻ if the solution contains Cl⁻.¹³ Nomura et al.⁸ reported that the complex state of Fe³⁺ in MeOH can be controlled by addition of Cl⁻; [FeCl₄]⁻ is formed above [Cl⁻] = 60 mM. Our idea to control the complex state is to bring the two complexes, e.g., [FeL₆]³⁺ and [FeCl₄]⁻, into competition and to unbalance them with heating and/or cooling.

In this work, we found that the α value of Fe²⁺/Fe³⁺ in DMSO with small amount of 19 M LiCl aqueous solution exhibits a crossover behavior from 1.4 mV K⁻¹ (20 °C ≤ T ≤ 40 °C) to ≈0 mV K⁻¹ (50 °C ≤ T ≤ 80 °C). The molar absorption (ε) spectra suggest that the crossover behavior of α can be ascribed to the temperature switch of the electrochemically-active redox pair from [FeL₆]²⁺/[FeL₆]³⁺ to [FeCl₄]²⁻/[FeCl₄]⁻. We further investigate the distribution of the redox potential against temperature and observed variation of the distribution.

2 Experimental methods

2.1 Solution

The solvent (DMSO) and solutes (dehydrated FeCl₂, dehydrated FeCl₃ and LiCl) were purchased from FUJIFILM Wako corp. and used as received. The solutions contain 0.5(1 − n_Fe³⁺) mM FeCl₂ and 0.5n_Fe³⁺ mM FeCl₃, where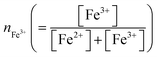 is the molar ratio of Fe³⁺. The sum of [Fe²⁺] and [Fe³⁺] was fixed at 0.5 mM. The [Cl⁻] value was controlled by adding small amount (0.1–0.4 vol%) of 19 M LiCl aqueous solution. We investigated DMSO solution containing 300 mM LiCl at n_Fe³⁺ = 0.5 as a prototypical solution of [FeCl₄]²⁻/[FeCl₄]⁻. We further investigate Cl⁻-free DMSO solution containing 0.25 mM Fe(ClO₄)₂·6.0H₂O (FUJIFILM Wako corp.) and 0.25 mM Fe(ClO₄)₃·7.1H₂O (FUJIFILM Wako corp.) as a prototypical solution of [FeL₆]²⁺/[FeL₆]³⁺.

2.2 UV-vis spectra

The ultraviolet-visible (UV-vis) absorption spectroscopy is a sensitive probe for the complex state, because Fe³⁺ complex exhibits characteristic absorption bands.^8,12–15 The absorption spectra were investigated with a spectrometer (V750, Jasco) equipped with a temperature control unit. The molar absorption coefficient (ε) was defined by −ln(I/I₀)/cd, where c, d (= 1 cm), I, and I₀ are [Fe³⁺], the thickness of the optical cell, transmission intensity of the solution, and that without cell.

2.3 Electrochemical properties

The thermal potential (V_T) at temperature difference (ΔT = T_H − T_L; T_H and T_L are the temperatures of hot and cold electrodes, respectively) was evaluated with use of a specially-designed thermocell.¹⁶ The electrolyte was filled in a 0.73 mm ϕ polytetrafluoroethylene (PTFE) cylinder. Both ends were sealed with Pt disks with an area of 0.42 cm². The two Pt electrodes were placed at a distance of 1.0 cm. T_H and T_L are monitored with T-type thermocouples and are independently controlled with Peltier modules. T_L was fixed at 22 °C T_H was manually controlled by stepwise variation of the input current to the Peltier device at intervals of ∼5 minutes.

To investigate the distribution of the redox potential, the redox potentials of Fe²⁺/Fe³⁺ in DMSO solution containing 0.3 vol% 19 M LiCl aqueous solution were investigated against n_Fe³⁺. The solutions contain 0.5(1 − n_Fe³⁺) mM FeCl₂ and 0.5n_Fe³⁺ mM FeCl₃. We prepared the sample cell at n_Fe³⁺ and reference cell at n_Fe³⁺ = 0.1. A Pt collecting electrode was inserted in each cell. The temperatures of the cells were the same in a constant temperature water bath. The two cells were connected with a salt bridge, which was prepared as follows. NaClO₄ (10 g per 100 mL) and agar (4 g per 100 mL) were added to water. Then, the solution was heated, dissolved, poured into a U-shaped tube, and cooled to harden. The relative potential between the sample and reference cells were measured every five minutes. The mean values and standard deviations were evaluated from nine data (Table S1†).

3 Results and discussion

3.1 Properties of the two Fe complex states

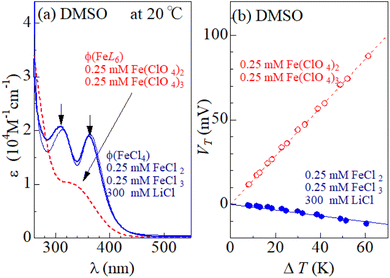
Fig. 1(a) shows molar absorption coefficient (ε) spectra of DMSO solution containing 0.25 mM FeCl₂, 0.25 mM FeCl₃, and 300 mM LiCl (solid curve) and that containing 0.25 mM Fe(ClO₄)₂6.0H₂O and 0.25 mM Fe(ClO₄)₃7.1H₂O (broken curve) at 20 °C. In the latter solution, [FeL₆]²⁺/[FeL₆]³⁺ is stable because there is no Cl⁻ in the solution. The ε spectra (broken curve) of the latter solution shows broad absorption at 340 nm due to electron transfer L and Fe³⁺. The ε spectra (solid curve) of the former solution that contains 300 mM Cl⁻ shows rather sharp absorption bands at 310 nm and 360 nm, which are ascribed to electronic transitions within [FeCl₄]⁻.^8,14 The intensities of the 310 nm and 360 nm bands are almost independent of T, as exemplified by the 80 °C spectrum (thin solid curve). Thus, [FeL₆]³⁺ and [FeCl₄]⁻ dominates the latter and former solutions, respectively. Hereafter, we refer the respective ε spectra as ϕ(FeL₆) and ϕ(FeCl₄). Fig. 1(b) shows the thermal voltage (V_T) against ΔT in each solution. In both the solutions, V_T changes in proportion to ΔT. In the solution of [FeL₆]²⁺/[FeL₆]³⁺ (open circles), α (= 1.4 mV K⁻¹) is positive and large. In the solution of [FeCl₄]²⁻/[FeCl₄]⁻ (closed circles), α (= −0.2 mV K⁻¹) is negative and small.

Fig. 1 (a) Molar absorption coefficient (ε) spectra of DMSO solution containing 0.25 mM FeCl₂, 0.25 mM FeCl₃, and 300 mM LiCl (thick solid curve) and that containing 0.25 mM Fe(ClO₄)₂6.0H₂O and 0.25 mM Fe(ClO₄)₃7.1H₂O (thick broken curve) at 20 °C. Thin solid curve represent the ε spectrum of the former solution at 80 °C. Downward arrows indicates optical transitions within [FeCl₄]⁻. (b) Thermal voltage (V_T) of Fe²⁺/Fe³⁺ against temperature difference (ΔT) in each solution. Broken and solid straight lines are results of the least-squares fitting.

3.2 Temperature control of Fe complex state

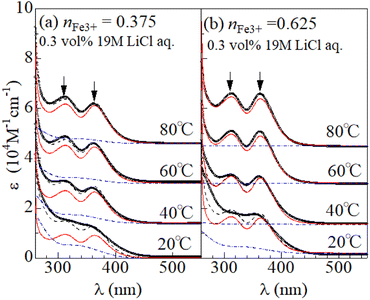
Fig. 2(a) shows temperature variation of the ε spectra (open circles) of DMSO solution containing 0.3 vol% 19 M LiCl aqueous solution ([Cl⁻] = 57 mM) at n_Fe³⁺ = 0.375. The spectrum at 20 °C shows broad absorption around 360 nm. The spectrum at 40 °C shows two sharp absorption bands at 310 nm and 360 nm (downward arrow), which can be ascribed to optical transitions within [FeCl₄]⁻.^8,14 The intensities of the 310 and 360 nm bands increases with further increase in T. A similar temperature variation is observed in the ε spectra at n_Fe³⁺ = 0.675 [Fig. 2(b)].

Fig. 2 Molar absorption coefficient (ε, open circles) spectra of DMSO solutions containing 0.3 vol% of 19 M LiCl aqueous solution at (a) n_Fe³⁺ = 0.375 and (b) 0.625. Downward arrows indicate electronic transition within [FeCl₄]⁻. The spectra were decomposed into ϕ(FeL₆) and ϕ(FeCl₄). Red, dashed blue, and broken black curves are (1 − n_FeCl4)ϕ(FeL₆), n_FeCl4ϕ(FeCl₄), and (1 − n_FeCl4)ϕ(FeL₆) + n_FeCl4ϕ(FeCl₄), respectively, where n_FeCl4 is the [FeCl₄]⁻ ratio.

To evaluate the [FeCl₄]⁻ ratio 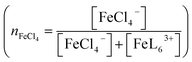, we decomposed the spectra into ϕ(FeL₆) and ϕ(FeCl₄) as (1 − n_FeCl4)ϕ(FeL₆) + n_FeCl4ϕ(FeCl₄). Red, dashed blue, and broken black curves in Fig. 2 are (1 − n_FeCl4)ϕ(FeL₆), n_FeCl4ϕ(FeCl₄), and (1 − n_FeCl4)ϕ(FeL₆) + n_FeCl4ϕ(FeCl₄), respectively. Fig. 3 shows the n_FeCl4 values against T. We tried to reproduce the n_FeCl4–T plot based on the equilibrium equation, [FeL₆]³⁺ + 4Cl⁻ ↔ [FeCl₄]⁻ + 6L. The equilibrium constant K is represented as 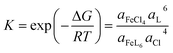, where ΔG, R, and a_i is, the standard reaction Gibbs energy, the gas constant, and activity of i, respectively. a_FeCl4, a_L, a_FeL6, and a_Cl are 0.0005n_Fe³⁺n_FeCl4, 1, 0.0005n_Fe³⁺(1 − n_FeCl4), and 0.057, respectively. The calculation fails to reproduce the experimental data, because 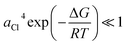for any positive ΔG (Fig. S1†). We suspect that the significant T dependence of n_FeCl4 is ascribed to change in the solution state possibly due to (1) 0.3 vol% water and/or (2) high melting point (= 19 °C) of DMSO.

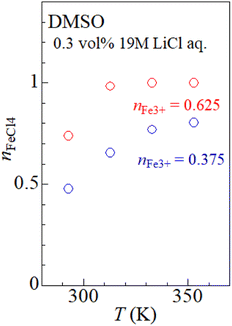Fig. 3 [FeCl₄]⁻ ratio (n_FeCl4) against temperature (T) at n_Fe³⁺ = 0.375 and 0.625. The n_FeCl4 values are evaluated by decomposition of the ε spectra (see text).

3.3 Distribution of redox potential

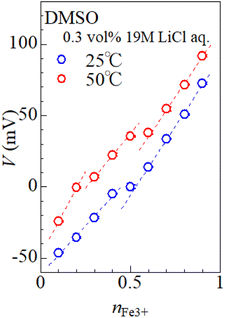
Fig. 4 shows relative potential (V) against n_Fe³⁺ in DMSO solution containing 0.3 vol% 19 M LiCl aqueous solution. The potential at n_Fe³⁺ = 0.5 and at 25 °C was set to be 0.0 mV. At n_Fe³⁺ = 0.5, the V value at 50 °C is 21.9 mV higher than the value at 25 °C. At 25 °C, V increases with n_Fe³⁺ below n_Fe³⁺ = 0.4, as indicated by broken line. The slope of the n_Fe³⁺–V plot is significantly suppressed at 0.4–0.5. With further increase in n_Fe³⁺ beyond 0.6, V again linearly increases with n_Fe³⁺. At 50 °C, V linearly increases with n_Fe³⁺ below n_Fe³⁺ = 0.2. The slope of the n_Fe³⁺–V plot is significantly suppressed at 0.2–0.3 and 0.5–0.6. With further increase in n_Fe³⁺ beyond 0.7, V again linearly increases with n_Fe³⁺. The overall increase in V with n_Fe³⁺ is reasonably ascribed to the second term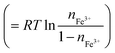 of the Nernst's equation.

Fig. 4 Relative potential (V) against n_Fe³⁺ in DMSO solution containing 0.3 vol% 19 M LiCl aqueous solution. The solutions contain 0.5(1 − n_Fe³⁺) mM FeCl₂ and 0.5n_Fe³⁺ mM FeCl₃. The potential at n_Fe³⁺ = 0.5 and at 25 °C was set to be 0.0 mV. Broken straight lines are eye-guided ones. The error bars are within the symbol size.

The origin of the flat regions in the n_Fe³⁺–V plot is considered as follows. When the redox potential of Fe²⁺/Fe³⁺ has a distribution, the Fe ions with lower potential are selectively oxidized. In this sense, the n_Fe³⁺–V plot contains information on the potential distribution. The flat region in the plot has a narrow potential distribution due to a well-defined redox process. At 25 °C, we observed a flat region at ≈0 mV. At 50 °C, we observed flat regions at ≈0 mV and 40 mV. We ascribed these regions to respective Fe complexes, i.e., [FeL₆]²⁺/[FeL₆]³⁺ and [FeCl₄]²⁻/[FeCl₄]⁻, because such complexes show well-defined redox processes. Recall that [FeCl₄]²⁻/[FeCl₄]⁻ becomes dominant at high T (Fig. 2). Then, it is reasonable to ascribe the flat regions at 0 and 40 mV to [FeL₆]²⁺/[FeL₆]³⁺ and [FeCl₄]²⁻/[FeCl₄]⁻, respectively. The present assignment apparently contradict with the previous report⁸ in MeOH that the redox potential of [FeCl₄]²⁻/[FeCl₄]⁻ is 200 mV lower than that of [FeL₆]²⁺/[FeL₆]³⁺. We note that in this report the [FeCl₄]²⁻/[FeCl₄]⁻ complex is stabilized with adding of excess Cl⁻, which can significantly alter the V value. In the present experiment, the stability of the complex is controlled only by temperature without changing the solution composition.

3.4 Temperature change of electrochemical Seebeck coefficient

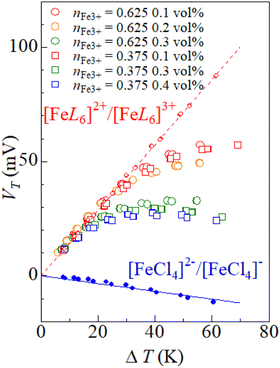
Fig. 5 shows the V_T values against ΔT in DMSO solution containing small amount of 19 M LiCl aqueous solutions. Broken and solid straight lines represent the relation in the solutions of [FeL₆]²⁺/[FeL₆]³⁺ and [FeCl₄]²⁻/[FeCl₄]⁻, respectively. In solutions with 0.1 vol% 19 M LiCl aqueous solution (red symbols), the ΔT–V_T plot traces the broken line in the small ΔT region (≤30 °C). The data points begins to deviate from the broken line above ΔT ≥ 30 °C. The α value in the high ΔT region (≥40 °C) is ≈0.4 mV K⁻¹. In solutions with 0.4 vol% 19 M LiCl aqueous solution (blue symbols), the ΔT–V_T plot traces the broken line in the small ΔT region (≤20 °C). The data points begin to deviate from the broken line above ΔT ≥ 30 °C. The α value in the large ΔT region (≥30 °C) is ≈0.0 mV K⁻¹. We emphasize that the α value (≈0.0 mV K⁻¹) in the high ΔT region is close to the value (= −0.2 mV K⁻¹) in the solution of [FeCl₄]²⁻/[FeCl₄]⁻ (broken line). This clearly indicates that the crossover behavior of α is ascribed to the temperature switch of the electrochemically-active redox pair from [FeL₆]²⁺/[FeL₆]³⁺ to [FeCl₄]²⁻/[FeCl₄]⁻.

Fig. 5 Thermal potential (V_T) of Fe²⁺/Fe³⁺ against temperature difference (ΔT) in DMSO solution containing small amount of 19 M LiCl aqueous solutions. The solutions contain 0.5(1 − n_Fe³⁺) mM FeCl₂ and 0.5n_Fe³⁺ mM FeCl₃. Small closed and open circles are the data points of solution containing 0.25 mM FeCl₂, 0.25 mM FeCl₃, and 300 mM LiCl and that containing 0.25 mM Fe(ClO₄)₂6.0H₂O and 0.25 mM Fe(ClO₄)₃7.1H₂O, respectively. Solid and broken straight lines are results of the least-squares fitting, which represent the prototypical behavior of the solutions of [FeCl₄]²⁻/[FeCl₄]⁻ and [FeL₆]²⁺/[FeL₆]³⁺, respectively.

Finally, let us quantitatively analyze the ΔT–V_T plot including the temperature switch of the electrochemically-active redox pair. In the small ΔT region where [FeL₆]²⁺/[FeL₆]³⁺ is dominant, V_T is expressed as V_T = V(FeL₆, T_H) − V(FeL₆, T_L) = α(FeL₆)ΔT, where V(FeL₆, T_H) and α(FeL₆) are the redox potential of [FeL₆]²⁺/[FeL₆]³⁺ at T_H and α of [FeL₆]²⁺/[FeL₆]³⁺, respectively. In the large ΔT region where [FeCl₄]²⁻/[FeCl₄]⁻ is dominant, V_T is expressed as V_T = V(FeCl₄, T_H) − V(FeL₆, T_L) = α(FeCl₄)ΔT + [V(FeCl₄, T_L) − V(FeL₆, T_L)], where V(FeCl₄, T_H) and α(FeCl₄) are the redox potential of [FeCl₄]²⁻/[FeCl₄]⁻ at T_H and α of [FeCl₄]²⁻/[FeCl₄]⁻, respectively. We note that the reference for the redox potential is V(FeL₆, T_L), not V(FeCl₄, T_L), even in the large ΔT region. With extrapolation of the ΔT–V_T plot toward T_L, V(FeCl₄, T_L) − V(FeL₆, T_L) is evaluated to be ≈30 mV. The value (≈30 mV) is close to the potential difference (≈40 mV; see Fig. 4) between [FeL₆]²⁺/[FeL₆]³⁺ and [FeCl₄]²⁻/[FeCl₄]⁻. This again indicates that the crossover behavior of α is ascribed to the temperature switch of the electrochemically-active redox pair from [FeL₆]²⁺/[FeL₆]³⁺ to [FeCl₄]²⁻/[FeCl₄]⁻. In the present solution system, V_T changes continuously with temperature because the potential difference (≈40 mV) between the two complexes is comparable to αΔT. If the potential difference could be made much larger than αΔT, a discontinuous change in V_T and a substantially large α could be realized.

4 Conclusion

In conclusion, we found that α of Fe²⁺/Fe³⁺ in DMSO with small amount of 19 M LiCl aqueous solution exhibits a crossover behavior from 1.4 mV K⁻¹ (20 °C ≤ T ≤ 40 °C) to ≈0 mV K⁻¹ (50 °C ≤ T ≤ 80 °C), which is ascribed to the temperature switch of the electrochemically-active redox pair from [FeL₆]²⁺/[FeL₆]³⁺ to [FeCl₄]²⁻/[FeCl₄]⁻. We believe that the temperature switch of the complex species is an effective strategy to develop a solvent–solute system that exhibits a substantially large α.

Author contributions

Y. N. has performed all the experiments and analyses. D. I. has set up the research equipment and assisted in the measurements. Y. M. has planned the research and wrote paper.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by JSPS KAKENHI (Grant Numbers 22J11837) and Murata Science foundation.

Notes and references

1. (a) T. Ikeshoji, Bull. Chem. Soc. Jpn., 2000, 60, 1505; (b) T. Kim, J. S. Lee, G. Lee, H. Yoon, J. Yoon, T. J. Kangd and Y. H. Kim, Nano Energy, 2017, 31, 160; (c) H. Zhou, T. Yamada and N. Kimizuka, J. Am. Chem. Soc., 2016, 138, 10502; (d) I. Quickenden and Y. Mua, J. Electrochem. Soc., 1995, 142, 3985; (e) Y. Mua and T. I. Quickenden, J. Electrochem. Soc., 1996, 143, 2558; (f) J. Kawamura, M. Shimoji and H. Hoshino, J. Phys. Soc. Jpn., 1981, 50, 194; (g) A. Schiraldi, E. Pezzati and P. Baldini, J. Phys. Chem., 1985, 89, 1528; (h) M. Sindhuja, B. Lohith, V. Sudha, G. R. Manjunath and S. Harinipriya, Mater. Res. Express, 2017, 4, 075513.
2. B. Yu, J. Duan, H. Cong, W. Xie, R. Liu, X. Ahuang, H. Wang, B. Qi, M. Xu and L. Wan, Science, 2020, 370, 342.
3. J. H. Kim, J. H. Lee, E. E. Palen, M.-S. Suh, H. H. Lee and R. J. Kang, Sci. Rep., 2019, 9, 8706.
4. J. Duan, G. Feng, B. Yu, J. Li, M. Chen, P. Yang, J. Feng, K. Liu and J. Zhou, Nat. Commun., 2018, 9, 5146.
5. S. W. Lee, Y. Yang, H.-W. Lee, H. Ghasemi, D. Kraemer, G. Chen and Y. Cui, Nat. Commun., 2014, 5, 3942.
6. M. A. Buckingham, F. Marken and L. Aldous, Sustainable Energy Fuels, 2018, 2, 20717.
7. A. Wake, D. Inoue and Y. Moritomo, Appl. Phys. Express, 2022, 15, 054002.
8. Y. Nomura, D. Inoue and Y. Moritomo, RSC Adv., 2022, 12, 17932.
9. D. Inoue, H. Niwa, H. Nitani and Y. Moritomo, J. Phys. Soc. Jpn., 2021, 90, 033602.
10. D. Inoue, Y. Fukuzumi and Y. Moritomo, Jpn. J. Appl. Phys., 2020, 59, 037001.
11. Y. Inada, H. Hayashi, K. Sugimoto and S. Funahashi, J. Phys. Chem., 1999, 103, 1401.
12. D. Inoue, T. Komatsu, H. Niwa, H. Nitani, H. Abe and Y. Moritomo, Jpn. J. Appl. Phys., 2022, 61, 1120003.
13. D. Inoue, T. Komatsu, H. Niwa, T. Ina, H. Nitani, H. Abe and Y. Moritomo, J. Phys. Soc. Jpn., 2022, 91, 0094605.
14. K. Asakura, M. Nomura and H. Kuroda, Bull. Chem. Soc. Jpn., 1985, 58, 1543.
15. (a) L. N. Mulay and P. W. Selwood, J. Am. Chem. Soc., 1955, 77, 2693; (b) R. J. Night and R. N. Sylva, J. Inorg. Nucl. Chem., 1975, 37, 779; (c) H.-J. Benkelberg and W. Peter, J. Phys. Chem., 1995, 99, 5214; (d) R. A. Danforth and B. Kohler, Chem. Phys. Lett., 2017, 683, 315; (e) G. Bunker, Nucl. Instrum. Methods Phys. Res., 1984, 207, 437.
16. Y. Fukuzumi, Y. Hinuma and Y. Moritomo, Jpn. J. Appl. Phys., 2019, 58, 065501.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra07886d

---