Open Access Article
Open Access ArticleRole of site selective substitution, magnetic parameter tuning, and self heating in magnetic hyperthermia application: Eu-doped magnetite nanoparticles
Krishna Priya Hazarika and
J. P. Borah *
*
Nanomagnetism Group, Department of Physics, National Institute of Technology Nagaland, Dimapur 797103, Nagaland, India. E-mail: jpborah@rediffmail.com
First published on 8th February 2023
Abstract
Various researchers have provided considerable insight into the fundamental mechanisms behind the power absorption of single-domain magnetic nanoparticles (MNPs) in magnetic hyperthermia applications. However, the role of all parameters pertinent to magnetic relaxation continues to be debated. Herein, to explore the role of magnetic anisotropy with the site selective substitution related to magnetic relaxation has generally been missing, which is critically essential in respective of hyperthermia treatment. Our study unravels contradictory results of rare earth (RE) interaction effects in ferrite to that of recently reported literature. Despite this, rare earth atoms have unique f-block properties, which significantly impact the magnetic anisotropy as well as the relaxation mechanism. Here, we use appropriate Eu doping concentration in magnetite and analyze its effect on the matrix. Furthermore, a positive SAR can effectively reduce the relative dose assigned to a patient to a minimal level. This study indicates that the introduction of Eu ion positively influenced the heating efficiency of the examined magnetite systems.
1. Introduction
Magnetic nanoparticles (MNPs) enable new biomedical strategies, including magnetic fluid hyperthermia (MFH), drug delivery, biosensing, and bioimaging.1–3 In order to determine the self-heating efficiency and magnetic relaxation of MNPs, it is essential to know and control intrinsic particle parameters, spatial arrangement, and colloidal properties. As a result, these parameters have an enormous impact on MFH as a cancer therapy, in which colloidal MNPs convert energy losses into heat under an AC magnetic field, limiting Hergt and Dutz criteria.4 Currently, MNPs with tuned properties, including their size, magnetic anisotropy, and saturation magnetization, are being designed for improved heating efficiency. The consequence of particle-intrinsic parameters and experimental specifications computed for optimum heating is yet to be fully understood in actual MFH experiments. It is well established that for their excellent biocompatibility, high thermal efficiency, and superparamagnetic properties, Fe3O4 MNPs have been studied extensively as a heating aid for MFH.5,6 In inclusion of all the properties mentioned above, Fe3O4 MNPs are still challenging due to the instability in oxidation states, which impact the structure, magnetic states, and optimal self-heating efficacy for MFH application.7,8Owing to the exceptional f-block arrangement and the remarkable optical and magnetic states of rare earth (RE) ions, researchers have been showing great interest; studies have shown that the addition of such dopants (Gd3+, Tb3+, Y3+, Eu3+, Dy3+) has profound effects on the final product matrix. Specially, RE ions substituted in spinel ferrite structure can lower the lattice deformation along with changes in the magnetization properties of specific materials.2,9–13 Moreover, from the previous literature, Slimani et al. reported the influence of Sm3+ and Er3+ doping on the CoFe2O4 system and found that saturation magnetization increases with an increase in doping concentrations.14 Additionally, the anisotropy-dependent magnetic coercive field is probably affected by the dopant concentration. However, when La3+ and Y3+ ions are both substituted in nano spinel ferrites, it will change the coercivity and magnetic anisotropy in an enhanced manner, as suggested by Almessiere et al.15
Among these, Eu-doped Fe3O4 MNPs draw significant attention, predominantly in clinical experimentations, due to the negligible toxicity of Eu3+ and its unique magnetic and optical properties.16 Therefore, engineered Eu-doped nanoparticles provoke interest in multimodal therapeutic applications owing to their enhanced magnetic resonance (MR) imaging properties and the nature of biocompatibility.16,17 Furthermore, because of the analogous ionic radii of Fe and Eu, the lesser doping concentration would not lead to the variation of the structural configuration, which pays a great deal of prominence to the researchers.
This work presents how a small amount of Eu doping in the Fe3O4 system can modify the crystal structure and magnetic states, which enhance the self-heating properties of MNPs, making it an excellent candidate for magnetic hyperthermia applications.
2. Materials and methods
2.1. Experimental details
The detailed procedure for synthesizing the studied materials is illustrated in our previous work.9 Therefore, we report only a concise expression of our primary procedure.All samples were synthesized via co-precipitation technique as follows: FeCl3 (ferric chloride), FeCl2 (ferrous chloride), and rare earth compound europium (Eu) acetate were dissolved in N2H4 (hydrazine) mixed double-deionized water in such ratios to form the final material with stoichiometric formula (Fe3+)A·[Eu3+x Fe2+(1−x) Fe3+]B·O4. In this paper, we take Eu percentages as 2%, 5%, and 7%, respectively, and they are further abbreviated as FE2, FE5, and FE7. The pH was kept constant for all the synthesized samples, which is 7–8. The precipitate obtained from the experiments was dehydrated in a vacuum oven and finally hand-milled to powder. In the experimental system, Eu3+ is expected to be substituted by the Fe3+/Fe2+ sites of the spinel ferrite (Fe3O4) matrix.
2.2. Characterization of magnetic nanoparticles
The crystallographic information and phase purity of the customized MNPs were examined via X-ray diffraction (Rigaku, Ultima IV) with Cu Kα radiation (λ = 1.5406 Å) varying 2θ from 10 to 90° in 0.02 steps. A Fourier transform infrared spectra (FTIR) (Cary 630, Agilent Technology) was exercised to identify the functional groups and states of elements. A scanning electron microscope (FESEM; ZEISS, Gemini 300) was used to examine the morphology of the processed MNPs. The compositional assay of the synthesized MNPs was computed by energy dispersive spectroscopy (EDS) attached with SEM. The average particle size and morphology, alongside d-spacing and SAED (selected area electron diffraction) inset, was studied via a high-resolution transmission electron microscope (TEM; JEOL, JEM 2100). X-ray photoelectron spectroscopy (XPS) (Thermo Fisher Scientific, Excalab Xi+ with Al Kα as the source of X-ray) is operated to investigate the chemical and electronic states of Eu in the Fe3O4 matrix. The thermogravimetric study (TGA) was conducted via Hitachi STA7300 thermal analyzer from room temperature to 800 °C under the N2 domain. Magnetic characteristics of the synthesized MNPs were analyzed by a vibrating sample magnetometer (VSM; Lakeshore, 7410 series) and electron spin resonance (ESR; JEOL, JES-FA200). An induction heating setup (Easy Heat-8310, Ambrell make, U.K.) is operated to examine the self-heating study of the processed samples.3. Results & discussion
3.1. Structural and morphological studies
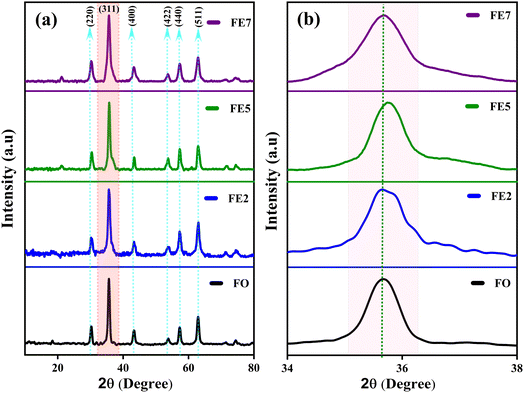
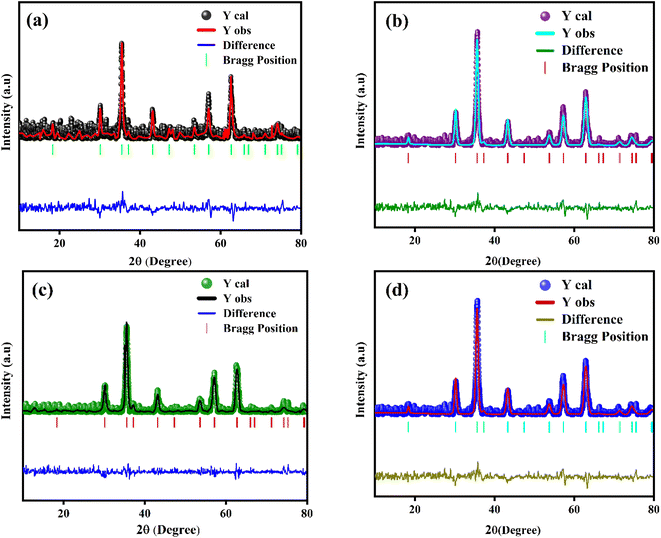
The powder XRD scans of prepared Eu-doped Fe3O4 MNPs are illustrated in Fig. 1. The observed XRD peak positions fit satisfactorily with the magnetite phase18 and also display the high crystallinity of these NPs. Furthermore, the reflections from the atomic planes (220), (311), (400), (422), (440), and (511) are identified and confirmed from the single-phase cubic spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Herein, we have noticed that the XRD peaks are shifted to a lower angle for the doped samples, indicating the impact of doping in the product matrix.16 Furthermore, we have employed Rietveld refinement (RR) via Full Proof software to understand the structural parameters, the distribution of cations, and cell constants, as depicted in Fig. 2.19,20 Fig. 2 shows the fine accordance of the experimental and theoretical graphs, with lower standards of numerous R-factors and Goodness of fit χ2 (∼2).14,20
m. Herein, we have noticed that the XRD peaks are shifted to a lower angle for the doped samples, indicating the impact of doping in the product matrix.16 Furthermore, we have employed Rietveld refinement (RR) via Full Proof software to understand the structural parameters, the distribution of cations, and cell constants, as depicted in Fig. 2.19,20 Fig. 2 shows the fine accordance of the experimental and theoretical graphs, with lower standards of numerous R-factors and Goodness of fit χ2 (∼2).14,20
Essentially, the synthesized product matrix comprises 56 atoms, containing 32 oxygen atoms, where 32 octahedral (B) and 64 tetrahedral (A) sites are in the unit cell, respectively. In the crystal structure of Eu doped Fe3O4 along with the different Wyckoff sites occupied by the Fe and O, respectively, shows Fe3+ cations occupying 8a sites at (1/8, 1/8, 1/8), Fe3+/Fe2+ cations occupying 16d sites at (1/2, 1/2, 1/2), and oxygen anions with reference to 32e position at (u,u,u).21,22
Moreover, from Fig. 3 (generated from VESTA) and the cation distribution from Rietveld Refinement (RR), it can be visualized that Eu ions opt to be in the octahedral (B) sites rather than the tetrahedral (A) sites. An increasing trend for lattice parameters and cell volume can be seen in Fig. 3, implying the developed strain and dislocation density with an enlargement in average crystallite size. There is a possibility that an increment of the lattice parameter is developed due to the slightly larger ionic radii of Eu in comparison to Fe. Additionally, the effective incorporation of Eu3+ ions in the magnetite system can be clarified from cation distribution, enclosed in Table 1. Based on cation distribution, the values of cationic radii per molecule at the tetrahedral (rA) and octahedral (rB), oxygen positional parameter, jump length of the tetrahedral (LA) and octahedral (LB), dislocation density (ρD), lattice strain (ε), cell volume, tetrahedral bond-length (A–O), octahedral bond length (B–O), and crystallite size for the characterized samples have been computed and enclosed in Table 1. According to Table 1, LA and LB follow an increasing manner with an increment of crystallite size. Increased bond length (A–O/B–0) can be predicted with this improved jumping length (LA and LB), which may be another reason for the increased cell volume. Aside from this, the LA value is also larger than LB, which further suggests that the electron hopping between cations at A and B sites is less likely than between B and B sites. The changing dislocation density with doping reflects the impact of the densification process with Eu doping concentration, as the physical properties of spinels are sensible to the cation's nature, valence state, and distribution on A and B sites. Following our cationic distribution analysis, the tetrahedral radii (rA) increment is almost trivial in comparison to the octahedral radii (rB), signifying that Eu ions prefer to alter Fe ions in the B sites. Furthermore, the strength of magnetic exchange interaction is directly dependent on bond angles and inversely dependent on interionic distances, and it can be inveterate by analyzing magnetic parameters.11,23 Besides, Eu doping in our respective ferrite systems enriched the bond length (A–O/B–O) and bond angle, as shown in Table 1. The rising trend of bond angle and bond length may arise due to cation/anion vacancies, finite size effect, lattice strain, lattice stress,24 etc. The aforementioned results indicate that Eu ions give primacy to B-sites rather than the A-sites of the Fe3O4 system.
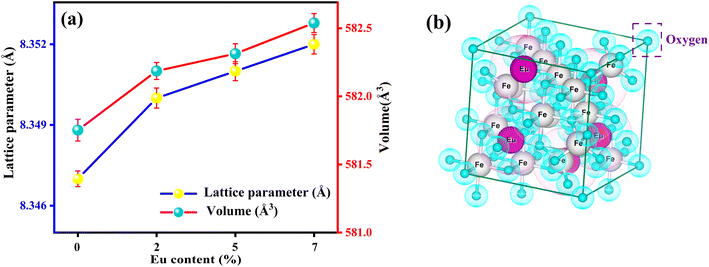 | ||
| Fig. 3 (a) Deviation of lattice constant and cell volume with the Eu-doping concentration (b) polyhedron representation of face-centered cubic (fcc) spinel structure of FE5 MNPs. | ||
| Eu content | 0.0 | 0.2 | 0.5 | 0.7 |
| Cation distribution | Fe3+[Fe2+Fe3+] O2 | δ = 0 [Fe3+0.996]A [Eu3+0.431Fe2+0.301Fe3+1.268]B O4 | δ = 0 [Fe3+0.998]A [Eu3+0.567Fe2+0.266Fe3+1.166]B O4 | δ = 0 [Fe3+0.999]A [Eu3+0.496Fe2+0.262Fe3+1.241]B O4 |
| Crystallite size (nm) | 13.13 | 15.37 | 15.71 | 18.79 |
| U | 0.25 | 0.25 | 0.26 | 0.25 |
| rA (Å) | 1.86 | 1.86 | 1.86 | 1.87 |
| rB (Å) | 2.04 | 2.05 | 2.06 | 2.08 |
| A–O (Å) | 0.06 | 0.07 | 0.07 | 0.08 |
| B–O (Å) | 3.09 | 3.11 | 3.13 | 3.16 |
| LA (Å) | 3.61 | 3.62 | 3.63 | 3.63 |
| LB (Å) | 2.95 | 2.95 | 2.96 | 2.97 |
| ε | 0.004 | 0.006 | 0.007 | 0.005 |
| Cell volume (Å) | 581.75 | 582.28 | 582.31 | 582.53 |
| ρD (×10−2) | 0.41 | 0.43 | 0.38 | 0.36 |
| θ1 (B–O–A)° | 123.75 | 123.79 | 123.80 | 123.82 |
| θ2 (A–O–B)° | 123.77 | 123.77 | 123.78 | 123.80 |
| θ3 (B–O–B)° | 92.12 | 92.13 | 92.13 | 92.14 |
| θ4 (B–O–B)° | 54.21 | 54.21 | 54.22 | 54.22 |
| θ5 (A–O–A)° | 78.92 | 78.94 | 78.95 | 78.97 |
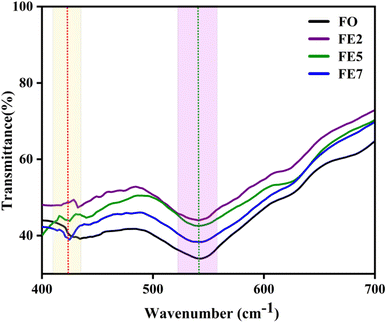
FTIR spectra of Eu-doped magnetite MNPs are shown in Fig. 4 within the frequency range of 400 to 700 cm−1. The spectrum of all the synthesized MNPs exhibits two distinct absorption bands, ∼428 and ∼540 cm−1, which upholds the structure of the spinel ferrite.25 The absorption bands (ν1) ∼540 cm−1 and (ν2) ∼428 cm−1 arise due to the Fe–O stretching vibration of the tetrahedral metal complex and an octahedral metal complex, respectively.26 It is expected that the metal–oxygen bond length at both tetrahedral and octahedral sites will change with doping concentration because of the stress/strain developed in the lattice site. Fig. 4 reflects the shifting of the absorption band (ν2) ∼428 cm−1 towards the higher wavenumber side, which affirms the effect of Eu ions on the octahedral sites of the Fe3O4 system, which upholds the calculated XRD results.
Fig. 5 shows the surface morphology of the characterized Eu-doped magnetite NPs. The SEM micrographs exhibit berry-like, non-uniform, and nearly spherical morphology towards agglomeration. As a result of their mutual magnetic interactions and high surface energies, the nanoparticles tend to agglomerate, which further matches the TEM analysis.
Fig. 6 portrays the TEM micrographs of the synthesized nanoparticles, which elucidates that the majority of the MNPs sound nearly spherical in shape and nearly agglomerated. The particle size calculated by lognormal distribution is 15 ± 2, 16 ± 2, 17 ± 3, and 18 ± 2 nm for FO, FE2, FE5, and FE7 MNPs, respectively, which is in accordance with the XRD results. There are concentric rings with spots on the SAED pattern, demonstrating the polycrystalline nature of the nanoparticles.27 The spotty rings correspond to the Bragg reflection planes (220), (311), (400), (422), (511), and (440), respectively, which upholds the XRD findings. Herein, the d-spacing corresponding to the (311) plane measured from the GATAN software perfectly fits the XRD analysis. It has been observed from Fig. 6 that Eu doping results in an apparent increase in particle size, which can be accredited to the replacement of Eu ions in the Fe ion sites in the Fe3O4 matrix, leading to the distortion in the lattice and affecting the particle size and shape. As shown in Fig. 7, the elemental mapping and composition of the nanoparticles are close to the stoichiometric one, which confirms the presence of Eu in the Fe3O4 system.
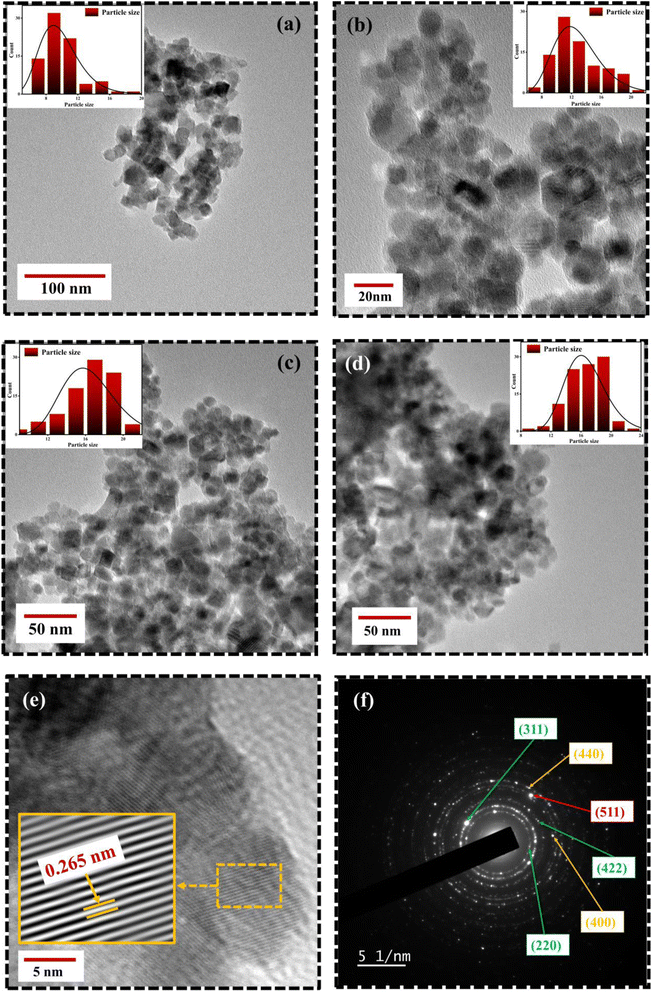 | ||
| Fig. 6 TEM micrographs of Eu doped Fe3O4 NPs (a) FO NPs (b) FE2 NPs(c) FE5 NPs (d) FE7 NPs (e) HRTEM image; d-spacing of (311) plane with IFFT zoom micrograph (f) SAED image of FE5 NPs. | ||
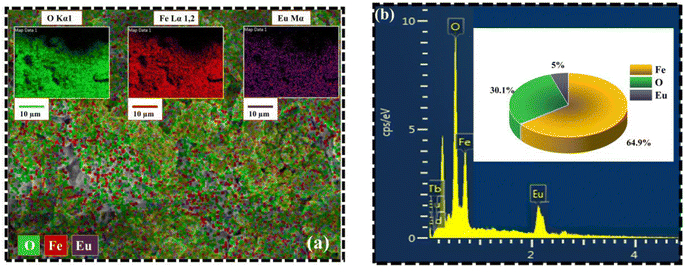 | ||
| Fig. 7 Elemental analysis of synthesized MNPs (a) Elemental mapping from SEM micrograph (b) EDX spectra of FE5 MNPs. | ||
The high-resolution Fe 2p core electron scan of the synthesized MNPs, directing the two spin–orbital characteristics of 2p3/2 and 2p1/2 at the peaks ∼710 eV and ∼723 eV, is illustrated in Fig. 8(a). The graph indicates that the valence states of Fe ions in the synthesized MNPs are 2+ and 3+10. The deconvolution of Fe 2p3/2 and Fe 2p1/2 at peaks ∼710 eV and ∼724 eV signifies the bond formation caused by the tetrahedral and octahedral sites. Moreover, we studied the effect of Eu ions in the Fe3O4 matrix. A peak at ∼134 eV indicates that Eu 4d5/2 ions are in octahedral bonding with oxygen. This study shows that Eu ion doping may cause alternations in cation rearrangement and is correlated with VSM analysis.28 An exemplary Eu 4d spectrum displaying the spin–orbital characteristics of 4d5/2 and Eu 4d3/2 at peaks of 134 eV and 143 eV is shown in Fig. 8(b). Accordingly, all synthesized samples exhibit a 3+ valence state. A deconvolution of the Eu 4d scan reveals the existence of two bonds that result from Eu ions occupying tetrahedral and octahedral sites. The complete survey spectra in Fig. 8(c) confirm that the Eu ion is appropriately substituted in the Fe3O4 structure.
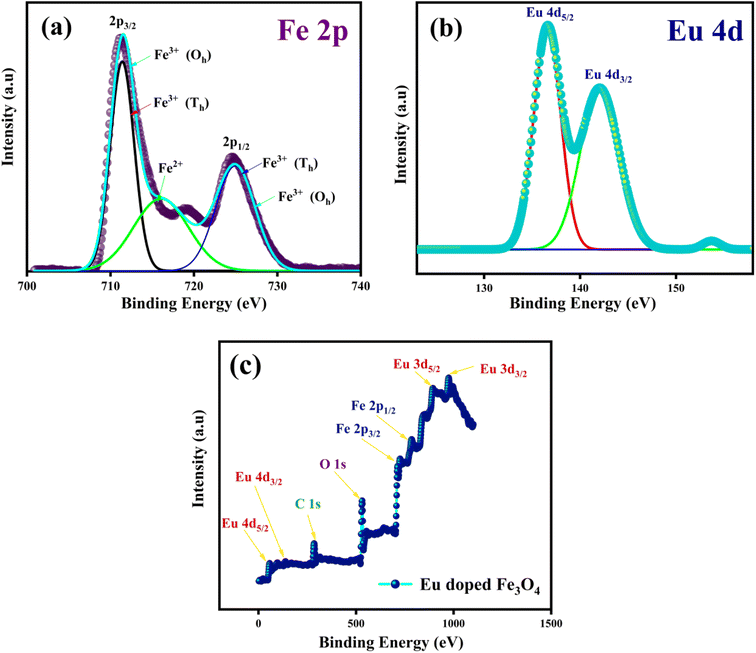 | ||
| Fig. 8 XPS scans of Eu doped Fe3O4 (FE7); (a) Fe 2p spectra (b) Eu 4d spectra (c) complete survey of FE7 MNPs. | ||
3.2. Thermogravimetric analysis (TGA)
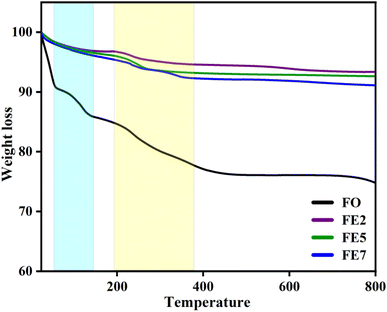
We performed a thermogravimetric analysis (TGA) in the range from room temperature to 800 °C in the N2 environment to examine the required temperature for the configuration of the well-crystalline phase. Fig. 9 displays the removal of nitrates and creation of a stable spinel ferrite phase.29 Moreover, the mass losses of the designed MNPs started from room temperature to 400 °C owing to the degradation of the watery compound and unreacted organic traces. A further observation is that doping affects the thermal stability of the MNPs, as weight loss decreases with Eu doping concentrations, which are 24%, 7%, 5%, and 3% for FO, FE2, FE5, and FE7, respectively. The TGA results summarize that doping incorporates phase purity and is free of residual reactants and carbonaceous matter.3.3. Magnetic study
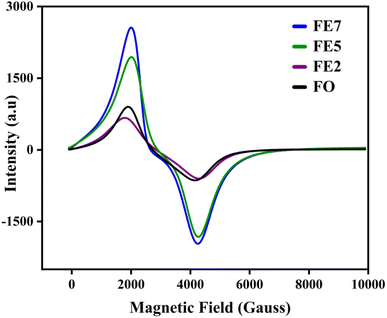
Electron spin resonance (ESR) is used to analyze the magnetic properties, spin-related phenomena, and relaxation mechanisms for the characterized MNPs. The magnetic field-dependent resonance spectra, at a fixed frequency of 9.44 GHz, are shown in Fig. 10. Table 2 lists the calculated ESR measurements, the spin–lattice relaxation time (τ1), spin–spin relaxation time (τ2), resonance linewidth (Hpp), FWHM of the absorption spectra (ΔH1/2), resonance field (Hres), and effective g value. The extracted Hres values show an increasing trend, excluding the 7% Eu doped one. FE7 MNPs exhibit reduced Hres value due to the continuous rise in magnetic anisotropy and saturation magnetization of their internal fields, further confirmed through VSM analysis. Secondly, resonance linewidth Hpp or ΔH1/2 follows the decreasing trend, signifying the strong super-exchange interaction, existence of dipolar–dipolar interaction, and conduction between the Eu3+/Fe3+–Fe2+.30 Moreover, there is a possibility of migration of ions in both tetrahedral and octahedral sites, respectively, which can be seen from cation distribution in the Rietveld refinement analysis. Additionally, the single broad ESR curve at g ∼ 2 directs that characterized MNPs are in the superparamagnetic phase.31 The lowering of g and Hpp values with the increment in Eu doping concentration implies the random alignment of the magnetic moments with the improvement of particle size. It is well known that for a magnetic hyperthermia study, specific absorption rate (SAR) is a key parameter to observe the heating efficiency of the magnetic ensemble, and it is inversely proportional to relaxation time. Based on ESR spectroscopy, we have calculated the spin–lattice relaxation time (τ1) and spin–spin relaxation time (τ2), enlisted in Table 3.32 As a result of spin–lattice fluctuations, MNPs exhibit spin–orbit coupling, whereas spin–spin relaxation corresponds to the exchange of energy among themselves rather than back to the lattice or molecular matrix. Hence, the superparamagnetic nature of the synthesized samples can be illustrated by spin–spin relaxation. According to the calculated data, the lower spin–spin relaxation time leads to a higher SAR, which is further confirmed via induction heating analysis, and the results make them an efficient candidate for hyperthermia application.| Doping concentration | τ1 ×10−12 (sec) | τ2 ×10−11 (sec) | g | Hpp (Gauss) | ΔH1/2 (Gauss) | Hres (Gauss) |
|---|---|---|---|---|---|---|
| 0 | 5.50 | 1.29 | 2.03 | 2495 | 4321 | 2706 |
| 2 | 4.85 | 1.47 | 2.02 | 2219 | 3843 | 2802 |
| 5 | 4.86 | 1.46 | 2.02 | 2218 | 3841 | 2873 |
| 7 | 4.89 | 1.45 | 2.02 | 2217 | 3839 | 2630 |
| Eu Doping concentration (%) | Ms (emu g−1) | Hc (Oe) | Mr (emu g−1) | k ×105 (erg cm−3) |
|---|---|---|---|---|
| 0 | 70.61 | 22 | 2.59 | 2.59 |
| 2 | 37.89 | 4 | 0.51 | 1.59 |
| 5 | 43.68 | 5 | 1.06 | 2.03 |
| 7 | 45.68 | 9 | 1.21 | 2.25 |
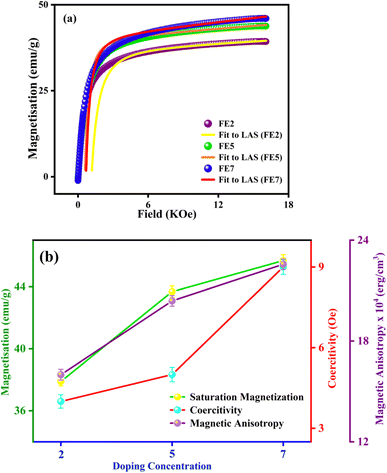
In order to quantify the magnetic states of synthesized MNPs, a vibrating sample magnetometer (VSM; Lakeshore, 7410 series) is used. The highlighted view of the hysteresis loop and the Langevin fit of the respective graphs depicts the superparamagnetic nature, as indicated in Fig. 11.33 For accurate estimation of the saturation magnetization (Ms) and effective magnetic anisotropy constant 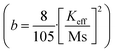 ,34 we have fitted the magnetization graph with the Law of approach to saturation magnetization (LAS). Albeit, the magnetization at the high field region complies well-fit with the LAS, as shown in Fig. 12(a).35 The obtained magnetic results, viz., saturation magnetization (Ms), coercivity (Hc), and retentivity (Mr) from the S-shaped M–H graphs, are enclosed in Table 3. The comparative behavior of magnetization (Ms), coercivity (Hc), and effective magnetic anisotropy (Keff) with Eu doping concentration is presented in Fig. 12(b).
,34 we have fitted the magnetization graph with the Law of approach to saturation magnetization (LAS). Albeit, the magnetization at the high field region complies well-fit with the LAS, as shown in Fig. 12(a).35 The obtained magnetic results, viz., saturation magnetization (Ms), coercivity (Hc), and retentivity (Mr) from the S-shaped M–H graphs, are enclosed in Table 3. The comparative behavior of magnetization (Ms), coercivity (Hc), and effective magnetic anisotropy (Keff) with Eu doping concentration is presented in Fig. 12(b).
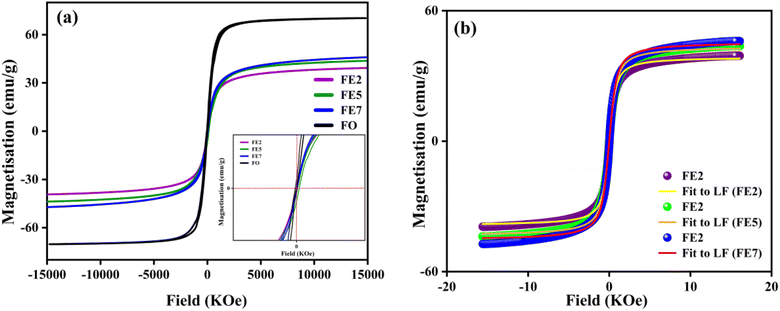 | ||
| Fig. 11 (a) M–H hysteresis loops of processed MNPs (b) Langevin fit of M–H hysteresis loop (Eu doped MNPs). | ||
 | ||
| Fig. 12 (a) LAS fit of the M–H hysteresis loop (Eu doped MNPs) (b) variation of saturation magnetization, coercivity, and magnetic anisotropy with different Eu doping concentrations. | ||
The obtained value of Ms and Keff is well coordinated with the previously reported Fe3O4 system. As shown in Table 3, the saturation magnetization of the processed Eu-doped MNPs exhibits lower saturation magnetization than the bare FO MNPs due to the size effect and spin disorder caused by spin canting at the surfaces.36,37 In particular, there is a direct correlation between the structural and magnetic states of the characterized NPs.38 As a result of the site-preferred substitution of Eu in place of Fe, the lattice parameter improves, which boosts the A–B superexchange interaction, and it can be the most probable reason for the upcharges of the Ms counterpart with the increment in Eu doping concentration.39–41 According to XRD analysis, Eu3+ cations substituting at octahedral Fe3+ sites initiate the increasing bond lengths Fe3+(Eu3+)–O2− and bond angles Fe3+(Eu3+)–O2−–Eu3+(Fe3+). As bond lengths and angles increase, the coordination of cations will be weaker, oxygen deficiency will be more pronounced, and most interestingly, it will reduce exchange interaction and magnetic parameters. The trend is consistent with previously documented Gd-doped Fe3O4 MNPs.10 Based on Table 3, the anisotropy values (k) for the Eu-doped samples were lower than those for the bare one since spinel ferrites have a trivial ligand field and all cations have high spin states.42 A weak interaction between Eu–Fe and weak crystal structure coupling could also be responsible for lowering the anisotropy constant. Consequently, an increase in Eu concentration enhanced the ratio of orbital to spin moments of 4f electrons, enhancing the spin–orbit coupling and progressing magnetic anisotropy.43 The improved coercivity (Hc) of the processed MNPs with doping concentration is correlated with the grain size, as in large grains, the binding of domain walls is less, and it lowers the volume of grain boundaries.44
In this regard, it is highly promising that Eu doping can tune the magnetic key parameters. The comparative study in Fig. 12(b) reveals that Ms, Hc, and Keff are improved by enhancing doping concentrations. The proposed MNPs ascertain an efficient tuning magnetic footprint in the way to magnetic hyperthermia.
3.4. Self-heating efficiency analysis of synthesized NPs
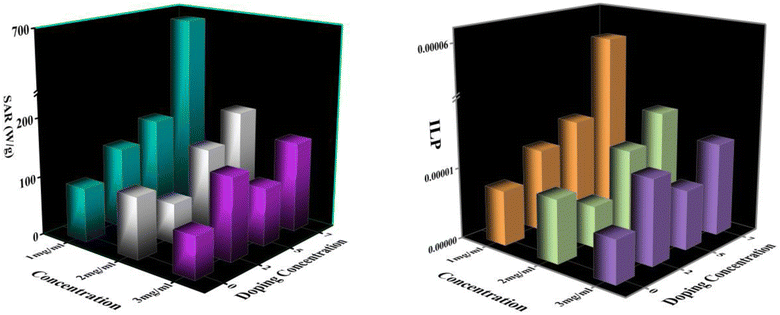
An induction heating setup is operated to examine the self-heating study of the synthesized samples at a fixed frequency of 337 kHz, magnetic field strength of 14.92 kA m−1, and an alternating current of 249 A, which are within the clinical limits (H.f ≤ 5 × 109 A m−1 s−1).45 The “self-heating” of magnetic nanoparticles is a procedure to generate heat with the help of an external AC magnetic field. The time-dependent temperature variant graph shows that the temperature increases exponentially with time at various concentrations (1, 2, and 3 mg mL−1) of the processed NPs, as portrayed in Fig. 13. It has been noted that the temperature rises rapidly in an early instant and then falls to a saturation regime after certain time.46,47 Moreover, increasing the concentration of the MNPs enhances the magnetic interaction between the nanoparticles during the heating process. Herein, we observed from Fig. 13 that only lesser concentrations (1 mg mL−1) of reference NPs exhibit the hyperthermic threshold regime (40 °C to 47 °C).48 On top of all, heat generation from the MNPs is an essential parameter for hyperthermia application. To do so, the heat generation competency can be examined by estimating SAR and intrinsic loss power (ILP) using a Box-locus model, which is shown in Fig. 14.49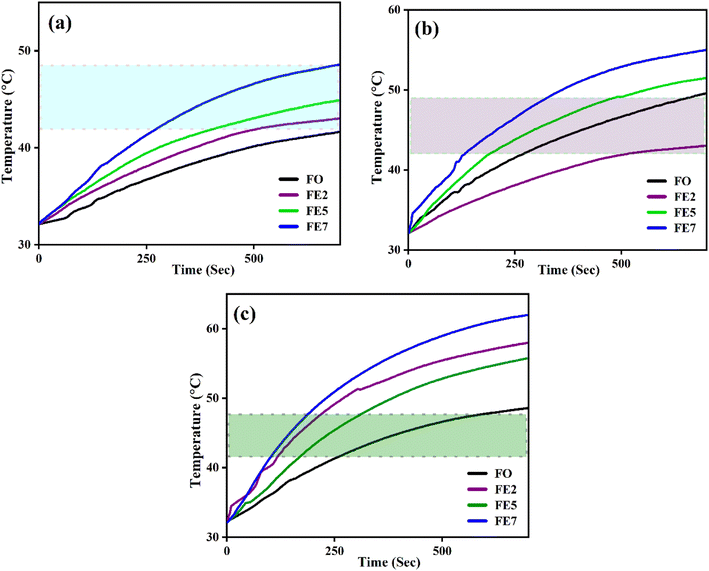 | ||
| Fig. 13 Time-dependent temperature deviation graph of processed MNPs for various concentrations (a) 1 mg mL−1 (b) 2 mg mL−1 (c) 3 mg mL−1. | ||
Fig. 14 depicts the increasing trend of SAR and ILP with the enhancement of Eu doping concentrations. Additionally, Fig. 15 shows that particle size portrays an imperative role in the heat generation mechanism as the SAR surges with the particle size. The following arguments substantiated our assumptions: (i) nanoparticle composition and size range comply with U.S. Drug and Food Administration50 requirements and correlate to in vivo studies of superparamagnetic MNPs. (ii) In practice, a living body may anchor nanoparticles to target tissues so that their ability to rotate their crystallographic axes is significantly reduced (e.g., MNPs in a cellular environment).51 Further, the XRD and TEM analysis confirms the particle size, which is in the range of ≥18 nm, and SAR increases with the particle size as illustrated in our comparative graph, as shown in Fig. 15. Zubarev et al. found the same result as observed via the theoretical model; calculations portray that intrinsic interaction of the MNPs with diameters in the range of 18–20 nm can enhance heat generation up to 30%.54,55 According to our findings, saturation magnetization increases with the increasing Eu concentration, which likely contributes to higher heating efficiency, as seen from the comparative analysis in Fig. 15.52 Herein, the replacement of Eu cations with Fe ions enhances the magnetocrystalline anisotropy, which can be noticed from the above-mentioned respective graph and can be the reason for the improved self-heating properties (SAR).53 Furthermore, in light of VSM analysis suggesting that MNPs are nearly superparamagnetic, relaxation losses (Brownian & Néel relaxation loss) govern the heat generation mechanism rather than Hysteresis loss.54 Brownian and Néel relaxation can endure together, but one with a shorter relaxation time rules the process. According to the prior study, the size of the MNPs in the range of critical size regime (in our case, we observed ∼20 nm) shows Néel relaxation's dominance over Brownian relaxation; hence our samples exhibit Néel relaxation rather than Brownian relaxation mechanism.55 Moreover, the ESR results reflect the predominance of spin–spin relaxation, which provides the importance of magnetic anisotropy for enhancing SAR in our system.56 The enrichment of the Eu substitution probably leads to a rise in the ratio of orbital to spin moments of 4f electrons and enhances the spin–orbit coupling and progressing magnetic anisotropy.43 Remarkably, the comparative analysis shows competent control over the particle size and tuning of magnetization with SAR for the processed MNPs. Henceforth, it is possible to diminution the relative dose assigned to the patient to a minimal level using MNPs with a maximum SAR value (Fig. 14).57,58
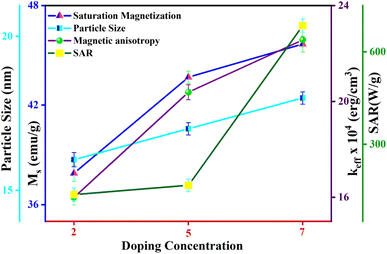 | ||
| Fig. 15 Variation of particle size, saturation magnetization, magnetic anisotropy, and SAR with different Eu doping concentrations. | ||
4. Conclusion
In summary, we demonstrate a simple co-precipitation technique for synthesizing phase-pure Eu-doped FO MNPs; the structure, morphology, and Eu doping of the MNPs have been confirmed from XRD FTIR, SEM, TEM, and XPS analyses. The Rietveld refinement of XRD patterns has portrayed the cation rearrangement and confirmed that Eu ions preferred octahedral sites rather than tetrahedral sites. We have examined the magnetic resonance over a fixed frequency of 9.44 GHz, and our results direct that the Lande g-factor is g ∼ 2, indicating that processed MNPs are in the superparamagnetic phase, supported by VSM analysis. Thus, one key achievement of the present study is that magnetic anisotropy and saturation magnetization have enhanced with the rising Eu doping concentrations. In addition, the heating efficiency for 7% Eu doped NPs has directed the maximum SAR (684.99 W g−1) value over all the doped NPs. Our strategy opens up a new avenue and is a promising starting point for future studies toward the application of magnetic hyperthermia.Conflicts of interest
The authors have no conflicts of interest.Acknowledgements
The authors would like to acknowledge the Central Instrument Facility (CIF), IIT Guwahati, for providing all the necessary facilities required for the characterization of the samples.References
- Z. Nemati, J. Alonso, I. Rodrigo, R. Das, E. Garaio, J. Á. García, I. Orue, M. H. Phan and H. Srikanth, J. Phys. Chem. C, 2018, 122, 2367–2381 CrossRef CAS.
- J. C. Park, G. T. Lee, H. K. Kim, B. Sung, Y. Lee, M. Kim, Y. Chang and J. H. Seo, ACS Appl. Mater. Interfaces, 2018, 10, 25080–25089 CrossRef CAS PubMed.
- E. Fantechi, C. Innocenti, M. Zanardelli, M. Fittipaldi, E. Falvo, M. Carbo, V. Shullani, L. Di Cesare Mannelli, C. Ghelardini, A. M. Ferretti, A. Ponti, C. Sangregorio and P. Ceci, ACS Nano, 2014, 8, 4705–4719 CrossRef CAS PubMed.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys. Condens. Matter, 2006, 18, 2919–2934 CrossRef.
- A. Rajan, M. Sharma and N. K. Sahu, Sci. Rep., 2020, 10, 1–15 CrossRef PubMed.
- R. Das, N. Rinaldi-Montes, J. Alonso, Z. Amghouz, E. Garaio, J. A. García, P. Gorria, J. A. Blanco, M. H. Phan and H. Srikanth, ACS Appl. Mater. Interfaces, 2016, 8, 25162–25169 CrossRef CAS PubMed.
- G. Keifer and F. Effenberger, Magnetic Oxides, Springer, 1967, vol. 6, pp. 107–150 Search PubMed.
- M. Nazari, N. Ghasemi, H. Maddah and M. M. Motlagh, J. Nanostructure Chem., 2014, 4, 2–6 Search PubMed.
- J. P. B. Krishna Priya Hazarika, J. Magn. Magn. Mater., 2022, 560, 251–256 Search PubMed.
- K. Priya, R. Fopase, L. M. Pandey and J. P. Borah, Phys. B Phys. Condens. Matter, 2022, 645, 414237 CrossRef.
- P. Thakur, R. Sharma, V. Sharma, P. B. Barman, M. Kumar, D. Barman, S. C. Katyal and P. Sharma, J. Magn. Magn. Mater., 2017, 432, 208–217 CrossRef CAS.
- A. A. Kadam, S. S. Shinde, S. P. Yadav, P. S. Patil and K. Y. Rajpure, J. Magn. Magn. Mater., 2013, 329, 59–64 CrossRef CAS.
- S. Satyanarayana, S. C. Sarma, S. C. Peter and S. Bhattacharya, J. Magn. Magn. Mater., 2019, 491, 165571 CrossRef CAS.
- Y. Slimani, M. A. Almessiere, S. Guner, B. Aktas, S. E. Shirsath, M. V. Silibin, A. V. Trukhanov and A. Baykal, ACS Omega, 2022, 7, 6292–6301 CrossRef CAS PubMed.
- M. A. Almessiere, Y. Slimani, A. D. Korkmaz, A. Baykal, H. Güngüneş, H. Sözeri, S. E. Shirsath, S. Güner, S. Akhtar and A. Manikandan, RSC Adv., 2019, 9, 30671–30684 RSC.
- T. Zhang, Z. Wang, H. Xiang, X. Xu, J. Zou and C. Lu, ACS Appl. Mater. Interfaces, 2021, 13, 33850–33861 CrossRef CAS PubMed.
- L. Yang, Z. Zhou, H. Liu, C. Wu, H. Zhang, G. Huang and H. Ai, Nanoscale, 2015, 3, 10715–10722 Search PubMed.
- S. Shatooti, M. Mozaffari, G. Reiter, D. Zahn and S. Dutz, Sci. Rep., 2021, 11, 16795 CrossRef CAS PubMed.
- B. Antic, A. Kremenovic, A. S. Nikolic and M. Stoiljkovic, J. Phys. Chem. B, 2004, 108, 12646–12651 CrossRef CAS.
- R.-C. Juan and R. Thierry, Mater. Sci. Forum, 2004, 444, 123–126 Search PubMed.
- K. Praveena, K. Sadhana, S. Srinath, S. R. Murthy, V. Chaudhari, S. E. Shirsath, M. L. Mane, R. H. Kadam, S. B. Shelke, D. R. Mane, K. Kamala Bharathi, J. Arout Chelvane, G. Markandeyulu, H. M. Tahir Farid, I. Ahmad, K. A. Bhatti, I. Ali, S. M. Ramay, A. Mahmood, A. F. Bakuzis and P. C. Morais, J. Magn. Magn. Mater., 2014, 321, 213–220 Search PubMed.
- X. Zeng, J. Zhang, M. Si, D. Cao, X. Deng, H. Ma, Q. Lan, D. Xue, X. Zhang, K. Tao and Y. Peng, Nanoscale, 2019, 11, 4385–4393 RSC.
- V. Jagadeesha Angadi, K. Manjunatha, K. Praveena, V. K. Pattar, B. Jeevan Fernandes, S. O. Manjunatha, J. Husain, S. V. Angadi, L. D. Horakeri and K. P. Ramesh, J. Magn. Magn. Mater., 2021, 529, 167899 CrossRef CAS.
- S. K. Paswan, S. Kumari, M. Kar, A. Singh, H. Pathak, J. P. Borah and L. Kumar, J. Phys. Chem. Solids, 2021, 151, 109928 CrossRef CAS.
- R. D. Waldron, Phys. Rev., 1995, 99, 1727 Search PubMed.
- S. M. Patange, S. E. Shirsath, S. P. Jadhav, V. S. Hogade, S. R. Kamble and K. M. Jadhav, J. Mol. Struct., 2013, 1038, 40–44 CrossRef CAS.
- Y. M. Abbas, A. B. Mansour, S. E. Ali and A. H. Ibrahim, J. Magn. Magn. Mater., 2019, 482, 66–74 CrossRef CAS.
- A. Hao, M. Ismail, S. He, N. Qin, R. Chen, A. M. Rana and D. Bao, Mater. Sci. Eng. B Solid-State Mater. Adv. Technol., 2018, 229, 86–95 CrossRef CAS.
- A. B. Kulkarni, S. N. Mathad and R. P. Bakale, Ovidius Univ. Ann. Chem., 2019, 30, 60–64 CrossRef CAS.
- R. Das, U. Chaudhuri, A. Chanda and R. Mahendiran, ACS Omega, 2020, 5, 17611–17616 CrossRef CAS PubMed.
- S. Mukherjee, A. K. Pal, S. Bhattacharya and S. Chattopadhyay, J. Phys.: Condens. Matter, 2008, 20, 055204 CrossRef.
- J. Massoudi, M. Smari, K. Nouri, E. Dhahri, K. Khirouni, S. Bertaina, L. Bessais and E. K. Hlil, RSC Adv., 2020, 10, 34556–34580 RSC.
- O. M. Lemine, N. Madkhali, M. Hjiri, N. A. All and M. S. Aida, Ceram. Int., 2020, 46, 28821–28827 CrossRef CAS.
- K. Y. Ho, X. Y. Xiong, J. Zhi and L. Z. Cheng, J. Appl. Phys., 1993, 74, 6788–6790 CrossRef CAS.
- A. Gholizadeh, J. Magn. Magn. Mater., 2018, 452, 389–397 CrossRef CAS.
- R. Aquino, J. Depeyrot, M. H. Sousa, F. A. Tourinho, E. Dubois and R. Perzynski, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 1–10 CrossRef.
- J. M. D. Coey, Phys. Rev. Lett., 1971, 27, 1140–1142 CrossRef CAS.
- Q. Li, C. W. Kartikowati, S. Horie, T. Ogi, T. Iwaki and K. Okuyama, Sci. Rep., 2017, 7, 1–4 CrossRef PubMed.
- S. Atta, M. Halder and A. K. Meikap, J. Mater. Sci.: Mater. Electron., 2021, 32, 6992–7008 CrossRef CAS.
- F. Benz, H. P. Strunk, J. Schaab, U. Künecke and P. Wellmann, J. Appl. Phys., 2013, 114, 6 CrossRef.
- B. P. Jacob, S. Thankachan, S. Xavier and E. M. Mohammed, J. Alloys Compd., 2013, 578, 314–319 CrossRef CAS.
- D. Jaison, E. Meher Abhinav, A. Gangwar, P. Nand Kishore, G. Chandrasekaran and M. Mothilal, Mater. Res. Express, 2020, 7, 064009 CrossRef CAS.
- C. Luo, W. Zhang, P. K. J. Wong, Y. Zhai, B. You, J. Du and H. Zhai, Appl. Phys. Lett., 2014, 105, 082405 CrossRef.
- T. Sodaee, A. Ghasemi, E. Paimozd, A. Paesano and A. Morisako, J. Magn. Magn. Mater., 2013, 330, 169–173 CrossRef CAS.
- S. Kossatz, R. Ludwig, H. Dähring, V. Ettelt, G. Rimkus, M. Marciello, G. Salas, V. Patel, F. J. Teran and I. Hilger, Pharm. Res., 2014, 31, 3274–3288 CrossRef CAS PubMed.
- A. Chalkidou, K. Simeonidis, M. Angelakeris, T. Samaras, C. Martinez-boubeta and L. Balcells, J. Magn. Magn. Mater., 2011, 323, 775–780 CrossRef CAS.
- E. D. Do, P. K. Manna, R. Nickel and J. Van Lierop, ACS Appl. Mater. Interfaces, 2019, 11, 6858–6866 CrossRef PubMed.
- R. E. Rosensweig, J. Urol., 2002, 252, 370–374 CAS.
- O. L. Lanier, O. I. Korotych, A. G. Monsalve, D. Wable, S. Savliwala, N. W. F. Grooms, C. Nacea, O. R. Tuitt, O. L. Lanier, O. I. Korotych, A. G. Monsalve, D. Wable, N. W. F. Grooms, C. Nacea, O. R. Tuitt and J. D. Evaluation, Int. J. Hyperthermia, 2019, 36, 687–701 CrossRef PubMed.
- D. Bobo, K. J. Robinson, J. Islam, K. J. Thurecht and S. R. Corrie, Pharm. Res., 2016, 33, 2373–2387 CrossRef CAS PubMed.
- R. Di Corato, A. Espinosa, L. Lartigue, M. Tharaud, S. Chat, T. Pellegrino, C. Ménager, F. Gazeau and C. Wilhelm, Biomaterials, 2014, 35, 6400–6411 CrossRef CAS PubMed.
- D. K. Mondal, S. Jonak, N. Paul and J. P. Borah, RSC Adv., 2021, 11, 12507–12519 RSC.
- S. Laurent, S. Dutz, U. O. Häfeli and M. Mahmoudi, Adv. Colloid Interface Sci., 2011, 166, 8–23 CrossRef CAS PubMed.
- E. Lima, T. E. Torres, L. M. Rossi, H. R. Rechenberg, T. S. Berquo, A. Ibarra, C. Marquina, M. R. Ibarra and G. F. Goya, J. Nanoparticle Res., 2013, 15, 1654 CrossRef.
- M. A. A. Kerroum, C. Iacovita, W. Baaziz, D. Ihiawakrim, G. Rogez, M. Benaissa, C. M. Lucaciu and O. Ersen, Int. J. Mol. Sci., 2020, 21, 1–24 Search PubMed.
- R. Hergt, S. Dutz and M. Zeisberger, Nanotechnology, 2010, 21, 015706 CrossRef PubMed.
- A. Shrivastava and A. K. Shrivastava, J. Nano- Electron. Phys., 2021, 13, 02002 CAS.
- K. P. Hazarika and J. P. Borah, J. Magn. Magn. Mater., 2022, 560, 251–256 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |