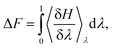Open Access Article
Open Access ArticleFormic and acetic acid pKa values increase under nanoconfinement†
Izaac Sita,
Bidemi T. Fashinab,
Anthony P. Baldob,
Kevin Leung b,
Vicki H. Grassian
b,
Vicki H. Grassian *c and
Anastasia G. Ilgen
*c and
Anastasia G. Ilgen *b
*b
aDepartment of Nanoengineering, University of California San Diego, La Jolla, CA 92093, USA
bGeochemistry Department, Sandia National Laboratories, Albuquerque, NM 87123, USA. E-mail: agilgen@sandia.gov
cDepartment of Chemistry & Biochemistry, University of California San Diego, La Jolla, CA 92093, USA. E-mail: vhgrassian@ucsd.edu
First published on 1st August 2023
Abstract
Organic acids are prevalent in the environment and their acidity and the corresponding dissociation constants can change under varying environmental conditions. The impact of nanoconfinement (when acids are confined within nanometer-scale domains) on physicochemical properties of chemical species is poorly understood and is an emerging field of study. By combining infrared and Raman spectroscopies with molecular dynamics (MD) simulations, we quantified the effect of nanoconfinement in silica nanopores on one of the fundamental chemical reactions—the dissociation of organic acids. The pKa of formic and acetic acids confined within cylindrical silica nanopores with 4 nm diameters were measured. MD models were constructed to calculate the shifts in the pKa values of acetic acid nanoconfined within 1, 2, 3, and 4 nm silica slit pores. Both experiments and MD models indicate a decrease in the apparent acid dissociation constants (i.e., increase in the pKa values) when organic acids are nanoconfined. Therefore, nanoconfinement stabilizes the protonated species. We attribute this observation to (1) a decrease in the average dielectric response of nanoconfined aqueous solutions where charge screening may be decreased; or (2) an increase in proton concentration inside nanopores, which would shift the equilibrium towards the protonated form. Overall, the results of this study provide the first quantification of the pKa values for nanoconfined formic and acetic acids and pave the way for a unifying theory predicting the impact of nanoconfinement on acid–base chemistry.
Introduction
Porous particles, natural or engineered, are commonly found in the environment and often have large surface to volume ratios that can sequester significant amounts of chemical species present in aqueous systems and facilitate their transformations at the solid–water interface inside nanopores. Many of these particles are silicates (e.g., pure minerals or sedimentary rocks and soils) with pores that reach nano-scale dimensions. Theoretical, computational, and experimental studies have shown that nanoconfinement of a solid–water interface within nanopores filled with aqueous solutions can often lead to unexpected chemical reactivities including: increase in gas solubilities,1 enhanced chemisorption reactions,2–4 and lower chemical reaction barriers.5 These deviations in reactivity when compared to unconfined counterparts have been tentatively explained by the disruption of the H-bonding network within nanopores and decreases in the dielectric response,6 melting point,7 density,7,8 surface tension,7,8 and H2O dissociation constant9 compared to bulk solutions.3,7,10–12 Here we hypothesize that nanoconfinement shifts apparent pKa values for acidic species, even when these species are not interacting with the pore surfaces. These nanoconfinement effects on the Ka equilibrium constant (pKa value, where pKa = −log(Ka)) may arise due to a decrease in the dielectric response inside silica nanopores leading to less effective charge screening. Additionally, it was reported recently that protons tend to accumulate in negatively charged silica nanopores,13 which would shift the equilibrium toward the protonated species in nanopores.Nanoconfinement effects on chemistry are poorly understood and constitute an emerging research field. So far the very few studies of nanoconfinement effects on acidity indicate that in highly charged clay mineral interlayers, acidity of water increases by ∼4 orders of magnitude.9 Similarly, recent study by Zhu et al. shows that the local pH inside silica nanopores is lowered, compared to adjacent bulk solution, due to selective uptake of protons inside the negatively charged SiO2 pores.13 Again, lower pH is reported for silica nanopores functionalized with 2-(dimethylamino)ethyl methacrylate (DMAEMA) and 2-(metacryloyloxy)ethyl phosphate (MEP) polymers, which was attributed to an increase in the deprotonation of these surface-bound species under nanoconfinement.5 Contrary to the studies above, Rubinovich et al. observed the equilibrium constants for the hybridization of single stranded DNA are shifted towards undissociated complexes in nanoconfined conditions due to entropic stabilization of these large molecules inside nanochannels.14 These limited studies on acidity in nanopores indicate that de-protonation reactions could be either enhanced or hindered under nanoconfinement, especially for those nanopores that have a negative surface change. The results we report here for silica nanopores show similar trends as observed for air–water interfaces, where protonated forms of organic acids are stabilized.15 Currently, there is no fundamental understanding of how acid dissociation is affected by nanoconfinement. Environmentally relevant molecules, such as organic acids, humic substances, nucleotides, amino acids, proteins and DNA, have one or more acid dissociation constants and therefore understanding the impact of nanoconfinement on various types of acidic groups is urgently needed.
For these reasons, here we quantify the effect of nanoconfinement on the pKa values for two simple organic acids, formic and acetic acids. Formic and acetic acids can be found in the environment from cellular processes cycle, fermentation and are the main constituents of volatile organic acids.16,17 These organic acids are also involved in many industrial processes like paper manufacturing, metal ore mining, and food production that can be in chemical runoff and introduced into aqueous environmental systems.18,19 Additionally, many environmentally prevalent organic molecules, biomolecules and humic substances contain one or more carboxylic acid functional groups, and their deprotonation can be sensitive to nanoconfinement.
Here we utilize these small organic acids as a convenient model system to investigate the effect of nanoconfinement on acid–base chemistry. In this study, Raman and attenuated total reflection Fourier transform infrared (ATR-FTIR) spectroscopy were employed to experimentally estimate the acid dissociation constants of formic and acetic acids when nanoconfined in cylindrical silica nanopores. In addition to experimental approach, molecular dynamics (MD) simulations were used to estimate pKa shifts for nanoconfined acetic acid in 1, 2, 3, and 4 nm silica slit pores.
Materials and methods
Materials
The templated SBA-15 silica (SiO2) with 4.4 ± 0.1 nm pores20 was purchased from Sigma Aldrich; all other chemicals were purchased from Fisher Scientific. Based on our earlier characterization, 4 nm SiO2 has pore volume of 0.67 ± 0.04 cm3 g−1, surface area of 580 ± 13 m2 g−1, with surface area contribution from internal (inside the pores) surfaces of 75% ± 6%.20 Therefore, we conclude that while we cannot isolate vibrational signals from inside the pores vs. from the external surfaces of silica particles, the overall contribution from inside the pores is ∼75%. All solutions were prepared using milliQ water with a resistivity of ≥18.2 MΩ cm and the pH electrode was calibrated daily with pH 1.68, 4 and 7 reference standards. Silica particles were washed in de-ionized milliQ H2O and dried at 40 °C prior to use, as in our earlier work.2,3,7 This treatment produced nanoporous SiO2 surfaces with an average Si–OH site density of 1.8–2.0 –OH nm−2; the pore diameters were 4.4 quantified in our earlier work.2,3,7Solution preparation
25 mM formic acid and 25 mM acetic acid solutions were prepared by diluting with milliQ H2O. pH was measured and titrated using an OAKTON pH 700 meter equipped with a temperature probe. 6 N HCl, 6 N NaOH, 1 N HCl, and 1 N NaOH were used to titrate solutions. Higher concentration of titrants was used to minimize solution dilution, which never fell below 24.6 mM.Attenuated total reflectance Fourier transform infrared (ATR-FTIR) spectroscopy
The ATR-FTIR spectroscopy set-up has been previously described.21–24 ATR-FTIR spectroscopy is based off the total internal reflection of an infrared beam between the optically dense medium (ATR crystal) and an optically rare medium (sample). This reflection at the interface creates an evanescent wave that propagates into the sample where absorption of infrared light occurs. The ATR accessory is a horizontal flow cell equipped with an amorphous material transmitting IR radiation (AMTIR) crystal (Pike Technologies). The AMTIR crystal has a refractive index of 2.5 and the number of reflections is 10. The IR spectra were collected using a Nicolet iS10 FTIR spectrometer (Thermo-Fisher) equipped with a mercury cadmium telluride detector (MCT/A). Spectral resolution was 4 cm−1 and averaged over 100 scans over the range of 750–4000 cm−1. All spectra were processed using OMNIC 9 software. Spectra were collected after a 30 minute purge with filtered CO2-free dry air.For solution phase spectra of the acids, 25 mM concentrations were prepared and titrated to pH ranging from 2–6 (formic acid) and 2–7 (acetic acid). About 800 μL of the titrated solution was pipetted onto the AMTIR crystal and a spectrum was recorded. A spectrum of milliQ water without pH adjustment was used as the background.
For collecting spectra of nanoconfined formic acid, a suspension containing 10 mg of SiO2 in 800 μL milliQ water was prepared and sonicated for 30 seconds. The suspension was drop casted on the AMTIR crystal and dried overnight under filtered CO2-free air. To initiate the experiment, the 700 μL milliQ water was pipetted on the dried SiO2 film and a background spectrum was collected. To collect spectra of SiO2 film saturated with acid solutions, a 700 μL aliquot of 25 mM formic acid at target pH was pipetted on the film and then removed; then another 700 μL aliquot of the same solution was pipetted on the film and a sample spectrum was collected. A similar step-wise addition method was used to collect spectra of nanoconfined 25 mM acetic acid, where acid at target pH value was added, then removed, followed by the fresh acid addition.
To determine the pKa values of the aqueous and the nanoconfined formic acid from the ATR-FTIR data, the intensities of ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and νas(COO−) vibrational bands were used because they represent the protonated and deprotonated formic acid forms, respectively. A linear baseline was used to determine peak heights (intensities). At pH 2, ν(C
O) and νas(COO−) vibrational bands were used because they represent the protonated and deprotonated formic acid forms, respectively. A linear baseline was used to determine peak heights (intensities). At pH 2, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) was considered to represent the 100 mol% of the expected protonated form, while at pH 6, νas(COO−) was considered to represent 100 mol% of deprotonated form. Sigmoidal functions were fit to the two measured acid and base line intensities, and the pKa value was determined independently for each at the 50% intensity value. The same method was used to determine the pKa of 25 mM acetic acid solution (bulk phase and nanoconfined in SiO2 pores). The intensity measured at pH 2 ν(C
O) was considered to represent the 100 mol% of the expected protonated form, while at pH 6, νas(COO−) was considered to represent 100 mol% of deprotonated form. Sigmoidal functions were fit to the two measured acid and base line intensities, and the pKa value was determined independently for each at the 50% intensity value. The same method was used to determine the pKa of 25 mM acetic acid solution (bulk phase and nanoconfined in SiO2 pores). The intensity measured at pH 2 ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) was considered to represent the 100 mol% of protonated form, and at pH 7 νas(COO−) to represent the 100 mol% of deprotonated form. The reported pKa value for formic acid is 3.75,25–27 and for acetic acid is 4.75.27–29
O) was considered to represent the 100 mol% of protonated form, and at pH 7 νas(COO−) to represent the 100 mol% of deprotonated form. The reported pKa value for formic acid is 3.75,25–27 and for acetic acid is 4.75.27–29
Raman spectroscopy
For solution and nanoconfined acid measurements, 500 mM formic and acetic acid was prepared and titrated between pH 2 and pH 7 using 18 N NaOH or 6 N HCl solutions.A 500 mg 4 nm silica sample was equilibrated in 10 mL of 500 mM formic or acetic acids at pH 2–7. The silica particles were equilibrated in centrifuge tubes for 48 hours at room temperature, with intermittent agitation every 12 hours. The particles were allowed to settle by gravity while the supernatant was discarded. The silica-acid slurry was placed in quartz crucible, excess acid was dabbed with Kim-wipe, and covered with microscope cover glass. Raman spectra were collected using a Horiba XploRA plus Raman spectrometer with a cooled CCD detector (Jobin Yvon's Synapse camera). An unpolarized HeNe laser was used with a 532 nm excitation and ∼10 mW radiation power. A 10× microscope objective lens was used with a laser spot diameter of ∼3 μm. An 1800 nm grating was used, and an average of 30 scans was collected between 1800 and 600 cm−1. For each silica-acid slurry, 10 spectra were acquired at different spots on the sample. Consistent with nanopore measurements, the bulk acid solutions at pH between pH 2 and 7 were also in the same quartz crucible during data collection. All spectra were processed by fitting linear segments under peaks to correct for baseline.
To calculate the pKa of the aqueous and the confined acids from the Raman data, the intensity of the Raman spectra corresponding to the deprotonated forms of acetic acid (927 cm−1) and protonated forms of formic acid (1219 cm−1) were plotted against pH for both the aqueous and the nanoconfined acids. These bands were chosen because (1) they are less susceptible to coupling effect by other bands, (2) they do not share bands with pristine silica, and (3) are very sensitive to changes in pH. The resulting plots were fitted with sigmoidal function. The half of the difference between the maximum and minimum intensity is the midpoint of the intensity plot. The point where the midpoint intercepts the sigmoidal function is equivalent to the pKa of the organic acid.
Potentiometric measurements
A solution of 25 mM formic acid was slowly titrated against 0.1 N NaOH while the solution is continuously stirred and the pH recorded after each addition of the titrant. The titration was continued until the pH did not change with further additions of the NaOH titrant. The pKa was determined to be the pH at half the volume used to reach the equivalence point using the 2nd derivative x-intercept. The same procedure was used to determine pKa value for 25 mM acetic acid.Molecular dynamics simulations
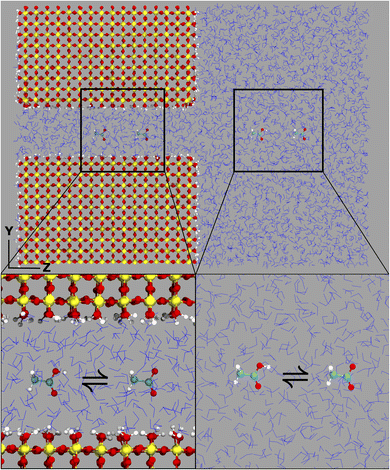
The computational system cell, as seen in Fig. 1, contains a 2D slit pore of beta-cristobalite with hydroxylated {110} faces for the inner and outer pore surfaces (hydroxyl site density is ∼5 –OH per nm2), occupying half of the periodically replicated simulation cell. The pore itself is periodic in the x, y directions and is finite in the z-direction. The 4 nm pore system dimensions were 3.7 × 9.1 × 8.3 nm, and the 1 nm pore system dimensions were 3.7 × 6.1 × 8.3 nm. This represents a nanoconfined environment. The remaining half consists of bulk solvent and therefore an unconfined environment. These simulation conditions are at the zero ionic strength limit.Thermodynamic integration calculations determined the free energy difference of the acetic acid/acetate transformation according to the following equation:
Molecular dynamics simulations were performed with the GROMACS30 software package version 2022.2. Force field parameters for the silicate were treated with Clayff,31,32 while the remainder of the system, including the acetic acid and acetate, were modelled with the CHARMM33 force field version 27 with TIP3P34 waters occupying the bulk and 2D pore channel. Each system representing any given λ value was initially subject to up to 5000 steps of minimization, followed by equilibration at 300 K, 1 bar for 1 ns with the Berendsen35 barostat. Afterwards, runs were continued at 300 K, 1 bar with the Parrinello–Rahman36 barostat in 10 ns increments. It is from these runs of which δH/δλ for each given thermodynamic state was considered. To compute the total free energy difference, Bennett acceptance ratio37 (BAR) was utilized to determine the free energy difference between the initial and final state. The total free energy and estimated variance are reported as computed within GROMACS with the command gmx bar. Volume scaling of the system cell both during equilibration and further runs was applied semi-isotropically to maintain the periodicity of the silicate slabs, with x and y dimensions of the simulation cell remaining fixed with variability in the z component of the volume. Full electrostatics were computed with the particle mesh Ewald38 method with a short-range cutoff of 12 Å. Related calculations have previously been conducted using Density Functional Theory Molecular Dyamics (DFT/MD).15
Results
Vibrational spectroscopy
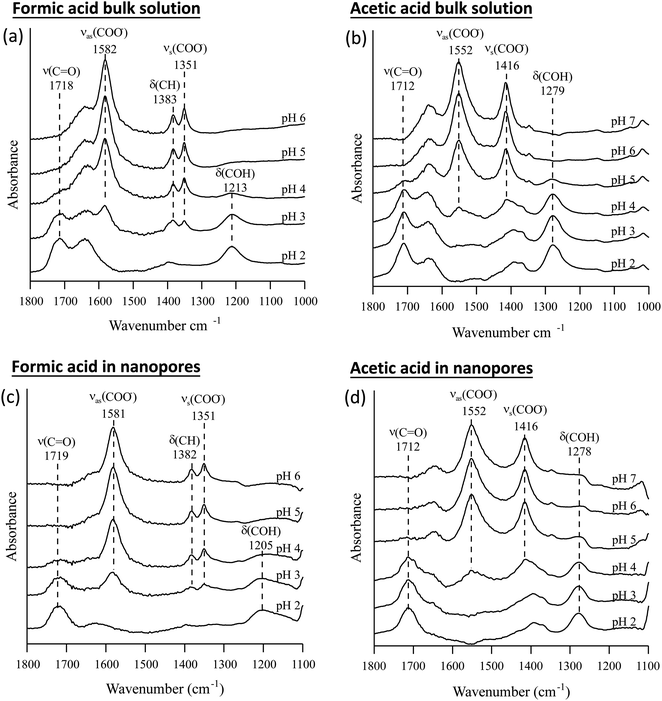
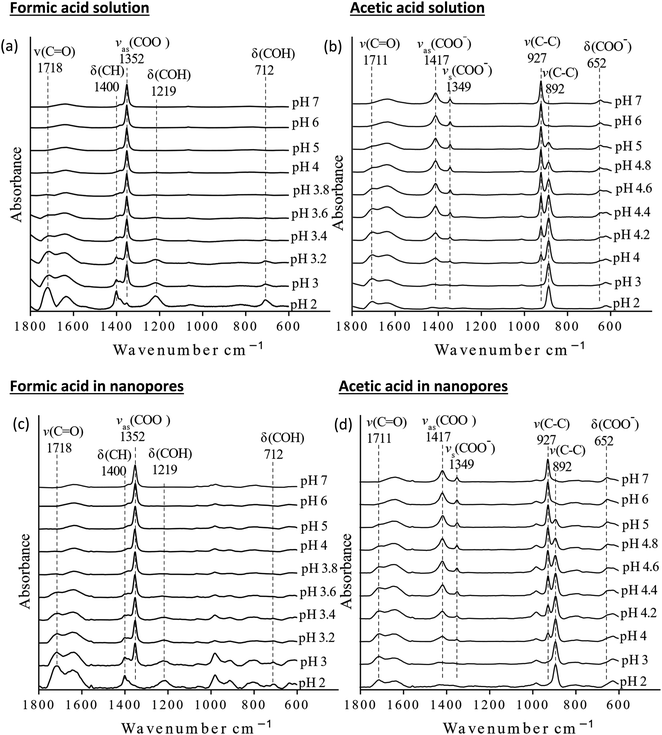
The pKa values of formic and acetic acid solutions in bulk and nanoconfined conditions in SiO2 nanopores were determined by monitoring ATR-FTIR and Raman characteristic band intensities of protonated and deprotonated forms. Fig. 2 shows the ATR-FTIR spectra of the organic acids in solutions and in SiO2 nanopores between pH 2–6 (formic acid) and 2–7 (acetic acid). For formic acid at pH 2, ATR-FTIR vibrational bands belonging to the protonated species are observed at 1718 and 1213 cm−1 which represent the ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and δ(COH) modes, respectively.39,40 As pH increases and formic acid deprotonates, the 1582, 1383 and 1351 cm−1 bands gained intensity. These absorption bands are assigned to the νas(COO−), δ(CH), and νs(COO−), respectively (ESI†).39–41 At pH ≥ 5 the characteristic deprotonated bands appear, and the characteristic protonated band disappear. The most pronounced changes in the intensities for the deprotonated and protonated forms occur between pH 3 and 4, which agrees with the reported formic acid pKa value of 3.75.25–27 As formic acid deprotonates into formate, the ν(C
O) and δ(COH) modes, respectively.39,40 As pH increases and formic acid deprotonates, the 1582, 1383 and 1351 cm−1 bands gained intensity. These absorption bands are assigned to the νas(COO−), δ(CH), and νs(COO−), respectively (ESI†).39–41 At pH ≥ 5 the characteristic deprotonated bands appear, and the characteristic protonated band disappear. The most pronounced changes in the intensities for the deprotonated and protonated forms occur between pH 3 and 4, which agrees with the reported formic acid pKa value of 3.75.25–27 As formic acid deprotonates into formate, the ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) 1718 cm−1 peak intensity decreases while the 1582 cm−1 νas(COO−) intensity increases.41,42 These two characteristic peaks were used to monitor the speciation form of formic acid. Similar observations can be made about acetic acid spectra, the protonated peaks can be seen at 1712 and 1279 cm−1 assigned to the ν(C
O) 1718 cm−1 peak intensity decreases while the 1582 cm−1 νas(COO−) intensity increases.41,42 These two characteristic peaks were used to monitor the speciation form of formic acid. Similar observations can be made about acetic acid spectra, the protonated peaks can be seen at 1712 and 1279 cm−1 assigned to the ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and δ(COH) vibrational modes, respectively. As pH increases, the deprotonated peaks appear at 1552 and 1416 cm−1 assigned to νas(COO−) and νs(COO−), respectively. The most pronounced changes in the spectra occur between pH 4 and 5, which agrees with the reported acetic pKa value of 4.76.27–29
O) and δ(COH) vibrational modes, respectively. As pH increases, the deprotonated peaks appear at 1552 and 1416 cm−1 assigned to νas(COO−) and νs(COO−), respectively. The most pronounced changes in the spectra occur between pH 4 and 5, which agrees with the reported acetic pKa value of 4.76.27–29
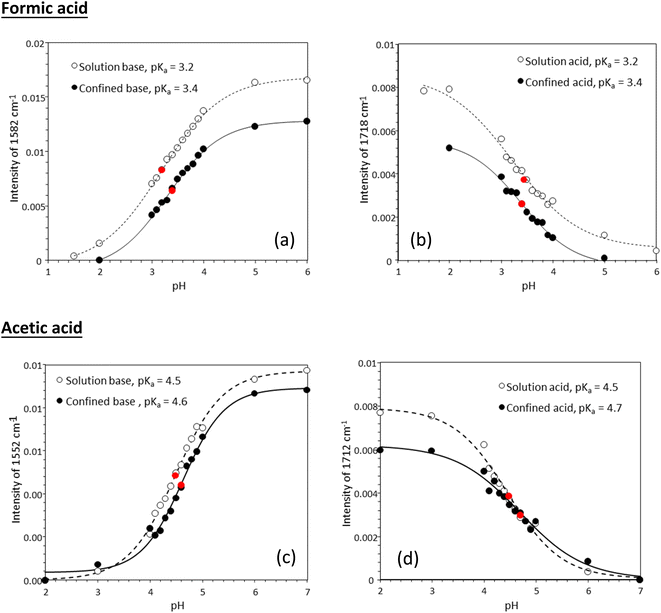
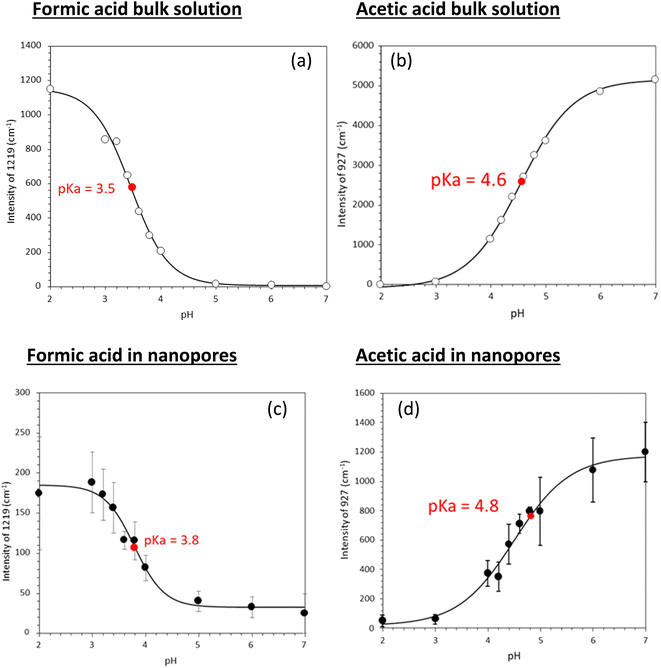
Fig. 3 shows experimentally determined speciation curves for formic and acetic acids at different pH values using characteristic vibrational bands in ATR-FTIR spectra. The mid-point for the protonated and de-protonated band intensities indicates the pKa value of formic and acetic acids in bulk solution are 3.2 and 4.5, respectively. Using the same data analysis approach, the pKa values of nanoconfined formic and acetic acids are 3.4 and 4.6, respectively. The measured solution pKa values for formic and acetic acid agree well with potentiometric measurements performed in our laboratory (Fig. S1†), supporting that spectroscopic method can be used as an effective technique to determine molecular acid dissociation constants. Our measured values deviate by approximately 0.3 units from the values in the literature, because these compiled literature values are for solutions with ionic strength close to zero,43,44 while the solutions in our study have the ionic strength of 0.25. As alkyl chain length increases, the acidity of the carboxylic acid decreases as the alkyl group destabilizes the carboxylate ion.45 However, as the alkyl group lengthens, the inductive effect lessens as the added carbons are farther away from the carboxylate. This inductive effect is apparent at the difference in measured pKa values for formic and acetic acid solutions of ca. one pH unit.
In general, in silica nanopores ATR-FTIR peaks for (de)protonated acid forms show the same response to increasing pH as was observed for bulk solutions, where protonated peaks disappear, and deprotonated peaks appear. Peak shifting, changes to spectral intensities, and broadening and/or narrowing can be indicative of surface complexation when compared to solution spectra; if molecules adsorb on SiO2 surfaces inside nanopores, molecular symmetry can change leading to peak shifting or full width half max (FWHM) changes.46,47 Additionally, if adsorption onto solid surface takes place, local concentrations are increased which can be observed in the significant increase in spectral intensities, sometimes as large as 100×.21,22 However, this is not observed as measured ATR-FTIR intensities are similar for bulk solution samples and those in SiO2 nanopores (Fig. 2).
The Raman spectra for solution phase formic and acetic acid have similar spectral responses to pH changes (Fig. 4). As pH increases for solution phase formic acid, the protonated bands represented by the 1721 cm−1 ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and 712 cm−1 δ(COH) peak intensities decrease while the deprotonated 1219 cm−1 and 1352 cm−1 ν(COO−) band intensity increases.42 The carboxylate band is very intense and when plotted on the same scale, swamps the δ(COH) band intensity. Significant spectral changes occur between pH 3 and pH 4 (see Fig. S3†), similar to what was observed in ATR-FTIR data. For solution phase acetic acid, as pH increases, the 1711 cm−1 ν(C
O) and 712 cm−1 δ(COH) peak intensities decrease while the deprotonated 1219 cm−1 and 1352 cm−1 ν(COO−) band intensity increases.42 The carboxylate band is very intense and when plotted on the same scale, swamps the δ(COH) band intensity. Significant spectral changes occur between pH 3 and pH 4 (see Fig. S3†), similar to what was observed in ATR-FTIR data. For solution phase acetic acid, as pH increases, the 1711 cm−1 ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) band and 891 cm−1 ν(C–C) decrease while the deprotonated carboxylate bands, 1416 cm−1 νas(COO−), 1349 cm−1 νs(COO−) and 927 cm−1 ν(C–C) bands increase. Again, significant spectra changes occur between pH 4 and pH 5.
O) band and 891 cm−1 ν(C–C) decrease while the deprotonated carboxylate bands, 1416 cm−1 νas(COO−), 1349 cm−1 νs(COO−) and 927 cm−1 ν(C–C) bands increase. Again, significant spectra changes occur between pH 4 and pH 5.
 | ||
| Fig. 4 Raman spectra of bulk and nanoconfined solutions (a) formic acid solutions, (b) acetic acid solutions, (c) nanoconfined formic acid solutions, and (d) nanoconfined acetic acid solutions. | ||
Using the approach earlier explained in the material and method section (i.e., plot of intensity ratios vs. pH), the pKa of the acids in solution were 3.5 and 4.6 for formic and acetic acid, respectively (Fig. 5). Under nanoconfinement, the pKa values increased to 3.8 and 4.8, respectively.
For Raman intensities, the intensities measured for acids nanoconfined in silica pores are smaller than in solution. Because of the absence of signal enhancement, we conclude that the organic acids are not complexing with the SiO2 surfaces to any significant degree, and the majority of the acids reside within the body of the nanopore. To show what the spectra would look like if the organic acids were strongly adsorbed to the surface, acetic acid was adsorbed onto alumina at various pH values using ATR-FTIR spectroscopy (Fig. S2†). The spectra did not change despite varying the solution pH and showed peak shifting of the carboxylate peaks, indicating adsorption onto alumina surfaces. In the case of formic and acetic acid nanoconfined in silica pores, spectral changes in response to changing pH was observed so the acids are not adsorbed to the silica surface.
The nanoconfined spectra behave similarly to solution spectra in terms of decreasing intensities of the protonated bands and increasing intensities of de-protonated bands as pH increases for both organic acids. However, the nanoconfined ATR-FTIR spectral intensities is ca. 30% of solution whereas Raman is ca. 50% of that measured in solution. Instead of the laser beam probing a volume of only organic acid and water, part of the sampled volume is being filled by silica, resulting in a lower concentration of acid molecules and lower intensity values. There is minimal peak shifting when solution and nanoconfined spectra are compared for either acid from both spectroscopic techniques. Additionally, the FWHM of protonated and deprotonated bands do not change significantly. Due to sensitivity issues, the concentration used for Raman spectra is 20× higher than used for ATR-FTIR.
Tabulated pKa values for vibrational measurements on solution and nanoconfined acids are shown in Table 1. Under nanoconfinement and using ATR-FTIR spectroscopy, formic acid has a pKa value of 3.4 and acetic acid has a pKa value of 4.6. Both pKa values are higher than those in bulk solution by 0.2 (6.3%) and 0.12 (2.7%) pH units for formic and acetic acid, respectively. For pKa values calculated using Raman spectroscopy data, both pKa values are higher than those in bulk solution by 0.4 (11.8%) and 0.26 (5.7%) pH units for formic and acetic acid, respectively. Our ATR-FTIR and Raman experimental results suggest that the protonated forms of the organic acids are more stable compared to their deprotonated forms, resulting in a decrease in dissociation constants and increase in pKa values.
| ATR-FTIR | Raman | |||
|---|---|---|---|---|
| Solution | Nanoconfined | Solution | Nanoconfined | |
| Formic acid | 3.2 | 3.4 | 3.5 | 3.8 |
| Acetic acid | 4.5 | 4.6 | 4.6 | 4.8 |
Molecular dynamics simulations
The thermodynamic cycle explored in the calculations follows:| CH3COOpore− + CH3COOHbulk → CH3COOHpore + CH3COObulk− |
In Table 2 we list the calculated free energy differences for the chemical transformation above and the corresponding ΔpKa values.
| Unconfined | 1 nm pore | 2 nm pore | 3 nm pore | 4 nm pore | |
|---|---|---|---|---|---|
| Acetate/acetic acid free energy difference (kJ mol−1) | 0 | –3.17 ± 0.11 | –0.98 ± 0.07 | –0.74 ± 0.06 | –0.85 ± 0.09 |
| Acetic acid pKa shifts | 0 | +0.54 ± 0.02 | +0.17 ± 0.01 | +0.13 ± 0.01 | +0.15 ± 0.02 |
In all the slit pores, pKa shifts to more positive values, indicating that acid strength decreases under nanoconfinement. There is a clear differentiation between the 1 nm pore and the remaining pore size systems. When slit pore size is 1 nm, pKa shifts by +0.54 ± 0.02 units, and the difference in the estimated free energy difference is 3 times larger than was observed in the 2 nm pore. For an organic molecule like acetic acid, the 1 nm pore represents an extreme nanoconfined environment where other factors like channel solvent density and surface adsorption would also likely have greater differential effects when compared to the other pore sizes, though these factors were not explicitly explored. When comparing the difference in energies between 2 nm and 3 nm pores, it is diminished. Most notably, the pKa shifts predicted by our MD simulations are in qualitative agreement with the experimentally measured pKa shifts for acetic acid in SiO2 nanopores with 4 nm diameter, although the experimental system is cylindrical, and not slit-like. Future MD work will consider other pore geometries and ionic strengths to attain better fidelity to experimental conditions and to investigate whether dielectric effects, which can be screened by salt, are solely responsible for this confinement effect.
Discussion
The increase in pKa value under nanoconfinement suggests that the stabilization of the organic acid conjugate base is not as favorable. Gao et al. demonstrated an increase in carboxylic acid pKa values in a confined nanochannel.48 It was suggested that the decrease in dissociation stemmed from neighboring carboxylic groups having to overcome an electrostatic repulsion interaction from neighboring negatively charged carboxylate groups. Not only do the carboxylic groups have to overcome neighboring carboxylate charges, but also deprotonated silica surface charge; the point of zero charge for silica is around 4.2.49,50 However, for electrostatic effects to be dominant, intermolecular interactions of organic acid–organic acid has to occur but this has not been observed in our study due to the low acid concentrations. It is recognized that formic and acetic acids can polymerize to form linear or cyclic complexes.51–53 However, this often occurs in gaseous phase or at very high concentrations (>5.25 M) of organic acid.54,55 Yang et al. used Raman spectroscopy to monitor peak shifting in the OH stretch in a binary system of acetic acid–water as the volume fraction of the acid (VAA) was varied.55 Notable peak shifts begin at VAA > 0.30 (∼5.25 M). It was also noted that this was due to formation of linear dimers while VAA < 0.30, hydrated monomers were the dominant species. Furthermore, another study concluded that the introduction of water into acetic acid cyclic dimer complexes, leads to water separated molecules, removing the hydrogen bonds formed in the dimer.56For our study, VAA = 0.0014 for ATR-FTIR spectroscopy and 0.035 for Raman spectroscopy, which is well below the onset of dimerization in solution. One could argue that under nanoconfinement, the organic acid could be sequestered or excluded from the pore, altering the volume fraction. However, the intensities of the characteristic solution and nanoconfined peaks are very similar (Fig. S3†). This suggests that the pores are not sequestering or excluding organic acids and that the solution concentration is similar to that of what is inside the pores. The caveat is that the VAA onset of dimerization can be different under nanoconfinement than in solution, however, it would require the difference to be ∼2 orders of magnitude. Thus, the interaction that is observed is of organic acid–water and not organic acid–organic acid nature. This means that electrostatic repulsion is not the dominant force for the observed increase in the pKa values. Additionally, molecular size of non-solvated formic acid is approximately 3.4 Å and 4.9 Å for acetic acid.57 The molecular size of solvated formic acid is approximately 11.4 Å and 12.5 Å for acetic acid.57–59 The solvated sizes are rough estimations based on molecular sizes and distances. Both non-solvated and solvated sizes are significantly smaller than the 4 nm pores in the experimental portion of this study, therefore we assume that steric effects are not dominant. As shown in our MD simulations, steric effects may become important when we reach 1 nm slit pore opening.
Under nanoconfinement, previous studies have shown that the dielectric response is significantly lowered (ε = 2)6 compared to bulk water (ε = 78).3,10,11 Confined water molecules are more ordered (have less rotational freedom) and since nanopores are spatially limited, the density of dipoles is reduced.7 These effects result in a reduced dielectric response for confined water. As the organic acid undergoes deprotonation in nanoconfined environments, the rearrangement and restructuring of water molecules to hydrate the conjugate base and proton is more difficult compared to hydrating the neutral acid. The reduced dielectric constant in a confined system could reduce the ability of water molecules to accept a proton from an organic acid, thus increasing the pKa of the acid. Nie et al. used ab initio calculations to show the increase in H-bond dissociation energy for carboxylic acids in protein interiors as the dielectric response of the media decreases.60 The low dielectric environments enhance H-bonding interactions and are more stable than in higher dielectric media. This suggests that the deprotonation of carboxylic acids becomes more difficult in low dielectric media, thus explaining the observed increase in the pKa value of two acids examined here. Talik et al. showed polypropylene glycols (PPG) hydrogen bonding strength between water molecules and the PPG–OH groups increased under nanoconfinement.61 Moreover, Ilgen et al. found that the solvation energy of dissolved cations is decreased in a nanoconfined system compared to bulk solutions, which causes an increase in the inner-sphere complexation reactions within SiO2 nanopores.3 A reduction in the solvation energy of nanoconfined species could lead to increased complexation, including protonation of organic acids reported here. Adams et al. probed the transport of protons in confined reverse micelles as a function of size and acid concentration.62 The authors reported an inability to execute a Grotthuss shuttling of protons due to the Eigen hydronium complex strong adsorption onto the polar surface. This causes a buildup of protons within confined environments and limits proton mobility suggesting that ability to deprotonate and transport a proton away through a network of water molecules from an organic acid is hindered, stabilizing the acid. Zhu et al. investigated the pH difference between bulk solutions and solutions within nanopores.13 The authors concluded that the pH of nanopores can be lower than in bulk, due to selective uptake of proton into the pore volume. With increasing proton activity inside nanopores, the de-protonation reaction equilibrium is expected to shift towards the un-dissociated species. Additionally, the carbonyl and acidic proton have been shown to be the main active sites for hydrogen bonding.57,60 Once the organic acids deprotonate, the electrons are delocalized in the carboxylate and the strong hydrogen bonding site is lost, reducing the stability of deprotonated acids. For these reasons, protonated organic acids are stabilized in nanopores, which is reflected in the increase of pKa value under nanoconfined environments.
Conclusions
Here we show that vibrational spectroscopy can be used to experimentally determine acid dissociation constants in solution and in nanoconfined matrices. Nanoconfinement can significantly alter molecular properties of aqueous species due to re-structuring of H-bonding in nanoconfined water. Using ATR-FTIR and Raman spectroscopies, acid dissociation constants for two small organic acids, formic and acetic acid, were experimentally determined. Under nanoconfinement, the pKa of formic and acetic acids is increased, stabilizing the protonated form. MD simulations for acetic acid nanoconfined within SiO2 slit pores are in agreement with experimental measurements. The observed and predicted increase in the pKa values is most likely due to the combination of factors, including (1) reduced dielectric response of water; (2) enhanced H-bonding interactions; and (3) concentration of protons in nanoconfined environments, which shifts the equilibrium towards protonated species in nanopores. Additionally, the H-bonding interactions between the strong H-bonding sites of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and OH group are lost when deprotonated. For these reasons, the stabilization of the protonated organic acid is reflected in the decrease in acid dissociation constant (increase in pKa) under nanoconfined conditions.
O and OH group are lost when deprotonated. For these reasons, the stabilization of the protonated organic acid is reflected in the decrease in acid dissociation constant (increase in pKa) under nanoconfined conditions.
Author contributions
The manuscript was written through contributions of all authors. IS collected and analyzed ATR-FTIR data and preliminary Raman data. BTF performed Raman experiments and analyzed data. APB ran MD models and analyzed data. KL conceptualized MD simulations. VHG designed the ATR-FTIR experiments and data analysis and oversaw research progress. AGI developed research hypothesis, designed Raman experiments, and oversaw research progress.Conflicts of interest
All authors declare no competing financial or non-financial interests.Acknowledgements
The authors thank Jacob G. Smith and Kadie M. Sanchez for help with sample preparation, and Jeffery Greathouse for technical discussions on the MD model setup. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences Division under Field Work Proposal #23-015452. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Workforce Development for Teachers and Scientists, Office of Science Graduate Student Research (SCGSR) program. The SCGSR program is administered by the Oak Ridge Institute for Science and Education (ORISE) for the DOE. ORISE is managed by ORAU under contract number DE-SC0014664. All opinions expressed in this paper are the author's and do not necessarily reflect the policies and views of DOE, ORAU, or ORISE. The experimental work was performed at the University of California San Diego and at Sandia National Laboratories. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA-0003525. The employees own all right, title and interest in and to the article and are solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.References
- C. Qiao, X. Yu, X. Song, T. Zhao, X. Xu, S. Zhao and K. E. Gubbins, Langmuir, 2020, 36, 8527–8536 CrossRef CAS PubMed.
- A. W. Knight, P. Ilani-Kashkouli, J. A. Harvey, J. A. Greathouse, T. A. Ho, N. Kabengi and A. G. Ilgen, Environ. Sci.: Nano, 2020, 7, 68–80 RSC.
- A. G. Ilgen, N. Kabengi, K. Leung, P. Ilani-Kashkouli, A. W. Knight and L. Loera, Environ. Sci.: Nano, 2021, 8, 432–443 RSC.
- D. R. Ferreira and C. P. Schulthess, Soil Sci. Soc. Am. J., 2011, 75, 389–396 CrossRef CAS.
- R. Brilmayer, S. Kübelbeck, A. Khalil, M. Brodrecht, U. Kunz, H.-J. Kleebe, G. Buntkowsky, G. Baier and A. Andrieu-Brunsen, Adv. Mater. Interfaces, 2020, 7, 1901914 CrossRef CAS.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed.
- A. W. Knight, N. G. Kalugin, E. Coker and A. G. Ilgen, Sci. Rep., 2019, 9, 8246 CrossRef PubMed.
- T. Takei, K. Mukasa, M. Kofuji, M. Fuji, T. Watanabe, M. Chikazawa and T. Kanazawa, Colloid Polym. Sci., 2000, 278, 475–480 CrossRef CAS.
- X. Liu, X. Lu, R. Wang, E. J. Meijer and H. Zhou, Geochim. Cosmochim. Acta, 2011, 75, 4978–4986 CrossRef CAS.
- S. Senapati and A. Chandra, J. Phys. Chem. B, 2001, 105, 5106–5109 CrossRef CAS.
- S. Varghese, S. K. Kannam, J. S. Hansen and S. P. Sathian, Langmuir, 2019, 35, 8159–8166 CrossRef CAS PubMed.
- E. Breynaert, M. Houlleberghs, S. Radhakrishnan, G. Grübel, F. Taulelle and J. A. Martens, Chem. Soc. Rev., 2020, 49, 2557–2569 RSC.
- Y. Zhu, H. G. Derami, P. Gupta, R. Gupta, S. Singamaneni and Y.-S. Jun, Chem, 2022, 8, 3081–3095 CAS.
- L. Rubinovich and M. Polak, Nano Lett., 2013, 13, 2247–2251 CrossRef CAS PubMed.
- D. Lesnicki, V. Wank, J. D. Cyran, E. H. G. Backus and M. Sulpizi, Phys. Chem. Chem. Phys., 2022, 24, 13510–13513 RSC.
- D. Mamlouk and M. Gullo, Indian J. Microbiol., 2013, 53, 377–384 CrossRef CAS PubMed.
- H. Farahani, M. Shokouhi, M. Rahimi-Nasrabadi and R. Zare-Dorabei, Toxicol. Environ. Chem., 2016, 98, 714–726 CAS.
- E. Budsberg, R. Morales-Vera, J. T. Crawford, R. Bura and R. Gustafson, Biotechnol. Biofuels, 2020, 13, 154 CrossRef CAS PubMed.
- G. Deshmukh and H. Manyar, in Biotechnological Applications of Biomass, eds. , T. P. Basso, T. O. Basso and L. C. Basso, IntechOpen, Rijeka, 2020 Search PubMed.
- A. W. Knight, A. B. Tigges and A. G. Ilgen, Geochem. Trans., 2018, 19, 13 CrossRef PubMed.
- I. Sit, H. Wu and V. H. Grassian, Annu. Rev. Anal. Chem., 2021, 14, 489–514 CrossRef CAS PubMed.
- I. Sit, S. Sagisaka and V. H. Grassian, Langmuir, 2020, 36, 15501–15513 CrossRef CAS PubMed.
- I. Sit, Z. Xu and V. H. Grassian, Polyhedron, 2019, 171, 147–154 CrossRef CAS.
- I. A. Mudunkotuwa, A. Al Minshid and V. H. Grassian, Analyst, 2014, 139, 870–881 RSC.
- M. H. Kim, C. S. Kim, H. W. Lee and K. Kim, J. Chem. Soc., Faraday Trans., 1996, 92, 4951–4956 RSC.
- X. Wang, H. Fu, D. Du, Z. Zhou, A. Zhang, C. Su and K. Ma, Chem. Phys. Lett., 2008, 460, 339–342 CrossRef CAS.
- F. R. Dutra, C. de S. Silva and R. Custodio, J. Phys. Chem. A, 2021, 125, 65–73 CrossRef CAS PubMed.
- R. N. Goldberg, N. Kishore and R. M. Lennen, J. Phys. Chem. Ref. Data, 2002, 31, 231–370 CrossRef CAS.
- L. Samuelsen, R. Holm, A. Lathuile and C. Schönbeck, Int. J. Pharm., 2019, 560, 357–364 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- R. T. Cygan, J. A. Greathouse and A. G. Kalinichev, J. Phys. Chem. C, 2021, 125, 17573–17589 CrossRef CAS.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, Phys. Rev. Lett., 1980, 45, 1196–1199 CrossRef CAS.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- M. A. Moreno, O. Gálvez, B. Maté, V. J. Herrero and R. Escribano, J. Phys. Chem. A, 2011, 115, 70–75 CrossRef CAS PubMed.
- J. Park and D. E. Woon, Astrophys. J., 2006, 648, 1285–1290 CrossRef CAS.
- K. Ito and H. Bernstein, Can. J. Chem., 2011, 34, 170–178 CrossRef.
- A. Olbert-Majkut, J. Ahokas, J. Lundell and M. Pettersson, Chem. Phys. Lett., 2009, 468, 176–183 CrossRef CAS.
- A. J. Eugene, E. A. Pillar-Little, A. J. Colussi and M. I. Guzman, Langmuir, 2018, 34, 9307–9313 CrossRef CAS PubMed.
- E. J. Cohn, F. F. Heyroth and M. F. Menkin, J. Am. Chem. Soc., 1928, 50, 696–714 CrossRef CAS.
- A. Chandra and S. Chattopadhyay, Colloids Surf., A, 2020, 589, 124395 CrossRef CAS.
- Y. Arai and D. L. Sparks, J. Colloid Interface Sci., 2001, 241, 317–326 CrossRef CAS.
- E. J. Elzinga and D. L. Sparks, J. Colloid Interface Sci., 2007, 308, 53–70 CrossRef CAS PubMed.
- H.-L. Gao, H. Zhang, C.-Y. Li and X.-H. Xia, Electrochim. Acta, 2013, 110, 159–163 CrossRef CAS.
- A. W. Knight, A. B. Tigges and A. G. Ilgen, Geochem. Trans., 2018, 19, 13 CrossRef PubMed.
- M. Kosmulski, J. Colloid Interface Sci., 2009, 337, 439–448 CrossRef CAS PubMed.
- P. Farfán, A. Echeverri, E. Diaz, J. D. Tapia, S. Gómez and A. Restrepo, J. Chem. Phys., 2017, 147, 44312 CrossRef PubMed.
- P. Rodziewicz and N. L. Doltsinis, J. Phys. Chem. A, 2009, 113, 6266–6274 CrossRef CAS PubMed.
- N. Nishi, T. Nakabayashi and K. Kosugi, J. Phys. Chem. A, 1999, 103, 10851–10858 CrossRef CAS.
- M. Tang, W. A. Larish, Y. Fang, A. Gankanda and V. H. Grassian, J. Phys. Chem. A, 2016, 120, 5609–5616 CrossRef CAS PubMed.
- B. Yang, Y. Li, N. Gong, X. Cao, S. Wang and C. Sun, Spectrochim. Acta, Part A, 2019, 213, 463–466 CrossRef CAS PubMed.
- J. Chocholoušová, J. Vacek and P. Hobza, J. Phys. Chem. A, 2003, 107, 3086–3092 CrossRef.
- S. Soffientini, L. Bernasconi and S. Imberti, J. Mol. Liq., 2015, 205, 85–92 CrossRef CAS.
- P. Krishnakumar and D. K. Maity, J. Phys. Chem. A, 2017, 121, 493–504 CrossRef CAS PubMed.
- S. Aloisio, P. E. Hintze and V. Vaida, J. Phys. Chem. A, 2002, 106, 363–370 CrossRef CAS.
- B. Nie, J. Stutzman and A. Xie, Biophys. J., 2005, 88, 2833–2847 CrossRef CAS PubMed.
- A. Talik, M. Tarnacka, M. Geppert-Rybczyńska, B. Hachuła, K. Kaminski and M. Paluch, J. Phys. Chem. C, 2020, 124, 17607–17621 CrossRef CAS.
- E. M. Adams, H. Hao, I. Leven, M. Rüttermann, H. Wirtz, M. Havenith and T. Head-Gordon, Angew. Chem., Int. Ed., 2021, 60, 25419–25427 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra07944e |
| This journal is © The Royal Society of Chemistry 2023 |