Open Access Article
Open Access ArticleStudy of physical properties of the Li0.5MgFe1.5O3.5 ferrite nanoparticles
Abddaim Jeidd *a,
Mohamed Amghar
*a,
Mohamed Amghar a,
A. Mabrouki
a,
A. Mabrouki a,
A. Benaliacd,
A. Trabelsia,
E. Dhahria,
K. Khirounib and
B. F. O. Costac
a,
A. Benaliacd,
A. Trabelsia,
E. Dhahria,
K. Khirounib and
B. F. O. Costac
aApplied Physics Laboratory, Faculty of Sciences of Sfax, University of Sfax, 3000 Sfax, Tunisia. E-mail: abddayem.jeyid@gmail.com
bMaterial Physics Laboratory and Environnement-Applied Nanomaterials, Faculty of Sciences of Gabes, University of Gabes, 6079 Gabes, Tunisia
cPhysics Department, CFisUC, University of Coimbra, Rua Larga, P-3004-516 Coimbra, Portugal
dI3N, Physics Department, University of Aveiro, Campus de Santiago, Aveiro, Portugal
First published on 26th April 2023
Abstract
In the present research study, the structural, optical, magnetic, electrical and dielectrical properties of the spinel ferrite Li0.5MgFe1.5O3.5, synthesized using a sol–gel auto-combustion method were studied. X-ray diffraction, Fourier transform infrared spectroscopy (FTIR), and Raman spectroscopy revealed that this sample crystallizes in a cubic spinel structure with space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Moreover, the optical investigation by UV-visible spectroscopy has revealed that the band gap for our sample is (Eg = 2.87 eV), which shows that our compound is a potential candidate for optoelectronic applications. The values of the remanent magnetization Mr = 0.13 emu g−1, of the coercive field HC = 4.65 Oe deduced from the hysteresis loop, are very low, suggesting the superparamagnetic behavior of our sample. Additionally, the temperature coefficient of resistance (TCR) is −19% affirmed that Li0.5MgFe1.5O3.5 ferrite is a good candidate for detecting infrared radiation and infrared bolometric applications. Indeed, the activation energies were calculated from the imaginary part of the impedance, the electrical conductivity, and the imaginary part of the modulus, thus demonstrating that the charge carriers involved in the processes of conduction and relaxation are the same.
m. Moreover, the optical investigation by UV-visible spectroscopy has revealed that the band gap for our sample is (Eg = 2.87 eV), which shows that our compound is a potential candidate for optoelectronic applications. The values of the remanent magnetization Mr = 0.13 emu g−1, of the coercive field HC = 4.65 Oe deduced from the hysteresis loop, are very low, suggesting the superparamagnetic behavior of our sample. Additionally, the temperature coefficient of resistance (TCR) is −19% affirmed that Li0.5MgFe1.5O3.5 ferrite is a good candidate for detecting infrared radiation and infrared bolometric applications. Indeed, the activation energies were calculated from the imaginary part of the impedance, the electrical conductivity, and the imaginary part of the modulus, thus demonstrating that the charge carriers involved in the processes of conduction and relaxation are the same.
1. Introduction
Iron-based spinels with the general formula AFe2O4, where A is a divalent transition metal (Ni, Cu, Mg, Zn, Co, Mn, Cd), have attracted the attention of researchers due to their structural, morphological, magnetic, optical, chemical, mechanical, thermal, and electrical properties.1–6 These materials are currently among the most successful magnetic nanoparticles for medical and technological applications, namely solar water oxidation, electrochemical supercapacitor applications, magnetic fluid hyperthermia, magnetic memory, biological applications, gas sensors, and contrast enhancement in magnetic resonance imaging.7–14 The magnesium ferrite (MgFe2O4) ferrite belongs to the family of spinel ferrites, well known for its use in magnetic technologies, sensors, heterogeneous catalysis, and adsorption.15 The introduction of metal transition ions leads to significant variations in physical properties depending on the method of synthesis and doping concentration.16,20 Nanoparticles ferrite spinel are characterized by an assembly of unrelated giant short range order (SRO) magnetic moments that can fluctuate when the thermal energy (KBT) exceeds the anisotropy energy is known as a superparamagnetic.17 These systems should ideally not exhibit remanence magnetic moments, coercivity, or long-range coherency; that is, the magnetization curve should not exhibit a hysteresis loop above the so-called blocking temperature (TB). Spinel cubic ferrimagnets, magnetic nanoparticles, and magnetic superlattices all have well-known size-dependent (50 nm) superparamagnetic properties. Complex systems with competing interactions between spin and charge ordering have been studied extensively for several years for the exposition of their multiferroic properties. Domains and domain wall sizes and their related anisotropic energy of the magnetic nanoparticles are important factors which decide the critical diameter.18To highlight the dielectric response of Li–Mg mixed ferrites, a systematic investigation of the dielectric properties as a function of temperature and frequency has been conducted.19 For example, Li–Mn,20 Li–Zn,21 L–Cd,22 Li–Ni,23 and Li–Ti24 have been found to generally exhibit excellent physicochemical properties. Not only do these properties depend on the processing parameters, but also on the preparation methods. An overview of the literature reveals that when other metal cations like (Co2+, Mg2+, Ni2+,…) are substituted for lithium, the characteristics of lithium ferrites are significantly altered. In fact, S. E. Shirsath et al. have reported a decrease in permeability and a decrease in saturation magnetization with Co2+ substitution in Li0.5Fe2.5O4.25 To synthesize ferrite nanoparticles, hydrothermal chemical treatment, condensation under inert gas, microwave or sonochemical, electrochemical, mechanical grinding, and sol–gel auto-combustion have been introduced.16 The reason behind using the sol–gel auto-combustion method is that it offers products with high chemical homogeneity, even at quite low temperatures.16 The present research work aims to study the structural, morphological, optical, magnetic, electrical and dielectric properties of the spinel ferrite oxide Li0.5MgFe1.5O3.5, which can be used in a variety of applications such as optoelectronics, photovoltaics and gas sensors.
2. Experimental
2.1 Synthesis of Li0.5MgFe1.5O3.5 nanoparticles
The Li0.5MgFe1.5O3.5 nanoparticle is synthesized by the sol–gel auto-combustion method,26 using nitrate precursors Mg(NO3)2·6H2O (98% purity, Sigma-Aldrich), Fe(NO3)3·9H2O (99% purity, Sigma-Aldrich) and LiNO3 (98% purity, Sigma-Aldrich), purchased from Sigma-Aldrich. First, these nitrates were dissolved separately in 100 ml of distilled water, followed by the addition of citric acid (C6H8O7 99% purity, Sigma-Aldrich) with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 molar ratio of the metal cation (Fe + Mg + Li). The resulting mixture was heated on a hot plate at 80 °C with magnetic stirring until a viscous gel was formed. Then, the gel was heated on a hot plate at 300 °C to obtain a dark powder, which was ground in an agate mortar. Finally, the obtained powder was annealed at 500 °C for 6 hours in an electric oven to crystallize the sample.
1.5 molar ratio of the metal cation (Fe + Mg + Li). The resulting mixture was heated on a hot plate at 80 °C with magnetic stirring until a viscous gel was formed. Then, the gel was heated on a hot plate at 300 °C to obtain a dark powder, which was ground in an agate mortar. Finally, the obtained powder was annealed at 500 °C for 6 hours in an electric oven to crystallize the sample.
2.2 Characterization
The phase purity and crystal structure of the prepared sample was verified by X-ray diffraction (XRD) using the Bruker D8 Advance diffractometer with CuKα radiation (λ = 1.5406 Å). The surface morphology and chemical compositions of the synthesized compound were studied using a Merlin scanning electron microscope (SEM) Hitachi S3500 Microanalysis EDS, Kevex (132 keV) equipped with a microanalyzer at energy dispersive X-rays (EDX). Transmission electron microscopy (TEM) images were obtained with an FEI Tecnai F20 microscope.In addition, the FT-IR spectrum for the studied spinel compound was recorded using a PerkinElmer Spectrum 1000 FT-IR spectrometer at room temperature, in the range of 400 to 4000 cm−1. The Raman spectroscopy was performed under backscattering geometry, using a Jobin Yvon HR 800 system and an excitation wavelength of 532 nm. For the RT absorption experiments, a Shimadzu UV 2100 spectrometer was used in transmission mode in a wavelength range from 170 to 800 nm. The Raman spectra were recorded with a modular double grating excitation spectrofluorimeter with a TRIAX 320 emission monochromator (Fluorolog-3, Horiba Scientific) coupled to an HR 980 Hamamatsu photomultiplier, using a front face acquisition mode. As an excitation source a 450 W X arc lamp was used. Next, the UV-vis absorption spectrum was recorded using a Shimadzu UV-3101PC UV-vis spectrophotometer. The magnetic measurements were made using a cryogen free Vibrating Sample Magnetometer (VSM) that allows measurements as a function of temperature (between 0 and 300 K), with a maximum value of magnetic field of 10 T. In addition, the electrical measurements of the prepared sample were performed by impedance spectroscopy using an Agilent 4294A impedance analyzer. Before starting this characterization, the sample must have the shape of dipoles; thus, we deposited a thin layer of silver of a few nanometers on the face of the pellet using a vacuum thermal evaporator. Then we glued a silver wire using silver lacquer on each side. The frequency range explored was between 40 Hz and 1 MHz. The temperature was 440 K to 600 K. The analyzed sample was characterized under an AC excitation signal of 50 mV.
3. Results and discussion
3.1 X-ray diffraction study
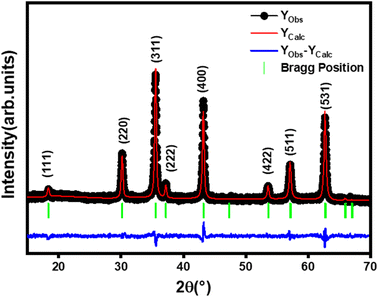
The X-ray diffraction (XRD) pattern of Li0.5MgFe1.5O3.5 powder recorded at room temperature is shown in Fig. 1. This figure shows the reflections allowed in the spinel cubic structure. In addition, the XRD pattern confirmed the single-phase formation of the prepared ferrite sample. A regards the Rietveld refinement by FULLPROF27 software, it confirmed the formation of a single-phase cubic spinel structure with the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, without any additional peaks of a secondary phase, thus indicating the high purity of our sample. The parameters obtained by the Rietveld method of Li0.5MgFe1.5O3.5 are shown in Table 1. The low value of χ2, suggests that the refinement of the developed compound is effective, and that the sample is of good quality.
m space group, without any additional peaks of a secondary phase, thus indicating the high purity of our sample. The parameters obtained by the Rietveld method of Li0.5MgFe1.5O3.5 are shown in Table 1. The low value of χ2, suggests that the refinement of the developed compound is effective, and that the sample is of good quality.
| Parameters | Li0.5MgFe1.5O3.5 |
|---|---|
| aR (Å) | 8.3773 |
| V (Å3) | 587.9041 |
| χ2 | 1.449 |
| aexp (Å) | 8.3773 |
| LA–A (Å) | 3.6274 |
| LB–B (Å) | 3.4730 |
| LA−B (Å) | 2.9618 |
| ρX-ray (g cm−3) | 3.966 |
| ρexp (g cm−3) | 5.8976 |
| P (%) | 32.7438 |
| S (m2 g−1) | 31 |
| δ × 10−3 | 0.434 |
| DDS (nm) | 48 |
| nB (μB) | 0.56 |
Furthermore, the lattice constant (aexp) was calculated using:28
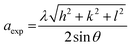 | (1) |
From the XRD data, the crystallite size Dsc of the Li0.5MgFe1.5O3.5 compound was calculated by the Scherrer method using the strongest peak (311) and following this equation:29–31
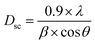 | (2) |
The mean crystallite size value of the prepared compound is 48 nm, confirming the obtaining of nanometric crystallites.
The X-ray density (ρX-ray) for the compound Li0.5MgFe1.5O3.5 was calculated taking into account that a basic unit cell of the spinel cubic structure contains eight ions, using the following relationship:
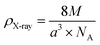 | (3) |
The apparent density (ρexp) was calculated using the following relationship:32
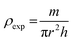 | (4) |
Porosity was defined as the difference between the X-ray density (ρX-ray) and the apparent density (ρexp) using the following relationship:33
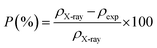 | (5) |
Assuming that the particles are spherical, the specific surface S was determined by the following expression:34
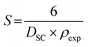 | (6) |
The number of defects, known as the length of dislocation lines per unit volume of the crystal, was calculated by the formula:35
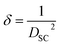 | (7) |
The lowest value of dislocation density, shown in Table 1, leads to an increase in the surface/volume ratio, and therefore to the good crystallinity of the synthesized compound.
X-ray density (ρX-ray), experimental density (ρexp), porosity (P), and specific surface (S), in the sample are listed in Table 1.
The notion of porosity and the specific surface area show that the particle size is uniformly distributed and well agglomerated over the entire surface of the sample Li0.5MgFe1.5O3.5. It is to be noted that the large surface area of spinel nanoparticles is required for the detection and application of gas sensors.32
3.2 SEM and EDX analysis
To obtain an accurate estimation of the microstructure and morphology of the Li0.5MgFe1.5O3.5 compound, scanning electron microscopy (SEM) was used. A SEM image that shows the surface of the Li0.5MgFe1.5O3.5 sample obtained at 500 °C is shown in Fig. 2(a). Due to electrostatic forces, the grains in this image have formed a sizable aggregation.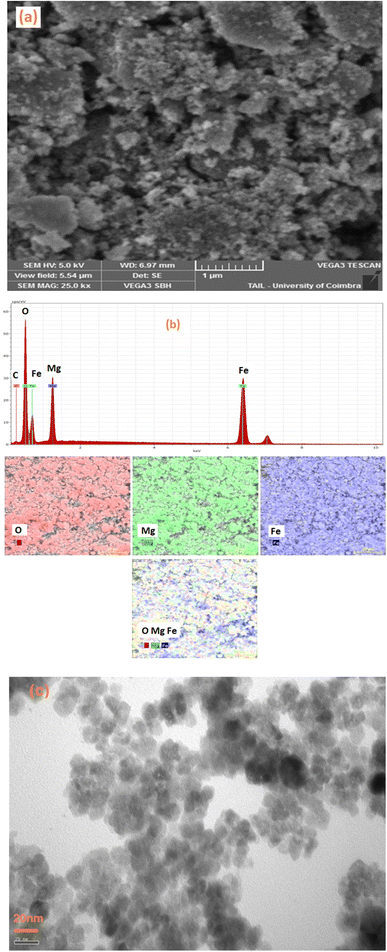 | ||
| Fig. 2 (a) SEM morphology image, (b) EDX spectrum of the compound Li0.5MgFe1.5O3.5, (c) TEM morphology image. | ||
The chemical analysis of the synthesized compound was performed by energy dispersive X-ray spectroscopy (EDX). The Fig. 2(b) shows the elemental analysis of the Li0.5MgFe1.5O3.5 sample at room temperature using EDX, whose spectra confirm the presence of all the constituent elements of Li0.5MgFe1.5O3.5, such as Fe, Mg, and O. This substantiates that no integrated elements were lost or contaminated. In fact, the small atomic number (Z) of the element lithium (Li),which is lower than the sensitivity of EDX, is the main cause of their invisibility in the spectrum.36,37
The Fig. 2(c) shows the TEM images for the Li0.5MgFe1.5O3.5 sample. This figure shows a symmetrical particle morphology with an almost spherical shape in the nanometer range with some crystallite agglomeration.
3.3 FTIR spectra analysis
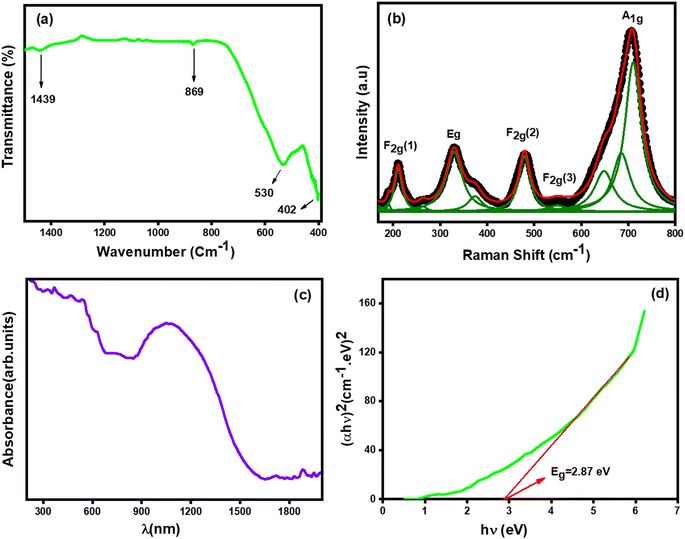
Fourier transform infrared (FTIR) spectroscopy of the compound Li0.5MgFe1.5O3.5, taken at room temperature, was presented in Fig. 3(a). This spectrum demonstrates that there are two absorption bands that appear in the region of 400–600 cm−1, as in the spinel ferrite structures.38 The absorption band around 532 cm−1 corresponds to the vibration of ions present in the tetrahedral site, and the absorption band around 402 cm−1 corresponds to the vibration of ions present in the octahedral site.39 These absorption bands reveal the formation of the spinel cubic structure, which is in agreement with the XRD results. Even in this figure, the peaks obtained around 1439 cm−1 are responsible for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrations,38 and the peak near 930 cm−1 is attributed to C–H bending vibrations.
O stretching vibrations,38 and the peak near 930 cm−1 is attributed to C–H bending vibrations.
 | ||
| Fig. 3 (a) FT-IR, (b) Raman spectra, (c) variation of absorbance versus wavelength, (d) variation [αhν]2 versus (hν) of Li0.5MgFe1.5O3.5 nanoparticle. | ||
3.4 Raman spectra analysis
The Raman spectrum of Li0.5MgFe1.5O3.5 has been studied at room temperature and presented in Fig. 3(b). This Raman spectrum has one feature in common, which is the presence of five Raman peaks (A1g + Eg + 3F2g) that are known for the cubic spinel structure belonging to the space group (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).40,41 In order to clarify the position of the peak, the experimental data were fitted with the Lorentzian function. While the (A1g) mode that appears around 700 cm−1 is associated with Fe–O tetrahedral bonds, those of Eg centered around 333 cm−1 are attributed to the symmetric curvature of O with respect to Fe. Whereas the F2g(2) mode centered at 479 cm−1 corresponds to asymmetric bending of Fe–O bonds, that of the F2g(1) mode centered at 210 cm−1 corresponds to the transnational motion of the whole tetrahedron. The F2g(3) modes at 550 cm−1 are attributed to the asymmetric curvature of O with respect to Fe.
m).40,41 In order to clarify the position of the peak, the experimental data were fitted with the Lorentzian function. While the (A1g) mode that appears around 700 cm−1 is associated with Fe–O tetrahedral bonds, those of Eg centered around 333 cm−1 are attributed to the symmetric curvature of O with respect to Fe. Whereas the F2g(2) mode centered at 479 cm−1 corresponds to asymmetric bending of Fe–O bonds, that of the F2g(1) mode centered at 210 cm−1 corresponds to the transnational motion of the whole tetrahedron. The F2g(3) modes at 550 cm−1 are attributed to the asymmetric curvature of O with respect to Fe.
3.5 UV-visible absorption study
The Fig. 3(c) shows the absorption spectra of the compound Li0.5MgFe1.5O3.5 in the 200–1900 nm range. The electronic transition from the valence band to the conduction band can be used to explain the strong absorption (O2p Fe3d). In other words, the electronic excitation from the O2p level (valence band) to the Fe3d level (conduction band) absorbed a significant amount of visible light.42The optical band gap energy (Eg) was calculated by the following Tauc relation:43,44
| (αhν) = A[hν − Eg]n | (8) |
The band gap energy value (Eg) was calculated by plotting the variation of [αhν]2 as a function of the photon energy [hν] as shown in Fig. 3(d). However, 2.87 eV is equivalent to the gap energy's (Eg) value. Our ferrite sample demonstrates semiconducting activity, according to the band gap energy value, and can be used in a variety of technical domains, including optoelectronics, photovoltaics, and gas sensors.
The refractive index (n0) is essential of semiconductor materials to determine the optical and electrical properties of the crystal. Understanding n0 is essential in the design of heterostructure lasers in optoelectronic devices and solar cell applications.45 Using Moss' empirical relationship,46 the refractive index (n0) can be calculated from the value of Eg:
| Egn04 = 104 eV | (9) |
| εα = n02 | (10) |
The values of refractive index (n0) and (εα) of the studied sample are 2.45 and 6.01, respectively.
3.6 Magnetic properties
To verify the existence of a magnetic order in Li–Mg ferrite nanoparticles, we discussed the variation of magnetic properties as a function of the temperature of Li0.5MgFe1.5O3.5 nanoparticles. Measurements of magnetization as a function of temperature, mode (ZFC) and mode (FC) under an applied field of 500 Oe in the temperature range of 5 to 300 K of our sample are shown in Fig. 4(a). It is well known that in sets of magnetic nanoparticles, the FC curve is superimposed on the ZFC curve, and the system exhibits a behavior of magnetic irreversibility below a given temperature (Tirr), which is related to the blockage of larger particles.48,49 However, nanoparticles are characterized by a large peak of the ZFC curve at Tmax temperature that decreases rapidly during cooling, while the FC curve remains roughly constant. Such a maximum characterizes a Tmax temperature proportional to the TB blocking temperature.48 This characteristic is the sign of superparamagnetic behavior with moderate dipolar interaction and easy random magnetization axis orientations.50 This maximum temperature corresponds to the blocking/freezing temperature of the super spins. The presence of this peak is clearly associated with a transition from the blocked state to the superparamagnetic state of individual isolated nanoparticles without interaction. Beyond Tmax, thermal energy (KBT) is superior to the magnetic energy barrier and thus materials become superparamagnetic according to the Curie–Weiss law. The effect of presence of nanoparticles and short range ordering in bigger magnetic nanoparticles due to broken chain may lead the magnetic frustration and spin fluctuation in the composite.17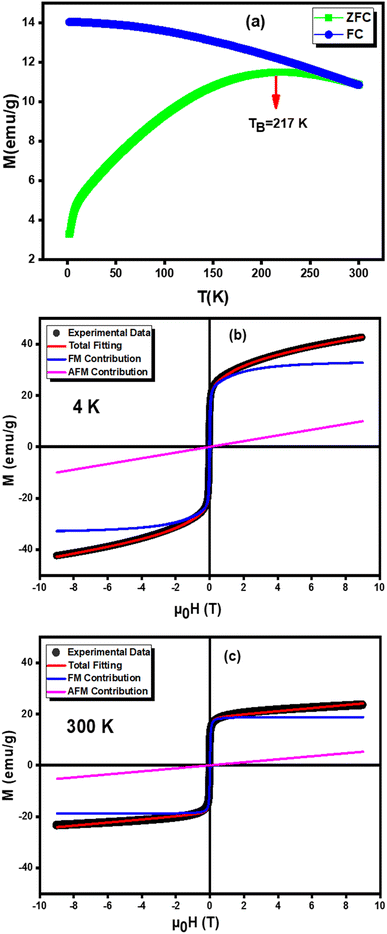 | ||
| Fig. 4 (a) ZFC/FC magnetization as a function of temperature, (b and c) the hysteresis loops of the nanoparticle of the nanoparticle Li0.5MgFe1.5O3.5 measured at 4 K and 300 K. | ||
The Fig. 4(b) and (c) show the magnetic hysteresis loop (M–H) for Li0.5MgFe1.5O3.5 sample measured under a magnetic field range up to 9 T at room temperature. In order to quantify the magnetic parameters (MS saturation magnetization, Mr residual magnetization and HC intrinsic coercive field), we adjusted the hysteresis loop (M–H) by the following equation:50,51
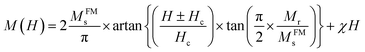 | (11) |
The first term quantifies the FM contribution while the second represents the AFM/PM contributions (linear contributions).
The values of the residual magnetization Mr = 0.13 emu g−1 and the coercive field HC = 4.65 Oe, and MFMs = 18.83 emu g−1. HC and Mr values are low, which also confirms the superparamagnetic character of our sample. In addition, we can conclude that this sample could be a potential candidate in many technological applications, such as recording heads, transformers, induction cores, spintronic devices, micro-devices waves because of its gentle nature.52,53
The magnetic moment nB (μB) calculated from the values of the saturation magnetization MS (emu g−1) and the molecular weigh MW (g mol−1) according to the following equation54 is reported in Table 1.
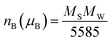 | (12) |
| ωm = γ8π2MS | (13) |
The studied compound Li0.5MgFe1.5O3.5 has a very significant value (4.158 GHz), showing that it can be used in high frequency microwave applications (ωm), This Li–Mg nano ferrite frequency value is within the ranges corresponding to the S and C bands. In addition, the ωm value is comparable to those of other ferrite systems, which can be considered as possible candidates for use in microwave frequency bands 41.56. In light of this, the Li0.5MgFe1.5O3.5 samples make excellent candidates for radiofrequency microwave devices.
3.7 Electrical results
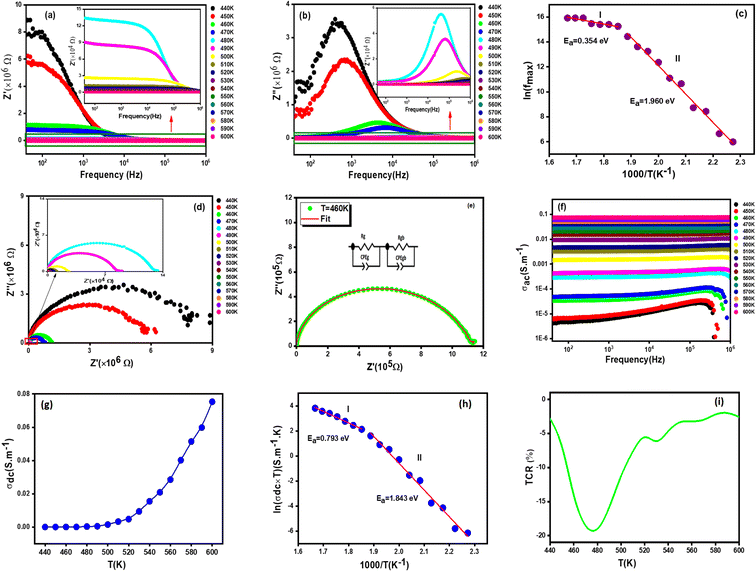
3.7.1.1 Real part of impedance. The Fig. 5(a) shows the frequency dependence of the real part of the impedance (Z′) at different temperatures of the sample Li0.5MgFe1.5O3.5. It can be noted that the values of Z′ are higher at low frequencies and gradually decrease with the increase in frequency. Indeed, the plots demonstrate that Z′ reaches a temperature-independent minimum value. According to the literature, this behavior can be explained by the space charge, which occurs when the material's potential barrier is reduced due to the temperature increase.56,57 It is also important to point out that Z′ decreases with the increase in temperature, which can be attributed to the decrease in the density of charge carriers and the increase in their mobility, suggesting a reduction in the localized character of charge carriers.58,59
3.7.1.2 Imaginary part of impedance. The frequency and temperature dependent plots of the imaginary part of the impedance (Z′′) for the Li0.5MgFe1.5O3.5 sample under study is shown in Fig. 5(b). These curves are characterized by the existence of a single peak that shifts to high frequencies, proving the presence of a relaxation phenomenon in the synthesized sample.60 It can be noted that for all temperatures, Z′′ increases and takes a maximum value that shifts to higher frequencies with the increase in temperature. This does not only indicate the increase of the relaxation time, but also shows that the decrease of the material's strength. Such a relaxation phenomenon is likely to be explained by the presence of electrons and/or immobile species at low temperature and defects at high temperature.61 Moreover, the increase in the frequency of relaxation peaks with the increase in temperature proves a non-Debye type relaxation,62 described by Arrhenius' law:63,64
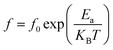 | (14) |
The logarithmic variation of fmax as a function of 1000/T is presented in Fig. 5(c). The obtained values of activation energy (Ea) estimated from the slope of the linear fitting curve are 0.354 eV for (I) and 1.960 eV for (II). This result is of the same order as those of other spinel ferrite materials reported in the literature.65
3.7.1.3 Equivalent circuit. The Fig. 5(d) represents the variation of the imaginary part (Z′′) of the complex impedance with the real part (Z′) at different temperatures for the Li0.5MgFe1.5O3.5 compound. These curves, known as Nyquist diagrams, allow us to distinguish the contributions of grain boundaries, electrodes, and grains to the transport phenomenon in the sample.66 The decrease in the diameters of the semicircles with the increase in temperature confirms a thermally activated conduction process,67 To better understand this process, the experimental data of the Nyquist plots were fitted using the Z-view software. Satisfactory fits are obtained using an equivalent circuit formed by the parallel combination of a (Rg)//(CPEg) and (Rbg)//(CPEbg) grain match and grain boundary respectively as shown in Fig. 5(e).
3.7.2.1 AC conductivity analysis. The spectra of conductivity (ac) versus frequency at different temperatures for the compound Li0.5MgFe1.5O3.5 are shown in Fig. 5(f). These conductivity spectra are composed of two distinct frequency regions, the first of which is at low frequency, where the conductivity is virtually independent of frequency, and thermally activated.68 As for the second frequency region, it is where electrical conductivity increases with frequency as described by Jonscher's law following this equation:69
| σac(ω) = σdc + Aωs | (15) |
3.7.2.2 DC conductivity analysis. The constant fluctuation of conductivity with temperature is shown in Fig. 5(g), demonstrating that the produced compound's Li0.5MgFe1.5O3.5 conductivity grows continuously with temperature. This is likely to confirm the behavior of a semiconducting material, which could be attributed to the increase in drift mobility and the charge carriers' jump frequency.
Usually, the conductivity of ferrites is described by the charge carrier hopping (SPH) model expressed by:71
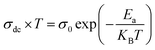 | (16) |
In Fig. 5(h), we present the product σdc × T as a function of 1000/T. We estimated the value of the activation energy by a linear fit of the curve which turns out to be Ea = 0.793 eV (I) and Ea = 1.843 eV (II), this value is similar to that found for other ferrites.65
The temperature coefficient of resistance (TCR) is one of the most important parameters for device applications involving infrared (IR) detectors for night vision bolometer technologies, determined by the following expression:72
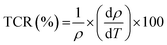 | (17) |
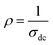 and T are respectively the resistivity and the absolute temperature.
and T are respectively the resistivity and the absolute temperature.
In Fig. 5(i), the temperature coefficient of resistivity for the compound is displayed along with calculation of the TCR factor. As can be seen according to the Li0.5MgFe1.5O3.5 material, a significant negative TCR value is equal to −19%, indicating a higher TCR value when compared to other TCR found in prior works. A simple comparison with published results for similar spinel materials is summarized in Table 2. Therefore, our samples are good candidates for infrared radiation detection.
| M* = M′ − iM′′ = i2πfC0Z* | (18) |
The real (M′), and imaginary (M′′) parts of the electric complex modulus are given by:
| M′ = 2πfC0Z′′ | (19) |
| M′′ = 2πfC0Z′ | (20) |
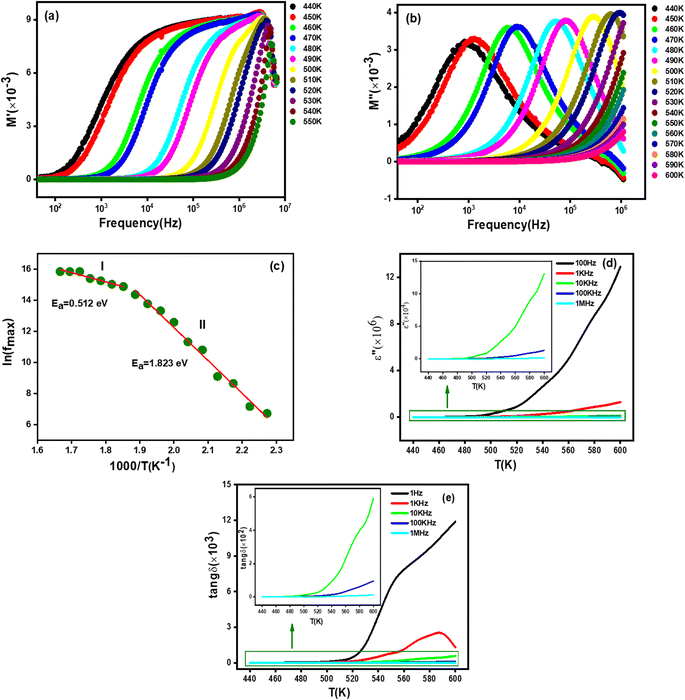
3.7.3.1 Real part of modulus. The frequency versus the real part (M′) of the complex modulus at different temperatures for the studied Li0.5MgFe1.5O3.5 compound is shown in Fig. 6(a). As can be seen in this figure, at low frequencies, the values of M′ approach zero and then shows an increase in dispersion with frequency, confirming that the electronic polarization has a negligible value74,75 Afterwards, in the high frequency region, M′ increases progressively with frequency, suggesting that the conduction technique may be due to the short-range mobility of charge carriers.74
3.7.3.2 Imaginary part of modulus. The Fig. 6(b) plots the variation of the imaginary part of the electric modulus (M′′) as a function of frequency at different temperatures for the synthesized material in order to better understand the dielectric relaxations. This figure shows that the M′′ plots show a single relaxation peak associated with a specific frequency called the relaxation frequency. The fact that this relaxation peak changed to higher frequencies as the temperature rose suggests that our compound experiences a relaxation phenomenon. Moreover, this behavior shows the dominance of the thermally activated jump process, which has been reported in several research investigations.1,64
In order to estimate the activation energy for the studied compound Li0.5MgFe1.5O3.5, we have plotted in Fig. 6(c) the logarithmic variation of the relaxation frequency (fmax) as a function of the inverse of the temperature 1000/T (K), from the data of the imaginary part of the modulus (M′′). This curve shows that this variation presents an activated behavior, according to the Arrhenius law:79
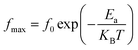 | (21) |
The extracted values of the activation energy are Ea = 0.512 eV (I) and Ea = 1.823 eV (II), respectively. We can see that all these values are quite similar to those calculated from the imaginary part of the impedance (Z′′) and the conductivity dc (σdc).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at different frequencies of the Li0.5MgFe1.5O3.5 compound is shown in Fig. 6(c) and (d), respectively.
δ) at different frequencies of the Li0.5MgFe1.5O3.5 compound is shown in Fig. 6(c) and (d), respectively.As can be clearly seen in Fig. 6(c), the variation of the imaginary part of the dielectric permittivity (ε′′) is independent of frequencies and temperatures over a small temperature range, and then it gradually increases with the increase in temperature. This behavior confirms the dominance of the interfacial polarization contribution in the studied material.76
However, the dielectric loss increases with the increase in temperature as shown in Fig. 6(d), which could be due to an increase in electronic conduction attributed to thermal activation of electrons.77 It is trusty to mention that similar behaviors have been reported in the literature.77,78,79
4. Conclusion
In conclusion, we have studied the structural, morphological, optical, magnetic, electrical, and dielectric properties of Li0.5MgFe1.5O3.5 ferrite, synthesized by the sol–gel auto-combustion route. The X-ray diffraction, FTIR spectroscopy, and RAMAN spectroscopy show that this compound crystallizes in a cubic structure at room temperature with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The scanning electron microscopy has proven that our material consists of grain agglomerates. Energy dispersive spectroscopy analysis confirmed the purity of the synthesized sample. Besides, the studied material exhibits a ferrimagnetic behavior at room temperature. The values of the remanent magnetization Mr, of the coercive field HC and of the magnetization at saturation deduced from the hysteresis loop are respectively Mr = 0,13 emu g−1, and HC = 4,65 Oe. These values of HC and Mr are very low, which suggests the superparamagnetic behavior of our sample. Finally, the impedance spectroscopy of this material was studied in the frequency range (40 Hz–1 MHz), in the thermal range (440 K to 470 K). Traces of the Nyquist diagram revealed semicircles not centered on the true axis, showing that the conduction of this material follows the Cole–Cole model. The equivalent electrical circuit is formed by a parallel R-CPE combination representing the grain and grain boundary contributions.
m. The scanning electron microscopy has proven that our material consists of grain agglomerates. Energy dispersive spectroscopy analysis confirmed the purity of the synthesized sample. Besides, the studied material exhibits a ferrimagnetic behavior at room temperature. The values of the remanent magnetization Mr, of the coercive field HC and of the magnetization at saturation deduced from the hysteresis loop are respectively Mr = 0,13 emu g−1, and HC = 4,65 Oe. These values of HC and Mr are very low, which suggests the superparamagnetic behavior of our sample. Finally, the impedance spectroscopy of this material was studied in the frequency range (40 Hz–1 MHz), in the thermal range (440 K to 470 K). Traces of the Nyquist diagram revealed semicircles not centered on the true axis, showing that the conduction of this material follows the Cole–Cole model. The equivalent electrical circuit is formed by a parallel R-CPE combination representing the grain and grain boundary contributions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by national funds from FCT – Fundação para a Ciência e a Tecnologia, I. P., within the projects UIDB/04564/2020 and UIDP/04564/2020. Access to TAIL-UC facility funded under QREN-Mais Centro Project No. ICT_2009_02_012_1890 is gratefully acknowledged.References
- A. Omri, E. Dhahri, B. F. O. Costa and M. A. Valente, J. Magn. Magn. Mater., 2020, 499, 166243 CrossRef CAS.
- T. Hyeon, Chem. Commun., 2003, 927–934 RSC.
- F. Elleuch, M. Triki, M. Bekri, E. Dhahri and E. K. Hlil, J. Alloys Compd., 2015, 620, 249–255 CrossRef CAS.
- M. A. Willard, L. K. Kurihara, E. E. Carpenter, S. Calvin and V. G. Harris, Int. Mater. Rev, 2004, 49, 125–170 CrossRef CAS.
- A. Dhahri, F. I. H. Rhouma, J. Dhahri, E. Dhahri and M. A. Valente, Solid State Commun., 2011, 151, 738–742 CrossRef CAS.
- M. A. Ahmed, E. Dhahri, S. I. El-Dek and M. S. Ayoub, Solid State Sci., 2013, 20, 23–28 CrossRef CAS.
- B. Rabi, A. Essoumhi, M. Sajieddine, J. M. Greneche, E. K. Hlil, A. Razouk and M. A. Valente, Appl. Phys. A, 2020, 126, 174 CrossRef CAS.
- A. C. Gandhi, P. M. Reddy, T.-S. Chan, Y.-P. Ho and S. Y. Wu, RSC Adv., 2015, 5, 84782–84789 RSC.
- N. Guijarro, P. Bornoz, M. Prévot, X. Yu, X. Zhu, M. Johnson, X. Jeanbourquin, F. Le Formal and K. Sivula, Sustainable Energy Fuels, 2018, 2, 103–117 RSC.
- A. M. Popov, T. A. Labutin, A. E. Goldt, O. V. Usovich, S. E. Bozhenko and N. B. Zorov, J. Anal. At. Spectrom., 2014, 29, 176–184 RSC.
- M. Colombo, S. Carregal-Romero, M. F. Casula, L. Gutiérrez, M. P. Morales, I. B. Böhm, J. T. Heverhagen, D. Prosperi and W. J. Parak, Chem. Soc. Rev., 2012, 41, 4306–4334 RSC.
- A. E. Reddy, T. Anitha, C. V. M. Gopi, S. S. Rao, B. Naresh and H.-J. Kim, Anal. Methods, 2018, 10, 223–229 RSC.
- J. Xie, K. Chen, H.-Y. Lee, C. Xu, A. R. Hsu, S. Peng, X. Chen and S. Sun, J. Am. Chem. Soc., 2008, 130, 7542–7543 CrossRef CAS PubMed.
- E. Céspedes, J. M. Byrne, N. Farrow, S. Moise, V. S. Coker, M. Bencsik, J. R. Lloyd and N. D. Telling, Nanoscale, 2014, 6, 12958–12970 RSC.
- V. K. Tripathi and R. Nagarajan, Adv. Powder Technol., 2016, 27, 1251–1256 CrossRef CAS.
- F. Gandomi, S. M. Peymani-Motlagh, M. Rostami, A. Sobhani-Nasab, M. Fasihi-Ramandi, M. Eghbali-Arani, R. Ahmadian, N. Gholipour, M. Rahimi-Nasrabadi and M. R. Ganjali, J. Mater. Sci.: Mater. Electron., 2019, 30, 19691–19702 CrossRef CAS.
- H. Borkar, R. J. Choudhary, V. N. Singh, M. Tomar, V. Gupta and A. Kumar, Mater. Res. Express, 2015, 2, 086101 CrossRef.
- A. Kumar, J. F. Scott and R. S. Katiyar, Appl. Phys. Lett., 2011, 99, 062504 CrossRef PubMed.
- D. Ravinder and P. V. B. Reddy, Mater. Lett., 2003, 57, 4344–4350 CrossRef CAS.
- S. A. Mazen and N. I. Abu-Elsaad, J. Magn. Magn. Mater., 2012, 324, 3366–3373 CrossRef CAS.
- S. K. Gurav, S. E. Shirsath, R. H. Kadam, S. M. Patange, K. S. Lohar and D. R. Mane, Mater. Res. Bull., 2013, 48, 3530–3536 CrossRef CAS.
- D. Ravinder and T. S. Rao, Cryst. Res. Technol., 1990, 25, 963–969 CrossRef CAS.
- M. F. Al-Hilli, S. Li and K. S. Kassim, Mater. Chem. Phys., 2011, 128, 127–132 CrossRef CAS.
- S. A. Mazen, A. H. Wafik and S. F. Mansour, J. Mater. Sci., 1996, 31, 2661–2665 CrossRef CAS.
- S. E. Shirsath, R. H. Kadam, M. L. Mane, A. Ghasemi, Y. Yasukawa, X. Liu and A. Morisako, J. Alloys Compd., 2013, 575, 145–151 CrossRef CAS.
- P. Sivakumar, R. Ramesh, A. Ramanand, S. Ponnusamy and C. Muthamizhchelvan, Mater. Res. Bull., 2011, 46, 2204–2207 CrossRef CAS.
- T. Roisnel and J. Rodríquez-Carvajal, in Materials Science Forum, Transtec Publications, 2001, vol. 378, pp. 118–123 Search PubMed.
- A. Iftikhar, M. U. Islam, M. S. Awan, M. Ahmad, S. Naseem and M. A. Iqbal, J. Alloys Compd., 2014, 601, 116–119 CrossRef CAS.
- R. Jenkins and R. L. Snyder, Introduction to X-ray Powder Diffractometry, Wiley Online Library, 1996, vol. 138 Search PubMed.
- A. A. Pandit, A. R. Shitre, D. R. Shengule and K. M. Jadhav, J. Mater. Sci., 2005, 40, 423–428 CrossRef CAS.
- F. Naaz, H. K. Dubey, C. Kumari and P. Lahiri, SN Appl. Sci., 2020, 2, 1–8 Search PubMed.
- S. Nasrin, S. M. Hoque, F. U. Z. Chowdhury and M. M. Hossen, IOSR J. Appl. Phys., 2014, 6, 58–65 CrossRef.
- N. Aggarwal and S. B. Narang, J. Alloys Compd., 2021, 866, 157461 CrossRef CAS.
- R. Tholkappiyan and K. Vishista, Mater. Sci. Semicond. Process., 2015, 40, 631–642 CrossRef CAS.
- J. Bennet, R. Tholkappiyan, K. Vishista, N. V. Jaya and F. Hamed, Appl. Surf. Sci., 2016, 383, 113–125 CrossRef CAS.
- I. Soudani, K. B. Brahim, A. Oueslati, H. Slimi, A. Aydi and K. Khirouni, RSC Adv., 2022, 12, 18697–18708 RSC.
- A. D. Jeidd, A. Bougoffa, A. Benali, A. Trabelsi, E. Dhahri, K. Khirouni and B. F. O. Costa, Ionics, 2023, 29(2), 603–615 CrossRef CAS.
- A. Nairan, M. Khan, U. Khan, M. Iqbal, S. Riaz and S. Naseem, Nanomaterials, 2016, 6, 73 CrossRef PubMed.
- C. Murugesan, L. Okrasa and G. Chandrasekaran, J. Mater. Sci.: Mater. Electron., 2017, 28, 13168–13175 CrossRef CAS.
- A. Ahlawat, V. G. Sathe, V. R. Reddy and A. Gupta, J. Magn. Magn. Mater., 2011, 323, 2049–2054 CrossRef CAS.
- A. Lassoued, F. Karolak, B. Dkhil, S. Ammar and A. Gadri, J. Mater. Sci.: Mater. Electron., 2017, 28, 18857–18864 CrossRef CAS.
- R. Sharma, S. Bansal and S. Singhal, RSC Adv., 2015, 5, 6006–6018 RSC.
- T. Tatarchuk, M. Bououdina, W. Macyk, O. Shyichuk, N. Paliychuk, I. Yaremiy, B. Al-Najar and M. Pacia, Nanoscale Res. Lett., 2017, 12, 1–11 CrossRef CAS PubMed.
- J. Massoudi, M. Smari, K. Nouri, E. Dhahri, K. Khirouni, S. Bertaina and L. Bessais, RSC Adv., 2020, 10, 34556–34580 RSC.
- L. Hannachi and N. Bouarissa, Phys. B, 2009, 404, 3650–3654 CrossRef CAS.
- A. O. Turky, M. M. Rashad, A. M. Hassan, E. M. Elnaggar and M. Bechelany, Phys. Chem. Chem. Phys., 2017, 19, 6878–6886 RSC.
- N. M. Ravindra and V. K. Srivastava, Infrared Phys., 1979, 19, 605–606 CrossRef CAS.
- A. G. Kolhatkar, A. C. Jamison, D. Litvinov, R. C. Willson and T. R. Lee, Int. J. Mol. Sci., 2013, 14, 15977–16009 CrossRef PubMed.
- A. Manikandan, J. J. Vijaya, L. J. Kennedy and M. Bououdina, Ceram. Int., 2013, 39, 5909–5917 CrossRef CAS.
- J. M. Vargas, A. Srivastava, A. Yourdkhani, L. Zaldivar, G. Caruntu and L. Spinu, J. Appl. Phys., 2011, 110, 064304 CrossRef.
- A. Mabrouki, H. Chadha, O. Messaoudi, A. Benali, T. Mnasri, E. Dhahri, M. A. Valente, S. Elgharbi, A. Dhahri and L. Manai, Inorg. Chem. Commun., 2022, 139, 109310 CrossRef CAS.
- X. Zeng, J. Zhang, S. Zhu, X. Deng, H. Ma, J. Zhang, Q. Zhang, P. Li, D. Xue, N. J. Mellors, X. Zhang and Y. Peng, Nanoscale, 2017, 9, 7493–7500 RSC.
- M. Junaid, J. Jacob, M. Nadeem, N. Jabbar, M. A. Khan, A. Manzoor, A. H. Chughtai, A. Ali, K. Mahmood and S. Hussain, Phys. B, 2021, 602, 412494 CrossRef CAS.
- A. S. Kakde, R. M. Belekar, G. C. Wakde, M. A. Borikar, K. G. Rewatkar and B. A. Shingade, J. Solid State Chem., 2021, 300, 122279 CrossRef CAS.
- M. N. Akhtar, M. Saleem and M. A. Khan, J. Phys. Chem. Solids, 2018, 123, 260–265 CrossRef CAS.
- N. Hamdaoui, Y. Azizian-Kalandaragh, M. Khlifi and L. Beji, Ceram. Int., 2019, 45, 16458–16465 CrossRef CAS.
- F. B. Abdallah, A. Benali, M. Triki, E. Dhahri, M. P. F. Graca and M. A. Valente, Superlattices Microstruct., 2018, 117, 260–270 CrossRef CAS.
- A. Dhahri, Y. Moualhi, C. Henchiri, A. Benali, P. Sanguino, M. P. F. Graça, M. A. Valente, N. Abdelmoula, H. Rahmouni and B. F. O. Costa, Inorg. Chem. Commun., 2022, 140, 109435 CrossRef CAS.
- A. Kumar, B. P. Singh, R. N. P. Choudhary and A. K. Thakur, J. Alloys Compd., 2005, 394, 292–302 CrossRef CAS.
- S. Hcini, A. Selmi, H. Rahmouni, A. Omri and M. L. Bouazizi, Ceram. Int., 2017, 43, 2529–2536 CrossRef CAS.
- A. Benali, M. Bejar, E. Dhahri, M. F. P. Graça and L. C. Costa, J. Alloys Compd., 2015, 653, 506–512 CrossRef CAS.
- S. El. Kossi, F. I. H. Rhouma, J. Dhahri and K. Khirouni, Phys. B, 2014, 440, 118–123 CrossRef.
- Z. Raddaoui, R. Lahouli, S. El Kossi, J. Dhahri, H. Belmabrouk and A. Bajahzar, J. Mater. Sci.: Mater. Electron., 2020, 31, 4836–4849 CrossRef CAS.
- M. Amghar, A. Bougoffa, A. Trabelsi, A. Oueslati and E. Dhahri, RSC Adv., 2022, 12, 20348–20359 RSC.
- R. Lahouli, J. Massoudi, M. Smari, H. Rahmouni, K. Khirouni, E. Dhahri and L. Bessais, RSC Adv., 2019, 9, 19949–19964 RSC.
- H. Nyquist, Bell Syst. Tech. J., 1932, 11, 126–147 CrossRef.
- H. Felhi, R. Lahouli, M. Smari, H. Rahmouni, K. Khirouni and E. Dhahri, J. Mol. Struct., 2019, 1179, 1–10 CrossRef CAS.
- H. Rahmouni, A. Benali, B. Cherif, E. Dhahri, M. Boukhobza, K. Khirouni and M. Sajieddine, Phys. B, 2015, 466, 31–37 CrossRef.
- A. K. Jonscher, J. Phys. D: Appl. Phys., 1999, 32(14), R57 CrossRef CAS.
- A. Zaouali, A. Dhahri, A. Boughariou, E. Dhahri, R. Barillé, B. F. O. Costa and K. Khirouni, J. Mater. Sci.: Mater. Electron., 2021, 32, 1221–1232 CrossRef CAS.
- J. Massoudi, D. Bouekkeze, A. Bougoffa, K. Khirouni, E. Dhahri and L. Bessais, Adv. Powder Technol., 2020, 31, 4714–4730 CrossRef CAS.
- M. D. Daivajna, A. Rao and G. S. Okram, J. Magn. Magn. Mater., 2015, 388, 90–95 CrossRef CAS.
- R. N. Bhowmik and A. G. Lone, J. Alloys Compd., 2016, 680, 31–42 CrossRef CAS.
- E. Oumezzine, S. Hcini, F. I. H. Rhouma and M. Oumezzine, J. Alloys Compd., 2017, 726, 187–194 CrossRef CAS.
- M. Amghar, A. Bougoffa, A. Trabelsi, A. Oueslati and E. Dhahri, RSC Adv., 2022, 12, 15848–15860 RSC.
- S. Saha and T. P. Sinha, J. Appl. Phys., 2006, 99, 014109 CrossRef.
- P. Anithakumari, B. P. Mandal, S. Nigam, C. Majumder, M. Mohapatra and A. K. Tyagi, New J. Chem., 2017, 41, 13067–13075 RSC.
- S. Ben Moumen, Y. Hadouch, Y. Gagou, D. Mezzane, M. Amjoud, E. Choukri, Z. Kutnjak, B. Rožič, N. Abdelmoula and H. Khemakhem, J. Mater. Sci.: Mater. Electron., 2020, 31, 19343–19354 CrossRef.
- H. S. Mohanty, T. Dam, H. Borkar, D. K. Pradhan, K. K. Mishra, A. Kumar, B. Sahoo, P. K. Kulriya, C. Cazorla, J. F. Scott and D. K. Pradhan, J. Phys.: Condens. Matter, 2019, 31, 075401 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2023 |