Open Access Article
Open Access ArticleTheoretical exploration of noncovalent interactions in Sc2C2@C2n (n = 40, 41, and 42)⊂[12]CPP, PF[12]CPP†
Yang Liua,
Wangchang Lia,
Peiying Lia,
Yanmin Guoa,
Peng Cui*b and
Zhuxia Zhang *c
*c
aCollege of Materials Science and Engineering, Key Laboratory of Interface Science and Engineering in Advanced Materials, Taiyuan University of Technology, Taiyuan 030024, China
bThe Novel Computer Architecture Laboratory, School of Information, Guizhou University of Finance and Economics, Guiyang 550025, China. E-mail: pcui@mail.gufe.edu.cn
cCollege of Chemistry, Taiyuan University of Technology, Taiyuan 030024, China. E-mail: zhangzhuxia@tyut.edu.cn
First published on 3rd February 2023
Abstract
The encapsulation of fullerenes by carbon nanorings has gained increasing attention because of the unique molecular structure and special properties of the formed complexes. The host–guest interactions between the fullerenes and the carbon nanorings can influence the metal ion orientation and the molecular electronic structure. In this study, we hooped a series of carbide cluster metallofullerenes, namely Sc2C2@C2v(5)-C80, Sc2C2@C3v(8)-C82, and Sc2C2@D2d(23)-C84, with molecular carbon nanorings of [12]cycloparaphenylene ([12]CPP) and perfluoro[12]cycloparaphenylene (PF[12]CPP). The formed complexes were computationally studied via dispersion-corrected density functional theory calculations. The results showed that the deformation rate of PF[12]CPP after the formation of the fullerene-containing complexes was significantly smaller than that of [12]CPP. The binding energy and thermodynamic information showed that PF[12]CPP was more suitable for fullerene encapsulation. Moreover, charge population analysis showed that PF[12]CPP transferred more electrons to Sc2C2@C2n (n = 40, 41, and 42) compared with [12]CPP. Energy decomposition and real-space function analyses of host–guest interactions revealed the characteristics and nature of the noncovalent interactions in the supramolecules. These results provide theoretical support for the study of host–guest systems based on metallofullerenes.
1. Introduction
Endohedral metallofullerenes (EMFs) have attracted increasing attention owing to their diverse chemical properties, related to the fullerene carbon cages, and several unique properties associated with the internal metal clusters, including their magnetic properties, photoluminescence, and quantum spin.1–5 However, owing to the ball-like fullerene cage, it is still a challenge to control the metallofullerene molecules and comprehensively explore their properties. Consequently, the discovery of suitable fullerene receptors for forming stable fullerene inclusion complexes has become an active field in fullerene chemistry.6–8One of the interesting approaches to this problem is the use of receptors based on the so-called concave–convex π–π interactions. Through the use of concave receptors capable of adapting to the convex surface of fullerenes, the number of atom contacts can be maximized at short distances, enabling the maximization of stabilization through dispersion.9 Considering the spherical form of metallofullerene, the circular carbon nanorings are a suitable host for accommodating metallofullerenes and altering their properties. Molecular carbon nanorings are distinct π systems resembling carbon nanotube (CNT) segments, and both can form stable supramolecular systems through concave–convex π–π interactions.10 The most representative examples of carbon nanorings are cyclophenylpropylenes (CPPs), which consist of conjugated multibenzene rings that represent the shortest armchair carbon nanotube segment. Since the discovery of C60 was trapped into [10]CPP by Yamago et al.,11 the following class of supramolecular systems has been developed: C59N⊂[10]CPP,12 C70⊂[10–11]CPP,13 La@C82⊂[11]CPP,14 Gd@C82⊂[11]CPP,15 Y2@C79N⊂[12]CPP,16 and Sc2C2@C82⊂[12]CPP17 etc.
Fluorine incorporation into organic compounds considerably modifies the properties of the compounds, including their polarity, solubility, and lipophilicity. Therefore, perfluorocycloparaphenylenes (PFCPPs), another class of carbon nanorings with a comparable structure to CPPs, have attracted extensive attention. PFCPPs are a class of highly strained ring-shaped perfluoroarenes in which all hydrogen atoms of the corresponding CPPs are replaced with fluorine atoms. The structural and electronic properties of PFCPPs are expected to change significantly following the replacement of hydrogen by fluorine.18 Thus, elucidating the implications of these changes in PFCPPs for supramolecular systems such as fullerene⊂CPP is vital. Moreover, clarifying the fullerene molecule accommodation property of PFCPPs as compared with CPPs is important. Recently, Itami et al. synthesized and isolated PFCPPs.19 However, studies on the combination of PFCPPs and fullerenes are few. In addition, experimentally elucidating the nature of these noncovalent interactions is difficult. Therefore, the computational groups have a good opportunity to explore in depth the fundamental properties of the π–π noncovalent interactions of these host–guest systems.
In this study, we hooped a series of carbide cluster metallofullerenes, namely Sc2C2@C2v(5)-C80, Sc2C2@C3v(8)-C82, and Sc2C2@D2d(23)-C84, with nanorings of [12]CPP and PF[12]CPP. Although Zhang and Lu et al.17,20 have used [12]CPP to encapsulate Sc2C2@C3v(8)-C82, its two isomers Sc2C2@C2v(5)-C80, and Sc2C2@D2d(23)-C84 have not been investigated. Thus, in the present study, a series of complexes formed by host molecules ([12]CPP and PF[12]CPP) and guest molecules Sc2C2@C2n (n = 40, 41, and 42) were computationally studied using the density functional theory (DFT). The molecular-level π–π interactions of two systems were theoretically assessed to explore the discrepancies between them. The results of this study can elucidate the structures and properties of these supramolecular complexes and contribute to the design of novel supramolecular nanoarchitectures for material chemistry applications.
2. Computational details
All of the geometric optimizations were performed using M06-2X exchange–correlation functional in conjunction with the 6-31G(d) basis set.21,22 Additionally, Grimme's DFT-D3 method,23 which provides an empirical dispersion correction for DFT, was employed. Harmonic frequency analyses were performed at the same level to confirm whether the structures were in local minima or transition states on the potential energy surface. Geometry optimizations and frequency analyses were implemented using the Gaussian 09 program.24 Cartesian coordinates of the studied systems are provided in the ESI† material.In order to obtain accurate binding energy for supramolecular complexes, the ωB97M-V functional in combination with a large def2-TZVPP basis set were employed in single-point calculations.25,26 The Counterpoise correction was used to solve the problem of basis set superposition error (BSSE).27 The ωB97M-V is fairly accurate for evaluating intermolecular interactions, and the single-point calculations were conducted using the ORCA 5.0.3 program28 via the RIJCOSX technique29 to accelerate the calculations.
To determine the nature of weak interactions in the supramolecular complexes, the physical components of intermolecular interactions were quantitatively analyzed via symmetry-adapted perturbation theory (SAPT) analysis using the PSI4 code.30 Considering the size of the studied systems, we had to use the simplest SAPT level, SAPT0,31 in combination with a small def2-SVP basis set. The adopted SAPT0 included the following terms:
| ESAPT0 = Eelest + Eexch + Eind + Edisp, | (1) |
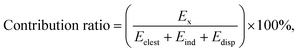 | (2) |
Electrostatic potential (ESP) and independent gradient model based on Hirshfeld partition (IGMH) analyses were all finished by Multiwfn 3.8(dev) code.32–37 Thermochemistry properties were calculated using the Shermo package.38 All isosurface and molecular structure maps were constructed using the VMD software.39
3. Results and discussion
3.1 ESP analysis and molecule orientation
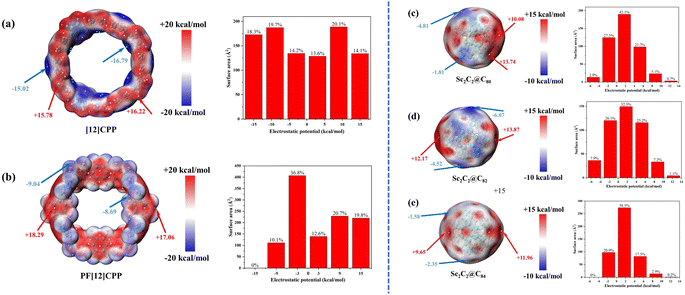
The ESP of a molecule represents the interaction energy between a unit charge at a given position and the system under study without considering the effects of charge transfer and polarization.40 The ESP is a rather common and useful tool to intuitively reveal the possible electrostatic interaction of a molecule with the external environment, which also affects complexation between the host and guest molecules.9 Fig. 1 shows the ESP of the host molecules [12]CPP and PF[12]CPP and the guest molecules Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84. The red (blue) area represents the surface local maxima (minima) of ESP.The [12]CPP featured negative regions associated with phenyl rings and positive regions on the rim of the ring, owing to hydrogen atoms (Fig. 1a). Therefore, the cavity was mostly negative and will favor the inclusion of electron-deficient species. The ESP of the van der Waals (vdW) surface of [12]CPP was distributed in the range of −16.79 to 16.22 kcal mol−1. The overall distribution characteristics of ESP can be found from the histogram of the area distribution of different ESP intervals. The relatively uniform distribution of the surface area in different ESP ranges for [12]CPP is shown in Fig. 1(a-right), and the positive and negative areas were calculated as 451.1 and 494.1 Å2, respectively, which correspond to 47.8% and 52.2% of the entire vdW surface, respectively. As the polarity of F atoms was much greater than that of H atoms, PF[12]CPP and [12]CPP considerably differed in ESP distribution. PF[12]CPP displayed positive regions in the internal region of the ring and negative regions on the ring rim (Fig. 1b). The ESP of the vdW surface of PF[12]CPP was distributed in the range −9.04 to 18.29 kcal mol−1, and the local minima and maxima of the ESP values were greater (more positive) than those of [12]CPP (−16.79 to 16.22 kcal mol−1). Fig. 1(b-right) displays the inhomogeneous surface area for different ESP ranges of PF[12]CPP compared with [12]CPP. The areas of the positive and negative parts of PF[12]CPP were respectively calculated as 587.7 and 518.1 Å2, corresponding to 46.9% and 53.1% of the entire vdW surface, respectively. The ESP of the vdW surface of PF[12]CPP was not distributed in the interval −18 to 12 kcal mol−1, whereas 18.3% of that of [12]CPP was distributed in this interval.
In previous studies, C60 and C70 showed almost zero ESP, with marginally positive regions, and C76 and C78 exhibited the same behavior.9 However, the occurrence of the endohedral unit in endofullerenes introduces larger asymmetries in the charge distribution, resulting in noticeable positive and negative ESP regions. Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84 (Fig. 1c–e) showed a markedly positive region, where the Sc atom contacted the carbon cage, while the carbon cages near the C–C bonds of the Sc2C2 endohedral cluster exhibited a negative region. Moreover, the positive region of Sc2C2@C80 was more concentrated than those of Sc2C2@C82 and Sc2C2@C84, attributable to the small size of C80, which resulted in a dihedral angle of only 112.7° for Sc–C2–Sc in the Sc2C2 cluster, which is significantly smaller than those of C82 and C84 (126.0° and 180.0°, respectively; see Table S1† for specific geometric parameters). The ESPs of the vdW surface of Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84 were distributed in the range −4.81 to 13.74 kcal mol−1, −6.07 to 13.87 kcal mol−1, and −2.35 to 11.96 kcal mol−1, respectively. The ESP of Sc2C2@C84 was not distributed in the interval of −7.0 to −3.5 kcal mol−1, whereas 2.9% and 7.9% of the ESPs of Sc2C2@C82 and Sc2C2@C84 were distributed in this interval. In addition, Sc2C2@C84 showed almost the largest marginally positive ESP regions (50.9% in the 0 to 3.5 kcal mol−1 interval); the corresponding percentages for Sc2C2@C80 and Sc2C2@C82 were 42.1% and 32.5%, respectively, consistent with the ESP diagram (Fig. 1e).
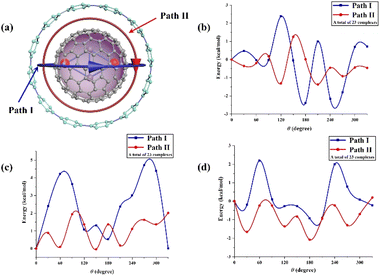
Furthermore, we explored the different orientations of guest molecules in the host molecule through the ESP study of host–guest molecules and according to the electrostatically complementary principle. We simulated two typical rotation processes by calculating the energy curves of Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84 along their rotation path inside [12]CPP (Fig. 2). All isomers were optimized at the M06-2X-D3/6-31G(d) level (a total of 69 complexes). Path I suggests that two Sc atoms move perpendicularly along [12]CPP plane, while Path II suggests that two Sc atoms remained adhered to the wall of the nanoring during the rotation process, indicating that the positive region where Sc atoms contacted the carbon cage could overlap maximally with the negative region inside the [12]CPP cavity. Path II was the best path to rotate because its energy curve was below that of Path I (Fig. 2c and d). When Sc2C2@C82 rotated in [12]CPP, the barrier difference between Paths I and II was 4.75 kcal mol−1, while for Sc2C2@C84, the barrier difference was 4.27 kcal mol−1. In contrast to both complexes, for Sc2C2@C80 (Fig. 2b), the energy curve of Path II was not significantly lower than that of Path I because the positive region of Sc2C2@C80 was more concentrated (Fig. 1) than those of Sc2C2@C82 and Sc2C2@C84, as mentioned earlier. Path II was still the best rotation path because its barrier was 2.13 kcal mol−1 lower than that of Path I. When both Sc atoms were on parallel sites of the [12]CPP plane (θ = 180°), the conformer possessed minimum energy for Path I, because the positive region could overlap maximally with the negative region. The results of our study agree with the findings by Zhao and Lu et al. and explain why metallofullerenes such as Sc3N@C80 and Y2@C79N have the best rotation paths when rotated horizontally within [12]CPP.16,20 Likewise, for Sc2C2@C2n⊂PF[12]CPP (n = 40, 41, and 42), we positioned Sc atoms in parallel and perpendicular to F atoms, where the positive and negative regions overlapped to the maximum and minimum extents. The energy of the isomers was reduced when Sc atoms were parallel to F atoms. Section 3.2 focuses on the structures of the supramolecular complexes. The above results show that the molecular ESP is useful for identifying the stable structures of supramolecular complexes such as metallofullerene⊂CPP.
3.2 Geometric configurations
The geometric configurations of the host–guest complexes Sc2C2@C2n⊂[12]CPP and Sc2C2@C2n⊂PF[12]CPP (n = 40, 41, and 42) are shown in Fig. 3. To further describe the complexes, the geometric parameters and dipole moments of the [12]CPP and PF[12]CPP hosts and all of the host–guest complexes are detailed in Table 1.| Species | Dc–ca (Å) | Long axis (Å) | Short axis (Å) | Aspect ratio | Rdb (%) | θc (deg) | Dipole (Debye) |
|---|---|---|---|---|---|---|---|
| a Dc–c is defined as the distance between the two centers of host and guest.b Rd (deformation ratio of the host ring) = (aspect ratio of the host in the complex – aspect ratio of the free host)/aspect ratio of the free host.c θ is defined as the dihedral angle range between ring units of the host [12]CPP and PF[12]CPP. | |||||||
| Free [12]CPP | — | 16.407 | 16.283 | 1.007 | — | 28.1–39.1 | 0 |
| Sc2C2@C80⊂[12]CPP | 1.519 | 18.000 | 14.384 | 1.251 | 24.2 | 27.5–47.3 | 1.647 |
| Sc2C2@C82⊂[12]CPP | 1.110 | 17.537 | 15.009 | 1.168 | 16.0 | 18.2–40.5 | 1.970 |
| Sc2C2@C84⊂[12]CPP | 1.102 | 17.278 | 15.160 | 1.140 | 13.2 | 25.2–36.2 | 1.160 |
| Free PF[12]CPP | — | 15.955 | 14.960 | 1.069 | — | 46.1–60.1 | 0.014 |
| Sc2C2@C80⊂PF[12]CPP | 0.608 | 16.866 | 14.929 | 1.130 | 5.7 | 44.1–55.7 | 1.297 |
| Sc2C2@C82⊂PF[12]CPP | 0.530 | 16.776 | 14.905 | 1.126 | 5.3 | 42.7–56.2 | 0.898 |
| Sc2C2@C84⊂PF[12]CPP | 0.674 | 16.400 | 15.667 | 1.047 | −2.1 | 40.5–54.0 | 0.536 |
As shown in Table 1, the free [12]CPP and PF[12]CPP were almost circular, with calculated aspect ratios of 1.007 and 1.069, respectively. Upon the encapsulation of the fullerenes, the hosts were deformed into an elliptical shape. The deformation ratio of the host ring (Rd), defined in the footnote of Table 1, is a parameter for describing the host ring deformation after the formation of the complexes. Rd decreased with increasing carbon cage size (Table 1).
The Rd values of Sc2C2@C80⊂[12]CPP, Sc2C2@C82⊂[12]CPP, and Sc2C2@C84⊂[12]CPP were 24.2%, 16.0%, and 13.2%, respectively. The Rd of Sc2C2@C2n⊂PF[12]CPP was significantly lower than that of Sc2C2@C2n⊂[12]CPP. The Rd of Sc2C2@C84⊂PF[12]CPP (−2.1%) was lower than that of Sc2C2@C80⊂PF[12]CPP (5.7%). The −2.1% Rd of Sc2C2@C84⊂PF[12]CPP indicates that the interaction between the PF[12]CPP host and Sc2C2@C84 guest makes PF[12]CPP closer to a circular geometry compared with the free PF[12]CPP. In addition, Table 2 calculates the deformation energy of the monomers. The deformation energy (ΔEdef) of PF[12]CPP is lower than that of [12]CPP. The dihedral angle (θ) between ring units of the host [12]CPP and PF[12]CPP is another necessary parameter for describing the structure and deformation of the host ring. The θ values of the free host PF[12]CPP were widely distributed (46.1–60.1°), whereas those of the free hosts [12]CPP were narrowly distributed (28.1–39.1°), because the steric repulsion between the F atoms was greater than that between the H atoms. Additionally, the dihedral angles in the complexes change to different extents, probably suggesting a larger deformation energy of the host and a very strong host–guest interaction based on repulsion deriving from steric energy. Furthermore, because of their quasi-symmetry, both the free [12]CPP and PF[12]CPP possessed small dipole moments nearly equal to zero. However, all of the host–guest complexes were polar supramolecules with a certain number of dipole moments, attributable to the electron-rich property of the host and the electron-deficient nature of the guest fullerene.
| Complexes | ΔEa | BSSEa | ΔEcpa | ΔEdef | ΔG | ΔH | ΔS | |
|---|---|---|---|---|---|---|---|---|
| Full | Ring | |||||||
| a Obtained at the ωB97M-V/TZVPP level//M06-2X-D3/6-31G(d) level; BSSE refers to basis set superposition error. | ||||||||
| Sc2C2@C80⊂[12]CPP | −45.66 | 1.47 | −44.19 | 0.55 | 5.43 | −102.09 | −178.97 | −257.88 |
| Sc2C2@C82⊂[12]CPP | −48.40 | 1.48 | −46.92 | 0.49 | 3.94 | −112.83 | −189.95 | −258.69 |
| Sc2C2@C84⊂[12]CPP | −49.45 | 1.37 | −48.08 | 0.58 | 1.46 | −123.22 | −195.02 | −240.81 |
| Sc2C2@C80⊂PF[12]CPP | −57.23 | 5.86 | −51.37 | 0.80 | 1.23 | −135.05 | −212.22 | −258.84 |
| Sc2C2@C82⊂PF[12]CPP | −58.00 | 5.90 | −52.10 | 0.19 | 1.15 | −136.34 | −215.65 | −266.00 |
| Sc2C2@C84⊂PF[12]CPP | −60.82 | 5.76 | −55.06 | 0.26 | 0.93 | −153.38 | −227.77 | −249.52 |
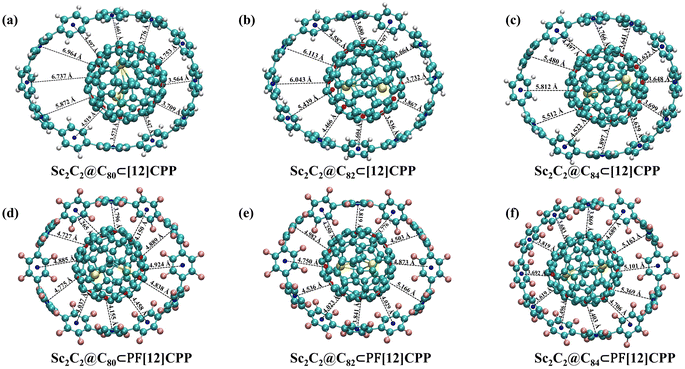
To accurately describe the position of the endofullerene guests in the [12]CPP and PF[12]CPP hosts, the distances (Dc–c) between the centers of host and guest were determined (Table 1). The Dc–c value is not zero, which indicates that the centers of the host and the guest did not completely overlap in all of the configurations of the complexes. A close relationship existed between the centers of the host and the guest (Dc–c) and the π–π interaction regions, and the shorter Dc–c was more advantageous to maximize the attractive interactions between the host and guests. The guest Sc2C2@C80 of Sc2C2@C80⊂[12]CPP, Sc2C2@C82 of Sc2C2@C82⊂[12]CPP, and Sc2C2@C84 of Sc2C2@C84⊂[12]CPP shifted to one side of the host ring by 1.519, 1.110, and 1.105 Å away from the [12]CPP center, respectively. The Dc–c values of Sc2C2@C80⊂PF[12]CPP, Sc2C2@C82⊂PF[12]CPP, and Sc2C2@C80⊂PF[12]CPP were 0.608, 0.530, and 0.674 Å, respectively. The Dc–c value of Sc2C2@C2n⊂PF[12]CPP was markedly smaller than that of Sc2C2@C2n⊂[12]CPP, suggesting that Sc2C2@C2n⊂PF[12]CPP exhibited stronger host–guest interaction.
All of the complexes of the Sc2C2@C2n⊂[12]CPP system exhibited similar general aspects (Fig. 3), with the fullerenes fitting within the [12]CPP cavity and establishing favorable interactions with all of the phenylene units. The fullerenes were oriented inside the cavity in such a way that the endohedral Sc atoms were in the plane of the nanoring which means that carbon atoms interacting with the endohedral unit were always oriented towards phenylene rings. All of the complexes of the Sc2C2@C2n⊂PF[12]CPP system also exhibited similar general features, with the fullerene suitably fitting within the PF[12]CPP cavity and establishing helpful interactions with F atoms of ring units. The Sc atoms were located close to F atoms in PF[12]CPP, which indicates that carbon atoms interacting with the endohedral unit were oriented toward the F atoms of ring units. Structures with other orientations relative to hosts were less stable. These behaviors were probably related to the asymmetry of the electron charge shown in Fig. 1. The ESP of endofullerenes was more positive in the regions where the endohedral unit contacted the carbon cage. Considering that the ESP of the [12]CPP cavity and the ring rim of PF[12]CPP were markedly negative, metallofullerenes were oriented such that their positive regions were directed toward those negative regions of hosts to facilitate the stabilization of electrostatic interactions. Fig. 3 also shows the interfacial distances (di) between hosts and guests. Here, di denotes the interfacial distance between the centroid of a ring unit of the host and the nearest centroid of a hexagon or pentagon of an endofullerene. The di values of Sc2C2@C80⊂[12]CPP, Sc2C2@C82⊂[12]CPP, and Sc2C2@C84⊂[12]CPP were 3.547–6.964 Å (Fig. 3a), 3.536–6.113 Å (Fig. 3b), and 3.622–5.812 Å (Fig. 3c), respectively, showing the wide distribution of di. This suggests that the attractive force of endofullerenes along the [12]CPP was nonuniform. A narrower interface will have a stronger force between Sc2C2@C2n and [12]CPP than a wider interface, because the interfacial distances were not significantly greater than 3.4 Å, the vdW distance between graphite sheets. The di values of Sc2C2@C80⊂PF[12]CPP, Sc2C2@C82⊂PF[12]CPP, and Sc2C2@C84⊂PF[12]CPP were 3.796–4.924 Å (Fig. 3d), 3.776–5.166 Å (Fig. 3e), and 3.619–5.369 Å (Fig. 3f), which shows a relatively narrow di distribution compared with the Sc2C2@C2n⊂[12]CPP system, respectively. Thus, the attractive force of endofullerenes along PF[12]CPP was relatively uniform compared with that along [12]CPP.
The effect of the host molecule on the endohedral unit is also of concern. The geometric parameters of Sc2C2 are presented in Table S1.† The cluster of Sc2C2@C80 was bent like a butterfly, with two tightly bonded C atoms in the cage center. The two Sc atoms existed between the C2 unit and the cage. The Sc–Sc distance in the Sc2C2@C80 cage was 3.692 Å, and the Sc–C2–Sc dihedral angle was 112.7°. Compared with the Sc2C2@C80 cage, the Sc2C2@C80⊂[12]CPP system exhibited a 0.006 Å higher Sc–Sc distance and a 0.4° lower Sc–C2–Sc dihedral angle, while the Sc2C2@C80⊂PF[12]CPP system exhibited a 0.015 Å lower Sc–Sc distance and 0.9° lower Sc–C2–Sc dihedral angle. Moreover, the Sc–Sc distance and dihedral angle of the Sc2C2 cluster of Sc2C2@C82 were 3.939 Å and 126.0°, greater than those of Sc2C2 cluster of Sc2C2@C80, which indicates that the values of both parameters increased with increasing carbon cage size. In addition, compared with Sc2C2@C82, the Sc–Sc distances of the Sc2C2@C82⊂[12]CPP and Sc2C2@C82⊂PF[12]CPP systems were reduced by 0.002 Å and 0.003 Å, respectively, while the Sc–C2–Sc dihedral angles were reduced by 0.4° and 0.2°, respectively. The Sc2C2 cluster of Sc2C2@C84 exhibited the largest Sc–Sc distance and dihedral angle: 4.473 Å and 180.0°, respectively. Compared with Sc2C2@C84, the Sc–Sc distances of the Sc2C2@C84⊂[12]CPP and Sc2C2@C84⊂PF[12]CPP systems were 0.004 Å and 0.003 Å higher, respectively, while the Sc–C2–Sc dihedral angles did not change. The C–C distance was almost constant for all complexes (around 1.265 Å). Overall, the weak interaction between the host and the guest did not significantly affect the endohedral clusters.
3.3 Binding energies and thermodynamic properties
Binding energy is a decisive and valuable factor to measure the stability and strength of intermolecular noncovalent interactions between the units of a complex. Table 2 presents binding energies with and without BSSE correction (ΔECP and ΔE). The counterpoise correction is calculated at the ωB97M-V/TZVPP level (two fragments are carbon nanorings and metallofullerenes, respectively). Here the binding energy is the difference in the electron energy between the complexes and the monomers, and considering the deformation energy (ref. 9). Regarding the Sc2C2@C2n⊂[12]CPP system, the ΔECP of Sc2C2@C84⊂[12]CPP was 48.08 kcal mol−1, which was distinctly greater than those of Sc2C2@C80⊂[12]CPP and Sc2C2@C82⊂[12]CPP, by 3.89 and 1.16 kcal mol−1, respectively. The Sc2C2@C2n⊂PF[12]CPP system exhibited a similar trend; the ΔECP of Sc2C2@C84⊂PF[12]CPP was 55.06 kcal mol−1, which was distinctly greater than those of Sc2C2@C80⊂PF[12]CPP and Sc2C2@C82⊂PF[12]CPP by 3.69 and 2.96 kcal mol−1, respectively.Sc2C2@C84 exhibited the greatest binding energy to the host molecule, attributable to the larger carbon cage size of C84 compared with C80 and C82, which allows for a large region of π–π contact between the host molecules ([12]CPP and PF[12]CPP) and C84. The binding energy of the Sc2C2@C2n⊂PF[12]CPP system was about 7 kcal mol−1 greater than that of the Sc2C2@C2n⊂[12]CPP system, which indicates that PF[12]CPP is more suitable for accommodating fullerenes than [12]CPP. In addition, to investigate the effect of Sc2C2 clusters on the noncovalent interactions between the host and guest, the binding of C80, C82, and C84 without Sc2C2 clusters to [12]CPP and PF[12]CPP was calculated (see Table S2†). The results show that Sc2C2@C2n binds more stable to [12]CPP and PF[12]CPP compared with C2n. This suggests that electrostatic interactions due to the introduction of endohedral clusters can promote the stabilization of supramolecular complexes. The thermodynamic information of all of the complexes at 298.15 K and 1 atm were obtained via DFT calculations at the M06-2X-D3/6-31G(d) level of theory (Table 2). The relative trends of the ΔG and ΔH of the Sc2C2@C2n⊂[12]CPP and Sc2C2@C2n⊂PF[12]CPP complexes were well consistent with those of ΔECP. The processes of Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84 binding to [12]CPP and PF[12]CPP at 298.15 K were spontaneous, with ΔG values of −102.09 to −123.22 kJ mol−1 and −135.05 to −153.38 kJ mol−1 for Sc2C2@C2n⊂[12]CPP and Sc2C2@C2n⊂PF[12]CPP complexes, respectively. The ΔG values of the Sc2C2@C2n⊂[12]CPP complexes were considerably smaller (more positive) than those of the Sc2C2@C2n⊂PF[12]CPP complexes, indicating that the [12]CPP molecule exhibited a weaker thermodynamic spontaneity of endofullerenes binding than PF[12]CPP. According to the ΔH values, all host–guest binding reactions were highly exothermic. The free molecules decreased by half after the formation of the host–guest complexes, and correspondingly, the entropies of the six complexes decreased by −240.81 to −266.00 J mol−1 K−1. All of this thermodynamic information indicates that the binding of Sc2C2@C2n to [12]CPP and PF[12]CPP in the vacuum was enthalpy-driven and entropy-opposed.
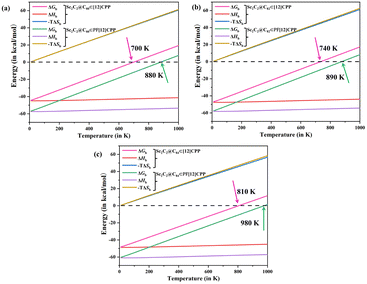
It is well known that the possibility of intermolecular binding depends entirely on the Gibbs free energy (ΔGb), and it is closely related to environmental temperature. At a given temperature, a negative and positive ΔGb correspond to thermodynamically spontaneous and infeasible complex formation, respectively. Therefore, further research on ΔGb is necessary. In this work, we calculated the ΔGb of all of the complexes and decomposed it as ΔGb = ΔHb − TΔSb, where ΔHb and ΔSb represent the changes in enthalpy and entropy upon binding, respectively, to illustrate the thermodynamic nature of the formation of the complex (Fig. 4).
The ΔHb curve shows that the binding of endofullerenes to [12]CPP and PF[12]CPP is primarily driven by a significant reduction in enthalpy, and the extent of which is less dependent on temperature. The formation of the host–guest complexes reduced the motion freedom of the system, so that the entropy of the system was significantly decreased, resulting in a clear increase in the −TΔSb terms. Overall, the ΔGb value of all of the complexes increased with increasing temperature. Supramolecular complexes Sc2C2@C80⊂[12]CPP, Sc2C2@C82⊂[12]CPP, and Sc2C2@C84⊂[12]CPP were spontaneously formed below 700, 740, and 810 K, respectively, because the calculated ΔGb of the system was negative in this temperature range. Sc2C2@C80⊂PF[12]CPP, Sc2C2@C82⊂PF[12]CPP, and Sc2C2@C80⊂PF[12]CPP were spontaneously formed below 880, 890, and 980 K, respectively. The ΔGb values of the Sc2C2@C2n⊂PF[12]CPP systems were higher than those of the Sc2C2@C2n⊂[12]CPP systems, indicating that the thermodynamic spontaneity of the Sc2C2@C2n⊂PF[12]CPP system was stronger than that of Sc2C2@C2n⊂[12]CPP, as previously described.
3.4 Frontier orbital features and electronic properties
Frontier orbitals play a decisive role in the reactions and properties of molecules. Fig. 5 provides the compositions and energy levels of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the most stable Sc2C2@C2n⊂[12]CPP and Sc2C2@C2n⊂PF[12]CPP (n = 40, 41, and 42) host–guest complexes. The frontier orbital gap of PF[12]CPP was larger than that of [12]CPP by 0.72 eV, and the frontier orbital gaps of both were much larger than those of the free fullerenes and their complexes (Fig. 5). During the binding between the free PF[12]CPP or [12]CPP and Sc2C2@C2n to form complexes, the frontier orbital gap decreased significantly compared with those of PF[12]CPP and [12]CPP. Moreover, the two systems Sc2C2@C2n⊂[12]CPP and Sc2C2@C2n⊂PF[12]CPP featured almost the same frontier orbital gap as Sc2C2@C2n. This indicates that the HOMOs and LUMOs of the complexes were entirely derived from those of Sc2C2@C2n and that the electronic properties of the complexes may be more related to the guest molecules.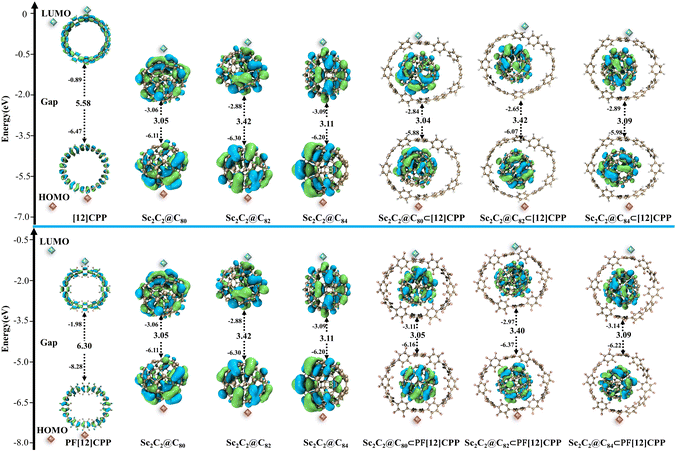 | ||
| Fig. 5 The frontier molecular orbital and the corresponding energy level diagram of the Sc2C2@C2n (n = 40, 41, and 42) and six complexes. | ||
To further investigate the electronic properties of the complexes, the ionization potential (IP) and the electron affinity (EA) of individual molecules and their complexes were determined from the energies of the corresponding charged and neutral species. Table 3 presents the computed IP and EA values of Sc2C2@C2n, [12]CPP, PF[12]CPP, and their complexes. The relative trends of the fundamental gap (i.e., IP minus EA, GapIP−EA) of the systems were well consistent with those of the frontier orbital gap (GapHOMO–LUMO, Table 3). Either the IP or EA of free PF[12]CPP was higher than that of the free [12]CPP, which indicates that [12]CPP exhibited a stronger electron-donating capacity but weaker electron-accepting capacity than PF[12]CPP in their isolated states. Additionally, the free host molecules [12]CPP and PF[12]CPP exhibited higher IPs but lower EAs than the free guest molecules Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84. This indicates that the free endofullerenes featured stronger electron-donating and electron-accepting capacities than the free [12]CPP and PF[12]CPP. Therefore, the fundamental gaps and frontier orbital gaps of [12]CPP and PF[12]CPP were distinctly larger than those of the three metallofullerenes. A careful examination of the results indicates that the electrons in the Sc2C2@C82 were more bound than those in Sc2C2@C80 and Sc2C2@C84; however, Sc2C2@C82 had a weaker electron-capturing capacity, as its EA was 2.38 eV, which was 0.14 and 0.18 eV lower than those of Sc2C2@C80 and Sc2C2@C84, respectively.
| Systems | IP | EA | GapIP−EA | GapHOMO–LUMO |
|---|---|---|---|---|
| [12]CPP | 6.86 | 0.50 | 6.36 | 5.58 |
| PF[12]CPP | 8.68 | 1.58 | 7.10 | 6.30 |
| Sc2C2@C80 | 6.61 | 2.52 | 4.09 | 3.05 |
| Sc2C2@C82 | 6.83 | 2.38 | 4.45 | 3.42 |
| Sc2C2@C84 | 6.66 | 2.56 | 4.10 | 3.11 |
| Sc2C2@C80⊂[12]CPP | 6.29 | 2.39 | 3.90 | 3.04 |
| Sc2C2@C82⊂[12]CPP | 6.51 | 2.24 | 4.27 | 3.42 |
| Sc2C2@C84⊂[12]CPP | 6.44 | 2.45 | 3.99 | 3.09 |
| Sc2C2@C80⊂PF[12]CPP | 6.52 | 2.68 | 3.84 | 3.05 |
| Sc2C2@C82⊂PF[12]CPP | 6.79 | 2.51 | 4.28 | 3.40 |
| Sc2C2@C84⊂PF[12]CPP | 6.69 | 2.66 | 4.03 | 3.09 |
As mentioned earlier, the frontier molecular orbitals of the six complexes were derived from those of endofullerenes and independent of [12]CPP and PF[12]CPP; that is, the IP or EA of the complexes was determined mainly by the concentration of endofullerenes Sc2C2@C2n. As expected, the IP and EA trends of the complexes were similar to those of the endofullerenes (Table 3). Among the Sc2C2@C2n⊂[12]CPP and Sc2C2@C2n⊂PF[12]CPP systems, Sc2C2@C82⊂[12]CPP and Sc2C2@C82⊂PF[12]CPP respectively exhibited both the highest IP and the lowest EA. The IP and EA of the Sc2C2@C2n⊂PF[12]CPP systems were higher than those of the Sc2C2@C2n⊂[12]CPP systems, which indicates that the Sc2C2@C2n⊂[12]CPP system possessed a stronger electron-donating capacity but weaker electron-accepting capacity than the Sc2C2@C2n⊂PF[12]CPP system.
Charge transfer commonly occurs in supramolecular systems. Charge transfer results in the additional stability of a complex in terms of interaction energy. In addition to the IP of the donor and the EA of the acceptor, the intermolecular distance and mutual orientation also highly influence the amplitude of charge transfer.41 Table 4 presents the amount of charge transfer as determined via Mulliken population analysis and natural population analysis (NPA). The Mulliken and NPA charge transfers of the Sc2C2@C2n⊂[12]CPP systems were around 0.07 and 0.04 e, respectively. The charge transfer amount of the Sc2C2@C2n⊂[12]CPP system as derived via Mulliken analysis was consistent with the charge transfer of the [11]CPP–La@C82 complex reported by Yamago et al.14 Sc2C2@C80⊂PF[12]CPP, Sc2C2@C82⊂PF[12]CPP, and Sc2C2@C84⊂PF[12]CPP exhibited Mulliken and NPA charge transfers of 0.19 and 0.10 e, 0.17 and 0.09 e, and 0.35 and 0.12 e, respectively, which were significantly greater than those of the Sc2C2@C2n⊂[12]CPP system. These results suggest that the amount of charge transfer between the host and guest molecules was more dependent on the species of the host molecule rather than the species and size of the fullerene.
| Host–guest | Mulliken | NPA |
|---|---|---|
| Sc2C2@C80⊂[12]CPP | 0.08 | 0.04 |
| Sc2C2@C82⊂[12]CPP | 0.07 | 0.04 |
| Sc2C2@C84⊂[12]CPP | 0.07 | 0.04 |
| Sc2C2@C80⊂PF[12]CPP | 0.19 | 0.10 |
| Sc2C2@C82⊂PF[12]CPP | 0.17 | 0.09 |
| Sc2C2@C84⊂PF[12]CPP | 0.35 | 0.12 |
3.5 Energy decomposition analysis and weak interaction regions
The energy components of the interaction between [12]CPP or PF[12]CPP and Sc2C2@C2n are presented in Table 5. Although the calculated ESAPT0 at the SAPT0/def2-SVP level was considerably different from the more accurate ωB97M-V/def2-TZVPP results (ΔEcp in Table 2), the relative contribution of its components was still helpful for clarifying the nature of the intermolecular interactions. Only the Eexch characterizing the steric effect contributed positively to the interaction, while the other terms, including Eelest, Eind, and Edisp, negatively affected the interaction, indicating that the ESAPT0 components played an attractive role in the intermolecular complexation.| Fragments | Eelest | Eind | Edisp | Eexch | ESAPT0 |
|---|---|---|---|---|---|
| [12]CPP-Sc2C2@C80 | −29.11 (22.19%) | −6.89 (5.25%) | −95.21 (72.56%) | 65.47 | −65.74 |
| [12]CPP-Sc2C2@C82 | −29.42 (22.40%) | −6.82 (5.19%) | −95.09 (72.41%) | 64.96 | −66.37 |
| [12]CPP-Sc2C2@C84 | −26.89 (21.11%) | −6.35 (4.99%) | −94.14 (73.90%) | 62.87 | −64.51 |
| PF[12]CPP-Sc2C2@C80 | −30.55 (25.26%) | −6.33 (5.23%) | −84.06 (69.51%) | 73.59 | −47.35 |
| PF[12]CPP-Sc2C2@C82 | −37.75 (27.68%) | −7.52 (5.51%) | −91.10 (66.80%) | 84.78 | −51.59 |
| PF[12]CPP-Sc2C2@C84 | −66.75 (32.60%) | −13.38 (6.46%) | −126.25 (60.94%) | 167.61 | −39.57 |
Furthermore, for all of the six complexes, Edisp dominated the attractive component of the interaction energy, and for most of these cases, it even contributed more than 60% to this part. Even though electrostatic interaction is not as important as dispersion interaction in the formation of dimers, its effect on binding should not be ignored, with Eelest accounting for more than 20% of all complexes. As depicted in Table 4, a small amount of charge transfer existed between the host and guest molecules, and thus, Eind contributed the least to the interaction, only about 5%.
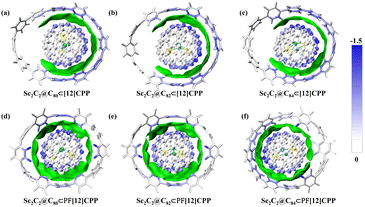
IGMH is a very intuitive method proposed to graphically depict the main interaction regions between specific fragments of compounds by using the isosurface of δginter function. Fig. 6 delineates the weak interaction regions of the host–guest complexes and the role played by each atom in the fragment. The atoms in the different fragments are colored according to their contributions to the dispersion interaction energy. The larger the contribution to the dispersion effect, the closer the bluer the hue. For all the complexes, the extended δginter isosurface in green suggests that the interaction between the host and guest molecules covered a wide spatial region and that the electron density on δginter isosurface was small (about 0.001 a.u). Thus, the interaction between host and guest molecules can be considered typical π–π stacking.7 The weak interaction region of the Sc2C2@C2n⊂[12]CPP system exhibited an open weak interaction region. The closer the interfacial distance (di) between the host [12]CPP and guest Sc2C2@C2n was to 3.4 Å (Fig. 3), the bluer the color of the atoms, indicating stronger π–π vdW interactions. In contrast, at an inter-atom distance considerably greater than 3.4 Å (corresponding to white atom color, the longest distance was >6 Å), vdW π–π interactions will no longer exist. Compared with the Sc2C2@C2n⊂[12]CPP system, the Sc2C2@C2n⊂PF[12]CPP system exhibited an almost closed weak interaction region, consistent with the relative trend of the binding energies. This trend was due to the relatively uniform distribution of the interfacial distance between PF[12]CPP and the fullerenes. IGMH not only visualizes the weak interaction regions but also identifies the weak interaction type as π–π stacking.
4 Conclusions
CPPs and the corresponding perfluorinated aromatic compounds, PFCPPs, are widely used in materials science. In this study, we investigated the structures and properties of the complexes formed between [12]CPP or PF[12]CPP and Sc2C2@C2n (n = 40, 41, and 42). The main findings and conclusions are summarized as follows:(1) ESP analysis showed that [12]CPP exhibited negative regions associated with phenyl rings and positive regions on the rim of the ring. However, PF[12]CPP exhibited positive regions in the internal region of the ring and negative regions on the ring rim because the polarity of F atoms was much greater than that of H atoms. In addition, the ESP can be useful for identifying the stabilized structure of the complexes.
(2) Three endofullerenes, namely Sc2C2@C80, Sc2C2@C82, and Sc2C2@C84, established favorable interactions with all of the phenylene units of the Sc2C2@C2n⊂[12]CPP system. For the Sc2C2@C2n⊂PF[12]CPP system, the three endofullerenes established favorable interactions with the F atoms of the ring units. This could be related to the greater polarity of the endofullerenes, which showed positive ESP regions around the carbon atoms contacting the endohedral units.
(3) With increasing carbon cage size, the binding energy of the complexes also increased, possibly because the larger carbon cage allowed for a large region of π–π contact between the host molecules ([12]CPP and PF[12]CPP) and guest molecules (Sc2C2@C2n). However, PF[12]CPP could more suitably accommodate Sc2C2@C2n than [12]CPP. Thermodynamic information indicated that the complexes of the two systems were enthalpy-driven and entropy-opposed. Moreover, the Sc2C2@C2n⊂PF[12]CPP system exhibited a stronger thermodynamic spontaneity than the Sc2C2@C2n⊂[12]CPP system.
(4) The frontier molecular orbitals of the six complexes were completely derived from those of the endofullerenes and independent of [12]CPP and PF[12]CPP. The IP and the EA showed that the electron-accepting capacities of the complexes were higher than those of the free [12]CPP and PF[12]CPP. Moreover, compared with [12]CPP, PF[12]CPP exhibited a stronger charge transfer with fullerenes.
(5) Energy decomposition analysis showed that the interaction between the host and guest molecules of the complexes was dominated by dispersion attraction. However, the intermolecular electrostatic interaction was considerable. The visualized weak interaction regions indicated that π–π vdW interaction would be nonexistent in the region with di much greater than 3.4 Å.
The elucidated structures and properties of those host–guest supramolecules, which are difficult to experimentally obtain, and the reported conclusions can provide useful theoretical guidance for materials chemistry applications.
Author contributions
Yang Liu: investigation, writing – original draft. Wangchang Li: validation. Peiying Li: validation. Yanmin Guo: validation. Peng Cui: supervision & resources. Zhuxia Zhang: writing – review & editing, resources.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the Plan Project for Guizhou Provincial Science and Technology (QKH-Basic [2018]1022), the Planted talent plan of Guizhou University of Finance and Economics (2020XSXMA09), and the National Natural Science Foundation of China (No. 21963004; 21903059).References
- Z. Hu, B. W. Dong, Z. Liu, J. J. Liu, J. Su, C. Yu, J. Xiong, D. E. Shi, Y. Wang, B. W. Wang, A. Ardavan, Z. Shi, S. D. Jiang and S. Gao, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed.
- F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Buchner and A. A. Popov, Nat. Commun., 2017, 8, 16098 CrossRef CAS PubMed.
- Z. Liu, B. W. Dong, H. B. Meng, M. X. Xu, T. S. Wang, B. W. Wang, C. R. Wang, S. D. Jiang and S. Gao, Chem. Sci., 2018, 9, 457–462 RSC.
- H. Meng, C. Zhao, M. Nie, C. Wang and T. Wang, Nanoscale, 2018, 10, 18119–18123 RSC.
- T. Wang, J. Wu, W. Xu, J. Xiang, X. Lu, B. Li, L. Jiang, C. Shu and C. Wang, Angew. Chem., Int. Ed., 2010, 49, 1786–1789 CrossRef CAS PubMed.
- S. Goswami, D. Ray, K. I. Otake, C. W. Kung, S. J. Garibay, T. Islamoglu, A. Atilgan, Y. Cui, C. J. Cramer, O. K. Farha and J. T. Hupp, Chem. Sci., 2018, 9, 4477–4482 RSC.
- Z. Liu, X. Wang, X. Wang, T. Lu, M. Zhao and X. Yan, ChemRxiv, preprint, 2022, DOI: DOI:10.26434/chemrxiv-2022-lb0dt.
- E. M. Perez and N. Martin, Chem. Soc. Rev., 2015, 44, 6425–6433 RSC.
- I. Gonzalez-Veloso, E. M. Cabaleiro-Lago and J. Rodriguez-Otero, Phys. Chem. Chem. Phys., 2018, 20, 11347–11358 RSC.
- G. Povie, Y. Segawa, T. Nishihara, Y. Miyauchi and K. Itami, Science, 2017, 356, 172–175 CrossRef CAS PubMed.
- T. Iwamoto, Y. Watanabe, T. Sadahiro, T. Haino and S. Yamago, Angew. Chem., Int. Ed., 2011, 50, 8342–8344 CrossRef CAS PubMed.
- A. Stergiou, J. Rio, J. H. Griwatz, D. Arcon, H. A. Wegner, C. P. Ewels and N. Tagmatarchis, Angew. Chem., Int. Ed., 2019, 58, 17745–17750 CrossRef CAS PubMed.
- K. Yuan, Y.-J. Guo and X. Zhao, J. Phys. Chem. C, 2015, 119, 5168–5179 CrossRef CAS.
- T. Iwamoto, Z. Slanina, N. Mizorogi, J. Guo, T. Akasaka, S. Nagase, H. Takaya, N. Yasuda, T. Kato and S. Yamago, Chem.–Eur. J., 2014, 20, 14403–14409 CrossRef CAS PubMed.
- Y. Nakanishi, H. Omachi, S. Matsuura, Y. Miyata, R. Kitaura, Y. Segawa, K. Itami and H. Shinohara, Angew. Chem., Int. Ed., 2014, 53, 3102–3106 CrossRef CAS PubMed.
- C. Zhao, H. Meng, M. Nie, X. Wang, Z. Cai, T. Chen, D. Wang, C. Wang and T. Wang, J. Phys. Chem. C, 2019, 123, 12514–12520 CrossRef CAS.
- J. Zhang, C. Zhao, H. B. Meng, M. Z. Nie, Q. Li, J. F. Xiang, Z. X. Zhang, C. R. Wang and T. S. Wang, Carbon, 2020, 161, 694–701 CrossRef CAS.
- J. Rio, D. Erbahar, M. Rayson, P. Briddon and C. P. Ewels, Phys. Chem. Chem. Phys., 2016, 18, 23257–23263 RSC.
- H. Shudo, M. Kuwayama, M. Shimasaki, T. Nishihara, Y. Takeda, N. Mitoma, T. Kuwabara, A. Yagi, Y. Segawa and K. Itami, Nat. Commun., 2022, 13, 3713 CrossRef CAS PubMed.
- Y. X. Lu, C. Zhao, J. Zhang, W. Li, J. Y. Liang, L. S. Liu, Y. G. Li, C. R. Wang and T. S. Wang, Sci. China. Chem., 2022, 65, 1601–1606 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Thermochim. Acta, 1973, 28, 213–222 CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215–241 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, W. F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09 Rev. D.01, Gaussian Inc., Wallingford, CT, 2013 Search PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12 DOI:10.1002/wcms.1606.
- S. Kossmann and F. Neese, Chem. Phys. Lett., 2009, 481, 240–243 CrossRef CAS.
- R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince 3rd, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer 3rd, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197 CrossRef CAS PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539–555 CrossRef CAS PubMed.
- T. Lu, Z. Liu and Q. Chen, Mater. Sci. Eng., B, 2021, 273 Search PubMed.
- S. Manzetti and T. Lu, J. Phys. Org. Chem., 2013, 26, 473–483 CrossRef CAS.
- J. Zhang and T. Lu, Phys. Chem. Chem. Phys., 2021, 23, 20323–20328 RSC.
- T. Lu and Q. Chen, Comput. Theor. Chem., 2021, 1200, 113249 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS PubMed.
- Z. Y. Liu, T. Lu and Q. X. Chen, Carbon, 2021, 171, 514–523 CrossRef CAS.
- J. Rezac and A. de la Lande, J. Chem. Theory Comput., 2015, 11, 528–537 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra08153a |
| This journal is © The Royal Society of Chemistry 2023 |