Open Access Article
Open Access ArticleAn ab initio investigation of the structural, mechanical, electronic, optical, and thermoelectric characteristics of novel double perovskite halides Cs2CaSnX6 (X = Cl, Br, I) for optically influenced RRAM devices
Saira Kirana,
Umair Mumtaz be,
Aymen Mustafad,
Muhammad Imran
be,
Aymen Mustafad,
Muhammad Imran *c,
Fayyaz Hussain
*c,
Fayyaz Hussain *e,
Umbreen Rasheede,
R. M. A. Khalile,
Ejaz Ahmad Kheraf and
Alia Nazira
*e,
Umbreen Rasheede,
R. M. A. Khalile,
Ejaz Ahmad Kheraf and
Alia Nazira
aInstitute of Physics, The Islamia University of Bahawalpur, 63100 Pakistan
bCentre of Excellence in Solid State Physics, University of the Punjab, Lahore, Pakistan
cDepartment of Physics, Govt. College University Faisalabad, 38000 Pakistan
dNishtar Medical University Multan, 66000 Pakistan. E-mail: imraniub86@gmail.com
eMaterials Simulation Research Laboratory (MSRL), Institute of Physics, Bahauddin Zakariya University Multan, 60800 Pakistan. E-mail: fayyazhussain248@yahoo.com
fDepartment of Physics Bahawalnagar Campus, The Islamia University of Bahawalpur, 63100 Pakistan
First published on 11th April 2023
Abstract
Hybrid lead halide perovskites have been considered as promising candidates for a large variety of optoelectronic applications. By exploring novel combinations of lead-free double perovskite halides, it is possible to find a suitable replacement for poisonous lead halide perovskites, enhancing electronic and optical response for their application as optically-influenced resistive switching random access memory (RRAM). In this work, the structural, mechanical, elastic, electronic, optical, and thermoelectric characteristics of lead-free double halide perovskites were investigated by Vienna ab initio simulation package (VASP) to explore their role in RRAM. From the analysis of mechanical constraints, it is clear that all three composites of Cs2CaSnX6 (X = Cl, Br, I) are mechanically stable and ductile in nature. The electronic bandgap with and without spin–orbit coupling (SOC), and total and sub-total density of states (TDOS, sub-TDOS) have been calculated using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) potentials. The observed direct band gaps of 3.58 eV, 3.09 eV, and 2.60 eV for Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6, respectively, reveal the suitability of these specified composites as resistive switching material for RRAM devices. Additionally, the optical characteristics, such as complex refractive index, absorption coefficient, and reflectivity of the compounds under consideration have been calculated under the action of incident photons of 0 to 14 eV energy. The thermoelectric properties of Cs2CaSnX6 (X = Cl, Br, I) double perovskite halide were computed and analyzed with the help of the BoltzTraP Code.
1. Introduction
In this advanced technological era, it is very important to find low-cost and less energy-consuming materials for the fabrication of primary optoelectronic devices, such as optically-influenced resistive switching random access memory devices (RRAM). In the last few years, the extraordinary performance of all-inorganic lead halide perovskites appealed much attention from various research groups to find their best use in optoresponsive memory devices (RRAM). Recently, Meng-Cheng Yen and his collaborators fabricated all-perovskite light-emitting memory (LEM) with the help of CsPbBr3 by pairing a RRAM and light-emitting electrochemical cell (LEC).1 No doubt, this is a ground-breaking innovation in the field of optoresponsive RRAM. Nonetheless, the drawbacks of lead halide perovskites, such as toxicity and instability, cannot be forbidden. These limitations of lead halide perovskites have become a hot topic of debate in the whole materials research community, which inspired an interest in the discovery of stable and nontoxic perovskites that can be as efficient as the lead halide perovskites.2 Replacement of Pb2+ with Sn2+ reduces the amount to lead contaminants with excellent properties, such as premium optoelectronic properties making Sn2+-based perovskites valuable for vast studies.3,4 The bandgaps of 4.8 eV and 1.4 eV were observed for Cs2SnCl6 and Cs2SnI6, respectively.5 However, the long-term stability of Sn(II)-based perovskites has been challenging for a long time due to the easy oxidation of Sn2+ into Sn4+.6,7 Exploring novel double perovskite halides is a suggested remedy for this problem. In recent years, the vacancy-ordered perovskite A2BX6, such as Cs2SnX6, in distorted cubic phase with the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m was characterized experimentally and computationally. The vacancy ordering in Cs2SnX6 solves the problem of Sn(II) to Sn(IV) oxidation, but the structural distortion still limits the true potential of tin-based perovskites.8 Therefore, it is necessary to find new ways to enhance the stability of tin-based double perovskite halides for their true potential in RRAM devices.
m was characterized experimentally and computationally. The vacancy ordering in Cs2SnX6 solves the problem of Sn(II) to Sn(IV) oxidation, but the structural distortion still limits the true potential of tin-based perovskites.8 Therefore, it is necessary to find new ways to enhance the stability of tin-based double perovskite halides for their true potential in RRAM devices.
Calcium is not a commonly used element in lead-halide perovskites. However, properties exhibited by this element, such as high carrier mobilities, low trap densities, and induced stability can be beneficial for perovskite-based applications in allied optoelectronic devices, especially RRAM devices, where stability is highly desired and challenging.9–12 In a recent study conducted by M. A. Irham et al., the effect of bivalent doping (Ca2+ and Mn2+) on the stability and optoelectronic properties of CsSnI3 was investigated. The results showed improved stability and enhanced photovoltaic behavior in the Sn(II)-based perovskite due to the incorporation of bivalent dopants (Ca2+ and Mn2+).13 These findings highlight the potential of bivalent doping to improve the performance of Sn(II)-based perovskite halides, which can play a vital role in the development of efficient and stable perovskites for various applications. This also suggests that incorporating calcium with tin halide perovskites such as Cs2CaSnX6 can improve the stability of tin halide perovskites as well their response to the incident electromagnetic radiations.
However, to the best of the author's knowledge and belief, the physical properties of Cs2CaSnX6 (X = Cl, Br, I) double perovskite halides are not investigated theoretically or experimentally from the perspective of optoelectronic RRAM devices. Therefore, we have conducted the first-principles calculations using density functional theory (DFT) for the investigation of the structural, elastic, optoelectronic, and thermoelectric characteristics of halides double perovskites Cs2CaSnX6 (X = Cl, Br, I) using the VASP and BoltzTraP code. The structural stability was determined with the help of elastic constraints. The mechanical characteristics of the compositions have been tested with the help of elastic constants such as Poisson's and Pugh's ratios. The optical characteristics were investigated in terms of complex refractive index, absorption coefficients, energy loss coefficient, and reflectivity. The thermoelectric properties were deliberate from the Seebeck coefficient, and thermal and electrical conductivities. Present, ab initio calculations motivated the experimental researchers to synthesize considered materials for the fabrication of RRAM.
2. Computational approach
The first principle investigation of structural, mechanical, electronic, optical, and thermoelectric properties of Cs2CaSnX6 (X = Cl, Br, I) using the VASP code14–17 was performed using the projector augmented wave (PAW)17 method. The PBE-GGA approximation18,19 was used to obtain the optimized structure, and mechanical, optical, and thermoelectric characteristics of Cs2CaSnX6 (X = Cl, Br, I). The electronic properties were studied with spin–orbit coupling (SOC) and without-SOC effect. The total energy convergence reached between two consecutive self-consistent electronic cycles was less than 1 × 10−8 eV. The cutoff energy of 400 eV and the Monkhorst–Pack k-point mesh grid of 4 × 4 × 4 were used to have converged values in the full Brillouin Zone. The thermoelectric properties were studied using the BoltzTraP Code.203. Results and discussions
3.1. Structural and mechanical properties
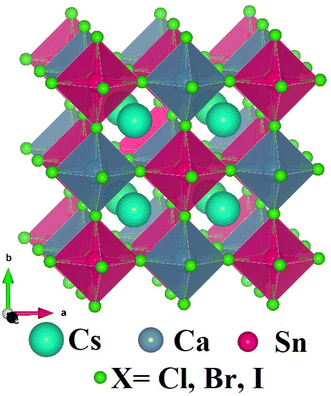
The cubic crystal structures with space group 225-Fm3m of novel double halide perovskites Cs2CaSnX6 (X = Cl, Br, I) are shown in Fig. 1. The alternate arrangement of two different octahedra CaX6 and SnX6, forming a network of corner-sharing octahedra with Cs-cation is having 12-fold coordination with X-anions (X = Cl, Br, and I) filling the cavities within this network. The Cs-atoms, Sn-atoms, Ca-atoms, and X-atoms (X = Cl, Br, and I) are located at the 8c, 4a, 4b, and 24e Wyckoff positions with their fractional coordinates (0.25, 0.25, 0.25), (0, 0, 0), (0.5, 0.5, 0.5) and (0.25, 0, 0), respectively. The considered double perovskite halides Cs2CaSnX6 (X = Cl, Br, I) have 40 atoms in their unit cell with four formula units, as shown in Fig. 1. All three composites have negative ground state energies Eo describes the structural stability of Cs2CaSnX6 (X = Cl, Br, I). The lattice parameters of the considered double halide perovskites increased from 11.10 Å to 12.51 Å for Cs2CaSnCl6 to Cs2CaSnI6 due to the increasing ionic radii of X-anion from Cl to I. The lattice parameters ao, Ground-state volume Vo, Elastic constants (Cij), Bulk modulus (B), Shear modulus (G), Young's modulus (E), Poisson's ratio (σ), Pugh ratio (B/G), Cauchy's pressure (GPa), and other elastic constraints are summarized in Table 1.| Material property | Cs2CaSnCl6 | Cs2CaSnBr6 | Cs2CaSnI6 |
| Lattice parameter (ao) | 11.10 | 11.70 | 12.51 |
| Ground state volume Vo (Å)3 | 1369.51 | 1600.52 | 1958.19 |
| Ground state energy Eo (eV) | −147.2962 | −134.3245 | −117.9079 |
| C11 (GPa) | 50.906 | 42.678 | 33.754 |
| C12 (GPa) | 9.727 | 8.279 | 6.735 |
| C44 (GPa) | 7.089 | 5.821 | 3.392 |
| Bulk modulus, B (GPa) | 23.453 | 19.745 | 15.741 |
| Shear modulus, G (GPa) | 11.049 | 9.144 | 6.141 |
| Young modulus, E (GPa) | 28.648 | 23.764 | 16.303 |
| Poisson ratio, σ (GPa) | 0.296 | 0.299 | 0.327 |
| Pugh ratio, B/G (GPa) | 2.123 | 2.159 | 2.563 |
| Cauchy's pressure (GPa) | 2.6 | 2.5 | 3.3 |
| Transverse wave velocity (m s−1) | 1890.677 | 1561.213 | 1235.524 |
| Longitudinal wave velocity (m s−1) | 3514.822 | 2917.691 | 2438.923 |
| Average wave velocity (m s−1) | 2110.888 | 1743.710 | 1384.941 |
| Debye temperature ΘD (K) | 193.5 | 151.8 | 112.7 |
| Linear compressibility | 14.213 | 16.882 | 21.175 |
The elastic constants are attention-grabbing parameters associated with the physical characteristics of any solid materials. The stiffness constants for considered double perovskites halides Cs2CaSnX6 (X = Cl, Br, I) are C11, C12, and C44. The decrease in bulk modulus, shear modulus, and young's modulus of Cs2CaSnCl6 (X = Cl, Br, I) were observed with the change in halogen atom from Cl to I. The mechanical stability of the materials in the cubic phase can be tested using the Born–Huang stability conditions:21,22
| C11 − C12 > 0; C11 > 0; C44 > 0; C11 + 2C12 > 0 |
All the results of the stability standard by Born–Huang stability conditions were fulfilled by all three materials, which verified the mechanical stability of the considered double perovskite halides Cs2CaSnX6 (X = Cl, Br, I). The nature of chemical bonding between atoms can be analyzed with the help of Cauchy's pressures, which can be calculated as C12–C44. The positive value of Cauchy's pressure revealed the ionic bonding. Moreover, the negative value of Cauchy's pressure showed covalent bonding. The values of calculated Cauchy's pressures for Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6 are positive, which specified that these double perovskite halides Cs2CaSnX6 (X = Cl, Br, I) are ionic compounds. The Poisson's ratio and the Pugh ratio were calculated to predict whether the considered materials are ductile or brittle in nature. If the value of Poisson's ratio is smaller than 0.26 Gpa, then the material is considered to be brittle, otherwise, the material is ductile. Similarly, if the calculated Pugh ratio is smaller than 1.75 Gpa, then the material is brittle, otherwise, the material is ductile. The computed Pugh ratio and Poisson's ratio in Table 1 specify the ductile nature of Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6.
3.2. Electronic properties
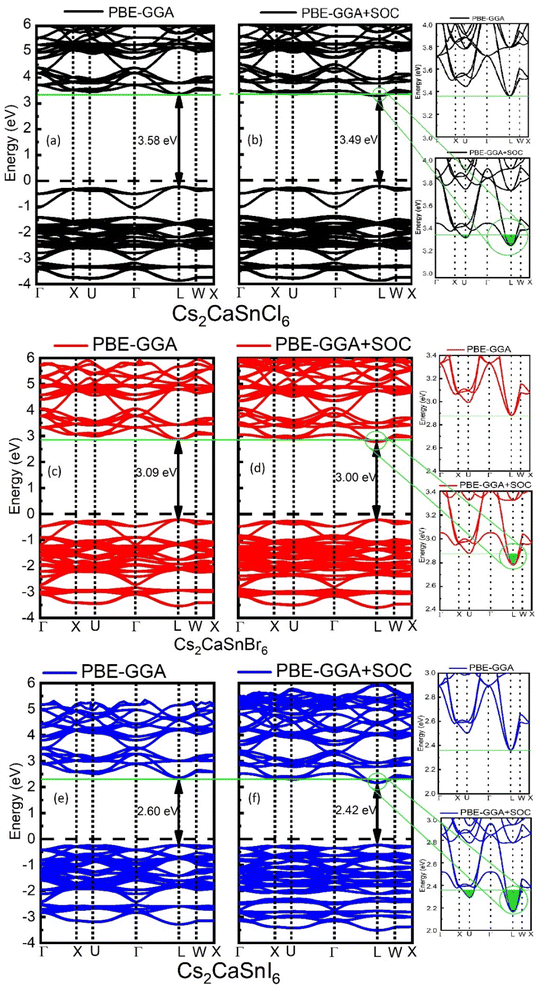
The electronic properties of Cs2CaSnX6 (X = Cl, Br, I) were studied by proper analysis of band structures and DOS, which are portrayed in Fig. 2 and 3, respectively. The electronic properties of Cs2CaSnX6 (X = Cl, Br, I) were calculated with SOC and without SOC. The without-SOC calculations show direct bandgaps of 3.58 eV, 3.09 eV, and 2.60 eV at the L point of symmetry for Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6, respectively. The SOC calculations show the direct bandgaps of 3.49 eV, 3.00 eV, and 2.42 eV were observed at the L point of symmetry for Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6, respectively. We found that the SOC effect resulted in a negligible improvement of only 0.09 eV for Cs2CaSnCl6 and Cs2CaSnBr6 and 0.18 eV for Cs2CaSnI6 in the electronic bandgap (as shown in the magnified portion of Fig. 2 with the green highlighted region). This means that the SOC effect in Cs2CaSnX6 is relatively small, as shown in Table 2, and therefore its effect on the electronic and optical properties can often be neglected.| Composite name | Non-SOC bandgap (Eg) | SOC bandgap (Eg) | Difference |
|---|---|---|---|
| Cs2CaSnCl6 | 3.58 | 3.49 | 0.09 |
| Cs2CaSnBr6 | 3.09 | 3.00 | 0.09 |
| Cs2CaSnI6 | 2.60 | 2.42 | 0.18 |
The decrease in the band gap was witnessed from Cs2CsSnCl6 to Cs2CaSnI6 due to an increase in the lattice parameter, which leads to the weaker ion-electron coulomb interaction of X-anions (X = Cl, Br, I) of Cs2CsSnCl6 to Cs2CsSnI6. The ionic radii are increasing from Cl to Br and Br to I-anion, leading to the fact that the Coulomb interaction of Cl-anion is stronger, as compared to that of Br and I, due to this weakening of ion-electron interaction of X-atoms (X = Cl, Br, I), the decrease in the electronic bandgap occurs. It is suggested that the band gap tailoring from a wide bandgap to a narrow bandgap decreases the amount of energy required to initiate the set and reset process, making it suitable for less energy-consuming memory devices.
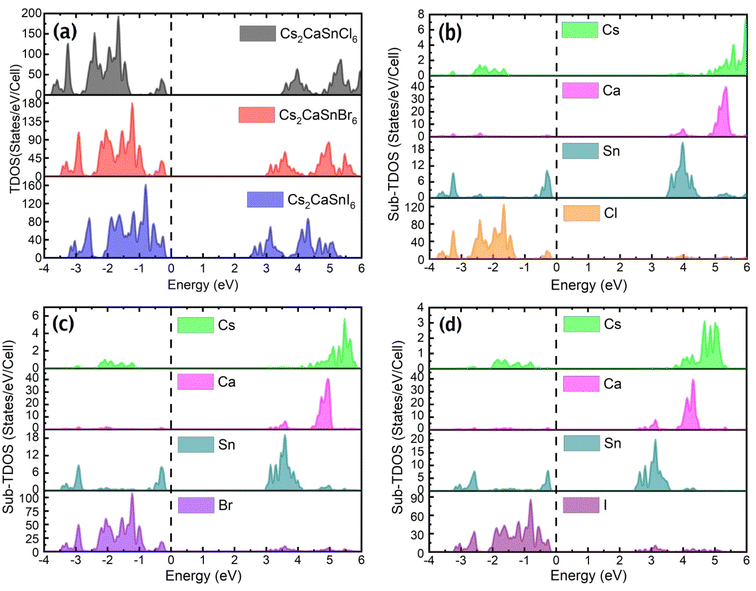
In Fig. 3(a) the TDOS of Cs2CaSnX6 (X = Cl, Br, I), Fig. 3(b) the Sub-TDOS of Cs2CaSnCl6, Fig. 3(c) the Sub-TDOS of Cs2CaSnBr6, and Fig. 3(d) the Sub-TDOS of Cs2CaSnI6 are displayed. Significant bandgaps were witnessed from TDOS as well between the uppermost valence band-edge and the lowermost conduction band-edge in each case. This semiconducting behavior makes the specified composites suitable RS material for RRAM applications. It is also suggested that these specified composites will initially exhibit a stable high resistance state desired for RRAM devices. Moreover, in the absence of any defect states in the bandgap, no initial leakage current might be present and hence prohibit the need for any forming voltage. Since the Fermi level is located near the valence band for all three composites, it is predictable that all three composites are p-type semiconductors, as shown in Fig. 3(a). So, the majority of charge carriers must be holes. The overall behavior of TDOS remains the same in all three compounds, except, for the observed downshift of the conduction band-edge with the change in the halide from Cl to Br and Br to I.
The Sub-DOS tells us about the contribution of Cs, Ca, Sn, and X-atoms (X = Cl, Br, and I) of each compound in the conduction and valence band formation. A very small contribution of Cs-atoms has been observed in the conduction and valence band formation of all three composites. Ca-atoms participated in the formation of the conduction band; however, Sn-atoms contributed to both the valence band and conduction band formation. The highest contribution of halogen atoms (X = Cl, Br, I) was observed on the valence band side, while some peaks were also present on the conduction band side. The majority of the peaks in the valence band are due to the halogen atoms but Sn and Ca contributed enough to the formation of the valence band. The change of the halogen atom from Cl to Br and then Br to I not only introduced available states at a lower energy level in the conduction band but also manipulated the available states of Ca-atoms and Sn-atoms on the conduction band side. This manipulation in the available states due to Ca-atoms and Sn-atoms along with the available states of halogen atoms (X = Cl, Br, I) at lower energy caused the observed downshift in TDOS. This manipulation in the available states and the addition of new states are the causes of the decrease in the bandgap from Cs2CaSnCl6 to Cs2CaSnI6.
3.3. Optical properties
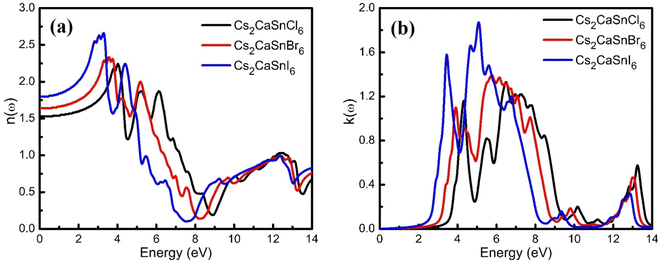
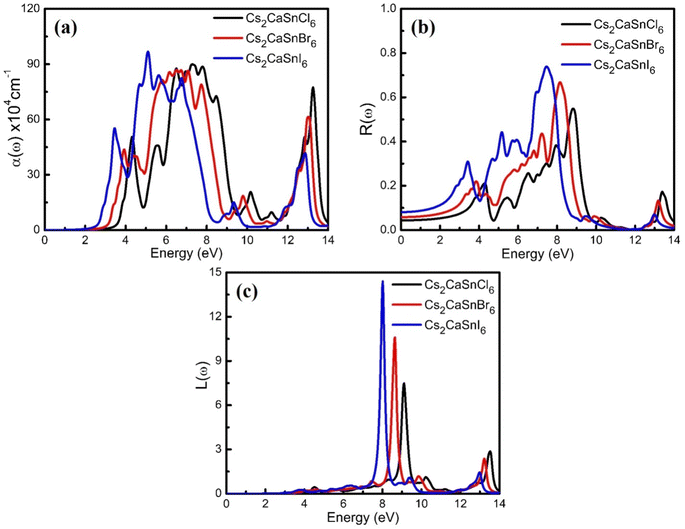
Optical properties are the properties that define the material's response under the influence of incident radiations, photons, or light. The optical properties of any material can be defined in terms of its complex refractive index (such as refractive index and extinction coefficient), reflectivity, absorption coefficient, and energy loss coefficient. All these parameters help portray the optical behavior of any material. We used the Kramer–Kronig relationship23,24 for the estimation of the optical response of Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6 in the energy range of 0 eV to 14 eV. A detailed discussion of these parameters has been accompanied to define the optical response of Cs2CaSnX6 (X = Cl, Br, I).In Fig. 4(b), the extinction coefficient for Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6 are shown for 0 to 14 eV, photonic energy. The extinction coefficient k(ω) can directly describe the attenuation of incident electromagnetic radiation in the material. The behavior of extinction coefficient k(ω) is quite analogous to the absorption coefficient, which can be seen in Fig. 5(a) where the absorption coefficient α(ω) has been shown for the energy range 0 to 14 eV energy. The absorption of incident electromagnetic radiations started after the corresponding absorption edge, which is equal to the band gap energies for each material. This justifies the above-mentioned semiconducting nature of these specified composites, as shown in Fig. 2 and 3. The extinction coefficient for all three materials increases toward higher values after their corresponding band gap energies showing the increasing rate of optical absorption in the high energy range. The higher value of extinction coefficient was observed for Cs2CaSnI6 between 2.6 eV and 6.5 eV than that of Cs2CaSnCl6 and Cs2CaSnBr6. This revealed the better capability of Cs2CaSnI6 to absorb the incident photons and hence more feasible for optoelectronic RRAM devices.
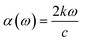 | (1) |
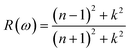 | (2) |
The ability to absorb incident electromagnetic radiation, light, or photons of suitable energy (E = ħω) of any material is directly associated with the absorption coefficient α(ω), and the energy loss function L(ω) defines the loss of energy while the material is interacting with high-speed incident photons. The absorption coefficients of Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6 are plotted in Fig. 5(a) for the energy range of 0 eV to 14 eV photonic energy. The absorption coefficient defines the absorption of the incident photons. The absorption coefficient for all three cases has been observed to be zero before their corresponding band gap energies signifying that no absorption occurs unless sufficient energy is achieved for the photoelectric effect. After corresponding band gap energies for related materials, the absorption coefficient takes its flight toward its higher values and kept on increasing with the increasing photonic energy. The small fluctuation in the absorption coefficient is due to the varying rate of transitions. A higher rate of absorption coefficient was observed for Cs2CaSnI6, which signifies the improved absorption of the incident photons, as compared to that on Cs2CaSnCl6 and Cs2CaSnBr6.
The reflectivity is shown in Fig. 5(b) for Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6. The reflectivity increases with the increase in the photonic energy with a slight fluctuation due to the varying rates of transitions. The reflectivity attained its maximum values in the same region where the absorption drastically dropped. The highest observed values of reflectivity were 54% at 8.83 eV for Cs2CaSnCl6, 66% at 8.15 eV for Cs2CaSnBr6, and 73% at 7.47 eV for Cs2CaSnI6, which started to decrease with further increase of photonic energy. The energy loss functional L(ω) is portrayed in Fig. 5(c) for Cs2CaSnX6 (X = Cl, Br, I). The energy loss functional L(ω) defines the loss of energy while the fast electrons move in the materials. The L(ω) for each composite demonstrates that maximum peaks have been observed at different energy ranges. Intense peaks were observed between the incident energy ranges of 7 to 10 eV and 12 to 14 eV. The results of energy loss functional describe that negligible energy loss occurs in the visible and low ultraviolet region (below 7 eV energy). The L(ω) is associated with the plasma resonance. The extreme energy loss L(ω) for each composite is in the energy range of incident electromagnetic radiation between 7 to 10 eV.
3.4. Thermoelectric properties
To check the thermoelectric characteristics of any material, key parameters such as the Seebeck coefficient, electrical conductivity, and thermal conductivity were calculated using the original BoltzTraP Code. We have calculated these parameters of all three compositions of Cs2CaSnX6 (X = Cl, Br, I) over a wide range of temperatures 300 to 1500 K. Fig. 6(a–c) depict the Seebeck coefficient, electrical conductivity, and thermal conductivity, respectively.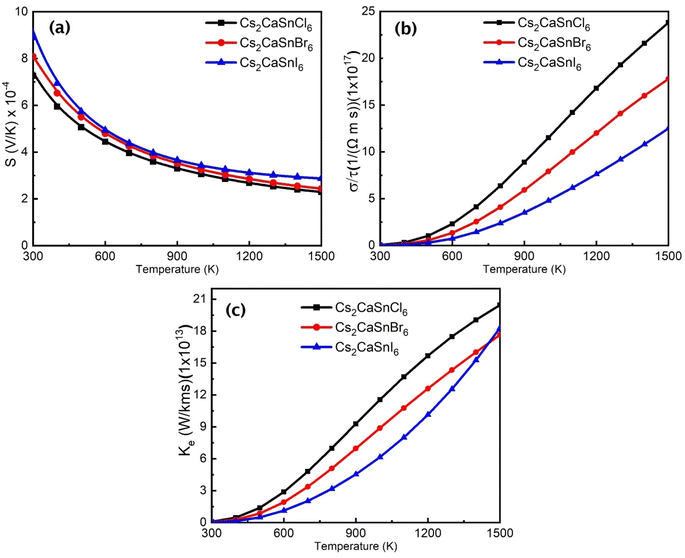 | ||
| Fig. 6 (a) Seebeck Coefficient, (b) electronic conductivity, and (c) thermal conductivity of Cs2CaSnX6 (X = Cl, Br, I). | ||
In perovskites, the most convenient thermoelectric parameter is the Seebeck coefficient to describe a thermoelectric characteristic of a considered composite. The Seebeck effect describes the potential induced in the material due to the change in temperature across the material due to the movement of available electrons. The positive or negative sign and the magnitude of the Seebeck coefficient are interrelated with the majority charge carrier type and their concentration. It is clear from Fig. 6(a) that the Seebeck coefficient for Cs2CaSnX6 (X = Cl, Br, I) is positive, which predicted that these are p-type semiconductors where holes are the majority charge carriers, as depicted in Fig. 3. The p-type behavior was also witnessed in DOS calculations. Furthermore, the linear increase in the Seebeck coefficient was seen with the increase in temperature. It is believed that the hole conduction in p-type Cs2CaSnX6 (X = Cl, Br, I) is due to Sn-atoms and X-atoms within the crystal structure because each of these atoms is majorly contributing to the valence band formation.
Electrical conduction and heat transport are closely linked with the Seebeck coefficient. The usual trend of electrical conductivity and the Seebeck coefficient is opposite, which means that the increase in the Seebeck coefficient will lead to a decrease in the electrical conductivity and vice versa. The increasing trend of electrical conductivity and decreasing trend of the Seebeck coefficient are exactly according to the trend. The Seebeck coefficients for both materials decrease with the increase in temperature, which means the electrical conductivity increase with the increase in temperature. Electrical conductivity defines the measure of electrons that are available for conduction with the increase in temperature. It is clear from Fig. 6(b), the electrical conductivity of Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6 increases with the increase in temperature because of the greater atomic radius of I, as compared to those of Br and Cl. The increasing atomic radii weaken the grip of the nuclei on valence electrons that easily push more electrons toward the conduction band, which increases the electrical conductivity in Cs2CaSnI6, as compared to that in Cs2CaSnBr6 and Cs2CaSnCl6. Thermal conductivity is also an important parameter in thermoelectric properties for device applications. The thermal conductivities of Cs2CaSnCl6, Cs2CaSnBr6, and Cs2CaSnI6 are plotted in the temperature range from 300 to 1500 K in Fig. 6(a). The electronic thermal conductivity also increased with the increase in temperature for all three materials.
4. Conclusion
The structural, mechanical elastic, electronic, optical, and thermoelectric characteristics of Cs2CaSnX6 (X = Cl, Br, I) were calculated using the DFT approach for application in the RRAM device. The mechanical stability and ductile nature of all three composites of Cs2CaSnX6 (X = Cl, Br, I) are clear from the analysis of elastic and mechanical constraints. The semiconductor behavior of Cs2CaSnX6 (X = Cl, Br, I) was confirmed by the presence of the direct band gap in the electronic band structures. The band structure and DOS plots revealed that the band gap of the considered p-type semiconductors occurs with the change of X-atoms from Cl to Br and Br to I. Furthermore, the increase in electronic as well as thermal conductivity has been observed with the increase in temperature for all three materials. Cs2CaSnI6 with the lowest band gap has the highest optical absorption in the low energy region, which can alter the resistance of the considered material between the high resistance state and low resistance state in optical memory devices. Therefore, Cs2CaSnI6 is recommended as the best composite among the other compositions of Cs2CaSnX6 (X = Cl, Br, I) for RRAM applications and other allied optoelectronic applications.Conflicts of interest
The authors declare that there are no conflicts of interest.Acknowledgements
No funding was received for this research.References
- M.-C. Yen, et al., All-inorganic perovskite quantum dot light-emitting memories, Nat. Commun., 2021, 12(1), 4460, DOI:10.1038/s41467-021-24762-w.
- D. E. Lee, S. Y. Kim and H. W. Jang, Lead-free all-inorganic halide perovskite quantum dots: review and outlook, J. Korean Ceram. Soc., 2020, 57(5), 455–479, DOI:10.1007/s43207-020-00058-5.
- H. Li, H. Dong, J. Li and Z. Wu, Recent Advances in Tin-Based Perovskite Solar Cells, Acta Phys. Chim. Sin., 2020, 2007006, DOI:10.3866/pku.whxb202007006.
- E. Aktas, et al., Challenges and strategies toward long-term stability of lead-free tin-based perovskite solar cells, Commun. Mater., 2022, 3(1), 104, DOI:10.1038/s43246-022-00327-2.
- M. M. S. Karim, et al., Anion Distribution, Structural Distortion, and Symmetry-Driven Optical Band Gap Bowing in Mixed Halide Cs2SnX6 Vacancy Ordered Double Perovskites, Chem. Mater., 2019, 31(22), 9430–9444, DOI:10.1021/acs.chemmater.9b03267.
- J. Sanchez-Diaz, et al., Tin perovskite solar cells with >1300 h of operational stability in N2 through a synergistic chemical engineering approach, Joule, Apr. 2022, 6(4), 861–883, DOI:10.1016/j.joule.2022.02.014.
- K. J. Savill, A. M. Ulatowski and L. M. Herz, Optoelectronic Properties of Tin–Lead Halide Perovskites, ACS Energy Lett., 2021, 6(7), 2413–2426, DOI:10.1021/acsenergylett.1c00776.
- H.-M. Huang, Z.-Y. Jiang and S.-J. Luo, First-principles investigations on the mechanical, thermal, electronic, and optical properties of the defect perovskites Cs2SnX6 (X = Cl, Br, I), Chin. Phys. B, 2017, 26(9), 096301, DOI:10.1088/1674-1056/26/9/096301.
- S. Ghosh, H. Shankar and P. Kar, Recent developments of lead-free halide double perovskites: a new superstar in the optoelectronic field, Mater. Adv., 2022, 3(9), 3742–3765, 10.1039/d2ma00071g.
- W. Xia, X. Liu, F. Jin, X. Jia, Y. Shen and J. Li, Evaluation of calcium codoping in double perovskite PrBaCo2O5+ as cathode material for IT-SOFCs, Electrochim. Acta, 2020, 364, 137274, DOI:10.1016/j.electacta.2020.137274.
- S. F. Hoefler, G. Trimmel and T. Rath, Progress on lead-free metal halide perovskites for photovoltaic applications: a review, Monatshefte für Chemie - Chem. Mon., 2017, 148(5), 795–826, DOI:10.1007/s00706-017-1933-9.
- C. F. J. Lau, et al., Enhanced performance via partial lead replacement with calcium for a CsPbI3 perovskite solar cell exceeding 13% power conversion efficiency, J. Mater. Chem. A, 2018, 6(14), 5580–5586, 10.1039/C7TA11154A.
- M. A. Irham, F. H. Tejo Baskoro, F. A. Permatasari and F. Iskandar, Toward Stable High-Performance Tin Halide Perovskite: First-Principles Insights into the Incorporation of Bivalent Dopants, J. Phys. Chem. C, 2022, 126(11), 5256–5264, DOI:10.1021/acs.jpcc.1c10315.
- G. Kresse, Ab initio molecular dynamics for liquid metals, J. Non-Cryst. Solids, 1995, 192–193, 222–229, DOI:10.1016/0022-3093(95)00355-X.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B, 1993, 48(17), 13115–13118, DOI:10.1103/PhysRevB.48.13115.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B, 1999, 59(3), 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- J. P. Perdew, K. Burke and Y. Wang, Generalized gradient approximation for the exchange-correlation hole of a many-electron system, Phys. Rev. B, 1996, 54(23), 16533–16539, DOI:10.1103/PhysRevB.54.16533.
- J. P. Perdew, Generalized gradient approximations for exchange and correlation: A look backward and forward, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 172(1–2), 1–6, DOI:10.1016/0921-4526(91)90409-8.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006 DOI:10.1016/j.cpc.2006.03.007.
- B. B. Karki, G. J. Ackland and J. Crain, Elastic instabilities in crystals from ab initio stress-strain relations, J. Phys.: Condens. Matter, 1997, 9(41), 8579–8589, DOI:10.1088/0953-8984/9/41/005.
- F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B, 2014, 90(22), 224104, DOI:10.1103/PhysRevB.90.224104.
- L. Kador, Kramers–Kronig relations in nonlinear optics, Appl. Phys. Lett., 1995, 66(22), 2938–2939, DOI:10.1063/1.114235.
- C. Vittoria and Kramers-Kronig Relations, in Microwave Properties of Magnetic Films, World Scientific, 1993, pp. 163–170. doi: DOI:10.1142/9789814354387_0007.
| This journal is © The Royal Society of Chemistry 2023 |