Open Access Article
Open Access ArticleAdsorption of singlet and triplet oxygen on B-doped graphene: adsorption and electronic characteristics†
A. Sahithi and
K. Sumithra *
*
Birla Institute of Technology and Science (BITS), Pilani, Hyderabad Campus, Shamirpet, Telangana State 500078, India. E-mail: sumithra@hyderabad.bits-pilani.ac.in
First published on 11th July 2023
Abstract
The density functional calculations of electronic and structural properties of the adsorption of dioxygen on boron-doped graphene surfaces are conducted using spin-polarized density functional theory methods, including van der Waals correction. The results show significant differences in the adsorption characteristics of singlet and triplet oxygen on boron-doped graphene surfaces. Both triplet and singlet show only weak attraction to intrinsic and singly doped graphene. The singlet oxygen adsorption on doped graphene shows fascinating features involving chemisorption with dioxetane ring formation with appreciable charge transfer. In contrast, the triplet oxygen is only weakly physisorbed on the boron-doped surfaces. Chemisorption of singlet oxygen occurs with noticeable charge transfer and leads to almost featureless band structures, while the triplet oxygen physisorption proceeds with a well-defined band structure. Chemisorption of the singlet oxygen is attributed to the enormous mixing of π* of dioxygen and the p-orbitals of dopant and carbon. Because of the difference in adsorption characteristics, chemically modified graphene can find use in detecting and trapping singlet oxygen, which has potential applications in photodynamic therapy.
1. Introduction
Considerable attention has been focused on studies involving monolayer graphene since its remarkable isolation in 2004.1 It has facilitated new research on two-dimensional materials with various novel properties and technological applications.2,3 It has been reported experimentally that graphene could be a potential gas sensor with appreciable sensitivity, showing transport property changes on exposure to gases like NO2 and NH3.4 It is seen that the electrical and optical properties of graphene and other similar 2D materials show deviations upon exposure to gases.4–7 Understanding the adsorption characteristics of gases on the surface is extremely important to envisage any two-dimensional based sensor devices. Following the experimental investigation4 with individual molecules, the adsorption of small molecules like O2, CO, H2O, NO2, NO, NH3, etc. has been explored8–12 to understand their influence on the electronic structure properties of pristine graphene.Nonetheless, most gas molecules can only weakly physisorb on pristine graphene.13–15 Such physisorptions cannot improve the semi-conducting properties of graphene and therefore forbid its potential use in gas sensors and other electronic devices. To enhance the sensitivity of gases towards the intrinsic graphene, doping the surface with either n- or p-type dopants are common and are expected to alter the electronic and transport properties.5,13 Regular practice is to replace one or more carbon atoms with either metal, transition metals, and non-metals,16,17 or by decorating the surface extrinsically with atoms.18 It is already established that B- or N-doped and B- and N- co-doped graphene can significantly improve the sensing of gases like NO, NO2, NH3, and CO.13,17,19–21 Metal and transition metal doped22,23 graphene are found to alter the electronic structure drastically and, therefore, cannot be employed in semiconductor devices. On the experimental front, several non-metals doped graphene-based materials were synthesized successfully with boron, nitrogen, etc.24,25
This section discusses an overview of oxygen adsorption on intrinsic and B-doped graphene. Using the computational first-principles technique, Nakamura et al.26 found that oxygen atoms selectively adsorb on intrinsic graphene, forming epoxide rings and modifying structural and electrical characteristics. There have been a few experimental5,27–29 and theoretical attempts13,16,30–37 to explore the sensing of molecular dioxygen, O2, on pristine and doped graphene monolayers. Some earlier literature reveals attempts to make oxygen sensors27,28 with monolayer graphene. Such oxygen sensors were made at room temperature by chemical vapor deposition, and rapid changes in the current were shown when the sensors were exposed to different oxygen concentrations at room temperature.27 Bagsican et al.29 employed temperatures programmed terahertz (THz) emission microscopy (TPTEM) to explore the local O2 adsorption and desorption dynamics on graphene and tungsten disulfide (WS2). They have found adsorption energy of about −0.15 eV for oxygen molecules on pristine graphene.
All the theoretical investigations predict only weak adsorptions with molecular oxygen,16,30–37 and some studies indicate increased oxygen sensitivity after doping with silicon.30,33 It is also suggested that Si-doped surfaces can be a metal-free catalyst for oxygen reduction reactions (ORRs).33 Diffusion Monte Carlo (DMC) calculations were also performed for O2 adsorption on single-layer graphene31 to describe the adsorption's nature accurately. They have obtained adsorption energy of −0.142 eV, close to the experimental value of −0.15 eV.29 The adsorption of O2 is also facilitated by topological defects and compressive mechanical strain.36
With their pioneering work, Dai and colleagues found that dioxygen adsorbs onto B-doped and N-doped (each with a single atom of dopant) weakly. In contrast, it is more robust with transition metal doped surfaces.13,16 The adsorption of singlet oxygen molecules onto aromatic hydrocarbon molecules like benzene, naphthalene, and pyrene, employing ab initio MO calculations, was also done previously.38 They have found dioxetane like metastable structures on adsorption of singlet O2 onto hydrocarbons. Even though it is clear that the theoretical studies on triplet dioxygen which is O2 in its natural state, 3Σg, were conducted on graphene and singly B-doped graphene, the investigations on the adsorption of singlet dioxygen, 1Δg, is hardly discussed irrespective of its importance. Additionally, the information on the electronic structure in terms of band structures and density of states (DOS) is not discussed previously in the literature for both triplet and singlet oxygen.
All previous investigations show that triplet O2 is unreactive to the surface. This theoretical investigation is the first to discuss the differences between the adsorption and electronic characteristics of both singlet and triplet dioxygen. Additionally, this work involves adsorption on graphene with various dopant concentrations and surfaces with different doping patterns. Therefore, it is vital to understand the scope of using boron-doped graphene to capture singlet oxygen for its potential uses as nano-catalysts, sensor platforms, and medical-related applications. Moreover, a boron-doped graphene surface exposed to singlet dioxygen may limit its use as a sensor for various other gaseous molecules.
2. Methodology
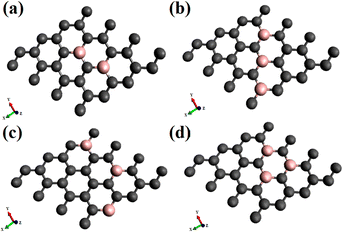
The adsorption and electronic characteristics are calculated following density functional theory, using periodic boundary conditions. The analyses with dioxygen, in both the spin states, triplet, and singlet on doped graphene are performed with spin-polarised density functional theory (DFT) calculations, using the PBE generalized gradient approximation (GGA)39 exchange–correlation functional. The density functional calculations are carried out using the Vienna ab initio simulation package (VASP).40 as integrated with the MedeA® computational environment.41 We used the PAW (projected augmented wave) potentials42 provided with the latest VASP distribution and included the semi-core states into the valence band.The calculations are performed with single dioxygen placed above the graphene surface. A supercell of 4 × 4 graphene supercell (32 carbon atoms) represents an isolated graphene sheet on which different substitutional doping concentrations and surface configurations are considered. In order to eliminate the periodic interaction between neighboring layers, the supercell is extended with a lattice parameter of 15 Å along the z-axis from the graphene to create the vacuum layer. Therefore, the dopant concentration with one boron substituting a carbon atom is 3.12%. The increased concentrations considered are 6.25 and 9.37%, with the dopants following different configurational arrangements on the surface, as shown in Fig. 1. To investigate the possibility of interactions of periodic image, calculations of adsorption of singlet and triplet oxygen were also done on a 5 × 5 graphene supercell.
To account for dispersion interactions, we used different approaches like DFT-D2 and DFT-D3.43 The initial set of calculations employing the DFT and DFT-D3 functionals43 revealed that van der Waals corrections are essential to describe surface oxygen adsorption. To get the best geometries, we used DFT theory with long-range dispersion correction in the DFT-D3 formulations of BJ damping.44 The adsorption energies obtained are calculated as:
| Eads = E0 [A@G] − E0 [G] − E0 [A], | (1) |
Cut-off energy of 520 eV and Gaussian smearing with a width of σ = 0.025 eV for the occupation of the electronic levels are used. A Monkhorst–Pack Γ-centered 9 × 9 × 1 k-point mesh was used, and the total energy values converged below 0.01 eV Å−1. The charge transfer difference Δρ between the gas molecule and graphene is calculated using the Bader charge analysis.45 Δρ can be calculated as the charge variation of gas molecules before and after the adsorption for oxygen employing eqn (2),
| Δρ = ρ (O2/surface) − (ρ (surface) + ρ (O2)). | (2) |
3. Results and discussion
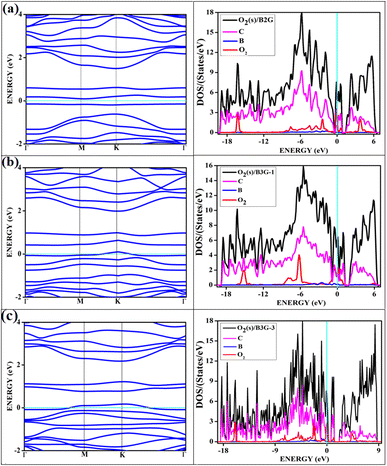
The results of electronic structure calculation of adsorption dioxygen, O2, on graphene chemically doped surfaces are discussed in this section. The adsorption studies explore oxygen in the paramagnetic triplet (3Σg) ground state and the diamagnetic singlet (1Δg) state on a variety of B-doped graphene. The effect of the surface doping concentrations, as well as configurations or the patterns made by the dopants on the electronic band gaps, has been discussed in our previous investigations.17,19 It has been reported that the doping concentrations and the configurations lead to appreciable variations in the electronic band gaps of the graphene, even without the adsorption of gaseous molecules. Based on the sub-lattice symmetry breaking, some configurations show improved electronic aspects. This study considers doping with boron atoms as it causes the least deformity to the two-dimensional planar surface on substitutional doping. The dopant concentrations studied are 3.12, 6.25, and 9.37%. The pristine graphene is indicated as PG, and the singly doped graphene with 3.12% boron is represented as BG. For 3.12% and 6.25% of dopant concentration the doped graphene surfaces are designated as BG and B2G, whereas for 9.37%, there are three patterns of doped surfaces, denoted as B3G-1, B3G-2, B3G-3. A few of the doped surfaces that show increased band gaps with 6.25% and all of 9.37% doping concentrations are shown in Fig. 1. The remaining patterns of –B–C–B– denoted as B2G-2 and –B–C–C–B– named as B2G-1 are shown in the ESI Fig S1.† The results of the calculations on 5 × 5 supercell are discussed in the ESI (Fig. S3–S8 and Tables S1 and S2†). The results of the calculation with 4 × 4 and 5 × 5 supercells do not differ much as can be seen from Tables S1 and S2.† This indicates that our study with 4 × 4 supercell is sufficient to discuss about the adsorption and electronic properties for the doped systems considered in this study.3.1. Adsorption of dioxygen
Although there are few studies on oxygen adsorption,13,16,36 the effect of the spin nature of the molecule on the electronic structure and the adsorption characteristics are not yet considered. The majority of the previous studies deal with adsorption on pristine graphene surfaces, other graphene-based materials,14 and a few on transition metal doped23,30 and on defective graphene.34,46 This article discusses the results of the adsorption of dioxygen in both triplet and singlet states. The adsorption studies are conducted for various dopant concentrations and patterns. A few geometries optimized configurations are given in Fig. 1. The results of the calculations, the adsorption energies, optimized distances, band gaps wherever necessary, and charge transfers for the triplet ground state and singlet are summarized in Tables 1 and 2, respectively.| System 3Σg on | Adsorption energy (eV) | Distance (Å) | Band gap (eV) | Charge transfer (e) |
|---|---|---|---|---|
| PG | −0.147 | 3.0 | 0 | 0.06 |
| BG | −0.265 | 2.93 | 0.20 (0.14) | 0.03 |
| B2G-1 | −0.144 | 2.86 | Flat line (0.21) | 0.02 |
| B2G-2 | −0.138 | 2.9 | 0.41 (0.37) | 0.04 |
| B2G-3 | −0.127 | 2.97 | 0.16 (0.15) | 0.01 |
| B3G-1 | −0.374 | 2.9 | 0.64 (0.57) | 0.07 |
| B3G-2 | −0.186 | 2.9 | 0.15 (0.16) | 0.014 |
| B3G-3 | −0.367 | 2.78 | 0.63 (0.58) | 0.05 |
| System 1Δg on | Adsorption energy (eV) | Distance (Å) | Charge transfer (e) |
|---|---|---|---|
| PG | −0.396 | 2.96 | 0.08 |
| BG | −0.718 | 2.20 | 0.22 |
| B2G-1 | −0.664 | 1.9 | 0.06 |
| B2G-2 | −1.222 | 1.53 | 0.32 |
| B2G-3 | −0.932 | 1.9 | 0.04 |
| B3G-1 | −1.747 | 1.52 | 0.55 |
| B3G-2 | −0.176 | 2.97 | 0.03 |
| B3G-3 | −1.504 | 1.54 | 0.63 |
Adsorption of the oxygen molecule on boron-doped graphene surfaces is expected to improve both the adsorption and electronic characteristics and thus may contribute to its potential application as a sensor for this molecule. Both triplet and singlet oxygen tend to physisorb onto the intrinsic graphene surface at a distance of about 3 Å, as shown in Tables 1 and 2. The adsorption energy for triplet oxygen on intrinsic graphene is found to be −0.147 eV, confirming weak physisorption. This result agrees very much with the previous experimental result29 of −0.15 eV and the earlier calculations of −0.142 eV.35
Therefore, the DFT-D3 method, including the dispersion correction, can be conveniently used to investigate adsorption on boron-doped systems. In Table 1, the electronic band gaps caused by triplet oxygen adsorption are also given. The corresponding doped, bare adsorbent band gaps are shown in parenthesis. With the triplet oxygen, the physisorptions are not strong enough to cause appreciable changes in the electronic band gaps. However, with surfaces ‘B3G-1’ and ‘B3G-3’, the band gaps are slightly more than the bare doped surface, as seen from Table 1. The equilibrium distances are around 2.9–3 Å with negligible charge transfers, suggesting physisorptions. On doping with boron, the adsorption energies are improved for certain surfaces by an amount of 0.05–0.07 eV because of the following reasons.
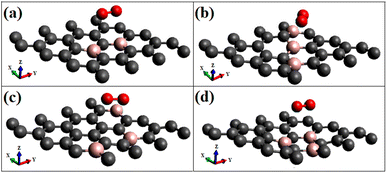
First, p-type doping makes it easier for the oxygen molecule to have the lone pair of electrons get attracted to the surface, irrespective of the spin nature of the molecule. The adsorption energies of triplet oxygen on various surfaces are slightly higher in the case of triplet adsorption on the doped surface configurations ‘B3G-1’ and ‘B3G-3’ compared to the other surface configurations. After doping with boron, the unpaired p orbitals on the surface are the most reliable sources of radical spins. The radical spin nature contributes to intermolecular interactions between graphene and oxygen molecules because of the high reactivity of unpaired electrons on triplet oxygen. It leads to a slightly larger band gap opening. The higher adsorption energies of triplet oxygen in these two cases, i.e., B3G-1 and B3G-3 systems with higher band gaps than other systems, are attributed to equivalent site doping, resulting in sub-lattice symmetry breaking. The optimized geometries of triplet oxygen on various doped surfaces are shown in Fig. 2. All of them exhibit physisorption at a distance of around 3 Å.
Comparing the adsorption energies of triplet and singlet oxygen on the same type of surfaces in Tables 1 and 2, we see that the singlet adsorptions are more stabilized. It leads to chemisorption on the doped graphene surface except for the pristine graphene (PG) and singly doped graphene (BG). By analyzing the adsorption energies, it is found that the magnitude of the adsorption energies of singlet oxygen is appreciable, compared to that of triplet oxygen adsorption, even on the pristine graphene surface. The adsorption energy value is −0.39 eV for singlet oxygen adsorption on pristine graphene compared to −0.147 for triplet. The reason for the same is easy to understand. The oxygen molecule in the triplet ground state is more stable than the singlet by 1 eV (experiment value is 0.97 eV), and the bond distance is smaller than in singlet oxygen. As the triplet oxygen is already in the lowest energy state, like other diatomic species near bare graphene surface, it is only weakly physisorbed.29,35 On the other hand, singlet oxygen is reactive, remains excited at higher energy, and therefore gets more attracted towards the bare surface to get stabilized. The charge transfer also indicates that there is stronger adsorption than in the case of triplet oxygen.
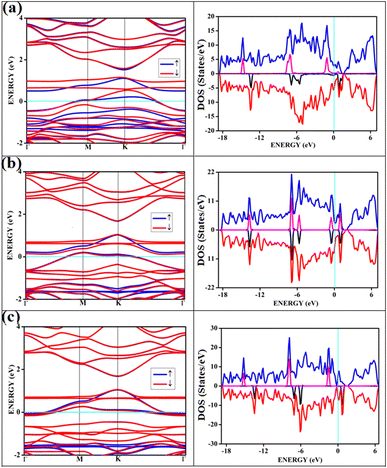
The band structures and the corresponding density of states of the relevant cases of triplet oxygen adsorption are shown in Fig. 3. The effect of dopant concentration on the band gap is discussed elaborately in our previous publications.17 However, we do not see a one-to-one correspondence of band gap with the dopant concentration and band gap does not necessarily vary linearly with the dopant concentration. The band gap of O2(t)/B2G-2 is 0.41 eV, close to the bare surface value of 0.37 eV. Similar behavior can be observed for the other two cases, O2(t)/B3G-1 and O2(t)/B3G-3 shown in Fig. 3. Though the band gaps for the bare surfaces B3G-1 and B3G-3 show an increase in band gaps, changes during adsorption of triplet oxygen are minimum without any appreciable changes in the band structure. It is clear that the π* orbitals are not taking part in any bond formation except for a weak mixing with the p-orbitals on the surface. The flat bands near the Fermi indicate the contribution from pz orbitals of the oxygen atoms creating bands above the Fermi, indicating p-type nature. The band gaps (in Table 1) are unaffected and remain similar to the bare surface.
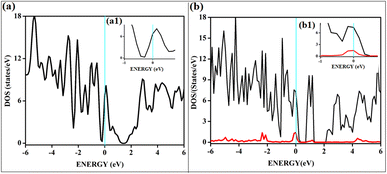
It shows physical adsorption and is confirmed by the density of states (DOS). The partial density of states (PDOS) for triplet oxygen is drawn together with the total DOS. The state not participating in bond formation appears as peaks slightly above the Fermi. It is also possible to see slight mixing and contribution from both π* orbitals and carbon and boron pz in Fig. 4. The oxygen pz orbitals remain without much mixing, with a small contribution from boron, and it appears as a straight band near 1 eV.
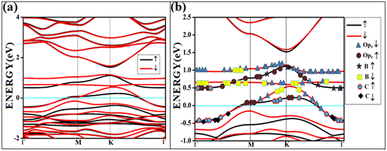 | ||
| Fig. 4 The band structure of triplet with the orbital contribution (a) O2(t)/B2G-2 (b) O2(t)/B2G-2 mixed orbitals. The line above 0.5 eV indicates oxygen pz and boron p orbitals. | ||
Three effects are to be considered while understanding the difference in the adsorptive behavior of triplet and singlet oxygen: repulsive, attractive, and spin–spin interactions. The triplet oxygen has two electrons occupying two π* antibonding molecular orbitals with parallel spins, and is a biradical. The same spin directions make it more repulsive. Attractive forces emerge from the tendency of the kinetic energy between the parallel spins moving apart. In the case of triplet oxygen, the repulsive forces between the biradical oxygen and the doped surface overcome the attractive interactions with the boron-doped graphene surface.
Most singlet oxygen adsorptions proceed through a dioxetane-like (with B–O bonds) ring formation except for the configuration ‘B3G-2’, where two carbon atoms separate the dopant borons. The B–O distances in the dioxetane ring ranged from 1.52 to 1.54 Å. The geometry of the optimized structure is shown in Fig. 5, and a detailed figure of the dioxetane ring formed on one of the patterns (B3G-3) is shown in Fig. 5(d).
The flat lines at around 0.59–0.85 eV correspond to the pz orbital of oxygen. In this model, the p-orbitals of boron, carbons, and π*-orbital of oxygen molecule interact for bonding. In the singlet oxygen adsorption, the electrons are arranged according to the Pauli exclusion principle. Therefore, it is more attracted to borons on the surface resulting in strong physisorption or chemisorption. The ‘B3G-2’ configured surface observed strong physisorption rather than chemisorption. In this surface pattern, the borons are separated by two carbons. Compared to the other configurations with a 9.37% dopant concentration, the lower band gap is due to the non-equivalent site doping in the B3G-2 surface configuration.
A study of adsorption of singlet oxygen onto aromatic hydrocarbon molecules38 found that singlet oxygen has the potential to chemisorb onto simple hydrocarbons. This attribute can be compared with the reaction of singlet oxygen with ethylene, where the dioxetane transition state is identified.47 A similar reaction path cannot be located for dioxetane for the triplet state of oxygen. In other words, the singlet oxygen does tend to oxidize the corresponding surfaces. The singlet oxygen is chemisorbed onto all surfaces except on intrinsic graphene and ‘B3G-2’ with the formation of dioxetane rings.
All the band structures for singlet O2 adsorptions are primarily featureless bands with ill-defined band gaps; a few are shown in Fig. 6, along with the corresponding DOS. The partial density of states (PDOS) of carbon and boron are added in the DOS plots to understand the contribution. An appreciable mixing of orbitals can be seen near the Fermi indicating strong chemisorption. The featureless bands result from the intense mixing of p-orbitals of boron, carbon, and molecular π* orbital of dioxygen formed from p-orbitals. The mixing is depicted in Fig. 7 for singlet oxygen adsorption on the surface B3G-1. From the density of states, it can be seen that the adsorbate orbitals are undergoing appreciable orbital mixing with that of the surface, especially with the vertical pz orbitals on boron, as can be seen from Fig. 7 due to chemical bond formation.
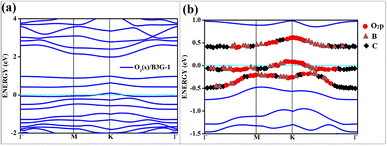 | ||
| Fig. 7 The band structure of singlet with the orbital contribution (a) O2(s)/B3G-1 (b) O2(s)/B3G-1 mixed orbitals. The line above −0.5 eV indicates oxygen pz and boron p orbitals. | ||
On intrinsic graphene, attractive forces are insufficient to form a dioxetane intermediate, even though such systems are predicted to form on aromatic hydrocarbons without doping.38 The effect of singlet oxygen adsorption on one of the surfaces is shown in Fig. 8. The total DOS of the B3G-3 surface before and after singlet oxygen adsorption is shown. The states near Fermi are magnified to show the intense orbital mixings due to chemisorption.
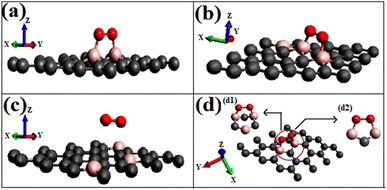
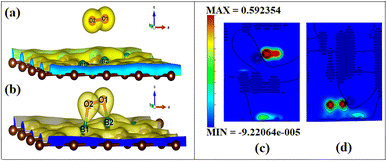
To visualize the difference in the charge transfers on adsorption, the VESTA (visualization for electronic and structure analysis) software is used.48 The charge density (Fig. 9a and b) and the difference density plots (Fig. 9c and d) with color coding shown in Fig. 9, respectively, explain both the physisorption of triplet oxygen and chemisorption with dioxetane ring formation in the case of singlet oxygen with the surface B3G-1.
For various partitions of electronic charge densities of O2(s)/B3G-1, the plane hkl (001) containing O–O–B bonds is employed. The charge density difference between the adsorbed complex, the surface, and the gas molecule O2 is computed using eqn (2). Charge density rearrangement can be seen in the case of chemisorptive adsorption. In comparison to the rest of the surface, electron-deficient patches may be seen near boron atoms. The red color reflects high charge density oxygen, the green iso-charge surfaces represent 8.95e-06e Å−3 charge buildup, and the bottom cyan color represents 0.55e Å−3 charge depletion on the graphene surface. Furthermore, the charge collected around the oxygen attracts it to the charge deficient area (cyan iso-surface, i.e., boron of graphene iso-surface), contributing to the energy preference of oxygen to connect with the specific borons doped in graphene. In this case, the valence charge (cyan) around the boron atoms is drawn to the oxygen atom (from the cyan toward the green iso-charge surface), leading to the covalent bond formation (dioxetane ring). O–O–B bonds with bonding states on top of the valence bands.
The graphic depicts how the charge concentration is spread among carbon atoms near the bond formation site with boron. In Fig. 9a, the charge transfers between triplet oxygen and boron are minimal, showing physisorption on the graphene surface of configuration B3G-1. In the case of triplet oxygen, the contour red color depicts the charge on oxygen. However, the charge accumulation is much lower than in the case of singlet oxygen, i.e., at 1.16e-05 of green color and bottom cyan color at 0.037, depicting charge depletion on graphene due to boron atoms.
4. Summary and conclusion
The spin-polarized calculations reveal that the results vary drastically upon considering triplet and singlet oxygen adsorption on doped surfaces. With the intrinsic graphene surface, both types of oxygen show weak attractions, as is evident from the previous investigations.38 The triplet oxygen is only physically adsorbed on all chemically doped surfaces, whereas singlet oxygen undergoes chemisorption. Chemisorption of the singlet follows with the dioxetane intermediate formation on the doped surface. This result can be best understood from the orbital structures of doped graphene and oxygen, in addition to the various possible interactions. A considerable amount of orbital mixing of the orbitals of singlet dioxygen and the orbitals of boron and carbons in the vicinity of bond formation is seen. The charge transfer is also appreciable, with charge density accumulation near the surface confirming the bond formations. It is interesting to see the different adsorption behavior with the different spin states of the adsorbate molecule. Though there are theoretical evidence to support the spin states and their occupancy on adsorption,15 the experimental evidence to suggest the importance of the spin states are still in premature state. Though there are few research on the effect of spin states on the catalytic activity of transition metal oxides,49 the experimental strategies to follow up the spin states are still under study. Whether the change of spin states change the adsorption configuration and reaction path are still unclear.Conflicts of interest
The authors declare that there are no conflicts to declare.Acknowledgements
Sahithi Andru acknowledges the BITS Pilani, Hyderabad campus, for financial support in the form of a Senior Research Fellowship.Notes and references
- K. S. Novoselov, A. K. Geims, V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef PubMed.
- K. Geim and P. Kim, Sci. Am., 2008, 298, 90–97 CrossRef PubMed.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsenelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652 CrossRef CAS PubMed.
- H. C. Chang, Y. J. Huang, H. Y. Chang, W. J. Su, Y. T. Shih, Y. S. Huang and K. Y. Lee, Appl. Phys. Express, 2014, 7, 055101 CrossRef CAS.
- C. J. Docherty, C. T. Lin, H. J. Joyce, R. J. Nicholas, L. M. Herz, L. J. Li and M. B. Johnston, Nat. Commun., 2012, 3, 1228 CrossRef PubMed.
- H. Nan, Z. Wang, W. Wang, Z. Liang, Y. Lu, Q. Chen, D. He, P. Tan, F. Miao, X. Wang, J. Wang and Z. Ni, ACS Nano, 2014, 8, 5738–5745 CrossRef CAS PubMed.
- Y. Sato, K. Takai and T. Enoki, Nano Lett., 2011, 11, 3468–3475 CrossRef CAS PubMed.
- L. Liu, S. Ryu, M. R. R. Tomasik, E. Stolyarova, N. Jung, M. S. S. Hybertsen, M. L. L. Steigerwald, L. E. E. Brus and G. W. W. Flynn, Nano Lett., 2008, 8, 1965–1970 CrossRef CAS PubMed.
- M. Zhou, Y. H. Lu, Y. Q. Cai, C. Zhang and Y. P. Feng, Nanotechnology, 2011, 22, 385502 CrossRef PubMed.
- F. Yavari, C. Kritzinger, C. Gaire, L. Song, H. Gulapalli, T. Borca-Tasciuc, P. M. Ajayan and N. Koratkar, Small, 2010, 6, 2535–2538 CrossRef CAS PubMed.
- T. O. Wehling, K. S. Novoselov, S. V. Morozov, E. E. Vdovin, M. I. Kats Nelson, A. K. Geim and A. I. Lichtenstein, Nano Lett., 2008, 8, 173–177 CrossRef CAS PubMed.
- J. Dai, J. Yuan and P. Giannozzi, Appl. Phys. Lett., 2009, 95, 232105 CrossRef.
- B. Kang, H. Liu and J. Y. Lee, Phys. Chem. Chem. Phys., 2014, 16, 974–980 RSC.
- O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
- J. Dai and J. M. Yuan, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 165414 CrossRef.
- A. Sahithi and K. Sumithra, RSC Adv., 2020, 10, 42318–42326 RSC.
- K. Nakada and A. Ishii, DFT Calculation for Adatom Adsorption on Graphene, Graphene Simulation, IntechOpen, London, 2011, pp. 1–18 Search PubMed.
- A. Sahithi and K. Sumithra, Mater. Today Commun., 2021, 27, 102417 CrossRef CAS.
- Y. H. Zhang, Y. B. Chen, K. G. Zhou, C. H. Liu, J. Zeng, H. L. Zhang and Y. Peng, Nanotechnology, 2009, 20, 185504 CrossRef PubMed.
- I. Choudhuri, N. Patra, A. Mahata, R. Ahuja and B. Pathak, J. Phys. Chem. C, 2015, 119, 24827–24836 CrossRef CAS.
- S. Yang, G. Lei, H. Xu, B. Xu, H. Li, Z. Lan and Z. Wang, Appl. Surf. Sci., 2019, 480, 205–211 CrossRef CAS.
- J. Ni, M. Quintana and S. Song, Phys. E, 2020, 116, 113768 CrossRef CAS.
- L. S. Panchakarla, K. S. Subrahmanyam, S. K. Saha, A. Govindaraj, H. R. Krishnamurthy, U. V. Waghmare and C. N. R. Rao, Adv. Mater., 2009, 21, 4726–4730 CAS.
- D. Wei, Y. Liu, Y. Wang, H. Zhang, L. Huang and G. Yu, Nano Lett., 2009, 9, 1752–1758 CrossRef CAS PubMed.
- J. Nakamura, J. Ito and A. Natori, J. Phys.: Conf. Ser., 2008, 100, 052019 CrossRef.
- C. W. Chen, S. C. Hung, M. D. Yang, C. W. Yeh, C. H. Wu, G. C. Chi, F. Ren and S. J. Pearton, Appl. Phys. Lett., 2011, 99, 243502 CrossRef.
- S. Rumyantsev, G. Liu, M. S. Shur, R. A. Potyrailo and A. A. Balandin, Nano Lett., 2012, 12, 2294–2298 CrossRef CAS PubMed.
- F. R. Bagsican, A. Winchester, S. Ghosh, X. Zhang, L. Ma, M. Wang, H. Murakami, S. Talapatra, R. Vajtai, P. M. Ajayan, J. Kono, M. Tonouchi and I. Kawayama, Sci. Rep., 2017, 7, 1774 CrossRef PubMed.
- Y. Zou, F. Li, Z. H. Zhu, M. W. Zhao, X. G. Xu and X. Y. Su, Eur. Phys. J. B, 2011, 81, 475–479 CrossRef CAS.
- H. Shin, Y. Luo and A. Benali, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 075430 CrossRef CAS.
- A. Pramanik and H. S. Kang, J. Phys. Chem. C, 2011, 115, 10971–10978 CrossRef CAS.
- Y. Chena, X. C. Yang, Y. Liua, J. Zhaoa, Q. Cai and X. Wang, J. Mol. Graphics, 2013, 39, 126–132 CrossRef PubMed.
- F. Mehmood, R. Pachter, W. Lu and J. J. Boeckl, J. Phys. Chem. C, 2013, 117, 10366–10374 CrossRef CAS.
- X. Zhu, K. Liu, Z. Lu, Y. Xu, S. Qi and G. Zhang, Phys. E, 2020, 117, 113827 CrossRef CAS.
- L. H. Qu, X. L. Fu, C. G. Zhong, P. X. Zhou and J. M. Zhang, Materials, 2020, 13, 4945 CrossRef CAS PubMed.
- J. Yan, B. Xu, S. Q. Shi and C. Y. Ouyang, J. Appl. Phys., 2012, 112, 104316 CrossRef.
- K. Kinoshita, T. Saito, A. Ito, T. Kawakami, Y. Kitagawa, S. Yamanaka, K. Yamaguchi and M. Okumura, Polyhedron, 2011, 30, 3249 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- MedeA®, Materials Exploration and Design Analysis, Software Package, Ver. 2.22, Materials Design, Inc., San Diego, CA, USA, 2019 Search PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- K. A. L. Lima, M. L. Pereira Jr., F. F. Monteiro, L. F. Roncaratti and L. A. Ribeiro Jr., Chem. Phys. Lett., 2021, 763, 138229 CrossRef CAS.
- T. Saito, S. Nishihara, Y. Kataoka, Y. Nakanishi, T. Matsui, Y. Kitagawa, T. Kawakami, M. Okumura and K. Yamaguchi, Chem. Phys. Lett., 2009, 483, 168 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- Z. Zhang, P. Ma, L. Luo, X. Ding, S. Zhou and J. Zeng, Angew. Chem., Int. Ed., 2023, 62, e202216837 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra00624g |
| This journal is © The Royal Society of Chemistry 2023 |