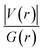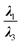Open Access Article
Open Access ArticleDensity functional theory computation of the intermolecular interactions of Al2@C24 and Al2@Mg12O12 semiconducting quantum dots conjugated with the glycine tripeptide
Hadi Mohammadi a,
S. M. Azamib and
Hashem Rafii-Tabar
a,
S. M. Azamib and
Hashem Rafii-Tabar *ac
*ac
aDepartment of Medical Physics and Biomedical Engineering, School of Medicine, Shahid Beheshti University of Medical Sciences, Tehran, Iran. E-mail: rafii-tabar@nano.ipm.ac.ir
bDepartment of Chemistry, Faculty of Sciences, Yasouj University, Yasouj, Iran
cThe Physics Branch of the Academy of Sciences of Iran, Tehran, Iran
First published on 28th March 2023
Abstract
The nature of intermolecular forces within semiconductor quantum dot systems can determine various physicochemical properties, as well as their functions, in nanomedical applications. The purpose of this study has been to investigate the nature of the intermolecular forces operating between Al2@C24 and Al2@Mg12O12 semiconducting quantum dots and the glycine tripeptide (GlyGlyGly), and also consider whether permanent electric dipole–dipole interactions play a significant role vis-à-vis these molecular systems. The energy computations, including the Keesom and the total electronic interactions and the energy decomposition, together with the quantum topology analyses were performed. Our results demonstrate that no significant correlation is found between the magnitude and orientation of the electrical dipole moments, and the interaction energy of the Al2@C24 and Al2@Mg12O12 with GlyGlyGly tripeptide. The Pearson correlation coefficient test revealed a very weak correlation between the quantum and the Keesom interaction energies. Apart from the quantum topology analyses, the energy decomposition consideration confirmed that the dominant share of the interaction energies was associated with the electrostatic interactions, yet both the steric and the quantum effects also made appreciable contributions. We conclude that, beside the electrical dipole–dipole interactions, other prominent intermolecular forces, such as the polarization attraction, the hydrogen bond, and the van der Waals interactions can also influence the interaction energy of the system. The findings of this study can be utilized in several areas in the field of nanobiomedicine, including the rational design of cell-penetrating and intracellular drug delivery systems using semiconducting quantum dots functionalized with a peptide.
1. Introduction
Intermolecular forces of semiconducting quantum dots (SCQDs) play a decisive role in diverse fields ranging from nanoscopic self-assembly1 to various nanofabrication processes, based on inter-particle forces,2–5 and supramolecular assembly of macromolecules as in bio-molecular recognition applications.6–9 They play a significant role in accounting for both structure-stability and structure–function in the above-mentioned fields. For instance, long-range electrostatic effects, either attractive or repulsive,10 perform a crucial role in related biological phenomena11,12 such as in the protein function13 and in the DNA repair process14 as well as DNA deformation.15 These intermolecular forces modulate the active sites of some enzymes.16 Similarly, they play a decisive role in the field of pharmacology, ranging from drug discovery to the investigation of drug-receptor coupling.17–21 The majority of scientists have paid a great deal of attention to the consequences of these classical intermolecular interactions.7,8,11,12,17–19,22,23From the perspective of cellular level, several research groups have carried out their study with reference to the field of nanomedicine, specifically the interactions of nanostructures, or quantum dots, with cells, biomolecules, and proteins.24–30 For instance, Forest et al.31 have pointed out the significant role of electrostatic interactions in relation to nano-bio systems, which consist of the interactions of cells with nanoparticles that are coupled to them via the surface of the cell membranes. Furthermore, Nel et al.32 have considered the biophysical interactions at the interface of nano-bio systems. Consequently, they have demonstrated that the nature of these biophysical interactions is the same as those between some colloidal particles that interact via electrostatic, hydrophobic, van der Waals(vdW), solvophobic, solvation interactions, as well as the depletion forces.32 Consequently, the majority of studies have indicated that specific intermolecular forces, such as those mentioned above, compared with nonspecific forces, such as the hydrophobic one, play a vital role vis-à-vis the cellular uptake of nanoparticles at the nano-bio interfaces.33
In addition to the cellular level, the electrostatic forces at the molecular level are defined by several types of interactions, i.e., the charge–charge, the charge–dipole and the permanent dipole–permanent dipole interactions, that are important in gas or liquid or solvent phases.34 Therefore, the electrical dipole–dipole interactions are categorized as electrostatic in nature, and they are more effective in connection with the interactions of nanostructures with biomolecules.35–37 As an example, Vovusha et al. have employed the density functional theory (DFT) to investigate the mutual interactions between the permanent electrical-dipole-moment orientations of the h-BN/graphene nanoflake with nucleobases. Their results indicate that not only the special orientation of the hybrid nanoflake in relation to nucleobases has a significant role in stabilizing the system, but also the most accessible configurations of the h-BN/graphene nanoflake with nucleobases were found to be the antiparallel orientation.38 Similarly, in the field of medicinal chemistry and drug design, the electrical dipole moment plays an important role as a descriptor in the quantitative-structure–activity-relationship (QSAR) in order to discover the biological activity of either the natural products or the synthetic compounds.39,40 For instance, Riahi and coworkers41 have computed the effect of Efavirenz drug (as a potentially anticancer drug) on DNA to reveal the nature of the intermolecular interaction between them. Their results showed that the appropriate interaction is composed of the electrostatic and dispersion forces at the drug–nucleobase interface leading to the stability of the complexes.
Summarizing the above-mentioned points, we can regard the electrical dipole–dipole intermolecular forces as playing a significant role either at the nano-bio interfaces or in pharma systems. Furthermore, the classical electrostatic interactions have been considered more extensively compared with the quantum effects.
Therefore, the aim of our paper has been to systematically explore the origin of the intermolecular forces through a molecular model via the DFT calculations, and asertain whether or not the electrical dipole–dipole interactions always play a decisive role in the stability of the selected molecular systems at the nano-bio interfaces including intercellular drug delivery design based on peptides as a target vector. When employing the quantum mechanical approach to study the nano-bio systems, we need to select an approach within this methodology which provides an adequate level of information by using a rather reasonable amount of computational time, and cost. Consequently, both the configuration interaction (CI)42,43 approach and the Møller–Plesset perturbation theory (MPn)44 are considered as higher wave function-based quantum mechanical approaches, compared with the Hartree–Fock (HF) approaches, which take into account the electron–electron correlation, but with a higher computational costs that could form a significant limitation for their use. Therefore, the rationale behind using the DFT method is associated with its exceptional level of accuracy with reduced computational time and being cost effective in comparison to the above-mentioned methods.
To the best of our knowledge, this is the first time that these two particular SCQDs, that have wide-ranging applications in biomedical fields,45–49 have been investigated. To implement this objective two sets of organic and inorganic SCQDs, including Al2@C24 and Al2@Mg12O12, interacting with (conjugated with) the GlyGlyGly tripeptide, are considered in order to carry out qualitative and quantitative analyses. Our results ascertain that in addition to the electrical dipole–dipole interactions, the intermolecular forces, such as the polarization attraction, the hydrogen bonding and the vdW interactions play a rather significant role in nanobiomedical systems, and that the intermolecular forces in these systems are not ignorable, vis-à-vis the stability, nor are they ignorable in relation to the properties of the molecular systems themselves.
The organization of this paper is as follows: in Section 2, we consider the theoretical and computational modeling that has been used to compute the dipole moments of the two quantum dots that have been considered. In Section 3, the results of our computations and their discussion are provided. Section 4 is the concluding part of the paper.
2. Theoretical and computational methods
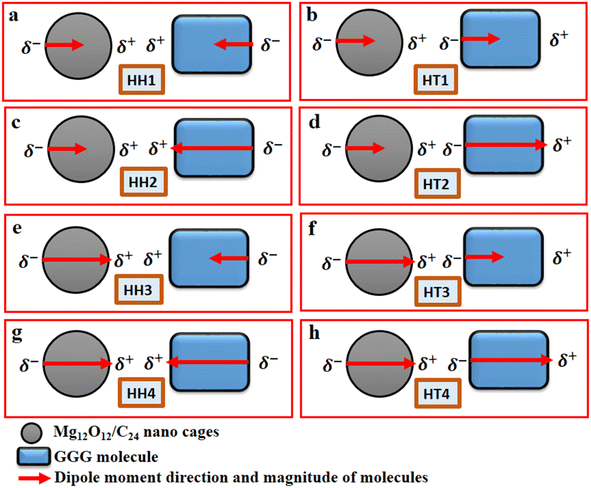
The Gaussian 16 software package50 and the Gauss View 6.1.1 version51 were employed to carry out all the relevant quantum-mechanical calculations and the corresponding visualization of all the structures that were considered. Furthermore, the ground-state calculations of the specific quantum dots, Al2@C24 and Al2@Mg12O12, and the GlyGlyGly tripeptide in the implicit solvent phase model were performed (Fig. 1a–c). The solvent model is represented by the conductor-like polarizable continuum model (CPCM) as well as by the self-consistent reaction field (SCRF).52,53 The calculations were optimized at M062X level of the DFT theory using the 6-31++G** basis set. The M062X function is a reliable method since it considers the dispersion long range interactions; it is therefore applied for studying the noncovalent interactions of various nanocages–pharma interfaces.54–60 In order to ascertain whether the structures are the optimized ones, frequency computations were performed to probe the nature of the stationary points of the structures.Our modeling consists of two parts. In the first part, the dipole moments of Al2@C24, Al2@Mg12O12, and GlyGlyGly under both optimized and fragmented conditions, and Al2@C24-GlyGlyGly, and Al2@Mg12O12-GlyGlyGly complexes under optimized conditions were computed. Furthermore the difference of the two dipole moments representing the (Pcompx − Psumopt) and the (Pcompx − Psumfrag) states were calculated. Initially the optimized states of Al2@C24-GlyGlyGly complexes as well as Al2@Mg12O12-GlyGlyGly systems were guessed with respect to both the orientation and magnitude of the dipole moments. For these calculations, as can be seen in Fig. 1, two sets of eight molecules are considered. In this way, the set of complexes consisting of vertically parallel and horizontally opposed directions of the dipole moments, such as the head-to-tail (HT) and the head-to-head (HH) horizontal orientations could be considered. We considered only the horizontal orientations. As far as the magnitude of the dipole moments of the SCQDs and tripeptide are concerned, according to Fig. 1 we have four HH/HT configurations, denoted by 1 to 4, wherein the numbers 1 and 4 pertain to the cases when the dipole moments are either both minimum or both maximum (as shown in Fig. 1a, b, g and h) and configuration numbers 2 and 3 pertain to the cases when one dipole moment is minimum and the other one is maximum (as shown in Fig. 1c–f). In addition to the dipole moments, two energy calculations are performed; one is the total electronic (TE) energy that represents the quantum interaction energy, and the other is the Keesom energy. At the end of this part, Pearson's regression coefficient was computed as a statistical index, via the Origin Pro 2021 software, in order to determine whether there is any correlation between the pertinent variables.
The Keesom (KE) energy is given by.10
KE = −P1P2[2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1cos θ1cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 − sinθ1 θ2 − sinθ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2cos θ2cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ]/4πε0d3 φ]/4πε0d3
| (1) |
The second part of our computations was concerned with the analyses of the electronic structures namely; the energy decomposition analysis (EDA), the quantum theory of atoms in molecules (QTAIM), the electron localized function (ELF), the localized orbital locator (LOL), the noncovalent interaction (NCI), and the reduced density gradient (RDG) for the eight selected complexes. These analyses were performed in order to obtain an explicit information concerning the nature of the interactions within the complexes.
Here we briefly state the theoretical basis of the EDA, QTAIM, ELF, LOL, NCI and RDG. The EDA is performed by employing the Shubin Liu (SBL) method.61 In this method, the interaction energy of the complexes can be decomposed into the electrostatic, steric and quantum terms as expressed by
| E = Eel + Es + Eq | (2) |
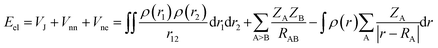 | (3) |
| ES = TW = |∇ρ(r)|2/[8ρ(r)] | (4) |
| Eq = Epauli + EXC | (5) |
The QTAIM, and both the ELF and the LOL, are the complementary electronic structure analyses used for investigating the nature of intermolecular force(s) between GlyGlyGly tripeptide and Al2@C24/Al2@Mg12O12 SCQDs via the AIM 2000 software62 and the MWfn 3.8 software.63 The QTAIM method is the based on Bader's theory64 and provides the electronic distribution features and the topological parameters of the selected SCQDs.
The NCI indices, as represented by eqn (6), depend on both the electron density (q) and the RDG,65 denoted by s, where s is given by eqn (6). The NCI is computed by using the interactive MWfn 3.8 software63 in order to determine the types of weak interactions among the complexes. The second largest Hessian matrix of eigenvalues (λ2) of q versus the RDG scatter plots obtained by the Multiwfn 3.8 software provides the noncovalent interactions within the complexes. The RDG isosurfaces and the maps of the scatter points are visualized and/or are plotted using the visual molecular dynamics (VMD1.9.4) package,66 and the gnu-plot software 5.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 67 respectively.
67 respectively.
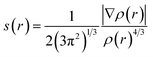 | (6) |
3. Results and discussion
3.1. Calculation of various dipole moments
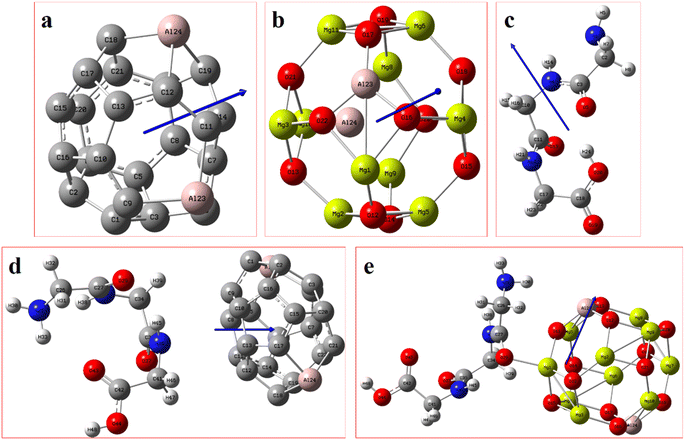
Fig. 2 displays the selection of some of the optimized structures under the isolated (Fig. 2a–c), and the complexes conditions (Fig. 2d and e) for both SCQDs and the GlyGlyGly biomolecule together with the orientations of their corresponding dipole moments. Here, we have solely taken into account the horizontally opposite states, including the HH as well as the HT directions, of the individual dipole moments as the initial conditions for the computations. Furthermore, we have applied geometry optimization not only for obtaining the possible ground state of the molecules, but also to extract the orientation and magnitude of the dipole moments for the SCQDs and GlyGlyGly. The optimization of the molecules was performed under different situations namely; the isolated, the combined, i.e., SCQDs and GlyGlyGly, and the frozen fragment conditions in which the Cartesian coordinates are fixed, whereas they change in the complex. Both the frozen fragment conditions and the complexes conditions are used to calculate the binding energy.Fig. 3 displays the minimum and maximum dipole moments of Al2@C24 and Al2@Mg12O12 together with their conjucation with the GlyGlyGly under the optimized conditions. The calculated values of the dipole moments of these molecules wer; 0.76 and 30.57 for Al2@C24-GlyGlyGly complexes, 4.43 and 50.44 for Al2@Mg12O12-GlyGlyGly complexes, 4.7 and 11.12 for Al2@C24 SCQDs, 0.09 and 34.70 for Al2@Mg12O12 SCQDs, 4.01 and 14.13 for GlyGlyGly tripeptides, all in the Debye (D) unit. Similarly, the pair of minimum and maximum values of the dipole moments for the frozen fragments of Al2@C24 and Al2@Mg12O12 SCQDs were obtained to be (5.00D, 10.64D), (4.04D, 50.34D) respectively. Therefore, it can be seen from the Fig. 3 that for both SCQD-GlyGlyGly complexes, the HT4 has the highest value, while the HH1 and the HT1 have the lowest values for these complexes. Likewise, for the frozen fragment condition, the highest and lowest values were the same as those under the optimized situation.
 | ||
| Fig. 3 Variations of the magnetiude of the dipole moments with configuration (a) for Al2@C24-GlyGlyGly and (b) for Al2@Mg12O12-GlyGlyGly. | ||
It should be pointed out that if the dipole–dipole interactions are dominant in the reagent interaction energy within the total electronic energy of the system, then we expect that all the HT configurations to have a higher value of the dipole moments compared to the HH configurations.34 As Fig. 3 shows only the HH1 and the HT4, which belong to Al2@C24-GlyGlyGly, appear at correct places at the beginning and the end of the graph, while the orders of the other configurations do not correspond to the locations that they should occupy on the graph. Similarly, for Al2@Mg12O12-GlyGlyGly cases, the HT4 and the HT3 have the highest values of the dipole moments, but instead of the HH1 configuration appearing on the minimum side of the graph, the HT1 is seen to be located on the minimum side, which is not its appropriate location.
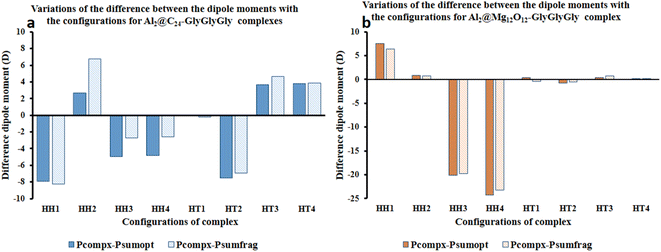
Fig. 4 represents the difference between the dipole moments of the complete Al2@C24-GlyGlyGly complexes (Pcompx) and the sum of the dipole moments of their constituent parts (Psumopt) under the optimized situation, and the difference between the complete dipole moments of Al2@C24-GlyGlyGly complexes and the sum of the dipole moments of their constituent parts under the frozen fragment condition (Psumfrag). The figure also shows the same differences for Al2@-Mg12O12-GlyGlyGly complexes.
As can be seen from this figure, all of the cases of Al2@C24-GlyGlyGly in the segment of head-to-head directions are subtractive except the HH2 complex, whereas for half of the cases (HT3 and HT4), in the head-to-tail sector, they appear to be additive. However, in case of Al2@Mg12O12-GlyGlyGly complexes, half of the cases are computed to be either subtractive or additive in both configurations. By “additive” and “subtractive”, we mean when two dipole moments are added together, and when they are subtracted from each other. It should be noted that when two charges, either with the same sign or the opposite sign, interact with each other, the results would appear as either subtractive or additive respectively. Therefore, we observe that for both the HH and the HT configurations of the SCQDs, it seems that there are some exceptional cases. As an example, although we expect that both the HH2 and the HH1 configurations of Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly should appear as subtractive, however, they appear to be additive. In other words, the results indicate that there might be some other intermolecular forces operating at the interfaces of such systems. Finally, some analysis from the energetic perspective maybe necessary in order to obtain a deeper insight.
Furthermore, considering the bar graph of Fig. 4 for Al2@C24-GlyGlyGly cases, all the calculated values of (Pcomplex − Psumopt) and (Pcompex − Psumfrag) are approximately the same, except for the HH2 configuration wherein the difference between Psumopt and Psumfrag is significant. Equally, for Al2@Mg12O12-GlyGlyGly complexes, there is no significant difference between the magnitude of the above-mentioned parameters, however, for the HT1 case, there is a significant change of orientation of (Pcomplex − Psumopt) relative to (Pcompex − Psumfrag) leading to their dipole moments change from 0.42D to −0.43D respectively. As a final point, it should be reiterated that this change of sign from positive to negative could be due to the appearance of density deformation phenomena.
3.2. Keesom energy and total electronic energy calculations
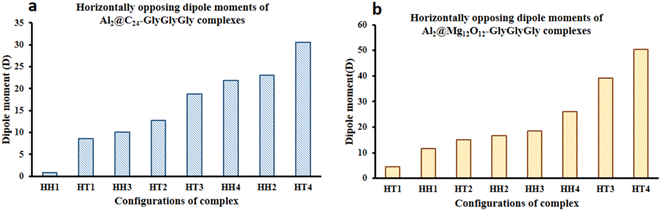
Fig. 5 displays both the calculated Keesom energy (KE) and the total electronic energy (TE) for the systems considered in this study. The KE energy represents the classical dipole–dipole interaction energy, and the total electronic energy provides the quantum interaction energy. Consequently, from Fig. 5 one can observe that the KE energy of both Al2@C24 and Al2@Mg12O12 SCQDs coupled to GlyGlyGly tripeptides, for the HH4 and the HT4 configurations, are most stable for the former, and least stable for the later. Additionaly, Fig. 5 shows that all of the HH configurations for Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly are the most stable complexes except for the HH1 of Al2@Mg12O12-GlyGlyGly.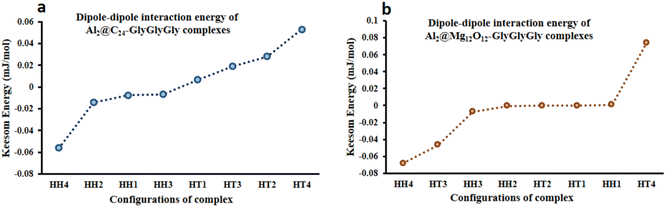 | ||
| Fig. 5 Variations of the calculated Keesom energy with the configurations of the complexes; (a) Al2@C24-GlyGlyGly and (b) Al2@Mg12O12-GlyGlyGly. | ||
From the quantum interaction energy point of view, as shown in Fig. 6, configurations such as (HT3, HT1) and (HH3, HT2) provide respectively the highest and the lowest pairs of values of the quantum interaction energy for Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly complexes. Additionaly, Fig. 6 shows that the TE energy for both organic and inorganic SCQDs conjugated with GlyGlyGly, a mixture of the HT and the HH configurations are located in the left segment of the figure (present the stable structures).
 | ||
| Fig. 6 Variations of the calculated total electronic interaction energy with the orientation of the complexes; (a) Al2@C24-GlyGlyGly and (b) Al2@Mg12O12-GlyGlyGly. | ||
Finally, we should mention that in our computation of the KE, we employed some approximations, vis-à-vis both the distance (d) and the angeles (θ and φ) between the dipole moments of the complexes in eqn (1). These approximations imply that the calculated Keesom interaction energy does not have the exact value that it should.
From Fig. 5 and 6 it can be seen that the majoraty of the HH configurations have the most negative values of the energy for both the dipole–dipole and quantum interaction energies, and are hence located in the left segment of the figures that present the most stable structures. However, for the TE energy of Al2@C24-GlyGlyGly SCQD the most stable configuration is of the HT type and not of the HH type. In contrast, all of the complexes with the most positive values of the quantum and dipole–dipole interaction energies, have the least stable structures. These are assigned to the HT type configurations of both Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly.
To summarize, our results from Fig. 5 and 6 show that the computed values of the KE and the TE energies for both Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly do not follow the same trend. Hence, it should be emphasized that the dipole–dipole interaction does not make a dominant contribution to the intermolecular force at the interface of the SCQDs with the tripeptide GlyGlyGly. Therefore, we could assume that other intermolecular interactions are operative at the interface. To elucidate this point, further analyses that will be reported in the following sections, are necessary. Furthermore, to determine the correlations between the values of:
1. The KE energy and the quantum interaction energy,
2. Dipole moment with the TE energy,
3. (Pcompx − Psumopt) with the TE energy,
4. (Pcompx − Psumfrag) with the TE energy,
we need to implement some specific statistical test to provide a quantitative relationship between all the calculated parameters. In the next section, these correlations are computed.
3.3. Calculated correlations
The statistical test is based on Pearson's correlation coefficient method68 to determine whether any correlation exists between the parameters in the above 1–4 list. The results obtained for the coefficient of correlation (R) for cases (1, 2, 3, 4) are listed in Table 1. In this table, the positive values of R indicate that the changes in the correlated parameters for the cases (1, 2, 3, 4) follow the same trend, whereas the negative values indicate that the changes follow the opposite trend. Additionally, from the R2 results in Table 1, we can state that the nearer these values are to 1, the stronger are the correlations and the nearer these values are to 0, the weaker are the correlations. Since the R2 values, shown in Table 1, for cases 1–4 are small, therefore the correlations between the corresponding parameters are weak. Consequently, the results show that the dipole–dipole interactions are not the only contribution to the interaction energy of the systems studied, and that the contributions of other interaction energies are also significant. It should be mentioned that as far as the calculated energies are concerned, our results do not show the same trend vis-à-vis the classical and quantum interaction energies.| Variables | R | R2 |
|---|---|---|
| KE energy and quantum interaction energy | 0.1 | 0.01 |
| Dipole moment with TE energy | −0.3 | 0.09 |
| (Pcompx − Psumopt) with TE energy | 0.2 | 0.04 |
| (Pcompx − Psumfrag) with TE energy | 0.3 | 0.09 |
3.4. Analyses of electronic structures
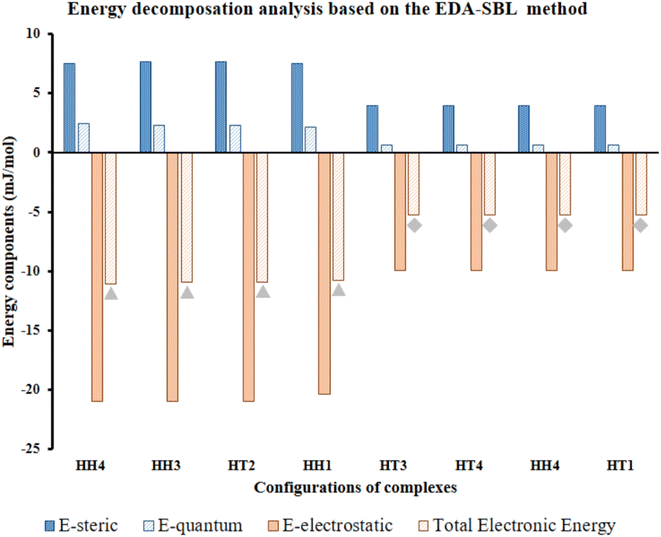 | ||
| Fig. 7 Calculated EDA components of selected Al2@C24-GlyGlyGly depicted by gray triangles and Al2@Mg12O12-GlyGlyGly shows by gray rhombuses according to the EDA-SBL method. | ||
Our calculations, therefore, reveal that there is a strong correlation, with R2 = 0.98, for the eight selected complexes, half for Al2@C24 cases and half for Al2@Mg12O12 cases as can be seen from Fig. 7. The values of components of E, i.e., Eelst, Estric, Equantum, are listed in Table 2. Moreover, Table 2 also shows the R-values of steric, electrostatic and quantum energies, and the total electronic energy of Al2@C24/Al2@Mg12O12 SCQDs coupled to GlyGlyGly systems. According to these results, the relationship between the values of all the components and the total electronic energy is linear and is in the same direction when R is positive, and in the opposite direction when R is negative.
| Variables | R | R2 |
|---|---|---|
| Esteric with TE | −0.99 | 0.98 |
| Eelst with TE | 0.99 | 0.98 |
| Equantum with TE | −0.99 | 0.98 |
| TE energy from DFT with EDA | 0.99 | 0.98 |
In order to reiterate the correlations between the interaction energy and the electrostatic, steric, and the quantum energies, from the energetic point of view, the calculated interaction energy either by the EDASBL method or with the M062X DFT method, shows a strong correlation with R2 = 0.98 as seen in Table 2 for all of the eight selected complexes mentioned above. Finally, major contribution to the interaction energy of the selected cases is assigned to the electrostatic effect. However, we cannot completely associate this effect with the contribution of the dipole–dipole interaction energy; since, previous research69 shows that the electrostatic energy, in addition to the dipole–dipole energy, consists of several other energies such as the dipole–quadrupole, the quadrupole–quadrupole energies etc. Therefore, performing specific analyses, like topological analysis, to ascertain the details of the nature of the intermolecular interactions are essential.
| Complex | Configurations | BCPs | ρ(r) | ∇2ρ(r) | V(r) | G(r) | H(r) | Ellipticity | ELF | LOL | sign λ2 × ρ(r) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al2@Mg12O12-GlyGlyGly | HH3 | Mg–O⋯H⋯N | 0.311 | −1.737 | −0.510 | 0.075 | −0.585 | 7.75 | 0.001 | 1.09 | 0.97 | 0.84 | −0.31 |
| O–Mg⋯O | 0.045 | 0.369 | 0.015 | 0.077 | −0.063 | 0.81 | 0.020 | 0.14 | 0.04 | 0.18 | −0.05 | ||
| Al–O⋯H–O | 0.331 | −1.956 | −0.561 | 0.072 | −0.632 | 8.83 | 0.005 | 1.14 | 0.98 | 0.86 | −0.33 | ||
| HT2 | Mg–O⋯H | 0.022 | 0.061 | −0.001 | 0.016 | −0.018 | 1.07 | 0.039 | 0.22 | 0.09 | 0.23 | −0.02 | |
| HH4 | O⋯H⋯N | 0.027 | 0.077 | 0.043 | 0.021 | 0.022 | 1.064 | 0.020 | 0.225 | 0.098 | 0.248 | −0.03 | |
| HH1 | O–Al⋯H | 0.005 | 0.008 | 0.000 | 0.002 | −0.002 | 0.910 | 0.428 | 0.193 | 0.115 | 0.217 | 0.00 | |
| O⋯H–N | 0.025 | 0.072 | −0.001 | 0.019 | −0.021 | 1.068 | 0.032 | 0.225 | 0.093 | 0.243 | −0.03 | ||
| Mg–O⋯C | 0.045 | 0.348 | 0.013 | 0.074 | −0.061 | 0.822 | 0.020 | 0.143 | 0.046 | 0.180 | −0.04 | ||
| O⋯H–O | 0.325 | −1.888 | −0.544 | 0.072 | −0.616 | 8.538 | 0.002 | 1.131 | 0.974 | 0.860 | −0.33 | ||
| Al2@C24-GlyGlyGly | HT3 | C–C⋯H | 0.012 | 0.035 | 0.001 | 0.008 | −0.007 | 0.85 | 0.329 | 0.19 | 0.05 | 0.18 | −0.01 |
| C–Al⋯O | 0.074 | 0.596 | 0.011 | 0.139 | −0.128 | 0.92 | 0.028 | 0.15 | 0.07 | 0.21 | −0.07 | ||
| HT4 | C–C⋯N | 0.008 | 0.022 | 0.001 | 0.005 | −0.004 | 0.79 | 1.146 | 0.20 | 0.04 | 0.17 | −0.01 | |
| C–C⋯O | 0.073 | 0.583 | 0.011 | 0.135 | −0.124 | 0.92 | 0.013 | 0.15 | 0.07 | 0.21 | −0.07 | ||
| HH4 | C–Al⋯N | 0.064 | 0.352 | −0.002 | 0.090 | −0.092 | 1.02 | 0.013 | 0.18 | 0.10 | 0.25 | −0.06 | |
| C–C⋯N | 0.006 | 0.016 | 0.000 | 0.004 | −0.003 | 0.92 | 0.839 | 0.10 | 0.02 | 0.13 | −0.01 | ||
| C–C⋯H | 0.015 | 0.041 | 0.001 | 0.010 | −0.009 | 0.94 | 0.091 | 0.21 | 0.07 | 0.21 | −0.01 | ||
| Al–C⋯H | 0.011 | 0.031 | 0.001 | 0.007 | −0.006 | 0.88 | 0.810 | 0.19 | 0.05 | 0.19 | −0.01 | ||
| HT1 | C–C⋯N | 0.008 | 0.023 | 0.001 | 0.005 | −0.005 | 0.88 | 0.253 | 0.15 | 0.03 | 0.16 | −0.01 | |
| Al–C⋯H | 0.004 | 0.013 | 0.001 | 0.003 | −0.002 | 0.72 | 0.651 | 0.14 | 0.02 | 0.11 | −0.004 | ||
| Al–C⋯O | 0.006 | 0.018 | 0.001 | 0.004 | −0.003 | 0.85 | 0.550 | 0.14 | 0.02 | 0.13 | −0.01 |
We should mention that the combination of the signs of the electron energy density and the Laplacian of the electron density is imperative for determination of the nature of the intermolecular interaction. According to Rozas et al.,70 the positive sign of H(r) alone represents the shared interactions, while the negative sign exhibits the closed-shell interactions. Likewise, the negative values of H(r) and ∇2ρ(r) are strong manifestations of the covalent nature of interactions, whereas the positive values of H(r) and ∇2ρ(r) determine the weak electrostatic nature of interactions. However, if H(r) has a negative sign and ∇2ρ(r) has a positive sign, the dominant form of interaction is partially covalent in nature. For instance, from Table 3 it can be seen that between Al2@C24 and Al2@Mg12O12 SCQDs with tripeptide, only Al2@Mg12O12-GlyGlyGly complexes that include the HH3 and the HH1 have negative values for both H(r) and ∇2ρ(r) topological parameters. Hence, we can attribute this to the sharing-interactions, such as the covalent bonding, which plays a significant role in the stability of the molecular systems.
From another perspective, the nature of the intermolecular forces can arise due to the balance that is established between the potential energy and the electron kinetic energy density at BCPs. Accordingly, the ratio |V(r)|/G(r) must be calculated in order to demonstrate the nature of the intermolecular interactions,70 since, when the value of this ratio is more than 2, the interaction is characterized as a covalent bond, and when it is between 1 and 2, the interaction is of mixed type, and finally when it is less than 1, it represents either a hydrogen bond (H-bond) or a vdW type of interaction. Table 3 shows that for the majority of the intermolecular interactions between GlyGlyGly and organic SCQDs, the ratio is less than 1, except for the HH4 configuration of Al2@C24-GlyGlyGly complex. By addressing this issue, the results show the dominancy of the weak interactions such as the vdW or the H-bond for Al2@C24-GlyGlyGly case. However, for the GlyGlyGly case and inorganic SCQDs, as shown in Table 3, the calculated values for the ratio involve all of the possible values, i.e., less than 1, between 1 and 2, and greater than 2. For the inorganic SCQDs case, a range of interactions, from the weak to mixed and covalent, can be present.
From another aspect, the character of the intermolecular forces can be determined by the ratio |λ1/λ3|, where λ3 presents the third largest Hessian matrix of eigenvalues, which serves as another AIM index.71 Therefore, when |λ1/λ3| is less than 1 and ∇2ρ(r) is greater than 0, this character is known as the outflow of ρ(r) that can represent the closed-shell interactions such as the highly-polarized bond, the ionic bond, the vdW bond as well as the H-bond. In contrast, if ∇2ρ(r) is less than 0 and |λ1/λ3| is greater than 1, then the compression of ρ(r) becomes significant and can be taken into account as the shared interactions representing the covalent bond.71,72 Since all of the complexes have positive values of the Laplacian, and |λ1/λ3| is less than 1, we can infer that the closed-shell interactions like the vdW and the hydrogen bond, and the high polarity bond play vital role vis-à-vis all of the selected cases except the HH3 configurations of Al2@Mg12O12-GlyGlyGly complex.
According to the QTAIM analyses, shown in Table 3, it can be deduced that among the selected complexes, the majority of structures have positive values of H(r) and the Laplacian, and |λ1/λ3| < 1. These values indicate that closed-shell interactions (the H-bond and the vdW) exist between the tripeptide and SCQDs. On the contrary, the minority of selected complexes, such as the HH3 and the HH1 configurations of Al2@Mg12O12-GlyGlyGly complexes, acquire negative values for H(r), the Laplacian as well as the ratio|λ1/λ3| > 1 which demonstrate covalent bonding as the shared interaction types. Finally, the selected cases, like the HH3 and the HH1 configurations belonging to Al2@Mg12O12-GlyGlyGly complexes, can be categorized as strong interactions with electron density values of more than 0.3 au and the ellipticity index approaching 0, while for the rest of the structures, the values of the electron density are less than 0.1 that indicate weak interactions.
Apart from the above indices, the ellipticity (ε = (λ1/λ2) − 1), where λ1 and λ2 present the first and the second largest Hessian matrix of eigenvalues respectively, is introduced in the AIM theory73 as an index to measure the deviation of ρ(r) from the cylindrical symmetry. Table 3 shows that the HH3 and the HT4 have the ellipticity of 0.001 and 1.146 for Al2@Mg12O12-GlyGlyGly and Al2@C24-GlyGlyGly i.e., the lowest and the highest values respectively. Additionally, to further illustrate this point, one can state that there is a relationship between the ellipticity and the nature of the intermolecular interactions for both SCQDs coupled to GlyGlyGly and surrounded by water as the solvent. Whenever the shared interaction and the strong interaction are dominant in the HH3 and the HH1 configurations, the values of ε approach 0. Nevertheless, for the rest of the complexes i.e., Al2@C24-GlyGlyGly or Al2@Mg12O12-GlyGlyGly that have closed-shell interactions, the values of ε deviate from 0 which imply a deviation from the cylindrical symmetry, and this can be attributed to a decrease in the π component of the bond.
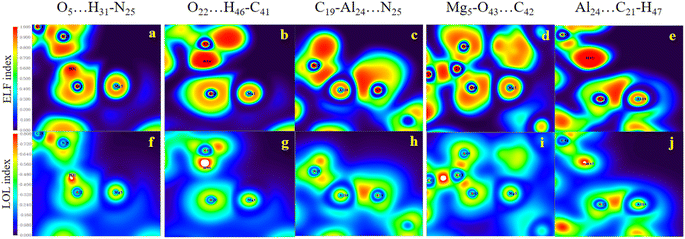
Evidently, in accordance with Fig. 8, which depicts the map of the ELF and the LOL for the selected complexes, such as the HH3, the HH1 and the HT2 configurations for Al2@Mg12O12-GlyGlyGly, the nature of the intermolecular interactions is computed to be covalent, partially-covalent-partially-electrostatic, and purely electrostatic respectively. While for the HH4, the HT3, and the HT1 configurations of Al2@C24-GlyGlyGly, the nature of the intermolecular interactions is computed to be partially-covalent-partially-electrostatic and purely electrostatic respectively. It has been shown by Becke et al.74 that the low (high) ELF values are attributed to fast (slow) electrons, and that the slow electrons serve as localized electrons like lone pairs and covalent bonds respectively. For this reason, the higher the values of the LOL and the ELF, the greater is the electron density. Similar points also apply to the LOL.
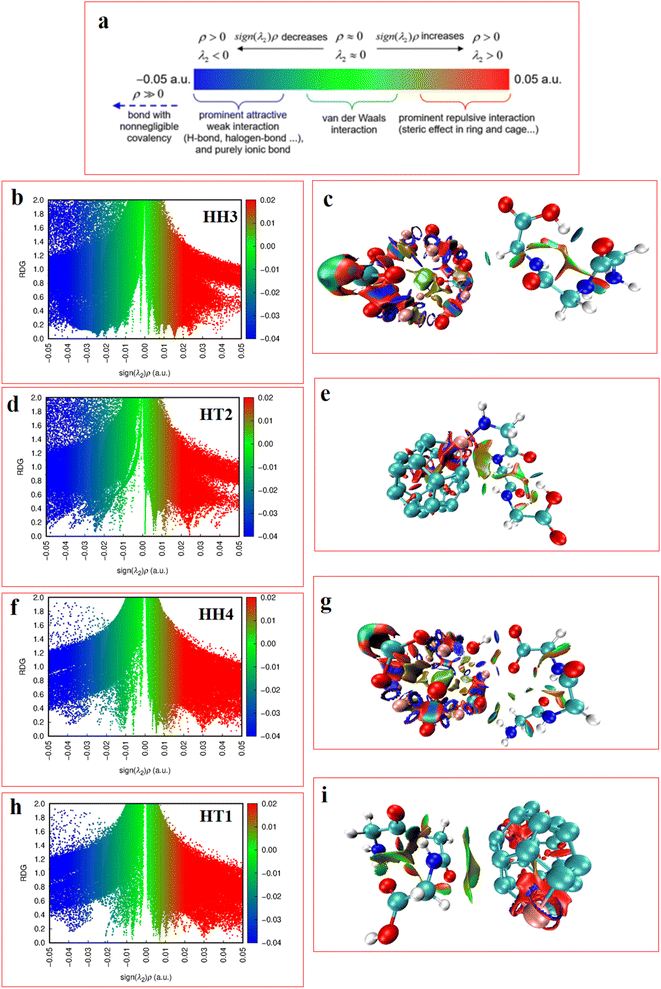
In the RDG scatter plots, shown in Fig. 9, there are various regions as well as colors such as blue, green and red with specific interpretation. Firstly, the data with positive values (spikes in the range of 0.1 to 0.5 au) indicate repulsive steric interactions. The next region, located around 0, relates to the vdW interactions. Finally, the weak attractive interactions appear in the negative zone of this plot. As a result, the values displayed by the RDG plots of the selected Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly complexes, and given in Table 3, all correspond to the negative sign of (λ2) × ρ(r). In addition, it should be emphasized that the negative values less than 0.1 au can be attributed to noncovalent interactions, such as those that appear for all of the Al2@C24-GlyGlyGly complexes, while for some of the Al2@Mg12O12-GlyGlyGly cases the values are more than −0.1 au that are indicative of covalent interactions. Finally, in the NCI analyses shown in Fig. 9, both the green and yellow patches that appear between GlyGlyGly and the SCQDs represent the vdW interactions, whereas the red patches in the Al2@C24 and Al2@Mg12O12 SCQDs depict the steric repulsion. Consequently, the vdW interactions, which are predominant interactions, compared to other intermolecular interactions, correspond to values in the range of −0.01 to 0.01 au on the RDG scatter plots. Ultimately, the small blue patches only emerge between the Al2@Mg12O12 SCQDs with GlyGlyGly for the cases of the HH3 and the HH1 configurations as shown in the RDG isosurface.
4. Conclusion
In this paper, we investigated systematically the relationship between the magnitude and the direction of the electrical dipole moments and the interaction energy at the interfaces of the Al2@C24-GlyGlyGly and Al2@Mg12O12-GlyGlyGly complexes. We employed the DFT method, based on the M062X and 6-31++G** as the level of the theory and the basis set respectively. It should be remarked that more sophisticated post-HF methods, such as the MPn and the QCI methods, provide higher accuracy than the general DFT-based methods. We also used the MP2 method for some of the quantum dot systems. For example, we optimized the Al2@Mg12O12–GlyGlyGly complex at the MP2/6-31++G** level using 32 processing cores (each having a clock rate of 2.6 GHz) and a total of 100 GB memory, with no frequency analysis. Under these conditions it took 2.5 real-time days (∼85 days of CPU time) to perform the computations. Furthermore, there exists some benchmarking of the M062X method in the literature77 that shows that this method provides reasonable results in comparison with the higher theoretical levels (such as the MPn etc.) and experimental observations. Our results also show that the values for the energy and the dipole moment obtained with the M062X method are close to those obtained from the MP2 in units of Hartree and Debye, respectively as shown in Table 4.| M062X | MP2 | Difference (%) | |
|---|---|---|---|
| Al2@Mg12O12 (energy) | −3514.14 | −3297.96 | 6.6% |
| Mg12O12-GlyGlyGly (dipole moment) | 39.08 | 45.32 | 13.7% |
Our calculated results of the dipole moments of the complexes indicate that there is no significant correlation between the values of the electrical dipole moments of complexes and their orientations. It should be pointed out that, according to the previously reported results, the combination of the dipole moments of selected complexes with the HT is of synergetic nature, and that of the HH is of an antagonistic nature. This is in contrast to the results that we have obtained; namely an antagonistic behavior for the HT and synergetic behavior for the HH. This is due to the fact that in previous research only the pure electrostatic interactions were taken into account, whereas in addition to electrostatic interactions we have also considered the quantum and steric interactions.
We have calculated both the Keesom and the total electronic interaction energies wherein the dipole–dipole and the quantum interaction energies are present. Furthermore, the Pearson correlation coefficient test reveals that the correlations between the classical interaction energy and the quantum energy (R2 = 0.01) as well as the variation in the difference of the dipole moments with the total electronic energy (with R2 equal to 0.03 and 0.01) are categorized as the weak correlation type. The EDA analysis, based on the SBU scheme, demonstrates that for all the selected complexes, the electrostatic effect has a significant role, but the quantum and steric effects also play important roles at the interfaces of molecular systems. All the three approaches, the QTAIM, the ELF and the LOL, to a large extend reveal the nature of the intermolecular interactions. Likewise, the NCI-RDG analyses confirm the above-mentioned findings and reveal that the dipole–dipole interactions at the surfaces of the molecular systems play an important role in the intermolecular interactions. However, there are other types of intermolecular forces such as the vdW, the H-bond and the polarization attraction that can have decisive contributions to the interaction energy of the complexes.
Our molecular modeling can be helpful to provide an insight into the nature of the intermolecular forces. Consequently, one approach to obtain these forces is via the DFT method due to its lower computational cost and acceptable accuracy in comparison with the MP2 method. As far as justification for the use of GlyGlyGly is concerned, it should be mentioned that since the limitations of the use of the quantum dots in clinical researches are related to their solvation capacity, therefore some biomolecules, like GlyGlyGly tripeptide, can play a significant role for overcoming these limitations. Finally, some tripeptides, like GlyGlyGly, can make contribution as a targeting agent in nano drug delivery vehicles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This paper has been extracted from the PhD thesis in the field of computational nanomedicine by Mr Hadi Mohammadi at the Department of Medical Physics and Biomedical Engineering in the School of Medicine, Shahid Beheshti University of Medical Sciences (Registration No: IR.SBMU.MSP.REC.1398.666). The authors gratefully acknowledge the help of Dr Reza Karbalaei for providing computing facilities and computer script codes checking.References
- D. Luo, C. Yan and T. Wang, Small, 2015, 11, 5984–6008 CrossRef CAS PubMed.
- Y. Sun, Chem. Soc. Rev., 2013, 42, 2497–2511 RSC.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed.
- T. Wang, D. LaMontagne, J. Lynch, J. Zhuang and Y. C. Cao, Chem. Soc. Rev., 2013, 42, 2804–2823 RSC.
- B. Abécassis, M. D. Tessier, P. Davidson and B. Dubertret, Nano Lett., 2014, 14, 710–715 CrossRef PubMed.
- K. Pahnke, O. Altintas, F. G. Schmidt and C. Barner-Kowollik, ACS Macro Lett., 2015, 4, 774–777 CrossRef CAS PubMed.
- A. Sikder, S. Chakraborty, P. Rajdev, P. Dey and S. Ghosh, Acc. Chem. Res., 2021, 54, 2670–2682 CrossRef CAS PubMed.
- I. Insua, J. Bergueiro, A. Méndez-Ardoy, I. Lostalé-Seijo and J. Montenegro, Chem. Sci., 2022, 13, 3057–3068 RSC.
- G. Chen and M. Jiang, Chem. Soc. Rev., 2011, 40, 2254–2266 RSC.
- J. N. Israelachvili, Intermolecular and surface forces, Academic press, 2011 Search PubMed.
- P. H. Maccallum, R. Poet and E. J. Milner-White, J. Mol. Biol., 1995, 248, 361–373 CAS.
- D. M. Smith and K. A. Woerpel, Org. Biomol. Chem., 2006, 4, 1195–1201 RSC.
- A. Warshel, Acc. Chem. Res., 1981, 14, 284–290 CrossRef CAS.
- Y. L. Jiang, Y. Ichikawa, F. Song and J. T. Stivers, Biochemistry, 2003, 42, 1922–1929 CrossRef CAS PubMed.
- L. D. Williams and L. J. Maher III, Annu. Rev. Biophys. Biomol. Struct., 2000, 29, 497–521 CrossRef CAS PubMed.
- J. A. Olsen, D. W. Banner, P. Seiler, U. Obst Sander, A. D'Arcy, M. Stihle, K. Müller and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 2507–2511 CrossRef CAS PubMed.
- I. Doytchinova, Molecules, 2022, 27, 1496 CrossRef CAS PubMed.
- P. Politzer and J. S. Murray, Chemical Reactivity in Confined Systems: Theory and Applications, 2021, pp. 113–134 Search PubMed.
- J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1326 Search PubMed.
- L. Schaeffer, in The practice of medicinal chemistry, Elsevier, 2008, pp. 464–480 Search PubMed.
- S. Shah, N. Rangaraj, S. B. Singh and S. Srivastava, Colloid Interface Sci. Commun., 2021, 42, 100406 CrossRef CAS.
- M. K. Mazumder, R. A. Sims, A. S. Biris, P. K. Srirama, D. Saini, C. U. Yurteri, S. Trigwell, S. De and R. Sharma, Chem. Eng. Sci., 2006, 61, 2192–2211 CrossRef CAS.
- A. Shurki, M. Strajbl, C. N. Schutz and A. Warshel, Methods Enzymol., 2004, 380, 52–84 CAS.
- Y. Wang, R. Cai and C. Chen, Acc. Chem. Res., 2019, 52, 1507–1518 CrossRef CAS PubMed.
- S. T. Johnston, M. Faria and E. J. Crampin, Nanoscale Adv., 2021, 3, 2139–2156 RSC.
- L. Abarca-Cabrera, P. Fraga-García and S. Berensmeier, Biomater. Res., 2021, 25, 1–18 CrossRef PubMed.
- J. Li, N. Lu, S. Han, X. Li, M. Wang, M. Cai, Z. Tang and M. Zhang, ACS Appl. Mater. Interfaces, 2021, 13, 21040–21050 CrossRef CAS PubMed.
- A. Hu, W. Zhang, G. Liao, D. Wang and Y. Peng, Environ. Sci.: Nano, 2020, 7, 2795–2808 RSC.
- I. Rouse, D. Power, E. G. Brandt, M. Schneemilch, K. Kotsis, N. Quirke, A. P. Lyubartsev and V. Lobaskin, Phys. Chem. Chem. Phys., 2021, 23, 13473–13482 RSC.
- J. Subbotina and V. Lobaskin, J. Phys. Chem. B, 2022, 126, 1301–1314 CrossRef CAS PubMed.
- V. Forest, M. Cottier and J. Pourchez, Nano Today, 2015, 10, 677–680 CrossRef CAS.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543–557 CrossRef CAS PubMed.
- G. Hu, B. Jiao, X. Shi, R. P. Valle, Q. Fan and Y. Y. Zuo, ACS Nano, 2013, 7, 10525–10533 CrossRef CAS PubMed.
- E. Silla, A. Arnau and I. TuñóN, Handbook Solvents, 2001, vol. 7 Search PubMed.
- J. E. Schoutens, J. Biol. Phys., 2005, 31, 35–55 CrossRef PubMed.
- S. J. Ganesan and S. Matysiak, J. Chem. Theory Comput., 2014, 10, 2569–2576 CrossRef CAS PubMed.
- E. J. Lien, Z.-R. Guo, R.-L. Li and C.-T. Su, J. Pharm. Sci., 1982, 71, 641–655 CrossRef CAS PubMed.
- H. Vovusha, R. G. Amorim, R. H. Scheicher and B. Sanyal, RSC Adv., 2018, 8, 6527–6531 RSC.
- A. Das, A. Das and B. K. Banik, J. Indian Chem. Soc., 2021, 98, 100005 CrossRef CAS.
- A. Das and B. K. Banik, in Green Approaches in Medicinal Chemistry for Sustainable Drug Design, Elsevier, 2020, pp. 921–964 Search PubMed.
- S. Riahi, S. Eynollahi, M. R. Ganjali and P. Norouzi, Int. J. Electrochem. Sci., 2010, 5, 815–827 CAS.
- J. C. Slater, Phys. Rev., 1929, 34, 1293 CrossRef CAS.
- E. U. Condon, Phys. Rev., 1930, 36, 1121 CrossRef CAS.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- B. Gidwani, V. Sahu, S. S. Shukla, R. Pandey, V. Joshi, V. K. Jain and A. Vyas, J. Drug Deliv. Sci. Technol., 2021, 61, 102308 CrossRef CAS.
- S. O. Souza, R. B. Lira, C. R. A. Cunha, B. S. Santos, A. Fontes and G. Pereira, Top. Curr. Chem., 2021, 379, 1–32 CrossRef CAS PubMed.
- Y. Fu, M.-S. Jang, T. Wu, J. H. Lee, Y. Li, D. S. Lee and H. Y. Yang, Carbohydr. Polym., 2019, 224, 115174 CrossRef CAS PubMed.
- A. M. Wagner, J. M. Knipe, G. Orive and N. A. Peppas, Acta Biomater., 2019, 94, 44–63 CrossRef CAS PubMed.
- E. Campbell, M. T. Hasan, R. Gonzalez Rodriguez, G. R. Akkaraju and A. V Naumov, ACS Biomater. Sci. Eng., 2019, 5, 4671–4682 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016, http://gaussian.com/citation/ Search PubMed.
- R. Dennington, T. A. Keith, and J. M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016, http://gaussian.com/citation/ Search PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- H. Ghafur Rauf, S. Majedi, E. Abdulkareem Mahmood and M. Sofi, Chem. Rev. Lett., 2019, 2, 140–150 Search PubMed.
- I. Ravaei, M. Haghighat and S. M. Azami, Appl. Surf. Sci., 2019, 469, 103–112 CrossRef CAS.
- Y. Cao, A. Khan, H. Balakheyli, A. N. K. Lup, M. R. Taghartapeh, H. Mirzaei, S. R. Khandoozi, A. Soltani, M. Aghaei and F. Heidari, Arabian J. Chem., 2021, 14, 103200 CrossRef CAS.
- M. Sheikhi, Y. Ahmadi, S. Kaviani and S. Shahab, Struct. Chem., 2021, 32, 1181–1196 CrossRef CAS.
- Y. Gao, F. Xu, J. Wu, H. Zhao and A. G. Ebadi, Comput. Theor. Chem., 2022, 1207, 113507 CrossRef CAS.
- B. L. Ndjopme Wandji, A. D. Tamafo Fouegue, N. K. Nkungli, R. A. Ntieche and A. Wahabou, R. Soc. Open Sci., 2022, 9, 211650 CrossRef PubMed.
- A. S. Rad, V. Samipour, S. Movaghgharnezhad, A. Mirabi, M. H. Shahavi and B. K. Moghadas, Surf. Interfaces, 2019, 15, 30–37 CrossRef CAS.
- S. Liu, J. Chem. Phys., 2007, 126, 244103 CrossRef PubMed.
- K. F. Biegler, J. Schnbohm and D. Bayles, J. Comput. Chem., 2001, 22(5), 545–559 CrossRef.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- P. Wu, R. Chaudret, X. Hu and W. Yang, J. Chem. Theory Comput., 2013, 9, 2226–2234 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- T. Williams and C. Kelley, Gnuplot 4.5: an interactiveplotting program., 2011, http://gnuplot.info Search PubMed.
- A. L. Edwards, Correl. Coeff., 1976, 33–46 Search PubMed.
- A. Volkov and P. Coppens, J. Comput. Chem., 2004, 25, 921–934 CrossRef CAS PubMed.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161 CrossRef CAS.
- R. F. W. Bader and H. Essén, J. Chem. Phys., 1984, 80, 1943–1960 CrossRef CAS.
- D. Cremer and E. Kraka, Croat. Chem. Acta, 1984, 57, 1259 Search PubMed.
- R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- H. L. Schmider and A. D. Becke, J. Mol. Struct.: THEOCHEM, 2000, 527, 51–61 CrossRef CAS.
- A. Otero-De-La-Roza, E. R. Johnson and J. Contreras-García, Phys. Chem. Chem. Phys., 2012, 14, 12165–12172 RSC.
- A. L. Hickey and C. N. Rowley, J. Phys. Chem. A, 2014, 118, 3678–3687 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |