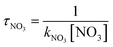A theoretical study of the gas-phase reactions of propadiene with NO₃: mechanism, kinetics and insights

Abstract

In this study, the conversion mechanisms and kinetics of propadiene (CH₂=C=CH₂) induced by NO₃ were researched using density functional theory (DFT) and transition state theory (TST) measurements. The NO₃-addition pathways to generate IM1 (CH₂ONO₂CCH₂) and IM2 (CH₂CONO₂CH₂) play a significant role. P3 (CH₂CONOCHO + H) was the dominant addition/elimination product. Moreover, the results manifested that one H atom from the –CH₂– group has to be abstracted by NO₃ radicals, leading to the final product h-P1 (CH₂CCH + HNO₃). Due to the high barrier, the H-abstraction pathway is not important for the propadiene + NO₃ reaction. In addition, the computed k_tot value of propadiene reacting with NO₃ at 298 K is 3.34 × 10⁻¹⁵ cm³ per molecule per s, which is in accordance with the experimental value. The computed lifetime of propadiene oxidized by NO₃ radicals was assessed to be 130.16–6.08 days at 200–298 K and an altitude of 0–12 km. This study provides insights into the transformation of propadiene in a complex environment.

---

1. Introduction

During daytime, the main oxidants in the troposphere are OH radicals; at night, because there is no photochemical reaction in the troposphere, the concentration of OH radicals decreases sharply, NO₃ radicals and O₃ become the main oxidants,^1–3 and nocturnal chemistry develops with NO₃ and N₂O₅ as the center. NO₃ can react with a series of volatile organic compounds to degrade them.⁴ However, NO₃ can be directly converted into nitrate via a heterogeneous reaction or converted into N₂H₅ and then reacted with water or aerosol to be removed from the atmosphere, resulting in the removal of NO_x.⁵ Propadiene (CH₂=C=CH₂) has been measured in planetary atmospheres and in combustion.^6,7 In recent years, the reactions of NO₃ with unsaturated hydrocarbons have been a subject of many experimental investigations.^8–16 The reactions of NO₃ with many other small hydrocarbons have been poorly characterized. For instance, propadiene (C₃H₄) was generated as an intermediate during the combustion of saturated^17,18 and unsaturated^19–23 hydrocarbons. Much less information has been published for the reaction of NO₃ with propadiene. However, Grosjean et al.²⁴ measured the rate coefficients at 298 K for the reaction of NO₃ with C₃H₄ (3.39 × 10⁻¹⁵ cm³ per molecule per s in air). Moreover, Arrhenius exponential factor, activation energy and product distribution have not yet been identified for the reaction of NO₃ with C₃H₄. Previous investigations of the reactions of NO₃ with saturated hydrocarbons have indicated that the H-abstraction pathways dominate the reaction,²⁵ and the addition/elimination pathways dominate the reactions of NO₃ with unsaturated hydrocarbons at room temperature.^26–29 According to similar size and structure, the reaction of NO₃ with propadiene could be estimated to be similar to those of ethylene and propylene based on their similar size and structure. To date, no theoretical work has been reported on the reaction of NO₃ with propadiene. Thus, we decided to employ a theoretical investigation of the reaction of NO₃ with propadiene for two purposes: (i) to rationalize the reported experimental data and (ii) to put forward a point of mechanistic view for exhaustive NO₃-oxidation processes.

2. Computational methods

Gaussian09 (ref. 30) procedure was applied for the electronic structure investigation, which consist of the optimization of the structure and calculation of vibration frequency by employing the density functional theory (DFT) method B3LYP^31,32 with the 6-311++G(d,p) basis set for the species referring to the CH₂=C=CH₂ + NO₃ reaction. Intrinsic reaction coordinate (IRC) theory^33,34 computation was implemented to ensure that the related products and reactants are glossy linked to the transition states along the reaction path. The dynamics studies have indicated that DFT with the B3LYP functional supplies the most favorable compromise scheme for gaining precise barrier height. It could also precisely forecast low-level PES information of all the species reliably. Furthermore, the high-level energy correction was implemented at the CCSD(T)³⁵/cc-pVTZ level to determine the precision of the DFT results and compute the thermodynamic properties of barrier height (ΔE), enthalpy (ΔH) and Gibbs free energy (ΔG) at room temperature and standard atmospheric pressure. In this work, the total and individual rate coefficients of the CH₂=C=CH₂ + NO₃ reaction are computed in the temperature range of 200–3000 K by employing the RRKM theory.^36–39 The detailed calculated process is given in the ESI.†

3. Results and discussion

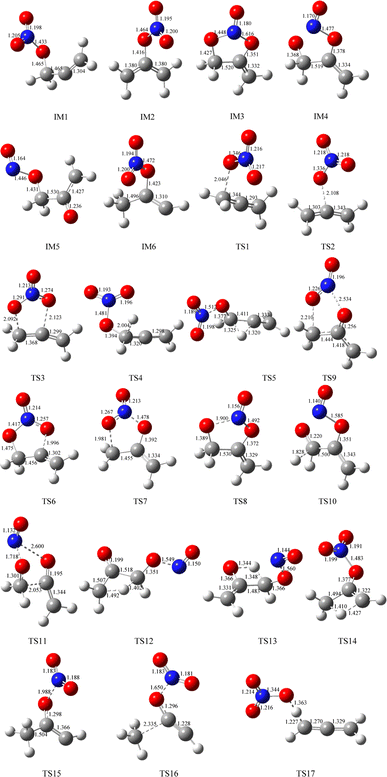
The geometric configurations of all the intermediates and transition states are depicted in Fig. 1. Fig. 2 displays the configurations for all the reactants and products. The potential energy surface (PES) for the CH₂=C=CH₂ + NO₃ reaction is described in Fig. 3. The zero-point correction energy (ZPE), and the relative energy, enthalpy, Gibbs free energy and the data of the T₁-diagnosis obtained at the CCSD(T)//B3LYP level are listed in Table 1. The moment of inertia and the harmonic vibrational frequencies, and the Cartesian coordinates for intermediates and transition states obtained at the B3LYP/6-311++G(d,p) level are summarized in Tables S1 and S4.†

Fig. 1 Optimized geometries including all intermediates and transition states on the PESs computed at the B3LYP/6-311++G(d, p) level for the CH₂=C=CH₂ (propadiene) + NO₃ system. The bond lengths are given in angstroms.

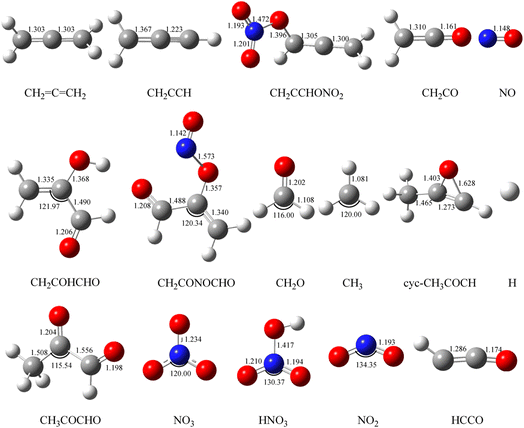Fig. 2 Optimized geometries of all reactants and products on the PESs computed at the B3LYP/6-311++G(d, p) level for the CH₂=C=CH₂ (propadiene) + NO₃ system. The bond lengths are given in angstroms.

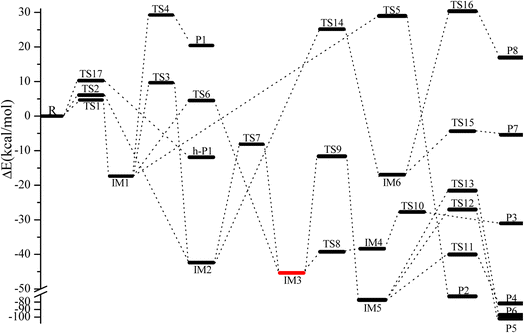Fig. 3 Energy profile of the CH₂=C=CH₂ + NO₃ reaction at the CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) level.

Table 1 Zero Point Energies (ZPE) without scaling factor, T₁ diagnostic values, relative Energies (ΔE), relative enthalpies (ΔH) and Gibbs free energy (ΔG) for the species involved in the CH₂=C=CH₂ + NO₃ reaction (energies in kcal mol⁻¹)

Species	ZPE	T1	ΔE	ΔH	ΔG	Gibbs activation enegries
CH2=C=CH2+NO3	41.17	0.012	0.00	0.00	0.00
		0.023
IM1	45.68	0.028	−17.37	−17.02	−6.36
IM2	45.19	0.025	−42.38	−40.52	−29.40
IM3	46.57	0.028	−45.34	−43.60	−31.43
IM4	45.16	0.326	−38.36	−36.57	−25.71
IM5	45.14	0.026	−77.37	−72.87	−62.52
IM6	45.30	0.028	−16.93	−16.57	−5.64
TS1	43.69	0.033	4.66	3.68	13.68	13.68
TS2	43.23	0.038	5.37	4.47	14.53	14.53
TS3	43.98	0.029	9.67	8.04	18.94	25.30
TS4	39.82	0.033	29.25	26.69	37.29	43.65
TS5	42.20	0.026	28.97	26.16	37.12	43.48
TS6	44.77	0.044	4.54	2.92	15.14	21.50
TS7	44.86	0.045	−8.14	−9.11	3.72	33.12
TS8	45.52	0.032	−39.25	−38.10	−25.54	5.89
TS9	43.00	0.038	−11.64	−11.41	−1.16	30.27
TS10	39.28	0.026	−27.70	−26.24	−15.88	9.83
TS11	42.25	0.028	−40.02	−37.57	−27.94	34.58
TS12	40.64	0.025	−27.02	−25.70	−15.47	47.05
TS13	41.70	0.027	−21.52	−20.85	−10.00	52.52
TS14	41.89	0.031	25.14	22.38	33.88	62.28
TS15	43.32	0.047	−4.36	−4.53	5.16	10.80
TS16	41.11	0.043	30.33	28.46	37.00	42.64
TS17	39.63	0.036	10.25	9.24	18.20	18.20
P1: (CH2CCHONO2 + H)	39.09	0.018	20.41	20.82	24.27
P2: (CH2CHCHO + NO2)	43.84	0.015	−72.60	−72.81	−73.17
P3: (CH2CONOCHO + H)	38.63	0.020	−33.39	−32.82	−29.28
P4: (CH2CO + CH2O + NO)	39.23	0.016	−84.51	−83.24	−94.46
		0.015
		0.025
P5: (CH3COCHO + NO)	43.25	0.015	−105.69	−105.37	−106.24
		0.025
P6: (CH2COHCHO + NO)	43.70	0.015	−99.42	−99.31	−99.18
		0.015
P7: (CH3COCH + NO2)	41.46	0.016	−5.39	−4.91	−6.60
		0.024
P8: (CH3+HCCO + NO2)	35.83	0.008	16.95	18.72	6.39
		0.024
		0.024
h-P1: (CH2CCH + HNO3)	42.20	0.035	−11.90	−11.93	−12.42
		0.018

---

3.1 Mechanism of the propadiene + NO₃ reaction

There exist two identical C=C bonds and one type of C–H bond in CH₂=C=CH₂ molecules. Here, we will research the pathways of NO₃-addition to the C=C bond and the H-extraction from the C–H bonds in detail.

As revealed in Fig. 1, the NO₃-association could react via two unequal reaction channels owing to the difference of the carbon atom in the C=C bond of CH₂=C=CH₂ molecules. The NO₃–C₃H₄ adduct isomers can be generated via NO₃ addition to α-C atom and β-C atom of CH₂=C=CH₂ via TS1 and TS2, respectively, as depicted in Fig. 1. The corresponding intermediates are denoted as IM1 (CH₂ONO₂CCH₂) and IM2 (CH₂CONO₂CH₂). In TS1 and TS2, the reactive C–O bonds are 2.046 and 2.108 Å, respectively. The energy of TS1 is 0.71 kcal mol⁻¹ lower than that of TS2, suggesting that the α-C-association is superior to the β-C-association. In addition, IM1 could rearrange as IM2 needing to overcome 27.04 kcal mol⁻¹ barrier via an annular transition state TS3, which is 5.01 kcal mol⁻¹ higher than TS1, indicating that this interconversion process might contribute less to the CH₂=C=CH₂ + NO₃ reaction. IM1 and IM2 are activated C-centered radicals, which are 17.37 and 42.38 kcal mol⁻¹ more stable than NO₃ + CH₂CCH₂. IM1 and IM2 in the atmosphere are possibly subject to unimolecular isomerization/elimination and decomposition processes to generate final products, and will be explicated in the following discussion.

As shown in Fig. 3, IM1 (CH₂ONO₂CCH₂) is subject to two decomposition and addition/elimination pathways. TS4 involves the direct cleavage of the C–H bond to generate P1 (CHONO₂CCH₂ + H), and TS5 refers to the 1,2-H shift associated with the scission of the O–N bond to generate P2 [propionaldehyde (CH₂=CHCHO) + NO₂]. This pathway of IM1 → TS4 → P1 is endothermic by 20.82 kcal mol⁻¹ and IM1 → TS5 → P2 is exothermic by 72.81 kcal mol⁻¹, and the barriers for these two processes are as high as 46.62 and 46.34 kcal mol⁻¹, which may be excluded.

The adding of the O atom to the center-C atom of IM1 via TS6 or to the terminal-C atom of IM2 via TS7 could generate the five-center ring intermediate IM3, which lies 45.34 kcal mol⁻¹ below the initial reactants. This cyclic association channel through TS6 and TS7 needs to surmount 21.91 or 34.24 kcal mol⁻¹ barriers. Subsequently, the open-chain adducts IM4 and IM5 from IM3 are generated via TS8 and TS9, which lie 39.25 and 11.64 kcal mol⁻¹ below the reactants CH₂=C=CH₂ + NO₃. The barriers of IM3 → TS8 → IM4 or IM3 → TS9 → IM5 processes are 6.09 and 33.70 kcal mol⁻¹, respectively, and these two processes are exothermic by 36.57 and 72.87 kcal mol⁻¹. IM4 and IM5 with internal energies of 38.36 and 77.37 kcal mol⁻¹ could experience one decomposition channel for IM4 and three decomposition channels for IM5. A simple C–H bond in IM4 could be easily cracked to generate P3 (CH₂CONOCHO + H) via TS10 surmounting to 10.66 kcal mol⁻¹ barrier. The IM4 → P3 (CH₂CONOCHO + H) rearrangement is exothermic by 3.75 kcal mol⁻¹.

Starting from IM5, there are three probable decomposition pathways resulting in three different products. The dissociation of IM5 via a simple transition state TS11 directly fracturing C–C and O–N bonds at the same time generates P4 (CH₂CO + CH₂O + NO) by surmounting 37.35 kcal mol⁻¹ barrier (Fig. 3). This IM5 → TS11 → P4 is exothermic by 83.24 kcal mol⁻¹. The second pathway begins with a 1,3-H shift from the C atom in the –CH₂ONO group to the other terminal-C atom in IM5, accompanied by the –NO group leaving away to generate P5 (CH₃COCHO + NO). This stepwise channel goes through a HCCC four-centered ring structure TS12 with 50.35 kcal mol⁻¹ barrier height. The third channel is to generate the P6 (CH₂COHCHO + NO) via a HCCO four-centered ring structure TS13 overcoming a barrier of 55.85 kcal mol⁻¹. The order of the barrier heights for the above-mentioned three decomposition pathways is TS11 (37.35 kcal mol⁻¹) < TS12 (50.35 kcal mol⁻¹) < TS13 (55.85 kcal mol⁻¹). Therefore, the most significant pathway from IM5 is generating P4 (CH₂CO + CH₂O + NO).

The pathways from IM2 (CH₂CONOCH₂) begin with one of the H atom in the –CH₂ group shifting to the other C atom in the –CH₂ group via an HCCC four-center transition state TS14 leading to the intermediate IM6 surmounting a barrier of 67.52 kcal mol⁻¹. In TS14, the length of the fracturing and generating C–H bonds are 1.410 and 1.427 Å, respectively. The internal energy of IM6 will be at least 16.93 kcal mol⁻¹, which will quickly dissociate through TS15 by cleavage of the O–N bond to generate P7 (CH₃COCH + NO₂), or through TS16 by cleavage of the C–C and O–N bonds simultaneously to generate P8 (CH₃ + HCCO + NO₂). The length of the fracturing O–N bond in TS15 is 1.988 Å, and that of the fracturing C–C and O–N bonds in TS16 is 2.335 and 1.650 Å. The barrier heights of IM6 → TS15 → P7 and IM6 → TS16 → P8 are 12.57 and 47.26 kcal mol⁻¹, respectively. Therefore, the pathway of generation of P7 (CH₃COCH + NO₂) from IM6 may be significant to the NO₃ + CH₂=C=CH₂ reaction. However, the high isomerization barrier of IM2 → TS14 → IM6 prevents the generation of the P7 pathway from taking place.

Only one H-extraction channel is discovered for the CH₂=C=CH₂ + NO₃ reaction. The oxygen atom of NO₃ could extract the H atom in the –CH₂ group of CH₂=C=CH₂ through TS17 to generate h-P1 (CH₂CCH + HNO₃), and the H-extraction is exothermic by 11.93 kcal mol⁻¹. The barrier of the H-extraction is 10.25 kcal mol⁻¹, which is 5.59 and 4.88 kcal mol⁻¹ higher than that of TS1 and TS2, respectively. Thus, the H-extraction pathway is less competitive than the addition/elimination pathway for the CH₂=C=CH₂ + NO₃ reaction.

3.2 Dynamic calculation

The rate coefficient of the cardinal addition/elimination pathways was computed within the temperature scope of 200–3000 K (see Table 2). The corresponding data of the rate coefficients for IM1 (k_IM1), IM2(k_IM2), IM3(k_IM3), IM4(k_IM4), P3(k_P3) and total rate coefficients (k_tot = k_IM1+ k_IM2+ k_IM3+ k_IM4+ k_P3) are described in Fig. 4. Fig. 5 draws the branching ratio for the generation of IM1-IM4, and P3, respectively. As represented in Fig. 4, our computed total rate constant at 298 K is 3.34 × 10⁻¹⁵ cm³ per molecule per s for the CH₂=C=CH₂ + NO₃ reaction, which matches well with the experimental data of 3.39 × 10⁻¹⁵ cm³ per molecule per s, implying that our computations are credible. k_IM1, k_IM2, k_IM3 and k_IM4 first increase and then decrease along with the increasing temperature. k_P3 and k_tot have positive temperature dependence. Fig. 5 reveals that the pathway of passing through the complex IM1 is more preponderant to the CH₂=C=CH₂ + NO₃ reaction between 200 and 1200 K, while the generation of P3 controls the entire reaction at T > 1200 K. In the entire temperature range, k_IM3 and k_IM4 have less weight to the CH₂=C=CH₂ + NO₃ reaction.

Table 2 The total and individual rate constants for generation of IM1, IM2, IM3, IM4, and P3 at 200–3000 K, as well as experimental value for the title reaction

T/K	kIM1	kIM2	kIM3	kIM4	kP3	ktot	k^refexp
200	1.48 × 10^−16	7.93 × 10^−18	9.77 × 10^−27	5.01 × 10^−27	4.02 × 10^−26	1.56 × 10^−16
250	8.63 × 10^−16	8.30 × 10^−17	5.44 × 10^−25	3.14 × 10^−25	5.94 × 10^−24	9.46 × 10^−16
298	2.93 × 10^−15	4.12 × 10^−16	1.19 × 10^−23	7.35 × 10^−24	2.7 × 10^−22	3.34 × 10^−15	3.39 × 10^−15
300	3.06 × 10^−15	4.36 × 10^−16	1.34 × 10^−23	8.25 × 10^−24	3.11 × 10^−22	3.50 × 10^−15
400	1.76 × 10^−14	4.11 × 10^−15	1.51 × 10^−21	9.7 × 10^−22	1.07 × 10^−19	2.17 × 10^−14
500	5.82 × 10^−14	1.83 × 10^−14	4.17 × 10^−20	2.58 × 10^−20	6.61 × 10^−18	7.65 × 10^−14
600	1.42 × 10^−13	5.46 × 10^−14	4.91 × 10^−19	2.78 × 10^−19	1.43 × 10^−16	1.97 × 10^−13
700	2.87 × 10^−13	1.28 × 10^−13	3.31 × 10^−18	1.68 × 10^−18	1.53 × 10^−15	4.17 × 10^−13
800	5.06 × 10^−13	2.55 × 10^−13	1.48 × 10^−17	6.72 × 10^−18	1.00 × 10^−14	7.71 × 10^−13
900	7.99 × 10^−13	4.53 × 10^−13	4.85 × 10^−17	1.98 × 10^−17	4.48 × 10^−14	1.30 × 10^−12
1000	1.14 × 10^−12	7.36 × 10^−13	1.24 × 10^−16	4.58 × 10^−17	1.50 × 10^−13	2.03 × 10^−12
1200	1.80 × 10^−12	1.58 × 10^−12	4.71 × 10^−16	1.46 × 10^−16	8.77 × 10^−13	4.26 × 10^−12
1400	2.13 × 10^−12	2.72 × 10^−12	1.10 × 10^−15	2.88 × 10^−16	2.94 × 10^−12	7.79 × 10^−12
1600	2.07 × 10^−12	3.86 × 10^−12	1.93 × 10^−15	4.35 × 10^−16	7.03 × 10^−12	1.30 × 10^−11
1800	1.8 × 10^−12	4.70 × 10^−12	2.85 × 10^−15	5.58 × 10^−16	1.36 × 10^−11	2.01 × 10^−11
2000	1.48 × 10^−12	5.09 × 10^−12	3.76 × 10^−15	6.51 × 10^−16	2.29 × 10^−11	2.95 × 10^−11
2200	1.20 × 10^−12	5.04 × 10^−12	4.57 × 10^−15	7.08 × 10^−16	3.45 × 10^−11	4.07 × 10^−11
2400	9.63 × 10^−13	4.69 × 10^−12	5.14 × 10^−15	7.27 × 10^−16	4.67 × 10^−11	5.24 × 10^−11
2600	7.73 × 10^−13	4.13 × 10^−12	5.35 × 10^−15	7.07 × 10^−16	5.72 × 10^−11	6.21 × 10^−11
2800	6.15 × 10^−13	3.49 × 10^−12	5.19 × 10^−15	6.50 × 10^−16	6.40 × 10^−11	6.81 × 10^−11
3000	4.8 × 10^−13	2.83 × 10^−12	4.71 × 10^−15	5.65 × 10^−16	6.58 × 10^−11	6.91 × 10^−11

---

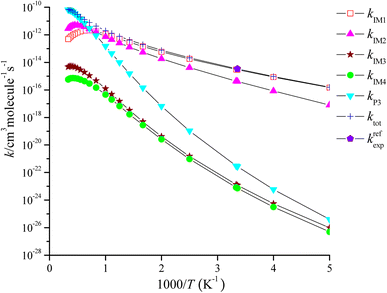Fig. 4 Temperature dependence of the total and individual rate constants for the CH₂=C=CH₂ + NO₃ reaction at 760 Torr N₂.

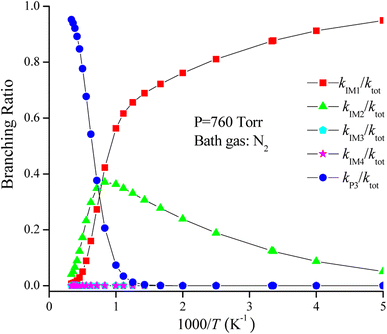Fig. 5 Branching ratios of the important product channels for the CH₂=C=CH₂ + NO₃ reaction in the temperature range of 200–3000 K.

The high-pressure limit rate coefficients denoted as k_inf are computed at P = 10¹⁰ Torr, as depicted in Fig. 6. k_inf(IM1), k_inf(IM2), k_inf(IM3) and k_inf(IM4) for the pathway through IM1-IM4 and k_inf(P3) for the dissociation of IM4 reveal with positive temperature dependence. The pathway through IM1 takes over the CH₂=C=CH₂ + NO₃ reaction, and the pathway through IM2 contributes to the title reaction, while the generation of other product channels could be ruled out. The fitting of the total high-pressure limit rate coefficients is represented as follows:

k_inf(tot)/(cm³ per molecule per s) = 2.02 × 10⁻⁷T^−0.70 exp(−6908.55/T) (200 ≤ T ≤ 3000 K)

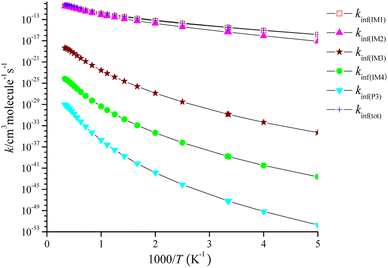Fig. 6 High-pressure limit rate constants for the CH₂=C=CH₂ + NO₃ reaction in the temperature range of 200–3000 K at 10¹⁰ Torr N₂.

Significantly, the tunneling effect was not taken into account in the above-mentioned dynamic computations. Due to the significant energy barriers in each reaction channel and the good separation of the addition and abstraction energy barriers, the rate constant mainly decided by the individual barrier height. Furthermore, there are several difficulties that prevent us from correcting the tunneling effect. Most of all, no suitable method was used to deal with the tunneling effect in our multichannel RRKM calculation. The one-dimensional tunneling effect method is often certificated to be qualitatively incorrect.⁴⁰ Other semi-classical approximations, for example, the small curvature tunnel (SCT) and large curvature tunnel (LCT) exploited by Truhlar et al.,^41,42 might be appropriate. Unfortunately, these methods are too complex to be used in our multi-channel RRKM program.

To check the reliability of such a simplification, we estimated the tunneling effect qualitatively. An asymmetric Eckart potential⁴³ was used to calculate the tunneling factor κ(T). For the addition mechanism, κ(T) was always in the range 1.2–1.0 from 200 to 3000 K. Therefore, the tunneling effect cannot influence our kinetic calculations significantly.

3.3 Subsequent reaction of IM1 and IM2 with O₂ and NO

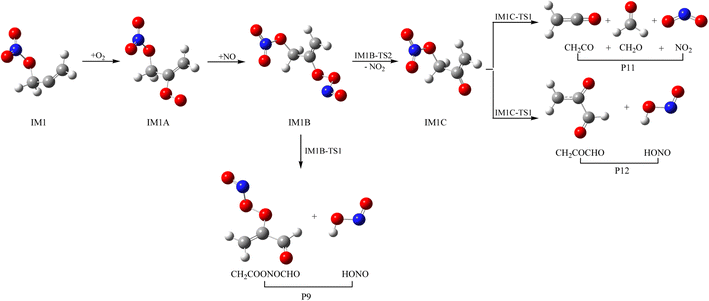
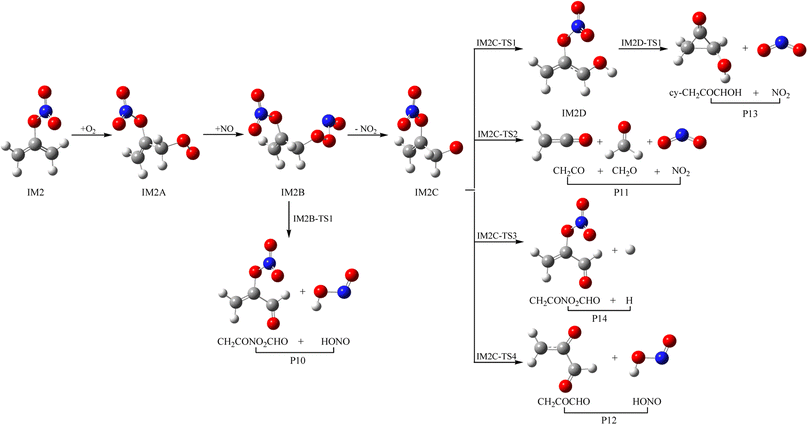
As a kind of high activity and open shell radical, IM1 and IM2 could react quickly with O₂ to generate organic peroxy adducts IM1A and IM2A, which are barrier-free with exothermicity of 94.93 and 93.92 kcal mol⁻¹, respectively (see Fig. 7, 8 and Table S2†). IM1A and IM2A will react instantly with omnipresent NO to generate IM1B and IM2B, which released 120.46 and 118.29 kcal mol⁻¹ of heat. IM1B and IM2B could directly decompose to P9 (CH₂COONOCHO + HONO) and P10 (CH₂CONO₂CHO + HONO) through IM1B-TS1 and IM2B-TS1 with the barrier of 41.43 and 26.24 kcal mol⁻¹. In addition, IM1B and IM2B could also experience unimolecular splitting through the direct scission of the O–O bond resulting in IM1C + NO₂ through IM1B-TS2 for IM1B, and leading to IM2C + NO₂ with no barrier for IM2B, respectively. IM1C could generate P11 (CH₂CO + CH₂O + NO₂) and P12 (CH₂COCHO + HONO) through IM1C-TS1 and IM1C-TS1 with barriers of 37.51 and 40.73 kcal mol⁻¹. IM2C are activated radicals, and their further reactions are ineluctable. There exist one rearrangement and three decomposition channels for IM2C. IM2C could isomerize to IM2D via the 1,2-H shift transition state IM2C-TS1 surmounting a barrier of 26.77 kcal mol⁻¹. IM2D, with an internal energy of 126.52 kcal mol⁻¹, could decompose to final products P13 (cy-CH₂COCHOH + NO₂) via IM2D-TS1 with a barrier of 17.28 kcal mol⁻¹. Moreover, IM2C could also directly decompose to products P11 (CH₂CO + CH₂O + NO₂), P14 (CH₂CONO₂CHO + H) and P12 (CH₂COCHO + HONO) via IM2C-TS2, IM2C-TS3 and IM2C-TS4 with barriers of 25.90, 24.06 and 30.14 kcal mol⁻¹, respectively.

Fig. 7 Schemes for IM1 with O₂ and NO reaction.

Fig. 8 Schemes for IM2 with O₂ and NO reaction.

3.4 Atmospheric effects

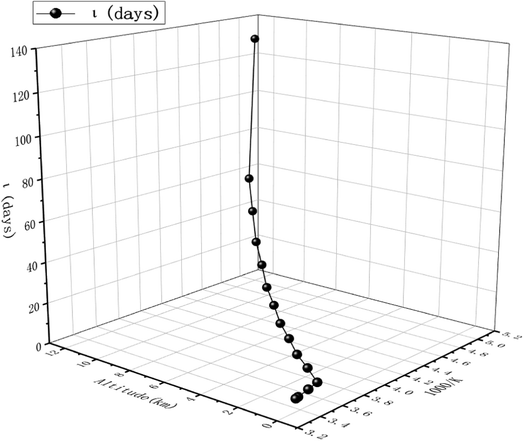
The obtained dynamics results were used to estimate the atmospheric lifetime of propadiene in the troposphere. The tropospheric lifetime (τ) of propadiene can be assessed by hypothesizing that its elimination from the troposphere takes place via the reaction with NO₃ radicals. The gained rate constant data are helpful to better define the tropospheric lifetime.⁴⁴ Natural and man-made pollutants in the atmosphere may cause environmental hazards such as acid rain, photochemical smog and ozone layer degradation.⁴⁵ Thus, it is significant to understand the residence time of these species in the atmosphere and their degradation mechanism in the tropospheric lifetime of propadiene with NO₃ radicals. The atmospheric lifetime was estimated using the following formula:
where k_NO3 is the rate coefficient of the reaction of propadiene with NO₃ radicals at 298 K as 3.34 × 10⁻¹⁵ cm³ per molecule per s. The lifetime of propadiene at CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) level of theory was estimated to be τ_NO3 ≈ 6.08 days at 298 K using the average atmospheric concentration of NO₃ (5.70 × 10⁸ molecule per cm³).⁴⁶ In the altitude range of 0–12 km and temperature range of 200–298 K, the estimated atmospheric lifetimes of propadiene were 130.16–6.08 days. As shown in Fig. 9 and Table S3,† the lifetime increased with the increase in altitude under the requirement of a constant NO₃ concentration (5.70 × 10⁸ molecule per cm³). Therefore, it degraded approaching the source of emission and the long-range transportation of propadiene was of non-ignorable importance.

Fig. 9 Atmospheric lifetime of CH₂=C=CH₂ at 217–298 K and an altitude of 0–12 km.

The global warming potentials (GWPs)^47,48 of propadiene to carbon dioxide (CO₂) were computed for further evaluation atmospheric implications. On account of the global lifetime (τ), intensities of the corresponding vibrational mode k (A_k) and the vibrational frequencies (v_k), we executed the following formula to compute the GWPs for propadiene:

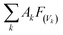is the radiative efficiency, and it is 0.0458 W m⁻² ppb⁻¹ for propadiene. AGWP represents the absolute global warming potential for CO₂.⁴⁹ The global warming potential (GWP) for propadiene (when the time horizon is 100 years) relative to CO₂ was predicted to be only 0.23 at 298 K, suggesting that the contribution of propadiene to the greenhouse effect is not significant.

4. Conclusion

The conversion mechanisms and environmental fate for the NO₃-initiated degradation of propadiene have been studied by the quantum chemistry method. Some concrete conclusions are summarized as follows:

(1) in the NO₃-induced oxidation procedure of propadiene, the NO₃-addition/elimination pathways are dominant rather than the H-abstraction pathway. The NO₃ radicals are more probable to attack the terminal-C atom than the central-C atom of propadiene. The primary product generated is P3 (CH₂CONOCHO + H).

(2) The computed k_tot value of propadiene reacting with NO₃ radicals is 3.34 × 10⁻¹⁵ cm³ per molecule per s under 298 K. The NO₃-addition/elimination channels occupy more predominate during the OH-induced procedure, of which the branching ratio accounts for 85.90%.

(3) At 298 K, the lifetime of propadiene degradation was assessed to be 6.08 days. The lifetime increased with the increase in altitude under the requirement of a constant NO₃ concentration.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the Natural Science Foundations of China (No. 21707062), Scientific Research Starting Foundation of Mianyang Normal University (No. QD2016A007), Science and Technology Project of Sichuan Province (2023NSFSC1119). Mianyang Normal University Graduate Innovation Practice Fund. Supported by the Open Project Program of Beijing Key Laboratory of Flavor Chemistr, Beijing Technology and Business University (BTBU), Beijing 100048, China.

References

1. U. Platt, A. M. Winer and H. W. Biermann, et al., Measurement of nitrate radical concentrations in continental air, Environ. Sci. Technol., 1984, 18, 365–369.
2. P. Warneck, Chemistry of the Natural Atmosphere, San Diego, Academic Press, 2nd ed., 2000.
3. N. Poisson, M. Kanakidou and B. Bonsang, et al., Global change science a revolutionary approach in climate change research, Chemosphere: Global Change Sci., 2001, 3(3), 353–366.
4. R. Atkinson, Atmospheric chemistry of VOCs and NO_X, Atmos. Environ., 2000, 34, 2063–2101.
5. B. J. Allan, N. Carslaw and H. Coe, et al., Observations of the Nitrate Radical in the Marine Boundary Layer, J. Atmos. Chem., 1999, 33, 129–154.
6. T. A. Cool, K. Nakajima and T. A. Mostefaoui, et al., Selective detection of isomers with photoionization mass spectrometry for studies of hydrocarbon flame chemistry, J. Chem. Phys., 2003, 119, 8356.
7. E. H. Wilson and S. K. Atreya, Current state of modeling the photochemistry of Titan's mutually dependent atmosphere and ionosphere, J. Geophys. Res., 2004, 109, E06002.
8. D. J. Stewart, S. H. Almabrok, J. P. Lockhart, O. M. Mohamed, D. R. Nutt, C. Pfrang and G. Marston, The kinetics of the gas-phase reactions of selected monoterpenes and cyclo-alkenes with ozone and the NO₃ radical, Atmos. Environ., 2013, 70, 227–235.
9. H. J. Cao, X. Li, M. X. He and X. S. Zhao, Computational study on the mechanism and kinetics of NO₃-initiated atmosphere oxidation of vinyl acetate, Comput. Theor. Chem., 2018, 1144, 18–25.
10. R. A. Taccone, A. Moreno, I. Colmenar, S. Salgado, M. P. Martín and B. Cabañas, Kinetic study of the OH, NO₃ radicals and Cl atom initiated atmospheric photo-oxidation of iso-propenyl methyl ether, Atmos. Environ., 2016, 127, 80–89.
11. J. Kerdouci, B. Picquet-Varrault and J. F. Doussin, Structure-activity relationship for the gas-phase reactions of NO₃ radical with organic compounds: Update and extension to aldehydes, Atmos. Environ., 2014, 84, 363–372.
12. B. Wei, J. F. Sun, Q. Mei and M. X. He, Theoretical study on gas-phase reactions of nitrate radicals with methoxyphenols: Mechanism, kinetic and toxicity assessment, Environ. Pollut., 2018, 243, 1772–1780.
13. I. Colmenar, S. Salgado, P. Martín, I. Aranda, A. Tapia and B. Cabañas, Tropospheric reactivity of 2-ethoxyethanol with OH and NO₃ radicals and Cl atoms. Kinetic and mechanistic study, Atmos. Environ., 2020, 224, 117367.
14. I. Aranda, S. Salgado, P. Martín, F. Villanueva, E. Martínez and B. Cabañas, Atmospheric degradation of 3-ethoxy-1-propanol by reactions with Cl, OH and NO₃, Chemosphere, 2021, 281, 130755.
15. B. Yang, H. X. Zhang, Y. F. Wang, P. Zhang, J. Shu, W. Q. Sun and P. K. Ma, Experimental and theoretical studies on gas-phase reactions of NO₃ radicals with three methoxyphenols: Guaiacol, creosol, and syringol, Atmos. Environ., 2016, 125, 243–251.
16. N. Zhao, X. L. Shi, F. Xu, Q. Z. Zhang and W. X. Wang, Theoretical investigation on the mechanism of NO₃ radical-initiated atmospheric reactions of phenanthrene, J. Mol. Struct., 2017, 1139, 275–281.
17. C. S. McEnally and L. D. Pfefferle, Aromatic and Linear Hydrocarbon Concentration Measurements in a N.on-Premixed Flame, Combust. Sci. Technol., 1996, 116, 183–209.
18. P. Dagaut, M. Cathonnet and J. C. Boettner, Kinetic modeling of propane oxidation and pyrolysis, Int. J. Chem. Kinet., 1992, 24, 813–837.
19. K. H. Homann and H. Schweinfurth, Kinetics and Mechanism of Hydrocarbon Formation in the System C₂H₂/H, Ber. Bunsen-Ges. Phys. Chem., 1981, 85, 569–577.
20. S. D. Thomas, A. Bhargava, P. R. Westmoreland, R. P. Lindstedt and G. Skevis, Propene oxidation Chemistry in laminar Premixed Flames, Bull. Soc. Chim. Belg., 1996, 105, 501–512.
21. J. D. Bittner and J. B. Howard, Composition profiles and reaction mechanisms in a near-sooting premixed benzene/oxygen/argon flame, Symposium on Combustion, 1981, 18, 1105–1116.
22. J. A. Miller and C. F. Melius, Kinetic and thermodynamic issues in the formation of aromatic compounds in flames of aliphatic fuels, Combust. Flame, 1992, 91, 21–39.
23. M. Frenklach, S. Taki, M. B. Durgaprasad and R. A. Matula, Soot formation in shock-tube pyrolysis of acetylene, allene, and 1,3-butadiene, Combust. Flame, 1983, 54, 81–101.
24. D. Grosjean and E. L. Williams, Environmental persistence of organic compounds estimated from structure-reactivity and linear free-energy relationships. Unsaturated aliphatics, Atmos. Environ., Part A, 1992, 26, 1395–1405.
25. G. Bravo-Perez, J. R. Alvarez-Idaboy, A. Cruz-Torres and M. E. Ruiz, Quantum Chemical and Conventional Transition-Sate Theory Calculations of Rate Constants for the NO₃ + Alkane Reaction, J. Phys. Chem. A, 2002, 106, 4645–4650.
26. T. L. Nguyen, J. Park, K. Lee, K. Song and J. R. Barker, Mechanism and Kinetics of the Reaction NO₃ + C₂H₄, J. Phys. Chem. A, 2011, 115, 4894–4901.
27. R. Cartas-Rosado, J. R. Alvarez-Idaboy, A. Galano-Jimenez and A. Vivier-Bunge, A theoretical investigation of the NO₃ addition of the mechanism to alkenes, J. Mol. Struct.: THEOCHEM, 2004, 684, 51–59.
28. H. Bandow, M. Okuda and H. Akimoto, Mechanism of the gas-phase reactions of C₃H₆ and NO₃ radicals, J. Phys. Chem., 1980, 84, 3604.
29. S. Paul, R. Chandra Deka and N. Kishor Gour, Kinetics, mechanism, and global warming potentials of HFO-1234yf initiated by O₃ molecules and NO₃ radicals: insights from quantum study, Environ. Sci. Pollut. Res., 2018, 25, 26144–26156.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
31. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648.
32. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
33. C. Gonzalez and H. B. Schlegel, An improved algorithm for reaction path following, J. Chem. Phys., 1989, 90, 2154–2161.
34. C. Gonzalez and H. B. Schlegel, Reaction path following in massweighted internal coordinates, J. Phys. Chem., 1990, 94, 5523–5527.
35. K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, A ffth-order perturbation comparison of electron correlation theories, Chem. Phys. Lett., 1989, 157, 479–483.
36. K. A. Holbrook, M. J. Pilling, and S. H. Robertson, Unimolecular Reactions, Wiley, Chichester, 1996.
37. N. T. Hoa, L. T. N. Van and Q. V. Vo, Reactions of nicotine and the hydroxyl radical in the environment: Theoretical insights into the mechanism, kinetics and products, Chemosphere, 2023, 314, 137682.
38. J. R. Alvarez-Idaboy, N. Mora-Diez, R. J. Boyd and A. Vivier-Bunge, On the Importance of Prereactive Complexes in Molecule-Radical Reactions: Hydrogen Abstraction from Aldehydes by OH, J. Am. Chem. Soc., 2001, 123, 2018–2024.
39. A. Galano, J. R. Alvarez-Idaboy, M. E. Ruiz-Santoyo and A. Vivier-Bunge, Rate Coefficient and Mechanism of the Gas Phase OH Hydrogen Abstraction Reaction from Formic Acid: A Quantum Mechanical Approach, J. Phys. Chem. A, 2002, 106, 9520–9528.
40. D. H. Lu, D. Maurice and D. G. Truhlar, What is the effect of variational optimization of the transition state on .alpha.-deuterium secondary kinetic isotope effects? A prototype: CD₃H + H .dblarw. CD₃ + H₂, J. Am. Chem. Soc., 1990, 112, 6206–6214.
41. Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, Molecular modeling of the kinetic isotope effect for the [1,5]-sigmatropic rearrangement of cis-1,3-pentadiene, J. Am. Chem. Soc., 1993, 115, 2408.
42. Y. P. Liu, D. H. Lu, A. Gonzalez-Lafont, D. G. Truhlar and B. C. Garrett, Direct dynamics calculation of the kinetic isotope effect for an organic hydrogen-transfer reaction, including corner-cutting tunneling in 21 dimensions, J. Am. Chem. Soc., 1993, 115, 7806–7817.
43. H. S. Johnston and J. Heicklen, Tunnelling corrections for unsymmetrical eckart potentical energy barriers, J. Phys. Chem., 1962, 66, 532.
44. R. C. Deka and B. K. Mishra, Theoretical studies on kinetics, mechanism and thermochemistry of gas-phase reactions of HFE-449mec-f with OH radicals and Cl atom, J. Mol. Graphics Modell., 2014, 53, 23–30.
45. O. B. Gadzhiez, S. K. Ignatov, B. E. Krisyuk, A. V. Maiorov, S. Gangopathyay and A. E. Masunov, Quantum Chemical Study of the Initial Step of Ozone Addition to the Double Bond of Ethylene, J. Phys. Chem. A, 2012, 116, 10420.
46. R. Atkinson, Kinetics and mechanisms of the gas phase reactions of the NO₃ radical with organic compounds, J. Phys. Chem. Ref. Data, 1991, 20, 459–507.
47. P. Blowers, K. F. Tetrault and Y. Trujillo-Morehead, Global Warming Potential Predictions for Hydrofluoroethers, Theor. Chem. Acc., 2008, 119, 369–381.
48. S. Pinnock, M. D. Hurley, K. P. Shine, T. J. Wallington and T. J. Smyth, Radiative Forcing of Climate by Hydrochlorofluor-ocarbons and Hydrofiuorocarbons, J. Geophys. Res.: Atmos., 1995, 100, 23227–23238.
49. D. J. Wuebbles, Weighing Functions for Ozone Depletion and Greenhouse Gas Effects on Climate, Annu. Rev. Energy Environ., 1995, 20, 45–70.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02523c

---