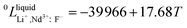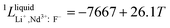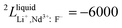Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental determination and thermodynamic optimization of the LiF-NdF3 system
ChunFa Liaoab,
ZanHui Fu ab,
LiangHua Queab,
Hao Tangab and
Xu Wang*ab
ab,
LiangHua Queab,
Hao Tangab and
Xu Wang*ab
aFaculty of Materials Metallurgy and Chemistry, Jiangxi University of Science and Technology, Ganzhou 341000, China. E-mail: sci_rech@163.com
bNational Rare Earth Functional Materials Innovation Center, Ganzhou 341000, China
First published on 11th August 2023
Abstract
Neodymium is mainly obtained by electrolysis of a molten LiF-NdF3-Nd2O3 system. LiF-NdF3 is a basic system, and the phase diagram of this system provides important information in the production of electrolytic neodymium. An accurate LiF-NdF3 binary phase diagram helps in the selection of the appropriate molten salt component in production and optimizing the production process, which is of great significance to improve the electrolysis efficiency and reduce the production cost. To obtain an accurate phase diagram of the LiF-NdF3 binary system, liquidus and solidus temperatures were experimentally determined in the LiF-NdF3 binary system by differential scanning calorimetry. The experimental results were used to construct the phase diagram and develop a new database for the LiF-NdF3 system using the FactSage software. The sub-regular solution model was used to describe the excess Gibbs free energy of the liquid phase, and the thermodynamic optimization calculation was carried out for the binary system. The binary interaction coefficients 0L = −39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 966 + 17.68 T, 1L = −7667 + 26.1 T, and 2L = −6000 were used to describe the system's excess Gibbs free energy. The results show that the eutectic point of the system is 68.4% LiF-31.6% NdF3 at 731.5 °C. The effects of industrial and high purity NdF3 and the presence of Nd2O3 on the liquidus temperature of the LiF-NdF3 system were also investigated, high liquidus temperatures have been observed in tests using industrial NdF3 and NdF3 feedstock that contains a specific quantity of Nd2O3.
966 + 17.68 T, 1L = −7667 + 26.1 T, and 2L = −6000 were used to describe the system's excess Gibbs free energy. The results show that the eutectic point of the system is 68.4% LiF-31.6% NdF3 at 731.5 °C. The effects of industrial and high purity NdF3 and the presence of Nd2O3 on the liquidus temperature of the LiF-NdF3 system were also investigated, high liquidus temperatures have been observed in tests using industrial NdF3 and NdF3 feedstock that contains a specific quantity of Nd2O3.
1. Introduction
Neodymium is a metal that is widely used in the field of key rare-earth functional materials, such as NdFeB magnetic materials, rare-earth alloys, and rare-earth hydrogen-storage materials.1,2 The main preparation method is molten salt electrolysis, and the electrolytic system mainly includes chloride and fluoride salt systems. The fluorine salt system is currently used for industrial production. In the molten salt electrolysis process, rare-earth fluoride is the electrolyte, and rare-earth oxide is electrolytic raw material. Currently, REF3-LiF and REF3-LiF-BaF2 electrolyte systems are commonly used.3,4 The solubility and eutectic temperature of rare-earth oxides in the REF3-LiF molten salt system are the key factors affecting electrolytic neodymium's production process.5 Research into phase diagrams can provide many useful pieces of information for developing new materials: Fedrov et al.6 reviewed lithium rare-earth fluorides as photonic materials, citing many phase diagrams that can provide theoretical guidance for optimizing production processes. The construction methods of phase diagrams mainly include the experimental determination method7 and the CALPHAD phase diagram calculation method.8,9 A large amount of experimental data is required to determine phase diagrams, and the accuracy of the phase diagram is greatly affected by the purity of the raw materials, as well as the accuracy of the analysis and experimental operation, which means that it has the disadvantages of a large workload and requires a high level of manpower, large quantities of materials, and substantial financial resources. Phase diagrams are difficult to determine through experiments only, and thermodynamic calculations of phase diagrams are often limited by a lack of accurate thermodynamic data. Experimental and thermodynamic data on the LiF-NdF3 system's binary phase diagrams are lacking, with Thoma data and Xue data among the few experimental data found so far. Marcelle Gaune-Escard et al.10 analyzed the enthalpy of mixing NdF3-MF (M = Li, Na, K) binary systems data using the Hoch–Arpshofen solution model, and with the development of CALPHAD phase diagram calculation technology, the construction of phase diagrams by combining experimental determination with phase diagram calculation has been widely adopted by scientific and technological workers.11,12Thoma et al.13 studied the phase diagram of LiF-NdF3 by thermal analysis experiments; however, the raw NdF3 material used in the experiments was prepared from the transformation of rare-earth oxide, which had a high level of rare-earth oxide (300 ppm). Nd2O3 in the raw material had considerable influence on the measurement result of liquidus temperatures. In terms of phase diagram calculation, Van der Meer et al.14 calculated the NdF3-LiF binary phase diagram by using the CALPHAD method and ChemSage software. They used the Redlich–Kister polynomial to describe the excess free energy of the liquid phase based on the literature experimental data.13 The calculated phase diagram is consistent with the experimental phase diagram in literature.13 M. Berkani et al.15 calculated the LiF-NdF3 binary phase diagram by thermal analysis and the Hoch–Arpshofen model. A. Abbasalizadeh et al.16 conducted experimental research and thermodynamic modeling on the LiF-NdF3-DyF3 ternary system, as well as Gibbs free energy modeling of the LiF-NdF3 and LiF-DyF3 systems by using the literature data.13 The phase diagram of the LiF-NdF3 binary system was calculated by the CALPHAD method. Xue et al. used DTA analysis to measure the liquidus temperature of the NdF3-LiF binary system at various compositions,17 drew the experimental phase diagram according to the results of the DTA, and finally optimized the LiF-NdF3 binary phase diagram according to CALPHAD calculation; however, the experimental materials used were all industrial grade with impurities. The peak temperature of the DTA curve was considered the result of liquidus temperature, and the optimized phase diagram of the LiF-NdF3 binary system obtained by this method still requires further discussion. Johnathon C. Ard et al.18 assessed and then reassessed the thermodynamics of 30 pseudo-binary and ternary salt systems, assessed the LiF-NdF3 binary phase diagram by modified quasi-chemical model in the quadruplet approximation with the data from literature,13 and determined relations for the liquid interaction parameters, and the phase diagram was in good agreement with literature.13 Regarding for the bivariate phase diagram of LiF-NdF3 that was previously described, the experimental method measured the phase diagrams,13,17 however, the raw material used in the ref. 17 experiment is industrial level, and its phase diagram is only suitable for guiding production. The other is a phase diagram that was calculated using experimental data found in literature.13 Additionally, the experimental NdF3 material utilized in ref. 13 is not high pure, which will significantly affect the experiment's results. For the purpose of obtaining more accurate phase diagram and thermodynamic data, this research combines the phase diagram calculation technique with higher purity raw materials to measure the solidus and liquidus temperature. Thermodynamic data consistent with the phase diagram can provide basic data for the study of the LiF-NdF3-Nd2O3 ternary phase diagram, which has important practical significance and economic value for optimizing the rare earth neodymium production process, improving current efficiency and reducing production costs. Therefore, differential scanning calorimetry was used to investigate the liquidus and solidus temperatures of the LiF-NdF3 system with different components. FactSage software was employed to calculate and optimize the phase diagram of the LiF-NdF3 molten salt system. The thermodynamic parameters of the system were optimized, and an accurate LiF-NdF3 phase diagram was constructed by combining the experiment with the CALPHAD method.
2. Experimental methods
2.1. Thermal analysis experiment
Raw materials for thermal analysis experiment: LiF, NdF3 and Nd2O3with purity ≥ 99.99% were obtained from Shanghai Macklin Biochemical Technology Co., Ltd. Industrial grade NdF3 obtained from Nanjing Chemical Reagent Co., Ltd.2.2. Phase diagram calculation
Based on the experimental phase diagram, the Gibbs freedom of the LiF-NdF3 system was calculated and optimized using the compound, solution, equilib, optisage, and phase diagram module of FactSage8.1 software. A new compound database and liquid phase database were created in the compound and solution modules, respectively. The interaction coefficient iL was optimized by the Bayesian optimization algorithm based on the probability model and constantly adjusted until the optimized phase diagram was in good agreement with the experimental phase diagram.19 The optimized thermodynamic data and optimized phase diagram of the system were obtained.3. Results and discussion
3.1. Experimental results and discussion of thermal analysis
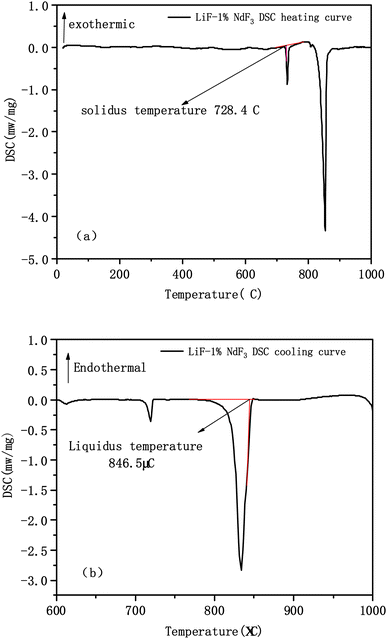
Table 1 shows the liquidus and solidus temperatures of the LiF-NdF3 molten salt system with different mass fractions tested experimentally. In accordance with the liquidus and solidus temperatures of the LiF-NdF3 system measured by thermal analysis, the experimental results show that, when the molar concentration of NdF3 is less than 31%, as the mole fraction of NdF3 in the system increases, the liquidus temperature of the LiF-NdF3 molten salt system gradually decreases. In addition, when the molar concentration of NdF3 is greater than 31%, as the increase in the mole fraction of NdF3 in the system increases, the liquidus temperature of the LiF-NdF3 system gradually increases. This finding shows that LiF can significantly reduce the liquidus temperature of the molten salt system, and with the increase in the mole fraction of NdF3, the liquidus temperature of the LiF-NdF3 system gradually increases mainly due to the high melting temperature of NdF3. The samples of different components have the same solidus temperature, which also indicates that the LiF-NdF3 system is a low eutectic system without the formation of intermediate compounds, which is consistent with the results of previous studies.
| No. | LiF mol% | NdF3 mol% | Liquidus temperature (°C) | Solidus temperature (°C) | Ref. |
|---|---|---|---|---|---|
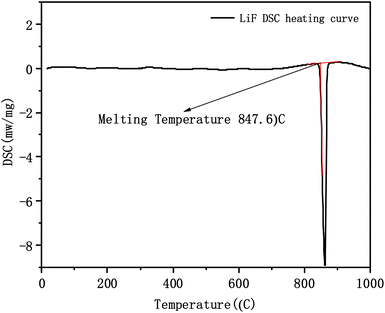
| 1 | 100 | 0 | 847.5 | 22 | |
| 2 | 99 | 1 | 846.5 | 728.4 | |
| 3 | 97 | 3 | 841.1 | 728.3 | |
| 4 | 95 | 5 | 832.6 | 727.1 | |
| 5 | 92 | 8 | 832.7 | 728.8 | |
| 6 | 90 | 10 | 821.8 | 726.1 | |
| 7 | 89 | 11 | 798.3 | 729.2 | |
| 8 | 84 | 16 | 793.6 | 728.2 | |
| 9 | 81 | 19 | 788.8 | 729.3 | |
| 10 | 77 | 23 | 776.9 | 729.7 | |
| 11 | 72 | 28 | 752.2 | 728.3 | |
| 12 | 69 | 31 | 734.6 | 729.1 | |
| 13 | 67 | 33 | 745.4 | 729.4 | |
| 14 | 66 | 34 | 751.1 | 728.4 | |
| 15 | 63 | 37 | 782.0 | 730.6 | |
| 16 | 60 | 40 | 790.5 | 724.4 | |
| 15 | 0 | 100 | 1374 | 22 |
Table 2 shows the regression equation, indicating that the intersection of the two fitted lines is the eutectic point of the LiF-NdF3 system. After calculation, the eutectic temperature of the system is 736.6 °C, and the eutectic components are divided into 68.62% LiF-31.38% NdF3.
| Range (mol%) | Fitted equation |
|---|---|
| a Note: Y—liquidus temperature (°C); C—mole fraction of NdF3. | |
| xNdF3 > 31% | Y = 577.59 + 374.2858 × C + 422.1014 × C2 |
| xNdF3 ≤ 31% | Y = 848.59 − 287.4729 × C − 220.8428 × C2 |
3.2. LiF-NdF3 phase diagram calculation and thermodynamic optimization
| G(T) = H(T) − S(T)T | (1) |
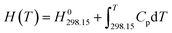 | (2) |
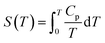 | (3) |
Cp function can be obtained by the fitting group experimental data:
| Cp = a + bT + cT−2 | (4) |
In the LiF-NdF3 binary molten salt system, the pure components are LiF and NdF3, the crystal structures are shown in Table 3, and the Gibbs free energy for pure components can be expressed as a function of temperature, as follows:
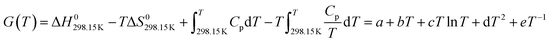 | (5) |
| Phase | Space groups | Crystal structure | Descriptive model |
|---|---|---|---|
| Liquid | — | — | [LiF, NdF3] |
| LiF | Fm3m | Cubic | LiF |
| NdF3 | P6c2 | Hexagonal | NdF3 |
| Phase | ΔH298.15 kJ mol−1 | S298.15 J mol−1 K−1 | Temperature, K | Cp J mol−1 K−1 |
|---|---|---|---|---|
| LiF (solid) | −616.931 | 35.65 | 298.15–1121.3 | Cp = 42.69 + 14.41 × 10−3 T − 5.30 × 105 × T−2 |
| LiF (liquid) | −594.58 | 43.00 | 1121.3–1900 | 64.183 |
| NdF3 (solid) | −1679.458 | 120.792 | 298.15–1650 | Cp = 92.697 + 23.43 × 10−3 × T − 6.456 × 105 × T−2 |
| NdF3 (liquid) | −1607.88 | 340.77 | 1650–1800 | Cp = 184.473 − 4.435 × 10−3 T − 119.244 ×105 × T−2 |
The most commonly used thermodynamic models for phase diagram calculation are the ideal solution, regular solution, compound energy, modified association models, as well as the modified quasi-chemical model in the quadruplet approximation.26 The regular solution model27 was proposed by Hildebrand in 1929, assuming the actual melt to be a replacement melt, and it is well simulated in some simple melt systems. The LiF-LuF3 molten salt systems (Lu = La, Ce, Pr, Nd, Sm, U and Pu) are all phase diagram systems with a low eutectic point without forming an intermediate, therefore, the thermodynamic LiF-NdF3 molten salt system can be described by the sub-regular solution model. Moreover, in the literature,15–17 the regular solution model was used to calculate the phase diagram of the LiF-NdF3 binary system.
For the liquid phase of the LiF-NdF3 binary system, the sub-regular solution model was used to describe the Gibbs free energy in the liquid phase. The Gibbs free energy is composed of pure-component mechanical mixing to Gibbs free energy, an ideal mixing contribution to Gibbs free energy, and excess Gibbs free energy.28–30 The expression is as follows:
| Gliquid = refGliquidm + idGliquidm + exGliquidm | (6) |
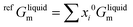 | (7) |
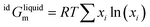 | (8) |
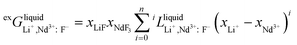 | (9) |
| iL = a + bT | (10) |
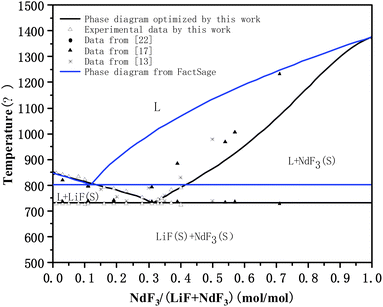 | ||
| Fig. 4 Comparison between optimized LiF-NdF3 binary phase diagram and experimental data. * The blue line was calculated directly by FactSage software, which was not optimized. | ||
Under the system's optimized thermodynamic data, the liquidus temperatures of each experimental component were calculated using the Equilib module in FactSage, with the maximum, minimum, and average deviations being 12.54 °C, −0.53 °C, and 3.28 °C, respectively. The eutectic temperature of the optimized phase diagram is 731.5 °C, and the eutectic point of the system is 68.4% LiF-31.6% NdF3. The result is very close to the intersection of the two fitted lines calculated in Section 3.1.2, showing that the calculated phase diagram is in good agreement with the experimental phase diagram. Moreover, describing the Gibbs free energy of the LiF-NdF3 molten salt system is feasible by using the sub-regular solution model. The calculated phase diagram is accurate and reliable.
Fig. 4 shows that the phase diagram obtained in this work (calculated directly by FactSage software (the blue line)) and the phase diagrams in the ref. 13 and 17 are all simple binary phase diagrams formed without intermediates. The liquidus trend is the same, but there are some differences. The eutectic point position and liquidus temperature at the low LiF side of the system are different. We also noticed that the obtained phase diagram was different from the literature,17 although the trend in the temperature of the liquids is consistent, and the composition of eutectics in this paper is 68.4% LiF-31.6% NdF3 and 77% LiF-23% NdF3 in literature.17 The difference might be caused by the equipment being tested, the purity of the raw materials, or other factors. At the same time, the final result may be slightly different because the phase diagram is optimized by different thermodynamic models. The phase diagram that calculated by FactSage directly is the phase diagram without thermodynamic evaluation and optimization, meaning it does not consider the influence of excess Gibbs free energy on the system. However, there is possibility of improvement in the FactSage LiF-NdF3 binary system database through the optimized thermodynamic data from the literature.
As is well known that NdF3 is primarily based on Nd2O3 as a raw material for fluorine conversion preparation, that its conversion rate is affected by the production process, that different production processes or requirements for purity are different, that its conversion rate will be different, and that for raw materials of industrial grade, it is typically believed that NdF3 purity must be greater than 99.0% to satisfy the requirements. To learn more about how various NdF3 raw materials affect the liquidus temperature of the LiF-NdF3 binary phase diagram, four comparison experiments were conducted using high-purity NdF3 (purity ≥ 99.99%) and industrial NdF3 (purity ≥ 99.0%) as the raw materials. Because the liquidus temperature of LiF-NdF3 obtained in this paper on the side with high NdF3 content is significantly lower than the data obtained in the literature.17 Table 6 displays the findings of the DSC test. According to the results of the experiments, when NdF3 is tested with industrial purity, the liquidus temperature is clearly higher than when NdF3 is tested with high purity raw material under the same conditions. The experiments show that when NdF3 is tested with industrial purity, for example, the industrial raw material tested this time had a liquidus temperature of 802.4 °C, which is almost identical to the 793.6 °C found in the literature17 for the LiF-31% mol NdF3 component. This discrepancy may be caused by the different raw material sources, though. The temperature of 734.6 °C that was tested using raw materials of high purity is substantially lower than both of the results.
| No. | Component | Liquidus temperature with high purity NdF3 (°C) | Liquidus temperature with industrial NdF3 (°C) |
|---|---|---|---|
| 1 | LiF-23% mol NdF3 | 776.9 | 805.0 |
| 2 | LiF-31% mol NdF3 | 734.6 | 802.4 |
| 3 | LiF-37% mol NdF3 | 782.0 | 797.6 |
| 4 | LiF-40% mol NdF3 | 790.5 | 798.2 |
Simultaneously, to demonstrate the influence of Nd2O3 impurities on the liquidus temperature of the LiF-NdF3 binary phase diagram, the liquidus temperature of the LiF-23% mol NdF3 system was 793.8 °C, 781.1 °C, and 803.0 °C after adding the mass fractions of Nd2O3 of 0.5%, 1.0%, and 2.0%, respectively. The experimental results demonstrate that, in comparison to the system without Nd2O3, the liquidus temperature of the LiF-NdF3 system rises with varied mass fractions of Nd2O3.
To sum up, on the low NdF3 side, the experimental data and optimized liquidus temperature in this work are basically consistent with those in ref. 13 and 17; however, on the low LiF side, the experimental data and optimized liquidus temperature obtained in this work are significantly lower than those in ref. 13 and 17, which may be related to the purity of the NdF3 used in the experiments mentioned above, because higher levels of Nd2O3 or other impurities will affect the liquidus temperature of the system and cause the eutectic point position to shift to the lower NdF3 position. This can also explain why the phase diagram in our work is basically consistent with the phase diagram in the literature on the low NdF3 side, while there is a larger difference on the low LiF side.
4. Conclusions
The thermal properties of the LiF-NdF3 binary molten salt system were examined in this study using differential scanning calorimetry. The results acquired from this analysis were utilized a relationship between the component's melting temperature and its NdF3 content. When xNdF3 > 31%, Y = 577.59 + 374.2858 × C + 422.1014 × C2, and when xNdF3 ≤ 31%, Y = 577.59 + 374.2858 × C + 422.1014 × C2. In LiF-NdF3-Nd2O3 molten salt systems, the regression equation can be used as a guide for altering and optimizing the rare-earth neodymium electrolysis process.The LiF-NdF3 binary system's liquidus temperature test findings are significantly influenced by the purity of NdF3, and they are likely to deviate greatly if Nd2O3 or other impurities are present in the raw material. As a result, the experimental phase diagram of the LiF-NdF3 binary system was chosen for this paper with a purity of at least 99.99% and is reliable.
The thermodynamic parameters of the basic molten salt LiF-NdF3 binary system for the electrolysis of molten salt fluoride and neodymium oxide were optimized using the CALPHAD phase diagram calculation technology, FactSage software, and sub-regular solution model. The thermodynamic data of the LiF-NdF3 system were improved, and an accurate LiF-NdF3 binary phase diagram was constructed in combination with the experimental data, providing basic data for the construction of the LiF-NdF3-Nd2O3 ternary phase diagram in the next procedure.
More studies are needed on the binary phase diagram of LiF-NdF3 that obtained by experimental and CALPHAD methods because the simulation of the system is a very complicated project. In future research, it is necessary to obtain additional experimental data and select more accurate thermodynamic models to optimize phase diagram simulations by comparing the optimization effects of different thermodynamic models. For example, the ref. 18 optimized the phase diagram of LiF-NdF3 binary systems by using the modified quasi-chemical model in quadruplet approximation. More thermodynamic data were needed to research the LiF-NdF3 binary system. When the experimental data is sufficient, the thermodynamic data is complete and the optimization is more reasonable, the phase diagram of LiF-NdF3 will become more and more accurate.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant numbers 52174335, 52074134).Notes and references
- H. C. Lin, Rare Earth, 2002, 23(2), 73–77 Search PubMed.
- L. Q. Ji, M. X. Chen, H. Gu, J. H. Zhao and X. Yang, Chin. J. Rare Earth, 2020, 38(2), 129–138 Search PubMed.
- W. Y. Wu and J. S. Zhang, Non-ferrous mining and metallurgy, 2000, 16(6), 34–36 Search PubMed.
- Y. J. Liu and S. H. Yan, Rare Earth, 2003, 4, 2–8 Search PubMed.
- C. F. Liao, S. M. Chen, X. Wang, B. Q. Cai, J. Y. Lin, Y. F. Jiao and Y. L. Zeng, J. Rare Earths, 2019, 37(2), 211–217 CrossRef CAS.
- P. P. Fedorov, V. V. Semashko and S. L. Korableva, Inorg. Mater., 2022, 58(3), 223–245 CrossRef CAS.
- L. Chi, MS thesis, Shanghai University, 2004.
- Y. W. Li, K. K. Chang, P. S. Wang, B. Hu, L. J. Zhang, S. H. Liu and Y. Du, Mater. Sci. Eng. Powder Metall., 2012, 17(1), 1–9 Search PubMed.
- Q. Luo, C. Zhai, D. K. Sun, W. Chen and Q. Li, J. Mater. Sci. Technol., 2019, 9(35), 309–314 Search PubMed.
- G. E. Marcelle and H. Michael, J. Alloys Compd., 2001, 321(2), 267–275 CrossRef.
- G. X. Lu, T. W. Lai, M. G. He and X. Y. Liu, Chin. Sci. Bull., 2020, 65(7), 641–648 CrossRef.
- G. Valerio, M. D. Erika, C. Marta, P. Mauro and B. Marcello, ACS Appl. Energy Mater., 2021, 4(7), 7327–7337 CrossRef.
- R. E. Thoma, G. D. Brunton, R. A. Penneman and T. K. Keenan, Inorg. Chem., 1970, 9(5), 1096–1101 CrossRef CAS.
- J. Van Der Meer, R. Konings, M. Jacobs and H. Oonk, J. Nucl. Mater., 2004, 335(3), 345–352 CrossRef CAS.
- M. Berkani and M. Gaune-Escard, MATEC Web Conf., 2013, 3, 01033 CrossRef CAS.
- A. Abbasalizadeh, S. Sridar, Z. Chen, M. Sluiter, Y. Yang, J. Sietsma, S. Seetharaman and K. H. Kumar, J. Alloys Compd., 2018, 753, 388–394 CrossRef CAS.
- J. Q. Xue, Z. F. Liu, J. Zhang, C. B. Tang and Q. Bi, Chin. J. Rare Met., 2014, 38(5), 832–838 CAS.
- C. A. Johnathon, S. P. Juliano, A. Mina, A. Y. Jacob, M. M. Amir, E. J. Kaitlin, M. D. Clara and M. B. Theodore, J. Chem. Thermodyn., 2022, 177, 106931 Search PubMed.
- X. Y. Ye, Q. Li, D. Wu, X. Huang and Y. Luo, J. Chin. Ceram. Soc., 2015, 43(1), 1597–1604 CAS.
- S. M. Chen, PhD thesis, Jiangxi University of Science and Technology, 2020.
- C. L. Wang, Phase diagrams and its application, 2008, p. 227–227 Search PubMed.
- Z. Y. Qiao, Handbook of Rare, 1992, p. 614 Search PubMed.
- Y. Y. Li, Physicochemical Constants of Rare Earth, Department of Metals, Sun Yat-Sen University, 1978, p. 93 Search PubMed.
- I. A. Santos, D. Klimm, S. L. Baldochi and I. M. Ranieri, J. Cryst. Growth, 2012, 360, 172–175 CrossRef.
- I. H. Jung and M. A. V. Ende, Metall. Mater. Trans. B, 2020, 51(5), 1851–1874 CrossRef CAS.
- S. Li, G. H. Ding, S. H. Wei and Z. M. Cao, ICPCM, Web of Conferences, 2014 Search PubMed.
- H. K. Hardy, Acta Metall., 1953, 1(2), 202–209 CrossRef CAS.
- M. Schick, A. Watson and K. Hack, J. Phase Equilib. Diffus., 2019, 40(1), 104–114 CrossRef CAS.
- S. Renhai, Thermochim. Acta, 2020, 683, 178461 CrossRef.
- K. H. Kumar and P. Wollants, J. Alloys Compd., 2001, 320(2), 189–198 CrossRef.
- O. Redlich and A. T. Kister, Ind. Eng. Chem., 1948, 40(2), 345–348 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |