First-principles investigation on multi-magnesium sulfide and magnesium sulfide clusters in magnesium-sulfide batteries

Abstract

Because of the abundance of magnesium and sulfur and their low cost, the development of magnesium sulfur batteries is very promising. In particular, the battery performance of nanoscale (MgS)_n clusters is much better than that of bulk sized MgS. However, the structures, stability, and properties of Mg_xS_y and (MgS)_n clusters, which are very important to improve the performance of Mg–S batteries, are still unexplored. Herein, the most stable structures of Mg_xS_y (x = 1–8, y = 1–8) and (MgS)_n (n = 1–10) are reliably determined using the structure search method and density functional theory to calculate. According to calculation results, MgS₃ and Mg₆S₈ may not exist in the actual charging and discharging products of magnesium sulfide batteries. The (MgS)_n (n ≥ 5) clusters exhibit intriguing cage-like structures, which are favorable for eliminating dangling bonds and enhancing structural stability. Compared to the MgS monomer, each sulfur atom in the clusters is coordinated with more magnesium atoms, thus lengthening the Mg–S bond length and decreasing the Mg–S bond activation energy. Notably, with the increase of dielectric constant of electrolyte solvent, compared to the DME (ε = 7.2), THF (ε = 7.6) and C₂H₄Cl₂ (ε = 10.0), Mg_xS_y and (MgS)_n clusters are most stable in the environment of C₃H₆O (ε = 20.7). It can delay the transformation of magnesium polysulfide to the final product MgS, which is conducive to improving the performance of Mg–S batteries. The predicted characteristic peaks of infrared and Raman spectra provide useful information for in situ experimental investigation. Our work represents a significant step towards understanding (MgS)_n clusters and improving the performance of Mg–S batteries.

---

1. Introduction

In modern society, rechargeable lithium-ion batteries and lithium-sulfur batteries are some of the most advanced electric energy storage technologies with high energy density, and have been widely used in many fields.^1,2 However, the application of large-scale energy storage of lithium batteries is limited by the small natural reserves of lithium, high production cost and safety issues. Magnesium, as the element on the diagonal line of lithium in the periodic table, has the characteristics of cheap price, no pollution to the environment and high safety.^3,4 In addition, magnesium ions also have a higher valence state than lithium ions, and magnesium sulfur batteries have a higher volume-theoretical capacity than lithium sulfur batteries (3833 vs. 2062 mA h cm⁻³).^5–7 The reserves of magnesium in Earth's crust are much higher than lithium (2.9% vs. 0.002%),^8,9 and magnesium and sulfur are easily obtained from by-products of a variety of minerals. Therefore, the combination of magnesium and sulfur is also considered a promising electrochemical system.^10,11

However, the development of magnesium sulfide batteries is still in the preliminary stage. One of the main obstacles is that during the discharge process, sulfur in the positive electrode and magnesium negative electrode form MgS solid on the magnesium surface,¹² resulting in the formation of a passivation layer on the surface of the magnesium negative electrode that is not conductive to the magnesium ion, which hinders the reversible deposition/dissolution of the magnesium ion.^13–15 Secondly, the compatibility between magnesium electrode and existing electrolyte is poor, many solvents and salts are easy to be reduced on the magnesium negative electrode.^4,16 Until now, the structure and electrochemical mechanism of polysulfide produced in the charge and discharge process of magnesium sulfide batteries have not been cleared. In 2014, Zhao et al.¹⁷ proposed for the first time a three-step electrochemical reaction formula in magnesium sulfide battery based on the electrochemical performance of magnesium sulfide battery and XPS analysis of cathode. In the first step, solid elemental sulfur was converted into liquid MgS₈, which was dissolved in electrolyte and further transformed into MgS₄ through electrochemical reaction. The second step is a reduction from low order polysulfide magnesium such as MgS₄ to MgS₂. In the final step, MgS₂ is reduced to MgS. In 2019, Xu et al.¹⁸ studied the evolution of chemical substances in the cathode of magnesium sulfide battery through in situ and non-in situ XAS experiments, measured the Mg : S ratio in MgS_x (x ≥ 3) through experiments, and then calculated by density functional theory (DFT) to obtain the polysulfide (Mg_xS₈, x = 1, 2, 3 and 8). They believe that finding a method to decompose inactive MgS and low polysulfides and promoting the conversion of MgS to low order MgS_x is the key to solve the problem of rapid capacity decline in magnesium sulfur batteries.¹⁹

To explore the structure and electrochemical mechanism of polysulfide in the charge and discharge process of magnesium sulfide batteries, activation of unreacted MgS by using electrolytes may be an important factor in improving the performance of Mg–S batteries, and the battery performance of nanoscale (MgS)_n clusters may be much better than that of bulk sized MgS. However, until now, the structure, relative stability and electronic properties of (MgS)_n clusters have not been determined. In addition, the growth pattern of (MgS)_n clusters can provide necessary guidance for the design of larger clusters. This motivation drives us to conduct further theoretical calculations of (MgS)_n (n ≤ 10) clusters. To obtain detailed bond length data and precise electronic properties, which are necessary prerequisites for optimizing its performance and understanding its discharge process. Few electrolytes are compatible with both Mg and S₈, and none are ideal. Organo-magnesium-based electrolytes, commonly used in Mg–Mo₆S₈ batteries, are likely too nucleophilic and will react with electrophilic S₈.²⁰ Efforts have therefore focused on the development of non-nucleophilic electrolytes. Understanding these fundamental questions is critical to addressing the obstacles to translating this promising electrochemical system into a useable technology.

In this article, the structure of magnesium polysulfide was predicted. The structure, stability and properties of (MgS)_n clusters, which are very important for improving the performance of Mg–S batteries, are investigated. We also provided the structural evolution of magnesium sulfide in the discharge process. In addition, the calculation of infrared and Raman spectra provides the description of characteristic spectral lines for the three basic structural units of MgS, Mg₂S and Mg₃S, and also provides useful information for experimental research. The solvation energy of magnesium polysulfide in electrolyte DME (ε = 7.2), THF (ε = 7.6), C₂H₄Cl₂ (ε = 10.0) and C₃H₆O (ε = 20.7) was calculated. With the increase of dielectric constant, the solvent energy of magnesium polysulfide gradually decreases, indicating that magnesium polysulfide is more stable in the electrolyte environment with large dielectric constant. It can promote the transformation of long chain magnesium polysulfide to short chain magnesium polysulfide, and delay the transformation of magnesium polysulfide to the final product MgS, which is conducive to improving the performance of Mg–S batteries. The work in this paper provides a good mechanism and theoretical support for understanding (MgS)_n clusters and improving the performance of Mg–S batteries.

2. Computational methods

In order to find the preferred structures of Mg_xS_y (x = 1–8, y = 1–8) and (MgS)_n clusters (n = 1–10), we employed the swarm-intelligence based ABCluster structure prediction method,^21,22 which can efficiently search for the stable structures of given cluster sizes. Furthermore, a global search should be an effective method to avoid missing candidates of ground state structures. To improve the search efficiency, point group symmetry and the bond characterization matrix technique were included to eliminate similar structures. The validity of the ABCluster method in cluster structure prediction has been demonstrated by its application for a series of cluster systems.

The underlying local structure optimization and electronic property calculations were performed at the density functional theory (DFT) level using the B3LYP²³ hybrid functional as implemented in the Gaussian 09 package. Since there are thousands of structures generated during the structure search, an economic basis set, i.e. 6-311G for Mg and S, was chosen to optimize these structures. These settings are enough for evaluating the relative energies of the generated structures. After the structure search, the accurate basis set of 6-311+G(d) was used for the refined structure optimization and vibrational frequency calculation for the isomers with low-lying energies. The absence of an imaginary frequency confirms that the predicted structures are stability.

First, we calculated the binding energy per atom, the formation energies were defined as

E_b = (E_MgxSy − xE_Mg − yE_S)/(x + y) (1)

where E_MgxSy is the lowest energy of structure Mg_xS_y, E_Mg and E_S are the energy of magnesium atom and sulfur atom respectively.

The solvent energy, ΔE^solven_b, was computed to measure the interaction strength between Mg_xS_y and electrolytes, the formula is as follows:

ΔE^solven_b = (E_MgxSy^vacuum − E_MgxSy^solven)/(x + y) (2)

In cluster physics, Δ²E_n, which was calculated as follows

Δ²E_n = E_n+1 + E_n−1 − 2E_n (3)

The second-order energy difference is a sensitive physical quantity that reflects the relative stability of considered clusters and can also be directly compared with the experimental relative abundance.

3. Results and discussion

3.1. Structural and thermal analysis of Mg_xS_y and (MgS)_n

The stability structures of Mg_xS_y molecule was determined by using the structure search method combined with density functional theory calculation and Gauss structure optimization.²³ As shown in Table 1, It can be seen that MgS_y is mainly plane chain structure and Mg_xS₈ is mainly cross ring structure. This can improve structural stability. In order to verify whether intermediate products exist in actual charge and discharge, we calculated E_b, as shown in Fig. 1.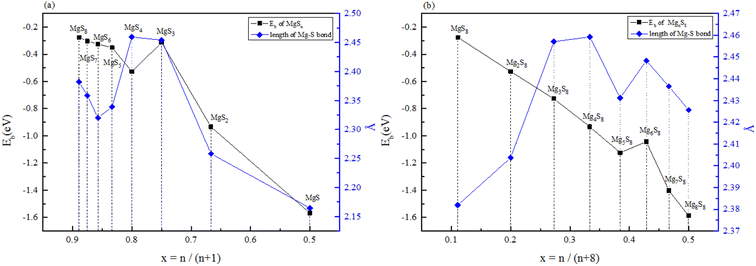

Table 1 Fully optimized structures of the Mg_xS_y

MgSy
	MgS	MgS2	MgS3	MgS4	MgS5	MgS6	MgS7	MgS8
Length of Mg–S bond	2.16 Å	2.26 Å	2.45 Å	2.46 Å	2.34 Å	2.32 Å	2.36 Å	2.38 Å
MgxS8
	MgS8	Mg2S8	Mg3S8	Mg4S8	Mg5S8	Mg6S8	Mg7S8	Mg8S8
Length of Mg–S bond	2.38 Å	2.40 Å	2.46 Å	2.46 Å	2.43 Å	2.45 Å	2.44 Å	2.43 Å

---

Fig. 1 (a) Binding energy and Mg–S bond length of MgS_y. (b) Binding energy and Mg–S bond length of Mg_xS₈.

Fig. 1(a) shows the binding energy and average Mg–S bond length of MgS_y. It can be seen that the binding energy of MgS₃ is higher than that of MgS₂ and MgS₄, this indicates that MgS₃ may not exist in the actual charging and discharging products of magnesium sulfide batteries, and the trend of average bond length of magnesium sulfide is basically consistent with that of MgS_y. Fig. 1(b) shows the binding energy and average Mg–S bond length of Mg_xS₈. It can be seen that the binding energy of Mg₆S₈ is higher than that of Mg₅S₈ and Mg₇S₈, so Mg₆S₈ may not exist in the actual charging and discharging products of magnesium sulfur batteries. It can be seen that with the increase of the number of magnesium atoms, the trend of Mg–S average bond length is in good agreement with the trend of binding energy of Mg_xS₈.

The structures of (MgS)_n clusters (n = 1–10) are completely optimized under vacuum environment. Based on thermodynamic stability analysis, the formation of (MgS)_n clusters are favorable. The lowest energy structure of (MgS)_n clusters determined by DFT structure optimization is shown in Fig. 2. An example of the simplest structure of (MgS)_n clusters is MgS. At the level of B3LYP/6-31+G(d), the shortest Mg–S bond length calculated is 2.65 Å, which is basically consistent with the 2.60 Å crystal bond length described in the literature.²⁴ According to the obtained (MgS)_n cluster complex structure, the analysis was conducted, as shown in Fig. 2(a). When n equals 5, the lowest energy structure underwent structural changes from two to three dimensions. With the further increase of cluster size (n ≥ 5) (MgS)_n clusters presented cage structure, which could improve the structural stability to a certain extent. In addition, the coordination number of sulfur atoms increases with the increase of cluster size. Specifically, the coordination number of the sulfur atom is 1 in the MgS monomer and 2 in (MgS)₂ and (MgS)₃; the highest is 3, which occurs in n = 5, 6, 7, 8, 9, and 10. The increase of coordination number also helps to improve structural stability. As shown in Fig. 2(b), the average Mg–S bond length in Mg-sulfur clusters is significantly larger than that in monomers. For example, the average Mg–S bond length in (MgS)₅ is 2.48 Å, while the average Mg–S bond length in MgS is 2.17 Å. Longer Mg–S bonds indicate reduced bond energy, which means that Mg–S bonds in the cluster are more easily dissociated, which is consistent with the lower activation energy of the (MgS)_n cluster as the cathode. In addition, we also calculated that the Mg–Mg bond length is about 2.64–2.88 Å, which is smaller than the Mg–Mg bond length (3.2 Å) in the crystal.²⁵ As shown in Fig. 2(b), the binding energy in the cluster is calculated with the formula (1). The relative stability of (MgS)_n clusters can be determined by analyzing their energy. The left ordinate of Fig. 2(b) shows the relationship between E_b of (MgS)_n clusters and the number of MgS units. E_b decreases monotonically with the increase of cluster size, indicating that the formation of (MgS)_n clusters is favorable.

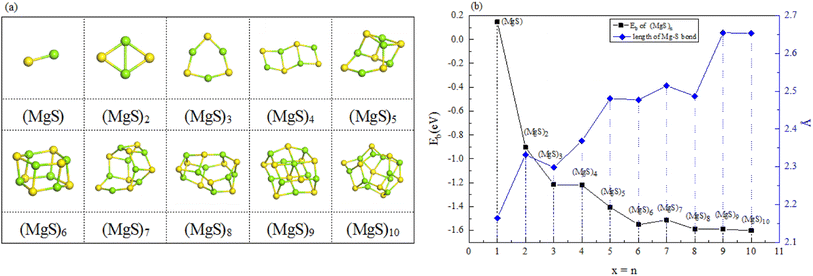Fig. 2 (a) Optimized structures of magnesium sulfide clusters; (b) binding energy of magnesium sulfide clusters (n = 1–10) and bond length of Mg–S bonds in the clusters.

The free energy of MgS unit of the clusters with the lowest energy structure is calculated. As shown in Fig. 3(a), the energy of MgS unit tends to converge with n increases. For example, the difference in binding energy between (MgS)₆ and (MgS)₁₀ is only 0.10 eV. In the physics of atomic clusters, the second-order energy difference, is a sensitive physical quantity that reflects the relative stability of the clusters under consideration and can also be compared directly with the experimental relative abundance. Fig. 3(b) shows the second-order energy difference as a function of cluster size. The results show that the second order energy difference shows an obvious odd-even oscillation when n = 5 is taken as the dividing line. The largest second-order energy difference is observed in clusters with n = 6. Therefore, among the clusters considered, (MgS)₆ should have a relatively high abundance.

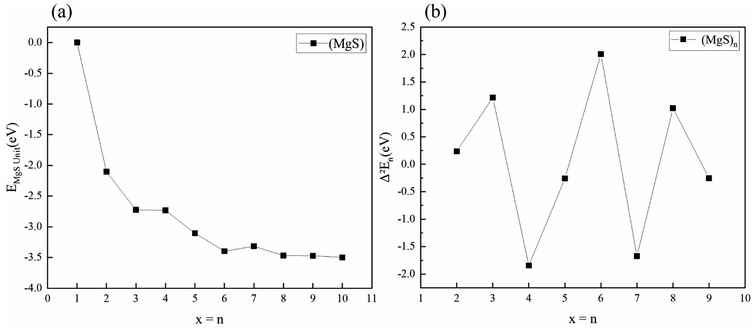Fig. 3 (a) Free energy of MgS unit of magnesium sulfide clusters (b) second-order energy difference Δ²E_b in magnesium sulfide clusters.

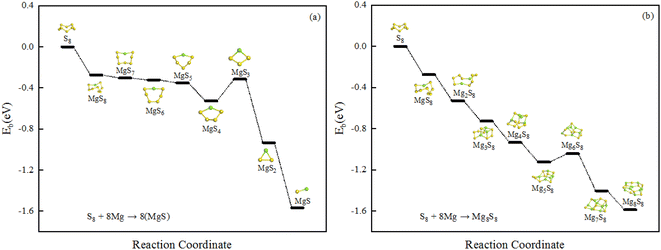
The structural evolution of magnesium sulfide in the discharge process are organized as shown in the Fig. 4(a) and (b), MgS₈ is first produced during the discharge of a magnesium sulfur battery, and the final product is MgS solid. There are two different processes shown in Fig. 4 respectively. Sulfur atoms undergo a reduction reaction, during which electrons are gradually obtained and the valence is gradually reduced. Fig. 4(a) shows the number of magnesium atoms does not change, Fig. 4(b) shows the number of sulfur atoms does not change, and the final product is MgS unit. We hope that our work can provide some basis for the experiment and provide some help for the subsequent magnesium sulfide clusters and their applications.

Fig. 4 (a) and (b) The structural evolution of magnesium sulfide in the discharge process.

3.2. Infrared absorption (IR) and Raman spectra of Mg_xS_y and (MgS)_n

To provide some useful information in experiment of Mg–S batteries, we simulated and calculated infrared absorption (IR) and Raman spectra. It is found that the shape of the Raman spectra strongly correlate with the size of the (MgS)_n (n = 1–10) clusters as Fig. 5 shown.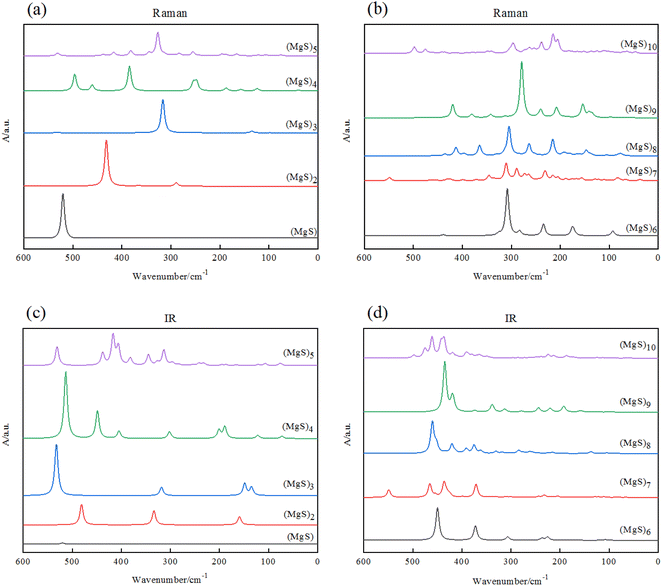

Fig. 5 (a) and (b) Raman spectra of (MgS)_n clusters; (c) and (d) infrared spectra of (MgS)_n clusters.

Fig. 5(a) and (b) are the Raman spectra of (MgS)_n clusters, Fig. 5(c) and (d) are the IR spectra of magnesium sulfide clusters. The calculation of infrared and Raman spectra provides the description of characteristic spectral lines for the three basic structural units of MgS, Mg₂S and Mg₃S, and also provides useful information for experimental research. By observing Raman spectra, we preliminarily guess that the corresponding frequency of the component unit MgS is about 500 cm⁻¹. When n = 2, there are peaks around 300 cm⁻¹, especially when (MgS)_n (n ≥ 5), the frequency of the main peaks is concentrated around 300 cm⁻¹. We guess that the corresponding frequency of Mg₂S may be about 300 cm⁻¹, and Mg₃S can be considered to be composed of multiple Mg₂S, and the intensity of the peaks is related to the number of Mg₃S. But this theory has yet to be tested experimentally.

We simulate infrared absorption (IR) and Raman absorption spectra. By observing the infrared spectrum in Fig. 5, we can see that the main characteristic peaks of (MgS)_n cluster are concentrated in the mid-infrared region (400–4000 cm⁻¹). And with the increase of n, the main characteristic peaks of (MgS)_n cluster produced a blue shift. It is found that the shape and intensity of infrared spectra are closely related to the size of (MgS)_n (n = 1–10) clusters. For example, the most stable cluster (MgS)₆, shows a strong band near 450 cm⁻¹, with many weak peaks in the wave number range of 100 to 400 cm⁻¹. This is in sharp contrast to the strong peak of MgS monomer (525 cm⁻¹).

3.3. Solven effect on the Mg_xS_y and (MgS)_n clusters

Since magnesium sulfide battery needs to work in electrolyte environment in practical application, we carried out density functional calculation on a series of magnesium sulfide clusters and polymagnesium sulfide products in vacuum state. The solvation energy and Mg–S bond length of magnesium sulfide clusters and polymagnesium sulfide in electrolyte DME, THF, C₂H₄Cl₂ and C₃H₆O solvents were analyzed. In ether-based electrolyte solvents, sulfur reduction and polysulfide formation occur at higher discharge voltages. However, the solvent properties of the dielectric constant may have a significant effect on the oxidation–reduction reaction of sulfur. In low dielectric constant solvents such as DME, the amount of polysulfide substances formed through chain growth and disproportionation reactions is expected to be large because of the low stability of these substances in such solvents.⁹

Firstly, magnesium sulfide clusters were optimized under four types solvent condition, and the solvation energy of magnesium sulfide clusters was calculated, as shown in Fig. 6(a). Compared with the energy of (MgS)_n clusters under vacuum, the cluster energy under solvent conditions was lower, indicating that the cluster stability in solvent environment was higher, and with the increase of dielectric constant of solvent, The solvation energy of the clusters decreases gradually. When n ≥ 6, it is obvious that solvation energy converges to about 1.0 eV. Secondly, the Mg–S bond length of magnesium sulfide clusters in the electrolyte environment was statistically analyzed. The average Mg–S bond length of the clusters in the electrolyte solvent increased with the increase of n, and with the increase of n, the average bond length remained at about 2.45 Å. In addition, the average Mg–S bond length of the same cluster increases with the increase of dielectric constant in the electrolyte solvent.

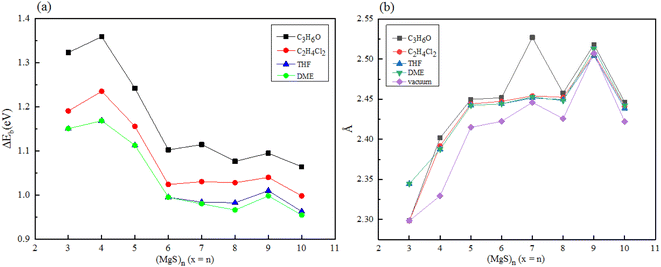Fig. 6 Solvation energy of (a) (MgS)_n in different electrolyte solvents (b) average Mg–S bond length of (MgS)_n in different electrolyte solvents.

In addition, the solvation energy of polysulfide Mg_nS₈ was calculated, as shown in Fig. 7(a). With the increase of the dielectric constant of the solvent DME, THF, C₂H₄Cl₂ and C₃H₆O, the solvation energy of Mg_nS₈ decreased gradually. These results indicate that Mg_nS₈ has lower energy and more stable structure in solvents with high dielectric constant coefficient, and the solvation energy of the same polysulfide decreases with the increase of dielectric constant in different solvents. In addition, with the increase of the number of magnesium atoms in the same solvent, the solvation energy gradually converges and finally stabilizes around 1.0 eV. As shown in Fig. 7(b), the average Mg–S bond length of polysulfide Mg_nS₈ under different electrolyte solvents was calculated. It can be seen that compared with the average Mg–S bond length of polysulfide under vacuum, the average Mg–S bond length of polysulfide under electrolyte solvent increased, and increased with the increase of electrolyte dielectric constant. In addition, with the increase of the number of Mg atoms, the average bond length of Mg–S converges to about 2.46 Å when the number of Mg atoms is greater than or equal to 5.

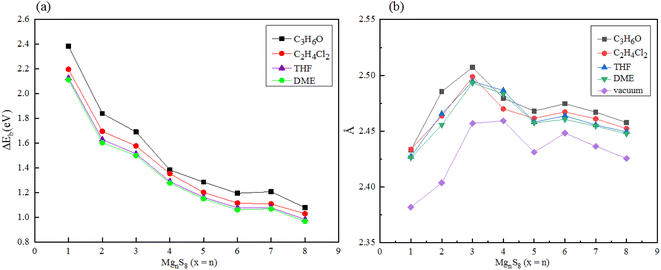Fig. 7 (a) Solvation energy of Mg_nS₈ in different electrolyte solvents (b) average Mg–S bond length of Mg_nS₈ in different electrolyte solvents.

4. Conclusions

The structure search method combined with density functional theory was used to predict the configuration of polysulfide magnesium, and the stable structure of polysulfide Mg_xS_y and (MgS)_n (n = 1–10) clusters was determined. The structure, stability and properties of (MgS)_n clusters, which are very important for improving the performance of Mg–S batteries, are investigated. The most stable structure, second order energy difference, binding energy, IR spectrum, Raman spectrum and solvation energy of the clusters are discussed. Second-order energy difference and gap analysis show that (MgS)₆ cluster is more stable than adjacent cluster. The weakening of the Mg–S bond means that (MgS)_n is more easily activated than the MgS monomer. We also provide a description of the structural evolution of magnesium sulfide in the discharge process, MgS₈ is first produced during the discharge of a magnesium sulfur battery, and the final product is MgS solid. The calculation of infrared and Raman spectra provides the description of characteristic spectral lines for MgS, Mg₂S and Mg₃S, and also provides useful information for experimental research. In addition, the solvation energy of magnesium polysulfide in electrolyte DME, THF, C₂H₄Cl₂ and C₃H₆O was calculated. With the increase of dielectric constant DME (ε = 7.2), THF (ε = 7.6), C₂H₄Cl₂ (ε = 10.0) and C₃H₆O (ε = 20.7), the solvent energy of magnesium polysulfide gradually decreases, indicating that magnesium polysulfide is more stable in the electrolyte environment with large dielectric constant. It can promote the transformation of long chain magnesium polysulfide to short chain magnesium polysulfide, and delay the transformation of magnesium polysulfide to the final product MgS, which is conducive to improving the performance of Mg–S batteries. The work in this paper provides a good theoretical support for the understanding of (MgS)_n clusters, and the research results have a certain guiding significance for further improving the performance of magnesium sulfide batteries.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JBW was supported by the National Natural Science Foundation of China (No. 11047164), the Shanghai College Foundation for Excellent Young Teachers of China (No. gjd10023), and the Academic Program of Shanghai Municipal Education Commission (No. 11XK11 and 2011X34). ZXY was supported by the National Natural Science Foundation of China (No. 62072296).

References

1. G. Bieker, et al., Influence of cations in lithium and magnesium polysulphide solutions: dependence of the solvent chemistry, Phys. Chem. Chem. Phys., 2017, 19(18), 11152–11162.
2. L. Wang, et al., Dual Role of Mo(6) S(8) in Polysulfide Conversion and Shuttle for Mg-S Batteries, Adv. Sci., 2022, 9(7), e2104605.
3. H. Fan, et al., Extending Cycle Life of Mg/S Battery by Activation of Mg Anode/Electrolyte Interface through an LiCl-Assisted MgCl2 Solubilization Mechanism, Adv. Funct. Mater., 2020, 30(9), 1909370.
4. Y. Xu, et al., Improving a Mg/S Battery with YCl(3) Additive and Magnesium Polysulfide, Adv. Sci., 2019, 6(4), 1800981.
5. R. Li, et al., Achieving high-energy-density magnesium/sulfur battery via a passivation-free Mg-Li alloy anode, Energy Storage Mater., 2022, 50, 380–386.
6. Y. Lu, et al., Progress and Perspective on Rechargeable Magnesium-Sulfur Batteries, Small Methods, 2021, 5(5), e2001303.
7. B. P. Vinayan, et al., Performance study of magnesium-sulfur battery using a graphene based sulfur composite cathode electrode and a non-nucleophilic Mg electrolyte, Nanoscale, 2016, 8(6), 3296–3306.
8. H. Xu, et al., Rational design of high concentration electrolytes and MXene-based sulfur host materials toward high-performance magnesium sulfur batteries, Chem. Eng. J., 2022, 428, 131031.
9. B. P. Vinayan, et al., Insights into the electrochemical processes of rechargeable magnesium-sulfur batteries with a new cathode design, J. Mater. Chem. A, 2019, 7(44), 25490–25502.
10. T. Gao, et al., Enhancing the reversibility of Mg/S battery chemistry through Li(+) mediation, J. Am. Chem. Soc., 2015, 137(38), 12388–12393.
11. D. T. Nguyen, et al., Material design strategies to improve the performance of rechargeable magnesium-sulfur batteries, Mater. Horiz., 2021, 8(3), 830–853.
12. J. Yang, et al., The potential application of VS2 as an electrode material for Mg ion battery: A DFT study, Appl. Surf. Sci., 2021, 544, 148775.
13. X. Zhou, et al., High Rate Magnesium-Sulfur Battery with Improved Cyclability Based on Metal-Organic Framework Derivative Carbon Host, Adv. Mater., 2018, 30(7), 1704166.
14. X. Yu and A. Manthiram, A Progress Report on Metal-Sulfur Batteries, Adv. Funct. Mater., 2020, 30(39), 2004084.
15. C. Wei, et al., Highly reversible Mg metal anodes enabled by interfacial liquid metal engineering for high-energy Mg-S batteries, Energy Storage Mater., 2022, 48, 447–457.
16. Z. Zhao-Karger, et al., Toward Highly Reversible Magnesium-Sulfur Batteries with Efficient and Practical Mg[B(hfip)(4)](2) Electrolyte, ACS Energy Lett., 2018, 3(8), 2005–2013.
17. Z. Zhao-Karger, et al., Performance Improvement of Magnesium Sulfur Batteries with Modified Non-Nucleophilic Electrolytes, Adv. Energy Mater., 2015, 5(3), 1401155.
18. Y. Xu, et al., In Situ X-ray Absorption Spectroscopic Investigation of the Capacity Degradation Mechanism in Mg/S Batteries, Nano Lett., 2019, 19(5), 2928–2934.
19. T. Gao, et al., Thermodynamics and Kinetics of Sulfur Cathode during Discharge in MgTFSI(2) -DME Electrolyte, Adv. Mater., 2018, 30(3), 1704313.
20. S. C. Bevilacqua, K. H. Pham and K. A. See, Effect of the Electrolyte Solvent on Redox Processes in Mg-S Batteries, Inorg. Chem., 2019, 58(16), 10472–10482.
21. J. Zhang and M. Dolg, ABCluster: the artificial bee colony algorithm for cluster global optimization, Phys. Chem. Chem. Phys., 2015, 17(37), 24173–24181.
22. J. Zhang and M. Dolg, Global optimization of clusters of rigid molecules using the artificial bee colony algorithm, Phys. Chem. Chem. Phys., 2016, 18(4), 3003–3010.
23. K. Raghavachari, Perspective on “Density functional thermochemistry. III. The role of exact exchange”, Theor. Chem. Acc., 2000, 103(3–4), 361–363.
24. M. K. Horton, et al., High-throughput prediction of the ground-state collinear magnetic order of inorganic materials using Density Functional Theory, npj Comput. Mater., 2019, 5(1), 64.
25. J. M. Munro, et al., An improved symmetry-based approach to reciprocal space path selection in band structure calculations, npj Comput. Mater., 2020, 6(1), 112.

---