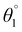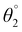Open Access Article
Open Access ArticleEffect of tailoring π-linkers with extended conjugation on the SJ-IC molecule for achieving high VOC and improved charge mobility towards enhanced photovoltaic applications†
Hira Zubaira,
Rana Farhat Mahmoodb,
Muhammad Waqasa,
Mariam Ishtiaqa,
Javed Iqbal *a,
Mahmoud A. A. Ibrahim
*a,
Mahmoud A. A. Ibrahim cd,
Shaban R. M. Sayede,
Sadia Noor
cd,
Shaban R. M. Sayede,
Sadia Noor f and
Rasheed Ahmad Khera
f and
Rasheed Ahmad Khera *a
*a
aDepartment of Chemistry, University of Agriculture, Faisalabad 38000, Pakistan. E-mail: rasheedahmadkhera@yahoo.com; rasheed.ahmad.khera@uaf.edu.pk
bDepartment of Chemistry, Division of Science and Technology, University of Education, Township, Lahore 54770, Pakistan
cComputational Chemistry Laboratory, Chemistry Department, Faculty of Science, Minia University, Minia 61519, Egypt
dSchool of Health Sciences, University of KwaZulu-Natal, Westville Campus, Durban 4000, South Africa
eDepartment of Botany and Microbiology, College of Science, King Saud University, P. O. Box 2455, Riyadh 11451, Saudi Arabia
fDepartment of Chemistry, University of Hohenheim, Stuttgart, 70599, Germany
First published on 1st September 2023
Abstract
The problem of low efficiency of organic solar cells can be solved by improving the charge mobility and open circuit voltage of these cells. The current research aims to present the role of π-linkers, having extended conjugation, between the donor and acceptor moieties of indacenodithiophene core-based A-π-D-π-A type SJ-IC molecule to improve the photovoltaic performance of pre-existing SJ-IC. Several crucial photovoltaic parameters of SJ-IC and seven newly proposed molecules were studied using density functional theory. Surprisingly, this theoretical framework manifested that the tailoring of SJ-IC by replacing its π-linker with linkers having extended π-conjugation gives a redshift in maximum absorption coefficient in the range of 731.69–1112.86 nm in a solvent. In addition, newly designed molecules exhibited significantly narrower bandgaps (ranging from 1.33 eV to 1.93 eV) than SJ-IC having a bandgap of 2.01 eV. Similarly, newly designed molecules show significantly less excitation energy in gaseous and solvent phases than SJ-IC. Furthermore, the reorganization energies of DL1–DL7 are much lower than that of SJ-IC, indicating high charge mobility in these molecules. DL6 and DL7 have shown considerably improved open circuit voltage (VOC), reaching 1.49 eV and 1.48 eV, respectively. Thus, the modification strategy employed herein has been fruitful with productive effects, including better tuning of the energy levels, lower bandgaps, broader absorption, improved charge mobility, and increased VOC. Based on these results, it can be suggested that these newly presented molecules can be considered for practical applications in the future.
1. Introduction
The impressive photoactivity of bulk heterojunction (BHJ) organic solar cells (OSCs) is linked to non-fullerene acceptors (NFAs) that possess easily tunable frontier energy levels. This characteristic is crucial in reducing the band gap and improving the absorption properties of photoactive materials.1–3 Fused-ring NFAs have upgraded the photovoltaic activity of OSCs. The photovoltaic performance of OSCs was limited due to fixed frontier energy levels and poor absorption of fullerene acceptors in the visible and near-infrared spectral ranges.4 Significant improvements in the performance of OSCs have been attained because of continuous efforts from both computational and synthetic approaches.5 Although noticeable advancements have improved fullerene-free OSCs, their efficiency is still insufficient for commercial applications.In order to bring about an improvement in the overall efficiency of fullerene-free OSCs, it is essential to focus on important factors such as narrowing the band gap, increasing the range of light absorption of chromophores, reducing excitation energy and reorganization energy, and increasing the open circuit voltage (VOC). Narrowing the band gap is vital as it increases the number of photons that can produce photovoltaic current.6–8 By expanding the light absorption range of chromophores, OSCs can capture a broader spectrum of sunlight, resulting in higher efficiency. Moreover, reducing excitation and reorganization energy can minimize energy loss during the charge transfer process and increase charge mobility.9 Increasing VOC is also essential as it is directly related to the maximum power output of a solar cell.10 By improving any of these crucial factors, researchers and scientists can work towards achieving greater efficiency in fullerene-free OSCs.11–14
Different computational and synthetic techniques have been used to improve the efficiency of fullerene-free OSCs. Among these techniques, increasing the conjugation length in molecules is an effective strategy that can be achieved by inserting π-bridges for further enhancement of the ability of the molecules to harvest light and, in turn, boost VOC of OSCs. Such a method also forms resultant channels for the transport of electrons between the donor core and acceptor units.15 Electrons are delocalized over the entire molecule surface in conjugated systems with extended π-electron systems. This results in many closely spaced energy levels, which can lead to light absorption at longer wavelengths, i.e., in the near-infrared region.16 Furthermore, π-bridges function as “conformational locks”; thus, they can improve planarity.17 Recently, Hai and coworkers investigated the effect of incorporating vinylene π-linkers in a central ladder-type fused core and developed two new molecules named BTP-2V-2F and BTP-1V-2F. BTP-2V-2F showed a power conversion efficiency (PCE) of 11.22% and a high short-circuit current of 26.50 mA cm−2, while the latter exhibited a remarkable PCE of 14.24%.18
In 2017, Li et al. used the strategy of π-linker insertion. They developed a novel compound named SJ-IC, having a ladder-type core of pentacyclic arene 4,9-dihydro-s-indaceno[1,2-b:5,6-b′]dithiophene (IDT) with four phenyl units as side chains to enhance its electron-donating character. In SJ-IC, the IDT donor part is separated from the IC acceptor via a vinyl group as a π-linker. Owing to the proficient structural fragments, SJ-IC exhibits strong absorption in chloroform solvent in the 560–800 nm wavelength range with a peak prominent at 720 nm. SJ-IC acting as acceptor along with J61 donor in a solar cell shows a high PCE of about 9.27%, notable JSC of approximately 16.99 mA cm−2, VOC of about 0.83 V, film factor with a value of 0.6595 and having an electron mobility of 5.73 × 10−4 cm2 V−1 s−1.19
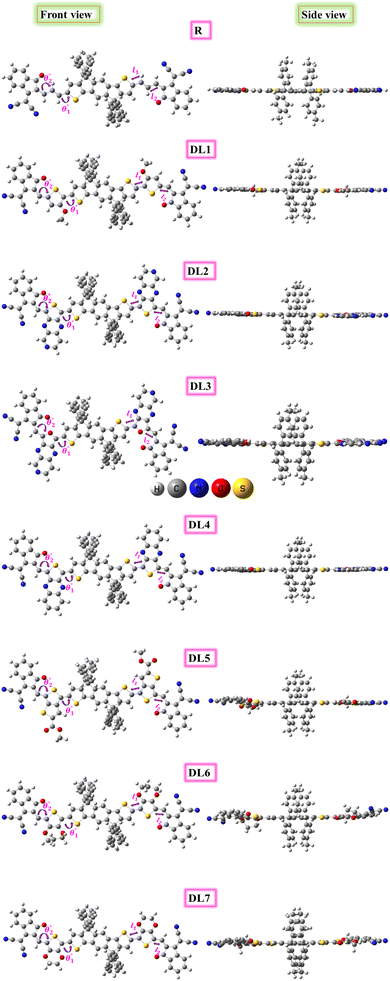
The current research further explores the effect of π-bridging in SJ-IC to enhance its already remarkable optoelectronic properties to design novel molecules for efficient OSCs. Until now, 19% PCE has been achieved in non-fullerene OSCs. But SJ-IC has significantly lagged in showing promising efficiency. SJ-IC (R) is structurally tailored to improve IDT core-based molecules by replacing vinyl spacers with other π-linkers with enhanced conjugation. Thus, seven new molecules have been designed. Herein, we derived all the investigated molecules from SJ-IC by replacing the simple π-bridge with methoxythiophene in DL1, 2-thia-4,6,9-triazacyclopenta [b]naphthalene in DL2, 2-oxa-4,6,9-triazacyclopenta [b]naphthalene in DL3, thieno [3,4-b]quinoxaline in DL4, methylthieno[3,4-b]thiophene-2-carboxylate in DL5, 3,4-dihydro-2H-thieno[3,4-b][1,4]dioxepine in DL6 and 2,3-dihydrothieno[3,4-b][1,4]dioxine in DL7 as shown in Fig. 1. These π-bridges have the potential to enhance crucial photovoltaic parameters such as increasing the light absorption ability, narrowing the bandgap, reducing reorganization and excitation energy, and enhancing VOC of these molecules.
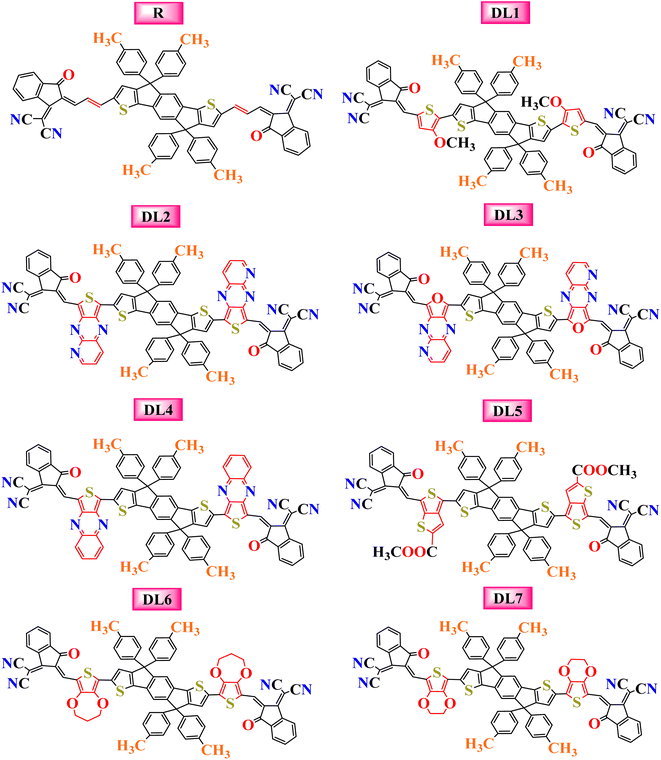 | ||
| Fig. 1 Pictorial representation of the molecular structures for the reference and the newly designed molecules with inserted linkers. | ||
2. Computational methodology
The 3D molecular frameworks of all the molecules involved in the current research work were designed with the help of GaussView 6.0 to study the various optical and electronic parameters. For simplicity, long alkyl substituents attached to the phenyls on the core of the reference (SJ-IC) molecule were replaced by methyl to save computational time and cost. The quantum simulations were progressed by Gaussian 09 software20 using DFT (density functional theory)21 and TD-DFT (time-dependent DFT)22 approaches, which are considered reliable for calculating ground state and excited state properties of OSC molecules. The reference (SJ-IC) molecule was optimized in the ground state with a restricted electronic spin by using four different functionals of the DFT, i.e., B3LYP,23 CAM-B3LYP,24 MPW1PW91,25 and WB97XD26 in conjunction with the 6-31G(d,p) basis set.27 After achieving geometry optimization with different functionals, the calculations in the solvent medium were performed by employing chloroform solvent via the IEFPCM28 model of the TD-DFT approach. Chloroform was used as a solvent because it was used initially for SJ-IC in the literature19 to check out the effect of solvent on the light absorption capability of molecules in the excited state.To determine the best molecular computational method, the obtained results with these different functionals were compared to the experimental results of the SJ-IC molecule. It was observed that experimental optoelectronic attributes of SJ-IC molecules, such as band gap and the maximum absorption (λmax), strongly agreed with the results obtained using the B3LYP/6-31G(d,p) level of theory. The λcalmax with B3LYP functional had a value of 731.69 nm, while the value of λcalmax was 546.11 nm with CAM-B3LYP functional, 691.11 nm with MPW1PW91, and 525.12 nm with WB97XD. This shows that use of B3LYP functional leads to more concordance with the experimental maximum spectral absorption (720 nm). For the convenience of comparison, Fig. S1 (ESI†) presents a graphical comparison of the results obtained using various functionals. Therefore, all the designed molecules were processed using the B3LYP functional of DFT to get all the results under similar conditions for parallel comparison.
Spectral illustrations for the absorption maxima (λmax) in gaseous and solvent phases were realized by Origin 6.0 software.29 Multiwfn 3.8 software30 was used to reconstruct TDM (transition density matrix) data into actual graphs to inspect exciton dynamics and their interactions. The same software was used for developing non-covalent interaction (NCI) graphs and isosurfaces and the VMD program21 was used to visualize isosurfaces. DOS (density of states) graphs were generated using the PyMOlyze1.1 (ref. 22) program to reveal the extent of each molecule's involvement of acceptors, linkers, and donor parts.
It is important to note that the reorganization energy influences the efficiency of a solar cell. It gives information about the charge transfer capability of OSC molecules, specifically the mobility of holes and electrons during excitation. This essential parameter can be calculated using the Marcus equation. Using the pre-selected level of theory, i.e., B3LYP/6-31G(d,p), all the studied molecules were optimized in cationic and anionic states, followed by simulations for energy calculations in cationic and anionic states. Eqn (1) and (2) (ref. 31) were applied to calculate the reorganization energy of electrons (λe) and holes λh of each molecule:
| λh = [E+0 − E+] + [E0+ − E0] | (1) |
| λe = [E−0 − E−] + [E0− − E0] | (2) |
3. Results and discussion
3.1 Geometry analysis
The SJ-IC molecule has three parts: a ladder-shaped donor or “push” part (IDT), C–C double bonds as π-bridges, and an electron-deficient acceptor, IC, “pull” fragment. As portrayed in Fig. 2, it can be observed that the SJ-IC molecule is optimized in one plane. The four phenyl moieties are arranged in another plane in order to minimize steric hindrance at low potential energy with 113° torsion angles. These phenyls lessen the intermolecular interactions due to steric hindrance and thus prevent self-aggregation.33 Lengths of the bonds connecting donor-linker and linker-acceptor parts of the SJ-IC molecule have values ranging from 1.42680 to 1.42034 Å. The dihedral angle between the donor and spacer is represented by θ1 while θ2 represents the dihedral angle between the spacer and acceptor. The dihedral angles between these connecting fragments have values of 0.00129° and 0.00476°, respectively. These values are very close to zero. The acquired outcomes indicate a higher degree of planarity and conjugation, both essential for charge transfer.Planarity is one of the vital factors responsible for charge transfer. Planarity is highly affected by the dihedral angle between the molecule's constituents. Planarity will be more prominent in molecules with smaller dihedral angles, increasing the possibility of charge transfer. The dihedral angle values for all our proposed molecules range from 0.00603° to 5.99593°, as summarized in Table 1. It is predicted that all the torsion angle values are considerably smaller for two reasons. One reason is the rotation restriction over single bonds due to the insertion of π-linkers with extended conjugation. The second reason for the smaller torsion angle can be the presence of conformation locks such as noncovalent interactions (S⋯O, S⋯H, O⋯H, and S⋯N) among subunits of each molecule which hold aromatic rings in the same plane.34 DL5 and DL6 have shifted slightly from the central plane due to lone pairs on the oxygen atoms of linkers.
| Molecule | Dihedral angle (θ°) | Bond length (LC–C) (Å) | ||
|---|---|---|---|---|
| l1 | l2 | |||
| R | 0.00129 | 0.00476 | 1.42680 | 1.42034 |
| DL1 | 0.37208 | 0.00603 | 1.43025 | 1.41556 |
| DL2 | 0.10320 | 0.02090 | 1.42059 | 1.40571 |
| DL3 | 0.36913 | 0.43839 | 1.40986 | 1.39471 |
| DL4 | 0.05060 | 0.00880 | 1.42106 | 1.40350 |
| DL5 | 5.91159 | 0.12303 | 1.43216 | 1.41254 |
| DL6 | 5.99593 | 0.65967 | 1.43451 | 1.40838 |
| DL7 | 2.32446 | 0.19666 | 1.43203 | 1.40981 |
The bond lengths between atoms that connect donor-spacer (l1) and spacer-acceptor (l2) were also calculated. Their values were observed to be in the 1.39471–1.43451 Å range. These data indicate that the bond lengths between molecule fragments are somewhere between those for C–C single (1.54 Å) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double (1.34 Å) bonds. This shows the presence of conjugation at these points.35 As these bonds connect the molecules' fragments, it can be inferred that charges can transfer from the donor to the acceptor portion in these molecules due to conjugation.
C double (1.34 Å) bonds. This shows the presence of conjugation at these points.35 As these bonds connect the molecules' fragments, it can be inferred that charges can transfer from the donor to the acceptor portion in these molecules due to conjugation.
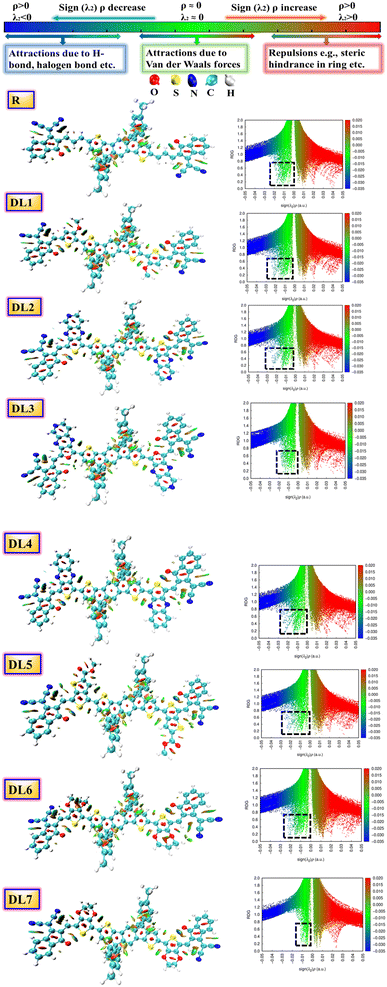 | ||
| Fig. 3 NCI graphs and isosurfaces for the researched molecules. Black dotted squares highlight the presence of non-covalent interactions for R and DL1–DL7. | ||
In this research, we focused on the appearance of peaks on the left y-axis of the graphs. These peaks have a negative sign(λ2) and correspond to various non-covalent interactions. When the electronegativity of atoms within a molecule increases, the peak spread of sign(λ2)ρ is shifted further towards negative values. This indicates that stronger hydrogen bonding is present in the molecule.
The presence of attractive non-covalent interactions in the newly designed molecules is evident from NCI graphs in Fig. 3. It can be seen that the green-colored peaks are spread toward the left. At the same time, the negative values of the effective density “(sign(λ2)ρ)” in all of our conceptualized molecules reveal the regions of electron depletion. Vastly reduced density gradients indicate strong interactions, whereas less reduced density gradients show weaker interactions.
It can be seen from the graphs that van der Waals forces of attraction are highly dominant in DL2 and DL6 molecules as compared to the other molecules. These weak forces are very much responsible for enhancing the stability of molecules. Furthermore, the blue line (on the left side) is above the red band (on the right side) for all the molecules, which signifies that attractive forces are more dominant than repulsive ones. The domination of attractive forces makes these molecules more stable.
Different colors of isosurfaces symbolize different interactions according to electron density. The labeled scale in Fig. 3 has the blue color showing strong, attractive interactions like strong H-bonding. The green color corresponds to medium–weak interactions, whereas red shows repulsive interactions. In DL1–DL7, disc-like blue isosurfaces depict the presence of various interactions, including S⋯O, S⋯H, S⋯N, O⋯H, etc. While remaining irregular patches symbolize some interactions, such as London dispersion and van der Waals forces.36 The small red patches inside the five-membered rings of the central donor core and linkers show repulsive interactions.
Similarly, among the phenyl substituents, large isosurface patches of red and green colors show the presence of repulsive and attractive forces. Repulsions push them out of the plane while the attractive interactions try to keep them in the plane with the rest of the molecule. It can be observed that green patches are present across each molecule in higher quantity, which confirms the dominance of attractive interactions in all these molecules leading towards enhanced stability.
3.2 Frontier molecular orbitals and absorption properties
Frontier molecular orbital (FMO) analysis is mandatory to study the excited state features of the computationally designed molecules. The efficiency of a solar cell is related directly to charge transfer.37 So, to gain insight into the electronic, optoelectrical, and conductive properties of the designed structures, we performed an FMO analysis.38 Band theory explains the push–pull mechanism of electrons by taking HOMO as an electron donor (valence band) and LUMO as an electron acceptor (conduction band).39,40 The difference between energy levels of HOMO and LUMO is called a band gap which is calculated using eqn (3):| Eg = ELUMO − EHOMO | (3) |
The lesser the distance between HOMO and LUMO, the smaller will be the band gap and, hence, the better will be charge transfer. Improved charge transfer boosts a device's overall efficiency.41 For narrower band gaps, the HOMO level of a molecule should lie at a higher energy state. The LUMO should lie at a low energy state, i.e., close to the HOMO. Stable LUMOs can hold maximum electrons in the acceptor vicinity for extended periods, allowing more photon absorption and lifting device performance.37
To reveal the impact of π-spacers on designed molecules DL1–DL7, we studied HOMO and LUMO energy levels along with their respective band gaps at B3LYP/6-31G(d,p) level of DFT, and results are summarized in Table 2. For SJ-IC, the HOMO and LUMO levels are present at −5.43 eV and −3.42 eV, respectively, resulting in a band gap of 2.01 eV. The HOMO levels for DL1–DL7 showed values of −5.02, −5.29, −5.34, −5.14, −5.30, −5.04, and −5.07 eV. On the other hand, energies of their LUMO appear to be at energy onset of −3.26, −3.95, −3.99, −3.73, −3.45, −3.11, and −3.12 eV, respectively. Meanwhile, the HOMO and LUMO of SJ-IC are present at energy levels of −5.43 and −3.42 eV, respectively. These data show that the LUMO of DL2, DL3, DL4, and DL5 reside at higher energy levels than the LUMO of the SJ-IC molecule. This indicates that these molecules have a higher probability of charge transfer from HOMO to LUMO than the reference SJ-IC molecule.
The ideality of the designed molecules is further confirmed by examining each studied molecule's energy difference among FMOs. The newly developed molecules (DL1–DL7) showed bandgap values of 1.76, 1.33, 1.35, 1.40, 1.85, 1.93, and 1.95 eV, respectively. These results show that energy gaps for all investigated molecules are smaller than that for reference (SJ-IC), having a bandgap of 2.01 eV.
DL2 seemed to have the narrowest band gap among all these investigated structures. This confirms that the spacer subunit with conjugated rings containing electronegative nitrogen and sulfur atoms performs better than the other spacers. Furthermore, DL3 and DL4 also show remarkable narrowing of the bandgap due to the presence of the extended conjugated network in spacer subunits. However, all the newly developed molecules (DL1–DL7) exhibited smaller bandgaps than the reference (SJ-IC). Hence, these molecules have marked charge transfer, confirming that inserting π-linkers with extended conjugation effectively modulates the molecules to boost their efficiency.
Further confirmation of the above observations was carried out by obtaining diagrams of FMOs from the relaxed geometry of each molecule. It visually represents intramolecular charge transfer41 and the relation between structure and energy levels.35 Dense colors have been used in FMO pictograms (Fig. 4) to express the flow pattern of the charges (electrons and holes) whose conduction provokes electric current. In R, HOMO is located on the donor part, representing that charge density is located on the donor in the ground state. In contrast, the LUMO part is mainly on the acceptor and π-bridges. It shows that the charges are attracted towards acceptor moieties of the molecule through π-bridges upon excitation. In all designed molecules, the pictures of their FMOs reveal that the donor units hold HOMO density more efficiently than the acceptors.
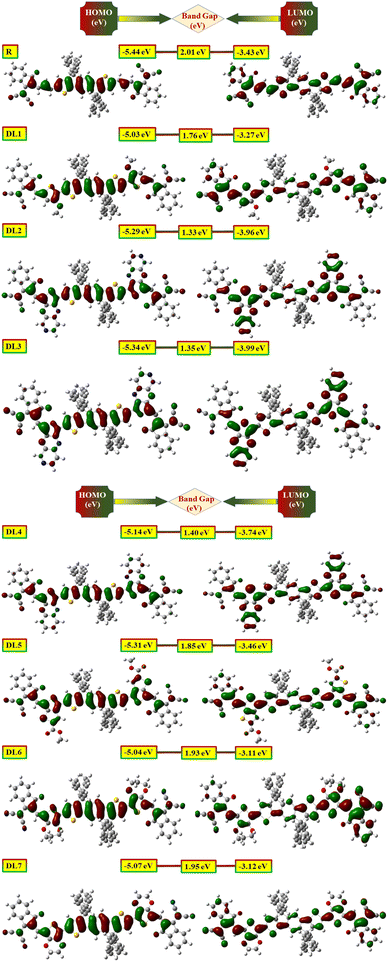 | ||
| Fig. 4 Visual display of highest occupied molecular orbital (HOMO) (left) along with lowest unoccupied molecular orbital (LUMO) (right) of reference and DL1–DL7 molecules. | ||
Likewise, LUMO density is mainly positioned on acceptor units (especially in DL1, DL6, and DL7). The charge density on π-bridges depicts their contribution to charge flow from HOMO to LUMO. These bridges are highly involved in pulling the electric charge density from the central donor core and passing these charges toward acceptor moieties. The above discussion clarifies the importance of our work, as electronic parameters show that these proposed molecules are appropriate candidates to be used for the construction of improved OSCs.
Optical properties play a pivotal role in estimating the overall performance of a device.42 Range of photon absorption, full width at half maximum (FWHM), excitation energy, oscillating strength, and involvement of orbitals contribute to the optical properties of the active layer of OSCs.43 All the studied molecules (R and DL1–DL7) were investigated with the B3LYP/6-31G(d,p) functional of DFT approach in gas and solvent phase. This study was performed to record spectra for the absorption in the UV-visible region and then translated into graphs using the Origin 6.0 program. These graphs are illustrated in Fig. 5 to visualize these molecules' maximum absorption of photons.
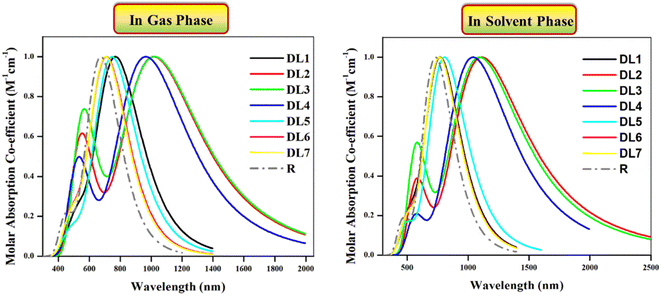 | ||
| Fig. 5 Absorption profiles of investigated molecules in UV-visible region in the gas phase (left) and in chloroform solvent (right) obtained through Origin 6.0 software at B3LYP functional. | ||
Experimental absorption coefficient (λexpmax) for R is reported at 720 nm, which is found to be in good agreement with DFT-based calculated absorption maximum (λcalmax) located at 731.69 nm. The literature shows that a molecule's absorption spectrum strongly depends on the nature of its substituents.35 As in all our planned molecules, building blocks differ regarding their π-linkers. The study of the optical properties helps to decide whether the insertion of investigated π-linkers is fruitful. In the gas phase, all the investigated molecules gave λcalmax in the range of 709–1023 nm. All the investigated molecules show redshifts ranging from 34 to 348 nm compared to R as evident from their λcalmax provided in Table 3.
| Molecule | λexpmax (nm) | λcalmax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (nm) a (nm) |
λcalmax![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b (nm) b (nm) |
Exa (eV) | Exb (eV) | fOSa | fOSb |
|---|---|---|---|---|---|---|---|
| a Gas phase.b Solvent phase. | |||||||
| R | 720 | 675.24 | 731.69 | 1.8362 | 1.6945 | 2.9570 | 3.2324 |
| DL1 | — | 772.38 | 772.38 | 1.6052 | 1.6052 | 2.6922 | 2.6922 |
| DL2 | — | 1018.32 | 1112.86 | 1.2175 | 1.1141 | 1.9092 | 2.2414 |
| DL3 | — | 1023.52 | 1094.78 | 1.2114 | 1.1325 | 1.5462 | 1.8899 |
| DL4 | — | 966.91 | 1040.86 | 1.2823 | 1.1912 | 2.0930 | 2.4747 |
| DL5 | — | 748.59 | 806.48 | 1.6562 | 1.5373 | 2.7547 | 3.0468 |
| DL6 | — | 715.02 | 768.28 | 1.7340 | 1.6138 | 2.583 | 2.8693 |
| DL7 | — | 709.70 | 765.72 | 1.7470 | 1.6192 | 2.7440 | 3.0080 |
We used chloroform for solvent-phase calculations to determine these molecules' working potential in a solvent medium. The parameters calculated for absorption in the solvent phase are illustrated in Table 3. It can be observed that λcalmax of each molecule is higher in the solvent phase than in the gas phase. The highest λcalmax values are exhibited by DL2 and DL3, i.e., 1112 nm and 1094 nm, respectively. UV-visible regions are important spectral regions that are responsible for high light-to-current transformation. Interestingly, λcalmax for DL2, DL3, and DL4 extend to the NIR region while covering the UV-visible range. DL2 exhibited a redshift of 381 nm in λcalmax compared to R. This can be due to the mutual electron withdrawal effect of nitrogen atoms in bridges along with CN groups of the acceptor. Similarly, in all designed molecules, the sulfur, nitrogen, and oxygen in linkers having an enormous electronegative difference provide good electron delocalization compared to a carbon atom in R, leading to higher absorption maxima. High values of λcalmax in the solvent phase also reveal that all these tailored molecules can be effectively used for solution processing of OSCs. Moreover, as all these molecules show light absorption in a broad range, they can produce more photoelectric current by absorbing radiation in a wide range which is beneficial for improving efficiency.
If we examine the graphs for λcalmax in the gas and solvent phases, it can be seen that two peaks characterize each molecule. One peak of smaller height located between 400 and 700 nm corresponds to π–π* transitions present in the respective molecule. In contrast, the heightened peak depicts absorption maxima for each molecule. The efficiency of introduced π-linkers is evident from the graphs via NIR region absorption peaks. Compared to R, the smaller peaks for the designed molecules are also increased due to the high number of π–π* transitions. The descending order of λcalmax in solvent phase calculated for reference and designed molecules (DL1–DL7) is: DL2 > DL3 > DL4 > DL5 > DL1 > DL6 > DL7 > R. This also shows that the decreased band gaps lead to enhanced absorption maxima as a lower band gap facilitates excitation of electrons from HOMO (ground state) to LUMO (excited state).
The photovoltaic properties of molecules of the photochemically active layer also depend on excitation energy.43 It is the amount of energy required for the transition of charge from a relaxed ground state to an excited state.44 For current generation, charge excitation is necessary as photocurrent is produced due to excited-state charges. The lower the excitation energy of charges, the higher the excitation of charges upon relaxation even for low energy radiations.43,44 So lower excitation energy causes accelerated transitions between HOMO and LUMO, leading to more charge transfer, guaranteeing efficient photovoltaic properties.44,45 The Ex values for the reference and DL1–DL7 are provided in Table 3. These calculated values show that the excitation energies range between 1.21 and 1.74 eV in the gas phase and 1.11 and 1.61 eV in the solvent phase. All the tailored molecules have smaller excitation energy values than R, which means these molecules have reasonable charge excitation potential. Furthermore, lower Ex in solvent phase indicates their capability of being solution-processable.
It can be noticed from Fig. 5 that molecules show significant absorption up to 1600 nm in a gaseous and solvent medium. The molecules possess multiple electronic transitions with different energies contributing to their absorption profile. The absorption at shorter wavelengths could be associated with higher energy transitions. While the absorption at longer wavelengths can be related to lower energy transitions.46,47 This broader absorption profile would allow the molecules to absorb light over various wavelengths.
In specific conjugated organic chromophores, excitonic effects can occur. Excitons are bound electron–hole pairs due to the coulombic interaction between an excited electron and a positively charged hole. These excitons can have lower energy than the calculated HOMO–LUMO gap and can contribute to the absorption profile at longer wavelengths.48,49
Furthermore, the presence of multiple excited states can also explain the broadening of the absorption profile.50 As these studies were carried out at multiple excited states, the absorption of light up to 1600 nm can be due to lower excited states.
Oscillator strength (fOS) measures the intensity of electromagnetic emission resulting from electronic transitions. Organic chromophores with higher oscillation strength show an enhanced probability for photon absorption resulting in higher light harvesting efficiency.43 For R and designed molecules, fOS values in gas and solvent phases are provided in Table 3. Although R exhibited higher fOS in both phases, fOS for the tailored molecules is also sufficient for successful transitions. Among all the newly designed molecules, DL5 and DL7 show the highest oscillator strength with values of 3.0468 and 3.0080, respectively, giving them superiority over other molecules.
3.3 Natural transition orbitals (NTOs)
For systems with extended conjugation, the consideration of NTOs is required in addition to simple FMO analysis. NTOs provide a more reliable description of inter- or intramolecular charge transfers and quantitatively explain electronic transitions. The study of NTOs can be considered an alternative method to simplify the complex descriptions of transitions obtained through the transition density matrix. Thus, it also helps to visualize the distribution pattern of the electrons and holes in a molecule's excited state. In the case of NTOs, the occupied orbital is named a “hole” as an electron is ejected from it. In contrast, the virtual orbital is said to be an “electron” as an ejected electron from the hole is occupied by the virtual orbital.51,52For all our studied molecules, we selected only those transition states with high oscillation strength and were found to be the first transition states. Fig. S3 (ESI†) shows that the hole area is predominantly spread on the donor regions in all designed molecules. In contrast, the electron area is localized on the bridge and acceptor fragments of the molecules. Thus, upon excitation, the charges from the orbital of the donor are transferred to unoccupied orbitals located on the acceptor or π-linker. This process ensures that a well-defined ICT is present among various fragments of each molecule.
We also noted the highest eigenvalue of transitions for each molecule. This represents the electron transport contributions (ETC) and is essential for understanding the extent of transitions. The calculated values of ETC as percentages are illustrated in Table 5. DL1 and DL4 show the most efficient electronic transitions, with the highest ETC values of 99.9%. The rest of the molecules also have better transport of electrons from HOMO to LUMO, as evidenced by their high value of transition characters, above 97% for all designed molecules. These data of electronic transitions from donor to acceptor regions confirm the high success rate of charge transfer in all these molecules, which is better for improving net efficiency.
3.4 Density of states
Results obtained by examining FMOs have been verified by DOS analysis. It was performed at B3LYP/6-31G(d,p) for the reference and structurally tailored (DL1–DL7) molecules. DOS depicts the contribution of various molecule fragments in forming the FMOs.45,53 The DOS determines the total number of states that electrons can occupy at a specific energy level. The higher the number of states that are occupied by electrons, the higher the value for DOS; hence, the higher will be the electron density.54 Thus, through DOS, we get insight into the contribution of the molecule's building blocks in constructing borderline molecular orbitals (FMOs). The DOS graphs for the reference and all designed molecules (DL1–DL7) are provided in Fig. 6.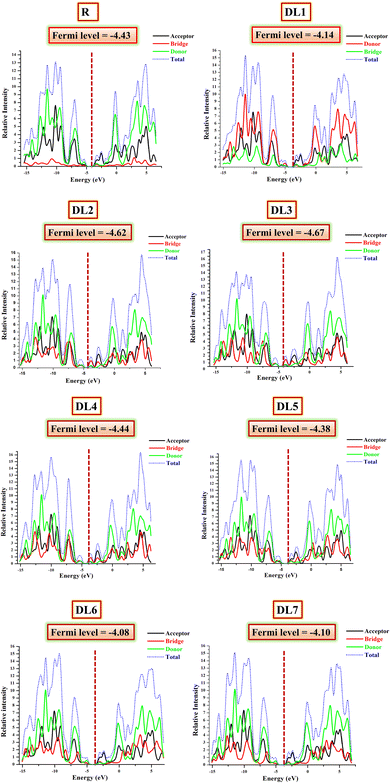 | ||
| Fig. 6 DOS graphs reveal the involvement of three fragments (donor, spacer, and acceptor) of the planned molecules (DL1–DL7) in raising HOMO and LUMO energy levels. | ||
The DOS graphs label the y-axis with the available states at specific energy levels, while the x-axis is labelled with three central values. Negative ones on the left side depict HOMO energy levels, and positive ones towards the right side represent LUMO. At the same time, the central region corresponds to the band gap between HOMO and LUMO.55 The zigzag lined curves represent HOMO–LUMO charge density, and the area under these curves corresponds to possible excitation states for charge density. DOS calculations have the advantage that in addition to total DOS, they also give partial density of states (PDOS) for each molecule fragment.
While inspecting PDOS, the individual participation of each fragment of a molecule in FMOs can be observed.44 On the other hand, the total DOS gives the total charge flow density of the whole molecule.40 For PDOS, the reference and our newly developed molecules were portioned into three parts: acceptor (shown with black), donor (represented by the red line), and bridge (highlighted with green color in graphs). All these fragments collectively constructed the total DOS, represented with the blue dotted line. The fragment that strongly contributes to forming HOMO or LUMO will have greater electron density. Such a fragment gives a peak with a higher crest in the DOS graph in the HOMO or LUMO region.56
The calculated values of DOS for each molecule involved in the current study are summarized in Table 4. If we examine the DOS data for the reference, it can be seen that the significant contribution for HOMO is from the donor part, i.e., 60.1%. In comparison, the acceptor has a minor (25.7%) contribution to the formation of HOMO. The bridge has the lowest contribution (14.3%) in the elevation of HOMO. In raising LUMO, the acceptor and bridge participate effectively in LUMO, contributing 52.6% and 17.5%, respectively.
| Molecule | HOMO | LUMO | ||||
|---|---|---|---|---|---|---|
| Acceptor (%) | Donor (%) | Linker (%) | Acceptor (%) | Donor (%) | Linker (%) | |
| R | 25.7 | 60.1 | 14.3 | 52.6 | 29.8 | 17.5 |
| DL1 | 20.0 | 23.3 | 56.8 | 56.7 | 18.6 | 24.7 |
| DL2 | 25.8 | 40.8 | 30.4 | 20.3 | 19.1 | 60.6 |
| DL3 | 33.7 | 35.8 | 30.5 | 19.4 | 20.0 | 60.6 |
| DL4 | 30.1 | 46.1 | 30.6 | 40.7 | 27.8 | 31.5 |
| DL5 | 23.3 | 46.1 | 30.1 | 40.7 | 27.8 | 31.8 |
| DL6 | 19.6 | 57.9 | 22.5 | 55.5 | 19.6 | 24.9 |
| DL7 | 20.2 | 57.3 | 22.5 | 53.1 | 21.4 | 25.5 |
Similarly, for all our designed molecules, the HOMO levels have been raised mainly due to donor parts. In contrast, the rise in LUMO levels can be seen due to the higher percentage contribution of acceptors and bridges. All the π-bridges in our planned molecules seem to be better charge distributors than a double-bond-containing bridge present in R. These outcomes are supported through their tabulated percentage participation obtained from Mulliken's calculations shown in Table 4. Interestingly, in the case of DL2 and DL3, it can be seen that the contribution of spacer subunits is up to 60.6% in forming the total LUMO. This means these highly conjugated spacers efficiently collect charges from the central donor portion.
The conductive property of any part corresponds to its location. If a part is located near LUMO, its involvement in conductivity will be higher due to the many available states. As inserted π-spacers have more conjugation and more π–π* transition possibilities, these spacers and acceptors gave higher output than SJ-IC (R). As a result, LUMO peaks showed suitable intensities, confirming that replacing the double bond in R with the above-mentioned π-spacers is a fruitful strategy.
3.5 Dipole moment
The dipole moment vector provides information regarding a molecule's planarity and solubility in a desired solvent.19 The dipole moments for R and all designed molecules in the gas and solvent phases are provided in Table 5. These values were computed through the B3LYP/6-31G(d,p) level of DFT. Our compounds are mostly planar except for the phenyl ring substituents attached to the core. Their dipole moments are lower due to their linear geometry attained via optimization. Due to symmetrical geometry, opposite charges come in front of each other in opposite directions. Thus, they cancel each other's effect to some extent. So, as revealed for all our planned structures, low dipole moments, higher planarity and more conjugation result in higher absorption maxima.| Molecule | μg (D) | μs (D) | Ebb (eV) | Interaction coefficienta | Interaction coefficientb | ETCa (%) |
|---|---|---|---|---|---|---|
| a Gas.b Chloroform solvent. | ||||||
| R | 0.04380 | 0.02930 | 0.316 | 0.7058 | 0.7025 | 99.6 |
| DL1 | 0.04160 | 0.04160 | 0.158 | 0.7069 | 0.7069 | 99.9 |
| DL2 | 0.09180 | 0.08630 | 0.224 | 0.7062 | 0.7036 | 99.7 |
| DL3 | 0.02460 | 0.13240 | 0.218 | 0.7031 | 0.7016 | 98.9 |
| DL4 | 0.01071 | 0.04260 | 0.215 | 0.7069 | 0.7035 | 99.9 |
| DL5 | 0.03478 | 0.05622 | 0.318 | 0.7045 | 0.7004 | 99.3 |
| DL6 | 2.17295 | 2.72379 | 0.325 | 0.7001 | 0.6973 | 98.0 |
| DL7 | 0.56570 | 0.67680 | 0.337 | 0.7058 | 0.6999 | 99.1 |
It is a fact that a higher dipole moment is necessary for improved movement of charges.37 The dipole moment values calculated in the solvent are slightly higher than those of the gas state. Interestingly, DL1 has a similar dipole moment in both gas and solvent phases, indicating that the solvent does not affect the dipole moment of this molecule. Such dipole moment vectors indicate that DL1–DL7 have positioned themselves to lower the charge recombination. Among all these molecules, DL6 shows the highest dipole moment in gas and solvent phases, with values of 2.17295 D and 2.72379 D, respectively. This shows that the DL6 molecule can have better charge mobility based on dipole moment than the other molecules.
The dipole moment also influences intramolecular charge transfer by affecting molecular fabrication. Two molecules with different dipole moments arrange such that their dipole moments are antiparallel. In this way, they create long tracks for the charges to move because their opposite faces attract each other due to the antiparallel alignment of their dipole moments.57,58 So, a higher dipole moment of a molecule enhances its solubility along with improved crystallinity leading toward closer molecular assemblages.40 The notable thing about our planned molecules is that they all have improved dipole moments compared to R. Thus, they are well compatible with chloroform solvent.
3.6 Exploration of physiochemical properties through an MEP map
To reveal the physiochemical properties of molecules such as three-dimensional electron density, reactive sites, and nucleophilic and electrophilic points,59 their molecular electrostatic surface potentials (MESPs) are portrayed. This study gives information about charge transfer across a molecule in the excited state.35 MESP surfaces appear like a cloud with three primary colors. Each color code corresponds to the specific strength of the electrostatic potential of the molecule.Red shades represent negative electrostatic potential. The red portion of the molecule is electron-rich, a possible attack site for electrophiles, and attractive points for protons due to aggregated electron density at these regions.60 In comparison, cyan and blue shades represent positive electrostatic potentials. It symbolizes that these areas correspond to electron-deficient sites, susceptible to nucleophilic attack, and repulsive areas for protons due to the atomic nuclei of molecules at these sites. In comparison, sites shaded with green represent areas with neutral electrostatic potential.
A color scale is also formed along with each MEP cloud with deep red color at one end, moving towards deep blue color at the other end.37 MEP plots for R and the structurally engineered molecules are displayed in Fig. S4 (ESI†). Fascinatingly, it can be seen that more red color exists at the acceptor regions of DL2, DL3, and DL5 molecules than the other molecules. This shows enhanced charge separation in these molecules depicting that these newly planned molecules can be efficiently designed for OSCs.
MEPs for the reference and designed molecules show cyan colors on the sides of the core, methyl groups of linkers, and phenyl rings of acceptors. Thus, these areas are susceptible to nucleophilic attack. In contrast, the negative potential represented by the red color is present on the acceptor and π-linkers having N, O, and S atoms. It shows that these regions provide a robust and attractive force for electrons and are responsible for better charge delocalization. But if we look at those N, O, and S atoms of various bridges facing towards the core, they do not show negative potential there, although they are still electronegative. The reason is the canceling effect produced by the positive potential of hydrogens and carbons of the core located in their vicinity. There is no high prevalence of blue color (positive electrostatic potential), while various areas of negative potential exist. So, it can also be inferred from obtained MESP surfaces that each of our planned molecules has the potential to behave as an acceptor molecule in the active layer of OSCs.
3.7 Chemical reactivity
There are five main parameters whose values give an idea about the reactivity of acceptor and donor molecules. These parameters also specify the charge transfer direction from one molecule to another. Namely, these are chemical potential (μ), chemical softness (S), chemical hardness (η), electrophilicity index (ω), and electronegativity (χ). We calculated these values using eqn (4)–(8) to get an insight into chemical reactivity.61–63For an acceptor, the chemical potential (μ) is the tendency to acquire a negative charge. For a donor, it is the electron-donating capacity of the molecule. The chemical potentials calculated for DL1–DL7 through eqn (4) are provided in Table 6.
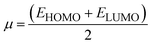 | (4) |
| Molecule | μ (eV) | η (eV) | S (eV−1) | χ (eV) | ω (eV) |
|---|---|---|---|---|---|
| R | −4.43 | 1.01 | 0.99 | 4.43 | 9.79 |
| DL1 | −4.14 | 0.88 | 1.13 | 4.14 | 9.75 |
| DL2 | −4.62 | 0.67 | 1.49 | 4.62 | 16.01 |
| DL3 | −4.66 | 0.67 | 1.48 | 4.67 | 16.14 |
| DL4 | −4.43 | 0.70 | 1.42 | 4.44 | 14.01 |
| DL5 | −4.38 | 0.93 | 1.08 | 4.38 | 10.38 |
| DL6 | −4.07 | 0.97 | 1.03 | 4.08 | 8.64 |
| DL7 | −4.09 | 0.98 | 1.02 | 4.09 | 8.58 |
| PTB1 | −4.05 | 0.85 | 1.17 | 4.05 | 9.64 |
| PCPDTBT | −4.42 | 0.72 | 1.38 | 4.42 | 661 |
| PTB7-Th | −4.40 | 0.80 | 1.25 | 4.40 | 12.10 |
PTB1, PCPDTBT, and PTB7-Th are selected as donors for our structurally engineered molecules and have a chemical potential of −4.05 eV, −4.42 eV, and −4.40 eV, respectively. PTB1 is selected for the reference, DL1, DL6, and DL7. PCPDTBT is selected for DL2, DL3, and DL4. PTB7-Th is selected for DL5 due to better matching of HOMO and LUMO energy levels. Except for DL5, all the other newly designed molecules have better chemical potential values than the donor used for them. DL2 and DL3 have significantly higher chemical potential than the corresponding donors, meaning that DL2 and DL3 are promising acceptor molecules.
Chemical potential further depends on the chemical softness (S) and hardness (η), which are inversely interlinked. Table 6 illustrates these parameters, which we obtained through eqn (5) and (6):
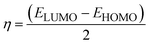 | (5) |
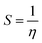 | (6) |
Higher softness is responsible for smooth electron transfer due to low resistance. As evident from softness values in Table 6, all our newly developed molecules (DL1–DL7) show higher softness than the reference. DL2, DL3, and DL4 show a remarkable improvement in softness with values of 1.49 eV, 1.48 eV, and 1.43 eV, respectively. This shows the probability of enhanced charge transfer rate in these designed molecules making our strategy of inserting conjugated π-linkers successful. All other newly designed molecules also show improvement in softness by lowering the hardness. This might be because these π-linkers have enhanced interactions of various molecular parts, resulting in an increase in ICT.
Electrophilicity (ω) and electronegativity (χ) explain excessive electron flow. The direction of electron flow depends on the values obtained from eqn (7) and (8):
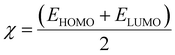 | (7) |
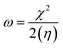 | (8) |
Table 6 illustrates the higher tendency of DL2, DL3, and DL4 for electrons with higher ω values of 16.0, 16.1, and 14.0 eV as compared to the other molecules. Similarly, the high electronegativity of the same molecules represents their better electron-accepting ability from donor molecules. These aspects of the mentioned molecules make them a superior choice for the development of efficient OSCs in the future.
3.8 Examination of charge transfer
| Eb = Eg − Ex | (9) |
Table 5 illustrates the values of the binding energy of excitons for the proposed molecules with values of 0.158 eV, 0.224 eV, 0.218 eV, 0.215 eV, 0.318 eV, 0.325 eV, and 0.337 eV for DL1–DL7 respectively. On the other hand, the binding energy of R is 0.316 eV. DL1 shows the lowest value of exciton binding energy. DL2, DL3, and DL4 also show lower exciton binding energy than the reference molecule. This means that these molecules have improved potential for the dissociation of excitons. Thus, based on the results of exciton Eb, it can be proposed that these molecules might have the potential for significant charge mobility.
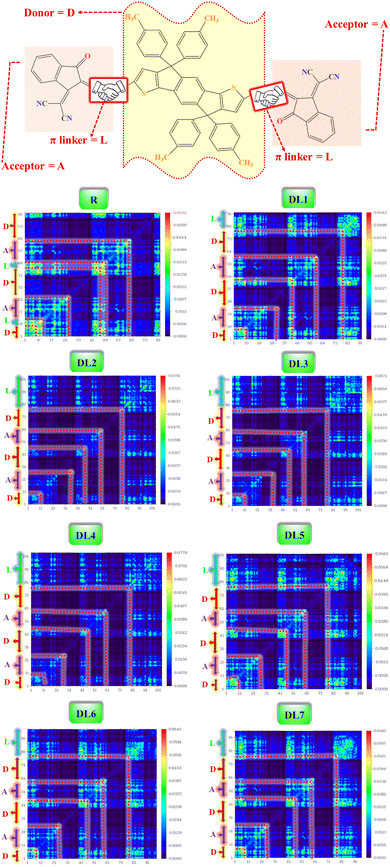 | ||
| Fig. 7 TDM heat maps for R and DL1–DL7 with red dotted lines partitioning the fragments of molecules. | ||
Atom numbers are displayed on the bottom x-axis and left y-axis. The electron density coefficient in the colored scale is also displayed for each molecule on the right y-axis. The bright blue-green areas against dark blue background symbolize charge transfer. From TDM plots for all of our proposed molecules, it can be observed that the electrons are distributed throughout the molecules due to extended conjugation. It can be observed that there is coherence in the regions of TDM maps which are specific for atoms of π-bridges and acceptor, separately. This confirms that π-linkers further facilitated charge transfer from one edge of the molecule to the other edge without charge trapping. Here π–π* transitions are represented through the coherence of electrons along the diagonal pathway. Like R, some core regions lack electronic transitions in all designed structures. Moreover, similar charge distribution behavior was revealed for R and the designed molecules, which shows the effectiveness of inserting π-linkers. From in-depth observations, it can be seen that there exist more electron interactions in the acceptor and spacer region of DL1 and DL5 molecules, indicated by more bright spots in the maps of these molecules.
Dissociation of excitons and capability of charges to migrate show inverse relation with interaction coefficient. A low interaction coefficient leads to fewer interactions among charges. Hence, molecules with low interaction coefficients have a high potential for the mobility of charges in various parts of the molecule. The interaction coefficient of all the studied molecules varies in chloroform solvent in increasing order as: DL6 < DL7 < DL5 < DL3< R < DL4 < DL2 < DL1.
DL6 and DL7 have small interaction coefficients; hence, the easiest charge transfer can occur in them in contrast to the others. However, it can be observed that a tiny difference exists in the values of all molecules' interaction coefficients. So, all these molecules have the probability of only a few interactions among charges which leads to a higher charge transfer rate in all these molecules. The cyanide groups present in the acceptor of each molecule improve the electron-withdrawing effect. These acceptor subunits possess electronegative nitrogen, sulfur, and oxygen atoms sp-hybridized in π-linkers. In conjunction with conjugated π-linkers, the cyanide groups further increase the conjugation of tailored structures. Hence, interactions among excitons are lowered, and excitons are easily separated, as evident from small values for the interaction coefficient of all designed molecules.
High EA is concerned with better electrophilicity and improved electron transport and injection.68 Molecules with high EA are used as efficient electron acceptors because they can take up electrons easily. However, donor materials should have low IP to donate electrons easily. Electron-donating moieties attached to a molecule cause a decrease in IP because HOMO levels are destabilized by facilitated electron transfer by these electron-donating groups. However, molecules having electron-withdrawing groups attached to them exhibit elevated IP because of the stabilization of HOMO, and electron removal becomes challenging.
We calculated IP and EA according to eqn (10) and (11), respectively,55 and summarize the results in Table 7:
| IP = [E+0 − E0] | (10) |
| EA = [E0 − E−0] | (11) |
| Molecule | λh (eV) | λe (eV) | EA (eV) | IP (eV) |
|---|---|---|---|---|
| R | 0.185 | 0.209 | 2.656 | 6.211 |
| DL1 | 0.188 | 0.129 | 2.536 | 5.766 |
| DL2 | 0.058 | 0.156 | 3.249 | 5.962 |
| DL3 | 0.139 | 0.154 | 3.274 | 6.009 |
| DL4 | 0.139 | 0.160 | 3.036 | 5.807 |
| DL5 | 0.161 | 0.182 | 2.753 | 6.013 |
| DL6 | 0.195 | 0.154 | 2.379 | 5.788 |
| DL7 | 0.186 | 0.147 | 2.396 | 5.814 |
All newly developed molecules (DL1–DL7) showed lower IP because their HOMO levels are at higher energy onsets than that of the reference. The least value of IP was shown by DL1 having an IP of 5.766 eV. Similarly, DL2 (3.249 eV), DL3 (3.274 eV), DL4 (3.036 eV), and DL5 (2.753 eV) showed significantly improved EA compared to R (2.656 eV). This is because the inserted π-linkers played a role in stabilizing the LUMOs, making electron injection easier. Hence, these are expected to have smooth electron flow.
The sum of ground- and excited-state reorganization energies (i.e., λ1 + λ2) gives λh as depicted in Fig. S5 (ESI†). λ1 (reorganization energy in ground state) equals the difference of energies of optimized neutral state and cationic geometry. On the other hand, λ2 represents the excited-state reorganization energy which is calculated as the energy difference of cationic energy of optimized molecule in charged state and neutral state geometry.
Charge mobility is inversely dependent on reorganization energy. Those molecules with lower reorganization energy have higher charge mobilities because they need a small driving force for exciton dissociation. A high value of reorganization energy results in non-radiative recombination.9 Our calculations revealed a decrease in reorganization energies for most of our structurally engineered molecules compared to the reference. These results are fruitful for enhancing exciton lifetime, improving charge transfer, and suppressing non-radiative recombination of charges. DL1 showed the lowest λe (0.129 eV), while DL2 showed minimum λh (0.058 eV). The λh of all the molecules increases in the order: DL2 (0.058 eV) < DL3 = DL4 (0.139 eV) < DL5 (0.161 eV) < R (0.185 eV) < DL7 (0.186 eV) < DL1 (1.88 eV) < DL6 (1.95 eV). On the other hand, all newly designed molecules show lower λe than the reference molecule. This means all these newly developed molecules have significantly improved electron transfer potential compared to R. The added π-linkers successfully reduced the energy barrier by conjugation, and as a result, charge mobility increased.
3.9 Light harvesting efficiency
Light harvesting efficiency (LHE) is another significant parameter that shows the photocurrent response of a molecule by absorption of radiation. When the LHE of a molecule is more significant, it will produce a high quantity short circuit current and intensify the molecule's photocurrent response. LHE is determined through oscillator strength (fOS) which measures the emission/absorption of radiation during the transition of electrons from one energy level to another. LHE of R and DL1–DL7 is presented in Table 8. It is calculated through eqn (12):70| LHE = 1 − 10−f | (12) |
| Molecule | ΔE (eV) | VOC (eV) | Normalized VOC | FF | LHE |
|---|---|---|---|---|---|
| R | 1.48 | 1.18 | 61.8357 | 0.9183 | 0.9994 |
| DL1 | 1.64 | 1.34 | 68.0193 | 0.9242 | 0.9971 |
| DL2 | 1.20 | 0.9 | 41.3527 | 0.8881 | 0.9943 |
| DL3 | 1.16 | 0.86 | 39.8068 | 0.8848 | 0.9871 |
| DL4 | 1.42 | 1.12 | 49.8551 | 0.9032 | 0.9967 |
| DL5 | 1.75 | 1.45 | 60.6763 | 0.9170 | 0.9991 |
| DL6 | 1.79 | 1.49 | 73.8164 | 0.9290 | 0.9987 |
| DL7 | 1.78 | 1.48 | 73.4300 | 0.9287 | 0.9990 |
Eqn (12) shows the direct dependence of LHE on oscillator strength fOS. A higher value of oscillator frequency of a molecule intensifies the absorption peak of that molecule.54 All our modelled molecules have comparable oscillator frequencies, and hence due to the direct relation of fOS with LHE, their LHEs also lie in a similar range. Among all the newly designed molecules, DL5 shows a maximum LHE value (0.991 eV), which is slightly better than those of the other designed molecules. These comparable values of LHE suggest that all these molecules can perform efficiently in OSC devices.
3.10 Open circuit voltage
Among the technical parameters which are most challenging to improve, open circuit voltage (VOC) is a crucial one. When the current flow is zero, the voltage value attained across a photovoltaic device is called open-circuit voltage.43 A higher value of a system's VOC leads to higher photocurrent conversion efficiency. To theoretically estimate the VOC of any photovoltaic system, Scharber's equation is used, which is given as:
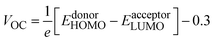 | (13) |
Hence, we calculated the VOC by computing the difference between the HOMO of the donor and the LUMO of designed acceptors (DL1–DL7), and the obtained results are portrayed in Fig. 8. The HOMO–LUMO of PTB1, PCPDTBT, and PTB7-Th lie at 4.90/3.20 eV, 5.15/3.70 eV, and 3.60/5.20 eV, respectively, as reported in the literature.72–74 The difference between the energy of HOMO and LUMO of donor and acceptor material is known as the electrochemical potential difference (ΔE), which signifies the interlayer bandgap.72,73 The tabulated values of ΔE of all molecules are also mentioned in Table 8.
It can be observed that there is a negative offset of the HOMO and LUMO levels between the donor and our acceptor molecules. A negative offset of HOMO means that the HOMO level of the acceptor is higher than that of the donor, i.e., in the case of PCPDTBT:DL4 blend. In this case, charge transfer is governed mainly by a hole transfer mechanism. Facilitated hole transfer occurs when a hole in the donor material is first transferred to an intermediate state. Then the hole can be transferred from the intermediate state to the acceptor material. Once the hole is transferred to the acceptor material, it can move from the acceptor material towards the electrode, generating a photocurrent.74,75
On the other hand, when the LUMO of the acceptor molecule is energetically lower than the LUMO of the donor molecule, a negative LUMO offset is created.76 The negative LUMO offset between the donor and acceptor molecules facilitates charge transfer by providing an energy gradient for electron movement.77 This offset ensures that the electron can quickly move from the donor to the acceptor, minimizing energy losses and enhancing the overall efficiency of the OSC.78 After absorbing light energy, electrons in the donor molecule are excited from the ground to a higher energy state, leaving behind a positively charged hole. The excited electron in the donor molecule absorbs enough energy to overcome the energy barrier created by the negative LUMO offset. It can then transfer from the donor molecule to the acceptor molecule. Once the electron is transferred to the acceptor molecule, it can move through the acceptor material, eventually reaching the electrode. Simultaneously, the positively charged hole left behind in the donor molecule can move in the opposite direction towards the other electrode. The movement of electrons and holes toward their respective electrodes creates an electric current.79,80 A negative offset of the LUMO energy level creates a separation of positive and negative charges, which is essential for the functioning of a solar cell.81
Table 8 shows that our designed molecules DL1, DL5, DL6, and DL7 have higher VOC with values of 1.34, 1.45, 1.49, and 1.48 eV, respectively, in comparison to the VOC of R (1.18 eV). The remaining proposed acceptors also show significant VOC, enough for electron transfer from the respective donors to the acceptors (DL1–DL7). The reason for better VOC is the low-lying HOMOs of donor materials while high-lying LUMOs of all planned NFAs. This increases the bandgap of the active layer, resulting in improved open circuit voltage.82 It can be noticed that the VOC of all these newly designed molecules is less than the active layer bandgap between the donor and acceptor molecules. This enhances the extent of their experimental applications. Due to this remarkable improvement in VOC, these newly designed molecules (especially DL6) should be considered for making advanced OSCs in the future.
3.11 Fill factor
The fill factor directly influences the light-to-electricity conversion efficiency of any photovoltaic device. It is mainly dependent on open circuit voltage. The higher the value of VOC, the higher will be the fill factor, and, consequently, the PCE of the device will also be higher. The ideal and perfect value for the fill factor is unity (i.e., 100%).83 We employed eqn (14) to calculate the fill factor of R and all optimized planned molecules:84,85
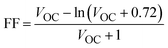 | (14) |
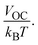 Normalized VOC is used for the theoretical calculations of FF. VOC represents open circuit voltage and kB is Boltzmann's constant (8.61733 × 10−5 eV K−1).
Normalized VOC is used for the theoretical calculations of FF. VOC represents open circuit voltage and kB is Boltzmann's constant (8.61733 × 10−5 eV K−1).
All the proposed molecules give FF values that are close to the ideal value for FF with 0.9242 for DL1, 0.8881 for DL2, 0.8848 for DL3, 0.9032 for DL4, 0.9170 for DL5 while 0.9290 and 0.9287 for DL6 and DL7, respectively, as evident from Table 8. DL1, DL6, and DL7 show remarkable improvement in FF compared to the reference SJ-IC. There can be several reasons that can lead to improved fill factor in OSCs. One theory suggests that optimizing the charge transport and reducing the recombination losses cause a higher fill factor.86 All the newly designed molecules have the potential for improved charge transport due to their lower reorganization energy than the reference. This can improve the fill factor in the newly designed molecules. Another scenario involves using low-bandgap polymers or small molecules, which can broaden the absorption spectrum and increase the open-circuit voltage, resulting in a higher fill factor.87 Enhanced light harvesting and increased light absorption in the active layer can improve the fill factor.88 As indicated from the absorption profiles of these studied molecules, newly designed molecules have broader absorption spectra which can enhance the fill factor of these molecules. Therefore, these molecules should be kept in focus for making efficient solar cells in the future as they emerge as potential candidates as a result of this study.
3.12 Short circuit current density
Short circuit current density (JSC) is an essential factor that influences the photovoltaic performance of solar cells. It measures the maximum current density that can be generated by a solar cell in the absence of any external resistance. Depending on several factors, JSC is the highest current that can be drawn from the solar cell. It is mainly affected by the number of photons, the incident light spectrum, the absorption coefficient of the active layer material, the charge carrier mobility, and the electron and hole diffusion lengths.89,90A higher JSC value generally results in a higher overall PCE of a solar cell. It is a direct measure of the quantity of current flowing through a circuit so that it can be accurately measured only by experimental methods. However, measuring other factors that affect JSC makes it possible to predict the improvement or decrement of JSC for the designed molecules compared to the reference molecule. It is noticed that higher absorption in the active layer leads to a higher JSC. Similarly, higher mobility allows for more efficient extraction of photogenerated charges, resulting in a higher JSC.91–93
The JSC value of the SJ-IC molecule is 13.70 mA cm−2.19 It can be observed that our newly proposed molecules show a significant improvement in light absorption owing to a broader absorption profile. This can lead to improved short-circuit current density in these proposed molecules. Similarly, higher charge mobility in the newly proposed molecules due to low reorganization energy can also improve the JSC of these molecules. It makes these molecules more suitable for developing efficient OSCs in the future.
4. Conclusion
In this quantum chemical approach, we studied the effect of inserting various π-linkers to reveal photovoltaic properties of SJ-IC. The conceptualized molecules outperformed the reference SJ-IC in the context of photovoltaic properties. All newly designed molecules exhibited significantly reduced band gap (Eg) between their respective FMOs in contrast to R. Furthermore, they show notably higher λcalmax, i.e., up to NIR in absorption spectra with broadened FWHM, thus having a better ability to harvest light. We studied various global descriptors, including chemical potential (μ), electronegativity (χ), chemical hardness (η), softness (S), along with electrophilicity (ω). The improved photovoltaic properties of designed molecules make them promising for use in OSCs. Lower excitation energies shown by the tailored molecules lead to easier charge excitation with a considerably better mobility rate for charges. The presence of NCI played the role of conformational locks to retain planarity, which was confirmed through NCI graphs and isosurfaces. The main challenge for OSCs is to achieve higher open-circuit voltage. Our results reveal that DL1 and DL6 can stand as the best acceptors out of those studied. The VOC values of these molecules range from 0.86 to 1.49 eV. The extent of improved charge mobility and photovoltaic efficiency shown by the newly designed molecules is remarkable. However, for conducive electron injection, these VOC values are considered acceptable. Lastly, the study of the J61:DL6 complex verified the acceptor nature of our designed molecules and confirmed the efficient charge transfer from donor to acceptor. Overall our research suggests that all the newly tailored molecules are efficient acceptor materials in contrast to the reported reference SJ-IC.Conflicts of interest
Authors have no conflict of interest.Acknowledgements
The authors extend their appreciation to the Researchers Supporting Project, number (RSPD2023R743), King Saud University, Riyadh, Saudi Arabia, for funding this work.References
- Y. Kervella, J. M. A. Castán, Y. A. Avalos-Quiroz, A. Khodr, Q. Eynaud, T. Koganezawa, N. Yoshimoto, O. Margeat, A. Rivaton, A. J. Riquelme, V. M. Mwalukuku, J. Pécaut, B. Grévin, C. Videlot-Ackermann, J. Ackermann, R. Demadrille and C. Aumaître, J. Mater. Chem. C, 2023, 11, 8161–8169 RSC.
- L. Yu, Y. Li, Y. Wang, X. Wang, W. Cui, S. Wen, N. Zheng, M. Sun and R. Yang, ACS Appl. Mater. Interfaces, 2019, 11, 31087–31095 CrossRef CAS PubMed.
- S. Sadiq, M. Waqas, A. Zahoor, R. F. Mehmood, M. Essid, Z. Aloui, R. A. Khera and S. J. Akram, J. Mol. Graphics Modell., 2023, 123, 108518 CrossRef CAS PubMed.
- J. Wang, G. Cai, B. Jia, H. Lu, X. Lu, X. Zhan and X. Chen, J. Mater. Chem. A, 2021, 9, 6520–6528 RSC.
- H. Wang, J. Cao, J. Yu, Z. Zhang, R. Geng, L. Yang and W. Tang, J. Mater. Chem. A, 2019, 7, 4313–4333 RSC.
- P. Cheng and Y. Yang, Acc. Chem. Res., 2020, 53, 1218–1228 CrossRef CAS PubMed.
- H. W. Cheng, Y. Zhao and Y. Yang, Adv. Energy Mater., 2022, 12, 2102908 CrossRef CAS.
- R. Q. Yang, W. Huang and M. B. Santos, Sol. Energy Mater. Sol. Cells, 2022, 238, 111636 CrossRef CAS.
- Y. Shi, Y. Chang, K. Lu, Z. Chen, J. Zhang, Y. Yan, D. Qiu, Y. Liu, M. A. Adil and W. Ma, Nat. Commun., 2022, 13, 3256 CrossRef CAS PubMed.
- M.-H. Lee, Sol. Energy, 2022, 234, 360–367 CrossRef CAS.
- J. H. Kim, T. Schembri, D. Bialas, M. Stolte and F. Würthner, Adv. Mater., 2022, 34, 2104678 CrossRef CAS PubMed.
- M. Ishtiaq, M. Waqas, H. Zubair, R. F. Mehmood, N. Al-Zaqri, R. A. Khera, M. A. A. Ibrahim and J. Iqbal, J. Mol. Liq., 2023, 386, 122473 CrossRef CAS.
- M. Majeed, M. Waqas, R. F. Mehmood, N. S. Alatawi, M. Essid and R. A. Khera, J. Phys. Chem. Solids, 2023, 181, 111495 CrossRef CAS.
- M. H. Maqsood, R. A. Khera, R. F. Mehmood, S. J. Akram, N. Al-Zaqri, M. A. A. Ibrahim, S. Noor and M. Waqas, J. Mol. Graphics Modell., 2023, 124, 108550 CrossRef CAS PubMed.
- L. Xu, W. Tao, H. Liu, J. Ning, M. Huang, B. Zhao, X. Lu and S. Tan, J. Mater. Chem. A, 2021, 9, 11734–11740 RSC.
- M. Khalid, M. U. Khan, S. Ahmed, Z. Shafiq, M. M. Alam, M. Imran, A. A. C. Braga and M. S. Akram, Sci. Rep., 2021, 11, 21540 CrossRef CAS PubMed.
- S. J. Akram, N. Hadia, J. Iqbal, R. F. Mehmood, S. Iqbal, A. M. Shawky, A. Asif, H. Somaily, M. Raheel and R. A. Khera, RSC Adv., 2022, 12, 20792–20806 RSC.
- J. Hai, W. Zhao, S. Luo, H. Yu, H. Chen, Z. Lu, L. Li, Y. Zou and H. Yan, Dyes Pigm., 2021, 188, 109171 CrossRef CAS.
- X. Li, T. Yan, H. Bin, G. Han, L. Xue, F. Liu, Y. Yi, Z.-G. Zhang, T. P. Russell and Y. Li, J. Mater. Chem. A, 2017, 5, 22588–22597 RSC.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- K. Ayub, J. Mater. Chem. C, 2016, 4, 10919–10934 RSC.
- D. Jacquemin, J. Preat and E. A. Perpète, Chem. Phys. Lett., 2005, 410, 254–259 CrossRef CAS.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Zhao, J. Pu, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2004, 6, 673–676 RSC.
- U. Salzner and A. Aydin, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef CAS PubMed.
- H. Sadki, M. Bourass, M. N. Bennani and M. Bouachrine, Res. Chem. Intermed., 2018, 44, 6071–6085 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- K. E. Mitchell, Science, 2000, 288, 1982 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- S. Rani, N. Al-Zaqri, J. Iqbal, S. J. Akram, A. Boshaala, R. F. Mehmood, M. U. Saeed, E. U. Rashid and R. A. Khera, RSC Adv., 2022, 12, 29300–29318 RSC.
- M. Waqas, N. M. A. Hadia, A. M. Shawky, R. F. Mahmood, M. Essid, Z. Aloui, N. S. Alatawi, J. Iqbal and R. A. Khera, RSC Adv., 2023, 13, 7535–7553 RSC.
- P. Wang, F. Bi, Y. Li, C. Han, N. Zheng, S. Zhang, J. Wang, Y. Wu and X. Bao, Adv. Funct. Mater., 2022, 32, 2200166 CrossRef CAS.
- A. Mahmood, A. Tang, X. Wang and E. Zhou, Phys. Chem. Chem. Phys., 2019, 21, 2128–2139 RSC.
- S. Ahmed and D. J. Kalita, Phys. Chem. Chem. Phys., 2020, 22, 23586–23596 RSC.
- P. R. Varadwaj, A. Varadwaj, H. M. Marques and K. Yamashita, Sci. Rep., 2019, 9, 1–29 CrossRef PubMed.
- N. S. Babu, Mater. Adv., 2022, 3, 3526–3535 RSC.
- M. U. Khan, M. Y. Mehboob, R. Hussain, R. Fatima, M. S. Tahir, M. Khalid and A. A. C. Braga, J. Phys. Org. Chem., 2021, 34, e4119 CrossRef CAS.
- M. Rafiq, R. A. Khera, M. Salim, M. Khalid, K. Ayub and J. Iqbal, Chem. Phys. Lett., 2021, 782, 139018 CrossRef CAS.
- M. Rafiq, M. Salim, S. Noreen, R. A. Khera, S. Noor, U. Yaqoob and J. Iqbal, J. Mol. Liq., 2022, 345, 118138 CrossRef CAS.
- M. Khalid, M. U. Khan, E.-t. Razia, Z. Shafiq, M. M. Alam, M. Imran and M. S. Akram, Sci. Rep., 2021, 11, 1–15 CrossRef PubMed.
- M. Y. Mehboob, R. Hussain, Z. Irshad and M. Adnan, J. Mol. Model., 2021, 27, 1–16 CrossRef PubMed.
- M. Haroon, A. A. Al-Saadi and M. R. S. A. Janjua, J. Phys. Org. Chem., 2022, 35, e4314 CrossRef CAS.
- U. Yaqoob, A. R. Ayub, S. Rafiq, M. Khalid, Y. A. El-Badry, Z. M. El-Bahy and J. Iqbal, J. Mol. Liq., 2021, 341, 117428 CrossRef CAS.
- M. U. Khan, M. Khalid, R. Hussain, A. Umar, M. Y. Mehboob, Z. Shafiq, M. Imran and A. Irfan, Energy Fuels, 2021, 35, 12436–12450 CrossRef CAS.
- C. Zhao, S. Ju, Y. Xue, T. Ren, Y. Ji and X. Chen, Carbon Neutrality, 2022, 1, 7 CrossRef.
- J. Vanderspikken, Q. Liu, Z. Liu, T. Vandermeeren, T. Cardeynaels, S. Gielen, B. Van Mele, N. Van den Brande, B. Champagne and K. Vandewal, Adv. Funct. Mater., 2022, 32, 2108146 CrossRef CAS.
- O. P. Dimitriev, Chem. Rev., 2022, 122, 8487–8593 CrossRef CAS PubMed.
- R. Shen, X. Li, C. Qin, P. Zhang and X. Li, Adv. Energy Mater., 2023, 13, 2203695 CrossRef CAS.
- B. Chettri, S. Jha and N. Dey, J. Photochem. Photobiol., A, 2023, 435, 114210 CrossRef CAS.
- S. Ahmed and D. J. Kalita, J. Mol. Graphics Modell., 2020, 100, 107631 CrossRef CAS PubMed.
- Y. Liu, L. Hua, S. Yan and Z. Ren, Nano Energy, 2020, 73, 104800 CrossRef CAS.
- M. Akram, S. A. Siddique, J. Iqbal, R. Hussain, M. Y. Mehboob, M. B. A. Siddique, S. Naveed, B. Ali, A. Hanif and M. Sajid, Comput. Theor. Chem., 2021, 1201, 113242 CrossRef CAS.
- M. Javed, A. Farhat, S. Jabeen, R. A. Khera, M. Khalid and J. Iqbal, Comput. Theor. Chem., 2021, 1204, 113373 CrossRef CAS.
- S. Zahid, A. Rasool, M. Ans, M. Yaseen and J. Iqbal, Energy Fuels, 2021, 35, 15018–15032 CrossRef CAS.
- K. Jaffar, Z. M. Elqahtani, Q. Q. Afzal, M. Ans, S. Riaz, M. A. Tahir, J. Iqbal, Z. M. Mahmoud, Z. Alrowaili and M. Al-Buriahi, Polymer, 2022, 245, 124675 CrossRef CAS.
- M. Y. Mehboob, M. U. Khan, R. Hussain, K. Ayub, A. Sattar, M. K. Ahmad, Z. Irshad and M. Adnan, Spectrochim. Acta, Part A, 2021, 244, 118873 CrossRef CAS PubMed.
- M. Khalid, M. U. Khan, E.-t. Razia, Z. Shafiq, M. M. Alam, M. Imran and M. S. Akram, Sci. Rep., 2021, 11, 19931 CrossRef CAS PubMed.
- K. M. Katubi, M. Saqib, A. Rehman, S. Murtaza, S. Hussain, Z. Alrowaili and M. Al-Buriahi, Chem. Phys. Lett., 2023, 140349 CrossRef.
- M. Raftani, T. Abram, N. Bennani and M. Bouachrine, Results Chem., 2020, 2, 100040 CrossRef CAS.
- A. H. Shntaif, Z. M. Rashi, Z. H. Al-Sawaff and F. Kandemirli, Russ. J. Bioorg. Chem., 2021, 47, 777–783 CrossRef.
- O. E. Oyeneyin, N. D. Ojo, N. Ipinloju, A. C. James and E. B. Agbaffa, Chem. Afr., 2022, 5, 319–332 CrossRef CAS.
- S. Zahid, A. Rasool, M. Ans, M. S. Akhter, J. Iqbal, M. Al-Buriahi, S. Alomairy and Z. Alrowaili, Sol. Energy, 2022, 231, 793–808 CrossRef CAS.
- L. Zhu, J. Zhang, Y. Guo, C. Yang, Y. Yi and Z. Wei, Angew. Chem., 2021, 133, 15476–15481 CrossRef.
- M. Schwarze, K. S. Schellhammer, K. Ortstein, J. Benduhn, C. Gaul, A. Hinderhofer, L. Perdigón Toro, R. Scholz, J. Kublitski and S. Roland, Nat. Commun., 2019, 10, 2466 CrossRef PubMed.
- F. Eisner and J. Nelson, Joule, 2021, 5, 1319–1322 CrossRef.
- A. A. Youssef, S. M. Bouzzine, Z. M. E. Fahim, İ. Sıdır, M. Hamidi and M. Bouachrine, Phys. B, 2019, 560, 111–125 CrossRef.
- Z. Zang, Q. Wang, P. Song, F. Ma and Y. Li, Sol. Energy, 2022, 231, 503–515 CrossRef CAS.
- S. Haseena and M. K. Ravva, Sci. Rep., 2022, 12, 15043 CrossRef CAS PubMed.
- M. Waqas, N. Hadia, M. Hessien, S. J. Akram, A. M. Shawky, J. Iqbal, M. A. Ibrahim and R. A. Khera, Comput. Theor. Chem., 2022, 1217, 113904 CrossRef CAS.
- A. Aboulouard, S. Mtougui, N. Demir, A. Moubarik and M. Can, Synth. Met., 2021, 279, 116846 CrossRef CAS.
- J. Bertrandie, J. Han, C. S. De Castro, E. Yengel, J. Gorenflot, T. Anthopoulos, F. Laquai, A. Sharma and D. Baran, Adv. Mater., 2022, 34, 2202575 CrossRef CAS PubMed.
- M. A. Ansari, A. Hafeez, M. Mustafa, R. P. Wijesundera and M. I. Malik, Mater. Sci. Semicond. Process., 2022, 150, 106919 CrossRef CAS.
- Z. Chen and H. Zhu, J. Phys. Chem. Lett., 2022, 13, 1123–1130 CrossRef CAS PubMed.
- M. Günther, N. Kazerouni, D. Blätte, J. D. Perea, B. C. Thompson and T. Ameri, Nat. Rev. Mater., 2023, 1–16 Search PubMed.
- S. Li, L. Zhan, C. Sun, H. Zhu, G. Zhou, W. Yang, M. Shi, C.-Z. Li, J. Hou and Y. Li, J. Am. Chem. Soc., 2019, 141, 3073–3082 CrossRef CAS PubMed.
- C. Sun, S. Qin, R. Wang, S. Chen, F. Pan, B. Qiu, Z. Shang, L. Meng, C. Zhang and M. Xiao, J. Am. Chem. Soc., 2020, 142, 1465–1474 CrossRef CAS PubMed.
- M. Madhu, R. Ramakrishnan, V. Vijay and M. Hariharan, Chem. Rev., 2021, 121, 8234–8284 CrossRef CAS PubMed.
- H. Derouiche and V. Djara, Sol. Energy Mater. Sol. Cells, 2007, 91, 1163–1167 CrossRef CAS.
- M. D. Ganji, M. Tajbakhsh, M. Kariminasab and H. Alinezhad, Phys. E, 2016, 81, 108–115 CrossRef CAS.
- S. Li, Y. Chen, Z. Wang, J. Chen, J. Zhang, J. Nie, Y. Duan, Y. Geng and Z. Su, Mater. Chem. Phys., 2023, 302, 127780 CrossRef CAS.
- X. Huang, J. Oh, Y. Cheng, B. Huang, S. Ding, Q. He, F. Wu, C. Yang, L. Chen and Y. Chen, J. Mater. Chem. A, 2021, 9, 5711–5719 RSC.
- B. Qi and J. Wang, Phys. Chem. Chem. Phys., 2013, 15, 8972–8982 RSC.
- M. Waqas, J. Iqbal, R. F. Mehmood, S. J. Akram, A. M. Shawky, M. Raheel, E. U. Rashid and R. A. Khera, J. Mol. Graphics Modell., 2022, 116, 108255 CrossRef CAS PubMed.
- M. Waqas, N. M. A. Hadia, M. M. Hessien, J. Iqbal, G. A. M. Mersal, S. Hameed, A. M. Shawky, Z. Aloui, M. A. A. Ibrahim and R. Ahmad Khera, J. Mol. Liq., 2022, 368, 120770 CrossRef CAS.
- C. Deibel, T. Strobel and V. Dyakonov, Adv. Mater., 2010, 22, 4097–4111 CrossRef CAS PubMed.
- T. H. Lee, M. H. Choi, S. J. Jeon, S. J. Nam, Y. W. Han, J. R. Haw and D.-K. Moon, Polym. J., 2017, 49, 177–187 CrossRef CAS.
- A. Furasova, E. Calabró, E. Lamanna, E. Tiguntseva, E. Ushakova, E. Ubyivovk, V. Mikhailovskii, A. Zakhidov, S. Makarov and A. Di Carlo, Adv. Opt. Mater., 2018, 6, 1800576 CrossRef.
- W. Qarony, M. I. Hossain, V. Jovanov, D. Knipp and Y. H. Tsang, Appl. Nanosci., 2018, 8, 339–346 CrossRef CAS.
- P. Hartnagel and T. Kirchartz, Adv. Theory Simul., 2020, 3, 2000116 CrossRef CAS.
- L. Ye, K. Weng, J. Xu, X. Du, S. Chandrabose, K. Chen, J. Zhou, G. Han, S. Tan, Z. Xie, Y. Yi, N. Li, F. Liu, J. M. Hodgkiss, C. J. Brabec and Y. Sun, Nat. Commun., 2020, 11, 6005 CrossRef CAS PubMed.
- M. Padilla, B. Michl, B. Thaidigsmann, W. Warta and M. C. Schubert, Sol. Energy Mater. Sol. Cells, 2014, 120, 282–288 CrossRef CAS.
- K. Wang, H. Wang, G. Li, Y. Hu, X. Guo, M. Zhang and Y. Li, Chem. Eng. J., 2021, 425, 130575 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra03317a |
| This journal is © The Royal Society of Chemistry 2023 |