Open Access Article
Open Access ArticleFirst-principle insight into the structural, electronic, elastic and optical properties of Cs-based double perovskites Cs2XCrCl6 (X = K, Na)
Jehan Y. Al-Humaidi a,
Abd Ullah*b,
Naimat Ullah Khanc,
Javed Iqbald,
Sajid Khane,
Ali Algahtanifg,
Vineet Tirth
a,
Abd Ullah*b,
Naimat Ullah Khanc,
Javed Iqbald,
Sajid Khane,
Ali Algahtanifg,
Vineet Tirth fg,
Tawfiq Al-Mughanamh,
Moamen S. Refati and
Abid Zaman
fg,
Tawfiq Al-Mughanamh,
Moamen S. Refati and
Abid Zaman *j
*j
aDepartment of Chemistry, College of Science, Princess Nourah bint Abdulrahman University, P.O. BOX 84428, Riyadh 11671, Saudi Arabia
bDepartment of Physics, Government Post Graduate College, Karak, 27200, Pakistan. E-mail: ktkshoraim@gmail.com
cDepartment of Physics, University of Science and Technology, Bannu, 28100, Pakistan
dDepartment of Physics, Gomal University, DI Khan, KP 29220, Pakistan
eDepartment of Physics, Kohat University of Science and Technology, Kohat 26000, Pakistan
fMechanical Engineering Department, College of Engineering, King Khalid University, Abha 61421, Asir, Kingdom of Saudi Arabia
gResearch Center for Advanced Materials Science (RCAMS), King Khalid University, Guraiger, P.O. Box 9004, Abha-61413, Asir, Kingdom of Saudi Arabia
hDepartment of Mechanical Engineering, College of Engineering, King Faisal University, P. O. Box 380, Al-Ahsa 31982, Kingdom of Saudi Arabia
iDepartment of Chemistry, College of Science, Taif University, P.O. Box 11099, Taif 21944, Saudi Arabia
jDepartment of Physics, Riphah International University, Islamabad 44000, Pakistan. E-mail: zaman.abid87@gmail.com
First published on 12th July 2023
Abstract
This study communicates the theoretical investigations on the cubic double perovskite compounds Cs2XCrCl6 (X = K or Na). Density functional theory (DFT) calculations were carried out using the TB-mBJ approximation. These compounds were found to be stable in the cubic perovskite structure having lattice constants in the range of 10.58–10.20. The stability of the investigated materials was assessed by the Gold-Schmidt tolerance method, which resulted in the tolerance factor values of 0.891 and 0.951 for Cs2KCrCl6 and Cs2NaCrCl6, respectively. The calculated values of the elastic constants C11, C12, and C44 of the cubic compounds studied by our research team confirm the elastic stability. The values of the formation energies were also calculated for both the compounds and were found in the range from −2.1 to −2.3. The electronic behavior of the presently investigated materials was examined by inspecting their band structures and the density of states. It was observed that both the materials have half-metallic nature. To check the suitability of the studied compounds in optical applications, we determined the real and imaginary parts of their respective dielectric functions, absorption coefficients, optical conductivities, refractive index, and reflectivity as a function of a wide range of incident photon energies up to 40 eV.
Introduction
More than 50% of the energy from primary energy sources is lost during their consumption, which has badly affected the GDP of the world and has brought enormous economic dividend. On the other hand, the increasing demand of fossil fuels has remarkably created environmental concerns, global warming being one of them. Therefore, researchers across the world have focussed on the discovery of clean, non-polluting, and renewable energy resources. The sun is the main source of clean and renewable energy, which has a great potential to replace the traditional fossil fuels in order to avoid the associated environmental problems and economic dividend. In fact, the hotspot of current research across the globe is the discovery of materials, which efficiently utilize solar energy.Silicon-based materials exhibit high photoelectric conversion efficiency (PCE); however, owing to their large volume and clumsy nature, scientists have diverted their attention to the development of thin and light perovskite solar cells (PSCs).1 Presently, hybrid halide perovskites owing to their very low cost, flexibility, and their thin-film formation, have proven to be promising materials as PSCs.2,3 The technology employed for the manufacturing of PSCs is simple, therefore, PSCs can be fabricated easily on a commercial-scale.4–6 Initially, the photoelectric conversion efficiency of PSCs was reported to be only 3.8%,7 however, in recent years it has been increased to 26.4%.8 Thus, owing to their cheap cost and high efficiency, these materials have attracted great attention for technological applications.9–12 Amongst the hybrid halide perovskites, considerable attention has been paid to CH3NH3PbI3 for its efficient solar cell applications.13,14 However, in spite of its high PEC, it is associated with many issues, such as toxicity and environmental problems. Perovskite CH3NH3PbI3 consists of lead, which is declared toxic and lethal for the health of human beings. In addition, it is very easily decomposed in humid environments, light, and heat, which limits its use on a large-scale.15,16 Hence, it is highly desired to find lead-free compounds, which have both high photoelectric conversion efficiency and good stability. For this purpose double perovskites with the general formula, A2M+M3+X6, have been investigated and found to be promising materials for solar cell applications, owing to their good photovoltaic properties and environmental stability.17–19 Among this family of perovskites, Cs2AgBiBr6 and Cs2AgBiCl6 were predicted to have good photovoltaic properties along with excellent stability.20,21 Xiao et al. investigated In1+-based CsInBiCl6 and CsInSbCl6 and found they have good photoelectric response on account of their small band gap nature, 1.02 eV and 0.91 eV, respectively.22 Volonakis and co-workers studied CsInAgCl6 for photoelectric applications. They reported that the understudy compound had a direct band gap of a semiconductor exhibiting good photoelectric conversion efficiency.23 Moreover, a literature study revealed that many researchers have also investigated materials of this nature for technological applications under the framework of density functional theory (DFT).24–27 Research of this kind has made it easy to filter materials with excellent photoelectric response for numerous optical devices.
Along with computational studies, recently, scientists have succeeded in synthesising Cs2AgSbBr6 and Cs2AgSbCl6 in the laboratory.28,29 Moreover, Lv et al. put forward the low dimensional study of Cs2AgSbBr/Cl6 and successfully fabricated their quantum dots using a surfactant-assisted approach.30 The electronic and optical properties of double perovskites Cs2PtX6 (X = Cl, Br, or I) were studied based on density functional theory. The calculated results reveal that Cs2PtI6 is a potential material for perovskite solar cells owing to the ideal band gap and high optical absorption.31
To the best of our literature review, there is no theoretical study available on lead-free double perovskite compounds Cs2XCrCl6 (X = K or Na). Therefore, in this study, we investigated the structural, electronic, and optical properties of Cs2XCrCl6 (X = K or Na) using first-principles calculations to discover potential materials for perovskite optoelectronics devices. It is expected that our study will enhance the comprehension of photoelectric properties and contribute to the optoelectronic application industries and also provide guidelines for the experimentalists.
Computational model
To accomplish the present study, all calculations were performed using Wien2k Software, which is based on full potential approach.32 In this method the Kohn–Sham equation is solved for electron–ion interaction with full-potential linearized augmented plane wave (FPLAPW) method.33 To address the exchange–correlation energy (Exc) (which is electron–electron interaction energy) in the Kohn–Shame equation, we have utilized the Tran–Blaha modified Becke–Johnson potential abbreviated as TB-mBJ. This method in general is useful in achieving a precise band gap. Moreover, for the optimization of structure, a cut-off energy of −6 Ry and k-point 2000 in Brillouin zone were selected. Furthermore, the muffin-tin radii (RMT) of 5 for both the Cs2KCrCl6 and Cs2NaCrCl6 was taken in-order to avoid the leakage current from the core. The parameters, RMT Kmax was considered as 7, the Gaussian-factor (Gmax) was retained at 12, while the expansion of wave function in the interstitial region was kept up to Imax = 10.Structural properties
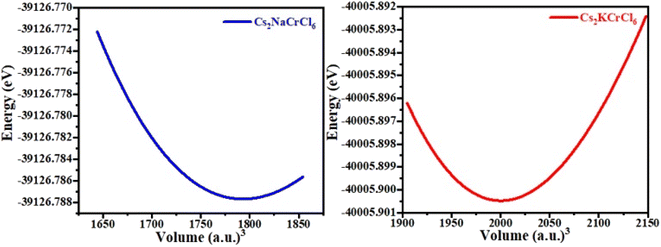
The structural properties and geometries of Cs-based double perovskites, Cs2KCrCl6 and Cs2NaCrCl6, were analyzed by utilizing the Birch–Murnaghan equation of state (Fig. 1). Both materials possess cubic structures with space group Fm![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3 (no. 225). The optimized lattice constants were obtained from the optimization of the unit cell for the ground state stable atomic configuration and presented in Table 1. The obtained optimization curves of the unit cells presented in Fig. 2 indicate the stability of the materials.
3 (no. 225). The optimized lattice constants were obtained from the optimization of the unit cell for the ground state stable atomic configuration and presented in Table 1. The obtained optimization curves of the unit cells presented in Fig. 2 indicate the stability of the materials.
| Structural parameters | Lattice constant | Bulk modulus | Ground state volume | Ground state energy | Bulk modulus derivative | Tolerance factor | Formation energy |
|---|---|---|---|---|---|---|---|
| Cs2KCrCl6 | 10.58 | 25.00 | 2000.20 | −40005.90 | 4.9 | 0.891 | −2.11 |
| Cs2NaCrCl6 | 10.20 | 30.9 | 1793.07 | −39126.78 | 5.1 | 0.951 | −2.23 |
In order to predict the stability of the perovskite materials, the Gold-Schmidt tolerance factor 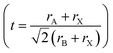 and the octahedral factor (μ = rA/rB) were typically calculated.34 In the case of double perovskite the average value of X (K or Na) and Cr were taken for rB.35 The calculated values of tolerance factor and octahedral factor are displayed in Table 1, indicating stable perovskite structures for both materials.36
and the octahedral factor (μ = rA/rB) were typically calculated.34 In the case of double perovskite the average value of X (K or Na) and Cr were taken for rB.35 The calculated values of tolerance factor and octahedral factor are displayed in Table 1, indicating stable perovskite structures for both materials.36
In order to determine the possibility of synthesizing these materials, their formation energies were computed using the formula:
| EFE = ECsXCrCl6 − (ECs + EX + ECr + 6ECl) |
The calculated values are presented in Table 1. The negative values of the formation energies show that these materials can be synthesized.37
Electronic properties
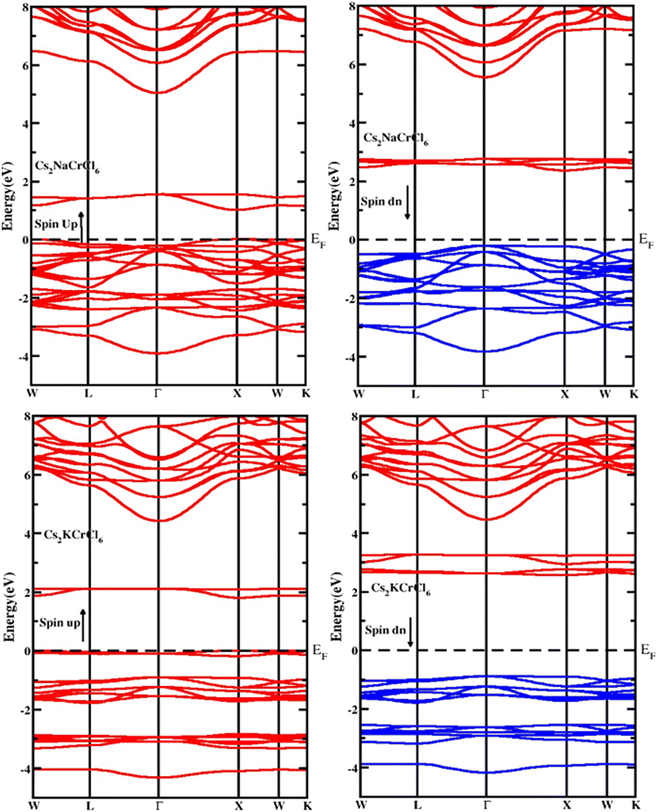
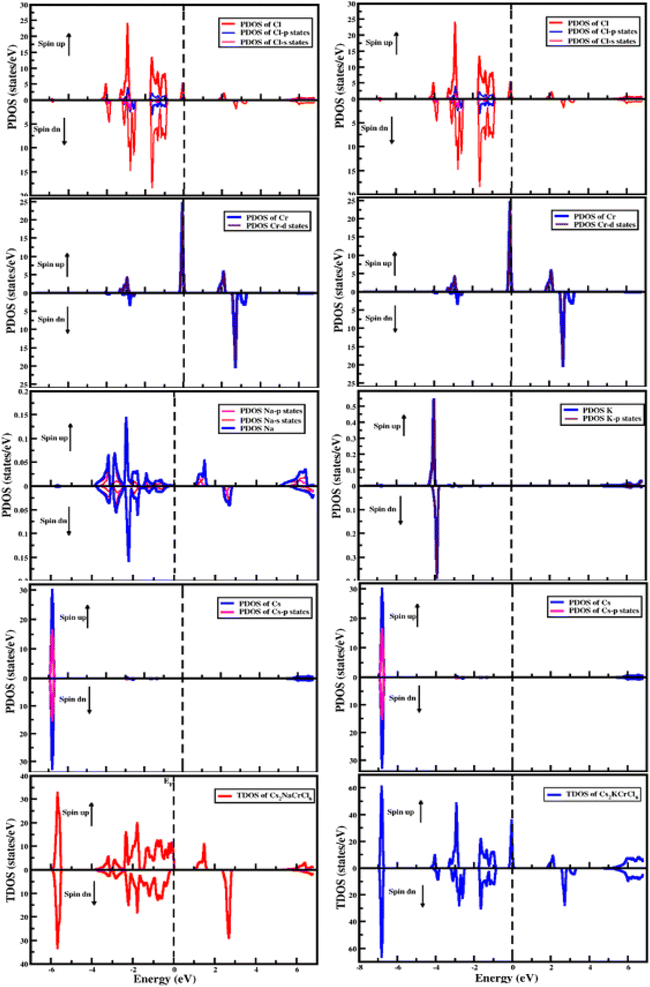
The electronic properties of the studied compounds are described in terms of their electronic band structure and the density of states. Fig. 3 shows the band structure profiles of Cs2XCrCl6 (X = K and Na) compounds. It is clear from Fig. 3 that both the investigated materials showed a dual nature of conductivity in their respective spin up and spin down configurations. The band curves of both the materials were found to overlap the Fermi level (i.e., zero level) in their spin up configuration and this nature of the two Cs2XCrCl6 (X = K or Na) materials authenticates their conducting behavior for the spin up configuration. However, for the spin down configuration it was deduced that they have the opposite behavior of conductivity compared to the spin up configuration. From the results of the band structures of the Cs2XCrCl6 (X = K or Na) compounds, it was concluded that both the studied materials have half-metallic nature. The density of state profiles gives us further insight into the distribution of electronic states. These states are contributed by various elements and their sub-shells as presented in Fig. 4. As, enough energy is provided to electrons, they make transitions from the valence to the conduction band. For complete understanding of these transitions, information regarding the contribution of individual states from various elements is desired. Especially, the states those are present at the top of the valence band and below the conduction band should be known. It is clear from Fig. 4 that the top of the valence band of both compounds is populated mainly by Cr-states. However, a small number of states due to Cl atom are also present. A similar behavior can be observed in the bottom portion of the conduction band with a slight difference. In addition to the Cr and Cl states in the lower portion of the conduction band, K states appeared in Cs2KCrCl6 while Na states were found for Cs2NaCrCl6.Optical properties
The frequency dependent dielectric function ε(ω) is a useful tool for describing the complex responses of the materials to electromagnetic radiation and this dielectric function can be represented mathematically as:| ε(ω) = ε1(ω) + iε2(ω) | (1) |
Fig. 5(a) shows a plot of the real part of the complex dielectric function ε1(ω). An important parameter known as the static dielectric constant, represented by the symbol ε1(0), is the value of the dielectric constant of a compound at zero frequency. Starting from the zero frequency limit, the real portion ε1(ω) of the examined chemicals attained its maximum value, then began to decline; and at a particular frequency range it fell below zero. When these materials were exposed to light having an energy of 2 eV or 6 eV, they show a metallic nature and the ε1(ω) values become negative. The peaks of the ε1,max spectra are observed for Cs2KCrCl6 at 6.2 (8 eV) and Cs2NaCrCl6 at 6.5 (9.5 eV). The peak values for Cs2KCrCl6 and Cs2NaCrCl6 were found to be 5.8 (14 eV) and 5.4 (13 eV), respectively, and can be confirmed in the imaginary part of the dielectric function ε2(ω) as shown in Fig. 5(b). Both compounds showed a broad range of absorption spectra, making them suitable for multiple optical applications.
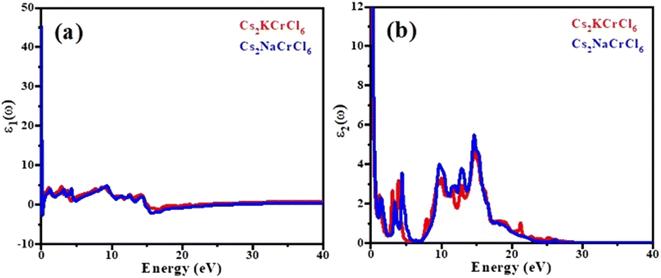 | ||
| Fig. 5 Calculated plots of the (a) real part and (b) imaginary part of dielectric function versus the energy of Cs2KCrCl6 and Cs2NaCrCl6 perovskites. | ||
Refractive index n(ω)
An important optical parameter to consider when investigating the possible uses of a material in the realm of optical and photonic devices is its refractive index n(ω).40 Mathematically refractive index can be expressed as:
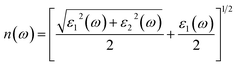 | (2) |
Fig. 6(a) displays the refractive index n(ω) spectra of Cs2KCrCl6 and Cs2NaCrCl6. The zero frequency refractive index n(0) for Cs2KCrCl6 and Cs2NaCrCl6 were determined to be 6.2 and 9.3, respectively. Beyond the zero frequency, the curves attained their highest values for Cs2KCrCl6 and Cs2NaCrCl6 at 8 eV and 9 eV, respectively. The fact that the values exceed unity, indicates that the photon slows down as a result of its interaction with the surface electrons in the materials.
 | ||
| Fig. 6 Calculated plots of (a) refractive index, (b) absorption coefficient, (c) optical conductivity, and (d) reflectivity versus energy for Cs2KCrCl6 and Cs2NaCrCl6 perovskites. | ||
Absorption coefficient I(ω)
An important optical indicator that provides insightful data on the absorption of optical energy per unit length is the absorption coefficient.41 It is possible to determine the absorption coefficient using the imaginary and real components of the dielectric function. The following relation may be used to get the absorption coefficient:
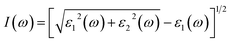 | (3) |
The band gap and molecular shape of the crystal affect the absorption values. When, an incoming frequency of photons resonates with the transition frequency of the atom, optical absorption occurs. Due to the frequency dependence of the absorption coefficient, certain frequency photons can only be absorbed by certain materials. The transition of electrons from the occupied states in the higher valence band to the accessible unoccupied levels in the lower conduction band causes the optical absorption.
The absorption coefficient curves are shown in Fig. 6(b). It can be seen, that the steps of the imaginary parts of the dielectric function are followed by the absorption curves. For Cs2KCrCl6 and Cs2NaCrCl6 compounds, the absorption coefficient displays small values up to 7.5 eV. However, as shown in Fig. 6(b) the maximum absorption coefficient values for Cs2KCrCl6 and Cs2NaCrCl6 are 245 at 15 eV and 280 at 16 eV, respectively.
Optical conductivity σ(ω)
The quantity of free electrons in a substance determines its optical conductivity. The optical conductivity increases as the free electron number increases.40 The optical conductivity is denoted by σ(ω) and is measured in units of (Ω m)−1. The following equation gives the mathematical expression for optical conductivity.42
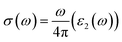 | (4) |
The above-mentioned eqn (4), demonstrates that the optical conductivity and optical absorption are directly related. Fig. 6(c) displays the optical conductivity graph for Cs2KCrCl6 and Cs2NaCrCl6. The optical spectra curves reveal that both materials exhibit a wide range of optical conductivity in the spectral region of 7–24 eV. For Cs2KCrCl6 and Cs2NaCrCl6, the highest optical conductivity was seen to be 9000 (Ω cm)−1 at 14 eV and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (Ω cm)−1 at 14.5 eV, respectively.
000 (Ω cm)−1 at 14.5 eV, respectively.
Reflectivity R(ω)
The surface behavior of any crystal is described by its reflectivity. The following relation can be utilized to calculate the reflectivity of a material:
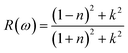 | (5) |
Elastic properties
The elastic properties of materials should be studied before their use in practical applications because many features of devices are the functions of the elastic properties of materials that are used in their manufacturing. Therefore, materials, which exhibit best elastic properties, are of great importance for their implementation in numerous devices. The elastic constant links mathematically the mechanical and dynamical characteristics of materials, and takes a crucial role in shaping the properties of any material and shows their reaction to external applied forces. For the complete description of the mechanical properties of any material, the three elastic constants C11, C12, and C44 are sufficient. We computed the elastic constants and correlated them with literature. The calculated values of all the elastic parameters are listed in Table 2.| Compounds | C11 | C12 | C44 | B | A | G | E | V | GV | GR |
|---|---|---|---|---|---|---|---|---|---|---|
| Cs2NaCrCl6 | 47 | 17.23 | 18.2 | 27.15 | 1.22 | 0.081 | 0.24 | 0.74 | 16.87 | 15.71 |
| Cs2KCrCl6 | 52.17 | 19.16 | 19.35 | 30.16 | 1.17 | 0.054 | 0.16 | 0.78 | 18.21 | 17.10 |
To ensure the mechanical stability of cubic compounds, the Burn-Haun criteria C11 > 0, C44 > 0, (C11 − C12) > 0, (C11 + 2C12) > 0, and C12 < B > C11 are checked for the determined elastic constant of the presently investigated materials and are presented in the Table 2. The fulfillment of the above criterion by both the compounds manifests their stability.43 Specific mechanical properties, such as bulk modulus, young modulus, anisotropy factor, and shear modulus, can be estimated by using the following relations:
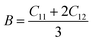 | (i) |
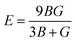 | (ii) |
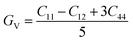 | (iii) |
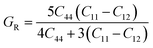 | (iv) |
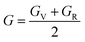 | (v) |
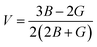 | (vi) |
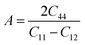 | (vii) |
The computed results presented in the Table 2, show that the value of the bulk modulus (B) for Cs2KCrCl6 (30.16) is greater than that calculated for Cs2NaCrCl6 (27.15); from this it was concluded that, when both compounds are compressed from all sides then Cs2KCrCl6 will resist more to the changes in its volume than Cs2NaCrCl6. Thus, Cs2KCrCl6 is more incompressible to external applied forces as compared to Cs2NaCrCl6.
The shear modulus (G) represents the toughness of any material. From the calculated values of the shear modulus it became evident that the value of G for Cs2NaCrCl6 (0.081) is greater than that of Cs2KCrCl6 (0.054) and the results of G conclude that Cs2NaCrCl6 is harder than Cs2KCrCl6. Thus, Cs2NaCrCl6 will show more resistance to the deformation in its shape than the Cs2KCrCl6 compound.
Young modulus (E) represents the stiffness of a material. From Table 2, it is evident that the value of E is greater for Cs2NaCrCl6 (0.24) than the Cs2KCrCl6 (0.16), which make Cs2NaCrCl6 more stiff than Cs2NaCrCl6.
The Poison ratio (V) enables researchers to know about the ductility and brittleness of a material. Materials having V > 0.33 are labeled as ductile, whereas those having V < 0.33 will be brittle. Herein, V was found to be greater than 0.33 for both the compounds and these results of V confirm that the investigated materials have a ductile nature.
The micro cracks in a material can be calculated from the anisotropic factor of any material. Anisotropy factor (A) is the parameter that indicates whether or not the structural properties of a material remain the same in all directions. For the medium to be isotropic, it must have A = 1, and A is not equal to 1 when the material is anisotropic. From the computed values of A shown in Table 2 for the recently studied materials, it became obvious that both materials are anisotropic in nature as they exhibit a value of A greater than 1.
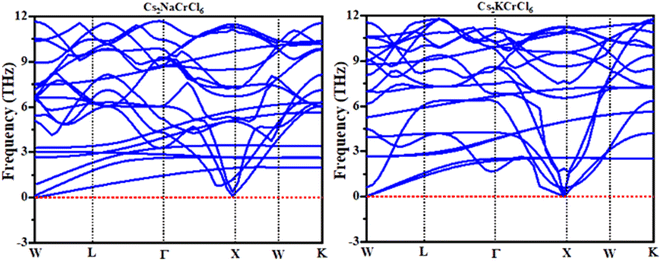
Phonopy spectra
Phonons are a crucial component of dynamic behaviors and thermal characteristics, which are the main aspects of the fundamental problems of materials science.44,45 The phonon dispersion band structure of cubic double perovskites Cs2KCrCl6 and Cs2NaCrCl6 was investigated using the WIEN2K package as depicted in Fig. 7. It can be seen from Fig. 7 that the phonon dispersion curves for both materials are positive and there are no negative values of dispersion curves (imaginary phonon frequencies). The positive dispersion curves confirm the phonon dynamic stability of these compounds.46Conclusion
We reported theoretical results on the structural, elastic, electronic, and optical properties of Cs2KCrCl6 and Cs2NaCrCl6 compounds by density functional theory using Wien2K software. The obtained values of the tolerance factor manifest that these compounds possess stability in the cubic structure. The values of the Poisson ratio deduced from the elastic constants indicate that both compounds are ductile in nature. In the top valence band region, Cr makes the major contribution to the electronic states. However, in the lower conduction band region, K and Na states for Cs2KCrCl6 and Cs2NaCrCl6, respectively, make their appearance along with Cr and Cl states. Optical parameters were calculated as a function of energy in the energy range of 0–40 eV. The behavior of the imaginary part of the dielectric function was found consistent with the optical conductivity curves of both investigated compounds. It was observed during the optical study of the presently studied materials that both exhibit a wide range of optical conductivity in the spectral region of 7–24 eV. The calculated properties of the studied materials make them attractive for implementation in various detectors and optoelectronic applications.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia for funding this work through the General Groups Project under grant number GRP/62/44. Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R24), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors acknowledge the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track [GRANT3711].References
- K. Bidai, M. Ameri, S. Amel, I. Ameri, Y. Al-Douri, D. Varshney and C. H. Voon, Chin. J. Phys., 2017, 55(5), 2144–2155 CrossRef CAS.
- W. S. Yang, B. W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. Seok, Science, 2017, 356, 1376–1379 CrossRef CAS PubMed.
- S. Kim, C. R. Lee, J. H. Im, K. B. Lee, T. Moehl, A. Marchioro and S. J. Moon, Sci. Rep., 2012, 2(1), 591 CrossRef PubMed.
- G. Hodes, Science, 2013, 342, 317–318 CrossRef CAS PubMed.
- H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630 CrossRef CAS.
- N. Moulay, M. Ameri, Y. Azaz, A. Zenati, Y. A. Douri and I. Ameri, Mater. Sci.-Pol., 2015, 33, 402–413 CrossRef CAS.
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- R. X. Lin, J. Xu, M. Y. Wei, Y. R. Wang, Z. Y. Qin, L. Zhou, J. L. Wu, K. Xiao, B. Chen, S. M. Park, G. Chen, H. R. Atapattu, K. R. Graham, J. Xu, J. Zhu, L. D. Li, C. F. Zhang, E. H. Sargent and H. Tan, Nature, 2022, 603, 73–78 CrossRef CAS PubMed.
- K. Akihiro, T. Kenjiro, S. Yasuo and M. Tsutomu, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef PubMed.
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007–15023 CrossRef CAS.
- C. Kdine, M. Nicolas and E. Jacky, Chem. Rev., 2019, 119, 3140–3192 CrossRef PubMed.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- H. Jun, S. Keitaro, H. Liyuan and T. Yoshitaka, J. Am. Chem. Soc., 2015, 137, 10048–10051 CrossRef PubMed.
- Z. Y. Deng, F. X. Wei, S. J. Sun, G. Kieslich, A. K. Cheetham and P. D. Bristowe, J. Mater. Chem., 2016, 4, 12025–12029 RSC.
- Z. F. Shi, Y. Zhang, C. Cui, B. H. Li, W. J. Zhou, Z. J. Ning and Q. X. Mi, Adv. Mater., 2017, 29, 1701656–1701661 CrossRef.
- A. H. Slavney, R. W. Smaha, I. C. Smith, A. Jaffe, D. Umeyama and H. I. Karunadasa, Inorg. Chem., 2017, 56, 46–55 CrossRef CAS.
- S. Wenwu, T. Cai, Z. Wang and O. Chen, J. Chem. Phys., 2020, 153, 141101 CrossRef.
- S. Zhao, K. Yamamoto, S. Iikubo, S. Hayase and T. Ma, J. Phys. Chem. Solids, 2018, 117, 117–121 CrossRef CAS.
- H. J. Feng, W. Deng, K. Yang, J. Huang and X. C. Zeng, J. Phys. Chem. C, 2017, 121, 4471–4480 CrossRef CAS.
- M. N. Tripathi, A. Saha and S. Singh, Mater. Res. Express, 2019, 6, 115517 CrossRef CAS.
- M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 2579 CrossRef CAS PubMed.
- Z. Xiao, K. Z. Du, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, J. Am. Chem. Soc., 2017, 139, 6054–6057 CrossRef CAS PubMed.
- G. Volonakis and A. A. Haghighirad, J. Phys. Chem. Lett., 2017, 8, 772–778 CrossRef CAS PubMed.
- D. Y. Hu, X. H. Zhao, T. Y. Tang, L. Li, L. K. Gao and Y. L. Tang, Opt. Mater., 2021, 119, 111316 CrossRef CAS.
- J. Su, T. Mou, J. Wen and B. Wang, J. Phys. Chem. C, 2020, 124, 5371–5377 CrossRef CAS.
- K. Boudiaf, A. Bouhemadou, Y. A. Douri, R. Khenata, S. Bin-Omran and N. Guechi, J. Alloys Compd., 2018, 759, 32–43 CrossRef CAS.
- D. Y. Hu, X. H. Zhao, T. Y. Tang, L. M. Lu, L. Li, L. K. Gao and Y. L. Tang, Sol. Energy, 2022, 231, 236–242 CrossRef CAS.
- E. Gonzalo, R. P. Daily, L. Rafael, C. Luis and M. D. Gustavo, Nanoscale, 2019, 11, 16650–16657 RSC.
- J. Zhou, X. Rong, M. S. Molokeev, Y. Wang, X. Yun, D. Xu and X. Li, Mater. Chem. Front., 2021, 5(13), 4997–5003 RSC.
- K. X. Lv, S. P. Qi, G. N. Liu, Y. B. Lou, J. X. Chen and Y. X. Zhao, Chem. Commun., 2019, 55, 14741 RSC.
- R. Sa, Q. Zhang, B. Luo and D. Liu, J. Solid State Chem., 2021, 304, 122602 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka and J. Luitz, An augmented plane wave+ local orbitals program for calculating crystal properties, 2001, vol. 60, pp. 1–302 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS.
- N. U. Khan, U. A. Khan, V. Tirth, J. Y. Al-Humaidi, M. S. Refat, A. Algahtani and A. Zaman, RSC Adv., 2023, 13(9), 6199–6209 RSC.
- Y. P. Fu, M. P. Hautzinger, Z. Y. Luo, F. F. Wang, D. X. Pan, M. M. Aristov, I. A. Guzei, A. L. Pan, X. Y. Zhu and S. Jin, ACS Cent. Sci., 2019, 5, 1377–1386 CrossRef CAS PubMed.
- T. Tang, D. Hu, X. Zhao, L. Li and Y. Tang, Phys. Scr., 2022, 97(12), 125821 CrossRef.
- J. Munir, M. Mustafa, H. Naeem, M. Yousaf, E. F. El-Shamy and Q. Ain, ECS J. Solid State Sci. Technol., 2022, 11(12), 123003 CrossRef.
- D. B. Melrose and R. J. Stoneham, J. Phys. A: Math. Gen., 1977, 10, L17 CrossRef.
- A. Amudhavalli, R. Rajeswarapalanichamy, K. Iyakutti and A. K. Kushwaha, Comput. Condens. Matter, 2018, 14, 55–66 CrossRef.
- S. Azam, S. Goumri-Said, S. A. Khan and M. B. Kanoun, J. Phys. Chem. Solids, 2020, 138, 109229 CrossRef CAS.
- A. Afaq, A. Bakar, S. Anwar, W. Anwar and F.-e. Aleem, Int. J. Mod. Phys. B, 2018, 32, 1850362 CrossRef CAS.
- R. Ahmad and N. A. Mehmood, J. Supercond. Novel Magn., 2018, 31(5), 1577e86 Search PubMed.
- D. Liu, W. Zha, R. Yuan, J. Chen and R. Sa, New J. Chem., 2020, 44(32), 13613–13618 RSC.
- C. Xie, Y. Liu, Z. Zhang, F. Zhou, T. Yang, M. Kuang and G. Zhang, Phys. Rev. B, 2021, 104(4), 045148 CrossRef CAS.
- C. Xie, H. Yuan, Y. Liu and X. Wang, Two-nodal surface phonons in solid-state materials, Phys. Rev. B, 2022, 105(5), 054307 CrossRef CAS.
- U. A. Khan, M. R. Sarker, N. U. Khan, S. Khan, J. Y. Al-Humaidi, V. Tirth and A. M. Alsuhaibani, J. Saudi Chem. Soc., 2023, 27(3), 101627 CrossRef.
| This journal is © The Royal Society of Chemistry 2023 |