Open Access Article
Open Access ArticleThe effects of ionic liquids on the ethanolysis of a chloroacenaphthene. Evaluation of the effectiveness of nucleofugality data to predict reaction outcome†
Andrew Y. Hsieh ,
Ronald S. Haines
,
Ronald S. Haines and
Jason B. Harper
and
Jason B. Harper *
*
School of Chemistry, University of New South Wales, UNSW Sydney, NSW 2052, Australia. E-mail: j.harper@unsw.edu.au; Fax: +61 2 9385 6141; Tel: +61 2 9385 4692
First published on 12th July 2023
Abstract
The reaction of a chlorobenzene in mixtures containing ethanol and eight different ionic liquids was investigated in order to understand the effects of varying proportions and constituent ions of an ionic liquid on the rate constant of the process. The results were found to be generally consistent with previously studied reactions of the same type, with small proportions of an ionic liquid resulting in a rate constant increase compared to ethanol and large proportions causing a rate constant decrease. Temperature dependent kinetic studies were used to interpret the changes in reaction outcome, particularly noting an entropic cost on moving to high proportions of ionic liquid, consistent with organisation of solvent around the transition state. While attempts to use empirical solvent parameters to correlate outcome with the ionic liquid used were unsuccessful, use of recently acquired nucleofugality data for chloride and estimations for the electrofuge allowed for excellent prediction of the effects of ionic liquids, with rate constants quantitatively predicted in systems containing both different proportions of ionic liquid (mean absolute error (MAE) log(k1) = 0.11) and different ionic liquids (MAE log(k1) = 0.33). Importantly, this demonstrates the ready application of these quantitative reactivity parameters.
Introduction
Ionic liquids, defined as salts with melting points below 100 °C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (though this definition has been broadened somewhat recently2) have been extensively investigated as potential alternatives to traditional molecular solvents.3 This interest is due to their desirable properties, such as low volatility4 and non-flammability,5 which are the result of the electrostatic interactions between the ionic components of the salt.1 However, ionic liquids can have vastly different solvent effects compared to traditional solvents and this problem has limited, at least initially, their application.
1 (though this definition has been broadened somewhat recently2) have been extensively investigated as potential alternatives to traditional molecular solvents.3 This interest is due to their desirable properties, such as low volatility4 and non-flammability,5 which are the result of the electrostatic interactions between the ionic components of the salt.1 However, ionic liquids can have vastly different solvent effects compared to traditional solvents and this problem has limited, at least initially, their application.
Many reactions have been studied in the presence of ionic liquids in order to rationalise, and ultimately predict, their effects on reaction outcomes.3,6–10 These studies have led to several key insights into the solvent effects of ionic liquids.11 Of particular note are that (i) different ionic liquids can have different effects on a given reaction, as demonstrated by systematically changing the constituents of the ionic liquid used;12–16 and that (ii) the proportion of ionic liquid present in a given reaction mixture affects the observed solvent effects.17–21 Importantly, these changes in reaction outcomes (such as rates and selectivities) on varying the amount and type of ionic liquid present can be explained using microscopic interactions involving components of the ionic liquid.8,22–25 With this knowledge in hand, there is the potential for the rational selection of an ionic liquid to give a desired reaction outcome.20,26–28
While the above arguments highlight the dramatic increase in understanding of solvent effects in ionic liquid mixtures, a key obstacle to the further utilisation of ionic liquids is the lack of a quantitative predictive framework for evaluating potential ionic liquid effects on the outcome of given reactions; while we might be able to say that an ionic liquid would increase the rate of a reaction, we can't say by how much.
There have been many different attempts to analyse these solvent effects in ionic liquid mixtures quantitatively using measurements such as solvent parameters (including Kamlet–Taft parameters,7,11,13,29–34 and Gutman donor numbers35), NMR relaxation data,36 charge distribution analysis,26 and machine learning methods.37 These attempts have been shown to be useful in certain contexts, but have proven to be reaction specific, and have variable quality of correlation. Of particular interest is that translating existing predictive models between different reactions is not possible; this is clearly demonstrated with the extremely different contributions of Kamlet–Taft parameters for extremely similar Diels–Alder7,29,32,33 and unimolecular substitution processes.13,30,34 Further, features of a solvent (such as apparent polarity), which might dramatically affect reaction outcome in molecular solvents, have been shown to poorly describe reaction outcomes in ionic solvents; for example, with SN1 processes.22,38 (For a review see, Hawker et al.11).
We have recently started to determine quantitative reactivity parameters in ionic liquids and their mixtures, particularly the nucleofugality of chloride.39 Nucleofugality measures the ability of a leaving group to depart with a bonding electron pair and can be quantified using the relationship:
| log10(k1)25 °C = sf (Nf + Ef) | (1) |
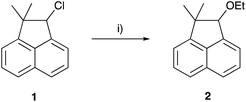
The ethanolysis of 2-chloro-1,1-dimethylnaphthalene 1 (Scheme 1) was chosen as the reaction for this study, due to the similarities between this reaction and the species used to determine the nucleofugality values in the original study; namely the chloride leaving group, and the ethanol cosolvent.39 With the above arguments in mind, the ethanolysis of chloride 1 was performed in a range of solvent mixtures and the rate constant of the reaction was determined through kinetic analysis of the solvolysis and compared to the data predicted using electrofugality measurements, to assess the potential of using such measurements to quantitatively predict reaction outcome.
Results and discussion
Initial kinetic analysis
As was discussed in the Introduction, the ethanolysis of the chloride 1 in ethanol (Scheme 1) proceeds through a unimolecular nucleophilic substitution (SN1) mechanism. This mechanism was confirmed using nucleophile dependence studies in which changing the amount of ethanol in the reaction mixture did not affect the rate constant for the process (see Table S1 in the ESI†).In order to study the effects of using an ionic liquid as the solvent for this reaction, the rate constant for the process was measured in mixtures containing different proportions of [bmim][N(SO2CF3)2] 3 (Fig. 1) in ethanol at 40 °C. The ionic liquid 3 was chosen as it is readily prepared and purified,39 and has been widely utilised in mechanistic studies;21,38,40–42 of particular note is its previous use to evaluate solvent effects on reactions that also proceed through the SN1 mechanism.13,18,19,34 The temperature was chosen such that the reactions could be readily followed based on previously observed solvent effects of ionic liquids.11 While this value is different to that used in nucleofugality studies,39 they would still be expected to provide useful quantitation data (vide infra). The reaction was followed in situ using 1H NMR spectroscopy and the kinetic data obtained are summarised as a plot showing the mole fraction dependence of the rate constant (Fig. 2). It is important to note that, while the chloride 1 has the potential to undergo rearrangement (potentially resulting in an alternative substitution product, or an elimination product43), these processes were not observed under any of the reaction conditions utilised.
 | ||
| Fig. 1 The ionic liquid 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([bmim][N(SO2CF3)2], 3) used in this study. | ||
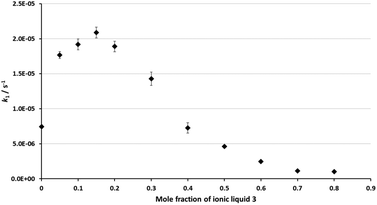 | ||
| Fig. 2 The rate constant for the reaction between the chloride 1 and ethanol (Scheme 1) in mixtures containing different proportions of ethanol and [bmim][N(SO2CF3)2] 3 (◆) at 40 °C. Uncertainties are the standard deviation of at least triplicate results; some error bars are smaller than the markers used. | ||
The rate constant increases at low mole fractions of the salt 3 compared to the neat molecular solvent case, and then decreases at higher mole fractions of the salt 3. The maximum rate constant increase occurs at χIL = 0.15, and is ca. three times the rate constant in the ethanol case. At χIL > 0.4, k1 is lower than the neat molecular solvent case, with the lowest rate constant at χIL = 0.8 being about half that in the neat ethanol case. Once again, these data demonstrate the effects of the proportion of salt 3 in the reaction mixture on the reaction outcome for this type of mechanism, and hence reinforce the importance of tailoring the proportion of ionic liquid present in order to achieve a desired reaction outcome.
This dependence of reaction outcome on solvent composition, with a rate constant increase followed by a decrease, is similar to what has been observed previously for other processes that proceed through an SN1 mechanism.13,18,19,22,30,34,39 Within this framework, there is significant variation in both the extent of rate constant increase (from 1.5 (ref. 30) to 40 (ref. 13) times), the proportion of salt at which the maximum rate constant occurs (from χIL = 0.02 (ref. 30) to 0.30 (ref. 13)) and the final rate constant relative to the neat molecular solvent (from 1000%13 of the rate in molecular solvent to 1%30). The data presented here are consistent with what has been seen previously for chloride nucleofuges with systems that have a significant degree of charge stabilisation of the carbocation intermediate.22,39
Temperature dependent kinetic studies
In order to identify the underlying interactions responsible for the changes in k1 when using an ionic liquid in the reaction mixture, temperature dependent kinetic studies were used to determine the activation parameters for this process in mixtures having different solvent compositions. These studies were carried out in ethanol and mixtures containing the ionic liquid 3 at either χIL = 0.15 or χIL = 0.8. The low mole fraction of the salt 3 was selected as it corresponds to the reaction mixture exhibiting the greatest increase in k1. The high mole fraction was chosen as it corresponds to the reaction mixture exhibiting the greatest decrease in k1, and is also the reaction mixture closest to neat ionic liquids that was considered. The temperature dependent kinetic data was analysed using an Eyring plot44 (see ESI†) and the activation parameters determined are shown in Table 1.| χIL | ΔH‡ /kJ mol−1 | ΔS‡ /J K−1 mol−1 |
|---|---|---|
| a Uncertainties quoted are derived from the fit of the linear regression. | ||
| 0 | 92.8 ± 1.7 | −47 ± 5 |
| 0.15 | 96.0 ± 1.5 | −30 ± 5 |
| 0.80 | 88.4 ± 4.0 | −79 ± 13 |
The enthalpy of activation for the reaction shown in Scheme 1 in ethanol is large and positive, and the entropy of activation is negative and relatively small in magnitude, consistent with previous values for equivalent reactions.22,39 These data are not unreasonable given the large extent of the bond breakage in the rate determining step (explaining the significant enthalpy of activation) and the significant charge build-up in the transition state, resulting in organisation of the polar ethanol molecules about the developing charges (consistent with the small, negative activation entropy). On moving from ethanol to χIL = 0.15, there is a small increase in both the enthalpy and the entropy of activation. A similar outcome has been seen previously for a related benzhydryl chloride.39 The origin of this increase in both parameters is not clear as it suggests either (i) greater stabilization of, and ordering about, the starting material, (ii) reduced stabilization of, and ordering about, the transition state, or (iii) some combination of both. Interactions of the cation of the ionic liquid 3 with the delocalised electron density in the substrate 1 (‘cation–π’ interactions, as reported to explain the solubility of aromatic species in ionic liquids45) could plausibly account for some of the increased interactions with, and organisation about, the starting materials. This argument is consistent with both our own previous work on π systems with opposite quadrupoles (see, for example, Tanner et al.46) and related benzhydryl bromide reactions,13,18 along with the work of D'Anna on ion–π interactions.47 In addition, a small amount of ionic liquid 3 might disrupt organisation of ethanol about the incipient charges in the transition state; the result of such disruption is a decrease in stabilisation of the transition state (increase in activation enthalpy) and a larger degree of disorder and hence an increase in activation entropy. It is likely that some combination of these effects leads to the observed activation parameter changes.
On increasing the proportion of ionic liquid 3 present to χIL = 0.80, the entropy of activation decreased relative to the other cases, whilst the enthalpy of activation also decreased on increasing the proportion of the salt from χIL = 0.15 to the same as in ethanol. The decrease in activation enthalpy can be attributed to stabilisation of the incipient charges in the transition state on moving to a high proportion of the salt 3 in the reaction mixture. This increased stabilisation is accompanied by increased organisation of the solvent mixture about the transition state, as indicated by the decrease in the entropy of activation. This ‘entropic cost’ outweighs any enthalpic benefit provided to the transition state by the salt 3, resulting in the decrease in observed rate at higher mole fractions of ionic liquid in the reaction mixture.
The effects of different ionic liquids
In order to better understand the microscopic interactions between the components of solution and the transition state, and hence the solvent effects of ionic liquids on the reaction being considered, a series of ionic liquids were selected that differ from ionic liquid 3 in either the cation or the anion (Fig. 3). Ionic liquids 4–7 contain the same cation as the parent salt 3 ([bmim]+) but differ in the anion; these anions were selected as they have a range of sizes and coordinating abilities and have been used in previous studies.13,30,39 Salts 8–10 have the same anion as the parent salt 3 ([N(SO2CF3)2]−) but differ in the cation; these were selected due to differences in charge localisation and accessibility of the charged centres, and again have been used in previous studies.13,30,39 A high proportion of ionic liquid (χIL = 0.80) was chosen in order to consider solutions that were as close as practical to neat ionic liquids. Notably, all of the selected ionic liquid mixtures have previously reported values for the nucleofugality of chloride.39 The rate constant for the reaction shown in Scheme 1 in mixtures containing each of the ionic liquids 4–10 (χIL = 0.80) was determined to evaluate how varying the constituents of the ionic liquid affects k1 (Table 2). Immediately clear from these data is that, at a high proportion of ionic liquid in the solvent mixture, the rate constant for the reaction shown in Scheme 1 is lower than that in the neat molecular solvent for almost all cases (the exception being salt 4). Importantly, however, there are significant differences in the solvent effects of the different salts 3–10, with the rate constant varying by a factor of ca. 30 from the fastest (salt 4) to the slowest (salt 9) cases.| Ionic liquid | k1/10−6 s−1 |
|---|---|
| a Uncertainties quoted are the standard deviation of triplicate results.b Neat ethanol, included for comparison. | |
| — | 7.4 ± 0.3 |
| [bmim][N(SO2CF3)2] 3 | 1.02 ± 0.11 |
| [bmim][C(CN)3] 4 | 6.5 ± 0.7 |
| [bmim][N(CN)2] 5 | 4.2 ± 0.2 |
| [bmim][PF6] 6 | 3.7 ± 0.3 |
| [bmim][BF4] 7 | 1.172 ± 0.011 |
| [bmpyr][N(SO2CF3)2] 8 | 0.84 ± 0.02 |
| [mTOA][N(SO2CF3)2] 9 | 0.22 ± 0.02 |
| [Li(G3)][N(SO2CF3)2] 10 | 1.10 ± 0.09 |
The effects of changing the anion of the ionic liquid on the reaction outcome can be seen by comparing the rate constants in the presence of salts 3–7. The previously considered salt 3 resulted in the smallest rate constant, though the outcome for the reaction in the tetrafluoroborate 7 was only slightly faster. The hexafluorophosphate salt 6 and the dicyandiamide salt 5 resulted in rate constants ca. 4 times greater than the parent bis(trifluoromethanesulfonyl)imide 3, whilst the tricyanomethanide 4 gave the largest observed rate constant. While these data demonstrate the effect of changing the anion on the observed rate constant, it is difficult to obtain any useful trends as there is no simple correlation with features of the anion such as coordinating ability, size and molecular shape.‡
The effect of changing the cation of the ionic liquid on solvent effects on the reaction in Scheme 1 can be assessed by comparing the outcomes in salts 3 and 8–10. The data for the pyrrolidinium salt 8 is slightly smaller, though comparable to, the parent imidazolium salt 3, while the presence of the quaternary ammonium salt 9 decreases k1 by 80% relative to the salt 3. Interestingly, the lithium glyme salt 10 resulted in the same reaction outcome as salt 3, within uncertainty. Though the data set is small, these examples do suggest that hindering the cationic centre reduces the rate constant. This argument is consistent with the observed activation enthalpy changes on moving to a high proportion of salt in the reaction mixture and suggests some interaction of the cation with the leaving group in the transition state.
While the above arguments allow some qualitative assessments of structure–activity relationships on solvent effect for the case shown here, it is difficult to predict the effects on the reaction of changing the ionic liquid. Previously,7,11,13,29–34 Kamlet–Taft parameters, which measure the hydrogen bond accepting48 and donating abilities,49 and the polarizability50 of a solvent, have been considered in attempts to quantify and predict solvent effects, as has been considered for molecular solvents.51 Where correlations exist, they can be used to identify the key interactions responsible for rate constant changes. However, this analysis is not always applicable to every system (and frequently gives different results for very similar reaction types7,13,29,30,32–34), as evidenced by the poor correlations obtained for this case (see ESI†). Thus, an alternative method of quantifying ionic liquid solvent effects needs to be considered.
Nucleofugality to predict rate constants
As outlined in the Introduction, the nucleofugality parameters of chloride in mixtures of ethanol and a range of different ionic liquids was recently determined.39 With these values, it is possible to use nucleofugality and electrofugality parameters to predict log(k1) (eqn (1)) for a given dissociation process if the electrofugality of the corresponding carbocation is known. In this case, the electrofugality of the acenaphthyl cation has not been reported, however it can be estimated based on literature comparisons to related systems to be ca. −7.5 (see ESI† for the full argument behind this value). Using that value (and a simple conversion that accounts for the different temperatures used here and in nucleofugality studies, see ESI†), the anticipated rate constants based on the reported chloride nucleofugalities in mixtures containing a high proportion (χIL = 0.8) of each of a range of ionic liquids 3–10 were determined (see ESI†). These predicted log(k1) values were then plotted against the experimental log(k1) values to evaluate the accuracy of the predictions (Fig. 4).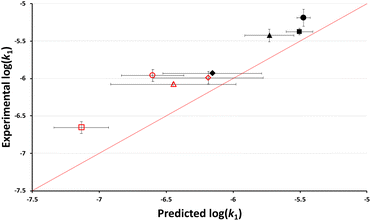 | ||
Fig. 4 The log of experimentally determined rate constant for the reaction between the chloride 1 and ethanol (Scheme 1) in mixtures containing ethanol and either [bmim][N(SO2CF3)2] 3 ( ), [bmim][C(CN)3] 4 (●), [bmim][N(CN)2] 5 (■), [bmim][PF6] 6 (▲), [bmim][BF4] 7 (◆), [bmpyr][N(SO2CF3)2] 8 ( ), [bmim][C(CN)3] 4 (●), [bmim][N(CN)2] 5 (■), [bmim][PF6] 6 (▲), [bmim][BF4] 7 (◆), [bmpyr][N(SO2CF3)2] 8 ( ), [mTOA][N(SO2CF3)2] 9 ( ), [mTOA][N(SO2CF3)2] 9 ( ), and [Li(G3)][N(SO2CF3)2] 10 ( ), and [Li(G3)][N(SO2CF3)2] 10 ( ) at χIL = 0.80 at 40 °C plotted against the corresponding predicted value based on reported nucleofugality data and Ef = −7.5. Uncertainties are the standard deviation of at least triplicate results for experimental data and are compounded from uncertainties in the reported nucleofugality data for the predicted values; some error bars are smaller than the markers used in the former case. The line shown is y = x and is present to guide the eye only. ) at χIL = 0.80 at 40 °C plotted against the corresponding predicted value based on reported nucleofugality data and Ef = −7.5. Uncertainties are the standard deviation of at least triplicate results for experimental data and are compounded from uncertainties in the reported nucleofugality data for the predicted values; some error bars are smaller than the markers used in the former case. The line shown is y = x and is present to guide the eye only. | ||
Immediately evident from this figure are two points: (i) that the model effectively predicts the rate constants for the process in different ionic liquids (mean absolute error (MAE) in log(k1) = 0.33) and (ii) as the points lie above the line y = x, the method systematically underestimates the value of log(k1). Both of these points can be addressed by considering the estimate of the electrofugality of the carbocation being formed; it is estimated to be −7.5 (see ESI†) but this method suggests that value is too small. Whilst alternative methods might be used to estimate the necessary Ef data, reducing the systematic error here (by assuming a correlation and optimising the fit, see below and ESI†), it should be noted that this simple model predicts reaction outcome with a MAE corresponding to a factor of ca. 2 in the rate constant. That is, it is possible to use available nucleofugality data and simple approximations of electrofugality to quantitatively predict rate constants for this process in mixtures containing different ionic liquids.
It should be noted that ionic liquid 10 might be considered an outlier in the above plot; it has the largest deviation from y = x and is the only case where the predicted rank of rate constants is differs from experimental. Salt 10 is the only ionic liquid which is significantly structurally different to the others used; this was identified in the original study,39 where it gave a notably different sf value compared to the other systems. As such, there is the potential that it might interact sufficiently differently with the electrofuge to affect the reactivity here.
It is worth considering not just whether the effects of different ionic liquids could be predicted, but also whether the effects of different proportions of an ionic liquid in the reaction mixture could be predicted. Using the same argument as above, the anticipated rate constants based on the reported chloride nucleofugalities in mixtures containing different proportions of the ionic liquid 3 in ethanol were determined (see ESI†). These predicted log(k1) values were then plotted against the experimental log(k1) values to evaluate the accuracy of the predictions (Fig. 5). In this case, compared to the example shown in Fig. 4, there is no readily apparent systematic error and while not all predicted values are within uncertainty of the experimental values, the overall efficacy of the model is clear. This efficacy is further demonstrated by a MAE in log(k1) = 0.11; which corresponds to a factor of 30%. Importantly, this plot shows that we can readily and quantitatively predict the rate constant for this process in mixtures containing different amounts of the ionic liquid 3.
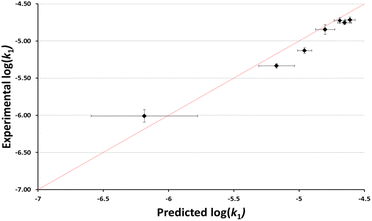 | ||
| Fig. 5 The log of experimentally determined rate constant for the reaction between the chloride 1 and ethanol (Scheme 1) in mixtures containing ethanol and [bmim][N(SO2CF3)2] 3 (◆) at 40 °C plotted against the corresponding predicted based on reported nucleofugality data and Ef = −7.5. Uncertainties are the standard deviation of at least triplicate results for the experimental data are compounded from uncertainties in the reported nucleofugality data for the predicted values; some error bars are smaller than the markers used in the former case. The line shown is y = x and is present to guide the eye only. | ||
It should be noted that an alternative way to calculate Ef would be to assume that the correlation held and to optimise the fit to a given value of electrofugality (see ESI†). Using the data in different ionic liquids gives a value of Ef of −7.17 (MAE = 0.11), while using the data for systems containing different proportions of the ionic liquid 3 gives a value of Ef of −7.60 (MAE = 0.08). Critically, that these separate datasets give estimates for Ef that are both (a) similar (differing by only 0.43) and (b) close to that determined from structural considerations (Ef = −7.5), supports the validity of the predicted Ef and demonstrates the robustness of the predictive model.
An interesting outcome from this plot is that the predictive method does not accurately order the rate constants in mixtures containing small proportions of ionic liquid (χIL < 0.3). Another way of representing this is that the maximum rate constant is observed at a different proportion of ionic liquid in the case of the chloride 1, compared to systems studied to determine the nucleofugality of chloride39 (χIL = 0.10 vs. χIL = 0.15 for substrate 1). The origin of this difference is not immediately clear but suggests that solvation of the two processes differs subtly as a result of the structure of the chlorides (acenaphthyl vs. benzhydryl), potentially indicating slight differences in measured electrofugality between species in solvent mixtures containing different proportion of ionic liquid in ethanol.
While the above caveats are important to consider, it is evident from Fig. 4 and 5 that the nucleofugality of chloride determined in mixtures containing ionic liquids can be used effectively to predict the rate constant for a related unimolecular process.
Conclusions
The work described here has investigated the ethanolysis of 2-chloro-1,1-dimethylnaphthalene 1 in the presence of each of a range of ionic liquids, along with the effect of changing the proportion of ionic liquid in the solvent mixtures. The reaction was found to be affected in a manner akin to other SN1 reactions in ionic liquids, with analyses such as mole fraction dependence of rate constants and the origin of those changes based on temperature dependent kinetic analyses being similar to that previously reported. This outcome is important as it demonstrates that the understanding of ionic liquid solvent effects on SN1 reactions as a whole can readily be transferred to other similar reactions.Previously determined nucleofugality data39 was exploited as a method to predict the solvent effects on the rate constant for this SN1 process. This methodology was able to predict the rate constant very effectively, both in mixtures containing different amounts of ionic liquid 3 but also in mixtures containing high proportions of each of the ionic liquids considered. These results are notable as they demonstrate a new method for the quantitative prediction of reaction outcomes in ionic liquids, one that is far more efficient than previous methods that were based on empirical solvent parameters and that also correlates with the understanding of solvation at the microscopic level. It is also noted that this method was effective even when the electrofugality of the carbocation generated was not known; it would be even more effective if that value has been reported.
In recognising this opportunity, it is important to acknowledge that the work herein to use nucleofugality to predict ionic liquid solvent effects is only preliminary. One of the biggest limitations currently is the lack of adequate nucleofugality data for ionic liquids. As the nucleofugality parameters are solvent dependent, further studies are needed to obtain the parameters for different nucleofuges and ionic liquid compositions.
Experimental
The chloride 1 was prepared from acenaphthene through oxidation, methylation, reduction and chlorination, as per literature procedures.52–56 Ethanol and triethylamine were purified through distillation according to literature procedures,57 and stored over activated 3 Å molecular sieves until use. The ionic liquids 3–5, 8 and 9 were prepared as per literature procedures,39 through alkylation of the appropriate amine followed by anion metathesis. The ionic liquids 6 and 7 were the generous gift of Dr Alyssa Gilbert.39 All ionic liquids were dried under reduced pressure (<0.1 mbar) and were found to have <100 ppm water using Karl Fischer titration methodology. The salts 3–10 contained <50 ppm residual halide as determined through ion chromatography. For full details of the preparations used, see ESI.†All 1H NMR characterization of products obtained from synthesis was done using a Bruker Avance III 300 (300 MHz, 1H), Bruker Avance III 500 (500 MHz, 1H), or Bruker Avance III 600 (600 MHz, 1H), NMR spectrometer. Multiplicities are reported as singlet (s), doublet (d), triplet (t), and multiplet (m). 1H NMR kinetic experiments were carried out on a Bruker Avance III 500 (500 MHz, 1H) NMR spectrometer calibrated with an Omega model HH23 thermometer. Where water bath kinetics methodologies were used, the temperature of the water bath was also calibrated using an Omega model HH23 thermometer.
Kinetic analyses were carried out in solutions containing the chloride 1 (ca. 0.005 mol L−1), triethylamine (ca. 0.02 mol L−1) and the appropriate mixture of ethanol and one of the ionic liquids 3–10. An aliquot (0.5 mL) of each stock solution was placed in an NMR tube and the reaction progress was followed using 1H NMR spectroscopy periodically. The reactions were kept at the appropriate temperature (40°C for all cases barring temperature dependent kinetic analyses) either in the spectrometer or in a water bath, depending on the reaction time. The extent of reaction was determined by following the decrease in the integration of the signal due to the benzylic proton on the chloride 1 (ca. 5.5 ppm) with time and fitting to either a first order decay (reactions that proceeded to >90% in 8 h) or an initial rate (other cases). Each rate constant was measured in triplicate. Activation enthalpies and entropies were determined by fitting the obtained temperature dependent rate constants to the Eyring equation.44 Further details of stock solutions compositions and kinetic experiments, including rate constants are in the ESI.†
1H NMR spectra were processed with Mestrelab MNova 14 software. Rate constants were calculated using Microsoft Office Excel in combination with the LINEST function. All rate constant data is provided in the ESI.†
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. Y. H. is grateful to the Australian Government for the award of a Research Training Program Scholarship. J. B. H. acknowledges financial support from the Australian Research Council discovery project funding scheme (project DP180103682). The support of the Mark Wainwright Analytical Centre and the UNSW NMR facility are gratefully acknowledged.Notes and references
- S. Zein El Abedin and F. Endres, Acc. Chem. Res., 2007, 40, 1106–1113 CrossRef PubMed.
- D. R. MacFarlane, A. L. Chong, M. Forsyth, M. Kar, R. Vijayaraghavan, A. Somers and J. M. Pringle, Faraday Discuss., 2018, 206, 9–28 RSC.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- M. Bier and S. Dietrich, Mol. Phys., 2010, 108, 1413 CrossRef CAS.
- D. M. Fox, W. H. Awad, J. W. Gilman, P. H. Maupin, H. C. De Long and P. C. Trulove, Green Chem., 2003, 5, 724–727 RSC.
- T. Welton, Chem. Rev., 1999, 99, 2071–2084 CrossRef CAS.
- R. Bini, C. Chiappe, V. L. Mestre, C. S. Pomelli and T. Welton, Org. Biomol. Chem., 2008, 6, 2522–2529 RSC.
- L. Crowhurst, N. L. Lancaster, J. M. Pérez Arlandis and T. Welton, J. Am. Chem. Soc., 2004, 126, 11549–11555 CrossRef CAS.
- G. Ranieri, J. P. Hallett and T. Welton, Ind. Eng. Chem. Res., 2008, 47, 638–644 CrossRef CAS.
- J. P. Hallett, C. L. Liotta, G. Ranieri and T. Welton, J. Org. Chem., 2009, 74, 1864–1868 CrossRef CAS PubMed.
- R. R. Hawker and J. B. Harper, Adv. Phys. Org. Chem., 2018, 52, 49–85 CrossRef CAS.
- A. George, A. Brandt, K. Tran, S. M. S. N. S. Zahari, D. Klein-Marcuschamer, N. Sun, N. Sathitsuksanoh, J. Shi, V. Stavila, R. Parthasarathi, S. Singh, B. M. Holmes, T. Welton, B. A. Simmons and J. P. Hallett, Green Chem., 2015, 17, 1728–1734 RSC.
- A. Gilbert, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2019, 17, 675–682 RSC.
- R. R. Hawker, M. J. Wong, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2017, 15, 6433–6440 RSC.
- I. Newington, J. M. Perez-Arlandis and T. Welton, Org. Lett., 2007, 9, 5247–5250 CrossRef CAS.
- E. E. L. Tanner, H. M. Yau, R. R. Hawker, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 6170–6175 RSC.
- X. Creary, E. D. Willis and M. Gagnon, J. Am. Chem. Soc., 2005, 127, 18114–18120 CrossRef CAS PubMed.
- S. T. Keaveney, B. P. White, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2016, 14, 2572–2580 RSC.
- S. T. Keaveney and J. B. Harper, RSC Adv., 2013, 3, 15698–15704 RSC.
- S. T. Keaveney, D. V. Francis, W. Cao, R. S. Haines and J. B. Harper, Aust. J. Chem., 2015, 68, 31–35 CrossRef CAS.
- K. S. Schaffarczyk McHale, R. R. Hawker and J. B. Harper, New J. Chem., 2016, 40, 7437–7444 RSC.
- H. M. Yau, S. A. Barnes, J. M. Hook, T. G. A. Youngs, A. K. Croft and J. B. Harper, Chem. Commun., 2008, 3576–3578 RSC.
- S. Tsuzuki, W. Shinoda, H. Saito, M. Mikami, H. Tokuda and M. Watanabe, J. Phys. Chem. B, 2009, 113, 10641–10649 CrossRef CAS PubMed.
- H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371 RSC.
- S. G. Jones, H. M. Yau, E. Davies, J. M. Hook, T. G. A. Youngs, J. B. Harper and A. K. Croft, Phys. Chem. Chem. Phys., 2010, 12, 1873–1878 RSC.
- A. Schindl, R. R. Hawker, K. S. Schaffarczyk McHale, K. T. C. Liu, D. C. Morris, A. Y. Hsieh, A. Gilbert, S. W. Prescott, R. S. Haines, A. K. Croft, J. B. Harper and C. M. Jäger, Phys. Chem. Chem. Phys., 2020, 22, 23009–23018 RSC.
- R. R. Hawker, J. Panchompoo, L. Aldous and J. B. Harper, ChemPlusChem, 2016, 81, 574–583 CrossRef CAS PubMed.
- K. T. C. Liu, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2020, 18, 7388–7395 RSC.
- R. Bini, C. Chiappe, D. Pieraccini, P. Piccioli and C. S. Pomelli, Tetrahedron Lett., 2005, 46, 6675–6678 CrossRef CAS.
- A. Gilbert, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2020, 18, 5442–5452 RSC.
- L. Crowhurst, R. Falcone, N. L. Lancaster, V. Llopis-Mestre and T. Welton, J. Org. Chem., 2006, 71, 8847–8853 CrossRef CAS PubMed.
- S. Tiwari, N. Khupse and A. Kumar, J. Org. Chem., 2008, 73, 9075–9083 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, V. L. Mestre, C. S. Pomelli and T. Welton, Theor. Chem. Acc., 2009, 123, 347–352 Search PubMed.
- A. Gilbert, G. Bucher, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2019, 17, 9336–9342 RSC.
- J. Alarcón-Espósito, R. Contreras, R. A. Tapia and P. R. Campodónico, Chem.–Eur. J., 2016, 22, 13347–13351 CrossRef.
- D. C. Morris, S. W. Prescott and J. B. Harper, Phys. Chem. Chem. Phys., 2021, 23, 9878–9888 RSC.
- T. L. Greaves, K. S. Schaffarczyk McHale, R. F. Burkart-Radke, J. B. Harper and T. C. Le, Phys. Chem. Chem. Phys., 2021, 23, 2742–2752 RSC.
- B. Y. W. Man, J. M. Hook and J. B. Harper, Tetrahedron Lett., 2005, 46, 7641–7645 CrossRef CAS.
- M. D. Coney, D. C. Morris, A. Gilbert, S. W. Prescott, R. S. Haines and J. B. Harper, J. Org. Chem., 2022, 87, 1767–1779 CrossRef CAS PubMed.
- C. E. Rosella and J. B. Harper, Tetrahedron Lett., 2009, 50, 992–994 CrossRef CAS.
- S. R. D. George, G. L. Edwards and J. B. Harper, Org. Biomol. Chem., 2010, 8, 5354–5358 RSC.
- K. S. Schaffarczyk McHale, R. S. Haines and J. B. Harper, ChemPlusChem, 2018, 83, 1162–1168 CrossRef CAS PubMed.
- G. A. Olah, G. Liang and P. Westerman, J. Am. Chem. Soc., 1973, 95, 3698–3705 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- J. B. Harper and R. M. Lynden-Bell, Mol. Phys., 2004, 102, 85–94 CrossRef CAS.
- E. E. L. Tanner, R. R. Hawker, H. M. Yau, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 7516–7521 RSC.
- F. D'Anna, S. Marullo, P. Vitale and R. Noto, Eur. J. Org. Chem., 2011, 2011, 5681–5689 CrossRef.
- M. J. Kamlet and R. W. Taft, J. Am. Chem. Soc., 1976, 98, 377–383 CrossRef CAS.
- R. W. Taft and M. J. Kamlet, J. Am. Chem. Soc., 1976, 98, 2886–2894 CrossRef CAS.
- M. J. Kamlet, J. L. Abboud and R. W. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038 CrossRef CAS.
- S. Spange, R. Lungwitz and A. Schade, J. Mol. Liq., 2014, 192, 137–143 CrossRef CAS.
- L. F. Fieser and J. Cason, J. Am. Chem. Soc., 1940, 62, 432–436 CrossRef CAS.
- A. Bosch and R. K. Brown, Can. J. Chem., 1968, 46, 715–728 CrossRef CAS.
- J. Chen, Z. Shi and P. Lu, Org. Lett., 2021, 23, 7359–7363 CrossRef CAS PubMed.
- S. D. Levine, J. Med. Chem., 1971, 14, 707–709 CrossRef CAS.
- F. McLure and R. Norris, Aust. J. Chem., 1987, 40, 523–537 CrossRef CAS.
- J. Leonard, B. Lygo and G. Procter, Advanced Practical Organic Chemistry, CRC Press, Boca Raton: United States of America, 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis of ionic liquids and precursors, experimental details for kinetic analyses, mixture composition and rate data for nucleophile dependence studies, mixture composition and rate data for mole fraction dependence studies, mixture compositions and rate data for analysis of temperature dependence, Eyring analyses, multivariate analysis for Kamlet–Taft correlations, estimation of the electrofugality of the acenaphthyl cation, comparison of predicted and experimental rate constant data, alternate methods to determine the electrofugality of the acenaphthyl cation and resultant predicted rate constant data, predicted NMR spectra for prepared compounds. See DOI: https://doi.org/10.1039/d3ra04302a |
| ‡ Kamlet–Taft parameters,48–50 which measure the solvent properties and can be related to the structures of the ionic liquid components,51 will be considered below. |
| This journal is © The Royal Society of Chemistry 2023 |