Alternating current properties of bulk- and nanosheet-graphitic carbon nitride compacts at elevated temperatures

Abstract

The investigations of temperature-dependent electrical properties in graphitic carbon nitride (g-C₃N₄) have been largely performed at/below room temperature on devices commonly fabricated by vacuum techniques, leaving the gap to further explore its behaviors at high-temperature. We reported herein the temperature dependence (400 → 35 °C) of alternating current (AC) electrical properties in bulk- and nanosheet-g-C₃N₄ compacts simply prepared by pelletizing the powder. The bulk sample was synthesized via the direct heating of urea, and the subsequent HNO₃-assisted thermal exfoliation yielded the nanosheet counterpart. Their thermal stability was confirmed by variable-temperature X-ray diffraction, demonstrating reversible interlayer expansion/contraction upon heating/cooling with the thermal expansion coefficient of 2.2 × 10⁻⁵–3.1 × 10⁻⁵ K⁻¹. It is found that bulk- and nanosheet-g-C₃N₄ were highly insulating (resistivity ρ ∼ 10⁸ Ω cm unchanged with temperature), resembling layered van der Waals materials such as graphite fluoride but unlike electronically insulating oxides. Likewise, the dielectric permittivity ε′, loss tangent tan δ, refractive index n, dielectric heating coefficient J, and attenuation coefficient α, were weakly temperature- and frequency-dependent (10³–10⁵ Hz). The experimentally determined ε′ of bulk-g-C₃N₄ was reasonably close to the in-plane static dielectric permittivity (8 vs. 5.1) deduced from first-principles calculation, consistent with the anisotropic structure. The nanosheet-g-C₃N₄ exhibited a higher ε′ ∼ 15 while keeping similar tan δ (∼0.09) compared to the bulk counterpart, demonstrating its potential as a highly insulating, stable dielectrics at elevated temperatures.

---

Introduction

Layered materials have received increasing attention due to their vast potential applications especially at elevated temperatures. For example, the thermal properties of graphite dictate its use as an electrical conductor, a thermal insulator, an inert coating/crucible material, and as a component of nuclear reactors.^1–3 Hexagonal boron nitride (hBN) possesses high thermal conductivity significantly larger than that currently used in thermal management.⁴ Graphite fluoride is a hydrophobic, electrically insulating, solid lubricant which starts to decompose at a temperature as high as 420 °C.⁵ Accordingly, it is important to uncover chemical/physical properties of these layered materials, including the nanosheets derived therefrom, to serve as guidelines for materials selection.

Graphitic carbon nitride (g-C₃N₄) are defect-rich, polymeric aromatic layered materials consisting mainly of sp²-bonded C and N atoms into neutral layers of tri-s-triazine units.⁶ The layers are linked by van der Waals interactions, adopting the A–B stacking and a misalignment to decrease the repulsive π–π interactions. g-C₃N₄ can be exfoliated into nanosheets by a facile HNO₃-assisted thermal exfoliation,⁷ and further constructed into a composite with metal oxide⁸ or metal.⁹ The electrical properties of g-C₃N₄-based devices^10–16 (typically prepared by vacuum techniques) or composites^8,17–20 (where the tested specimens can be easily prepared by pelletizing the powder) have been widely investigated at/below room temperature. It is acknowledged that g-C₃N₄ is highly insulating (resistivity ρ larger than 10⁸ Ω cm),^11,14,17,21 with the in-plane electrical conductivity two orders of magnitude smaller than that out-of-plane through the stacked layers.²² The dielectric permittivity ε′ of g-C₃N₄ typically varies from 2–7 in thin films^14,23,24 up to ∼60 in the bulk.^18,19 However, unusually large ε′ (∼10³) has also been reported⁹ especially at low frequency (<10² Hz) where electrode polarization could occur.

Interestingly, the investigations on the charge/dipole conduction of g-C₃N₄ at elevated temperatures are rather limited, or the temperature range is narrow and skewed towards the low-temperature side (i.e., below RT). For example, Patra and Mohapatra¹⁵ investigated the dielectric properties of the g-C₃N₄/Al₂O₃ heterostructure at 10⁵ Hz, showing that the capacitance (which is proportional to ε′) increased as T increased from −93 to 25 °C. Meanwhile, ε′ of g-C₃N₄ was practically T-independent from −73 to 23 °C,¹⁴ but it decreased from 16 to 10 as the frequency f increased (10² → 10⁶ Hz). The electric field-dependence of conductance^25,26 provided similar results. In the metal/amorphous carbon nitride/metal devices,^27,28 the conductance varied with T^−1/4 from −183 to 27 °C. (A similar T^−1/4 dependence was reported in a four-point probe measurement,²⁹ revealing that the charge transport was dominated by variable-hopping conduction). In addition, the conductance increased with f (10¹–10⁶ Hz) at −173 °C, but it was f-independent at 23 °C. In these works, impedance spectroscopy^30,31 is an important tool to elucidate the nature of charge transport, since different presentations highlight distinct parts of the responses and provide complementary information. In addition, impedance spectroscopy enables the simple derivation of some other parameters such as refractive index,³² dielectric heating coefficient,³² and attenuation coefficient,³³ but these have not been performed on g-C₃N₄.

Herein, we reported the impedance measurements and deduced several AC properties of polycrystalline g-C₃N₄ in bulk and nanosheet forms from 400 → 35 °C and at f = 10⁵, 10⁴, and 10³ Hz. The results are compared to graphite fluoride⁵ which is selected because it is a readily available, highly insulating, carbon-based, heteroatom-substituted layered material, where the layers are linked by van der Waals forces as with g-C₃N₄. In addition, we have theoretically investigated the complex dielectric function via first-principles calculation, supplementing the recent computational works.^34–40 Due to the anisotropic nature, values from the in-plane and out-of-plane direction (i.e. along the stacks) were typically reported, although the direct comparison with experimental values were not straightforward because of the difference in temperature and in frequency. Our work suggested that g-C₃N₄ could be a promising candidate as a thermally stable, temperature-independent insulator and dielectric (ε′ ∼8 and 15 for bulk and nanosheet forms, respectively, with similar tan δ ∼0.09).

Experimental

Synthesis

Bulk graphitic carbon nitride was prepared by a direct heating of urea powder (125 g) in an alumina crucible with a cover at 600 °C (heating rate 10 °C min⁻¹) for 4 h.^7,8 After cooling down to room temperature (RT), the pale-yellow product was collected and ground into powder. The nanosheet analog was produced by immersing the bulk powder (2.5 g) in 100 mL of HNO₃ (65%) for 12 h. The obtained sample was filtered and washed with deionized water, and heated at 500 °C for 4 h. Graphite fluoride (>61 wt% F) was a product from Sigma Aldrich, and its basic characterization results can be found in Fig. S1 in ESI.†

Characterization

X-Ray diffraction (XRD) was performed using CuKα radiation at 2θ = 10–60° (Bruker model D2 PHASER). The morphology of the samples was characterized by transmission electron microscopy at 200 kV (JEOL, JEM 2010). FTIR spectra in the attenuated total reflectance (ATR) mode were collected using a PerkinElmer spectrometer (Spectrum Two) at the resolution of 4 cm⁻¹. ¹H solid state NMR spectra were acquired using a JEOL 400YH operating at 400 MHz. TGA was performed under the flow of N₂ gas (20 mL min⁻¹) from RT to 800 °C (10 °C min⁻¹) using a PerkinElmer, Pyris-1 instrument.

The variable temperature X-ray diffraction was performed using a Rigaku SmartLab diffractometer operated from 25–350 °C under static air with the Bragg–Brentano geometry. The powder was directly placed onto an aluminum pan (7 × 7 mm²) placed on the heating stage, which was subsequently covered with stage cap chamber for heating (5 °C min⁻¹). The XRD patterns were collected at 2θ = 10–50° at a scan speed of 40° (2θ)·min⁻¹ with a 0.02° step-size.

Electrical properties measurements

The bulk or nanosheet-g-C₃N₄ powder, or graphite fluoride, was pressed without a binder into a pellet with the diameter of ∼0.5 cm and the thickness of ∼0.2 cm. All pellets were gold-sputtered on both sides to form electrical contacts. The impedance measurements were conducted using a precision LCR meter (HP-4284A, Hewlett-Packard, Palo Alto, CA) covering the frequency f = 20 to 10⁶ Hz. To avoid complication due to water from the atmosphere,⁸ the specimens were heated to 400 °C prior to cool down to 35 °C employing the heating/cooling rates of 2 °C min⁻¹. All electrical properties shown in this work were acquired from the cooling process 400 → 35 °C.

Computational method

The structural and electronic properties of g-C₃N₄ were performed based on first-principles calculation using the HSE06 hybrid functional^41,42 as implemented in the Vienna ab initio simulation package (VASP).^43,44 To accurately account for the van der Waals interaction, Grimme's empirical correction approach (GGA-D3)⁴⁴ was also applied. The lattice parameters, electronic band structure, and the band gap are consistent with those in the literature, see Fig. S2.† The optical properties of g-C₃N₄ were calculated using the Random Phase Approximation (RPA) method based on the HSE06 functional with the assistance of the VASPKIT tool,^45,46 employing an 18 × 18 × 1 gamma-centered k-point mesh.

Results and discussion

Samples characteristics

Fig. 1a shows the XRD patterns of bulk- and nanosheet-g-C₃N₄ samples which are similar to JCPDS 87-1526. They show two prominent peaks at ∼13.0° and 27.5° due to the in-plane motif (100 reflection) and the stacking of the graphitic carbon nitride sheet (002 reflection) respectively.^6–8,47 TEM images in Fig. 1b and c display thin sheets typical of layered materials with the lateral dimension of ∼200 nm. The sheets are buckled, reflecting their flexibility and confirming a successful HNO₃-assisted thermal exfoliation. The FTIR spectra in Fig. 1d show many characteristic peaks of g-C₃N₄.⁴⁷ These include the aromatic C–N stretching (1231, 1314, 1473 cm⁻¹), the C=N stretching (1536 and 1631 cm⁻¹), and the N–H and O–H stretching (from absorbed H₂O) at 3087, 3159 and 3254 cm⁻¹. Interestingly, the breathing mode of s-triazine units shifts from 813 cm⁻¹ in bulk-g-C₃N₄ to 803 cm⁻¹ in nanosheet-g-C₃N₄, suggesting a slight modification to the tri-s-triazine building block.

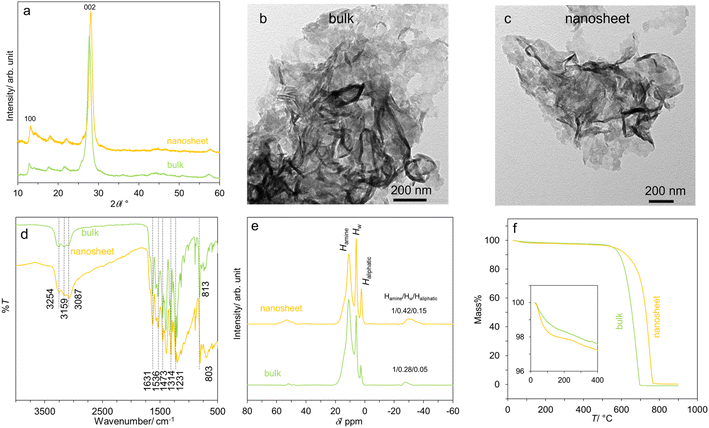Fig. 1 Some characteristics of the bulk- and nanosheet-g-C₃N₄ samples: (a) XRD patterns, (b and c) TEM images, (d) FTIR spectra, (e) ¹H NMR spectra, and (f) mass loss curves.

The modification is further supported by the ¹H NMR spectra in Fig. 1e, which comprise of three signals at ∼10.8, 5.8 and 2.6 ppm. There signals are ascribed respectively to the H atoms attached to N atoms from the triazine unit (H_amine), residual H₂O (H_W), and H attached to C atom (H_aliphatic) presumably at the edge or defect.^8,48,49 The peak area ratio H_amine/H_W/H_aliphatic for bulk-g-C₃N₄ equals 1/0.28/0.05, but it is 1/0.42/0.15 for nanosheet-g-C₃N₄. Accordingly, it can be deduced that there are more water molecules in the nanosheets, and that there is an increasing relative proportion of aliphatic region/edges in the nanosheets, consistent with the exfoliation. Lastly, Fig. 1f shows the mass loss curves. The two samples show the first mass loss due the removal of loosely bound, physisorbed water at T < 200 °C: 1.68 wt% for bulk-g-C₃N₄, and 2.09 wt% for nanosheet-g-C₃N₄. At T > 400 °C, a significant mass loss is observed possibly due to structural degradation. The hydrophilic nature of the g-C₃N₄ samples is consistent with earlier works on their protonic conduction⁸ and humidity detection.^10,11,17

To further conform the thermal stability of the samples, we conducted the variable-temperature XRD measurement employing the temperature the sequence 25 → 350 → 25 °C. Fig. 2a and b focus on the interlayer distance (d₀₀₂) of bulk- and nanosheet-g-C₃N₄ samples respectively, showing that the peak left-shifts with increasing T, reflecting the typical thermal expansion. Upon cooling down, d₀₀₂ right-shifts close to the original position indicating the reversible expansion/contraction and ensuring the thermal stability within this range. This finding indicates no phase change or structural degradation at least up 350 °C. Accordingly, water (cc. Fig. 1e and f) is most likely on the surface but not intercalated into the interlayer space. The T-dependence of d₀₀₂ is shown in Fig. 2c, varying from 3.193–3.202 Å, where there is no significant difference between bulk- and nanosheet-g-C₃N₄ samples.

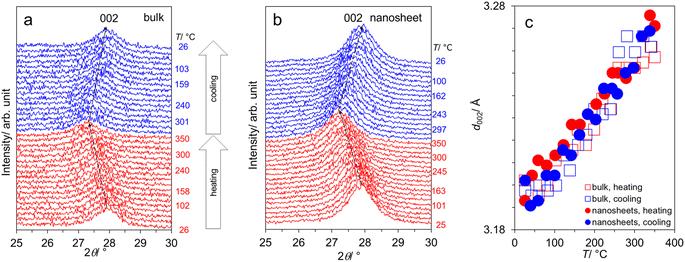Fig. 2 (a) Variable-temperature XRD patterns from the sequence 25 → 350 → 25 °C: (a) bulk-g-C₃N₄, (b) nanosheet-g-C₃N₄; and (c) the T-dependence of the interlayer spacing d₀₀₂.

The coefficient of thermal expansion (CTE) is calculated as:

CTE = [((d₀₀₂(350 °C) − d₀₀₂(25 °C))/d₀₀₂(25 °C)]/ΔT (1)

where d₀₀₂(350 °C) and d₀₀₂(25 °C) are the interlayer spacing at 350 °C and 25 °C, respectively; and ΔT is the temperature range of the measurement. It is found that CTE values are 2.2 × 10⁻⁵-3.1 × 10⁻⁵ K⁻¹ (Table S1†). This is the same order of magnitude with the values previously reported from first principles investigations,³⁵ and with those experimentally obtained from amorphous carbon nitride,⁵⁰ natural graphite sheet,⁵¹ hBN,⁵² see Table S1.†

Temperature dependence of AC properties

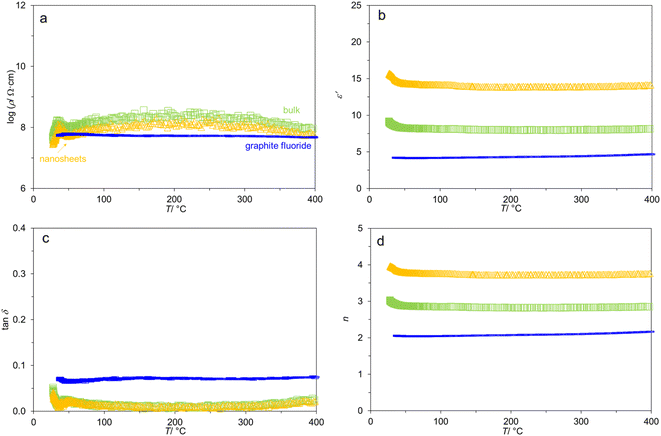
It is found that the Nyquist plots (real part Z′ vs. imaginary part −Z′′) of the two samples from 400 → 50 °C appeared almost as a straight line (Fig. S3†). This does not allow the fitting by equivalent circuit or a theoretical model. Considering the limited information from the f-dependence of the complex impedance, we investigated the T-dependence of AC properties from 400 → 35 °C at selected frequencies instead. As shown in Fig. 3a for the data at 10⁵ Hz, log ρ(T) is relatively constant throughout 400 → 50 °C for both bulk- and nanosheet-g-C₃N₄ samples alike. The variation of resistivity is not more than a factor of four (Fig. S4†) despite of the wide temperature window of investigation. This fluctuation can be explained by the simple powder pressing into pellets and the accompanying porosities (apparent densities 37–44% of the theoretical values). Meanwhile, the spike at <50 °C is most likely caused by proton conduction due to the (re)adsorption of atmospheric water.⁸ For comparison, the variation of log ρ(T) in typical oxides such as the insulating ceramics BaTiO₃–Bi_1/2Na_1/2TiO₃ (BT-BNT)⁵³ is up to four orders of magnitude. The stable log ρ(T) might be common for layered van der Waals materials such as graphite³ or graphite fluoride (Fig. 3a and also in Fig. S5†) The flat log ρ(T) of graphite fluoride might be due to the higher apparent density (71%) of the specimen. The absence of proton conduction at <50 °C can be well explained by the well-known water repellent nature of graphite fluoride.

Fig. 3 Temperature dependence of (a) log ρ, (b) ε′, (c) tan δ, and (d) n for bulk- and nanosheet-g-C₃N₄ samples, in comparison to graphite fluoride. Data shown here were at 10⁵ Hz and were obtained in the cooling process.

It is observed (Fig. 3a) that log ρ at 10⁵ Hz is in the order: bulk-g-C₃N₄ (up to 8.5 Ω cm) > nanosheet-g-C₃N₄ (8.1 Ω cm) > graphite fluoride (7.6 Ω cm). It is known that g-C₃N₄ shows high in-plane resistivity but low out-of-plane resistivity.^12,13,22 This is because the carriers are localized at the N atoms for the in-plane direction, but they can hop between the layers (out-of-plane), leading to the anisotropic transport characteristics.¹³ Accordingly, the nanosheet-g-C₃N₄ with smaller number of stacks should possess a facilitated charge/dipoles transport, as indeed experimentally detected by the smaller log ρ. The different behaviors of bulk-vs. nanosheet-g-C₃N₄ have been observed by other techniques such as ab initio calculations³⁷ and time resolved photoluminescence.⁵⁴ This is also consistent with the modifications to the graphitic structure as shown by IR and ¹H NMR spectroscopies, warranting further investigations. The different AC behavior suggests that the nanosheets would not reassemble back to the bulk form by a simple pressing during specimen preparation.

Despite of the small variation in log ρ(T), Fig. 3b shows that ε′ is practically T-independent from 400 → 50 °C, and equals to 14 (nanosheets), 8 (bulk), and 4 (graphite fluoride). While the specimens contain porosities, the ε′ values of g-C₃N₄ samples are comparable to those in the literature.^{8,14,15,23,55} For example, Patra and Mohapatra¹⁴ reported ε′ = 12 (also at 10⁵ Hz) in the low-temperature measurement (−3 to 23 °C). Moreover, Fig. 3c shows that the loss tangents tan δ of the two g-C₃N₄ samples are similar (0.009 at 200 °C) and comparable to that in carbon nitride films on Si,²³ which are seven times smaller than that of graphite fluoride. The dielectric loss is typically due to dipole relaxation (energy dissipation) and resistive loss (due to mobile charge carriers). Apparently, the latter is insignificant in nanosheet-g-C₃N₄. Also, the larger ε′ of the nanosheet-compared to the bulk-g-C₃N₄ is consistent with the larger σ (i.e., smaller ρ, Fig. 3a) and the same loss tangent (Fig. 3c), because σ = ωε′ε₀ tan δ.

The T-dependence impedance measurements allowed the calculation of some other parameters, see ESI.† Fig. 3d shows that the refractive indices n [eqn (S8)†] at 10⁵ Hz are similarly T-independent at 3.7 (nanosheet-g-C₃N₄), 2.8 (bulk-g-C₃N₄), and 1.6 (graphite fluoride) (vs. 1.85 for amorphous carbon nitride).⁵⁵ Notably, n of nanosheet-g-C₃N₄ is larger than that of the bulk, presumably reflecting the complex scatterings which require in-depth investigations. Nevertheless, similar finding is available⁵⁶ where n of graphite (2.56) is smaller than that of graphene (2.65–2.71), although the difference is small in this case. The T-dependence of the dielectric heating coefficient³² J, and the attenuation coefficient³³ α has been calculated as shown in Fig. S6.†

First-principles calculation

We also investigated the complex dielectric function (real part ε′ and the imaginary part ε'') of bulk-g-C₃N₄ at absolute zero temperature by first-principles calculation. Because the polarization along the x- and y-axes (i.e., in-plane) is isotropic, it is represented as a single line E_xx(yy) shown by the blue line in Fig. 4a and b. The polarization along the z-axis (i.e., out of plane) is represented by the red line E_zz. The average polarization was calculated by assuming that the off-diagonal elements contribute less to the average compared to the diagonal ones:

E_avg = 2/3(E_xx + E_yy) + 1/3(E_zz) (2)

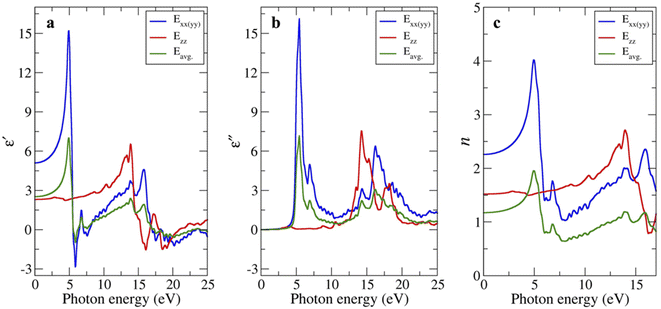Fig. 4 (a) Real and (b) imaginary parts of the complex dielectric function, and (c) refractive index of bulk-g-C₃N₄ as a function of photon energy.

The strong peak is observed for E_xx(yy) at 4.9 eV, while another peak with medium intensity is observed for E_zz at 15.8 eV. The peaks positions are broadly consistent with the reports in g-C₃N₄ (ref. 39 and 40) or amorphous carbon.³⁴

The static dielectric permittivity (i.e., ε′ close to zero energy) were calculated to be 5.10, 2.31, and 2.52 for the in-plane, out-of-plane, and the average value, respectively, which are comparable to 6.15, 2.84, and 5.05 reported by Rignanese et al.³⁶ Notably, the value along the in-plane direction (which was derived theoretically at absolute zero temperature) better matched the experimentally observed value (ε′ ∼8), the latter being weakly T-dependent from 400 → 50 °C. Meanwhile, the imaginary part near zero energy is on the order of 10⁻² (not clearly visible in Fig. 4b). Accordingly, the ratio of imaginary part over real part (i.e., tan δ) will be small, qualitatively consistent with the impedance measurements.

It is natural to assume that thin sheets of layered materials would approximately (but not neatly) stack on top of each other upon pelletization. Because the in-plane resistivity is higher than the out-of-plane resistivity,^12,13,22 charges/dipoles will be mostly confined to the in-plane direction, explaining to the reasonable agreement between the measurement and the calculated polarization along the xx(yy) direction. Likewise, the calculated (static) n values for the xx(yy) direction of 2.26 (vs. 2.0 by Reshak et al.)³⁹ are closer to n = 2.8 experimentally determined from bulk-g-C₃N₄ (Fig. 3d). The n values of 1.52 (zz) and 1.17 (averaged) are smaller.

Frequency dependence of AC properties

Table 1 compares log ρ, ε′, tan δ, and n at f = 10⁵, 10⁴ and 10³ Hz, all acquired upon cooling down (see also Fig. S7 and S8†). The values shown were averaged from 400 → 50 °C, with the standard deviation of the last digit in parenthesis. In all cases, log ρ increases with decreasing f (i.e., the samples become more insulating). This finding agrees with Jonscher's universal power law due to interacting charges/dipoles^33,57,58 (σ = Afⁿ; ρ = 1/σ). However, ε′ increases with decreasing f because dipoles have more time to reorient in response to the alternating field.^8,32,33 The increased ε′ leads to an increasing tan δ. Interestingly, tan δ remains similar between bulk- and nanosheet-g-C₃N₄ (0.01 at 10⁵ Hz, and 0.08 at 10³ Hz) while the ε′ values of the nanosheets are almost two times larger, 15 vs. 8. The results suggest that nanosheet-g-C₃N₄ could be a promising candidate for a highly insulating, stable dielectrics at elevated temperature.

Table 1 Comparison of the log ρ, ε′, tan δ, and n of the samples averaged from 400 → 50 °C (with the standard deviation of the last digit in parenthesis) at selected frequencies (in Hz), obtained during the cooling process

Sample	f/Hz	log(ρ/Ω cm)	ε′	tan δ	n
Bulk-g-C3N4	10^5	8(1)	8.07(9)	0.014(5)	2.84(2)
	10^4	8.8(1)	8.3(2)	0.04(1)	2.88(3)
	10^3	9.5(2)	8.8(5)	0.08(3)	2.97(9)
Nanosheet-g-C3N4	10^5	8.0(1)	14.0(2)	0.014(4)	3.75(2)
	10^4	8.6(1)	14.5(3)	0.04(1)	3.81(4)
	10^3	9.2(2)	15(1)	0.08(3)	3.9(1)
Graphite fluoride	10^5	7.73(3)	4.3(1)	0.070(3)	2.08(3)
	10^4	8.8(1)	4.8(1)	0.065(7)	2.19(3)
	10^3	9.8(2)	5.2(3)	0.05(2)	2.29(6)

---

Lastly, n is practically T-invariant in both g-C₃N₄ samples. The insignificant change of n(T) was long known in other layered materials such as graphite⁵⁹ from 25 to 600 °C. When f decreased from 10⁵ to 10³ Hz, the variation with T is more pronounced with the standard deviations 0.5–0.7%, 1%, and 3% of n, comparable to that of graphite fluoride also shown in Table 1.

Conclusions

Bulk- and nanosheet-g-C₃N₄ were thermally stable at least up to 350 °C with reversible interlayer expansion/contraction upon heating/cooling. They exhibited relatively stable resistivity, ε′, tan δ, and n invariant with temperature from 400 → 50 °C which were also weakly f-dependent from 10⁵–10³ Hz.

The experimental values (ε′ and n) of bulk-g-C₃N₄ are in reasonable agreement with the values along the in-plane direction as extracted from first-principles calculation, further showcasing the anisotropic charge/dipole transport.

Notably, nanosheet-g-C₃N₄ is more conducting than the bulk counterpart, in addition to exhibiting almost two time larger ε′ (15 vs. 8) but similar tan δ (0.09). This is contributed to the facilitated charge transfer in nanosheets with decreased stack numbers, ascribed to structural modifications suggested by IR and ¹H NMR spectroscopies. The nanosheet-g-C₃N₄ could be a promising candidate for a highly insulating, stable dielectrics at elevated temperature. The weak temperature-dependence of electrical properties, and the demonstrated structural/thermal stabilities, would minimize the impact of varying temperature on the device performances.

Author contributions

Tosapol Maluangnont: conceptualization; writing, review, and editing; funding acquisition; project administration, and supervision. Phieraya Pulphol, Kanokwan Chaithaweep, Klichchupong Dabsamut, and Thawanrat Kobkeatthawin: investigation. Siwaporn Meejoo Smith, Adisak Boonchun and Naratip Vittayakorn: supervision. All authors have reviewed and approved of the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work is supported by King Mongkut's Institute of Technology Ladkrabang (KREF 046403) (T. Maluangnont). The work of N. Vittayakorn is funded by KMITL under grant No. KREF 116501. We also acknowledge the facilities and technical assistance from Nanotechnology and Materials Analytical Instrument Service Unit (NMIS) of College of Materials Innovation and Technology, KMITL.

References

1. D. K. L. Tsang, B. J. Marsden, S. L. Fok and G. Hall, Graphite thermal expansion relationship for different temperature ranges, Carbon, 2005, 43, 2902–2906.
2. J. B. Nelson and D. P. Riley, The thermal expansion of graphite from 15 °C to 800 °C: part I. experimental, Proc. Phys. Soc., 1945, 57, 477–486.
3. M. Okada, N. Ohta, O. Yoshimoto, M. Tatsumi and M. Inagaki, Review on the high-temperature resistance of graphite in inert atmospheres, Carbon, 2017, 116, 737–743.
4. J.-C. Zheng, L. Zhang, A. V. Kretinin, S. V. Morozov, Y. B. Wang, T. Wang, X. Li, F. Ren, J. Zhang and C.-Y. Lu, et al., High thermal conductivity of hexagonal boron nitride laminates, 2D Mater., 2016, 3, 011004.
5. R. L. Fusaro and H. E. Sliney, Graphite fluoride (CF_x)_n—a new solid lubricant, ASLE Trans., 1970, 13, 56–65.
6. F. Fina, S. K. Callear, G. M. Carins and J. T. S. Irvine, Structural investigation of graphitic carbon nitride via XRD and neutron diffraction, Chem. Mater., 2015, 27, 2612–2618.
7. T. Kobkeatthawin, J. Trakulmututa, T. Amornsakchai, P. Kajitvichyanukul and S. M. Smith, Identification of active species in photodegradation of aqueous imidacloprid over g-C₃N₄/TiO₂ Nanocomposites, Catalysts, 2022, 12, 120.
8. T. Maluangnont, P. Pulphol, S. Pongampai, T. Kobkeatthawin, S. M. Smith and N. Vittayakorn, TiO₂/graphitic carbon nitride nanosheet composite with enhanced sensitivity to atmospheric water, RSC Adv., 2023, 13, 6143–6152.
9. S. Khasim, A. Pasha, M. Lakshmi, C. Panneerselvam, A. A. A. Darwish, T. A. Hamdalla, S. Alfadhli and S. A. Al-Ghamdi, Conductivity and dielectric properties of heterostructures based on novel graphitic carbon nitride and silver nanoparticle composite film for electronic applications, Dig. J. Nanomater. Biostruct., 2022, 17, 1089–1098.
10. L. M. Zambov, C. Popov, M. F. Plass, A. Bock, M. Jelinek, J. Lancok, K. Masseli and W. Kulisch, Capacitance humidity sensor with carbon nitride detecting element, Appl. Phys. A, 2000, 70, 603–606.
11. Z. Zhang, J. Huang, Q. Yuan and B. Dong, Intercalated graphitic carbon nitride: a fascinating two-dimensional nanomaterial for an ultra-sensitive humidity nanosensor, Nanoscale, 2014, 6, 9250–9256.
12. N. Urakami, K. Ogihara, H. Futamura, K. Takashima and Y. Hashimoto, Demonstration of electronic devices in graphitic carbon nitride crystalline film, AIP Adv., 2021, 11, 075204.
13. K. Takashima, N. Urakami and Y. Hashimoto, Electronic transport and device application of crystalline graphitic carbon nitride film, Mater. Lett., 2020, 281, 128600.
14. P. C. Patra and Y. N. Mohapatra, Dielectric constant of thin film graphitic carbon nitride (g-C₃N₄) and double dielectric Al₂O₃/g-C₃N₄, Appl. Phys. Lett., 2021, 118, 103501.
15. P. C. Patra and Y. N. Mohapatra, Graphitic carbon nitride (g-C₃N₄)/Al₂O₃ heterostructure as double dielectric: a comparative study in MIS based on a-IGZO, IEEE J. Electron Devices Soc., 2021, 9, 618–622.
16. M. Aono and S. Nitta, High resistivity and low dielectric constant amorphous carbon nitride films: application to low-k materials for ULSI, Diamond Relat. Mater., 2002, 11, 1219–1222.
17. X. Guo, D. Kuang, Z. Zhu, Y. Ding, L. Ge, Z. Wu, B. Du, C. Liang, G. Meng and Y. He, Humidity sensing by graphitic carbon nitride nanosheet/TiO₂ nanoparticle/Ti₃C₂T_x nanosheet composites for monitoring respiration and evaluating the waxing of fruits, ACS Appl. Nano Mater., 2021, 4, 11159–11167.
18. S. Pareek, M. Sharma, S. Lai and J. K. Quamara, Polymeric graphitic carbon nitride-barium titanate nanocomposites with different content ratios: a comparative investigation on dielectric and optical properties, J. Mater. Sci.: Mater. Electron., 2018, 29, 13043–13051.
19. S. Pareek and J. K. Quamara, Dielectric and optical properties of graphitic carbon nitride-titanium dioxide nanocomposite with enhanced charge separation, J. Mater. Sci., 2018, 53, 604–612.
20. S. Liu, T. Ye, Y. Liu, H. Cheng and X. Liu, Graphitic-carbon nitride nanosheets as a new inorganic filler for improving energy storage density of PVDF-based dielectric composites, J. Mater. Sci.: Mater. Electron., 2020, 31, 13063–13069.
21. X. Kang, A. Chatzitakis, T. Aarholt, X. Sun, C. Negri and T. Norby, Facet-engineered TiO₂ nanomaterials reveal the role of water–oxide interactions in surface protonic conduction, J. Mater. Chem. A, 2022, 10, 218–227.
22. Y. Noda, C. Merschjann, J. Tarábek, P. Amsalem, N. Koch and M. J. Bojdys, Directional charge transport in layered two-dimensional triazine-based graphitic carbon nitride, Angew. Chem., Int. Ed., 2019, 58, 9394–9398.
23. N. Konofaos, E. K. Evangelou, S. Logothetidis and M. Gioti, Electrical properties of carbon nitride films on silicon, J. Appl. Phys., 2002, 91, 9915–9918.
24. S. Pareek, S. Waheed and S. Karak, The effect of UV-ozone treatment on structural, optical, and dielectric properties of thermally evaporated graphitic carbon nitride thin film, J. Electron. Mater., 2023, 52, 1104–1112.
25. C. Godet, J. P. Kleider and A. S. Godovskikh, Electric field-controlled sign of the capacitance in metal-carbon nitride-metal devices, J. Non-Cryst. Solids, 2008, 354, 2637–2640.
26. S. Kumar, C. Godet, A. Goudovskikh, J. P. Kleider, G. Adamopoulos and V. Chu, High-field transport in amorphous carbon and carbon nitride films, J. Non-Cryst. Solids, 2004, 338–340, 349–352.
27. J. P. Kleider, A. S. Gudovskikh and C. Godet, DC and AC hopping transport in metal/amorphous carbon nitride/metal devices, J. Non-Cryst. Solids, 2006, 352, 1323–1326.
28. C. Godet, J. P. Kleider and A. S. Gudovskikh, Frequency scaling of ac hopping transport in amorphous carbon nitride, Diamond Relat. Mater., 2007, 16, 1799–1805.
29. Z. Qin, P. Wang, H. Shen, L. Mi and X. Ying, Microstructure and electronic properties of pulsed-discharge-deposited amorphous carbon-nitride films, Diamond Relat. Mater., 2015, 14, 1616–1622.
30. J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: characterization by impedance spectroscopy, Adv. Mater., 1990, 2, 132–138.
31. R. Gerhardt, Impedance and dielectric spectroscopy revisited: distinguishing localized relaxation from long-range conductivity, J. Phys. Chem. Solids, 1994, 55, 1491–1506.
32. T. Maluangnont, S. Sriphan, T. Charoonsuk and N. Vittayakorn, Dielectric spectroscopy and electric modulus analyses of Ti_0.8O₂ nanosheets–Ag nanoparticles–cellulose filter paper composites, Integr. Ferroelectr., 2022, 224, 214–224.
33. S. Sriphan, P. Pulphol, T. Charoonsuk, T. Maluangnont and N. Vittayakorn, Effect of adsorbed water and temperature on the universal power law behavior of lepidocrocite-type alkali titanate ceramics, J. Phys. Chem. C, 2021, 125, 12910–12920.
34. M. Gioti and S. Logothetidis, Dielectric function, electronic properties and optical constants of amorphous carbon and carbon nitride films, Diamond Relat. Mater., 2003, 12, 957–962.
35. S. P. Sun, S. Gu, J. H. Sun, F. F. Xia and G. H. Chen, First principles investigation of the electronic properties of graphitic carbon nitride with different building block and sheet staggered arrangement, J. Alloys Compd., 2018, 735, 131–139.
36. G.-M. Rignanese, J.-C. Charlier and X. Gonze, First-principles study of vibrational and dielectric properties of C₃N₄ polymorphs, Phys. Rev. B, 2002, 66, 205416.
37. S. Agrawal, W. Lin, O. V. Prezhdo and D. J. Trivedi, Ab initio quantum dynamics of charge carriers in graphitic carbon nitride nanosheets, J. Chem. Phys., 2020, 153, 054701.
38. B. Zhu, B. Cheng, L. Zhang and J. Yu, Review on DFT calculation of s-triazine-based carbon nitride, Carbon Energy, 2019, 1, 32–56.
39. A. H. Reshak, S. A. Khan and S. Auluck, Linear and nonlinear optical properties for AA and AB stacking of carbon nitride polymorph (C₃N₄), RSC Adv., 2014, 4, 11967–11974.
40. L.-W. Ruan, Y.-J. Zhu, L.-G. Qiu, Y.-P. Yuan and Y.-X. Lu, First principles calculations of the pressure affection to g-C₃N₄, Comput. Mater. Sci., 2014, 91, 258–265.
41. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215.
42. J. Heyd, G. E. Scuseria and M. Ernzerhof, Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys., 118, 8207, 2003], J. Chem. Phys., 2006, 124, 219906.
43. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B, 1996, 54, 11169–11186.
44. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
45. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code, Comput. Phys. Commun., 2021, 267, 108033.
46. K. Dabsamut, I. Chatratin, T. Thanasarnsurapong, T. Maluangnont and A. Boonchun, Theoretically proposed stable polymorph of two-dimensional pentagonal β-PdPSe, Phys. Chem. Chem. Phys., 2023, 25, 3815–3819.
47. T. Narkbuakaew and P. Sujaridworakun, Synthesis of tri-s-triazine based g-C₃N₄ photocatalyst for cationic rhodamine B degradation under visible light, Top. Catal., 2020, 63, 1086–1096.
48. P. Zhang, Y. Tong, Y. Liu, J. J. M. Vequizo, H. Sun, C. Yang, A. Yamakata, F. Fan, W. Lin and X. Wang, et al., Heteroatom dopants promote two-electron O₂ reduction for photocatalytic production of H₂O₂ on polymeric carbon nitride, Angew. Chem., Int. Ed., 2020, 59, 16209–16217.
49. W. Li, Z. Guo, L. Jiang, L. Zhong, G. Li, J. Zhang, K. Fan, S. Gonzalez-Cortes, K. Jin and C. Xu, et al., Facile in situ reductive synthesis of both nitrogen deficient and protonated g-C₃N₄ nanosheets for the synergistic enhancement of visible-light H₂ evolution, Chem. Sci., 2020, 11, 2716–2728.
50. A. Champi, R. G. Lacerda and F. C. Marques, Thermal expansion coefficient of amorphous carbon nitride thin films deposited by glow discharge, Thin Solid Films, 2002, 420–421, 200–204.
51. M. Cermak, N. Perez, M. Collins and M. Bahrami, Material properties and structure of natural graphite sheet, Sci. Rep., 2020, 10, 18672.
52. W. Paszkowicz, J. B. Pelka, M. Knapp, T. Szyszko and S. Podsiadlo, Lattice parameters and anisotropic thermal expansion of hexagonal boron nitride in the 10–297.5 K temperature range, Appl. Phys. A, 2002, 75, 431–435.
53. T. Shimada, K. Touji, Y. Katsuyama, H. Takeda and T. Shiosaki, Lead free PTCR ceramics and its electrical properties, J. Am. Ceram. Soc., 2007, 27, 3877–3882.
54. P. C. Patra and Y. N. Mohapatra, Exfoliated and evaporated thin films of graphitic carbon nitride (g-C₃N₄): evolution of photoelectronic properties from bulk, Mater. Lett., 2021, 302, 130374.
55. M. Aono, Y. Naruse, S. Nitta and T. Katsuno, The effect of hydrogen- and oxygen-plasma treatments on dielectric properties of amorphous carbon nitride films, Diamond Relat. Mater., 2001, 10, 1147–1151.
56. S. Cheon, K. D. Kihm, H. G. Kim, G. Lim, J. S. Park and J. S. Lee, How to reliably determine the complex r efractive Index (RI) of graphene by using two independent measurement constraints, Sci. Rep., 2014, 4, 6364.
57. A. K. Jonscher, Dielectric relaxation in solids, J. Phys. D: Appl. Phys., 1999, 32, R57–R70.
58. A. K. Jonscher, The 'universal' dielectric response, Nature, 1977, 267, 673–679.
59. B. J. Stagg and T. T. Charalampopoulos, Refractive indices of pyrolytic graphite, amorphous carbon, and flame soot in the temperature range 25° to 600 °C, Combust. Flame, 1993, 94, 381–396.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra04520j

---