Open Access Article
Open Access ArticleInvestigation of the structural, electronic, mechanical, and optical properties of NaXCl3 (X = Be, Mg) using density functional theory
Aiman Jehana,
Mudasser Husain *b,
Vineet Tirth
*b,
Vineet Tirth cd,
Ali Algahtanicd,
Muhammad Uzaire,
Nasir Rahman
cd,
Ali Algahtanicd,
Muhammad Uzaire,
Nasir Rahman *b,
Aurangzeb Khana and
Saima Naz Khana
*b,
Aurangzeb Khana and
Saima Naz Khana
aDepartment of Physics, Abdul Wali Khan University, Mardan, 23200, Pakistan
bDepartment of Physics, University of Lakki Marwat, 28420, Lakki Marwat, KPK, Pakistan. E-mail: mudasserhusain01@gmail.com; nasir@ulm.edu.pk
cMechanical Engineering Department, College of Engineering, King Khalid University, Abha 61421, Asir, Kingdom of Saudi Arabia
dResearch Center for Advanced Materials Science (RCAMS), King Khalid University, Guraiger, P. O. Box 9004, Abha 61413, Asir, Kingdom of Saudi Arabia
eDepartment of Physics, University of Peshawar, 25120, Pakistan
First published on 26th September 2023
Abstract
In our pursuit of enhancing material performance, our focus is centered on the investigation of sodium-based halide perovskites, specifically NaXCl3 (where X = Be & Mg). We are utilizing first-principles methods based on density functional theory (DFT) to delve into these materials' properties and potential improvements. This investigation is executed using the WIEN2K code, aiming to uncover a deeper understanding of these materials' properties and potential enhancements. In this study, we utilize the Full Potential Linear Augmented Plane Wave (FP-LAPW) approach to analyze the structural, mechanical, electronic, and optical properties of cubic perovskite materials NaXCl3 (X = Be, Mg). We employ the Birch–Murnaghan fitting curve to assess the structural stability of these compounds, and in each case, the compound demonstrates structural stability in its optimal or ground state. The existence of real frequencies serves as confirmation of the phonon stability for both compounds. To determine the elastic characteristics, the IRelast Package is used. This involves calculating the elastic constants, which demonstrates that the compounds have anisotropic, ductile properties and demonstrate mechanical stability. We investigate the electronic properties by analyzing the density of states and the band structure. Both compounds exhibit an indirect band gap energy of 4.15 eV for NaBeCl3 and 4.16 eV for NaMgCl3. We analyze both the total and partial density of states to gain insight into the contributions of different electronic states to the band structure. Furthermore, optical characteristics, including the dielectric function, absorption coefficient, refractive index, and reflectivity, are investigated across an energy spectrum ranging from 0 to 15 eV. These findings can offer a comprehensive insight into the development of advanced electronic devices with improved efficiency and enhanced capabilities. Furthermore, they have the capacity to inspire experimental researchers to delve further into this field for subsequent explorations.
1. Introduction
Within the domain of science and technology, the focus of researchers has shifted towards a category of compounds referred to as perovskites, encompassing a broad spectrum of chemical compositions. These compounds exhibit a crystalline structure similar to that of CaTiO3, a mineral discovered by a Russian mineralogist named Provski. To encompass the diverse array of compounds in this group, a universal formula, ABX3, is currently employed. Here, “A” and “B” denote the positions of cationic atoms, while X signifies the arrangement of anionic atoms. In perovskite compounds, the X site is typically occupied by either oxide or halide ions.1–3 Perovskites are a category of compounds known for their distinct crystal structure and remarkable physical and chemical properties.4,5 These materials have attracted significant attention from researchers due to their flexible structure and exceptional electromagnetic, elastic, thermal, and electrical behaviors.6,7 Among the properties exhibited by perovskite materials are thermoelectricity, dielectricity, superconductivity, ferroelectricity, optical properties, and various other distinctive characteristics.8–10 A particular class of perovskites, recognized as chloroperovskites or metal halide perovskites, involve the replacement of the X-anion with a halogen element, commonly chlorine (Cl). Chloroperovskites, which are widely found in perovskite structures, are represented by the formula ABCl3, where “A” and “B” can represent alkali metals, alkaline earth metals, transition metals, and “Cl” represents chlorine. Extensive research has been conducted on various compositions and structures of cubic perovskite compounds due to their potential advantages in various industrial applications.11–13 Recent investigations have highlighted the exceptional photo-physical properties of perovskites, including strong absorption coefficients, prolonged carrier lifetimes, and robust photoluminescence quantum yields.14–17 These unique characteristics make them highly desirable for applications in optoelectronics such as LEDs, solar cells, and other photonic devices.18–20 Furthermore, chloroperovskites have gained attention as scintillating materials due to their high band gaps, remarkable absorption coefficients, and cost-effective manufacturing.21,22 The utilization of scintillating materials and scintillators with high intensity, directional emission, and high-energy properties finds numerous applications.23,24 Chloroperovskites demonstrate exceptional adaptability for diverse optoelectronic uses, owing to the facile adjustability of their bandgap through manipulation of the halogen content.25–27 Additionally, their strong photocatalytic activity in visible light has prompted investigations into their use for photocatalytic reactions.28Density functional theory (DFT) stands as extensively employed computational approach for predicting the structural and electronic properties of materials. Several researchers have employed DFT to explore the properties of chloroperovskites. Wu et al. utilized DFT approach to analyze the electronic and optical properties of perovskites CsPbX3 (X = Cl, Br, I). Their observations unveiled a substantial reduction in the bandgap energy upon chlorine substitution. This phenomenon was ascribed to the existence of localized defect states.29 In a study carried out by Li et al. in 2019, they synthesized and characterized CsPbCl3 chloroperovskite crystals, employing X-ray diffraction and UV-Vis spectroscopy techniques. The research encompassed an examination of the crystal structure and optical properties of these chloroperovskite crystals. Their outcomes unveiled robust UV-Vis range absorption in the crystals, which was associated with the existence of an optical band gap.30 Zhou et al. conducted an extensive review of the most recent progress in the synthesis and characteristics of chloroperovskites. They discussed various synthesis methods employed for chloroperovskite production, as well as delved into the analysis of their structural, electrical, and optical features.31–33 In a study led by M. Hussain et al., a comprehensive investigation was undertaken to explore the optical attributes of BaMCl3 (M = Ag, Cu) compounds, delving into their structural features, electronic properties, and elasticity. The findings of the research unveiled the semiconductor nature of these compounds. The study demonstrated that these perovskite compounds display anisotropic properties, are ductile, and possess mechanical stability.34 A. A. Mubarak et al. investigated the electrical and optical properties of perovskite BaXF3 (X = Li, Na, K, and Rb). The study revealed that these materials exhibit a direct band gap, classifying them as semiconductors. The researchers also anticipated the potential use of these compounds as metals under high-energy photon exposure.35 The motivation of the given work is to enhance material performance, our focus is on investigating sodium-based halide perovskites NaXCl3 (where X = Be and Mg) by utilizing first-principles techniques. This exploration is conducted using the WIEN2K code, with the intention of gaining a more profound insight into the properties of these materials and identifying possibilities for improvements. The structural features of both materials are determined through optimization curves. The electronic properties are evaluated by analyzing the band gap and density of states (DOS). Mechanical stability is determined based on the elastic constants. Additionally, the optical properties, including refractive index, reflectivity, absorption coefficient, optical conductivity, and extinction coefficient, are investigated using the FP-LAPW approach.
2. Computational methodology
First-principle calculations offer a remarkable level of accuracy, enabling researchers to conduct precise analyses and unveil material characteristics at the atomic or electronic level with increasing precision. To investigate the structural, electrical, elastic, and optical properties of NaXCl3 (X = Be, Mg), the FPLAPW approach,36 based on Density Functional Theory (DFT)37,38 is employed. This approach allows for a comprehensive exploration of these characteristics, leveraging the principles of electronic structure calculations. The simulation code from WIEN2K is used to do the computations.39 The electron exchange and correlation potential for structural and elastic characteristics are calculated using the generalized gradient approximation.40 Wien2k is a versatile software program that can effectively handle various types of materials, including insulators, metals, and semiconductors. It is particularly useful when dealing with materials for which experimental data is unavailable. In these cases, WIEN2K can calculate the forces on atoms and determine optimized structural parameters, even when the atom positions are constrained by crystal symmetry. The structural properties are find out by using Birch–Munaghan41 equation of state. A lattice constant of NaXCl3 (X = Be, Mg) that has been optimised is used to assess the density of states (DOS) and band energy utilizing the FP-LAPW approach as implemented inside WIEN2K program. The IRelast package is used in this study to compute mechanical characteristics.42 The RMT value is set to “5” for the analysis of these compounds, and the first Brillouin zone in reciprocal space is sampled using 2000 K-points.43 The −6 Ry cut-off energy is used for both molecules. Understanding how well the material under consideration performs optically depends on its dielectric function ε(ω), because it has connections with the electrical structure's band gap. Additionally, it is necessary to derive relationships for the following parameters: refractive index n(ω), energy loss function L(ω), absorption coefficient I(ω), extinction coefficient K(ω), optical conductivity α(ω), and reflectivity R(ω). Real ε1(ω) and imaginary ε2(ω) portions make up the dielectric function, given as ε(ω) = ε1(ω) + iε2(ω).44 The surface of the material is utilized to depict how light is absorbed using the imaginary section of the dielectric function, and real portion describes how the material's surface disperses.45,46 The programs used in research for graphing are xmgrace,47 xcrysden,48 and origin.49 For the first-time, the physical properties of ternary NaXCl3 (X = Be, Mg) choloroperovskites are revealed by the use of the computational method indicated above.3. Results and discussion
The structural, electrical, elastic and optical characteristics of perovskites NaXCl3 (X = Be, Mg) will be discussed thoroughly in the next part, by utilizing the techniques mentioned above.3.1. Structural properties
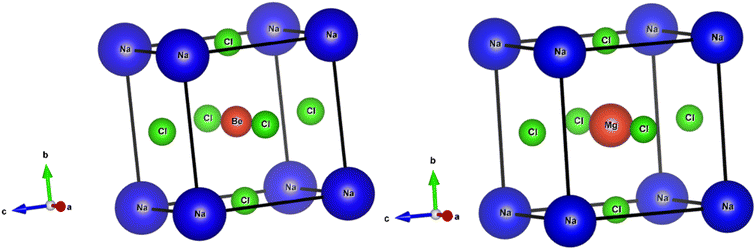
The perovskite structures of NaXCl3 (X = Be, Mg) were initially constructed, and their entire structures were optimized. Fig. 1 presents the optimized and relaxed structures of both compounds. Both structures belong to the pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (221) space group and exhibit cubic geometry. The Wyckoff positions for Na, X, and Cl atoms are (0, 0, 0), (0.5, 0.5, 0.5), and (0, 0.5, 0.5), respectively. The crystallographic structures for both compounds are depicted in Fig. 1.
m (221) space group and exhibit cubic geometry. The Wyckoff positions for Na, X, and Cl atoms are (0, 0, 0), (0.5, 0.5, 0.5), and (0, 0.5, 0.5), respectively. The crystallographic structures for both compounds are depicted in Fig. 1.
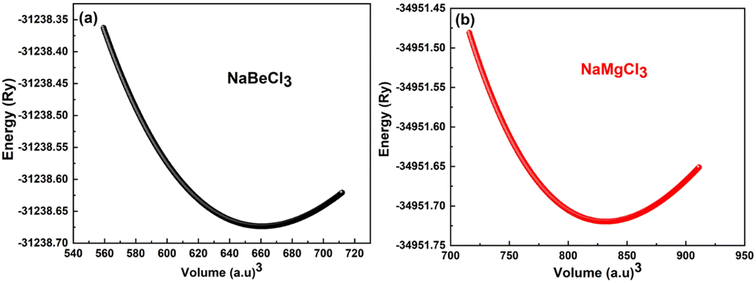
To minimize the total energy of the unit cell relative to its volume, volume optimization is performed for each substance. This process helps stabilize the entire system and is incorporated into the Birch–Murnaghan equation of state. These optimized values are then utilized in the Murnaghan equation of state to determine the volume density and bulk modulus under varying pressure conditions. The optimization procedure takes into account exchange and correlation effects using the GGA approximation. As shown in Fig. 1, the initial energy of the unit cell decreases during the optimization process. It is observed that the investigated compounds exhibit similar behavior. The system reaches its lowest energy state as it approaches the ground state energy E0. The volume at this lowest energy state is referred to as the ground state volume. The graph depicts a pattern where, up to a certain volume (V0), the energy of the unit cell decreases as the volume increases. Beyond this point, however, as the volume continues to expand, the system's energy starts to rise, suggesting an unstable condition. In first principle computations, the structural parameters are derived from the unit cell's most stable state, which aligns with the state of minimum energy (Fig. 2).
Table 1 presents the specific values for various structural parameters of NaXCl3 (X = Be, Mg), including lattice constants a0, bulk moduli at zero pressure B, B′ which represents their pressure derivatives, as well as the ground state volume V0 and ground state energy E0. Despite the absence of experimental or sufficient theoretical data, our results are in agreement with the available information from AFLOW.50
| Structural parameters | Our work | Other work Aflow50 | ||
|---|---|---|---|---|
| NaBeCl3 | NaMgCl3 | NaBeCl3 | NaMgCl3 | |
| a0 | 4.55 Å | 4.94 | 4.52 | 4.89 |
| B | 44.35 GPa | 32.16 | 41.45 | 30.09 |
| B′ | 4.16 GPa | 5.08 | 4.45 | 4.98 |
| Energy at ground state, E0 | −3123.86 Ry | −3495.17 | Eg = 4.17 | Eg = 4.18 |
| Ground state volume, V0 | 660.73 au3 | 831.89 | 663.43 | 826.13 |
The provided equation is employed to calculate the formation energies of cubic-phase NaXCl3 ternary compound halide perovskites, where “X” represents either Be or Mg. This calculation demonstrate the chemical stability of these complex compounds. To determine the chemical potential of each atom in compounds like NaBeCl3 and NaMgCl3, you would typically use computational methods, such as density functional theory (DFT) calculations or other quantum chemical simulations. These methods allow to calculate the electronic structure and properties of molecules and solids, including the chemical potential of individual atoms within the compounds. By optimizing the geometry of the compounds, which involves finding the most stable arrangement of atoms by minimizing the total energy of the system. After optimizing the geometry, electronic structure is calculated. This results in yielding the electronic energy, electronic density, and wavefunction of the system. The total energy of the compound is then calculated using the optimized geometry and electronic structure. The total energy accounts for both the kinetic and potential energy of all electrons and nuclei in the system.
The negative formation of energy is calculated as following51
| Ef = (Etotal − nμAs − mμ0)/(n + m) | (1) |
The chemical potential (μ) of each atom in the compound can be calculated using the formula:
| μ = E_total(N + 1) − E_total(N) |
3.2. Mechanical properties
The mechanical properties of solids offer insights into how interatomic potentials respond to external forces and play a crucial role in various fundamental phenomena in solid-state materials, including stability, strength, ductility, brittleness, and other characteristics. These properties encompass parameters such as Young's modulus (Y), bulk modulus (B), shear modulus (G), anisotropy factor, and other elastic parameters, which provide valuable information about the material's behavior under different conditions. Materials used in research, medicine, and engineering need to possess specific elastic properties. In the case of cubic materials, only three fundamental elastic constants, namely C11, C12, and C44, are required to determine all the aforementioned properties. These constants allow for the calculation of various mechanical properties and phenomena associated with the material, providing a concise and efficient approach for characterizing its behavior. Additionally, elastic constants establish a connection between the mechanical and dynamic characteristics of crystals.52Since our compounds exhibit a cubic crystal structure, their mechanical properties, such as structural stability and other relevant parameters, can be effectively described by three specific elastic constants: C11, C12, and C44. The mechanical stability of compounds with a cubic crystal structure can be ensured if the prescribed limitation formulas are met.53
| C44 > 0 | (2) |
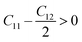 | (3) |
| C12 < B < C11 | (4) |
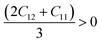 | (5) |
Our current results demonstrate that all the analyzed compounds, NaXCl3 (X = Be, Mg), satisfy the listed criteria for mechanical stability, indicating that our compounds are mechanically stable. The mechanical properties of NaXCl3 (X = Be, Mg) are presented in Table 2.
| Parameters | NaBeCl3 | NaMgCl3 |
|---|---|---|
| C11 (GPa) | 62.17 | 56.63 |
| C12 (GPa) | 45.53 | 25.01 |
| C44 (GPa) | 30.47 | 10.69 |
| B (GPa) | 20.56 | 20.59 |
| A | 3.6 | 0.6 |
| G (GPa) | 18.18 | 12.45 |
| E (GPa) | 47.98 | 33.08 |
| v | 0.31 | 0.43 |
| B/G | 2.43 | 2.58 |
In order to study mechanical properties, the cubic ECs of crystals with various symmetries are computed using the IRelast program. The elasto-cubic constants C11, C12, and C44, the letters “B” stand for the bulk modulus, “A” for anisotropy, “G” shear modulus, “E” young's modulus, “ν” the Poisson ratio, and “B/G” Pugh ratio are calculated by using the expressions given below:54
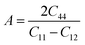 | (6) |
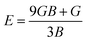 | (7) |
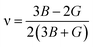 | (8) |
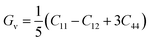 | (9) |
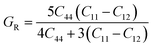 | (10) |
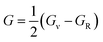 | (11) |
The shear modulus (G) serves as an indicator of the system's resilience. From the computed values in Table 2, NaBeCl3 exhibits a shear modulus of 18.18, whereas NaMgCl3 has a shear modulus of 12.45. This implies that NaBeCl3 is harder than NaMgCl3, indicating a greater resistance to material deformation in the former. On the other hand, Young's modulus (E) is employed to quantify the stiffness of a material.55 The NaBeCl3 compound has a Young's modulus (E) of 47.98 GPa, while NaMgCl3 has a value of 33.08 GPa. The higher value of “E” for NaBeCl3 signifies its greater stiffness in comparison to NaMgCl3. In engineering, the ductility of a material is a critical consideration, and it can be evaluated using the B/G Pugh ratio. According to specifications, ductile materials should have a B/G ratio greater than 1.75, whereas brittle materials typically have a B/G ratio lower than 1.75.56 The analysis reveals that all of the studied chemicals exhibited B/G ratios exceeding 1.75, which indicates their ductile behavior. Additionally, the Poisson ratio (ν) serves as another characterization parameter for ductility and brittleness, with a threshold value of 0.26. When the Poisson ratio is above 0.26, it indicates ductility, whereas values below 0.26 suggest inherent brittleness. In this study, all the examined chemicals displayed Poisson ratios higher than 0.26, affirming their ductile nature. The Cauchy pressure (CP) symbol is often used to represent the elasticity of a material, where a positive CP value signifies ductility, while a negative value indicates brittleness.
| CP = C12 − C44 | (12) |
From Table 2, it is evident that all the materials exhibit positive values for the Cauchy pressure (CP), indicating the presence of ductile properties. To assess whether a material's structural properties are consistent in all directions, the anisotropy factor (A) is considered. An isotropic material has an “A” value of 1, while materials with “A” values different from 1 are referred to as anisotropic media.57
3.3. Electronic properties
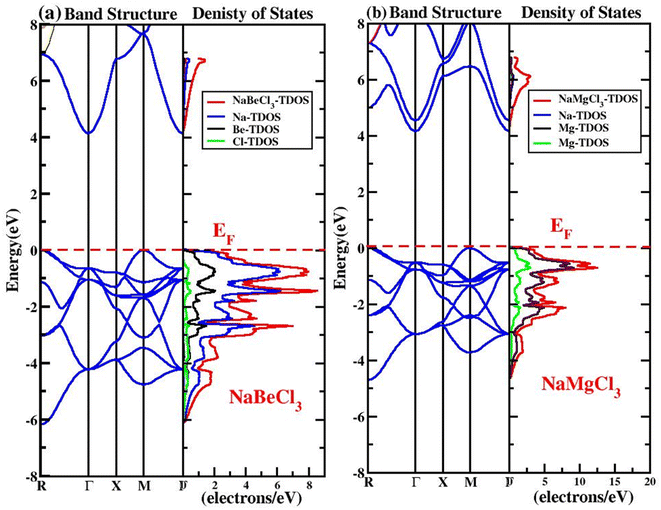
Studying energy band structure and the accompanying density of states is mostly necessary for understanding electronic characteristics. These findings shed light on the crystal's metallic, insulator, or semiconductor nature as well as the creation of the electron distribution in the valence states. The magnetic, optical, and thermal response of the unit cells may be explored further owing to an electronic study. It was easier to understand the orbital and spin character in detail after simulation of the total and partial density of states (TDOS, PDOS).The accessible states for electrons inside a system's structure will be discussed and explored in this section. A very detailed representation of the material is displayed by DOS, together with an overview of the states' main and minor contributions to the valence band and conduction band. This provides information on the structure of VB and CB, describes the arrangement of states, and suggests that what the states of the valence band and the conduction band are comprised off.58 Fig. 3 depicts the partial density of states (PDOS) and total density of states (TDOS) of the NaXCl3 (X = Be, Mg) compounds. From Fig. 3a it is clear that in the VB of NaBeCl3, Be-s, Be-p, Cl-p, Cl-d, and Cl-f are participating. In the CB, Be-s, Be-p and Cl-d are contributing. Fig. 3b shows that in the VB of NaMgCl3 there is the participation from Mg-s, Mg-p, Cl-p, Cl-d and Cl-f states. While in the CB, Na-s state, Mg-s and Cl-d states are participating but have little contribution from Mg-p state and Cl-f state.
3.4. Optical properties
To enhance our understanding of the electronic properties of NaXCl3 (X= Be, Mg), it is crucial to examine the optical characteristics of these compounds. Investigating the optical properties provides valuable insights into how the compounds interact with light, thereby contributing to a comprehensive understanding of their behavior. Therefore, in order to use a compound effectively in optoelectronic devices i.e. solar cells, diodes, lasers etc., one must have a thorough understanding of the optical characteristics. There has been limited research conducted on the optical properties of the chemical components comprising perovskites.59 By utilizing the FP-LAPW technique within the context of density functional theory, the optical characteristics of the NaXCl3 (X = Be, Mg) are thoroughly elucidated in this paper.| ε(ω) = ε1(ω) + iε2(ω) | (13) |
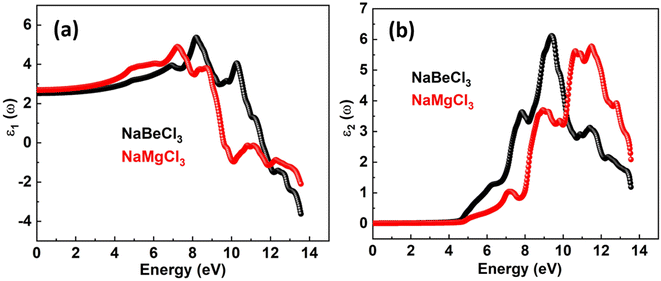
The real and imaginary components of the dielectric function are denoted by ε1(ω) and ε2(ω). A material's storage capacity is represented by the real component, which specifies polarization. The measured light absorption in the imaginary section represents the optical transitions within the energy bands. The electrical component of the ε1(ω) limit at zero frequency is included in the ε1(0) limit, which is 2.52 for NaBeCl3 and 2.684 for NaMgCl3 as depicted in the Fig. 3. The ε1(ω) spectra for each of the compounds studied begin to rise to their major maximum point after ε1(0). The peak of ε1(ω) for NaBeCl3 is 5.37 at 8.2 eV and 4.9 for NaMgCl3 at 7.2 eV. NaBeCl3 and NaMgCl3 both revealed maximum values of 5.8 at 11.5 eV and 6.1 at 9.4 eV, respectively, as demonstrated by the ε2(ω) spectra in the Fig. 4.
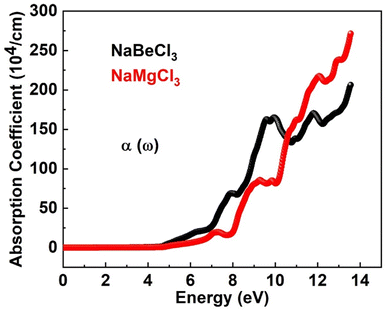
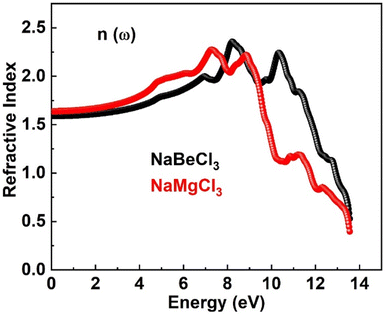
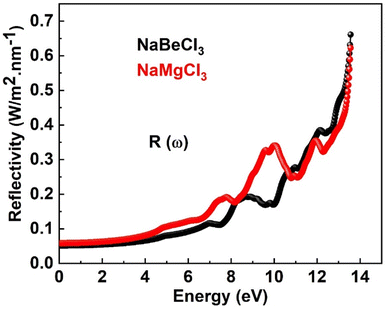
Numerous optical parameters, including refractive index, absorption coefficient, extinction coefficient, optical conductivity, and reflectivity, are calculated from the real and imaginary parts of dielectric functions. Some of these optical properties are investigated for NaXCl3 (X = Be, Mg) below.
4. Phonon dispersion
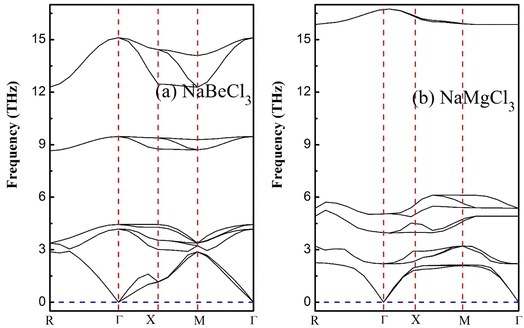
Emphasizing the importance of understanding phonon dispersion is crucial to grasp the intricate interplay between dynamic properties, thermodynamics, and vibrational Raman spectroscopy in crystalline solids.60 To address this facet, we employ the widely embraced and efficient approach known as density functional perturbation theory (DFPT), integrated within the pseudopotential framework of Quantum Espresso.61,62 This technique empowers us to explore the dynamic stability within the primitive unit cells of NaXCl3 (X= Be, Mg) perovskites. Upon delving into the dynamical context of these molecular crystal structures, it becomes evident that a dynamically stable compound inherently exhibits three acoustic branches with zero frequency at the Γ-point, corresponding to k = 0 in reciprocal space. The remaining branches, characterized by non-zero frequencies, are identified as optical phonons. Specifically, within the realm of acoustics, we observe a distinct longitudinal acoustic (LA) mode and two transverse acoustic (TA) modes. For a crystal composed of a unit cell containing N atoms, the optical modes tally to 3N − 3. Shifting our focus to the present investigation, the arrangement of 10 constituent atoms results in the emergence of 30 distinct frequency branches. Among these, precisely 3 branches converge at the Γ-point and are categorized as acoustic, while the remaining 27 are designated as optical, as visually depicted in Fig. 8. Notably, the lower frequency branches can be attributed to the pronounced vibrations of the heavier elements within the structure, while the optical branches predominantly stem from the vibrational behavior of the lighter atoms. Applying the principles of factor theory, we discern that the optical branches encompass a spectrum of Raman, Infrared, and Silent modes contingent upon their respective frequency bands. Importantly, the absence of negative or imaginary frequencies in the subsequent band dispersions accentuates the inherent dynamical stability of the studied systems.5. Electronic charge density
In crystalline materials, the characterization of chemical bonds can be carried out using contour plots of electronic charge density. This proves to be a highly effective method for elucidating the bonding nature between different atoms within crystalline compounds. This characteristic produces a structural map of valence electron charge density, illustrating the overall charge distribution within a unit cell of a compound. The examination of the overall electronic charge density map is utilized to analyze the manner in which chemical bonding occurs within a compound. Fundamentally, the charge density map or curve is comprised of structural atoms/ions that signify the involvement of orbital electrons in electronic properties by accumulating the charges of these atoms/ions. Afterward, the distinct color density map establishes a connection between the electronic DOS spectra of constituent elements by incorporating their respective charge contributions. The electronic density distribution of contour maps are calculated along 2D with TB-mBJ approximation for NaXCl3 (X= Be, Mg) chloroperovskites compounds are shown in Fig. 9.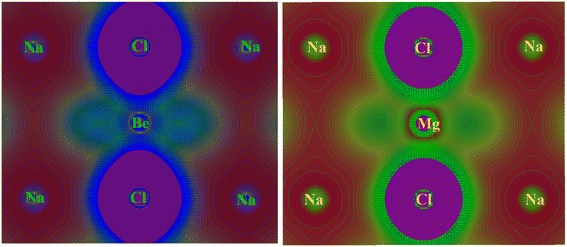 | ||
| Fig. 9 Investigated total 2D electronic charge densities with TB-mBJ approximation for NaXCl3 (X = Be, Mg) chloroperovskites compounds. | ||
The “Na” and “Cl” has almost spherical shape electronic charge density and the bonding between “Na” and “Cl” are ionic because very less overlapping is seen within “Na” and “Cl”. It is observed that the shape of electronic charge densities for “Cl” and “Be” is elongated and thus predict covalent bonding nature. Based on contour plots of electronic charge density, it is concluded that majority of the bonding is ionic with minor covalent bonding behavior. The major ionic bonding is attributed to the fact that Beryllium (Be) is in group 2 of the periodic table, and sodium (Na) is in group 1. Chlorine (Cl) is in group 17. Beryllium is a metal, sodium is also a metal, and chlorine is a non-metal. Na+ (sodium ion), Be2+ (beryllium ion) and 3Cl− (chloride ions). The bonding in this compound would involve the electrostatic attraction between the positive sodium and beryllium ions and the negative chloride ions. It would have an ionic bond character because of the transfer of electrons from sodium and beryllium to chlorine atoms. Beryllium would typically lose its two valence electrons to achieve a stable electron configuration, while sodium would lose one electron. Chlorine, on the other hand, would gain one electron to achieve stability. Magnesium (Mg) is also in group 2 of the periodic table, similar to beryllium. Sodium (Na) and chlorine (Cl) are the same as in the previous compound comprising Na+ (sodium ion), Mg2+ (magnesium ion) and 3Cl− (chloride ions). Just like in the case of NaBeCl3, the bonding in NaMgCl3 would also involve ionic interactions. Both sodium and magnesium would lose electrons to chlorine atoms, forming positively charged ions (Na+ and Mg2+), while chlorine would become negatively charged by gaining electrons.63,64
In essence, both NaBeCl3 and NaMgCl3 would demonstrate ionic bonding due to electron transfer between the metallic elements (sodium, beryllium, and magnesium) and the non-metallic chlorine, leading to the creation of positively and negatively charged ions that are attracted to each other through electrostatic forces.
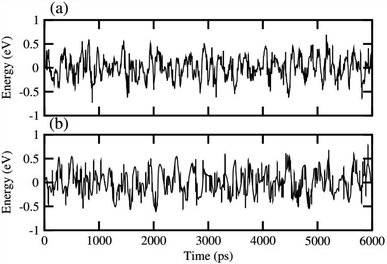
In order to assess the thermal stability of NaBeCl3 and NaMgCl3, we conducted ab initio molecular dynamics simulations (AIMD)65 at room temperature for a duration of 6 ps, with a time step of 1 fs. The results, as illustrated in Fig. 10, demonstrate minimal energy fluctuations throughout the simulation. Additionally, both perovskite structures maintained their original geometries without any noticeable structural distortions. This observation unequivocally confirms the stability of NaBeCl3 and NaMgCl3 at room temperature.
6 Conclusion
In this study, we have undertaken a novel exploration of the structural, elastic, electrical, and optical properties of NaXCl3 (X = Be, Mg) compounds, specifically focusing on the cases where X is Be and Mg. Here are the significant findings we have obtained:• Firstly, by analyzing the optimized structural parameters, we have determined that NaXCl3 (X = Be, Mg) compounds exhibit a stable cubic crystal structure, indicating their structural robustness.
• Secondly, utilizing the IRelast package, we have conducted a comprehensive analysis of the fundamental elastic properties of these compounds. Our results indicate that both materials are elastically stable, anisotropic, and possess ductile characteristics. These findings strongly support the potential application of these materials in various contemporary electrical systems.
• Moving on to the electronic characteristics, our investigations on the band structures and density of states (DOS) have revealed that NaXCl3 compounds are wide indirect band gap semiconductors, specifically from the X–X symmetry points. The calculated energy gaps are approximately 4.15 eV for NaBeCl3 and 4.16 eV for NaMgCl3, with an indirect (R–Γ) transition.
• Furthermore, we have examined the optical properties within the energy range of 0 eV to 15 eV. Both compounds exhibit photon transparency, suggesting their potential utility as lenses and anti-reflection coatings based on their favorable optical characteristics.
These findings contribute valuable insights into the structural, elastic, electrical, and optical properties of NaXCl3 (X = Be, Mg) compounds, opening up possibilities for their application in various technological fields.
Conflicts of interest
No conflict of interests.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia for funding this work through the Large Groups Project under grant number RGP.2/498/44.References
- C. Zhao, C. F. Cheung and P. Xu, High-efficiency sub-microscale uncertainty measurement method using pattern recognition, ISA Trans., 2020, 101, 503–514 CrossRef PubMed.
- J. Luo, et al., Single-atom Nb anchored on graphitic carbon nitride for boosting electron transfer towards improved photocatalytic performance, Appl. Catal., B, 2023, 328, 122495 CrossRef CAS.
- R. L. Z. Hoye, J. Hidalgo, R. A. Jagt, J. Correa-Baena, T. Fix and J. L. MacManus-Driscoll, The role of dimensionality on the optoelectronic properties of oxide and halide perovskites, and their halide derivatives, Adv. Energy Mater., 2022, 12(4), 2100499 CrossRef CAS.
- M. Husain, et al., Structural, electronic, elastic, and magnetic properties of NaQF3 (Q= ag, Pb, Rh, and Ru) flouroperovskites: A first-principle outcomes, Int. J. Energy Res., 2022, 46(3), 2446–2453 CrossRef CAS.
- M. Husain, et al., Examining computationally the structural, elastic, optical, and electronic properties of CaQCl 3 (Q= Li and K) chloroperovskites using DFT framework, RSC Adv., 2022, 12(50), 32338–32349 RSC.
- M. Husain, et al., The comparative investigations of structural, optoelectronic, and mechanical properties of AgBeX3 (X= F and Cl) metal halide-perovskites for prospective energy applications utilizing DFT approach, Opt. Quantum Electron., 2023, 55(10), 920 CrossRef CAS.
- M. Husain, et al., Predicting structural, optoelectronic and mechanical properties of germanium based AGeF3 (A= Ga and In) halides perovskites using the DFT computational approach, Opt. Quantum Electron., 2023, 55(6), 536 CrossRef CAS.
- Q. Liao, et al., High-performance silicon carbon anodes based on value-added recycling strategy of end-of-life photovoltaic modules, Energy, 2023, 281, 128345 CrossRef CAS.
- X. Fan, et al., Reversible switching of interlayer exchange coupling through atomically thin VO2 via electronic state modulation, Matter, 2020, 2(6), 1582–1593 CrossRef.
- N. Rahman, et al., Exploring the Structural, Optoelectronic, Elastic, and Thermoelectric Properties of Cubic Ternary Fluoro-perovskites Sodium Based NaMF3 (M= Si and Ge) Compounds for heterojunction solar cells applications, Phys. Scr., 2023, 065929 CrossRef.
- S. Khan, S. U. Zaman, R. Ahmad, N. Mehmood, M. Arif and H. J. Kim, Ab initio investigations of structural, elastic, electronic and optical properties of the fluoroperovskite TIXF3 (X= Ca, Cd, Hg, and Mg) compounds, Mater. Res. Express, 2020, 6(12), 125923 CrossRef.
- F. T. Tahir, M. Husain, N. Sfina, A. A. Rached, M. Khan and N. Rahman, Probing the physical properties for prospective high energy applications of QMnF 3 (Q= Ga, In) halide perovskites compounds employing the framework of density functional theory, RSC Adv., 2023, 13(27), 18788–18798 RSC.
- X. He, S. Xie, J. Xu, X.-B. Yin and M. Zhang, Reactive Template-Engaged Synthesis of NiS x/MoS2 Nanosheets Decorated on Hollow and Porous Carbon Microtubes with Optimal Electronic Modulation toward High-Performance Enzyme-like Performance, Inorg. Chem., 2023, 130225 Search PubMed.
- L. Kong, et al., Enhanced red luminescence in CaAl 12 O 19: Mn 4+ via doping Ga 3+ for plant growth lighting, Dalton Trans., 2020, 49(6), 1947–1954 RSC.
- L. Kong, et al., Luminescent properties and charge compensator effects of SrMo0. 5W0. 5O4: Eu3+ for White Light LEDs, Molecules, 2023, 28(6), 2681 CrossRef CAS PubMed.
- S. Du, et al., Auger scattering dynamic of photo-excited hot carriers in nano-graphite film, Appl. Phys. Lett., 2022, 121(18), 181104 CrossRef CAS.
- J. Wang, J. Liu, Z. Du and Z. Li, Recent advances in metal halide perovskite photocatalysts: Properties, synthesis and applications, J. Energy Chem., 2021, 54, 770–785 CrossRef CAS.
- L. Cai, Y. Lu and H. Zhu, Performance enhancement of on-chip optical switch and memory using Ge2Sb2Te5 slot-assisted microring resonator, Opt. Lasers Eng., 2023, 162, 107436 CrossRef.
- F. Yu, et al., Molecular engineering of biomimetic donor-acceptor conjugated microporous polymers with full-spectrum response and an unusual electronic shuttle for enhanced uranium (VI) photoreduction, Chem. Eng. J., 2023, 466, 143285 CrossRef CAS.
- J. Wang, et al., High-entropy ferroelastic (10RE0. 1) TaO4 ceramics with oxygen vacancies and improved thermophysical properties, J. Mater. Sci. Technol., 2023, 157, 98–106 CrossRef.
- M. N. Murshed, M. E. El Sayed, S. Naji and A. Samir, Electronic and optical properties and upper light yield estimation of new scintillating material TlMgCl3: Ab initio study, Results Phys., 2021, 29, 104695 CrossRef.
- Q. Zhao, et al., Double U-groove temperature and refractive index photonic crystal fiber sensor based on surface plasmon resonance, Appl. Opt., 2022, 61(24), 7225–7230 CrossRef CAS PubMed.
- Q. Zhao, J. Liu, H. Yang, H. Liu, G. Zeng and B. Huang, High birefringence D-shaped germanium-doped photonic crystal fiber sensor, Micromachines, 2022, 13(6), 826 CrossRef.
- N. Rahman, et al., Appealing perspectives of the structural, electronic, elastic and optical properties of LiRCl 3 (R= Be and Mg) halide perovskites: a DFT study, RSC Adv., 2023, 13(27), 18934–18945 RSC.
- X. Zhang, Y. Tang, F. Zhang and C. Lee, A novel aluminum–graphite dual-ion battery, Adv. Energy Mater., 2016, 6(11), 1502588 CrossRef.
- R. K. Pingak, S. Bouhmaidi and L. Setti, Investigation of structural, electronic, elastic and optical properties of Ge-halide perovskites NaGeX3 (X= Cl, Br and I): A first-principles DFT study, Phys. B: Condens. Matter, 2023, 663, 415003 CrossRef CAS.
- J. Gao, H. Sun, J. Han, Q. Sun and T. Zhong, Research on recognition method of electrical components based on FEYOLOv4-tiny, J. Electr. Eng. Technol., 2022, 17(6), 3541–3551 Search PubMed.
- R. Guo, S. Zhang, H. Gao, G. S. Murugan, T. Liu and Z. Cheng, Blazed subwavelength grating coupler, Photonics Res., 2023, 11(2), 189–195 CrossRef.
- W. Wang, et al., Improved synthesis of perovskite CsPbX3@ SiO2 (X= Cl, Br, and I) quantum dots with enhanced stability and excellent optical properties, ES Mater. Manuf., 2019, 4, 66–73 Search PubMed.
- D. Chen and X. Chen, Luminescent perovskite quantum dots: synthesis, microstructures, optical properties and applications, J. Mater. Chem. C, 2019, 7(6), 1413–1446 RSC.
- Y. Huang, et al., Sensing studies and applications based on metal halide perovskite materials: current advances and future perspectives, TrAC, Trends Anal. Chem., 2021, 134, 116127 CrossRef CAS.
- L. Cao, et al., Recent progress in all-inorganic metal halide nanostructured perovskites: Materials design, optical properties, and application, Front. Phys., 2021, 16, 1–20 Search PubMed.
- D. Wan, et al., Hyperuniform Disordered Solids with Morphology Engineering, Laser Photon. Rev., 2023, 2300398 CrossRef.
- M. Husain, et al., Insight into the Structural, Mechanical and Optoelectronic Properties of Ternary Cubic Barium-Based BaMCl3 (M= Ag, Cu) Chloroperovskites Compounds, Crystals, 2023, 13(1), 140 CrossRef CAS.
- A. A. Mubarak and A. A. Mousa, The electronic and optical properties of the fluoroperovskite BaXF3 (X= Li, Na, K, and Rb) compounds, Comput. Mater. Sci., 2012, 59, 6–13 CrossRef CAS.
- M. Petersen, F. Wagner, L. Hufnagel, M. Scheffler, P. Blaha and K. Schwarz, Improving the efficiency of FP-LAPW calculations, Comput. Phys. Commun., 2000, 126(3), 294–309 CrossRef CAS.
- I. B. Obot, D. D. Macdonald and Z. M. Gasem, Density functional theory (DFT) as a powerful tool for designing new organic corrosion inhibitors. Part 1: an overview, Corros. Sci., 2015, 99, 1–30 CrossRef CAS.
- M. Yang, W. Liu, Z. Liu, C. Cai, Y. Wang and J. Yang, Binocular Vision-Based Method Used for Determining the Static and Dynamic Parameters of the Long-Stroke Shakers in Low-Frequency Vibration Calibration, IEEE Trans. Ind. Electron., 2022, 70(8), 8537–8545 Search PubMed.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k: An Augmented Plane Wave plus Local Orbitals Program for Calculating Crystal Properties, 2001, p. 60 Search PubMed.
- J. P. Perdew, A. Ruzsinszky, J. Tao, V. N. Staroverov, G. E. Scuseria and G. I. Csonka, Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits, J. Chem. Phys., 2005, 123(6), 62201 CrossRef PubMed.
- V. G. Tyuterev and N. Vast, Murnaghan's equation of state for the electronic ground state energy, Comput. Mater. Sci., 2006, 38(2), 350–353 CrossRef CAS.
- M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B, 1976, 13(12), 5188 CrossRef.
- E. Sakalauskas, et al., Dielectric function and optical properties of Al-rich AlInN alloys pseudomorphically grown on GaN, J. Phys. D Appl. Phys., 2010, 43(36), 365102 CrossRef.
- L. Kong and G. Liu, Synchrotron-based infrared microspectroscopy under high pressure: An introduction, Matter Radiat. Extremes, 2021, 6(6), 068202 CrossRef CAS.
- J. Zhong, M. Han, C. Li, R. Li and H. He, Facile and scalable fabrication process of electroluminescent filament with high luminescent efficiency, Mater. Lett., 2023, 350, 134868 CrossRef CAS.
- A. Vaught, Graphing with Gnuplot and Xmgr: two graphing packages available under linux, Linux J., 1996, 28, 7 CrossRef.
- A. Kokalj, XCrySDen—a new program for displaying crystalline structures and electron densities, J. Mol. Graphics Modell., 1999, 17(3–4), 176–179 CrossRef CAS PubMed.
- P. M. Edwards, Origin 7.0: scientific graphing and data analysis software, J. Chem. Inf. Comput. Sci., 2002, 42(5), 1270–1271 CrossRef CAS.
- S. Curtarolo, et al., AFLOW: An automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- Y. Z. Abdullahi, R. Caglayan, A. Mogulkoc, Y. Mogulkoc and F. Ersan, New stable ultrawide bandgap As2O3 semiconductor materials, J. Phys. Mater., 2023, 6(2), 25003 CrossRef.
- A. H. Reshak and M. Jamal, DFT calculation for elastic constants of orthorhombic structure within WIEN2K code: A new package (ortho-elastic), J. Alloys Compd., 2012, 543, 147–151 CrossRef CAS.
- M. Born, On the stability of crystal lattices. I, in Mathematical Proceedings of the Cambridge Philosophical Society, 1940, vol. 36, no. 2, pp. 160–172 Search PubMed.
- M. A. Ali, A. Wahab, G. Murtaza and A. Khan, First principles calculations for structural, elastic, mechanical, electronic and optical properties of CsYbCl3, Mater. Res. Express, 2019, 6(6), 65905 CrossRef CAS.
- F. Litimein, R. Khenata, A. Bouhemadou, Y. Al-Douri and S. Bin Omran, First-principle calculations to investigate the elastic and thermodynamic properties of R BRh3 (R= Sc, Y and La) perovskite compounds, Mol. Phys., 2012, 110(2), 121–128 CrossRef CAS.
- P. Wachter, M. Filzmoser and J. Rebizant, Electronic and elastic properties of the light actinide tellurides, Phys. B: Condens. Matter, 2001, 293(3–4), 199–223, DOI:10.1016/S0921-4526(00)00575-5.
- D. H. Chung and W. R. Buessem, The elastic anisotropy of crystals, J. Appl. Phys., 1967, 38(5), 2010–2012 CrossRef CAS.
- A. Habib, et al., Insight into the Exemplary Physical Properties of Zn-Based Fluoroperovskite Compounds XZnF3 (X= Al, Cs, Ga, In) Employing Accurate GGA Approach: A First-Principles Study, Materials, 2022, 15(7), 2669 CrossRef CAS PubMed.
- M. Roknuzzaman, K. Ostrikov, H. Wang, A. Du and T. Tesfamichael, Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations, Sci. Rep., 2017, 7(1), 14025 CrossRef PubMed.
- Y. Cai, J. Lan, G. Zhang and Y.-W. Zhang, Lattice vibrational modes and phonon thermal conductivity of monolayer MoS 2, Phys. Rev. B, 2014, 89(3), 35438 CrossRef.
- P. Giannozzi, et al., QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens.Matter, 2009, 21(39), 395502 CrossRef PubMed.
- P. Giannozzi, et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens.Matter, 2017, 29(46), 465901 CrossRef CAS.
- Y. Z. Abdullahi and F. Ersan, Theoretical design of porous dodecagonal germanium carbide (d-GeC) monolayer, RSC Adv., 2023, 13(5), 3290–3294 RSC.
- Y. Z. Abdullahi, A. Bakhtatou, Y. Mogulkoc and F. Ersan, Giant band gap bowing in two dimensional Pb1−xSnxO alloys and Janus PbSnO monolayers, J. Phys. Chem. Solids, 2023, 175, 111203 CrossRef CAS.
- R. Yuan, J. A. Napoli, C. Yan, O. Marsalek, T. E. Markland and M. D. Fayer, Tracking aqueous proton transfer by two-dimensional infrared spectroscopy and ab initio molecular dynamics simulations, ACS Cent. Sci., 2019, 5(7), 1269–1277 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |