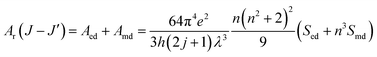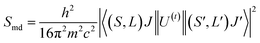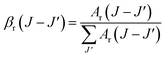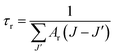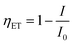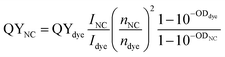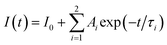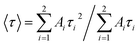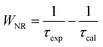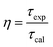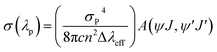DOI:
10.1039/D3RA05005J
(Paper)
RSC Adv., 2023,
13, 27292-27302
New insights on the luminescence properties and Judd–Ofelt analysis of Er-doped ZnO semiconductor quantum dots
Received
24th July 2023
, Accepted 5th September 2023
First published on 12th September 2023
Abstract
In this study, Er3+ doped ZnO semiconductor quantum dots (QDs) were synthesized using a wet chemical method. The successful doping of Er3+ ions into the ZnO host lattice and the elemental composition was confirmed by X-ray diffraction (XRD) and X-ray photoelectron spectroscopy (XPS). The ZnO and Er3+ doped ZnO QDs with a hexagonal structure, spherical shape, and particle size of approximately 5 nm were revealed by XRD and transmission electron microscopy (TEM). The absorption, luminescence properties, and fluorescence lifetimes of the samples were studied as the concentration of Er3+ ions varied. The intensity parameters, emission transition probabilities, branching ratios, and emission lifetimes of the excited levels of Er3+ ions in the ZnO host were determined using the Judd–Ofelt theory, which provided insight into the covalent relationship between the ions and ligands as well as the nature of the ZnO host lattice. Moreover, the energy transfer process from the ZnO host to Er3+ ions and the yield of this process are explained in detail along with specific calculations. The Er3+ doped ZnO QDs displayed a significantly longer lifetime than undoped ZnO, which opens up many potential applications in fields such as photocatalysis, optoelectronics, photovoltaics, and biosensing.
Introduction
In recent years, semiconductor quantum dots (QDs) have attracted significant attention from numerous scientists due to their remarkable optical properties and potential applications.1–4 The unique properties of QDs originate from their size-dependent physical characteristics. They are exceptional and noticeably differ from those of bulk semiconductors. Their size-dependent characteristics confer excellent optical features, such as a wide absorption spectrum, narrow emission spectrum, high photoexcitability, and anti-bleaching.5,6 Their unique optical properties make them suitable for various applications, including light-emitting devices, optoelectronics, catalysis, biomarkers, and solar cells.3,4,7,8
Semiconductor QDs such as CdS, CdTe, CdTeSe, CdSe, PbS, and PbSe… are often quite toxic because they contain heavy metals such as Cd, and Pb in their composition. Their toxicity seriously affects human health and limits their potential application in biology. Semiconductor materials that do not contain heavy metals are a good solution for this problem. ZnO QDs provide a solution to this problem because they do not contain heavy and toxic metals such as Cd or Pb. ZnO is a significant semiconductor material that emits ultraviolet and violet light and has a wide bandgap energy of 3.3 eV.9,10 To broaden the radiative ability, and improve the radiative efficiency and lifetime, QDs are frequently doped with rare earth (RE) ions. ZnO is a suitable host material for doping rare earth ions such as Eu3+, Ce3+, Sm3+, Tb3+, and Er3+.11–13 Researchers have demonstrated that RE ion-doped semiconductor QDs can be used in various applications such as optical converters, solid lasers, and optical amplifiers…
Among rare earth ions, Er3+ ions are considered suitable dopants for enhancing up-conversion fluorescence because of their colorfastness.13 The emission of Er3+ ions is mainly in the visible light region.14 The Er3+ ion exhibits three emission peaks in the short-wavelength region including 490 nm (4F7/2 → 4I15/2, blue), 525–545 nm (2H11/2/4S3/2 → 4I15/2, green), and 662 nm (4F9/2 → 4I15/2, red). In addition, the Er3+ ion has an emission peak around 1540 nm (corresponding to the absorption minimum of optical fibers), which makes it suitable for information transmission. The addition of Er3+ ions to the ZnO QDs significantly enhanced their optical properties. Trivalent Er3+ ion-doped ZnO QDs exhibit exceptional luminescence owing to the 4f–4f transitions of electrons in Er3+ ions.15 Some studies have been conducted on the optical properties of Er3+ ion-doped ZnO QDs.16–18 However, there have been no studies on the optical parameters of Er3+ doped ZnO QDs using the Judd–Ofelt theory and the energy transfer from the ZnO host to Er3+ ions, which are the new points of this study.
In this study, the optical characteristics of Er3+ doped ZnO QDs were studied in detail through both the UV-VIS-NIR and photoluminescence spectra using the Judd–Ofelt theory. The parameters of the excited states of the Er3+ ions, such as the intensity parameters (Ωλ), branching ratios (βr), radiative transition probabilities (Ar), and radiative lifetime (τr) were calculated to gain insight into the optical properties of the Er3+ ions in ZnO. Additionally, the energy transfer processes from the ZnO host to Er3+ ions were thoroughly investigated and explained.
Experimental description
Materials
Zn(OAc)2 (zinc acetate–Zn(CH3COO)2·2H2O, 99.99%), OLA (oleylamine–C18H37N, 97%), ODE (1-octadecene–CH3(CH2)15CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 95%), TOP (tri-n-octylphosphine–C24H51OP 97%), erbium acetate–(CH3CO2)3Er·xH2O (99.9%), isopropanol (70%), and toluene (99.8%) were purchased from Sigma–Aldrich.
CH2, 95%), TOP (tri-n-octylphosphine–C24H51OP 97%), erbium acetate–(CH3CO2)3Er·xH2O (99.9%), isopropanol (70%), and toluene (99.8%) were purchased from Sigma–Aldrich.
Synthesis of Er3+ doped ZnO quantum dots
Er3+ doped ZnO QDs were prepared using a wet-chemical method in a typical synthesis:8,19 Zn(OAc)2 and erbium acetate (Er3+ concentration depends on the ratio between Er3+ and Zn2+) werre mixed with 0.01 mol of TOP and 30 ml of ODE in a three-necked flask. This mixture was continuously blown with Ar gas to remove air from the flask. At this stage, 0.01 mol OLA was injected into reaction flask. The reaction solution was heated to 280 °C and maintained at that temperature for 30 minutes to obtain monodisperse Er3+ doped ZnO QDs. The solution containing QDs was cooled to room temperature and centrifuged in isopropanol (volume ratio of solution containing QDs/isopropanol = 1/4) at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 7 min to remove supernatant remnants. Sediments were collected and carefully preserved for further measurements. The samples ZnO, ZnO: 1 mol% Er, ZnO: 2 mol% Er, and ZnO: 4 mol% Er are denoted as ZE0, ZE1, ZE2, and ZE4, respectively.
000 rpm for 7 min to remove supernatant remnants. Sediments were collected and carefully preserved for further measurements. The samples ZnO, ZnO: 1 mol% Er, ZnO: 2 mol% Er, and ZnO: 4 mol% Er are denoted as ZE0, ZE1, ZE2, and ZE4, respectively.
Characterization
Ultraviolet visible (UV-vis) and near infrared (NIR) absorption spectra of the samples were measured using a Jasco V-770 spectrometer (Varian). Photoluminescence excitation (PLE) spectra, photoluminescence (PL) spectra, and luminescence lifetime were analyzed using a spectrophotometric system FLS1000 with a 450 W Xe lamp. The morphologies of the ZnO and Er doped ZnO QDs were observed using transmission electron microscopy (TEM, Joel-JEM 1010) operating at 80 kV. X-ray photoelectron spectroscopy (XPS) was performed using a Thermo VG Escalab 250 photoelectron spectrometer. The crystal structure and lattice parameters of the fabricated quantum dots were analyzed using X-ray diffraction (D5005) in the 2θ range of 20° to 80° with scan speed of 2° min−1 and equipped with a Cu-Kα radiation source.
Results and discussion
X-ray diffraction studies
The X-ray diffraction (XRD) patterns of ZE0, ZE1, ZE2, and ZE4 samples are shown in Fig. 1. The observed peaks, such as (100), (002), (101), (102), (110), (103), and (112), correspond to the standard reported in JCPDS number #89-0510 and confirm the hexagonal structure of all samples with the P63mc space group.20 The unit-cells scheme of Er-doped ZnO with hexagonal structure is showed in Fig. 2. Hexagonal structures are common for ZnO QDs, which are fabricated using the wet chemical method.16–18 In comparison to pure ZnO (ZE0), the diffraction peaks of ZE1, ZE2, and ZE4 shifted slightly towards lower 2θ angles, indicating an increase in the crystal lattice constant. This slight shift is due to the substitution of small radius Zn ions (0.74 Å) by larger radius Er ions (0.89 Å).21 This substitution causes internal stress in the material and shifts the diffraction peaks. The shift of the diffraction peaks towards the smaller 2θ angle with increasing Er concentration indicates that Er ions have replaced the positions of Zn ions. This result is called substitution doping. The crystallite size (D) of QDs can be determined using X-ray line broadening and the Debye–Scherrer equation:22| |
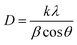 | (1) |
where, λ (=1.54 Å) is the wavelength of the X-ray, k = 0.9, θ is Bragg's diffraction angle, and β is the broadening of the diffraction line (measured at half of its maximum intensity). Table 1 presents the crystallite sizes of ZnO:Er3+ QDs. The lattice constants (a and c) of the WZ structure were calculated using the equation:23| |
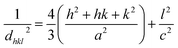 | (2) |
where h, k, and l are Miller indices, and dhkl is calculated from Bragg's equation: nλ = 2dhklsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The effective crystallite strain in the nanostructures was determined using the Stokes–Wilson equation:24
θ. The effective crystallite strain in the nanostructures was determined using the Stokes–Wilson equation:24| |
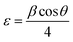 | (3) |
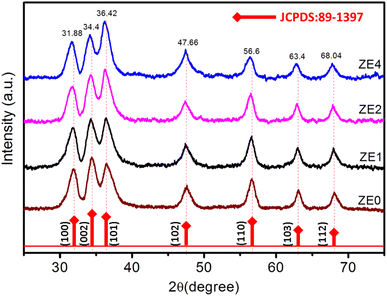 |
| | Fig. 1 XRD patterns of ZE0, ZE1, ZE2, and ZE4 samples. | |
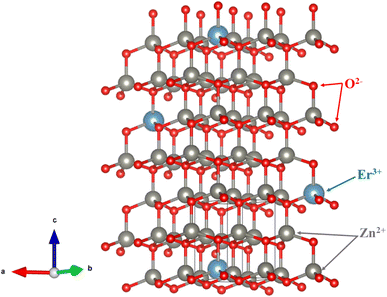 |
| | Fig. 2 The unit-cells scheme of Er-doped ZnO with hexagonal structure. | |
Table 1 The diffraction angle (2θ) of the preferred orientation of (101), lattice constants (a, c), cell volume, β, crystallite size (D), crystallite strain (ε) of ZE0, ZE1, ZE2, and ZE4 QDs
| Sample |
a (Å) |
c (Å) |
2θ (101) |
β × 10−2 |
Cell volume (Å3) |
D (nm) |
ε × 10−3 |
| ZE0 |
3.242 |
5.192 |
36.49° |
2.77 |
47.258 |
5.257 |
6.57 |
| ZE1 |
3.244 |
5.196 |
36.48° |
3.01 |
47.353 |
4.843 |
7.15 |
| ZE2 |
3.247 |
5.201 |
36.46° |
3.15 |
47.486 |
4.623 |
7.48 |
| ZE4 |
3.248 |
5.203 |
36.42° |
3.44 |
47.533 |
4.239 |
8.17 |
Table 1 summarizes all the parameters calculated from the XRD data, including a, c, 2θ, β, and ε. Table 1 indicates that the lattice strain increased and the crystallite size of the Er3+ doped ZnO quantum dots decreased with an increase in the Er3+ concentration. Chemingui and his colleagues suggested that when the Er concentration increases, an excess of Er3+ ions leads to the formation of Er–O–Zn bonds on the surface of ZnO, which may inhibit crystal growth and result in stress being transferred from the outside to the inside of the crystal.20
Morphological
To gain further insight into the morphological characteristics of the ZnO QDs, Transmission Electron Microscopy (TEM) was utilized. TEM are presented in Fig. 3, which show the images of three representative samples of the ZE0, ZE1, and ZE4 QDs. It can be observed that the QDs exhibit nearly spherical and monodisperse shapes. The average size of the QDs was approximately 5 nm and hardly changed even when doping Er3+ with a concentration of 4%. These findings support the XRD results and confirm the successful fabrication of ZnO and Er3+ doped ZnO QDs with stable sizes and shapes.
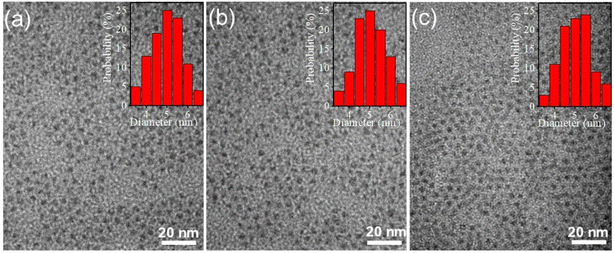 |
| | Fig. 3 TEM images of: (a) ZE0, (b) ZE1, and (c) ZE4 QDs. | |
Elemental and chemical composition analysis
The XPS spectrum provides valuable information on the chemical states and elemental composition, which are crucial for verifying the successful doping of elements in a host material. Fig. 4a displays typical XPS survey scans of the ZE0, ZE1, ZE2, and ZE4 samples. The XPS survey scan of the samples showed five peaks corresponding to the levels of Er 4d, C 1s, O 1s, Zn 2p3/2, and Zn 2p1/2. Fig. 4b shows a high-resolution Er 4d XPS spectrum. The peak at 169.2 eV demonstrates the existence of Er in the trivalent state in ZnO QDs.25 The binding energy peaks at 284.5 and 530.6 eV (in Fig. 4c and d) are indexed to the C 1s and O 1s levels, respectively. C element is detected, indicating the existence of precursors, that were used in the fabrication process of QDs. Fig. 4e shows the two peaks at 1022.2 and 1045.4 eV are ascribed to two levels Zn 2p3/2 and Zn 2p1/2 of Zn element.26 Zn-2p peak position was unchanged for all the samples. This result indicates that Er doping does not affect the electronic states of Zn; therefore, the presence of Zn vacancies was neglected.27 The binding energies of these two peaks are separated by a distance of 23.2 eV, which is in agreement with the reported values.28 The atomic percentages of the elements in the samples were determined using the peak areas of the corresponding high-resolution spectra and the calibrated atomic sensitivity factor, as shown in Table 2.
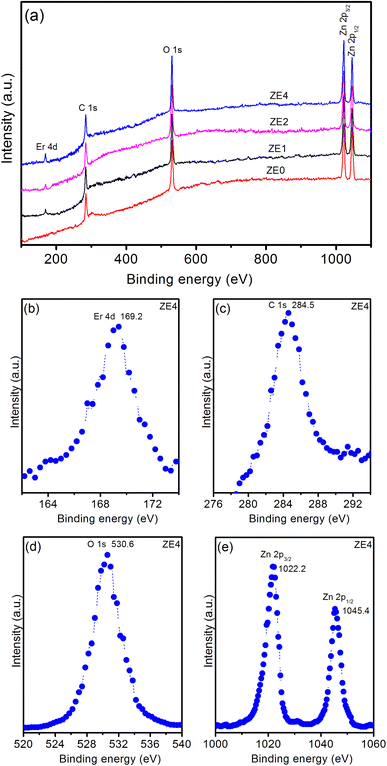 |
| | Fig. 4 (a) Survey XPS spectrum of ZE0, ZE1, ZE2, and ZE4 QDs. High-resolution XPS spectra of ZE4 QDs: (b) Er 4d, (c) C 1s, (d) O 1s, and (e) Zn 2p. | |
Table 2 Atomic (%) and weight (%) of ZE0, ZE1, ZE2, and ZE4 samples
| Samples |
Atomic (%) |
Weight (%) |
| Zn |
Er |
C |
O |
Zn |
Er |
C |
O |
| ZE0 |
51.2 |
— |
6.82 |
41.98 |
81.62 |
— |
2.01 |
16.37 |
| ZE1 |
50.67 |
0.86 |
5.7 |
42.77 |
78.7 |
3.42 |
1.63 |
16.25 |
| ZE2 |
49.95 |
1.13 |
7.51 |
41.41 |
77.62 |
4.49 |
2.14 |
15.75 |
| ZE4 |
48.93 |
3.23 |
6.12 |
41.72 |
71.4 |
12.06 |
1.64 |
14.9 |
Judd–Ofelt analysis
In Fig. 5, the optical absorption spectra of undoped and doped samples with Er3+ ions were measured in the 350–1550 nm range. The absorption spectra of ZE1, ZE2, and ZE4 QDs showed 11 peaks, corresponding to the transitions from the ground level to excited levels of Er3+ ion:8 4I15/2–4G9/2, 4I15/2–4G11/2, 4I15/2–4F3/2, 4I15/2–4F5/2, 4I15/2–4F7/2, 4I15/2–2H11/2, 4I15/2–4S3/2, 4I15/2–4F9/2, 4I15/2–4I9/2, 4I15/2–4I11/2, and 4I15/2–4I13/2. These peaks were centered at 364, 385, 440, 450, 499, 522, 545, 650, 799, 976, and 1536 nm. Among them, the 4I15/2 → 4I13/2 band (1536 nm) is the contribution of both electric and magnetic dipole transitions (ED and MD). The remaining bands are yielded by the pure ED transitions.
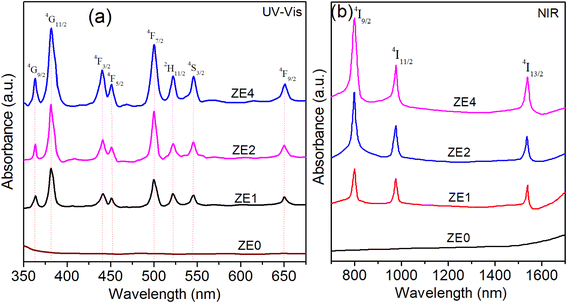 |
| | Fig. 5 UV-Vis (a) and NIR (b) spectra of: ZE0, ZE1, ZE2, and ZE4 QDs. | |
It is known that the Judd–Oflet (JO) theory has been widely used to evaluate the properties of ligand field as well as optical parameters of trivalent rare earth (RE3+) ions.29,30 The key of this theory is based on the three intensity parameters Ωλ (λ = 2, 4, 6) which are usually calculated from the absorption spectra. According to the JO theory, the relationship between the oscillator strength fcal of an ED transition and Ωλ parameters is given by the expression:31,32
| |
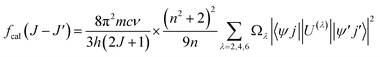 | (4) |
where ‖
U(t)‖ are matrix elements of the unit tensor operator that are calculated from the intermediate coupling approximation between the initial state 〈
ψj| and final state |
ψ′
j′〉.
h is Planck's constant,
n is the measured refractive index. The refractive index of the ZnO host (
n) is approximately 2.0 and is considered constant across all wavelengths.
33
From the absorption spectra, experimental oscillator strength (fexp) of an ED transition is calculated using the following expression:31,32
| | |
fexp(J − J′) = 4.318 × 10−9∫α(ν)dν
| (5) |
where
α(
ν) is the molar absorptivity for a band at energy
ν. The
α(
ν) value can be calculated from the absorbance
A by using Lambert–Beer's law:
A(
ν) =
α(
ν)
Cd.
34 Then the
fexp was calculated by:
| |
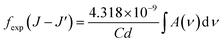 | (6) |
where
C is concentration [dim:
L−3, units: mol
−1];
d is the optical path length [dim:
L, units: cm] which is thickness of the sample. The
C concentration is calculated through expression:
34| |
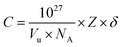 | (7) |
where
Vu is the volume of the crystallographic unit cell,
NA is Avogadro's number,
Z is the number of formula units per unit cell, and
δ is the doping fraction.
Using the eqn (5) and the absorption spectra, the experimental oscillator strengths of all the ED transitions were calculated. The obtained results for the ZE1 sample are presented in Table 3. For the transition including both MD and ED (4I15/2 → 4I13/2 transition), the oscillator strength is calculated by ftot = fED + fMD, in which ftot is computed from the eqn (5), and fMD is determined by the following formula:
| |
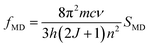 | (8) |
where
SMD is the line strengths of a MD transition which does not depend on the host. Thus, the
fMD value can be calculated using the relationship:
| |
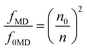 | (9) |
where
f0MD and
n0 are the oscillator strength and refractive index of any material which were published. In this study, we used data of the Er
3+ ions-doped HClO
4 solution, in which the
f0MD = 0.308 × 10
−6 and
n0 = 1.419.
34 Using the
eqn (8), the
fMD of the
4I
15/2 →
4I
13/2 transition was found to be 0.15 × 10
−7. After determining the
ftot (0.72 × 10
−7) and
fMD, the
fED of the
4I
15/2 →
4I
13/2 transition was calculated by
fED =
ftot −
fMD.
Table 3 Transition energies (ν, cm−1), experimental (fexp, 10−6) and calculated (fcal, 10−6) oscillator strengths for the absorption transitions from the Er3+:4I15/2 level in ZE1 sample
| Transition |
ν (cm−1) |
fexp |
fcal |
| 4I15/2 → 4I13/2 |
6502 |
0.57 |
0.72 |
| 4I11/2 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
0.76 |
0.49 |
| 4I9/2 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516 516 |
1.28 |
0.62 |
| 4F9/2 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 385 |
0.85 |
1.16 |
| 4S3/2 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349 349 |
1.13 |
0.86 |
| 2H11/2 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 157 |
1.12 |
1.83 |
| 4F7/2 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
3.12 |
2.41 |
| 4F5/2 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222 222 |
0.76 |
0.52 |
| 4F3/2 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 727 |
1.47 |
0.94 |
| 4G11/2 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974 974 |
10.25 |
10.51 |
| 4G9/2 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 472 |
1.41 |
1.15 |
| |
RMS = 0.52 × 10−6 |
By solving the system of equations fexp = fcal through the least square fitting method, the Ωλ (λ = 2, 4, 6) parameters as well as their error were determined and are listed in Table 4. It can be seen that the deviation of the Ωλ parameters is smaller than 20% which is within the allowable error range of the JO theory.
Table 4 Judd–Ofelt intensity parameters Ω2,4,6 (10−20 cm2) and R ratio of Er3+ in some matrices
| Sample |
Ω2 |
Ω4 |
Ω6 |
R |
Trend |
Reference |
| ZE1 |
2.64 ± 0.42 |
0.85 ± 0.16 |
0.61 ± 0.13 |
1.39 |
Ω2 > Ω4 > Ω6 |
This work |
| ZE2 |
2.68 ± 0.32 |
0.82 ± 0.14 |
0.56 ± 0.12 |
1.46 |
Ω2 > Ω4 > Ω6 |
This work |
| ZE4 |
2.54 ± 0.35 |
0.93 ± 0.14 |
0.51 ± 0.11 |
1.82 |
Ω2 > Ω4 > Ω6 |
This work |
| Fluorophosphate |
7.36 |
2.01 |
1.11 |
1.81 |
Ω2 > Ω4 > Ω6 |
36 |
| Antimony |
4.05 |
1.14 |
0.73 |
1.56 |
Ω2 > Ω4 > Ω6 |
37 |
| Germanate |
4.48 |
2.15 |
0.73 |
2.94 |
Ω2 > Ω4 > Ω6 |
38 |
| Bismuth borate |
5.86 |
1.37 |
2.15 |
0.63 |
Ω2 > Ω6 > Ω4 |
39 |
| Phosphate |
3.91 |
1.97 |
2.57 |
0.76 |
Ω2 > Ω6 > Ω4 |
40 |
| Fluoride |
3.08 |
1.46 |
1.69 |
0.86 |
Ω2 > Ω6 > Ω4 |
41 |
| Tellurite |
4.93 |
1.30 |
1.31 |
0.99 |
Ω2 > Ω6 > Ω4 |
42 |
The Ω2, Ω4, and Ω6 parameters can provide useful information about the local coordination around RE3+ ions.29,30 The covalency of the RE3+–ligand bond and ligand asymmetry can be inferred from the Ω2 parameter, with higher values indicating stronger bonds. Meanwhile, Ω4 and Ω6 are largely independent of the local environment but are influenced by factors such as viscosity and rigidity. Additionally, the value of Ω6 demonstrates an inverse correlation with the covalent nature of the (Er–O) bonds. The Ωλ parameters of the Er3+ ions in the ZnO QDs were compared with those in several other host matrices. For the ZnO:Er3+ QDs, the order of the Judd–Oflet parameters are Ω2 > Ω4 > Ω6 for all samples. This trend is similar to that of some host materials such as fluorophosphate, antimony, germanate,36–38 but is different from that in ref. 39–42. The root mean square (RMS) deviation between the fexp and fcal oscillator strengths of the ZnO:Er3+ QDs is presented in Table 3. A small value of RMS deviation indicates the reliability of our calculations.
To estimate the stimulated emission for the laser medium, the spectroscopic quality factor, R = Ω4/Ω6 is introduced. R is a very important factor that can be used to predict potential performance of laser,34,35 it is within the range of 0.63–2.94 for Er3+-doped samples.36–42 In this study, R showed an increasing trend with increasing Er3+ ion concentration. It is noted that the Ω2 parameter is sensitive to changes in the features of the local environment around the RE3+ ions such as ligand asymmetry and ligand–RE3+ bonding nature. A large value of Ω2 indicates high asymmetry of the ligand field as well as the high covalency of the ligand–RE3+ bond.35,37–39 As shown in Table 4, the Ω2 parameter of the ZnO:Er QDs was much lower than that of the compared hosts. This implies that the ligand asymmetry and covalence of the Er3+–ligand bond in ZnO:Er3+ QDs are higher than those in the compared matrices.
Radiative properties, such as the radiative transition probabilities of electric dipole transitions (Ar), radiative lifetimes (τr), and branching ratios (βr) can also be determined based on the Judd–Oflet theory. The probability of an electric dipole transition from j state to j′ state is determined using the following equation:29,30
| |
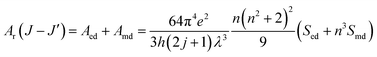 | (10) |
| |
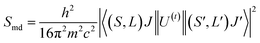 | (11) |
The branching ratio is important for all emission transitions. This provides an insight into how efficiently the transitions can be stimulated. The branching ratio is an essential factor to be considered when assessing the gain performance of a material. The branching ratio (βr) can be used to describe the probability of obtaining stimulated emissions. The branching ratio was calculated from the transition probability using the following equation:29,30
| |
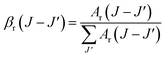 | (12) |
The emission lifetime (τr) of the excited states was determined from the emission transition probability (Ar) using the following equation:29,30
| |
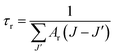 | (13) |
The values of Ar(J → J′) (s−1), βr(J → J′), and τr (ms) were calculated for some excited levels of Er3+ ions in the ZnO:Er3+ samples. The results are shown in Table 5.
Table 5 The parameters of Ar (s−1), βr, and τr (ms) for the excited levels of Er3+ ions in ZE1, ZE2, and ZE4 samples
| |
ZE1 |
ZE2 |
ZE4 |
| Ar (s−1) |
βr (%) |
τcal (ms) |
Ar (s−1) |
βr (%) |
τcal (ms) |
Ar (s−1) |
βr (%) |
τcal (ms) |
| 4F3/2→ |
— |
— |
0.358 |
— |
— |
0.387 |
— |
— |
0.394 |
| 4F5/2 |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
| 4F7/2 |
0.71 |
∼0 |
— |
0.68 |
∼0 |
— |
0.75 |
∼0 |
— |
| 2H11/2 |
0.16 |
∼0 |
— |
0.15 |
∼0 |
— |
0.15 |
∼0 |
— |
| 4S3/2 |
7.37 |
0.26 |
— |
7.48 |
0.29 |
— |
7.09 |
0.28 |
— |
| 4F9/2 |
21.86 |
0.78 |
— |
20.17 |
0.78 |
— |
19.47 |
0.77 |
— |
| 4I9/2 |
335.57 |
12.02 |
— |
321.25 |
12.43 |
— |
356.11 |
14.03 |
— |
| 4I11/2 |
995.12 |
35.63 |
— |
922.88 |
35.67 |
— |
911.05 |
35.89 |
— |
| 4I13/2 |
108.87 |
3.92 |
— |
100.42 |
3.88 |
— |
95.04 |
3.74 |
— |
| 4I15/2 |
1322.08 |
47.39 |
— |
1213.72 |
46.95 |
— |
1148.7 |
45.29 |
— |
| 4F5/2→ |
— |
— |
0.325 |
— |
— |
0.349 |
— |
— |
0.350 |
| 4F7/2 |
1.29 |
0.04 |
— |
1.28 |
0.05 |
— |
1.25 |
0.04 |
— |
| 2H11/2 |
3.98 |
0.13 |
— |
3.71 |
0.13 |
— |
3.73 |
0.13 |
— |
| 4S3/2 |
1.41 |
0.05 |
— |
1.43 |
0.05 |
— |
1.37 |
0.05 |
— |
| 4F9/2 |
132.68 |
4.31 |
— |
124.83 |
4.35 |
— |
129.78 |
4.55 |
— |
| 4I9/2 |
116.66 |
3.79 |
— |
111.42 |
3.89 |
— |
112.75 |
3.95 |
— |
| 4I11/2 |
134.45 |
4.36 |
— |
129.59 |
4.52 |
— |
146.59 |
5.14 |
— |
| 4I13/2 |
1208.13 |
41.55 |
— |
1200.21 |
41.86 |
— |
1232.91 |
43.20 |
— |
| 4I15/2 |
1410.27 |
45.77 |
— |
1294.67 |
45.15 |
— |
1225.32 |
42.94 |
— |
| 4F7/2→ |
— |
— |
0.244 |
— |
— |
0.261 |
— |
— |
0.256 |
| 2H11/2 |
0.92 |
∼0 |
— |
0.89 |
∼0 |
— |
0.85 |
∼0 |
— |
| 4S3/2 |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
| 4F9/2 |
24.02 |
0.58 |
— |
23.86 |
0.62 |
— |
24.04 |
0.62 |
— |
| 4I9/2 |
156.88 |
3.83 |
— |
148.18 |
3.86 |
— |
146.68 |
3.75 |
— |
| 4I11/2 |
245.65 |
6.00 |
— |
234.18 |
6.10 |
— |
252.58 |
6.46 |
— |
| 4I13/2 |
550.72 |
13.45 |
— |
531.28 |
13.86 |
— |
602.52 |
15.42 |
— |
| 4I15/2 |
3114.89 |
76.14 |
— |
2895.52 |
75.56 |
— |
2879.88 |
73.75 |
— |
| 2H11/2→ |
— |
— |
0.119 |
— |
— |
0.118 |
— |
— |
0.121 |
| 4S3/2 |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
| 4F9/2 |
44.33 |
0.53 |
— |
44.71 |
0.53 |
— |
43.37 |
0.52 |
— |
| 4I9/2 |
135.43 |
1.61 |
— |
133.97 |
1.58 |
— |
129.70 |
1.57 |
— |
| 4I11/2 |
122.62 |
1.45 |
— |
120.49 |
1.42 |
— |
125.22 |
1.51 |
— |
| 4I13/2 |
450.37 |
5.34 |
— |
446.81 |
5.28 |
— |
448.34 |
5.42 |
— |
| 4I15/2 |
7683.34 |
91.07 |
— |
7721.36 |
91.19 |
— |
7529.61 |
90.98 |
— |
| 4S3/2→ |
— |
— |
0.565 |
— |
— |
0.615 |
— |
— |
0.628 |
| 4F9/2 |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
∼0 |
∼0 |
— |
| 4I9/2 |
68.74 |
3.88 |
— |
64.11 |
3.94 |
— |
64.59 |
4.18 |
— |
| 4I11/2 |
35.24 |
1.99 |
— |
32.48 |
2.00 |
— |
31.26 |
2.02 |
— |
| 4I13/2 |
492.98 |
27.84 |
— |
452.57 |
27.82 |
— |
428.33 |
27.74 |
— |
| 4I15/2 |
1172.81 |
66.29 |
— |
1076.68 |
66.24 |
— |
1018.9 |
66.04 |
— |
| 4F9/2→ |
— |
— |
0.606 |
— |
— |
0.639 |
— |
— |
0.603 |
| 4I9/2 |
9.14 |
0.55 |
— |
9.17 |
0.59 |
— |
8.97 |
0.54 |
— |
| 4I11/2 |
83.33 |
5.05 |
— |
78.86 |
5.04 |
— |
75.43 |
4.55 |
— |
| 4I13/2 |
72.7 |
4.42 |
— |
69.97 |
4.46 |
— |
74.89 |
4.53 |
— |
| 4I15/2 |
1486.25 |
89.98 |
— |
1407.22 |
89.91 |
— |
1497.846 |
90.38 |
— |
| 4I9/2→ |
— |
— |
4.357 |
— |
— |
4.568 |
— |
— |
4.201 |
| 4I11/2 |
3.18 |
1.39 |
— |
3.14 |
1.44 |
— |
3.16 |
1.33 |
— |
| 4I13/2 |
50.23 |
21.88 |
— |
46.17 |
21.09 |
— |
43.89 |
18.44 |
— |
| 4I15/2 |
176.11 |
76.73 |
— |
169.55 |
77.47 |
— |
191.01 |
80.23 |
— |
| 4I11/2→ |
— |
— |
4.862 |
— |
— |
5.134 |
— |
— |
5.373 |
| 4I13/2 |
40.17 |
19.53 |
— |
38.82 |
19.93 |
— |
38.39 |
20.63 |
— |
| 4I15/2 |
165.52 |
80.47 |
— |
155.95 |
80.07 |
— |
147.68 |
79.37 |
— |
| 4I13/2→ |
— |
— |
5.016 |
— |
— |
5.237 |
— |
— |
5.341 |
| 4I15/2 |
199.38 |
100 |
— |
190.93 |
100 |
— |
187.21 |
100 |
— |
As shown in Table 5, for the luminescence transitions from any excited level, the transition to the 4I15/2 ground usually exhibits a much larger branching ratio than the others. These results are in good agreement with those obtained from the measured luminescence spectra (Fig. 6).
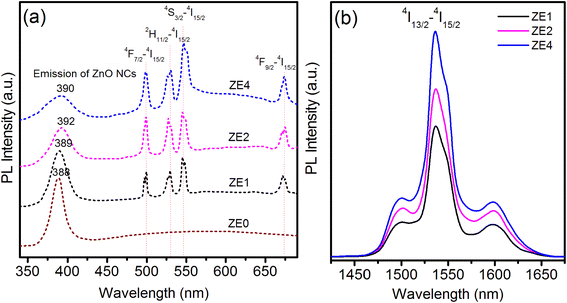 |
| | Fig. 6 PL spectra of ZE0, ZE1, ZE2, and ZE4 QDs: (a) in visible region, λexc = 325 nm; (b) in NIR region, λexc = 980 nm. Samples were dispersed in toluene. | |
Photoluminescence spectra and energy transfer
The photoluminescence (PL) spectra in visible region of the ZE0, ZE1, ZE2, and ZE4 samples were recorded under the same conditions with an excitation wavelength of 325 nm as shown in Fig. 6a. The purpose of using an excitation wavelength of 325 nm was to observe the emission of the ZnO host and Er3+ ions simultaneously. The PL spectrum of ZE0 QDs exhibited a strong and narrow emission peak at approximately 388 nm. This radiative emission originates from the recombination of electrons in the conduction band with holes in the valence band, and is referred to as excitonic emission. In addition, there is a weak and wide emission peak in the longer wavelength region, which is attributed to the emission from the surface state of the NC.43 Meanwhile, ZE1, ZE2 and ZE4 QDs displayed five emission peaks related to the transition of Er3+ ions at 500, 532, 547, and 672 nm, corresponding to the transitions 4F7/2 → 4I15/2, 2H11/2 → 4I15/2, 4S3/2 → 4I15/2, and 4F9/2 → 4I15/2, respectively.8 As shown in Fig. 6a, the intensity of the transitions of Er3+ ions increased with an increase in the concentration of Er3+ for all studied samples. This proves that the fluorescence quenching did not occur when the Er ion concentration was up to 4% in the ZnO QDs. Fig. 6(b) shows the PL spectra in NIR region of the ZE1, ZE2, and ZE4 samples under 980 nm excitation. The emission peaks at approximately 1540 nm corresponding to 4I13/2 → 4I15/2 level transition and their FWHM are very important and useful for NIR laser applications and optical communication.
Fig. 7 presents the photoluminescence spectra of the ZE0 sample and the excitation spectra of the ZE4 sample. The PLE spectrum of ZE4 QDs showed 8 peaks, corresponding to the transitions from the ground state 4I15/2 to the excited states 4G9/2, 4G11/2, 2H9/2 2F3/2, 2F5/2, 4F7/2, 2H11/2, and 4S3/2 of Er3+ ions.8,41,42 Energy transfer from a donor to an acceptor only occurs when there is an overlap between the emission spectra of the donor and the excitation spectra of the acceptor.2 The emission peak of the ZnO host (ZE0) at 388 nm was very close to the strongest excitation peak of Er (ZE4) at 385 nm. It can be seen that the overlapping area between these two peaks is quite wide. This indicates a clear possibility for the transfer of energy excitation from the ZnO host to Er3+ ions in Er doped ZnO QDs. The PLE spectrum due to the 4f–4f intraregional level transitions of Er3+ ions reveals that the excitation wavelength of 325 nm does not effectively excite the Er3+ ion, as shown in Fig. 7.
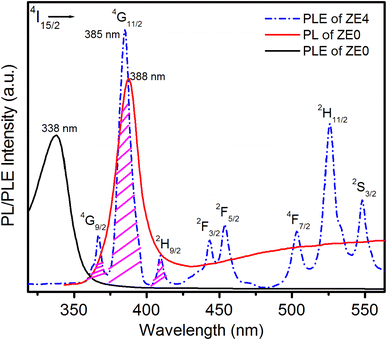 |
| | Fig. 7 PLE spectrum of ZE4 QDs measured at emission wavelength 1540 nm, PL spectrum of ZE0 QDs was excited at 325 nm, and PLE spectrum of ZE0 QDs. | |
Hence, the emission of the Er+3 ions in Fig. 6(a) is primarily due to energy transfer from the ZnO host to the Er3+ ion. The nature of this energy transfer process is observed in Fig. 8 and explained in detail as follows. When the ZnO QDs were excited at 325 nm, they absorbed photons, moved to a higher energy level and created electron–hole pairs. The recombination of these electron–hole pairs releases energy in the form of photons at 388 nm, which are absorbed by the Er3+ ions and excited to a higher energy state (4G11/2). After the Er3+ ions are excited and reach the 4G11/2 energy level, they can either relax non-radiatively (i.e., without emitting light) or undergo radiative decay by emitting photons at lower energies, corresponding to transitions to the 2H9/2, 4F3/2, 4F7/2, 2H11/2, 4S3/2, and 4F9/2 energy levels, eventually returning to the ground state and emitting photons with wavelengths of 500, 532, 547, and 672 nm, corresponding to the level transitions of 4F7/2 → 4I15/2, 2H11/2 → 4I15/2, 4S3/2 → 4I15/2, and 4F9/2 → 4I15/2.
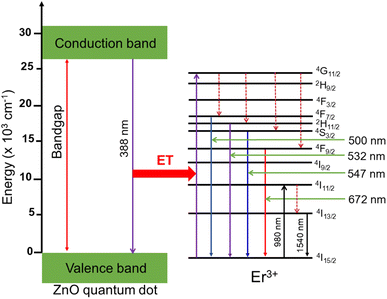 |
| | Fig. 8 Schematic energy level diagram of ZnO QDs, and transfer energy mechanism from ZnO host to Er3+ ion. | |
The energy diagram in Fig. 8 can be used to explain the mechanism of energy transfer from the ZnO host to the Er3+ ions in Er doped the ZnO QDs. The specific transitions and emission wavelengths depend on the local crystal field and morphology of the Er doped ZnO QDs, as well as the concentration of Er3+ ions. As the concentration of Er3+ ions increased, the intensity of the ZnO emission peak (approximately 388 nm) gradually decreased, while the intensity of the Er3+ ion emission peaks increased. This proves that the energy transfer from the ZnO host to the Er3+ ions became more efficient, leading to a greater proportion of the excitation energy being transferred to the Er3+ ions. This phenomenon can be used to control the emission properties of Er doped ZnO QDs and to tune their emission spectra for specific applications.
The efficiency of energy transfer (ET) from the ZnO host to Er3+ ions can be calculated using the following equation:2
| |
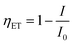 | (14) |
where,
I0 is the integrated radiative intensity of ZnO QDs and
I is the integrated radiative intensity of the ZnO QDs in the presence of Er
3+ ion. The intensities of the emission peaks of the ZE0, ZE1, ZE2, ZE4 QDs, and
ηET were calculated and these values are presented in
Table 6. The obtained results show that
ηET increases from 11.8 to 30.71% when the concentration of Er
3+ ions increases from 1.0 to 4.0 mol%. This result proves that the rate of energy transfer from the ZnO host to the Er
3+ ions increases with increasing Er concentration.
Table 6 The integral emission intensity (a.u.), ηET (%), QYZnO (%), and QYEr (%) of the samples
| Sample |
I388-ZnO |
I500 |
I532 |
I547 |
I672 |
I1540 |
ηET |
QYZnO |
QYEr |
| ZE0 |
3012 |
— |
— |
— |
— |
— |
— |
32.65 |
— |
| ZE1 |
2657 |
242 |
256 |
412 |
244 |
342 |
11.8 |
28.8 |
16.26 |
| ZE2 |
2223 |
392 |
417 |
563 |
276 |
411 |
26.19 |
24.1 |
22.32 |
| ZE4 |
2087 |
413 |
421 |
844 |
289 |
513 |
30.71 |
22.62 |
26.88 |
The quantum yield (QY) is an important parameter to determine the emission ability of materials. Photoluminescence (PL) quantum yield of a sample was measured relative to an organic dye with known QY and was calculated according to the following equation:43
| |
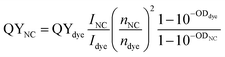 | (15) |
where
I is the integrated emission intensity of the PL spectrum and was obtained by fitting the PL spectrum using the combined function of Gauss and Lorentz.
n is the refractive index, and OD is the optical density of the NC/QD or the dye samples. To determine QY, QDs were dispersed in toluene and the used organic dye is Rodamin 6G (Rh 6G) with QY of 95% in ethanol. The optical density of QD and dye were determined to be equal (=0.037 at 325 nm). The refractive index of toluene and ethanol are 1.496 and 1.361, respectively. QYs of ZnO and Er ion emission are calculated and given by
Table 6.
Photoluminescence decay and radiative parameters of the 5I13/2 → 5I15/2 transition
The optical amplification efficiency of Er-doped materials depends on several factors, including the lifetime and bandwidth of the metastable state of Er3+ ions. The metastable state is the long-lived excited state of erbium ions that is responsible for the amplification of the optical signal. The longer the lifetime of this state, the more time the erbium ions must emit light, resulting in higher amplification. Fig. 9 displays the photoluminescence decay curves for the three samples at an excitation wavelength of 980 nm for the 4I13/2 → 4I15/2 transition at 1540 nm. It is noteworthy that the decay curves for the three samples were multi-exponential. This result is different from the decay curves of Er-doped glass or phosphor hosts, which exhibit a single-exponential nature.36–40 The emission process of Er3+ ions in hosts is due to different recombination mechanisms or energy transfer. The lifetimes of the samples were determined from the PL decay curve by fitting with a bi-exponential function, which is given as:44,45| |
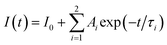 | (16) |
where, τi is the lifetime, and Ai is the pre-exponential factor. The average lifetime can be calculated using the following equation:46,47| |
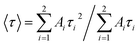 | (17) |
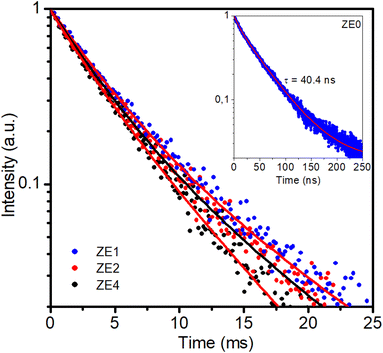 |
| | Fig. 9 PL decay curves of ZE1, ZE2, ZE4 QDs measured at 1540 nm (4I15/2–4I13/2) using an EPL-405 in an FLS1000. Measurement parameters: repetition rate = 200 kHz, excitation pulse width = 1 μs, λex = 980 nm, Δλex = 5 nm, resolution = 10 ns per channel. | |
The average lifetime depends on the pre-exponential factor and the lifetime of each exponential component.
The experimental lifetimes Ai, τi, and τ of the 4I13/2 state were calculated for all concentrations and are listed in Table 7. For the ZnO QDs undoped, the luminescence lifetime was found to be 40.4 ns (see inset of Fig. 9). Thus, by doping Er3+ ions into ZnO quantum dots, the fluorescence decay of the material was significantly lower than that of the undoped ZnO QDs. The enhancement of the fluorescence lifetime makes Er3+ doped ZnO QDs highly suitable for photovoltaic and biosensing applications. It was found that the lifetime of the 4I13/2 level slightly decreased with the increasing Er3+ ion concentration. In addition, the experimental lifetime was always shorter than the calculated lifetime (τcal).
Table 7 Fitting time constants of PL decay kinetics of ZE1, ZE2, ZE4 QDs
| Sample |
τ1 (ms) |
τ2 (ms) |
〈τ〉 (ms) |
| ZE1 |
1.98 (74.85%) |
6.57 (25.15%) |
4.4 |
| ZE2 |
2.35 (27.6%) |
4.63 (72.4%) |
4.26 |
| ZE4 |
2.53 (51.38%) |
4.84 (48.62%) |
4.02 |
In fact, the difference between the calculated and experimental lifetimes relates to the nonradiative processes such as reabsorption, multiphonon relaxation via impurities (e.g. OH groups and rests of acetates), energy transfer between Er3+ ions or from an Er3+ ion to face states and killer centers which always exist in quantum dots, etc.48 The nonradiative probability (WNR) and quantum efficiency (η) of the 4I13/2 level were calculated using the following formulas:29,44
| |
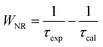 | (18) |
| |
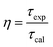 | (19) |
The calculated results are listed in Table 8. The WNR increased whereas the η with the increase in the Er3+ concentration doped into the ZnO QDs.
Table 8 Radiative parameters from the 4I13/2 level in ZnO:Er3+ QDs: the calculated lifetime (τcal, ms), experimental lifetime (τexp, ms), energy transfer rate (WNR, s−1), quantum efficiency (η, %), effective bandwidth (Δλeff, nm), stimulated emission cross section (σ(λp), 10−21 cm2), optical gain (σ(λp) × τcal, 10−23 cm2 s−1), and gain bandwidth (σ(λp) × Δλeff, 10−26 cm3)
| Sample |
τcal |
τexp |
WNR |
η |
Δλeff |
σ(λp) |
σ(λp) × τcal |
σ(λp) × Δλeff |
| ZE1 |
5.02 |
4.40 |
28.07 |
87.65 |
28.2 |
53.40 |
26.81 |
150.59 |
| ZE2 |
5.24 |
4.26 |
43.90 |
81.29 |
29.3 |
51.14 |
26.79 |
149.84 |
| ZE4 |
5.34 |
4.02 |
61.49 |
75.28 |
27.5 |
50.14 |
26.77 |
137.88 |
As shown in Fig. 6, the luminescence spectra of the ZnO:Er3+ QDs exhibit a strong emission band at 1540 nm. This band can be used for laser action and optical amplifiers.49 In order to estimate the applicability of the 1540 nm luminescence band of ZnO:Er3+ QDs, some radiative parameters such as the stimulated emission cross section (σ(λp)), optical gain (σ(λp) × τcal), and gain bandwidth (σ(λp) × Δλeff) of the 5I13/2 → 5I15/2 transition were calculated. The stimulated emission cross section of a radiative transition is defined as:50
| |
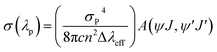 | (20) |
where Δ
λeff is the effective bandwidth, and
λp is the wavelength at the peak of the emission band.
The calculation results for the radiative parameters of the 4I13/2 level are presented in Table 8. It can be observed that the quantum efficiency decreases whereas the energy transfer rate increases when the Er3+ concentration increases. This may result in an increase in the interaction between Er3+ ions and the face states in the ZnO:Er3+ QDs. The radiative parameters of the 4I13/2 level in ZnO:Er3+ QDs are higher than those in the matrices presented in ref. 45, in which the ZE1 sample expresses the radiative parameters better than those of the other samples. This suggests the potential application of the ZnO:Er3+ QDs in optical amplifiers.
Conclusion
Er3+ doped ZnO QDs were successfully synthesized by a wet chemical method using Zn(OAc)2 as the precursor and OLA, TOP as the ligands. XRD and XPS analyses demonstrated that Er ions were successfully doped into the ZnO host and replaced the Zn ions. The XRD results show that Er-doped ZnO and ZnO QDs both have a hexagonal structure and the lattice constants (a and c) increase slightly with increasing Er concentration. The J–O theory was used to calculate and predict the emission parameters of the Er3+ ions. When the Er concentration changes, the order of the Judd–Ofelt parameters is Ω2 > Ω6 > Ω4, the maximum value of the Ω2 parameter indicates that the vibrational frequencies of the present samples are relatively low. The energy transfer process from the ZnO host to Er3+ ion has been explained and calculated in detail. The energy transfer efficiency from ZnO to Er3+ increased from 11.8 to 30.71% when the Er3+ concentration increased from 1 to 4%. The quantum efficiency decreases whereas the energy transfer rate increases when the Er3+ concentration increases. The long fluorescence lifetimes of Er3+ doped ZnO QDs make them have many potential applications in fields such as photocatalysis, optoelectronics, photovoltaics, and biosensing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research is funded by Ministry of Education and Training of Vietnam under grant number B2022-TNA-36. Assoc. Prof. N. X. Ca would like to thank for the support from Kunming Boren Precious Metals Co. Ltd.
References
- K. V. Chandekar, M. Shkir, A. Khan and S. AlFaify, Mater. Sci. Semicond. Process., 2020, 118, 105184 CrossRef CAS.
- P. M. Tan, N. X. Ca, N. T. Hien, H. T. Van, P. V. Do, L. D. Thanh, V. H. Yen, V. P. Tuyen, Y. Peng and P. T. Tho, Phys. Chem. Chem. Phys., 2020, 22, 6266 RSC.
- N. T. Hien, N. X. Ca, N. T. Kien, N. T. Luyen, P. V. Do, L. D. Thanh, H. T. Van, S. Bharti, Y. Wang, N. T. M. Thuy and P. M. Tan, J. Phys. Chem. Solid., 2020, 147, 109638 CrossRef CAS.
- J. P. Arago, E. Cordoncillo, R. A. S. Ferreira, L. D. Carlosb and P. Escribano, J. Mater. Chem., 2011, 21, 1162–1170 RSC.
- T. K. Nideep, M. Ramya and M. Kailasnath, Superlattices Microstruct., 2020, 141, 106477 CrossRef CAS.
- N. T. M. Thuy, V. T. K. Lien, P. V. Do, V. T. K. Oanh, N. X. Truong, N. X. Ca, N. T. Hien and P. M. Tan, J. Lumin., 2023, 255, 119538 CrossRef CAS.
- M. Kouhnavard, S. Ikeda, N. A. Ludin, N. B. A. Khairudin, B. V. Ghaffari, M. A. Mat- Teridi, M. A. Ibrahim, S. Sepeai and K. Sopian, Renewable Sustainable Energy Rev., 2014, 37, 397–407 CrossRef CAS.
- M. Kouhnavard, S. Ikeda, N. A. Ludin, N. B. A. Khairudin, B. V. Ghaffari, M. A. Mat- Teridi, M. A. Ibrahim, S. Sepeai and K. Sopian, Mater. Sci. Semi. Save Proc., 2018, 81, 113–117 CrossRef.
- E. Cerrato, C. Gionco, I. Berruti, F. Sordello, P. Calza and M. C. Paganini, J. Solid State Chem., 2018, 264, 42–47 CrossRef CAS.
- S. Sakthivel, B. Neppolian, M. V. Shankar, B. Arabindoo, M. Palanichamy and V. Murugesan, Sol. Energy Mater. Sol. Cells, 2003, 77, 65–82 CrossRef CAS.
- A. Kumawat, S. Chattopadhyay, R. K. Verma and K. P. Misra, Mater. Lett., 2022, 308, 131221 CrossRef CAS.
- L. Arda, J. Magn. Magn. Mater., 2019, 475, 493–501 CrossRef CAS.
- M. Achehboune, M. Khenfouch, I. Boukhoubza, I. Derkaoui, L. Leontie, A. Carlescu, B. M. Mothudi, I. Zorkani and A. Jorio, J. Lumin., 2022, 246, 118843 CrossRef CAS.
- M. H. M. Abdelrehman, R. E. Kroon, A. Yousif, H. A. A. S. Ahmed and H. C. Swart, J. Alloys Compd., 2022, 902, 163856 CrossRef CAS.
- M. Toma, O. Selyshchev, Y. Havryliuk, A. Pop and D. R. T. Zahn, Photochem, 2022, 2, 515–527 CrossRef CAS.
- S. R. Calderon, Mater. Lett., 2022, 315, 131988 CrossRef.
- S. Bhatia, N. Verma and R. K. Bedi, Opt. Mater., 2016, 62, 392–398 CrossRef CAS.
- S. Farhat, M. Rekaby and R. Awad, J. Supercond. Novel Magn., 2018, 31, 3051–3061 CrossRef CAS.
- N. T. Hien, Y. Y. Yu, K. C. Park, N. X. Ca, T. T. K. Chi, B. T. T. Hien, L. D. Thanh, P. V. Do, P. M. Tan and P. T. T. Ha, J. Phys. Chem. Solid., 2021, 148, 109729 CrossRef CAS.
- H. Chemingui, J. C. Mzalia, T. Missaouia, M. Konyarc, M. Smiria, H. C. Yatmaze and A. Hafiane, Desalin. Water Treat., 2021, 209, 402–413 CrossRef.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- A. Kocakusakoglu, M. Daglar, M. Konyar, H. C. Yatmaz and K. Öztürk, J. Eur. Ceram. Soc., 2015, 35, 2845–2853 CrossRef CAS.
- N. X. Ca, N. D. Vinh, S. Bharti, P. M. Tan, N. T. Hien, V. X. Hoa, Y. Peng and P. V. Do, J. Alloys Compd., 2021, 883, 160764 CrossRef CAS.
- R. Viswanath, H. S. B. Naika, G. S. Y. Kumar, P. N. P. Kumar, K. N. Harisha, M. C. Prabhakara and R. Praveen, Appl. Surf. Sci., 2014, 301, 126 CrossRef CAS.
- H. M. Chen, X. C. Liu, S. Y. Zhuo, Z. Xiong, R. W. Zhou, F. Li and E. W. Shi, AIP Adv., 2014, 4, 047121 CrossRef.
- S. Senapati and K. K. Nanda, ACS Appl. Mater. Interfaces, 2017, 9, 16305–16312 CrossRef CAS PubMed.
- P. Kumar, V. Sharma, A. Sarwa, A. Kumar, S. Sharma, R. Goyal, K. Sachdev, S. Annapoorni, K. Asokan and D. Kanjilal, RSC Adv., 2016, 6, 89242–89249 RSC.
- K. Parmod, K. M. Hitendra and K. Asokan, Europhys. Lett., 2015, 110, 67006 CrossRef.
- V. P. Tuyen, V. X. Quang, N. M. Khaidukov, L. D. Thanh, N. X. Ca, N. V. Hao, N. V. Nghia and P. V. Do, Opt. Mater., 2020, 106, 109939 CrossRef CAS.
- V. X. Quang, P. V. Do, N. X. Ca, L. D. Thanh, V. P. Tuyen, P. M. Tan, V. X. Hoa and N. T. Hien, J. Lumin., 2020, 221, 117039 CrossRef CAS.
- B. R. Judd, Phys. Rev., 1962, 127, 750 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511 CrossRef CAS.
- W. L. Bond, J. Appl. Phys., 1965, 36, 1674–1677 CrossRef CAS.
- K. A. Gschneidner and L. R. Eyring, Handbook on the Physics and Chemistry of Rare Earths, Elsevier, 1998, vol. 25, ISBN: 978-0-444-82871-2 Search PubMed.
- C. M. Reddy, G. R. Dillip and B. D. P. Raju, J. Phys. Chem. Solid., 2011, 72, 1336–1441 Search PubMed.
- M. Liao, L. Hu, Z. Duan, L. Zhang and L. Wen, Appl. Phys. B, 2006, 86, 83–89 CrossRef.
- M. Hamzaoui, M. T. Soltani, M. Baazouzi, B. Tioua, Z. G. Ivanova, R. Lebullenger, M. Poulain and J. Zavadil, Phys. Status Solidi B, 2012, 249, 2213–2221 CrossRef CAS.
- T. Wei, F. Chen, Y. Tian and S. Xu, J. Quant. Spectrosc. Radiat. Transfer, 2014, 133, 663–669 CrossRef CAS.
- D. Rajesh, Y. C. Ratnakaram and A. Balakrishna, J. Alloys Compd., 2013, 563, 22–27 CrossRef CAS.
- A. Langar, C. Bouzidi, H. Elhouichet and M. Ferid, J. Lumin., 2014, 148, 249–255 CrossRef CAS.
- Y. Tian, R. Xu, L. Hu and J. Zhang, Opt. Mater., 2011, 34, 308 CrossRef CAS.
- I. Jlassi, H. Elhouichet, M. Ferid and C. Barthou, J. Lumin., 2010, 130, 2394–2401 CrossRef CAS.
- H. T. Van, N. D. Vinh, P. M. Tan, U. T. D. Thuy, N. X. Ca and N. T. Hien, Opt. Mater., 2019, 97, 109392 CrossRef CAS.
- N. X. Ca, N. D. Vinh, P. V. Do, N. T. Hien, V. X. Hoa and P. M. Tan, Phys. Chem. Chem. Phys., 2021, 23, 15257 RSC.
- P. V. Do, T. Ngoc, N. X. Ca, L. D. Thanh, P. T. T. Nga, T. T. C. Thuy and N. V. Nghia, J. Lumin., 2021, 229, 117660 CrossRef CAS.
- N. X. Ca, H. T. Van, P. V. Do, L. D. Thanh, P. M. Tan, N. X. Truong, V. T. K Oanh, N. T. Binh and N. T. Hien, RSC Adv., 2020, 10, 25618–25628 RSC.
- N. X. Ca, N. T. Hien, P. N. Loan, P. M. Tan, U. T. D. Thuy, T. L. Phan and Q. B. Nguyen, J. Electron. Mater., 2019, 48, 2593–2599 CrossRef CAS.
- K. Linganna, K. Suresh, S. Ju, W. T. Han, C. K. Jayasankar and V. Venkatramu, Mater. Express, 2015, 5, 1692 Search PubMed.
- V. B. Sreedhar, N. Vijaya, D. Ramachari and C. K. Jayasankar, J. Mol. Struct., 2017, 1130, 1001–1008 CrossRef CAS.
- P. V. Do, V. P. Tuyen, V. X. Quang, N. T. Thanh, V. T. T. Ha, N. M. Khaidukov, Y. Lee and B. T. Huy, J. Alloys Compd., 2012, 520, 262–265 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
N. T. Hien
*a,
N. T. Hien a,
Xingxiang Fanbc,
P. V. Do
a,
Xingxiang Fanbc,
P. V. Do d,
V. H. Yene,
P. V. Haof,
L. K. Quynh
d,
V. H. Yene,
P. V. Haof,
L. K. Quynh f,
T. T. T. Huong
f,
T. T. T. Huong g and
V. X. Quang*hi
g and
V. X. Quang*hi
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 95%), TOP (tri-n-octylphosphine–C24H51OP 97%), erbium acetate–(CH3CO2)3Er·xH2O (99.9%), isopropanol (70%), and toluene (99.8%) were purchased from Sigma–Aldrich.
CH2, 95%), TOP (tri-n-octylphosphine–C24H51OP 97%), erbium acetate–(CH3CO2)3Er·xH2O (99.9%), isopropanol (70%), and toluene (99.8%) were purchased from Sigma–Aldrich.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 7 min to remove supernatant remnants. Sediments were collected and carefully preserved for further measurements. The samples ZnO, ZnO: 1 mol% Er, ZnO: 2 mol% Er, and ZnO: 4 mol% Er are denoted as ZE0, ZE1, ZE2, and ZE4, respectively.
000 rpm for 7 min to remove supernatant remnants. Sediments were collected and carefully preserved for further measurements. The samples ZnO, ZnO: 1 mol% Er, ZnO: 2 mol% Er, and ZnO: 4 mol% Er are denoted as ZE0, ZE1, ZE2, and ZE4, respectively.
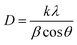
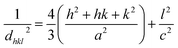
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The effective crystallite strain in the nanostructures was determined using the Stokes–Wilson equation:24
θ. The effective crystallite strain in the nanostructures was determined using the Stokes–Wilson equation:24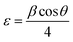

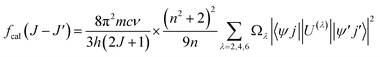
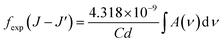
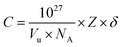
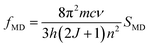
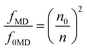
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246
246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516
516![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385
385![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349
349![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157
157![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040
040![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 222
222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727
727![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974
974![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472
472