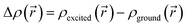Open Access Article
Open Access ArticleMetallo-dithiaporphyrin pigments for bulk-heterojunction solar cell applications: ab initio investigation of structural and optoelectronic properties†
Mohamed Yassine Dogguiab,
Mohamed Oussama Zouaghia,
Gilles Frapper b,
Frédéric Guegan
b,
Frédéric Guegan b and
Youssef Arfaoui
b and
Youssef Arfaoui *a
*a
aLaboratory of Characterizations, Applications & Modeling of Materials (LR18ES08), Department of Chemistry, Faculty of Sciences, University of Tunis El Manar, 2092 Tunis, Tunisia. E-mail: Youssef.arfaoui@fst.utm.tn
bIC2MP UMR 7285, Université de Poitiers – CNRS, 4, Rue Michel Brunet TSA 51106–86073 Cedex 9, Poitiers, France
First published on 20th November 2023
Abstract
Metallo-dithiaporphyrin small molecules have been designed by substituting Ru(II) with various transition metals at the same oxidation state (M = Mn, Fe, Ni, Cu) as donor materials for Bulk Heterojunction Organic Solar Cells (BHJ-OSCs). Density functional theory (DFT) and time-dependent DFT (TD-DFT) have been used to study the optoelectronic properties of metallo-dithiaporphyrin at various functionals and basis sets. We discovered that the open-circuit voltage (VOC) value increases when Ru(II) in Ru(S2TTP)Cl2 (S2TTP = tetra-p-tolyldithiaporphyrin) is substituted. In addition, the light harvesting efficiency (LHE) of nickel, manganese, and iron complexes was found to be similar to that of ruthenium, and the iron complex furthermore presented a comparable charge transfer in the excited state corresponding to the Q-band, compared to Ru(S2TTP)Cl2. Hence M(S2TTP)Cl2 (M = Mn, Fe, Ni) appear to be potential low cost candidate donor molecules within a bulk heterojunction solar cell. We further propose suitable engineered acceptor pigments, fitted to provide a good overall solar cell efficiency.
Introduction
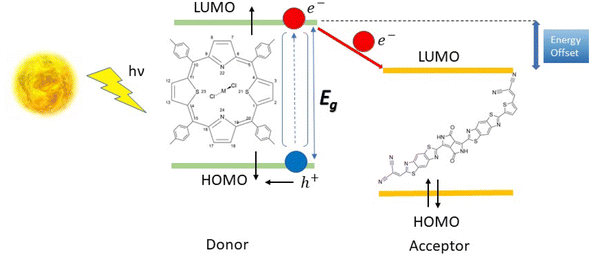
Nowadays, the most commonly used photovoltaic solar cells are made of mineral semiconductors like silicon. These cells have energy conversion efficiencies of up to 10% for amorphous silicon and 26% for crystalline silicon.1–3 However, their heavy and brittle nature makes installation expensive, and the energy required to purify and crystallize them increases their energy payback time, reducing their energy return on investment. Thus, it is necessary to find alternative materials that are more cost-effective and energy-efficient.Organic molecules-based photovoltaic cells offer greater flexibility to optimize their opto-electronic properties. Small molecule Heterojunction-Organic Solar Cells (SMH-OSCs), which consist of donor and acceptor molecules in separate phases but in close contact with the solid semiconductor phases, are particularly interesting.4–7 The efficiency of these cells depends on various parameters, including the energy gap (ΔεL–H), oscillator strength (f), and open-circuit voltage (VOC) of the donor–acceptor pair, which can be modified through chemical engineering techniques.
To improve the efficiency of the donor–acceptor pair, the donor must have a strong absorption band in the visible range and its chemical potential in the first excited state should be higher than that of the acceptor. This ensures that the electron transfer from donor to acceptor is favourable. In terms of the frozen molecular orbital framework, this can be stated as the acceptor's lowest unoccupied molecular orbital (LUMO) energy being lower than that of the donor for a favourable electron transfer (Scheme 1).
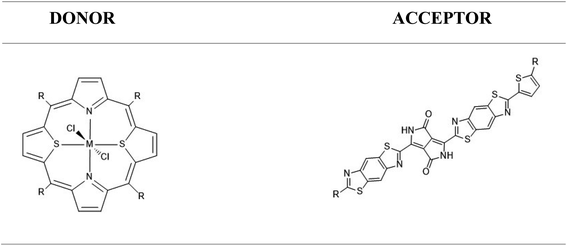
Porphyrins and their related coordination complexes are often brightly coloured and have strong UV-visible absorptions, which make them potential candidates for use in organic solar cells. Previous studies have shown that ruthenium-based dithiaporphyrin complexes can act as efficient donors in organic solar cells.8–11 However, the scarcity and high cost of ruthenium limit its application in solar cells.12 The synthesis of heteroporphyrins, especially dithiaporphyrins, has been widely studied,13–18 and these studies revealed the difficulty of inserting a metal within the molecule because of its ring size, until a recent study of the ruthenium-based dithiaporphyrin complex was conducted by Hang et al.19 The substitution of ruthenium by cheaper and more abundant metals appears desirable, but the aforementioned experimental difficulties in the complexation of dithiaporphyrins may be a strong limitation to their study. With this in mind, we thus considered conducting a theoretical preliminary work, studying first whether the proposed metal substitution at Ru(S2TTP)Cl2 would affect the donor properties of the complex, and second whether a suitable acceptor molecule could be proposed to afford a SMH-OSC.
Our main focus was on transition metals, and iron was our initial choice because it is part of the same group as ruthenium. Thanks to this identical valence configuration, it is more likely to form a stable complex like that of the Ru.19 We also considered other elements from the fourth period, based on their cost and natural abundance. As a result, the metals Ni, Mn and Cu were selected.‡20
In a first part, we calibrated our theoretical methodology against experimental data obtained for Ru(S2TTP)Cl2. We then discussed the structural parameters of all complexes (sketched in Scheme 2) and their optical properties, among which their computed UV-visible spectra and light harvesting efficiency (LHE). Then, a charge transfer (CT) study gave us more visibility into the nature of the CT and its orientation within the organometallic pigment.
Finally, we studied a promising acceptor material derived from (poly{3,6-bis(5-hexyldecyl-2thenyl)-2,5-dihydro-2,5-di(alkyl)pyrrolo[3,4]pyrrolo-1,4-dionethiazole}) (PDPP2TzT) which was synthesized by Janssen and co-workers.21,22 PDPP2TzT is a very good candidate as an acceptor material thanks to its low energy frontier molecular orbitals (−5.63 eV and −4.00 eV as computed at the B3LYP/DEF2-TZVP level of theory), broad infrared absorption (300–900 nm).
Methodology and methods
All geometries were optimized using density functional theory DFT23,24 with several exchange–correlation functionals: B3LYP,25 CAM-B3LYP,26 ωB97X-D,27 M05,28 and M05-2X29 and various combinations of basis sets and pseudopotentials: either 6-311G(d)30,31 for dithiaporphyrin and LANL2DZ32 or LANL2TZ33 for the metals, or a non-mixed basis-set DEF2-TZVP for all atoms (with appropriate pseudopotentials).34 All used basis-sets and pseudopotentials were recovered from the Basis Set Exchange library.35 All DFT calculations were performed with the Gaussian A16 program package.36The performance of an organic chromophore is affected by the energy barrier for the charge injection process. Ionization potential (IP), electron affinity (EA), and reorganization energy (λ) are the key parameters that determine the energy barrier for the charge injection process of organic molecules.37
Electron affinities and vertical ionization potentials have been computed by using eqn (1) and (2).38
| EA = E0 − E− | (1) |
| IP = E+ − E0 | (2) |
The HOMO and LUMO analyses are carried out to explain the molecular characteristics of molecules. ΔεL–H is defined as the electronic gap energy and it is given by the eqn (3)
| ΔεL–H = εLUMO − εHOMO | (3) |
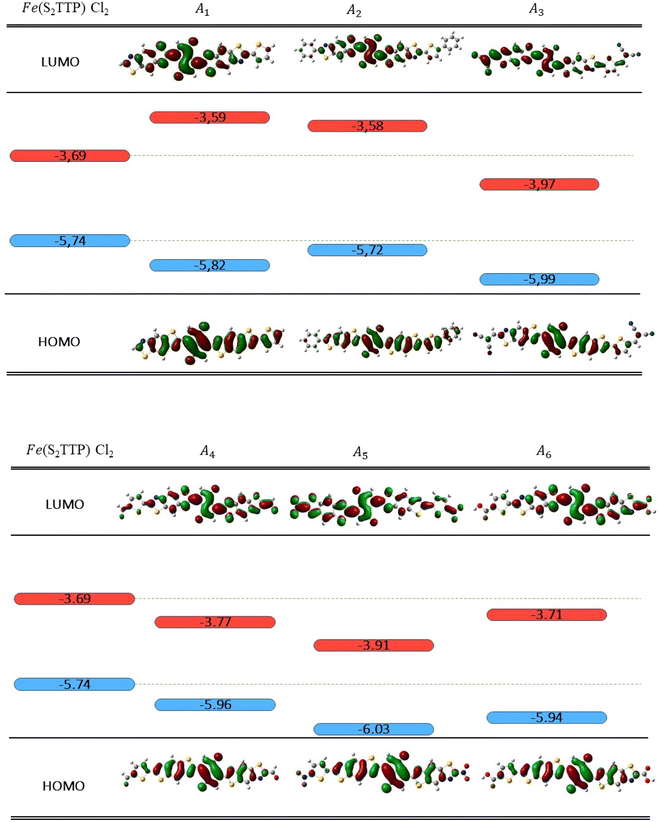
To more thoroughly investigate the performance of the organic pigment and acceptor, other key parameters should be studied, namely the open-circuit voltage VOCwhich has been calculated from the following expression:39
| VOC = |εDHOMO| − |εALUMO| − 0.3 | (4) |
In addition, a favourable energy alignment of HOMO–LUMO orbitals is required (conditions (5) and (6)):40
| εALUMO < εDLUMO | (5) |
| εAHOMO < εDHOMO | (6) |
Condition (5) describes the injection process, as expressed by the free enthalpy of injection (ΔGinj) as follows:
| ΔGinj = εALUMO − εDLUMO | (7) |
The molecules which exhibit the smallest values of reorganization energies show large mobilities of charge transfer between the donor and acceptor units of devices.37 The reorganization energies for electrons and holes are determined as follows:
(i) Electron reorganization energy:
| λe = [E0− − E−] + [E0− − E0] | (8) |
(ii) Hole reorganization energy:
| λh = [E0+ − E+] + [E0+ − E0] | (9) |
Using the ground state optimized geometries, the 35 lowest electronic excitation energies, their vertical transition energy (ΔE0–0) and oscillator strengths (f) were computed using the TD-DFT method,42–44 again with B3LYP and CAM-B3LYP functionals and the DEF2-TZVP basis set. The optical UV-visible absorption spectra were simulated by considering Gaussian functions and a FWHM of 0.1 eV. Besides, Natural Transition Orbital analysis (NTO) was carried out in order to investigate the most important transition for each complex, which allows to study each transition individually and to characterize the associated electron density distortion in a very compact manner (pairs of donor and acceptor orbitals).45
Excited state charge transfer (ESCT)
For push–pull systems like metallo-porphyrins, the UV absorption spectra are dominated by charge transfer excitations and the latter have been analysed in more detail.46Each transition is characterized by excitation energy, between the ground (0) and nth excited states, (ΔEopt = ΔE0n = En − E0), and is associated to a transition dipole moment:
μ0n = 0|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |n |n
| (10) |
Radiative processes are governed by the oscillator strength of the transition, which is related to the transition dipole moment:
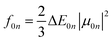 | (11) |
The CT character of the excitations can be determined from an analysis of the difference of electronic density between the ground and excited states, 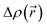 , following the procedure described by Le Bahers et al.46 Using this method, the distance between the barycentre of the negative and positive values of
, following the procedure described by Le Bahers et al.46 Using this method, the distance between the barycentre of the negative and positive values of 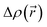 defines the charge-transfer distance (dCT), their integration over the whole space gives the amount of charge transferred (qCT), while their product gives the CT dipole moment,
defines the charge-transfer distance (dCT), their integration over the whole space gives the amount of charge transferred (qCT), while their product gives the CT dipole moment,
| ΔμCT = qCT × dCT | (12) |
It may however be noted that this approach is expected to fail in the case of symmetric molecules, since barycentres of the electron density depletion and relocation areas will collapse. This issue was recently acknowledged by Ciofini et al., who proposed an alternative charge transfer index, ADCT. The latter is based on the computation of a partial charge-transfer distance, restricted on the subset of atoms that constitutes the smallest asymmetric fragment of the molecule. By this symmetry restriction and a careful design of a weight function to piece back together all molecular fragments, it is then possible to evaluate a molecular symmetry-adequate charge distance.47
Results and discussion
Methodological calibration
We initially looked for an appropriate level of theory for our study. To do so, we first evaluated how efficiently the selected functionals could reproduce the geometry of the starting complex Ru(S2TTP)Cl2. We provide in Table S1 in ESI† the most relevant geometrical parameters for all considered functionals (B3LYP, CAM-B3LYP, M05, M05-2X, ωB97xD), used in conjunction with the def2-TZVP basis set (and effective core potential for Ru), as well as the experimental values obtained from X-ray diffraction. In line with experimental data, a singlet multiplicity was considered for Ru(S2TTP)Cl2.As one may note, all functionals offer a quite comparable reproduction of the experimental structure, small deviations being observed. B3LYP offering the shortest computation time, we thus opted for this functional for the second part of the calibration.
In the second stage, we then evaluated the impact of the basis set, again against the reproduction of the experimental structure. Three basis sets and pseudopotentials were considered here:
- 6-311G(d) for all atoms of the dithiaporphyrin and a double-zeta quality basis set and associated pseudopotential for the Ru atom (LanL2DZ);
- 6-311G(d) for all atoms of the dithiaporphyrin and a triple-zeta quality basis set and associated pseudopotential for the Ru atom (LanL2TZ);
- A triple-zeta basis sets with polarisation functions and adapted pseudopotential for the Ru atom (def2-TZVP).
We report in Table S2 in ESI† the same geometrical parameters as previously. Here again a limited impact of the level of theory is observed, although quite expectedly the deviations are larger when the basis set on Ru is only of double-zeta quality. A more complete analysis on all geometrical parameters reveals that root-mean-square deviations (RMSD) are in all cases quite low, but the best agreement to the experimental structure is reported for the “homogeneous” basis set def2-tzvp (RMSD of 0.03 against 0.07 for the split 6-311G(d)/LanL2DZ or LanL2TZ) (Fig. 1).
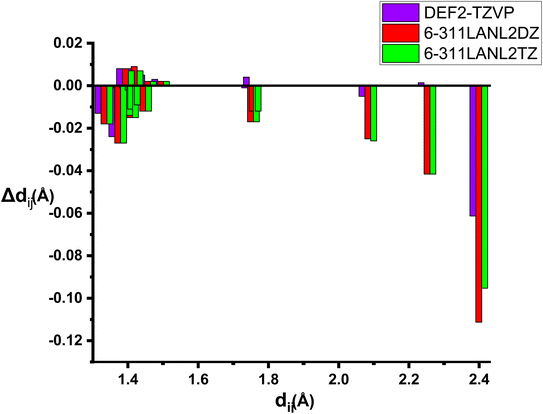 | ||
| Fig. 1 Bond distances deviations forRu(S2TTP) Cl2 with several basis-sets with B3LYP functional Δdij = dij (experimental) − dij (theoretical). | ||
At this stage, B3LYP/def2-TZVP thus appears to be a quite efficient level of theory for this study. We then finally evaluated its efficiency in the reproduction of the absorption spectrum of Ru(S2TTP)Cl2. We report in Fig. 2 the spectrum we obtain at the TD-B3LYP/def2-TZVP level of theory, in vacuum (for the first 35 excited states). We also report in inset the experimental electronic absorption spectrum of Ru(S2TTP)Cl2, measured in a CH2Cl2 solution at room temperature by Hung et al.19 As one may note, computed data meets the experimental one, up to a slight upshift. Indeed, we retrieve a near-IR band with a moderate absorption intensity (maximum at 782 nm against 810 nm experimentally), a low absorption massif around 600 nm (peaks at 586 and 602 nm, experimental peaks at 563 and 594 nm), and a high-intensity Soret band from 472 to 511 nm.
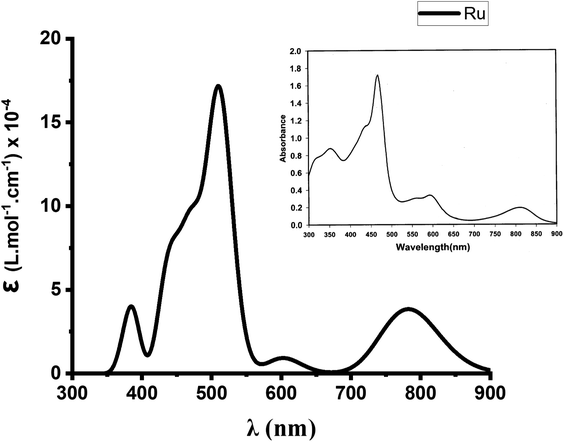 | ||
| Fig. 2 Experimental (inset) and calculated UV-visible spectra (35 excited states, Gaussian broadening) of Ru(S2TTP)Cl2 at the TD-B3LYP/DEF2-TZVP level. UV-vis peak half-width at half height 0.1 eV. | ||
Overall, (TD-DFT)B3LYP/def2-TZVP seems to confirm as an adequate level of theory for our study.
Effect of the nature of the transition metals on the geometrical and electronic structures
The level of theory being fixed, we then optimized the geometries of the different complexes M(S2TTP)Cl2 (Scheme 2) (M(II) = Mn, Fe, Ni, Cu). For each complex, we have considered different spin multiplicities. When considering the Mn(II) complex, which forms a quasi-octahedral geometry, it is anticipated that the valence configuration will be 4s03d5, resulting in three distinct electronic configurations determined by the octahedral crystal field: (t2g)3(eg)2, (t2g)4(eg)1, (t2g)5(eg)0, hence three spin multiplicities can be proposed following Hund's rule (sextet, quartet or doublet).The multiplicity associated with the lowest ground state energy is considered for the next calculations. The geometrical parameters such as bond lengths and dihedral angles characterizing the distortion of the thiophene as well as the energy of the ground state for each multiplicity are summarized in Table 1. Similar information for Ru(S2TTP)Cl2 are also given for the sake of comparison.
| M | Parameter | Experimental | DFT | ||
|---|---|---|---|---|---|
| Ru19 | 2S + 1 | — | 1 | 3 | 5 |
| Ru–N | 2.082 | 2.082 | 2.085 | 2.113 | |
| Ru–S | 2.251 | 2.247 | 2.280 | 2.296 | |
| Ru–Cl | 2.399 | 2.458 | 2.396 | 2.394 | |
| ΔE (kcal mol−1) | — | 0 3.5 | 38.5 | ||
| Dihedral angle of thiophen ring | 12.7 | 12.4 | 14.5 | 10.0 | |
| Mn | 2S + 1 | — | 4 | 6 | |
| Mn–N | — | 2.037 | 2.147 | ||
| Mn–S | — | 2.454 | 2.386 | ||
| Mn–Cl | — | 2.364 | 2.591 | ||
| ΔE (kcal mol−1) | — | 16.1 | 0 | ||
| Dihedral angle of thiophen ring | — | 11.7 | 12.6 | ||
| Fe | 2S + 1 | — | 1 | 3 | 5 |
| Fe–N | — | 2.061 | 2.081 | 2.143 | |
| Fe–S | — | 2.181 | 2.184 | 2.335 | |
| Fe–Cl | — | 2.407 | 2.656 | 2.506 | |
| ΔE (kcal mol−1) | — | 9.6 | 11.8 | 0 | |
| Dihedral angle of thiophen ring | — | 12.1 | 12.3 | 11.3 | |
| Ni | 2S + 1 | — | 1 | 3 | |
| Ni–N | — | 2.002 | 2.114 | ||
| Ni–S | — | 2.362 | 2.322 | ||
| Ni–Cl | — | 2.321 | 2.552 | ||
| ΔE (kcal mol−1) | — | 22.2 | 0 | ||
| Dihedral angle of thiophen ring | — | 11.2 | 11.9 | ||
| Cu | 2S + 1 | — | 2 | ||
| Cu–N | — | 2.059 | |||
| Cu–S | — | 2.360 | |||
| Cu–Cl | — | 2.560 | |||
| ΔE (kcal mol−1) | — | — | |||
| Dihedral angle of thiophen ring | — | 11.8 | |||
It may be noted from Table 1 that coordination environments for all metal centres are expectedly similar; noticeably the dihedral angle in the dithiaporphyrin moiety is only marginally impacted by the nature of the metal. This angle being instrumental in the electronic delocalisation within the dithiaporphyrin and between the metal and the dithiaporphyrin,48 we may at this stage expect the optical properties of the M(S2TTP)Cl2 series will be quite comparable.
Additionally, we note that open-shell electronic configurations appear to become the most stable ones for the Mn–Ni series. This was quite expected (energy gaps tending to decrease when going up the periodic table, and the value for Ru being already low). Eventually, the spin multiplicities that relate to the most stable geometries are quintet for Fe, triplet for Ni, doublet for Cu and sextet for Mn.
We provide in Table 2 the computed frontier molecular orbital energies (distinguishing spin up and spin down electrons in the case of open-shell systems) for the M(S2TTP)Cl2 complexes and all considered acceptor molecules (vide infra).
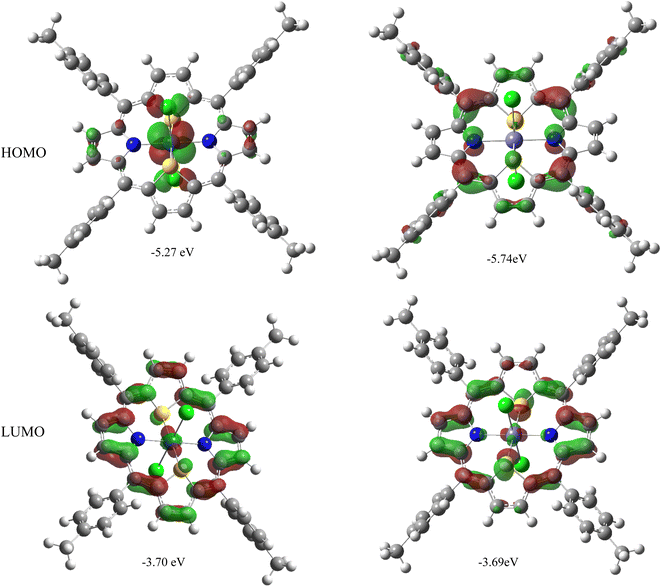
| M | 2S + 1 | εHOMO (eV) | εLUMO (eV) | ΔεL–H (eV) |
|---|---|---|---|---|
| Ru | 1 | −5.27 | −3.70 | 1.57 |
| Mn | 6 | α −5.59 | −3.50 | 2.09 |
| β −5.77 | −3.72 | 2.05 | ||
| Fe | 5 | α −5.75 | −3.45 | 2.30 |
| β −5.74 | −3.69 | 2.05 | ||
| Ni | 3 | α −5.80 | −3.54 | 2.27 |
| β −5.78 | −3.81 | 1.97 | ||
| Cu | 2 | α −5.78 | −3.54 | 2.24 |
| β −5.76 | −3.87 | 1.90 | ||
| A1 | 1 | −5.82 | −3.59 | 2.23 |
| A2 | 1 | −5.72 | −3.58 | 2.14 |
| A3 | 1 | −5.99 | −3.97 | 2.02 |
| A4 | 1 | −5.96 | −3.77 | 2.19 |
| A5 | 1 | −6.03 | −3.91 | 2.21 |
| A6 | 1 | −5.94 | −3.71 | 2.23 |
It may be noted that the electronic gap energies (defined here as the energy difference between the LUMO and HOMO) are larger in all M(S2TTP)Cl2 complexes (with M = Mn, Fe, Ni, Cu) than in Ru(S2TTP)Cl2, by approximately 0.5 eV. This effect is quite expected in the framework of the Hard and Soft Acids and Bases theory of Pearson:49 as one goes down the periodic table, chemical hardness (which can be approximated as the electronic gap energy)50 is expected to drop, as observed here. In fact, if we focus on the iron and ruthenium cases (which are isoelectronic), we observe the variation in the gap energy is seemingly largely due to the HOMO, since LUMOs are found at quite comparable energies. A closer look at these molecular orbitals (MOs), represented in Fig. 3, shows that the HOMOs of Ru and Fe complexes are different (π with no metal contribution in the case of Fe, 4d + π for the Ru complex), while the LUMOs are comparable (mostly π with a little contribution from the metal), explaining the observed trends.
Optical properties
In order to confirm their potential in a heterojunction solar cell, the optical parameters of M(S2TTP)Cl2 (M = Mn, Fe, Ni, and Cu) were then calculated at the TD-DFT level.We provide in Fig. 4 the calculated absorption spectra for each complex M(S2TTP)Cl2, at the most stable multiplicities and compared to that of Ru(S2TTP)Cl2.
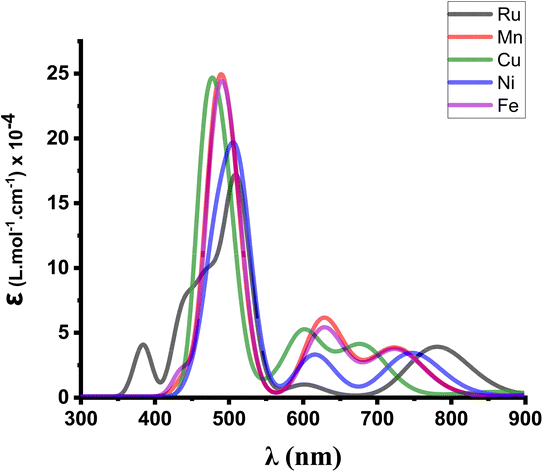 | ||
| Fig. 4 Modeled UV-visible absorption spectra of M(S2TTP)Cl2 (M = Mn, Fe, Ni, Cu, Ru) at the TD-B3LYP/DEF2-TZVP level. | ||
We notice that the Soret band around 500 nm is always present for all complexes and slightly shifts depending on the metal, which is expected since this transition is essentially a ligand-centred π–π* transition and thus is only weakly influenced by the coordination. We also report that all metal-complexes showed a higher molar absorption coefficient (ε) value compared to the Ru complex.
Encouraged by the efficient reproduction of the experimental spectrum for the ruthenium complex, we conducted Natural Transition Orbitals (NTO) analysis at the same level of theory in order to investigate electron contributions in excited states of the Soret band for each complex. The obtained results are summarized in Table 3. For Ru(S2TTP)Cl2 the principal excited state (ES9) that describes the Soret band (ε = 1.8 × 105 L mol−1 cm−1 and the highest oscillator strength for this complex) can be divided into two main electron density displacements (Scheme S1†). Both principally involve a reorganization of the π electron cloud (as expected for the Soret band), but additionally comprise a ligand-to-metal charge transfer (MLCT), with an electron transfer to a S/Ru and N/Ru antibonding accepting orbital (respectively accounting for 0.55 and 0.44 electrons). Similarly, Mn, Fe, Ni and Cu complexes also exhibit a ligand to metal charge transfer in addition to a delocalization within the dithiaporphyrin core.
| State number | λ (nm)/ΔE0–0 (eV) | Spin | Transition | Occupancy | f | LHE | |
|---|---|---|---|---|---|---|---|
| Ru | 9 | 511, 1/2, 43 | — | π → π* | 0.55 | 1,23 | 0.94 |
| +S → Ru | |||||||
| π → π* + (nN → dz2Ru) | 0.44 | ||||||
| Mn | 14 | 503.4/2.48 | α | π → π* + (N → Mn) | 1.09 | 1.00 | 0.9 |
| π → π* + (S → Mn) | 0.18 | ||||||
| β | π → π* + (Ni → S) | 0.50 | |||||
| π → π* (nN → dz2Ni, nS → dz2Ni) | 0.24 | ||||||
| 20 | 481.2/2.58 | α | π → π* + (N → Mn) | 1.13 | 1.26 | 0.95 | |
| π →π*+ (S→Mn) | 0.13 | ||||||
| β | π → π* + (N → Mn) | 0.6 | |||||
| π →π* + (S → Mn) | 0.12 | ||||||
| Fe | 18 | 504.9/2.46 | α | π → π* +(nN → dzFe) | 1.12 | 1.06 | 0.91 |
| π → π* | 0.20 | ||||||
| β | π → π* + (nS → dz2Fe) | 0.54 | |||||
| π → π* + (nN → dz2Fe) | 0.15 | ||||||
| 22 | 481.5/2.58 | α | π → π* | 1.08 | 1.24 | 0.94 | |
| π → π* + (nN → dz2Fe) | 0.14 | ||||||
| β | π → π*(nN → dz & Fe) | 0.64 | |||||
| π → π*(nS → dz2Fe) | 0.14 | ||||||
| Ni | 20 | 512.9/2.42 | α | π → π*+(nN → dz2Ni) | 0.96 | 1.22 | 0.94 |
| π → π* +(nS → d + z2Ni) | 0.32 | ||||||
| β | π → π*+ (Ni → S) | 0.50 | |||||
| π → π* (nN → dz2Ni, nS → dz2Ni) | 0.24 | ||||||
| 25 | 483.3/2.57 | α | π → π* +(N → Ni) | 0.78 | 0.78 | 0.84 | |
| π → π* +(S → Ni)/+(N → Ni) | 0.16 | ||||||
| β | π → π* +(S → Ni) | 0.73 | |||||
| π → π* + (N → Ni) | 0.27 | ||||||
| π → π*+ (S → Mn) | 0.13 | ||||||
| Cu | 24 | 496.0/2.5 | α | π → π* (nS → dz2Cu) | 0.67 | 1.04 | 0.91 |
| π → π* (nN → dz2Cu) | 0.16 | ||||||
| β | π → π* (nN → dz2Cu) | 0.97 | |||||
| π → π* (nS → dz2Cu) | 0.18 | ||||||
| 27 | 473.2/2.62 | α | π → π* (nN → dz2Cu) | 0.50 | 0.63 | 0.77 | |
| π → π* (Cu → S) | 0.4 | ||||||
| β | π → π* (nN → Cu, Cl → Cu, Cu → S) | 0.57 | |||||
| π → π*(N → Cu) | 0.40 | ||||||
| 29 | 468.6/2.65 | α | π → π*(Cl → Cu, N → Cu) | 0.56 | 0.76 | 0.82 | |
| π → π*(Por → Cu) | 0.31 | ||||||
| β | π → π* + (nN → dz2Cu) | 0.52 | |||||
| π → π*(nN → dz2Cu) | 0.48 |
The principal difference is the slightly higher oscilator strength obtained following the substitution of ruthenium by iron and manganese, (about +0.01 and +0.03, respectively), giving these new complexes comparable to slightly higher performance than the Ru complex. This small difference slightly improves the LHE value (Table 3). Ni and Cu show oscillator strength values very close to that of Ru and consequently close LHE values, which makes these metals potentially efficient in converting light into electrical energy at a lower cost. However, these optical properties resulting from TD-DFT are not sufficient to define which complex is the most efficient candidate for the design of a solar cell. A detailed CT character analysis should indeed be conducted to evaluate whether these complexes afford significant charge separation in the excited state. This can be achieved by computing the CT dipolar moment (eqn (13)).
Excited states CT analysis
In this part, we describe the special properties of charge transfer (CT) states. CTs are generally present in molecules in which electro-donating and electro-accepting moieties are electronically connected via a conjugated skeleton. Porphyrins can present a push–pull structure.51 In push–pull molecules, the most fundamental process is the intramolecular charge transfer (ICT), whereby electron density is transferred from the donor to the acceptor through a π-conjugated linker.52 Besides the highest LHE values, in order to assign a dye as efficient for PV applications, the excited states should present a large charge transfer, which can be evaluated by using the TD-DFT method.53 According to the data in Table 4, we have found that all M(S2TTP)Cl2 complexes display larger charge transfer in the Soret band than Ru(S2TTP)Cl2, as indicated by the qCT values. Among all complexes, Ni(S2TTP)Cl2 possesses the highest qCT value, which reveals large charge reorganization between the ground state (GS) and ES. Nevertheless, this alone is not sufficient to characterise efficient CT, as discussed by Le Bahers et al.46 In addition, one should study the electron density reorganization in space, in order to probe “how far are the electrons reshuffled”. This can in principle be analysed through the charge transfer distance dCT and/or the CT dipole momentum, but here an additional difficulty arises: because of the molecular symmetry, most excitations are expected to present very low values of dCT, even though locally the electron density movement in space can be quite large. Indeed, as can be seen in Table 4, almost all excitations present dCT values close to 0, while the electron density movements in Fig. 5 are quite significant.| Compound | 2S + 1 | Number of state | dCT | ΔμCT | qCT |
|---|---|---|---|---|---|
| Ru | 1 | 9 | 0.002 | 0.003 | 0.277 |
| Cu | 2 | 24 | 0.007 | 0.026 | 0.806 |
| 27 | 0.004 | 0.006 | 0.315 | ||
| 29 | 0.004 | 0.011 | 0.662 | ||
| Ni | 3 | 20 | 0.012 | 0.049 | 0.850 |
| 25 | 0.011 | 0.050 | 0.938 | ||
| Fe | 5 | 18 | 0.002 | 0.006 | 0.655 |
| 22 | 0.006 | 0.024 | 0.793 | ||
| Mn | 6 | 14 | 0.017 | 0.058 | 0.697 |
| 20 | 0.007 | 0.024 | 0.709 |
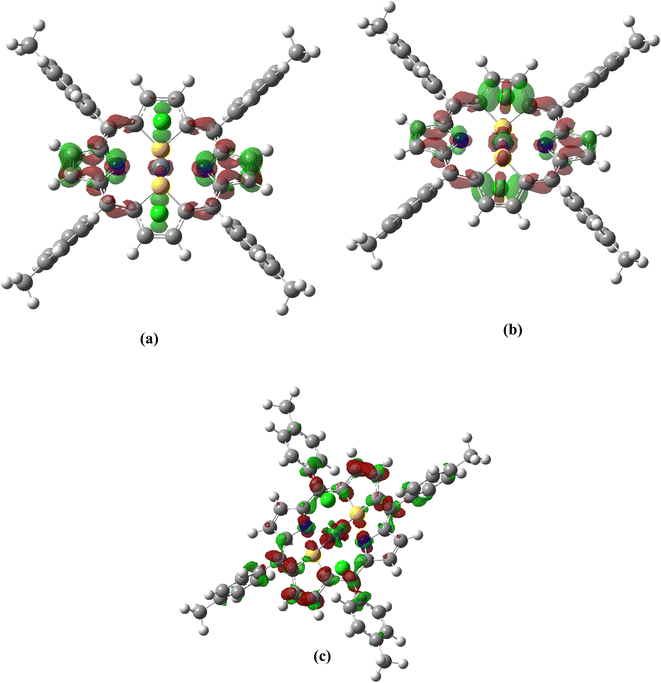
Using the generalized ADCT distance proposed by Ciofini et al.,47 we find more relevant charge transfer distances, as listed in Table 5.
| Complex | Excited state N° | ADCT (Å) |
|---|---|---|
| Ru | 9 | 6.3 |
| Fe | 18 | 4.8 |
| 22 | 4.2 | |
| Ni | 20 | 5.5 |
| 25 | 4.3 | |
| Mn | 14 | 4.7 |
| 20 | 4.1 | |
| Cu | 24 | 4.5 |
| 27 | 4.3 | |
| 29 | 4.2 |
The calculated ADCT values are consistent for all molecules. We find that, for ADCT values ranging from 4.1 to 4.5 Å, the electron density movements are indeed mainly localized on the central ring of dithiaporphyrin surrounding the metal (see Fig. 5 for the case of the Fe complex, see Scheme S1† for all complexes). For higher ADCT values, ranging from 4.6 to 6.3 Å, since the accepting NTOs are localized on the dithiaporphyrin ring as well as on the metal, the charge transfer distance increases. In the case of Ru(S2TPP)Cl2, contributions of the peripheral tolyl groups are also observed, which explain the additional extent of the charge transfer. Overall, all M(S2TTP)Cl2 complexes present strong charge transfer in the excited states associated with the Soret band, the largest values being observed in the case of the Ru derivative.
Study of acceptor tuning
As is well known, exciton excitation, separation, and transfer can be closely correlated with MO energies in the donor and acceptor, particularly with HOMO and LUMO energy levels.54 Schematically, after the initial excitation of the donor, considered to be in a closed-shell state, relaxation to the first singlet excited state is expected to occur (Kasha's rule). If we assume the MO diagram remains unperturbed by excitation (frozen orbital approximation), this singlet state is constructed by the promotion of one electron from the HOMO to the LUMO. To allow an electron transfer to the acceptor molecule, it is then desirable for the donor LUMO to be located higher in energy than the acceptor LUMO. As shown in Scheme 3, the LUMO of A1is too high in energy to allow the transfer of an electron.In order to tune the energy level of the acceptor's FMOs according to those of the donor, we substituted the hydrogen, located in the α position of the thiophene and thiazole of A1 by a phenyl (A2), a dicyanovinyl (A3), a carbonyl (A4), a nitro (A5) and a carboxylic acid (A6) group.
The substitution of R with a phenyl group A2 affects the delocalization. As seen in Scheme 3, the LUMO is mostly delocalized on the central part of the molecule, but not on the site of the modification, leading to a very slight stabilization of the LUMO at A2 (0.01 eV). This leads us to exclude A1 and A2 as potential acceptors in this work, since their LUMOs remain too high in energy.
On the other hand, the addition of the dicyanovinyl group (A3),which is a strongly attractive group, expectedly stabilizes both LUMO and HOMO, pushing the LUMO at a lower energy than that of Fe(S2TTP)Cl2 and all other donor complexes. The same effect is observed for A5 where a nitro group is added, which makes these two acceptors compatible with all the studied donors. In addition, we notice that the addition of an aldehyde group (A4) stabilizes the LUMO, which makes it compatible with Ru, Fe and Mn complexes, but not enough to form a heterojunction with Cu(S2TTP)Cl2 and Ni(S2TTP). Moreover, the low value of ΔGinj observed for the A4/Fe pair considerably decreases the efficiency of the cell since it is lower than 0.3 eV.54
Lastly, the addition of a carboxylic acid group stabilizes the LUMO of the acceptor ((A6) but not enough to allow an efficient injection of the electron with any of the selected donors.
In this evaluative part, we have calculated the hole and electron reorganization energies (λh and λe) for each M(S2TTP)Cl2 with the aim of investigating the hole and electron mobilities and the electron recombination after the injection (Table 6). We have found that Ni and Ru show the lowest λe and λh values of all donors. According to the Marcus theory55,56 smaller reorganization energy corresponds to a higher charge hopping rate constant, and hence higher charge mobility. Besides, λe of the Fe and Cu complexes is relatively high, while their hole reorganization energy, especially for iron, is acceptable with a value of 0.35 eV. Based on these results, we can conclude that Ru and Ni complexes are potential higher mobility materials compared to Fe, Cu and Mn complexes.
| λe | λh | |
|---|---|---|
| Cu | 1.08 | 0.78 |
| Ni | 0.28 | 0.26 |
| Fe | 0.94 | 0.35 |
| Mn | 0.35 | 1.18 |
| Ru | 0.28 | 0.21 |
We also calculated the open circuit voltage (Voc) values and ΔGinj for each compatible donor/acceptor pair (based on HOMO/LUMO energy levels) and the obtained results are summarized in Table 7. We notice at first sight that all complexes have a higher Voc value than Ru which makes recombination phenomenon more likely to be present in the latter. This result is a good confirmation that the substitution of Ru by other metals may be efficient. The highest Voc are those of the couples Fe(S2TTP)Cl2/A6,Ru(S2TTP)Cl2/A6, Mn(S2TTP)Cl2/A4, Fe(S2TTP)Cl2/A4and Ni(S2TTP)Cl2/A5, Cu(S2TTP)Cl2/A5. Nevertheless, their injection is very low (lower than 0.3 eV) which makes the injection phenomenon more difficult to be present within the bulk heterojunction solar cell. Assuming that an energy gap of 0.3 eV between the LUMO of the acceptor and the LUMO of the donor is sufficient for efficient charge separation,54 we conclude that the most promising pairs found in this part are Mn(S2TTP)Cl2/A3; Ni(S2TTP)Cl2/A3and Ru(S2TTP)Cl2/A3. Fe(S2TTP)Cl2/A3is also promising considering its high Voc value, although ΔGinj is relatively weak.
| A3 | A4 | A5 | A6 | |||||
|---|---|---|---|---|---|---|---|---|
| Voc | ΔGinj | Voc | ΔGinj | Voc | ΔGinj | Voc | ΔGinj | |
| Ru | 1.3 | −0.30 | −1.5 | −0.30 | −1.4 | −0.20 | −1.6 | −0.01 |
| Fe | 1.8 | −0.20 | −2.0 | −0.10 | −1.8 | −0.20 | −2.0 | −0.03 |
| Ni | 1.8 | −0.30 | — | — | −1.9 | −0.10 | — | — |
| Cu | 1.8 | −0.10 | — | — | −1.9 | −0.04 | — | — |
| Mn | 1.8 | −0.30 | −2.0 | −0.05 | −1.9 | −0.20 | — | — |
Conclusion
In this work, we investigated the impact of substituting ruthenium with other transition metals in the M(S2TTP)Cl2 complex, and characterized the resulting metallo-dithaporphyrin series in terms of their optical and electronic properties. Using density functional theory and time-dependent density functional calculations, we determined the most suitable functional and basis-set for our study. All modeled dithiaporphyrin complexes strongly absorb light in the visible range. Furthermore, we found that Fe and Mn have slightly higher oscillator strengths than Ru, which leads to an increase in the light harvesting efficiency (LHE) value.In addition to these findings, we calculated the electron reorganization energy λe, hole reorganization energy λh, free energy change of injection ΔGinj and open-circuit voltage VOC for each complex. Our results showed that Mn(S2TTP)Cl2/A3; Ni(S2TTP)Cl2/A3 pairs are the most effective, due to their high LHE value and optimal energy levels of the acceptor's HOMO/LUMO.
Overall, our study provides insights into the design of more efficient donor/acceptor pairs and paves the way for further investigations into the electron injection process in dithiaporphyrin complexes combined with semiconductor surfaces. In this study, we have demonstrated that small molecules based on dithiaporphyrin are potential candidates for applications as donors in BHJ-OSCs and substitution of Ru by cheaper metals improves productivity and lowers cell expenses. Besides, the effective strategy for designing efficient and effective next-generation BHJ-OSC devices is by modifying acceptor units, this is why acceptor A3 molecule is highly recommended for experimentalists to develop highly efficient solar cell devices. However, the challenge that is presented is to synthesize these complexes experimentally in order to confirm their kinetic and thermodynamic stabilities and evaluate their performance within solar cells offering new opportunities for designing efficient and sustainable energy conversion systems.
Conflicts of interest
There are no conflicts to declare.References
- M. A. Green, Y. Hishikawa, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger and A. W. Y. Ho-Baillie, Solar Cell Efficiency Tables (Version 51), Prog. Photovolt.: Res. Appl., 2018, 26(1), 3–12, DOI:10.1002/pip.2978
.
- M. A. Green, Y. Hishikawa, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger, M. Yoshita and A. W. Y. Ho-Baillie, Solar Cell Efficiency Tables (Version 53), Prog. Photovolt.: Res. Appl., 2019, 27(1), 3–12, DOI:10.1002/pip.3102
.
- M. A. Green, E. D. Dunlop, D. H. Levi, J. Hohl-Ebinger, M. Yoshita and A. W. Y. Ho-Baillie, Solar Cell Efficiency Tables (Version 54), Prog. Photovolt.: Res. Appl., 2019, 27(7), 565–575, DOI:10.1002/pip.3171
.
- J. Min, Y. N. Luponosov, A. Gerl, M. S. Polinskaya, S. M. Peregudova, P. V. Dmitryakov, A. V. Bakirov, M. A. Shcherbina, S. N. Chvalun, S. Grigorian, N. Kaush-Busies, S. A. Ponomarenko, T. Ameri and C. J. Brabec, Alkyl Chain Engineering of Solution-Processable Star-Shaped Molecules for High-Performance Organic Solar Cells, Adv. Energy Mater., 2014, 4(5), 1301234, DOI:10.1002/aenm.201301234
.
- A. Leliège, P. Blanchard, T. Rousseau and J. Roncali, Triphenylamine/Tetracyanobutadiene-Based D-A-D π-Conjugated Systems as Molecular Donors for Organic Solar Cells, Org. Lett., 2011, 13(12), 3098–3101, DOI:10.1021/ol201002j
.
- Y. Liu, Y. Yang (Michael), C.-C. Chen, Q. Chen, L. Dou, Z. Hong, G. Li and Y. Yang, Solution-Processed Small Molecules Using Different Electron Linkers for High-Performance Solar Cells, Adv. Mater., 2013, 25(33), 4657–4662, DOI:10.1002/adma.201301716
.
- Solution-Processable Organic Molecule Photovoltaic Materials with Bithienyl-benzodithiophene Central Unit and Indenedione End Groups | Chemistry of Materials, https://pubs.acs.org/doi/full/10.1021/cm400782q?casa_token=lasEAq810owAAAAA%3ASZPMlUXNsYFmd_AqKFB7vg9jLueGz-OD9Ihjn12dFge-YAc0F9VamQE6nN0o_Jwaoxbw3b90FrfWu5dy, (accessed 2022-08-04) Search PubMed.
- R. W. Wagner, T. E. Johnson and J. S. Lindsey, Soluble Synthetic Multiporphyrin Arrays. 1. Modular Design and Synthesis, J. Am. Chem. Soc., 1996, 118(45), 11166–11180, DOI:10.1021/ja961611n
.
- D.-L. Jiang and T. Aida, Morphology-Dependent Photochemical Events in Aryl Ether Dendrimer Porphyrins: Cooperation of Dendron Subunits for Singlet Energy Transduction, J. Am. Chem. Soc., 1998, 120(42), 10895–10901, DOI:10.1021/ja9823520
.
- K. M. Kadish, K. M. Smith, R. Guilard, The Porphyrin Handbook, 1999, vol. 21 Search PubMed
.
- S. Daoudi, A. Semmeq, M. Badawi, X. Assfeld, Y. Arfaoui and M. Pastore, Electronic Structure and Optical Properties of Isolated and TiO2-Grafted Free Base Porphyrins for Water Oxidation: A Challenging Test Case for DFT and TD-DFT, J. Comput. Chem., 2019, 40(29), 2530–2538, DOI:10.1002/jcc.26027
.
- P. Chmielewski, M. Grzeszczuk, L. Latos-Grazynski and J. Lisowski, Studies of the Reduction of the Nickel(II) Complex of 5,10,15,20-Tetraphenyl-21-Thiaporphyrin to Form Corresponding Nickel(I) Complexes, Inorg. Chem., 1989, 28(18), 3546–3552, DOI:10.1021/ic00317a030
.
- A. Ulman and J. Manassen, Synthesis of New Tetraphenylporphyrin Molecules Containing Heteroatoms Other than Nitrogen. I. Tetraphenyl-21,23-Dithiaporphyrin, J. Am. Chem. Soc., 1975, 97(22), 6540–6544, DOI:10.1021/ja00855a042
.
- A. Ulman, Synthesis of new tetraphenylporphyrin molecules containing heteroatoms other than nitrogen. Iii. tetraphenyl-21-tellura-23-thiaporphyrin: an internally-bridged porphyrin, Tetrahedron Lett., 1978, 21, 1885–1886, DOI:10.1016/S0040-4039(01)94699-4
.
- Z. Gross, I. Saltsman, R. P. Pandian and C. M. Barzilay, The First Metal Chelation by a Neutral Porphyrin Analogue, Tetrahedron Lett., 1997, 38(13), 2383–2386, DOI:10.1016/S0040-4039(97)00357-2
.
- K. K. Lara, C. R. Rinaldo and C. Brückner, Meso-Tetraaryl-7,8-Diol-21,23-Dithiachlorins and Their Pyrrole-Modified Derivatives: A Spectroscopic Comparison to Their Aza-Analogues, Tetrahedron, 2005, 61(9), 2529–2539, DOI:10.1016/j.tet.2004.12.043
.
- Synthesis of Newer Mercury(II) Complexes of Meso-Tetraaryl-21,23, Ingenta Connect Search PubMed.
- N. Agarwal, S. P. Mishra, A. Kumar, C.-H. Hung and M. Ravikanth, Synthesis and Crystal Structure of 2,3,12,13-Tetraalkoxy-21, 23-Dithiaporphyrins, Chem. Commun., 2002, 22, 2642–2643, 10.1039/B208017F
.
- C.-H. Hung, C.-K. Ou, G.-H. Lee and S.-M. Peng, Structure and Characterization of the First Metal Complex of Dithiaporphyrin: Ru(S 2 TTP)Cl 2, Inorg. Chem., 2001, 40(26), 6845–6847, DOI:10.1021/ic010705h
.
- O. Kahn, Molecular Magnetism, VCH, New York, NY, 1993 Search PubMed
.
- H. Bronstein, Z. Chen, R. S. Ashraf, W. Zhang, J. Du, J. R. Durrant, P. Shakya Tuladhar, K. Song, S. E. Watkins, Y. Geerts, M. M. Wienk, R. A. J. Janssen, T. Anthopoulos, H. Sirringhaus, M. Heeney and I. McCulloch, Thieno[3,2-b]Thiophene−Diketopyrrolopyrrole-Containing Polymers for High-Performance Organic Field-Effect Transistors and Organic Photovoltaic Devices, J. Am. Chem. Soc., 2011, 133(10), 3272–3275, DOI:10.1021/ja110619k
.
- J. Pan, H. Yin, Y.-Z. Xie, G.-Y. Sun and Z.-M. Su, The Conversion of Donor to Acceptor and Rational Design for Diketopyrrolopyrrole-Containing Small Molecule Acceptors by Introducing Nitrogen-Atoms for Organic Solar Cells, RSC Adv., 2017, 7(51), 31800–31806, 10.1039/C7RA02360J
.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871, DOI:10.1103/PhysRev.136.B864
.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138, DOI:10.1103/PhysRev.140.A1133
.
- A. D. Becke, Density-functional Thermochemistry. I. The Effect of the Exchange-only Gradient Correction, J. Chem. Phys., 1992, 96(3), 2155–2160, DOI:10.1063/1.462066
.
- A Simplified Time-Dependent Density Functional Theory Approach For Electronic Ultraviolet And Circular Dichroism Spectra Of Very Large Molecules - ScienceDirect, https://www.sciencedirect.com/science/article/abs/pii/S2210271X14000942, (accessed 2022-04-04) Search PubMed.
- Long-Range Corrected Hybrid Density Functionals With Damped Atom–Atom Dispersion Corrections - Physical Chemistry Chemical Physics (RSC Publishing), https://rsc.66557.net/en/content/articlelanding/2008/cp/b810189b/unauth, (accessed 2022-04-04) Search PubMed.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, Exchange-Correlation Functional with Broad Accuracy for Metallic and Nonmetallic Compounds, Kinetics, and Noncovalent Interactions, J. Chem. Phys., 2005, 123(16), 161103, DOI:10.1063/1.2126975
.
- Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions | Journal of Chemical Theory and Computation, https://pubs.acs.org/doi/abs/10.1021/ct0502763, (accessed 2022-04-04) Search PubMed.
- A. D. McLean and G. S. Chandler, Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z =11–18, J. Chem. Phys., 1980, 72(10), 5639–5648, DOI:10.1063/1.438980
.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions, J. Chem. Phys., 1980, 72(1), 650–654, DOI:10.1063/1.438955
.
- S. Chiodo, N. Russo and E. Sicilia, LANL2DZ Basis Sets Recontracted in the Framework of Density Functional Theory, J. Chem. Phys., 2006, 125(10), 104107, DOI:10.1063/1.2345197
.
- L. E. Roy, P. J. Hay and R. L. Martin, Revised Basis Sets for the LANL Effective Core Potentials, J. Chem. Theory Comput., 2008, 4(7), 1029–1031, DOI:10.1021/ct8000409
.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297, 10.1039/b508541a
.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community, J. Chem. Inf. Model., 2019, 59(11), 4814–4820, DOI:10.1021/acs.jcim.9b00725
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
.
- Designing Benzodithiophene-Based Donor Materials with Favorable Photovoltaic Parameters for Bulk Heterojunction Organic Solar Cells – Zara – 2017 – ChemistrySelect – Wiley Online Library, https://chemistry-europe.onlinelibrary.wiley.com/doi/10.1002/slct.201701008, (accessed 2022-01-17) Search PubMed.
- S. Ahmed and D. J. Kalita, End-Capped Group Manipulation of Non-Fullerene Acceptors for Efficient Organic Photovoltaic Solar Cells: A DFT Study, Phys. Chem. Chem. Phys., 2020, 22(41), 23586–23596, 10.1039/D0CP03814H
.
- (PDF) Designing Four Naphthalene Di-Imide Based Small Organic Solar Cells With 5,6-Difluoro-3-oxo-2,3-Dihydro-Indene Non-Fullerene Acceptors | Usman Ali – Academia.edu, https://www.academia.edu/51081101/Designing_four_naphthalene_di_imide_based_small_organic_solar_cells_with_5_6_difluoro_3_oxo_2_3_dihydro_indene_non_fullerene_acceptors, (accessed 2022-01-17) Search PubMed.
- C. Yan, S. Barlow, Z. Wang, H. Yan, A. K.-Y. Jen, S. R. Marder and X. Zhan, Non-Fullerene Acceptors for Organic Solar Cells, Nat. Rev. Mater., 2018, 3(3), 18003, DOI:10.1038/natrevmats.2018.3
.
- Dye-Sensitized Solar Cells Based on a Push–Pull Zinc Phthalocyanine Bearing Diphenylamine Donor Groups: Computational Predictions Face Experimental Reality | Scientific Reports, https://www.nature.com/articles/s41598-017-15745-3, (accessed 2022-05-24) Search PubMed.
- Time-Dependent Density Functional Response Theory for Molecules | Recent Advances in Density Functional Methods, https://www.worldscientific.com/doi/abs/10.1142/9789812830586_0005, (accessed 2022-01-17) Search PubMed.
- R. Bauernschmitt and R. Ahlrichs, Treatment of Electronic Excitations within the Adiabatic Approximation of Time Dependent Density Functional Theory, Chem. Phys. Lett., 1996, 256(4), 454–464, DOI:10.1016/0009-2614(96)00440-X
.
- J. D. Tozer and C. N. Handy, Improving virtual Kohn–Sham orbitals and eigenvalues: application to excitation energies and static polarizabilities, J. Chem. Phys., 1999, 109, 23, DOI:10.1063/1.477711
.
- R. L. Martin, Natural Transition Orbitals, J. Chem. Phys., 2003, 118(11), 4775, DOI:10.1063/1.1558471
.
- T. Le Bahers, C. Adamo and I. Ciofini, A Qualitative Index of Spatial Extent in Charge-Transfer Excitations, J. Chem. Theory Comput., 2011, 7(8), 2498–2506, DOI:10.1021/ct200308m
.
- L. Huet, A. Perfetto, F. Muniz-Miranda, M. Campetella, C. Adamo and I. Ciofini, General Density-Based Index to Analyze Charge Transfer Phenomena: From Models to Butterfly Molecules, J. Chem. Theory Comput., 2020, 16(7), 4543–4553, DOI:10.1021/acs.jctc.0c00296
.
- S. Holliday, Introduction, in Synthesis and Characterisation of Non-Fullerene Electron Acceptors for Organic Photovoltaics, ed. Holliday S., Springer International Publishing, Cham, 2018, Springer Theses, pp. 1–21, DOI: DOI:10.1007/978-3-319-77091-8_1
.
- R. G. Pearson, Hard and Soft Acids and Bases, ACS Publications, DOI: DOI:10.1021/ja00905a001.
- R. G. Parr and R. G. Pearson, Absolute Hardness: Companion Parameter To Absolute Electronegativity, ACS Publications, DOI: DOI:10.1021/ja00364a005.
- A. D’Aléo, F. Pointillart, L. Ouahab, C. Andraud and O. Maury, Charge Transfer Excited States Sensitization of Lanthanide Emitting from the Visible to the Near-Infra-Red, Coord. Chem. Rev., 2012, 256(15), 1604–1620, DOI:10.1016/j.ccr.2012.03.023
.
- Intramolecular Charge Transfer And Solvation Dynamics Of Push–Pull Dyes with Different π-Conjugated Linkers – Physical Chemistry Chemical Physics (RSC Publishing), https://rsc.66557.net/en/content/articlelanding/2019/cp/c9cp02559f/unauth, (accessed 2022-07-13) Search PubMed.
- M. O. Zouaghi, Y. Arfaoui and B. Champagne, Density Functional Theory Investigation of the Electronic and Optical Properties of Metallo-Phthalocyanine Derivatives, Opt. Mater., 2021, 120, 111315, DOI:10.1016/j.optmat.2021.111315
.
- M. C. Scharber, D. Mühlbacher, M. Koppe, P. Denk, C. Waldauf, A. J. Heeger and C. J. Brabec, Design Rules for Donors in Bulk-Heterojunction Solar Cells—Towards 10% Energy-Conversion Efficiency, Adv. Mater., 2006, 18(6), 789–794, DOI:10.1002/adma.200501717
.
- R. A. Marcus, Chemical and Electrochemical Electron-Transfer Theory, Annu. Rev. Phys. Chem., 1964, 15(1), 155–196, DOI:10.1146/annurev.pc.15.100164.001103
.
- R. A. Marcus, Electron Transfer Reactions in Chemistry. Theory and Experiment, Rev. Mod. Phys., 1993, 65(3), 599–610, DOI:10.1103/RevModPhys.65.599
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05063g |
| ‡ Cobalt could have been included in this study, but it is known experimentally to form complexes with a quite large magnetic anisotropy due to the orbital magnetic momentum, which require multi reference methods to be correctly modelled. Since we were interested in running DFT calculations here (single reference), we thus preferred to avoid Co. |
| This journal is © The Royal Society of Chemistry 2023 |