Open Access Article
Open Access ArticleUnleashing the piezoelectric potential of PVDF: a study on phase transformation from gamma (γ) to beta (β) phase through thermal contact poling†
Alban Morali a,
Arijit Mandala,
Maksim Skorobogatiyb and
Sampada Bodkhe
a,
Arijit Mandala,
Maksim Skorobogatiyb and
Sampada Bodkhe *a
*a
aLaboratory for Intelligent Structures, Department of Mechanical Engineering, Centre for Applied Research on Polymers and Composites (CREPEC), Polytechnique Montréal, Montréal, QC H3T 1J4, Canada. E-mail: sampada.bodkhe@polymtl.ca
bDepartment of Engineering Physics, Polytechnique Montréal, Montréal, QC H3T 1J4, Canada
First published on 25th October 2023
Abstract
Polyvinylidene fluoride (PVDF) is known for its piezoelectric properties. This material has different crystalline phases, alpha (α), beta (β) and gamma (γ), where the β-phase, in particular, is related to the piezoelectric behavior of PVDF. While the transformation from the α-phase to β-phase in PVDF is well-documented and widely studied, the transformation from γ- to β-phase has not yet been fully explored. However, when PVDF is produced by certain solution-based methods it can adopt its γ-form, which is not as piezoelectric as the β-phase. Hence, this study aims to bridge this gap by investigating the transformation from γ- to β-phase in PVDF nanocomposites films obtained from solution-based techniques. Our PVDF nanocomposite is made by solvent evaporation-assisted 3D printing of PVDF's nanocomposite with barium-titanate nanoparticles (BTO). To achieve the γ- to β-phase transformation, we first highlight the importance of annealing in the successful poling of PVDF samples. We then perform an in-depth analysis of the α-, β- and γ-crystallographic phases of PVDF-BTO using Fourier transform infrared spectroscopy (FTIR), X-ray diffraction (XRD) and differential scanning calorimetry (DSC). We observed that after annealing but before poling, the PVDF-BTO nanocomposite contains 76% of β + γ phases, the majority of which is the γ-phase. Poling of these samples resulted in the combination of the β + γ phases reaching 93% with the appearance of 40% of absolute fraction of the β-phase. We then demonstrated that the fraction of β-phase in the nanocomposite – as indicated by the 1275 cm−1 peak in PVDF's FTIR spectra – is not uniform on the surface area of the film. Additionally, the value of the absolute β-phase content also depends on the poling field's direction. Our work reveals that while considering PVDF's piezoelectric behavior, it is critical to be aware of these nuances and this article offers essential insights on how to address them. Overall, this study provides a step-by-step guideline to enhance the piezoelectricity of PVDF-based nanocomposites for sensing applications.
Introduction
Multi-material additive manufacturing (AM) is a promising potential tool to embed sensors into biomedical structures given the complexity and personalization required in orthotics, prosthetics, exoskeletons, and other biomedical equipment.1 Bodkhe et al. have invented a technique to fabricate ready-to-use piezoelectric sensors printed directly on top of the structures to be sensed.2,3 AM of these PVDF nanocomposite sensors has shown promising results in detecting human motion, breathing,2 and gait.4 AM further allows the precise deposition of PVDF-based sensors, knowing exactly where and how it will be placed each time which is in stark contrast to methods like electrospinning, where fibers are dispersed randomly.5Piezoelectricity is a physical phenomenon in which a material generates electric charges in response to an applied mechanical strain. The phenomenon of piezoelectricity, which has been studied for several decades,6,7 has a wide range of applications, in pressure sensing,8,9 strain sensing,10,11 actuation,12,13 and energy harvesting.14,15 Among piezoelectric materials, the polymer polyvinylidene fluoride (PVDF, chemical formula (C2H2F2)n) has been at the core of research owing to its biocompatibility, flexibility, and chemical inertness.16–18 This semi-crystalline polymer exists in 5 different molecular conformations, i.e., α (TGTG′, form II), β (TTTT, form I), γ (T3GT3G′, form III), δ and ε.19 In β-phase, the electronegative fluorine and electropositive hydrogen atoms are located on opposite sides of the polymer's carbon–carbon backbone. This configuration creates a net dipole moment within the molecule, which renders the piezoelectric properties to PVDF.20 However, PVDF naturally crystallizes into the thermodynamically stable α-phase, which being non-polar is not piezoelectric. That is why, a variety of processing steps like annealing, stretching,21–24 filler addition,25–27 or thermal poling4,21,28 are required to transform the α-phase into the β-phase. According to Bodkhe et al. the addition of BTO nanoparticles facilitates the nucleation of the electroactive β-phase in PVDF.9 Moreover, recent studies have demonstrated that 3D printing enables the mechanical stretching of PVDF,9,29 which can be further leveraged to achieve higher amount of β-phase. During the extrusion-based printing process, the PVDF nanocomposite solution is subjected to high extrusion pressures, up to 1 MPa, which induces a transition from α- to β-phase. Molecular dynamics simulations conducted by Yang et al. showed that it is further efficient to add a stretching step before poling because it creates a synergistic effect resulting in a greater alignment of molecular chains, consequently, higher transition to the β-phase of PVDF.30 Extensive research has been conducted to establish the relationship between the phases of PVDF and the specific peaks present in the polymer's Fourier transform infrared spectroscopy (FTIR) spectra. Despite minor discrepancies across different studies, there is a broad consensus that FTIR peaks corresponding to the α-phase are 763, 614, and 1071 cm−1 (ref. 31) to the β-phase are 840 and 1275 cm−1,32,33 and to the γ-phase are 840 and 1234 cm−1.34,35 Eqn (1) quantifies the amount of β-phase present in the material by analyzing the acquired FTIR spectra using the Beer–Lambert law:34
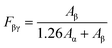 | (1) |
However, as the absorption peak at 840 cm−1 is common for both the β- and γ-phases, eqn (1) no more solely serve as an accurate representation of the β-phase proportion in the material but rather a combination of the β- and γ-phases.41 Therefore, according to Cai et al., when both β- and γ-phases are present in PVDF, it is necessary to use a more specific formulation, like the one below in order to obtain the true proportion of β- and γ-phases (Fβ and Fγ) in PVDF:41
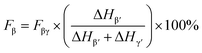 | (2) |
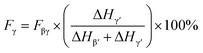 | (3) |
In this work, we additively manufacture polyvinylidene fluoride barium-titanate (PVDF-BTO) nanocomposite films according to the procedure developed by Bodkhe et al.9 The selection of a composite incorporating BTO in PVDF as a filler, instead of using pure PVDF was aimed at enhancing the piezoelectric properties of the material. We characterize the different phases in the films through X-ray diffraction (XRD), Fourier transform infrared spectroscopy (FTIR), and differential scanning calorimetry (DSC). We then present a comprehensive investigation of the effect of poling on the phase composition of PVDF using the eqn (1) and (2) to determine the true content of β-phase.41,49–51 Specifically, we focus on analyzing the changes in the peak intensities of the spectra obtained from these techniques: first qualitatively to extract meaningful insights and then quantitatively using eqn (1) and (2). This study embarks on a pioneering exploration of the transition from the γ-phase to the β-phase in PVDF, a topic that hasn't been addressed in the literature till date. We have achieved significant results in understanding the crystallization behavior of PVDF when manufactured using solution-based techniques, particularly highlighting the differences in piezoelectric coefficients between the γ- and the β-phases. Our study builds upon the work of Cai et al., published in 2017, and adds to it by offering a quantitative distinction between the two phases, a perspective believed to have been neglected for long in the field. Finally, the study goes a step further by not only studying the differences in analyses of the two phases but also investigating the variations of the content of the two phases across the surface of a 3D printed and poled PVDF nanocomposite film. We believe that this study deepens the understanding of the physicochemical properties of polymeric piezoelectric materials and their potential applications.
Results and discussion
We used a direct-ink-write (DIW) 3D printing process to fabricate square (30 × 30 mm2) PVDF-BTO films as defined by Bodkhe et al.9 The treatment and processing steps for the film are listed in Fig. 1 and described in the Experimental section. Samples that were removed from the 3D printer's build plate without any additional processing are referred to as neat (N), while those dried in a vacuum oven for 5 h at 90 °C are referred to as annealed (A). Subsequently, the annealed samples that were subjected to poling are designated as either glass side (PG) or air side (PA), depending on the side of the film studied. As shown in Fig. 1, the glass side refers to the side of the sample that was in contact with the 3D printer's glass build plate, while the air side refers to the one in contact with air during the printing process. During the poling process, the glass side was always in contact with the negative electrode, while the air side was in contact with the positive electrode. Only for the samples in the ESI (Fig. S1†) an inverse configuration was used, i.e. the glass side was in contact with the positive electrode, while the air side was in contact with the negative electrode.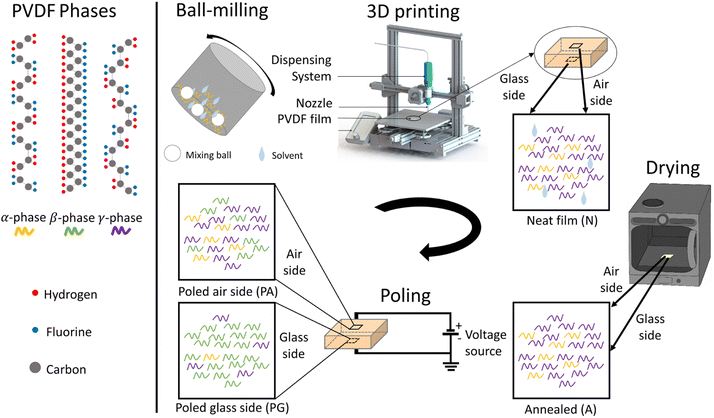 | ||
| Fig. 1 Schematic illustrating the processing steps involved in the fabrication of the PVDF nanocomposite sensors. | ||
Effect of drying
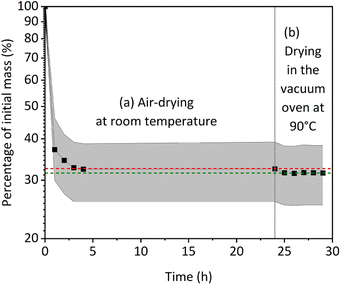
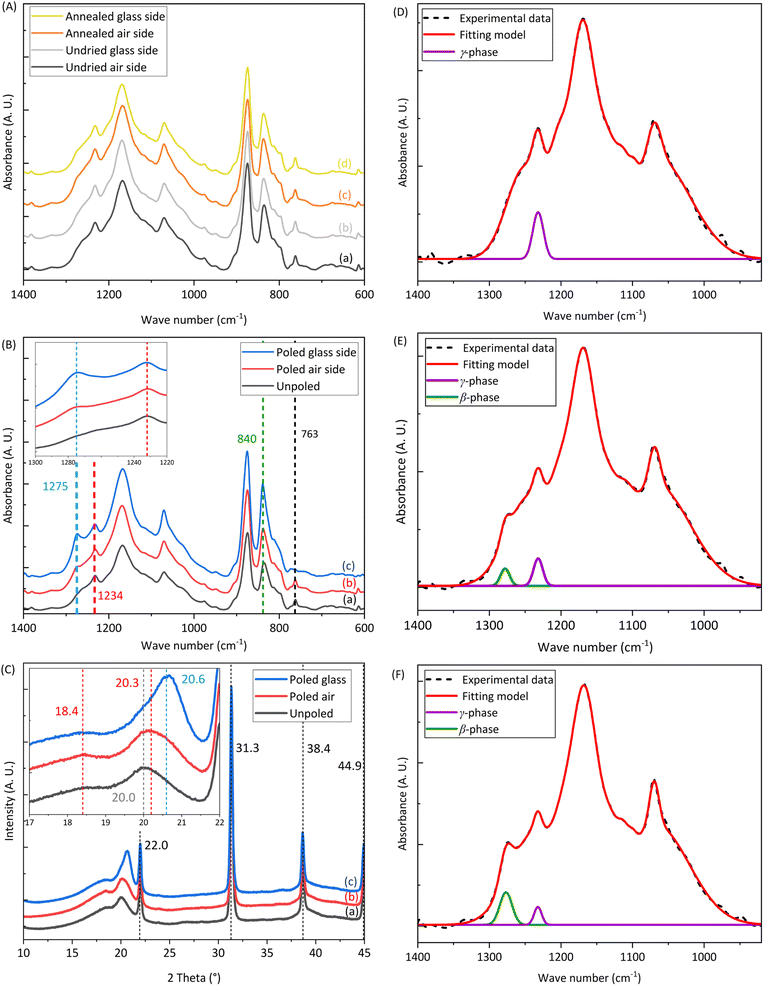
We study the effect of drying on the PVDF-BTO films by measuring their weight over time. Weight measurements were initiated immediately after printing the samples, and we considered the weight thus measured as the initial weight of the samples. After 4 h of drying in air, the weight of the samples no longer varied during the rest of the time (up to 24 h), meaning that no more evaporation occurred under ambient temperature and pressure conditions (Fig. 2). Samples were then placed in a vacuum oven at 90 °C, which led to a further decrease in the sample's weight, indicating that more solvent evaporated at elevated temperatures. Therefore, this drying step is critical for the success of the subsequent poling process since short-circuiting occurs immediately while attempting to pole neat samples. The solvents used to dissolve the PVDF-BTO, namely, acetone, DMF, and DMSO are all polar, so any residual solvent in the sample acts as an electric conductor, causing the charges to flow through the material. This is consistent with the measured finite resistances (in the 1–10 MΩ range) of the neat samples. Whereas, once the samples are completely dry, their resistance significantly increases reaching the instrument detection limit.The attenuated total reflectance Fourier transform infrared spectroscopy (ATR-FTIR) spectra of the neat and annealed samples before poling are presented in Fig. 3A. The peaks at 763 cm−1 correspond to the α-phase, while the peaks at 840 cm−1 represent a mixture of the β- and γ-phases. Additionally, the peak at 1234 cm−1 signify the presence of the γ-phase alone. It is significant to note that the ATR-FTIR spectra from all the samples are similar (Fig. 3A), and no statistically significant difference is observed between them. In all the samples the total fraction of the β- and γ-phases was found to be, Fβγ = 76 ± 1%. Therefore, we conclude that the drying process does not affect the physicochemical composition of the samples in our experimental conditions.
Effect of poling
Poling is a crucial step in the fabrication of piezoelectric materials as it is responsible for the alignment of molecular dipoles and the resultant piezoelectric response. In this section, we investigate the effect of poling on the molecular structure of the PVDF-BTO films using ATR-FTIR, XRD, DSC, and finally the piezoelectric coefficient with a d33-meter.We initially approach the piezoelectric response qualitatively to derive valuable understanding and subsequently quantify it using eqn (1) and (2). We have separated the analysis based on the location of the tests for a deeper understanding of the impact of poling on the piezoelectric properties throughout the PVDF-BTO samples.
Variations across sides
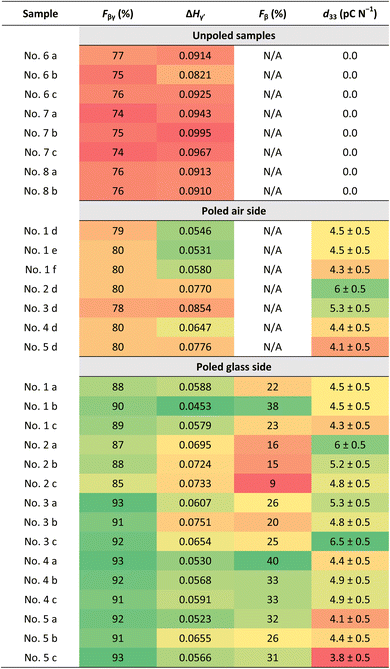
Fig. 3B shows the ATR-FTIR spectra of the annealed and poled PVDF-BTO films. We conducted analyses on both sides of the poled films: the air side (marked as b) and the glass side (marked as c). The inset provides an enlarged view of the peaks highlighting the increased intensity of the β-phase at 1275 cm−1 from the unpoled to poled samples and a clear reduction in the peak of α-phase at 763 cm−1. To better illustrate these changes, a deconvolution of the FTIR spectra was performed using the Origin software (Fig. 3D–F). In unpoled samples, only the γ-phase is present (Fig. 3D, purple curve). On the air side of the poled samples – the side with the smallest amount of β-phase (as shown in Fig. 3E), – the amount of γ-phase decreases when the β-phase shows up (represented by the green curve). On the other hand, in Fig. 3F, which depicts the glass side of the samples – the side with the largest amount of β-phase, – the amount of β-phase further increases, while the γ-phase and the α-phase both decrease. Table 1 shows the values of Fβγ, ΔHγ′, Fβ and d33 of unpoled films and both sides of poled films at the same locations as shown in Fig. 4A. The Fβγ values obtained for the air side of poled samples were 80 ± 2% (Table 1), whereas those for the unpoled samples were 76 ± 2% (Table 1), which, considering the errors in the measurements (value = ±2%), are relatively close. On the other hand, for the ATR-FTIR curves corresponding to the poled samples along the glass side (Fig. 3B(c)), due to the appearance of the exclusive β-peak at 1275 cm−1, we could use eqn (2) to calculate the Fβ values.4,21,28 Consequently, on the glass side of poled samples (Fig. 3B(c)), the Fβγ values reach up to 93% (Table 1). At the same time, ΔHγ′ values (Table 1) – related to the presence of γ-phase – are reduced, meaning that the γ-phase content is also reduced compared to unpoled samples. Hence we can conclude, that it is the electrical poling that results in the γ- to β-phase transformation.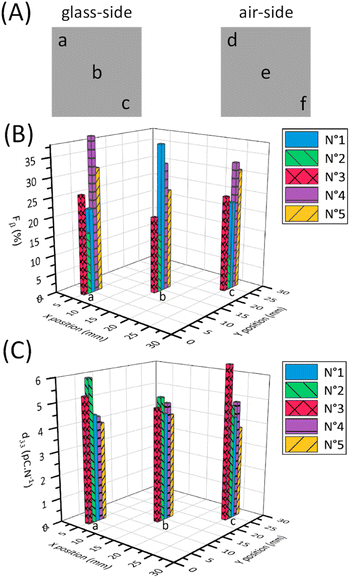 | ||
| Fig. 4 (A) Schematic of the measurement's locations on the samples area. Mapping bar chart of Fβ (B) and d33 (C) values of samples (1–5) depending on the locations (a–c). | ||
Fig. 3C presents the XRD spectra for the films, with a magnified view in the inset to better illustrate the peaks corresponding to the β-phase at 20.6° and the γ-phase at 18.4° and 20.3°. The analysis of X-ray diffractograms leads to consistent conclusions with the ATR-FTIR observations (Fig. 3C), i.e., that the crystalline-phase composition of the air side of poled samples (Fig. 3C(b)) is similar to unpoled samples (Fig. 3C(a)), while the glass side of poled samples (Fig. 3C(a)) shows the β-phase signature at 20.6°. The shift in the 20° peak to 20.6° and the presence of a peak at 36.5° for the glass side of poled sample (Fig. 3C(c)) confirms the appearance of β-phase. Meanwhile, the air side of the poled samples (Fig. 3C(b)) do not exhibit this shift. The three peaks at 24°, 32°, and 39° (Fig. 3C) are related to the presence of BTO, which was added to the PVDF as a filler in order to improve the Fβγ value.52
Therefore, the surface-sensitive analytical techniques such as ATR-FTIR and XRD (curves (b) and (c) in Fig. 3B and C) reveal that there are differences in the physicochemical structure of the material between the two sides of the poled samples. As from Fig. 3A, before the poling process, there is no difference between the unpoled glass side and unpoled air side of the samples, the difference in β-phase of the two sides of the poled samples is indeed obtained through the poling process.
We carried out additional experiments to confirm if the poling process contributed to the observed differences between the sides of the sample. We used an inverted setup where the side facing the glass was in contact with the positive electrode during poling and the side exposed to air was in contact with the negative electrode. Fig. S1† lists the Fβγ, ΔHγ′ and Fβ values of all the samples hence prepared. Again, a correlation is observed between the β-phase content and the side of the sample that was in contact with the electrode during the poling process. It can be seen that for these particular samples, the air side shows Fβ values while the glass side does not. This relationship implies that the electrode contact side during the poling process directly influences the distribution of the β-phase in the material.
This non-uniformity of poling across the film thickness on the sides, to our knowledge has not been discussed in the existing literature on this subject, pushing the need for further investigation and characterization of this phenomenon.
Variation across surface area
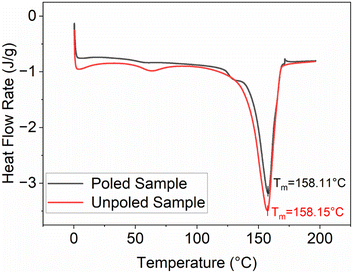
We then investigated how the local value of the piezoelectric coefficient, d33, is related to the local phase content across a sample surface. The d33 coefficient was measured locally using a d33-meter, while reflection mode ATR-FTIR spectroscopy was used to measure Fβ and Fβγ with a sample placed in the focal point of the ATR-FTIR beam. As the placement of the sample has to be done manually for these two methods, during the measurements we took care to always probe the samples at the same locations as shown in Fig. 4A. As seen from the values in Table 1 and Fig. 4, we see that it is difficult to establish a clear correlation between the d33 and Fβ values due to possible spatial mismatch in their measurement locations. These measurements are performed by two different instruments, which can cause misalignment and complicate spatial correlation between the two measurands. In our FTIR spectra we observe similar strong local variations in the d33 and Fβ values, in contrast to an almost constant spatially independent value of Fβγ. To better illustrate this variation, Fig. 4B and C depict plots displaying the Fβ and d33 values at locations a, b, and c across five different samples. Using these figures, we can see the pronounced discrepancies in the final Fβ and d33 across the samples and along their surfaces despite employing the uniform and consistent poling procedure for all samples and throughout their surfaces. This leads us to conclude that the poling isn't consistent across the surface as well. Thus, special care must be taken to ensure successful and uniform poling when embedding PVDF sensors via 3D printing into components.We used the DSC to study the changes in the crystallinity of the samples. It can be seen from Table 2, that there is no observable difference in the melting temperature and the crystallinity for the poled and unpoled samples. According to the literature, it is difficult to determine the phase from the DSC melting peaks (Fig. 5) as their melting temperatures overlap.33,45,53–56 Since the total crystallinity, which is about 43%, did not change for both poled and unpoled samples (Table 2), we can conclude that poling has no impact on the growth of new crystals in the samples. Therefore, there is only an interchange within the crystalline content between the phases from γ- to β-phase and α- to β-phase.
| No. | Sample type | Melting temperature | Crystallinity |
|---|---|---|---|
| 1 | Poled sample | 158.11 °C | 43.62% |
| 2 | Unpoled sample | 158.15 °C | 43.47% |
All these experiments show that the poling step not only creates polymer chain alignment but also transforms both α- and γ-phase to β-phase in the poled samples.
Conclusion
This study provides significant contributions to understanding the role of the poling process in increasing the piezoelectric properties in PVDF-based nanocomposites. Firstly, we show that an additional drying process in vacuum for the piezoelectric films is essential to eliminate solvents and render the nanocomposite films non-conductive to allow poling at higher electric fields of up to 50 MV m−1. Secondly, through ATR-FTIR analysis, focusing on the peak exclusively associated with the β-phase, i.e., 1275 cm−1, we show that the poling process is not uniform along the two surfaces of the sample. In particular, the Fβ values vary significantly from one point to another on the same surface of the sample. Therefore, we highlight the need for careful consideration of spatial variations of the piezoelectric phases because of the poling process.This is essential because, successful achievement of uniform piezoelectric properties within the film is an indispensable in integrating/embedding sensors into components via 3D printing. Moreover, as it is close to impossible to replace the integrated sensors they must be fabricated and analyzed accurately. Therefore, effective tools are essential to successfully analyze the resulting piezoelectric material and standardize the response of the PVDF-based sensors. This research introduces one of those tools, ultimately leading to advances in the development and application of PVDF-based materials with enhanced piezoelectric properties.
Experimental section
Sample preparation
1.8 g of polyvinylidene fluoride (PVDF; average Mw ∼ 534![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 by GPC, Sigma-Aldrich) powder, 0.2 g of barium titanate (BTO, BaTiO3; 99.9% purity, 100 nm, tetragonal; Nanostructured & Amorphous Materials Inc.) powder were poured into a ball-milling container. 4 mL of dimethylformamide (DMF; Alfa Aesar), 0.6 mL of dimethyl sulfoxide (DMSO; Sigma-Aldrich; 65 g L−1), and 6 mL of acetone were added to the container. The mixture was mixed in a high-energy shaker ball-mill (SPEX SamplePrep 8000, Series Mixer/Mill) at 1080 cycles per minute for 20 min with 3 zirconia balls (3.2 g each).
000 by GPC, Sigma-Aldrich) powder, 0.2 g of barium titanate (BTO, BaTiO3; 99.9% purity, 100 nm, tetragonal; Nanostructured & Amorphous Materials Inc.) powder were poured into a ball-milling container. 4 mL of dimethylformamide (DMF; Alfa Aesar), 0.6 mL of dimethyl sulfoxide (DMSO; Sigma-Aldrich; 65 g L−1), and 6 mL of acetone were added to the container. The mixture was mixed in a high-energy shaker ball-mill (SPEX SamplePrep 8000, Series Mixer/Mill) at 1080 cycles per minute for 20 min with 3 zirconia balls (3.2 g each).
3D printing of samples
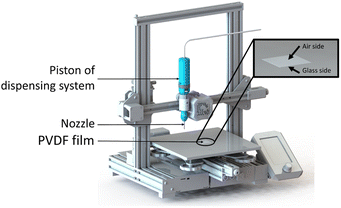
The printing setup is illustrated in Fig. 6. The ink was poured into a syringe (3 mL; Nordson EFD) with a cylindrical steel nozzle (0.1 mm inner diameter, 6.35 mm nozzle length; Nordson EFD), which was placed into a pneumatically operated dispensing system (Ultimus V combined with HP-7X; Nordson EFD). The dispensing system was mounted on a conventional fused filament fabrication (FFF) 3D printer (Creality, Ender 3 v2) using a 3D printed holder. The deposition pattern was programmed using the Cura slicer. The film was fabricated by depositing the material in a series of zigzag infill patterns, with the lines spaced 0.1 mm apart from each other. The dimensions of all the films were 30 × 30 mm2. The printing speed was 20 mm s−1 and a dispensing pressure was ≈ 1 MPa.Drying
After printing, the film was left to dry on the glass plate to avoid shrinkage and curling of the edges. After 24 h, the film was removed from the plate. Except for those labeled as “neat”, other samples were placed in a vacuum oven at 90 °C (at 10.1 kPa) for 5 h. The final thickness of all the films was 0.070 ± 0.010 mm.Poling process
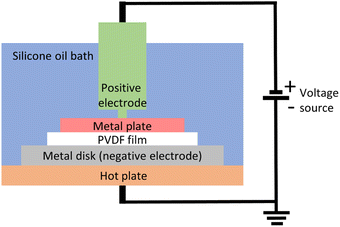
The in-house poling station similar to that used by Tao et al.,21 as shown in Fig. 7, was used to pole the samples. The setup consists of a heating plate, a silicone bath, and a voltage generator (ES60N-10W, Gamma High Voltage Research Inc.). It was ensured that the side in contact with the glass plate during 3D printing was the one facing the bottom metal disk in the silicone bath. On top side of the film (the air side), a 20 × 20 mm2 metal plate was used as the second electrode. A 3 kV voltage was applied at 100 °C for 1 h. After 1 h, the heat was turned off but the electric field was maintained until the temperature dropped to 60 °C. The film was taken out of the silicone bath and washed with detergent (Alconox, Powdered Precision Cleaner) to completely remove the silicone oil.Characterization
ATR-FTIR was performed using a PerkinElmer, Spectrum 65 ATR-FTIR spectrometer. The range of wavenumbers was set from 600 cm−1 to 1400 cm−1 with a resolution of 4 cm−1. All membranes were scanned on both sides with ATR (attenuated total reflection) mode. A picture of the ATR-FTIR is provided in Fig. S2.† Five samples for every type (neat, annealed, poled and unpoled) were tested at 3 different positions on each side of the film as shown in Fig. 4A.XRD was carried out using a Bruker, D8 advanced diffractometer with a copper anode at 40 kV and 40 mA. The samples were scanned in a 2-theta range of 10° to 45° with a step size of 0.0167°. Two samples every type (neat, annealed, poled and unpoled) were tested.
The crystallinity of poled and unpoled PVDF-BTO samples was measured using Differential Scanning Calorimetry (DSC) with TA Instruments differential scanning calorimeter, DSC Q100. Approximately 5 mg of samples were cut from the nanocomposite film, weighed and placed in an aluminum pan. Heating scans were carried out from 0 to 200 °C at the rate of 10 °C min−1. The total crystallinity was calculated using the following equation:
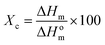 | (4) |
The d33 values were obtained using a d33-meter (YE2730, Sinocera Piezotronics, Inc.). A photograph of the d33-meter is presented in Fig. S3.† The samples are placed between two small clamps and the equipment applied dynamic stress while measuring the signal output. In Fig. 4, average d33 refers to the average of the absolute values measured on both sides of the PVDF film. Five samples for every type (neat, annealed, poled and unpoled) were tested on 3 different positions on each side of the film as shown in Fig. 4A.
Author contributions
This manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support from Fonds de recherche du Québec (FRQNT) Établissement de la relève professorale, NSERC (Natural Sciences and Engineering Research Council of Canada) Discovery Grants program and the MITACS Globalink research internship program. The authors would also like to thank M.Sc. Médéric Dégardin and M.Sc. Reza Damansabz for their valuable suggestions to the improvement of this article.References
- M. A. Ali, C. Hu, E. A. Yttri and R. Panat, Adv. Funct. Mater., 2022, 32, 2107671 CrossRef CAS PubMed
.
- S. Bodkhe, C. Noonan, F. P. Gosselin and D. Therriault, Adv. Eng. Mater., 2018, 20, 1800206 CrossRef
.
- S. Bodkhe, D. Therriault, F. Gosselin and T. Rui, US Pat. 11466169B2, 2017 Search PubMed
.
- S. Bodkhe, P. S. M. Rajesh, F. P. Gosselin and D. Therriault, ACS Appl. Energy Mater., 2018, 1, 2474–2482 CrossRef CAS
.
- A. Ziabicki, Fundamentals of fibre formation: The science of fibre spinning and drawing, 1976 Search PubMed
.
- G. Lippmann, Principe de la conservation de l’électricité, ou second principe de la théorie des phénomènes électriques, J. Phys. Theor. Appl., 1881, 381–394 CrossRef
.
- J. Curie and P. Curie, Bull. Soc. Fr. Mineral., 1880, 3, 90 Search PubMed
.
- Z. Wang, X. Yuan, J. Yang, Y. Huan, X. Gao, Z. Li, H. Wang and S. Dong, Nano Energy, 2020, 73, 104737 CrossRef CAS
.
- S. Bodkhe, G. Turcot, F. P. Gosselin and D. Therriault, ACS Appl. Mater. Interfaces, 2017, 9, 20833–20842 CrossRef CAS PubMed
.
- X. Lu, H. Qu and M. Skorobogatiy, ACS Nano, 2017, 11, 2103–2114 CrossRef CAS PubMed
.
- Z. Huo, X. Wang, Y. Zhang, B. Wan, W. Wu, J. Xi, Z. Yang, G. Hu, X. Li and C. Pan, Nano Energy, 2020, 73, 104744 CrossRef CAS
.
- X. Wang, X. He, H. Zhu, L. Sun, W. Fu, X. Wang, L. C. Hoong, H. Wang, Q. Zeng, W. Zhao, J. Wei, Z. Jin, Z. Shen, J. Liu, T. Zhang and Z. Liu, Sci. Adv., 2016, 2, e1600209 CrossRef PubMed
.
- Y. Wu, J. K. Yim, J. Liang, Z. Shao, M. Qi, J. Zhong, Z. Luo, X. Yan, M. Zhang, X. Wang, R. S. Fearing, R. J. Full and L. Lin, Sci. Robot., 2019, 4, eaax1594 CrossRef PubMed
.
- N. Li, Z. Yi, Y. Ma, F. Xie, Y. Huang, Y. Tian, X. Dong, Y. Liu, X. Shao, Y. Li, L. Jin, J. Liu, Z. Xu, B. Yang and H. Zhang, ACS Nano, 2019, 13, 2822–2830 CrossRef CAS PubMed
.
- Y. Zhang, C. R. Bowen, S. K. Ghosh, D. Mandal, H. Khanbareh, M. Arafa and C. Wan, Nano Energy, 2019, 57, 118–140 CrossRef CAS
.
- M. Yuan, L. Cheng, Q. Xu, W. Wu, S. Bai, L. Gu, Z. Wang, J. Lu, H. Li, Y. Qin, T. Jing and Z. L. Wang, Adv. Mater., 2014, 26, 7432–7437 CrossRef CAS PubMed
.
- S. Bodkhe and P. Ermanni, Multifunct. Mater., 2019, 2, 022001 CrossRef CAS
.
- G. Kalimuldina, N. Turdakyn, I. Abay, A. Medeubayev, A. Nurpeissova, D. Adair and Z. Bakenov, Sensors, 2020, 20, 5214 CrossRef CAS PubMed
.
- J. B. Lando and W. W. Doll, J. Macromol. Sci., Part B: Phys., 2006, 2, 205–218 CrossRef
.
- A. J. Lovinger, Science, 1983, 220, 1115–1121 CrossRef CAS PubMed
.
- R. Tao, J. Shi, M. Rafiee, A. Akbarzadeh and D. Therriault, Mater. Adv., 2022, 3, 4851–4860 RSC
.
- A. Salimi and A. A. Yousefi, Polym. Test., 2003, 22, 699–704 CrossRef CAS
.
- B. Mohammadi, A. A. Yousefi and S. M. Bellah, Polym. Test., 2007, 26, 42–50 CrossRef CAS
.
- S. Kasap, Principles of Electronic Materials and Devices, 2005 Search PubMed
.
- S. H. Lee and H. H. Cho, Fibers Polym., 2010, 11, 1146–1151 CrossRef CAS
.
- W. Huang, K. Edenzon, L. Fernandez, S. Razmpour, J. Woodburn and P. Cebe, J. Appl. Polym. Sci., 2010, 115, 3238–3248 CrossRef CAS
.
- S. Bodkhe, P. S. M. Rajesh, S. Kamle and V. Verma, J. Polym. Res., 2014, 21, 2474–2482 Search PubMed
.
- Y. Zhao, Q. Liao, G. Zhang, Z. Zhang, Q. Liang, X. Liao and Y. Zhang, Nano Energy, 2015, 11, 719–727 CrossRef CAS
.
- X. Yuan, A. Yan, Z. Lai, Z. Liu, Z. Yu, Z. Li, Y. Cao and S. Dong, Nano Energy, 2022, 98, 107340 CrossRef CAS
.
- J. Yang, X. Yao and Z. Meng, Polymer, 2022, 245, 124691 CrossRef CAS PubMed
.
- P. Martins, A. C. Lopes and S. Lanceros-Mendez, Prog. Polym. Sci., 2014, 39, 683–706 CrossRef CAS
.
- G. Cortili and G. Zerbi, Spectrochim. Acta, Part A, 1967, 23, 2216–2218 CrossRef CAS
.
- L. Ruan, X. Yao, Y. Chang, L. Zhou, G. Qin and X. Zhang, Polymers, 2018, 10, 228 CrossRef PubMed
.
- T. Boccaccio, A. Bottino, G. Capannelli and P. Piaggio, J. Membr. Sci., 2002, 210, 315–329 CrossRef CAS
.
- J. Zheng, A. He, J. Li and C. C. Han, Macromol. Rapid Commun., 2007, 28, 2159–2162 CrossRef CAS
.
- H. Li, Y. S. Song, T. W. Kim, M. H. Lee and S. Lim, Macromol. Mater. Eng., 2022, 307, 2200235 CrossRef CAS
.
- H. Li, S.-W. Jin, J. H. Lim and S. Lim, Appl. Mater. Today, 2022, 29, 101633 CrossRef
.
- H.-J. Ye, W.-Z. Shao and L. Zhen, J. Appl. Polym. Sci., 2013, 129, 2940–2949 CrossRef CAS
.
- H. Li and S. Lim, J. Mater. Chem. A, 2022, 10, 14894–14905 RSC
.
- H. Li and S. Lim, Nanomaterials, 2021, 11, 1908 CrossRef CAS PubMed
.
- X. Cai, T. Lei, D. Sun and L. Lin, RSC Adv., 2017, 7, 15382–15389 RSC
.
- G. Cortili and G. Zerbi, Spectrochim. Acta, Part A, 1967, 23, 285–299 CrossRef
.
- Y. Bormashenko, R. Pogreb, O. Stanevsky and E. Bormashenko, Polym. Test., 2004, 23, 791–796 CrossRef CAS
.
- R. Gregorio, J. Appl. Polym. Sci., 2006, 100, 3272–3279 CrossRef CAS
.
- D. M. Dhevi, A. A. Prabu and K. J. Kim, J. Mater. Sci., 2015, 51, 3619–3627 CrossRef
.
- K. Tashiro, M. Kobayashi and H. Tadokoro, Macromolecules, 2002, 14, 1757–1764 CrossRef
.
- Tashiro K., Tadokoro H. and M. Kobayashi, Macromolecules, 1975, 8, 158–170 CrossRef
.
- Cai X., T. Lei, X. Wang, L. Yu, X. Hu, G. Zheng, W. Lv, L. Wang, D. Wu, D. Sun and L. Lin, RSC Adv., 2017, 7, 15382–15389, 10.1039/C3RA42622J
.
- J. Fan, N. Deneke, S. Xu, B. Newell, J. Garcia, C. Davis, W. Wu, R. M. Voyles and R. A. Nawrocki, Addit. Manuf., 2022, 60, 103248 CAS
.
- S. Mahmoodi, P. Hamedi, S. Zhong, D. Weidner and W. Li, Phys. Chem. Chem. Phys., 2022, 24, 17577–17592 RSC
.
- S. Verma, M. Sharma and R. Vaish, Environ. Sci.: Nano, 2022, 9, 3885–3899 RSC
.
- S. Nayak, B. Sahoo, T. K. Chaki and D. Khastgir, RSC Adv., 2014, 4, 1212–1224 RSC
.
- A. Bužarovska, M. Kubin, P. Makreski, M. Zanoni, L. Gasperini, G. Selleri, D. Fabiani and C. Gualandi, J. Polym. Res., 2022, 29, 272 CrossRef
.
- Y. Chen, R. Feng, Y. Li, N. Dan, C. Yang, G. Yu, Y. Huang, H. Wen and W. Dan, Int. J. Polym. Anal. Charact., 2019, 24, 684–695 CrossRef CAS
.
- M. Neidhöfer, F. Beaume, L. Ibos, A. Bernès and C. Lacabanne, Polymer, 2004, 45, 1679–1688 CrossRef
.
- C. Leonard, J. L. Halary, L. Monnerie and F. Micheron, Polym. Bull., 1984, 11, 195–202 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05068h |
| This journal is © The Royal Society of Chemistry 2023 |