Open Access Article
Open Access ArticleManganese vacancies and tunnel pillars synergistically improve the electrochemical performance of MnO2 in aqueous Zn ion batteries
Lanxiang Huang†
 abcd,
Yilin Chen†c,
Pu Dengc,
Bo Zhaoc,
Xufeng Luobc,
Chang Chenc and
Yu Hu*abc
abcd,
Yilin Chen†c,
Pu Dengc,
Bo Zhaoc,
Xufeng Luobc,
Chang Chenc and
Yu Hu*abc
aCrystalline Silicon Photovoltaic New Energy Research, Leshan Normal University, Leshan, Sichuan 614000, China. E-mail: 120678486@qq.com
bLeshan West Silicon Materials Photovoltaic and New Energy Industry Technology Research Institute, Leshan, Sichuan 614000, China
cSchool of New Energy Materials and Chemistry, Leshan Normal University, Leshan, Sichuan 614000, China
dMaterial Corrosion and Protection Key Laboratory of Sichuan Province, Zigong, 643000, China
First published on 17th October 2023
Abstract
High-oxidation niobium was used for the first time in manganese dioxide cation doping to reduce the diffusion resistance of zinc ions, in order to improve its kinetic and electrochemical properties. The results show that using a simple hydrothermal process, all niobium ions were doped into the manganese dioxide lattice. As niobium(V) was incorporated into the [2 × 2] tunnel of α-MnO2, it induced manganese vacancies, which reduced the diffusion resistance of Zn2+ in manganese dioxide, improving the migration kinetics. It acted as a tunnel pillar, avoiding the collapse of the tunnel structure during the repeated insertion/extraction of the Zn2+ process, and prevented a rapid degradation of the cycling performance. In particular, the sample with the Nb/Mn molar ratio of 0.003 exhibited the best kinetic reversibility and rate performance. After 400 cycles at 1C, the capacity retention of Nb-doped MnO2 significantly increased to 89%, which was only 55% for the undoped sample. Meanwhile, at a power density of 400 W kg−1, it presented the highest energy density of 765 W h kg−1 due to the existing doping of metal ions.
1. Introduction
The development of solar and wind energy requires energy storage devices to help the power grid to achieve peak shaving and valley filling. Rechargeable batteries are considered the best energy storage device because of their good mobility and easy installation. Until now, lithium-ion batteries have been widely used in energy storage secondary batteries. For an energy storage battery, high safety, low cost, and long life are the most basic requirements. Although lithium-ion batteries have a high energy density, they are expensive, and the safety performance is relatively poor due to the high activity of lithium and the flammability of organic electrolytes.1,2 In order to find a suitable secondary battery for energy storage, researchers have made great efforts and the rechargeable aqueous battery with high ionic conductivity, and high safety has attracted great attention.Among them, the rechargeable aqueous zinc-ion batteries (ZIBs) based on the Zn2+ insertion/extraction reaction are considered the most attractive energy storage batteries with the advantages of abundant zinc reserves, environmental friendliness, multivalent carriers, low reduction potential (−0.76 V vs. SHE), and high theoretical specific capacity (825 mA h g−1).3,4 At present, the main cathode materials of ZIBs are Prussian blue, vanadium-based materials, and manganese-based materials. As Prussian blue is used as cathode material in ZIBs, the capacity decays rapidly, and its high operating voltage (1.7 V vs. Zn2+/Zn) leads to an oxygen evolution reaction.5 Vanadium-based materials (such as Zn0.3(NH4)0.3V4O10·0.91H2O, V2S, and Sr0.19V2O5·1.3H2O) and manganese-based materials have a moderate operating range compatible with the electrochemical window of water electrolyte.6–8 In view of the harmful effect of vanadium and its slow Zn2+ intercalation kinetics, manganese-based cathode materials with open crystal structures are more promising for practical applications of ZIBs.
Until now, the research on manganese-based materials has mainly been focused on manganese dioxides, such as α-MnO2, β-MnO2, γ-MnO2, δ-MnO2, λ-MnO2, and ε-MnO2.9–17 Because of Jahn–Teller distortion, manganese ions will be dissolved in water-electrolytes, leading to a decrease of active substances and the rapid decay of cycling performance. The preaddition of MnSO4 to the electrolyte can effectively alleviate this problem.18,19 However, the slow ion/electron transfer kinetics of MnO2 lead to the poor rate and cycling performance of ZIBs, and the repeated insertion/extraction of Zn2+ in MnO2 may lead to the collapse of its tunnel structure, resulting in a rapid degradation of cycling performance.20,21 Therefore, taking effective measures to solve these problems can make the practical application of ZIBs possible. The results show that doping is an effective approach for improving the electrochemical properties of MnO2.
According to the valence state of the doped ions, the cationic doping of manganese dioxide can be divided into univalent (K0.48Mn2O4·0.49H2O (ref. 17)), bivalent (Co-doped δ-MnO2,22 Ni-doped Mn2O3,23 Ni and Co co-substituted spinel ZnMn2O4,24 Zn/Co co-doped MnO/C,16 Ca0.28MnO2·0.5H2O,25 MgMn2O4 (ref. 26)), and trivalent ions (Al-intercalation MnO2,27 La3+ and Ca2+ co-doped MnO2 (ref. 28)). As can be seen, all of the selected doped cations (K+, Co2+, Ni2+, Zn2+, Ca2+, Mg2+, Al3+, and La3+) have low oxidation states, which can improve the electrochemical properties of manganese-based cathode materials to some extent, but none of them is ideal.
High oxidation state vanadium(V) has been doped into MnO2, inducing a large number of manganese vacancies and oxygen vacancies, greatly improving the performance of MnO2.29 Niobium and vanadium belong to the same subfamily and, therefore, may produce the same effect. High oxidation state cation doping will cause numerous manganese vacancy defects in the MnO2 lattice due to the principle of electrical neutrality, which can reduce the electrostatic barrier of Zn2+ and promote the diffusion of Zn2+ effectively, finally improving the electrochemical properties of ZIBs.30
2. Experimental
2.1 Material preparation
LiNbO3 was used as a source of niobium with a high oxidation state. Niobium-doped manganese dioxide was prepared by a hydrothermal method.29 Equal moles of KMnO4 and MnSO4·H2O solution were mixed, adding a certain amount of LiNbO3, and the redox reaction occurred simultaneously. With the hydrothermal reaction at 180 °C, a large amount of H+ was produced, leading to a strong acidic solution (pH = 1), thus ensuring the existence of a high oxidation state of niobium. The dispersed solution was vacuum filtered and washed until the pH was 7, then, it was vacuum dried at 100 °C for 12 h. After cooling to room temperature, the obtained material was used for electrode fabrication. A series of niobium-doped MnO2 samples were prepared according to Nb/Mn molar ratios of 0, 0.003, 0.005, and 0.01, and were labeled as 0, 0.003, 0.005, and 0.01 samples.2.2 Structure characterization
The phase of the materials was characterized using X-ray diffraction (XRD, DX-2600X, Cu-Kα1) and the chemical structure was analyzed using Raman spectroscopy (Thermo Fisher Dxr2xi). X-ray photoelectron spectroscopy (XPS, Thermo Scientific Nexsa, Al-Kα) was used to analyze the surface elements, chemical structures, and surface defects of the materials. The molar ratio of Nb to Mn was determined using inductively coupled plasma emission spectroscopy (ICP-OES, Agilent 730). Transmission electron microscopy (TEM) and high-resolution transmission electron microscopy (HRTEM, JEM2100) were used to observe and analyze the microstructure, crystal plane spacing, and crystal defects. The morphology of the electrode was characterized using scanning electron microscopy (SEM, FEI Inspect F50).2.3 Electrochemical test
A two-electrode battery system was used to test the electrochemical performance of the prepared materials. The active substance (different Nb/Mn molar ratios materials), acetylene black, and polytetrafluoroethylene (PTFE) binder were mixed with a mass ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and then pasted in a stainless steel mesh with a diameter of 12 mm. The mass of an active substance per piece of the electrode was approximately 3.0 mg. A zinc plate with a thickness of 0.2 mm was used as the negative electrode, and an aqueous solution of 1 mol L−1 ZnSO4 and 0.2 mol L−1 MnSO4 was used as the electrolyte. The dynamic performance (including cyclic voltammetry (CV) and electrochemical impedance spectroscopy (EIS)) of the ZIBs was measured using an electrochemical workstation (DongHua Analytical, DH7000), and all the electrochemical performances (including the charge and discharge curves, rate performance, cycle performance and constant-current intermittent titration (GITT)) of the ZIBs were tested by blue battery system (LAND, CT3001A). The voltage range was 0.8–1.9 V for all tests and were carried out at room temperature.
1 and then pasted in a stainless steel mesh with a diameter of 12 mm. The mass of an active substance per piece of the electrode was approximately 3.0 mg. A zinc plate with a thickness of 0.2 mm was used as the negative electrode, and an aqueous solution of 1 mol L−1 ZnSO4 and 0.2 mol L−1 MnSO4 was used as the electrolyte. The dynamic performance (including cyclic voltammetry (CV) and electrochemical impedance spectroscopy (EIS)) of the ZIBs was measured using an electrochemical workstation (DongHua Analytical, DH7000), and all the electrochemical performances (including the charge and discharge curves, rate performance, cycle performance and constant-current intermittent titration (GITT)) of the ZIBs were tested by blue battery system (LAND, CT3001A). The voltage range was 0.8–1.9 V for all tests and were carried out at room temperature.
3. Results and discussions
3.1 Morphology and structure
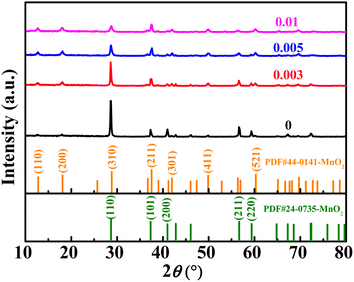
The XRD diffraction patterns of the samples are shown in Fig. 1. The XRD patterns of the undoped samples could be divided for β-MnO2 (PDF #24-0735) and α-MnO2 (PDF #44-0141). The diffraction peaks of (110), (200), (211), and (220) crystal faces of β-MnO2 are gradually weakened after Nb incorporation. However, the diffraction peaks of the (101) crystal plane are not weakened, which may be attributed to the increased amount of α-MnO2. As can be seen, the peak location of the (101) crystal face of β-MnO2 is very close to that of the (211) crystal plane of α-MnO2, so the fitting peak of the two crystal faces did not weaken. The characteristic peaks of (110), (200), (301), (411), and (521) crystal faces of α-MnO2 were gradually strengthened, indicating the increased content of α-MnO2. When the molar ratio of Nb/Mn increased to 0.005 or even 0.01, the amount of α-MnO2 dominated the mass of the mixture. In short, the product was a mixture of β-MnO2 and α-MnO2 under the hydrothermal reaction at 180 °C, and β-MnO2 was the dominant one. With the incorporation of Nb, the content of β-MnO2 gradually decreased, while α-MnO2 increased. In the reaction solution, KMnO4 was reduced to {MnOx}. Nb5+ could not exist as ions in the aqueous solution, so the complexation reaction occurred, and a complex Nb5+{MnOx}4 was formed. In the complex, Nb5+ ions were four-coordinated in a square planar. The complex formed the 2 × 2 tunnel structure, and Nb ions occupied the centre of the tunnel. Based on the complex, Nb5+ ions were used as permanent templates, and the crystal then grew in the c direction, which generated α-MnO2.31,33 When the doping content was low, the samples showed a mixture of β-MnO2 and α-MnO2. When the doping content was increased, the dominant products were α-MnO2. A similar crystal transformation was observed in the cerium-doped manganese dioxide.32 Meantime, compared with a high resistance of the [1 × 1] tunnel in β-MnO2, Zn2+ can be reversibly inserted/extracted in the [2 × 2] tunnel of α-MnO2.10,33,34The Raman spectra of MnO2 with Nb doping are shown in Fig. 2a. The three characteristic peaks at 500–510, 575–585, and 625–650 cm−1 were attributed to the bending vibration of Mn–O–Mn in [MnO6], telescopic vibration of ν3(Mn–O) at the base of octahedral structure, and symmetric telescopic vibration ν2(Mn–O) of group [MnO6], respectively.35,36 The absence of the Raman activity signature of Nb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds (NbO2+, NbO2+, amorphous Nb2O5) in the 1000 cm−1 region suggests that no additional niobium oxide was present.29,35,37 The binding energy (BE) values of the Nb 3d5/2 peaks were concentrated at 206 eV (Fig. 2b), indicating that the oxidation state of niobium in all doped samples was +5.29,38 The empirical formula for the average oxidation state (AOS) of manganese was 8.956–1.126 × ΔE (ΔE is the difference of binding energy between the two characteristic peaks of Mn 3s in the XPS spectrum),39 whereas ΔE for all the samples can be available from Fig. 2c. The AOS of Mn in MnO2 with different Nb/Mn molar ratio are 3.84, 3.81, 3.78, and 3.76, respectively (listed in Table 1), suggesting that Mn in the synthesized compounds had mixed valences of +4 and +3. The decrease in AOS compared with the undoped one means that Mn vacancies were created by Nb doping. Meanwhile, the proportion of manganese vacancies was created with the increase in Nb doping. The results show that the diffusion of Zn2+ in an ideal spinel structure is very difficult. The manganese vacancies in the spinel structure can reduce the electrostatic barrier of Zn2+ and increase the diffusion of Zn2+.40
O bonds (NbO2+, NbO2+, amorphous Nb2O5) in the 1000 cm−1 region suggests that no additional niobium oxide was present.29,35,37 The binding energy (BE) values of the Nb 3d5/2 peaks were concentrated at 206 eV (Fig. 2b), indicating that the oxidation state of niobium in all doped samples was +5.29,38 The empirical formula for the average oxidation state (AOS) of manganese was 8.956–1.126 × ΔE (ΔE is the difference of binding energy between the two characteristic peaks of Mn 3s in the XPS spectrum),39 whereas ΔE for all the samples can be available from Fig. 2c. The AOS of Mn in MnO2 with different Nb/Mn molar ratio are 3.84, 3.81, 3.78, and 3.76, respectively (listed in Table 1), suggesting that Mn in the synthesized compounds had mixed valences of +4 and +3. The decrease in AOS compared with the undoped one means that Mn vacancies were created by Nb doping. Meanwhile, the proportion of manganese vacancies was created with the increase in Nb doping. The results show that the diffusion of Zn2+ in an ideal spinel structure is very difficult. The manganese vacancies in the spinel structure can reduce the electrostatic barrier of Zn2+ and increase the diffusion of Zn2+.40
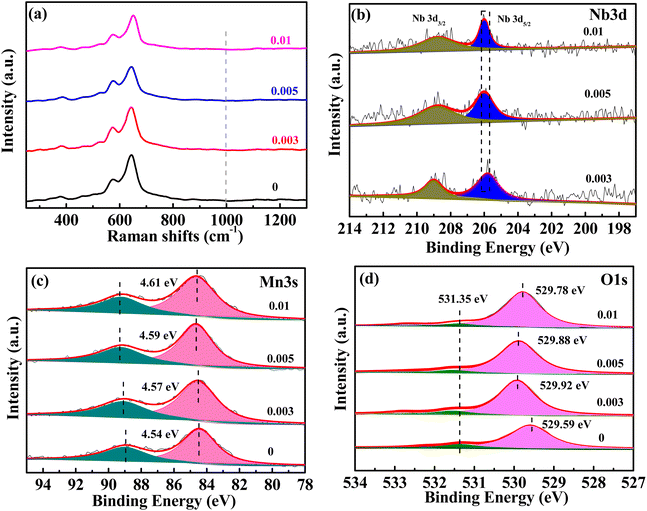 | ||
| Fig. 2 Raman spectra (a), XPS spectra for Nb 3d (b), Mn 3s (c), and O 1s (d) of MnO2 with different Nb/Mn molar ratios. | ||
| Sample | AOS of Mn | BE of OL | Nb/Mn molar ratio (ICP-OES) | Specific surface area (m2 g−1) |
|---|---|---|---|---|
| 0 | 3.84 | 529.59 | 4.7 | |
| 0.003 | 3.81 | 529.92 | 0.004 | 15.6 |
| 0.005 | 3.78 | 529.88 | 0.006 | 21.5 |
| 0.01 | 3.76 | 529.78 | 0.01 | 40.9 |
The XPS spectra of O 1s (Fig. 2d) can be resolved to lattice oxygen (OL) at approximately 529 eV and adsorbed oxygen (labeled as OA) at approximately 531–532 eV.37 As the Nb ions were doped into MnO2, the BE of O 1s was increased to a higher value, which indicated that Nb5+ doping enhanced the stability of MnO2. The BE of the lattice oxygen was 529.92 eV for the 0.003 sample, which was the highest for the doped samples, indicating the most stability. As the Nb/Mn molar ratio was increased to 0.005 and 0.01, the BE decreased gradually. Inserting Nb into the tunnel space of α-MnO2 has a dual effect, one creates manganese vacancies, which causes structural instability, and the other acts as tunnel pillars, which can stabilize the structure. With increased Nb doping, the instability caused by a higher amount of manganese vacancies outweighs the structural stability caused by tunnel pillars, thus, leading to the decreasing trend of the binding energy of lattice oxygen for 0.005 and 0.01 samples. The Nb/Mn molar ratio was measured by ICP-OES and the corresponding values are 0.004, 0.006, and 0.01 (Table 1), which are very close to the theoretical values of 0.003, 0.005, and 0.01, respectively, indicating that the niobium in LiNbO3 is almost completely doped into MnO2. Nb doping results in the creation of manganese vacancy defects, thus increasing the specific surface area of the material (Table 1).
Based on the previous analysis, the 0.003 sample was selected for further TEM and HRTEM morphology characterization and compared with the undoped one, as shown in Fig. 3. The samples were all nanorod-like structures (Fig. 3a and c); however, the Nb-doped material was shorter and thicker (Fig. 3c). The lattice stripes of α-MnO2 and β-MnO2 can be observed in Fig. 3b, meaning that the undoped sample is a mixture of the two types of MnO2, which is consistent with the detection results of XRD. The picture shows good crystallinity with few defects. As for the Nb-doped sample (Fig. 3d), the (200) crystal plane spacing of α-MnO2 was measured as 0.54 nm, which is higher than that of 0.49 nm. As shown in Fig. 3b, the (101) crystal plane spacing of β-MnO2 was measured as 0.25 nm, which is close to that of 0.24 nm in Fig. 3b, indicating that Nb(V) was mainly doped into the α-MnO2 crystal lattice. This may be due to the fact that the [2 × 2] tunnel in α-MnO2 can accommodate Nb (+5), with a large ion radius of 69 pm. Meanwhile, the lattice fringes in Fig. 3d are very blurry, and only a few areas can be observed clearly, indicating the poor crystallization of the material and more defects. According to the explanation of XPS, these defects are related to manganese vacancies induced by high oxidation niobium doping.
 | ||
| Fig. 3 TEM and HRTEM morphology of samples with Nb/Mn molar ratios of 0 (a and b), and 0.003 (c and d). | ||
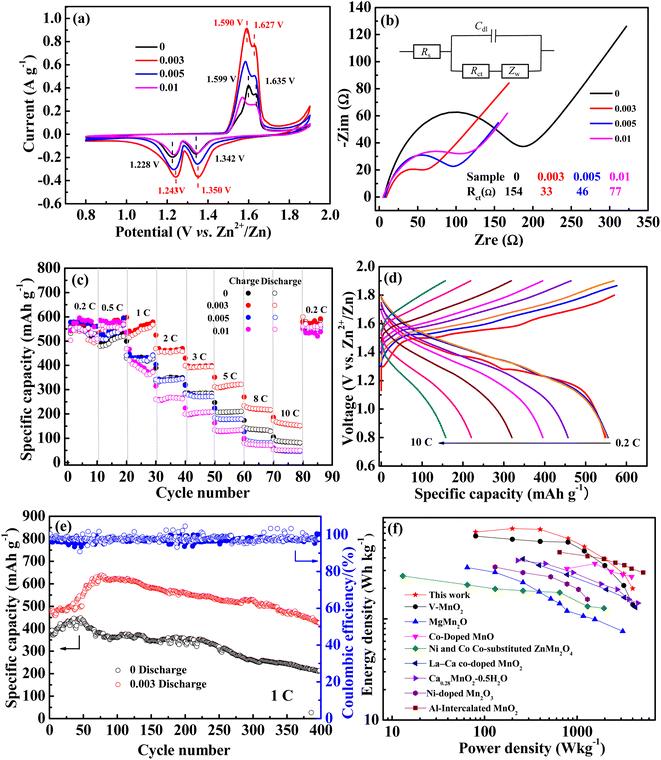
Cyclic voltammetry (CV) was performed and the results are shown in Fig. 4a. The reduction peaks of the undoped sample are located at 1.342 V and 1.228 V (denoted as R1 and R2), which are widely believed to be the insertion of H+ and Zn2+, respectively, into the crystal lattice of MnO2. The oxidized peaks are located at 1.599 and 1.635 V (denoted as O2 and O1), corresponding to the deintercalation of H+ and Zn2+, respectively.41 The related potential difference of the redox peaks was calculated to be 0.293 and 0.371 V. With niobium doping, the CV curves exhibited a similar shape to that of undoped MnO2, but the peak potential varies to different degrees. As for the 0.003 sample, the reduction potentials of R1 and R2 shift positively and the oxidation potentials of O2 and O1 shift negatively, which are 1.350, 1.243, 1.590, and 1.627 V, respectively. The corresponding potential difference of the redox peak values are 0.277 and 0.347 V, which are less than those of the undoped ones. Meanwhile, the peak current was the highest. All the analysis indicated the better reversibility of the sample with an Nb/Mn mole ratio of 0.003. Something else to note is that no other redox peaks appeared in all CV curves, indicating that Nb(V) doped in MnO2 was not involved in the charge–discharge reaction.
EIS tests were employed to study the kinetic performance. The corresponding Nyquist curves are displayed in Fig. 4b and the related equivalent circuit is presented as the inset. In addition, the fitted charge transfer impedances (Rct) are listed. As can be seen, the Rct of undoped MnO2 was 157 Ω and the Nb-doped MnO2 showed much lower values, arranged in an order of 0.003 sample (33 Ω) < 0.005 sample (46 Ω) < 0.01 sample (77 Ω). This indicated that Nb doping is indeed beneficial in reducing the charge transfer impedance, thus enhancing the electrochemical kinetic performance of MnO2.
The rate performance is shown in Fig. 4c. At low rates of 0.2 and 0.5C, the charge–discharge curves of all samples are highly superimposed, with similar performance and little deviation. With the rate increasing, the specific capacity gradually decreased and it was back to 0.2C again, it returned to the original level. For the undoped MnO2, the discharge-specific capacities gradually decreased to 416, 346, 283, 208, 135, and 86 mA h g−1 at 1, 2, 3, 5, 8, and 10C. However, as for the 0.003 sample, it was 567, 453, 393, 322, 227, and 167 mA h g−1 respectively, which was significantly higher than that of undoped MnO2. The corresponding charge–discharge curves at various rates are shown in Fig. 4d. The specific capacities are nearly equal at 0.2, 0.5, and 1C, suggesting that when charged and discharged at low and medium rates, the battery has good rate performance. In general, for all samples, the order of rate performance is 0.003 > 0.005 ≈ 0 > 0.01.
Through the above analysis, it can be seen that the 0.003 sample has better kinetic performance and rate performance. Inserting Nb into the tunnel of MnO2 can reduce the diffusion resistance of Zn2+ by the produced Mn vacancies. However, as tunnel pillars, they can also increase the resistance for the insertion/deintercalation of Zn2+. With a higher Nb doping amount, the resistance increases with more Nb pillars in the tunnel, which counteracts the reduction of the resistance by Mn vacancies, thus leading to the inferior performance of 0.005 and 0.01 samples.
The cycle performances of 0.003 and 0 samples at 1C are shown in Fig. 4e. For both, the specific capacity gradually increases in the initial cycle. For the undoped sample, it increased from 388 to 488 mA h g−1 after 48 cycles, and for the 0.003 sample, it changed from 480 to 638 mA h g−1 after 80 cycles. The increased specific capacity as proceeded cycles should be attributed to MnSO4 pre-added in the electrolyte. As is known, Mn2+ in manganese oxide will be dissolved in an aqueous electrolyte gradually as a discharge process, thus leading to the reduction of the active substances and the decay of cycling properties, and the pre-added MnSO4 can effectively inhibit the dissolution of Mn2+.18,19 Meanwhile, the pre-added Mn2+ will result in the electrodeposition of manganese oxide in the charged process, thereby causing an increment of the active substance and specific capacity.41 Obviously, compared with the undoped sample (100 mA h g−1, 25%), the higher increment specific capacity of the doped MnO2 (158 mA h g−1, 33%) may be attributed to its relatively high specific surface area caused by the manganese vacancy defects. After the initial increase in specific capacity, it gradually began to decline. After 400 cycles, the remaining specific capacity for the 0.003 and undoped samples was 426 and 214 mA h g−1, with 89% and 61% of the capacity retention rate, respectively. It can be concluded that Nb doping can effectively reduce the performance degradation of manganese-based materials in the cycling process, which may be attributed to the niobium that pre-intercalated into the tunnel space as pillars.
A comparison of high-oxidization Nb(V) doping with other studies on the modification of MnO2 by cationic doping is shown in Fig. 4f. A sample with an Nb/Mn molar ratio of 0.003 exhibited better energy densities than other low-oxidization cationic doping electrodes at power densities of 80, 200, 400, 800, 1200, and 2000 W kg−1 (based on the mass of the active material in the cathode). Even compared with the electrode doped with high oxidization vanadium(V), its energy density is much higher.
The structure of the 0.003 sample after cycling at 1C was characterized to evaluate its stability. ε-MnO2 (PDF #30-0820) was detected by XRD tests (Fig. 5a), and the stronger the characteristic peaks were as the cycles increased, indicating the deposition of more ε-MnO2. As can be seen from Fig. 5b, ε-MnO2 deposited as nano-sheets, resulting in an increase in the active substance, thus increasing the discharge capacity. As the cycle number was increased to 50 times (Fig. 5c), the nanosheets became more regular and smooth with a larger specific surface area and higher capacity. As cycles continued to increase (Fig. 5d), the nanosheets were gradually granulated, leading to the enhancement of electron/ion conduction resistance; therefore, the cycle performance decreased. After 200 cycles (Fig. 5e), the nanosheet structure collapsed, and the specific surface area of the nanoparticles on the electrode decreased significantly, resulting in the further deterioration of the cycling performance (Fig. 4e).
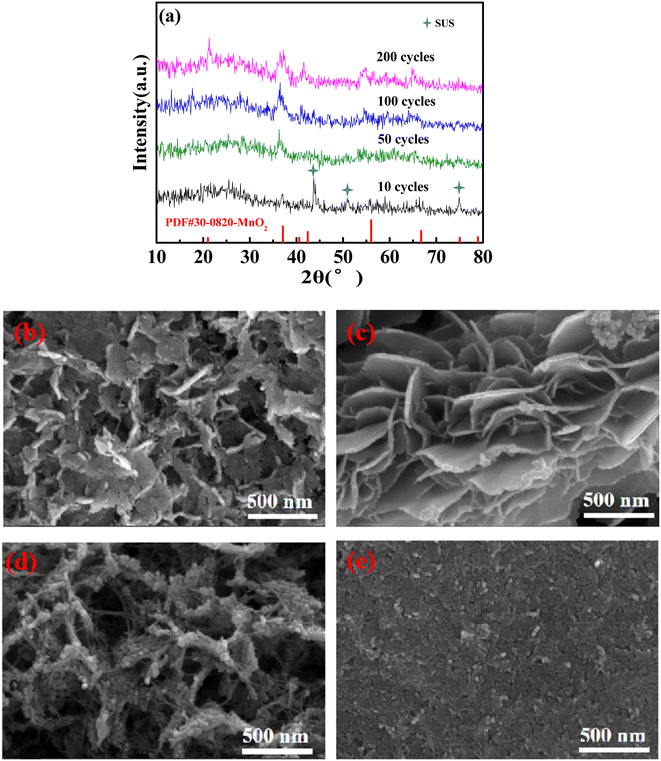 | ||
| Fig. 5 XRD patterns (a) and SEM morphology of the 0.003 sample recharging 1.9 V after 10 cycles (b), 50 cycles (c), 100 cycles (d), and 200 cycles (e) at 1C. | ||
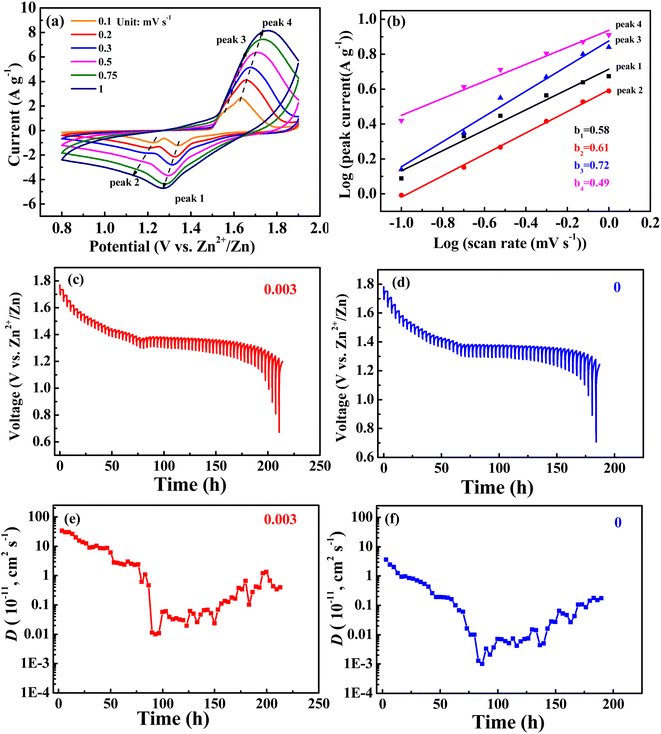
CV curves at different sweep velocities (0.1, 0.2, 0.3, 0.5, 0.75, and 1 mV s−1) and constant current intermittent titration (GITT) curves for the 0.003 sample are shown in Fig. 6. In the CV curve, the relationship between peak current (i) and scanning speed (υ) is as follows: i = aυb, that is, log(i) = log(a) + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(υ), when the slope b of the fitting curve between log(i) and log(υ) is 0.5, representing a diffusion-controlled reaction, and 1.0 represents a capacitive behavior.31 The fitting curves of the peak currents with sweep velocities for peaks 1, 2, 3, and 4 from Fig. 6a are shown in Fig. 6b, with corresponding b values of 0.58, 0.61, 0.72, and 0.49, respectively. The results suggest that the electrode reaction is not only controlled by diffusion but also by capacitance behavior, however, diffusion controls dominate.
log(υ), when the slope b of the fitting curve between log(i) and log(υ) is 0.5, representing a diffusion-controlled reaction, and 1.0 represents a capacitive behavior.31 The fitting curves of the peak currents with sweep velocities for peaks 1, 2, 3, and 4 from Fig. 6a are shown in Fig. 6b, with corresponding b values of 0.58, 0.61, 0.72, and 0.49, respectively. The results suggest that the electrode reaction is not only controlled by diffusion but also by capacitance behavior, however, diffusion controls dominate.
For the GITT test, the battery was first cycled at 0.2C until a state of equilibrium was reached and then discharged at 0.1C for 20 min. Thereafter, it was rested for 3 h until the battery reached equilibrium. The process was repeated until 0.8 V of the discharge voltage was reached. The GITT curves are shown in Fig. 5c and d. The formula for obtaining the diffusion coefficient D from the GITT curve is as follows:31
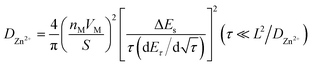 | (1) |
4. Conclusion
For the first time, high-oxidation niobium(V) was used for doping manganese dioxide and it completely doped into the manganese dioxide lattice by a simple hydrothermal reaction process. As niobium(V) was incorporated into the [2 × 2] tunnel of α-MnO2, it induced manganese vacancies, which reduced the diffusion resistance of Zn2+ in manganese dioxide, improved the migration kinetics; and in the meantime, it acted as tunnel pillars, avoiding the collapse of the tunnel structure during the repeated insertion/extraction of the Zn2+ process, preventing a rapid degradation of the cycling performance. As for the Nb–Mn molar ratio of the 0.003 sample, it presented the best rate and cycling performance. Its energy density was higher than that of other cationic-doped manganese dioxide at the same power density.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by the High-Level Talent Introduction Project (Grant No. 205190161) of Leshan Normal University, supported by Innovation Training Program for College Students (Grant No. S202310649200) of Leshan Normal University, supported by the Opening Project of Material Corrosion and Protection Key Laboratory of Sichuan Province (Grant No. 2022CL30), supported by the Opening Project of Crystalline Silicon Photovoltaic New Energy Research Institute (Grant No. 2022CHXK003), and 2022-Key Research Project of Leshan Science and Technology Bureau (Grant No. 22ZDYJ0091).References
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC.
- J. F. Parker, C. N. Chervin and I. R. Pala, Science, 2017, 356, 415–418 CrossRef CAS PubMed.
- M. H. Alfaruqi, V. Mathew and J. Song, Chem. Mater., 2017, 29, 1684–1694 CrossRef CAS.
- Y. Sun, Z. Xu, X. Xu, Y. Nie, J. Tu, A. Zhou, J. Zhang, L. Qiu, F. Chen, J. Xie, T. Zhu and X. Zhao, Energy Storage Mater., 2022, 48, 192–204 CrossRef.
- T. He, S. Weng, Y. Ye, J. Cheng, X. Wang and B. Wang, Energy Storage Mater., 2021, 38, 389–396 CrossRef.
- M. Du, Z. Miao, H. Li, F. Zhang, Y. Sang, L. Wei, H. Liu and S. Wang, Nano Energy, 2021, 89, 106477 CrossRef CAS.
- Y. Du, X. Liu, X. Wang, J. Sun, Q. Lu, J. Wang, A. Omar and D. Mikhailova, Rare Met., 2022, 41, 415–423 CrossRef CAS.
- X. Gao, H. Wu and W. Li, Small, 2020, 16, 1905842 CrossRef CAS PubMed.
- W. Liu, X. Zhang, Y. Huang, B. Jiang, Z. Chang, C. Xu and F. Kang, J. Energy Chem., 2021, 56, 365–373 CrossRef CAS.
- M. H. Alfaruqi, V. Mathew and J. Gim, Chem. Mater., 2015, 27, 3609–3620 CrossRef CAS.
- M. H. Alfaruqi, J. Gim and S. Kim, Electrochem. Commun., 2015, 60, 121–125 CrossRef CAS.
- C. Yuan, Y. Zang and Y. Pan, Electrochim. Acta, 2014, 116, 404–412 CrossRef CAS.
- L. Huang, X. Luo and C. Chen, Ionics, 2021, 27, 3933–3941 CrossRef CAS.
- R. Liang, J. Fu, Y. Deng, Y. Pei, M. Zhang, A. Yu and Z. Chen, Energy Storage Mater., 2021, 36, 478–484 CrossRef.
- K. Sun, Y. Shen, J. Min, J. Pang, Y. Zheng, T. Gu, G. Wang and L. Chen, Chem. Eng. J., 2023, 454, 140394 CrossRef CAS.
- X. Zhai, J. Qu, J. Wang, W. Chang, H. Liu, Y. Liu, H. Yuan, X. Li and Z. Yu, Energy Storage Mater., 2021, 42, 753–763 CrossRef.
- C. Qiu, X. Zhu, L. Xue, M. Ni, Y. Zhao, B. Liu and H. Xi, Electrochim. Acta, 2020, 351, 136445 CrossRef CAS.
- M. Chamouna, W. R. Brantb, C. Taia, G. Karlssonc and D. Noréus, Energy Storage Mater., 2018, 15, 351–360 CrossRef.
- C. Xu, B. Li, H. Du and F. Kang, Angew. Chem., Int. Ed., 2012, 51, 933–935 CrossRef CAS PubMed.
- M. H. Alfaruqi, S. Islam, D. Y. Putro, V. Mathew, S. Kim, J. Jo, S. Kim, Y. Sun, K. Kim and J. Kim, Electrochim. Acta, 2018, 276, 1–11 CrossRef CAS.
- F. Kataoka, T. Ishida, K. Nagita, V. Kumbhar, K. Yamabuki and M. Nakayama, ACS Appl. Energy Mater., 2020, 3, 4720–4726 CrossRef CAS.
- D. Zhang, J. Cao, X. Zhang, N. Insin, S. Wang, J. Han, Y. Zhao, J. Qin and Y. Huang, Adv. Funct. Mater., 2021, 1, 2009412 CrossRef.
- Y. Tao, Z. Li, L. Tang, X. Pu, T. Cao, D. Cheng, Q. Xu, H. Liu, Y. G. Wang and Y. Xi, Electrochim. Acta, 2020, 331, 135296 CrossRef CAS.
- T. Sun, Q. Nian, S. Zheng, J. Shi and Z. Tao, Small, 2020, 16, 2000597 CrossRef CAS PubMed.
- V. Soundharrajan, B. Sambandam, S. Kim, V. Mathew, J. Jo, S. Kim, J. Lee, S. Islam, K. Kim, Y. K. Sun and J. Kim, ACS Energy Lett., 2018, 3, 1998–2004 CrossRef CAS.
- C. Chen, M. Shi, Y. Zhao, C. Yang, L. Zhao and C. Yan, Chem. Eng. J., 2021, 422, 130375 CrossRef CAS.
- W. Wu, J. Luo, H. Zhang, J. Liu, X. Liu, Y. Yang, X. Lu and M. Zhang, J. Mater. Chem. A, 2020, 8, 11642–11648 RSC.
- L. Huang, L. Yi, Y. Chen, Y. Wu, Y. Hu, X. Luo and C. Chen, J. Alloys Compd., 2023, 946, 169386 CrossRef CAS.
- T. Xiong, Y. Zhang, W. S. V. Lee and J. Xue, Adv. Energy Mater., 2020, 1, 2001769 CrossRef.
- L. Song, Y. Duan, J. Liu and H. Pang, Nano Res., 2020, 13, 95–104 CrossRef CAS.
- J. Wang, X. Sun, H. Zhao, L. Xu, J. Xia, M. Luo, Y. Yang and Y. Du, J. Phys. Chem. C, 2019, 123, 22735 CrossRef CAS.
- C. Xu, B. Li, H. Du and F. Kang, Angew. Chem., Int. Ed., 2012, 51, 933–935 CrossRef CAS PubMed.
- H. R. Lee, H. Kim, K. Y. Chung, B. W. Cho and S. H. Oh, Chem. Commun., 2015, 51, 9265–9268 RSC.
- M. Polverejan, J. C. Villegas and S. L. Sui, J. Am. Chem. Soc., 2004, 126, 7774–7775 CrossRef CAS PubMed.
- C. Juliena, M. Massot, R. B. Hadjean, S. Franger, S. Bach and J. P. Pereira-Ramos, Solid State Ionics, 2003, 159, 345–356 CrossRef.
- L. Sun, Q. Cao, B. Hu, J. Li, J. Hao, G. Jing and X. Tang, Appl. Catal., A, 2011, 393, 323–330 CrossRef CAS.
- G. Silversmit, D. Depla, H. Poelman, G. B. Marin and R. D. Gryse, J. Electron Spectrosc. Relat. Phenom., 2004, 135, 167–175 CrossRef CAS.
- V. R. Galakhov, M. Demeter and S. Bartkowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 113102 CrossRef.
- N. Zhang, F. Cheng, Y. Liu, Q. Zhao, K. Lei, C. Chen, X. Liu and J. Chen, J. Am. Chem. Soc., 2016, 138, 12894–12901 CrossRef CAS PubMed.
- W. Sun, F. Wang, S. Hou, C. Yang, X. Fan, Z. Ma, T. Gao, F. Han, R. Hu, M. Zhu and C. Wang, J. Am. Chem. Soc., 2017, 139, 9775–9778 CrossRef CAS PubMed.
- H. L. Pan, Y. Y. Shao and P. F. Yan, Nat. Energy, 2016, 1, 16039–16045 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |