Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
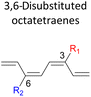
A computational investigation towards substitution effects on 8π electrocyclisation of conjugated 1,3,5,7-octatetraenes†
Nur Hazimah B. Z. Arfan,
Malai Haniti S. A. Hamid and
Nadeem S. Sheikh
and
Nadeem S. Sheikh *
*
Chemical Sciences, Faculty of Science, Universiti Brunei Darussalam, Jalan Tungku Link, Gadong, BE1413, Brunei Darussalam. E-mail: nadeem.sheikh@ubd.edu.bn
First published on 20th October 2023
Abstract
A computational investigation using M06-2X/6-31+G(d) method is reported for the substitution effects on 8π electrocyclisation of conjugated octatetraene. This systematic study describes the mono- and di-substitution effect across the 1,3,5,7-octatetraene skeleton. A general preference of the outward substitution over the inward, at C1 position of the monosubstituted system is observed. However, mesomerically electron donating group (–NH2 and –OH) display an opposite effect with respect to secondary orbital interaction (SOI) between the lone pair on the substituent and the 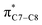 orbital. A comparative evaluation on the computed activation energies for the 1-, 2-, 3-, and 4-monosubstituted system showed an insignificant impact on the rate of the reaction, in contrast to the electrocyclic ring closure of the unsubstituted compound. Computations of disubstituted system are more pronounced, where a remarkable acceleration is observed for 2-NO2–7-NO2 substituted octatetraene at 4.9 kcal mol−1, and a noticeable deceleration for 4-CH3–5-CH3 substituted octatetraene at 25.4 kcal mol−1 from the parent molecule, 17.0 kcal mol−1. A visible accelerated effects are commonly exhibited by the substitution on the terminal double bonds (C1, C2, C7, and C8), that are 1,2-, 1,7-, 1,8-, and 2,7-patterns, in regard to the greater orbital interaction for the new σ-bond formation. Despite the unfavourable steric clashes of the substituents in the 1,8-system, an apparent reduction in the energy barrier up to 7.4 kcal mol−1 is computed for 1-NH2–8-NO2 system from 17.0 kcal mol−1. This is due to the synergistic effect of the electron donor and electron acceptor, enhancing the stability of the transition structure. The electrocyclic ring closure involving vicinal substitution patterns, such as 1,2-, 2,3-, 3,4-, and 4,5-systems are critically dominated by steric crowding between the adjacent functional groups. In certain cases of the 1,2-substituted system, a noticeable accelerated effects are found for 1-NH2–2-NH2-substituted compound (9.7 kcal mol−1) due to an increased in electronic density on the substituted terminal double bond (C1–C2), hence favouring the formation of the new σ-bond.
orbital. A comparative evaluation on the computed activation energies for the 1-, 2-, 3-, and 4-monosubstituted system showed an insignificant impact on the rate of the reaction, in contrast to the electrocyclic ring closure of the unsubstituted compound. Computations of disubstituted system are more pronounced, where a remarkable acceleration is observed for 2-NO2–7-NO2 substituted octatetraene at 4.9 kcal mol−1, and a noticeable deceleration for 4-CH3–5-CH3 substituted octatetraene at 25.4 kcal mol−1 from the parent molecule, 17.0 kcal mol−1. A visible accelerated effects are commonly exhibited by the substitution on the terminal double bonds (C1, C2, C7, and C8), that are 1,2-, 1,7-, 1,8-, and 2,7-patterns, in regard to the greater orbital interaction for the new σ-bond formation. Despite the unfavourable steric clashes of the substituents in the 1,8-system, an apparent reduction in the energy barrier up to 7.4 kcal mol−1 is computed for 1-NH2–8-NO2 system from 17.0 kcal mol−1. This is due to the synergistic effect of the electron donor and electron acceptor, enhancing the stability of the transition structure. The electrocyclic ring closure involving vicinal substitution patterns, such as 1,2-, 2,3-, 3,4-, and 4,5-systems are critically dominated by steric crowding between the adjacent functional groups. In certain cases of the 1,2-substituted system, a noticeable accelerated effects are found for 1-NH2–2-NH2-substituted compound (9.7 kcal mol−1) due to an increased in electronic density on the substituted terminal double bond (C1–C2), hence favouring the formation of the new σ-bond.
1. Introduction
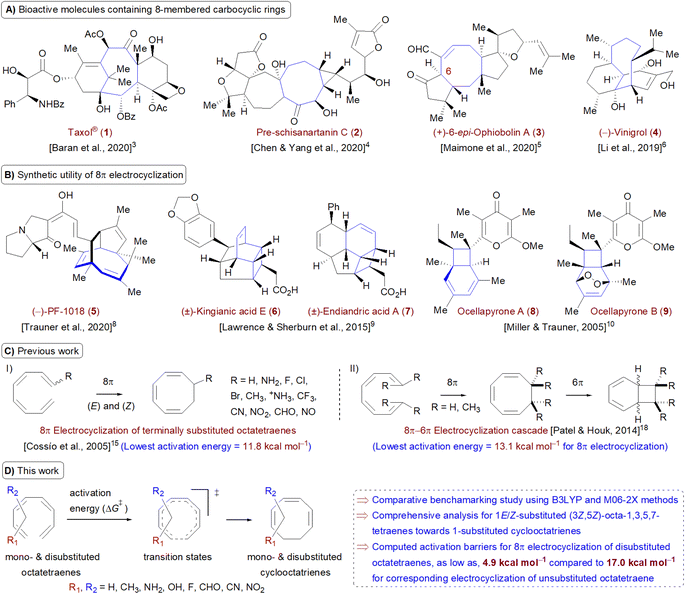
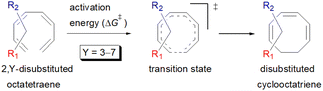
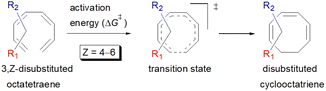
Carbocycles1 are structurally diversified motifs, which are ubiquitously present in bioactive natural products and cytotoxic molecules. Amongst them, 8-membered carbocyclic compounds2 such as taxol® (1),3 pre-schisanartanin C (2),4 (+)-6-epi-ophiobolin A (3)5 and (−)-vinigrol (4,6 Fig. 1A) are of great synthetic interest due to presence of synthetically challenging architectural features and substantial medicinal relevance. One of the elegant approaches to access these carbocycles is 8π electrocyclisation7 of conjugated tetraenes, which has been elegantly applied to synthesize several structurally complex potent compounds including (−)-PF-1018 (5),8 (±)-kingianic acid E (6),9 (±)-endiandric acid A (7),9 ocellapyrone A (8)10 and ocellapyrone B (9, Fig. 1B).In general, electrocyclisation11 is a powerful methodology to construct polycyclic scaffolds with highly efficient atom economy.12 It proceeds with an excellent and predictable regio- and stereocontrol, governed by Woodward–Hoffmann's rules.13 According to these rules, electrocyclic ring closure of conjugated octatetraenes with 8π system is a thermally induced conrotatory process, which involves spontaneous rotation of the terminal olefin bonds of a tetraene. Particularly, the steric effect, electronic properties and torquoselectivity14 (inward/outward rotation) of the substituents located at the C-atoms subjected to electrocyclic transformation (ring-opening or closure) play a vital role in orchestrating the observed stereoselectivities. For the conrotatory electrocyclisation of 1-substituted 1,3,5,7-octatetraenes, a pronounced steric effect of the substituents influences the stereochemical outcomes as reported by Houk and colleagues using ab initio molecular orbital theory.14b In addition, electronic properties of the substituents renders an insignificant effect on stereoselectivities for the octatetraene cyclisation due to dearth of rotational preference caused by the inward and outward substituents located at the terminal C-atoms involved in the bond formation. These findings are in sharp contrast to the conrotatory ring-opening of 3-substituted cyclobutenes, in which, the stereoselectivities are primarily mediated by the electronic nature of the substituents.
Building on the pioneer work championed by Houk et al.,14 Cossío and co-workers exploited the application of density functional theory (DFT) to further elaborate the electrocyclic ring closure for variously 1-substituted octatetraenes (Fig. 1C(I)).15 A detailed investigation suggests complete periselective electrocyclic ring closure of octatetraenes via Möbius aromatic transition structure. With a couple of exceptions (–NH2 and –NH3+ substituents), lower barriers have been found for the transition structures which have substituents at the outward positions and this is independent of the electronic nature of the substituents.
The lowest activation energy (11.8 kcal mol−1) is computed for inward NH3+-substituted octatetraene, which is considerably lower than the measured activation energy for the unsubstituted octatetraene i.e., 17.0 kcal mol−1.16 In addition, rate of reactions for 1,8-dimethyl substituted octatetraene isomers have also been computed, which require substantially higher barrier compared to that of the parent compound. Later, the groups of Schreiner and Suffert applied a computational approach to explore the origin of high torquoselectivities and complete diastereoselectivities observed during the competing synthesis of cyclooctatrienes vs. fenestradienes via 8π electrocyclic transformations.17 As expected, Möbius aromatic transition structures having different P- and M-helical topologies led to origin of observed selectivities in the cyclooctatrienes, formed as a result of 8π conrotatory electrocyclisation of tetraenes. However, the corresponding fenestradienes are the products of the 8π–6π electrocyclic cascade reactions.
Owing to synthetic utilities and increasing research interests towards 8π–6π electrocyclisation cascade, an inclusive and efficient computational investigation dealing with terminally CH3-substituted 1,3,5,7-octatetraenes has been elegantly reported by Patel and Houk (Fig. 1C(II)).18 The influence of steric crowding at terminal positions of the tetraene is directly linked with the reaction thermodynamics. Formation of corresponding 1,3,5-cyclooctatrienes via 8π electrocyclisation from the un- and monosubstituted tetraenes proceeds rapidly however, 6π electrocyclization leading to highly diastereoselective bicyclic product is relatively slow and reversible. In addition, initial 8π electrocyclisation for di- and trisubstituted reactants is comparatively less exergonic due to destabilization rendered by the steric effect. This leads to an endergonic 8π electrocyclic product for tetrasubstituted tetraene however, the overall reaction involving this cascade still remains exergonic and yields a bicyclic product containing two vicinal quaternary centers.
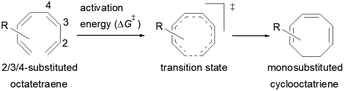
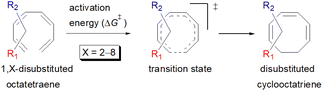
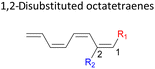
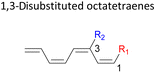
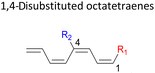
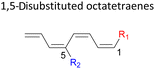
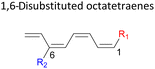
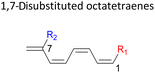
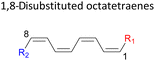
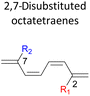
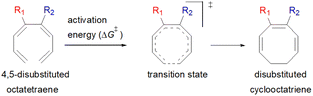
Here, a systematic and succinct DFT study is reported which delineates the mono- and disubstitution effect across the skeleton of 1,3,5,7-octatetraenes (Fig. 1D). Such an effect has already been reported for thermal conrotatory 4π electrocyclic ring-opening of substituted cyclobutenes19 and thermal disrotatory 6π electrocyclic ring-closure of 1,3,5-hexatrienes.20
To start with, a selection of commonly used substituents ranging from electron donating to withdrawing substituents have been subjected to this study. A remarkable accelerated substitution effect has been noticed that lowers the activation free energy for the 8π electrocyclisation up to 4.9 kcal mol−1 compared to 17.0 kcal mol−1, experimentally measured for the unsubstituted 1,3,5,7-octatetraenes.16 At the same time, certain disubstituted patterns produce negative effect, leading to a noticeable increase in the activation barriers; the maximum computed to be 23.6 kcal mol−1.
2. Results and discussion
2.1 8π electrocyclisation of unsubstituted 1,3,5,7-octatetraenes
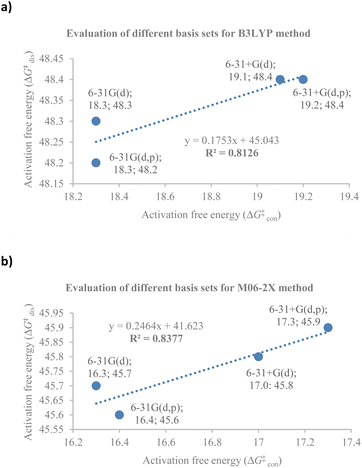
At the outset, a detailed comparative benchmarking study was envisaged as both B3LYP and M06-2X methods have been reported for the electrocyclisation of octatetraenes (Table 1).15,18 For an extensive and systematic study of a particular transformation, as it is, computational expense plays a crucial role, as well as, evaluation of calculations with the experimental values. Several basis sets were selected for both methods to find an appropriate computational approach for further investigation. It is evident from this study that B3LYP method overestimates the barrier for tetraene by ∼2 kcal mol−1 compared to M06-2X method. With the same time, a significant difference in reaction energies have been observed for both methods. Apparently, B3LYP method fails to accurately compute the reaction thermodynamics by showing approximate thermoneutral behaviour of electrocyclisation while M06-2X method, as expected, describes the exergonic nature of the 8π electrocyclisation of unsubstituted 1,3,5,7-octatetraenes.| Entry | Basis set | B3LYP | M06-2X | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ΔG‡ | ΔΔG‡a | ΔG | C1–C8b | ΔG‡ | ΔΔG‡a | ΔG | C1–C8b | ||
| a Activation energy difference between the disrotatory and conrotatory electrocyclic ring closures.b Bond distance values are for the conrotatory and disrotatory (in parentheses) electrocyclic transition states and in Å. | |||||||||
| 1 | 6-31G(d) | 18.3 (48.3) | 30.0 | −3.8 (−1.3) | 2.36301 (2.37609) | 16.3 (45.7) | 29.4 | −11.3 (−9.1) | 2.34510 (2.30942) |
| 2 | 6-31+G(d) | 19.1 (48.4) | 29.3 | −2.2 (0.3) | 2.36304 (2.39441) | 17.0 (45.8) | 28.8 | −9.9 (−7.8) | 2.34147 (2.32612) |
| 3 | 6-31G(d,p) | 18.3 (48.2) | 29.9 | −3.4 (−0.9) | 2.35405 (2.37660) | 16.4 (45.6) | 29.2 | −10.9 (−8.7) | 2.33886 (2.31052) |
| 4 | 6-31+G(d,p) | 19.2 (48.4) | 29.2 | −1.6 (0.9) | 2.33727 (2.39580) | 17.3 (45.9) | 28.6 | −9.2 (−7.2) | 2.33415 (2.32772) |
| 5 | Experimental16 | 17.0 | |||||||
Compared to experimental result, M06-2X/6-31+G(d) is the most appropriate basis set for the unsubstituted 1,3,5,7-octatetraenes (entry 2, Table 1). It is worth noticing that an absence of diffused function (entry 1, Table 1) and addition of polarization function to the hydrogen atoms (entry 3, Table 1) result in lower activation barriers compared to experimental value. At the same time, basis set containing both diffused and polarizations functions for heavy and hydrogen atoms offer slightly higher barrier (entry 4, Table 1). The reaction preferably proceeds through the helical shaped TS,21 which is associated with the conrotatory electrocyclisation of tetraene. In addition, disrotatory movement of molecular orbitals would undergo via deformed boat-shaped TS of the 1,3Z,5E,7-octatetraenes and has significantly higher activation barrier, as reported by Cossío et al.15
For the optimum method concluded from this benchmarking study [M0-62X/6-31+G(d)], the activation energy difference between the conrotatory and disrotatory TSs is 28.8 kcal mol−1, which is substantially higher than the measured activation energy i.e., 17.0 kcal mol−1.16 More or less, similar difference in the activation barriers is observed for all the basis sets considered for this study.
Further comparative analysis between B3LYP and M06-2X methods reveals a good correlation between the activation barriers for the conrotatory and disrotatory electrocyclisation using different basis sets for B3LYP method (Fig. 2a) and the corresponding M06-2X method (Fig. 2b). There is a strong correlation between the activation and reaction energies for the conrotatory electrocyclisation, however poor correlation was found for the disrotatory process.
2.2 8π electrocyclisation of monosubstituted 1,3,5,7-octatetraenes
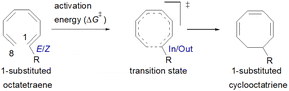
The computational results of thermally allowed conrotatory 8π electrocyclic ring closure of terminally monosubstituted system using M06-2X/6-31+G(d) method are shown in Table 2. The rate of these octatetraene cyclisation is determined by the outward or inward arrangement of the substituent on the system. Cossío et al. has identified a general preference of the outward attachment over the inward, as a consequence of lower steric crowding experienced by the substituent in the transition state.15 Such interaction renders slight stabilization to the outward transition structure, which was reflected by the lower computed activation barrier regardless of its electron donating or electron accepting character. Our computational findings have also shown similar trends. A minor preference of 1.5 to 2.6 kcal mol−1 lower than the computed activation energies for the substituent to be in the inside position are recorded. Consequently, the stereochemical outcomes of these electrocyclic reactions are directed by the steric effects.| Entry | R | ΔG‡(out TS)b | ΔG‡(In TS)c | ΔG‡(in–out)d | ΔG(1E)e | ΔG(1Z)e | C1–C8(out TS)f | C1–C8(In TS)f | R–C8(out TS)f | R–C8(In TS)f |
|---|---|---|---|---|---|---|---|---|---|---|
| a For computed values using M06-2X/6-31+G(d,p), see ESI.b Activation barriers (kcal mol−1) for conrotatory electrocyclisation of (1E)-substituted octatetraenes (outward-substituted transition structures).c Activation barriers (kcal mol−1) for conrotatory electrocyclisation of (1Z)-substituted octatetraenes (inward-substituted transition structures).d Activation energy difference (kcal mol−1) between the inward- and outward-substituted transition structures.e Reaction energies (kcal mol−1) for the electrocyclisation of (1E)- and (1Z)-substituted octatetraenes.f Bond distances are from the corresponding transition states and the values are in Å (for optimized geometries, see ESI). | ||||||||||
| 1 | CH3 | 19.2 | 20.7 | 1.5 | −5.9 | −7.4 | 2.30891 | 2.32493 | 3.09747 | 3.03689 |
| 2 | NH2 | 19.2 | 16.0 | −3.2 | −2.8 | −3.4 | 2.19929 | 2.18498 | 2.94978 | 2.95553 |
| 3 | OH | 17.3 | 14.9 | −2.2 | −7.9 | −7.6 | 2.24732 | 2.20575 | 2.96520 | 2.87002 |
| 4 | F | 16.5 | 19.1 | 2.6 | −12.2 | −11.0 | 2.30316 | 2.27767 | 2.97892 | 2.80513 |
| 5 | CHO | 17.0 | 17.9 | 0.9 | −5.0 | −7.5 | 2.29083 | 2.33002 | 2.97881 | 2.88939 |
| 6 | CN | 18.2 | 19.9 | 1.7 | −5.1 | −5.9 | 2.30282 | 2.31697 | 3.00091 | 2.89120 |
| 7 | NO2 | 16.9 | 18.5 | 1.6 | −9.6 | −12.3 | 2.32672 | 2.38439 | 2.99101 | 2.84308 |
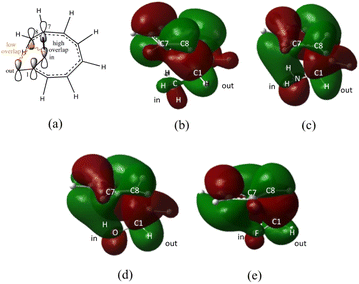
On the other hand, installation of mesomerically electron donating group, –NH2 and –OH group, shows an opposite preference of the torquoselectivity in the electrocyclisation process. Presumably, a secondary orbital interaction (SOI)15 between the lone pair on the functional group and the localized 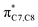 orbital, as shown in Fig. 3, provide extra stabilization to the transition structure. This interaction is favoured by the excellent overlap of the atomic orbital of the inward substituent with the atomic orbital on C7 (Fig. 3a). Moreover, it depends on the capacity of the electron donor character. Introduction of other mesomerically electron donating groups, –CH3 and –F, at the terminal position with an inward substitution does not offer a stabilizing SOI to the transition structures (Fig. 3b and e), particularly due to the weaker electron donating effect. Despite the presence of lone pairs on –F, the large electronegativity demonstrates an inductive effect that lowers the π-donor capability towards the
orbital, as shown in Fig. 3, provide extra stabilization to the transition structure. This interaction is favoured by the excellent overlap of the atomic orbital of the inward substituent with the atomic orbital on C7 (Fig. 3a). Moreover, it depends on the capacity of the electron donor character. Introduction of other mesomerically electron donating groups, –CH3 and –F, at the terminal position with an inward substitution does not offer a stabilizing SOI to the transition structures (Fig. 3b and e), particularly due to the weaker electron donating effect. Despite the presence of lone pairs on –F, the large electronegativity demonstrates an inductive effect that lowers the π-donor capability towards the 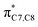 orbital of the terminal double bond (Fig. 3e).
orbital of the terminal double bond (Fig. 3e).
It is noteworthy that the carbonyl (–CHO) and hydroxyl (–OH) functional groups can be oriented in two possible conformations on the tetraene molecule, as was reported in the computational investigation of substituted 4π system paper.19 Hence, lowest energy conformation is used to study the reaction energies. In contrast to the unfunctionalised octatetraene (17.0 kcal mol−1), electronic properties of the substituent in a 1-substituted system hardly affect the rate of the transformation, ranging from 14.9 to 20.7 kcal mol−1. The mild steric effects do bring about the minute preference for the outward mode of rotation of the terminal substituent.
We have also computed the activation and reaction energies of the transition structure with functionality located at 3 other possible positions (C2-, C3-, and C4-position) to extensively study the mono-substituent effect on the reactivity of electrocyclization of the tetraene molecule (Table 3). Based on the computations, electronic properties of the functionality at C2-position are maximized, while the steric effects are minimized. A much larger reduction in the activation energies is observed, contrary to the other monosubstituted systems. At C3- and C4-monosubstituted octatetraenes, the energies are practically indistinguishable from the terminally monosubstituted system. The reasons may be attributed to the inconsequential electronic interaction of the substituent due to an indirect interaction with the terminal double bonds that are involved in the formation of the new σ-bond.
| Entry | R | ΔG‡a | ΔG‡b | Entry | R | ΔG‡a | ΔG‡b | Entry | R | ΔG‡a | ΔG‡b |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a For computed values using M06-2X/6-31+G(d).b For computed values using M06-2X/6-31+G(d,p). | |||||||||||
| 1 | CH3 | 14.5 (−12.4) | 14.7 (−11.9) | 8 | CH3 | 19.1 (−8.3) | 19.2 (−7.7) | 15 | CH3 | 18.0 (−12.0) | 18.0 (−11.5) |
| 2 | NH2 | 15.7 (−12.5) | 15.7 (−12.1) | 9 | NH2 | 19.4 (−6.3) | 19.5 (−5.7) | 16 | NH2 | 18.5 (−11.1) | 18.6 (−10.5) |
| 3 | OH | 17.8 (−11.6) | 18.3 (−10.7) | 10 | OH | 19.1 (−7.6) | 18.2 (−8.0) | 17 | OH | 17.5 (−11.3) | 18.0 (−10.6) |
| 4 | F | 15.8 (−13.5) | 16.0 (−12.9) | 11 | F | 17.3 (−9.8) | 17.5 (−9.2) | 18 | F | 15.1 (−12.2) | 15.3 (−11.6) |
| 5 | CHO | 11.4 (−16.8) | 11.6 (−16.3) | 12 | CHO | 14.9 (−12.5) | 14.1 (−10.7) | 19 | CHO | 14.1 (−13.7) | 14.2 (−13.2) |
| 6 | CN | 14.2 (−13.3) | 14.4 (−12.6) | 13 | CN | 17.9 (−9.1) | 18.0 (−8.5) | 20 | CN | 15.2 (−12.7) | 15.4 (−12.1) |
| 7 | NO2 | 10.2 (−17.2) | 10.5 (−16.6) | 14 | NO2 | 12.1 (−15.2) | 12.3 (−14.7) | 21 | NO2 | 14.8 (−13.4) | 14.8 (−12.9) |
Particularly, incorporating a strong electron-withdrawing group (–CHO and –NO2) at these positions (C2, C3 or C4) reveals an increase in the rate of the tetraene ring closure. A noticeable reduction is shown especially by the substitution at position C2, where the electronic properties are maximized and steric congestion are minimized.
The reaction of 2-CHO (Table 3, entry 5) and 2-NO2 (Table 3, entry 7) system are accelerated to 11.4 kcal mol−1 and 10.2 kcal mol−1, respectively, from 17.0 kcal mol−1 as reported for the unsubstituted 1,3,5,7-tetraene. It is worth mentioning that the strength of the electron withdrawing character is directly linked with facilitating the re-arrangement of the π-bonds and generation of the new σ-bond, to form a ring structure. Overall, a comparative evaluation of the results extracted for C1- to C4-substituted tetraenes with the unsubstituted parent 1,3,5,7-octatetraenes substrate shows a trivial impact on the acceleration of the 8π electrocyclisation reaction.
With regard to further verify the suitability of the selected DFT method for this investigation, calculations using the M06-2X/6-31+G(d,p) level of theory are conducted for all the monosubstituted patterns. The computed values (refer to ESI†) express only minor variation by up to 0.5 kcal mol−1 and 0.9 kcal mol−1 for the activation energies and the reaction energies, respectively when compared with M06-2X/6-31+G(d) level of theory. Henceforth, we conclude that the use of a lower basis set which is less computationally expensive is suitable to generate a reliable information for this organic transformation.
2.3 8π electrocyclisation of disubstituted 1,3,5,7-octatetraene
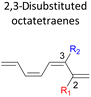
We have also extensively explored the disubstituted 1,3,5,7-octatetraenes using the M06-2X/6-31+G(d) method (Table 4). All possible substitutional patterns of different combinations at different site on the tetraene backbone are computed. Such investigation aims to understand the activation barrier requirements for the 8π electrocyclisation of the conjugated difunctionalised system.In the case of dinitro functionalized system (1-NO2–2-NO2), it is not surprising that only minor reduction in the activation barrier by 3.3 kcal mol−1 from 17.0 kcal mol−1 is recorded, in spite of their strong electron withdrawing effect. It arises from the steric congestion between the vicinal nitro groups that slightly destabilizes the transition structure. Greater destabilization leading to a higher energy barrier is presented by 1-CHO–2-OH substituted compound at 21.0 kcal mol−1 due to the unfavourable adjacent side groups clashes.
In 1,3-disubstituted model systems, the strain experience between the motifs becomes less eminent as they no longer feature in vicinal clashing. The reaction energies are seen to slightly be driven by the electronic properties of the substituents due to their minor electronic contribution at C3 position to the terminal double bonds to facilitate the formation of the new σ-bond. Hence, a decrease in reaction reactivity is recorded by the 1,3-diamino substituted system (1-NH2–3-NH2) to 21.2 kcal mol−1, in contrast to the corresponding 1,2-disubstituted (9.7 kcal mol−1) and also the unsubstituted system (17.0 kcal mol−1). Similar trends are also observed for some other 1,3-difunctionalized tetraenes. However, reverse trend is observed when functionalities with high electron withdrawing character are incorporated. An obvious increased in the activation barrier up to 8.5 kcal mol−1 and 9.6 kcal mol−1 from 17.0 kcal mol−1, are shown by the 1-NO2–3-F and 1-NO2–3-NO2 system, respectively. The effect of the functional groups installed at positions C4, C5 and C6 on the tetraene skeleton of the 1,X-disubstituted octatetraene become less significant during the cyclisation step. The location of these installation inconsequentially delegates effective electronic contribution with the molecular orbital for the newly formed C1–C8 bond. The energy trends observed for 1,7-disubstituted octatetraene are more pronounced than the other 1,X-systems (Table 4). It is the electronic effect of both substituents at these positions that are responsible for the observed accelerated transformation. Direct attachment of these groups on the terminal carbon double bonds promotes the orbital interactions between the forming C1–C8 σ-bond. A measurable decrease in the activation energies of 1-R1–7-CHO and 1-R1–7-NO2 systems are observed, particularly as a result of the R2 side group's strong electronic nature and their position on the tetraene skeleton where the electronic contributions are maximized and steric effects are minimized. The most accelerated transformation is observed by the 1-NH2–7-NO2 system, in which the activation energy is 8.0 kcal mol−1 compared to 17.0 kcal mol−1 for unsubstituted system. The synergistic effect between the two substituents with opposite electronic characteristics (–NH2 having electron donating effect, and –NO2 having electron withdrawing effect) and the magnitude of these properties effectively promotes the rate of ring closure. Greater orbital interaction with the terminus carbon atoms renders better stabilization to the transition structure, hence favouring the cyclooctatriene formation. Similar reactivity trends of such effects is also observed for 1-CH3–7-NO2 and 1-OH–7-NO2 substituted systems at 8.6 kcal mol−1 and 10.7 kcal mol−1, respectively.
In addition, a slightly more enhanced reactivity resulted by this synergistic effect is shown by 1-NH2–8-NO2 functionalized octatetraene. The computed activation free energy for this combination is 7.4 kcal mol−1. Despite the slight destabilization by the steric crowding between the vicinal functional groups at the transition state, the capacity of the electron donating and electron withdrawing characters, together with the direct attachment to the terminus position leads to a more stabilized and favourable orbital interaction. On the contrary, the highest activation barrier is shown by 1-CN–8-CN system at 21.4 kcal mol−1, that is governed by the greater steric clashes between the adjacent nitrile groups on the transition structure. The clashing of these substituents outweighs the electronic properties, that lead to the destabilization of the transition state by 4.4 kcal mol−1 from the unsubstituted tetraene.
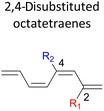
A remarkably lower activation energy of 6.3 kcal mol−1 is computed by the 2-NO2–5-NO2 octatetraene (Table 5). In the case of 2,7-disubstitution pattern, a much more prominent decrease in the reaction energies is observed which is the most accelerated transformation in this investigation. The lowest activation barrier is computed for 2-NO2–7-NO2 at 4.9 kcal mol−1 compared to the unsubstituted parent molecule (17.0 kcal mol−1). In general, any substituent attached at these positions (C2 and C7) offer maximized electronic contribution towards the formation of the new terminal σ-bond. Thus, a decrease in activation barriers of the difunctionalised octatetraene from 17.0 kcal mol−1 are depicted. In addition, an increase in the reactivity via lower barrier of certain substitutional pattern with the involvement of opposite electronic nature, presumably arises as a result of the synergistic effect between the attached substituents. For example, the 2-CH3–7-NO2, 2-NH2–7-NO2 and 2-OH–7-NO2 reveals an apparent decrease in the energy barriers to 6.9 kcal mol−1, 7.7 kcal mol−1, and 8.6 kcal mol−1, respectively, contrary to 17.0 kcal mol−1 for unsubstituted tetraene.
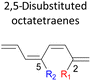
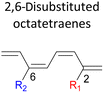
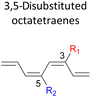
In the event of 3,5- and 3,6- patterns, only few combinations reveal a noticeable decrease in the reaction rate, as shown when nitro group is/are incorporated (Table 6). This could be explained in terms of the high electron accepting capacity that is strong enough to facilitate the 8π electrocyclic ring closure. On the other hand, the reaction reactivity for the other attachments is shown to be insignificantly affected by the electronic properties, as shown by the trivial variation from the unfunctionalised octatetraene.
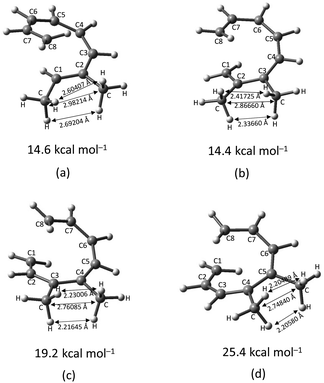
The transition structure of the 4,5-dimethyl substitution features relatively shorter interatomic distances between the adjacent functional groups than the 1,2-dimethyl substitution (Fig. 4). In accordance to the position of the attached functional groups, the rate of the electrocyclisation reaction is dominantly controlled by steric effect and considerably unaffected by the electronic characters of the substituents, as demonstrated by the increased in the activation energies from 17.0 kcal mol−1 (unsubstituted molecule).
In the event of the vicinal attachment involving strongest electron donating group (–NH2), similar trend of increasing activation barriers is observed (from 1,2- to 4,5-disubstitution). However, it is as a result of the decreasing electronic effect on the 8π electrocyclic ring closure in regards to their position on the tetraene skeleton.
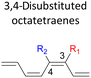
Moreover, reactivity trend involving –NO2 substitution (the strongest electron withdrawing group) also shows a general increase in the activation energies. However, an anomaly is identified whereby the 3-NO2–4-NO2-substituted octatetraene display an opposite effect (decrease in activation energy to 12.1 kcal mol−1). Presumably, extra stabilization of the 3,4-disubstitution favoring the electrocyclisation arise from the greater resonance structures at the transition states, compared to the 2,3- and 4,5-disubstituted octatetraene transition structures. Further investigation is underway to explore the crucial aspects pertinent to 8π electrocyclization of 1,3,5,7-octatetraene motifs.
3. Conclusions
Salient conclusions drawn from this computational study towards 8π electrocyclic ring closure of conjugated 1,3,5,7-octatetraenes include:(a) An extensive benchmarking studies reveal that M06-2X/6-31+G(d) method is one of the appropriate DFT methods for this investigation. This was supported by the accurate computed value with the measured activation energy (17.0 kcal mol−1) of the 8π electrocyclisation of 1,3,5,7-octatetraenes.
(b) Monosubstituted 1,3,5,7-octatetraenes shown to selectively prefer the transition structure with an outward substituent over the inward. The lower steric clashes stabilize the transition structure towards the 8π ring closure process. However, the opposite effects are also observed for some of the mesomerically electron donating groups (–NH2 and –OH). The SOI between the substituent lone pair and 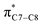 orbital results in the extra stabilization to the inward transition structure. Therefore, this exceptional case depends strongly on the capacity of the electron donating characters. Amidst the four possible monosubstitution patterns, attachment at C2 position displayed a more pronounced effect on the acceleration of the electrocyclic process due to greater electronic contributions with the terminal carbon double bonds. Therefore, they enhanced the orbital interaction for the generation of new σ-bond between the C1 and C8 atom. Contrary to the unfunctionalized 1,3,5,7-octatetraenes molecule, a single substitution does not result much impact on the efficiency of the 8π electrocyclic ring closure of studied tetraenes.
orbital results in the extra stabilization to the inward transition structure. Therefore, this exceptional case depends strongly on the capacity of the electron donating characters. Amidst the four possible monosubstitution patterns, attachment at C2 position displayed a more pronounced effect on the acceleration of the electrocyclic process due to greater electronic contributions with the terminal carbon double bonds. Therefore, they enhanced the orbital interaction for the generation of new σ-bond between the C1 and C8 atom. Contrary to the unfunctionalized 1,3,5,7-octatetraenes molecule, a single substitution does not result much impact on the efficiency of the 8π electrocyclic ring closure of studied tetraenes.
(c) In the case of disubstitution systems, attachments on the terminal double bonds renders a general reduction in the activation energies. This is due to the greater electronic interaction from both substituents that stabilizes the transition structure. Particularly, the involvement of strong electron withdrawing group (–NO2) often proceeds with reduced energy barriers. A remarkable decrease in the activation barrier up to 4.9 kcal mol−1 from 17.0 kcal mol−1 (parent molecule) is observed for 2-NO2–7-NO2 system. Moreover, the synergistic effect between the attached substituents of opposite electronic nature in a disubstituted environment also reveals an apparent accelerated effect on the reactivity of the functionalised tetraene molecule. For example, a decrease in the activation barrier to 7.4 kcal mol−1 is observed in the 1-NH2–8-NO2-disubstituted octatetraene.
(d) In the event of vicinal substitution (1,2-, 2,3-, 3,4-, and 4,5-systems), the eight electron conrotatory electrocyclisation reaction is disfavoured by the destabilization of the transition state, as a result of the sterically congested vicinal functional group arrangements. Greatest decelerated effect is observed by the 4-CH3–5-CH3 substituted octatetraene at 25.4 kcal mol−1, which is 8.4 kcal mol−1 higher than the unsubstituted compound (17.0 kcal mol−1). A much severe steric clashes are observed in the 4,5-pattern over the other vicinal disubstituted patterns because of the less important electronic effect of the substituents, and the greater steric clashes experienced between the adjacent side groups.
4. Computational methods
Density functional theory (DFT)22 calculations were performed using Gaussian 16 (revision C.01)23 and the GaussView (Version 6)24 was used to generate input geometries and visualize output structures. For the calculations related to the comparative benchmarking study for the electrocyclisation of unsubstituted octatetraene, hybrid three-parameter functional commonly known as B3LYP25 and metahybrid functional M0-62X26 levels of theory with different basis sets were used to locate all the stationary points involved. Both B3LYP/6-31G(d)15 and M0-62X/6-31+G(d,p)18 levels of theory have already been reported for the 8π electrocyclisation of tetraenes. Geometry optimization for mono- and disubstituted octatetraenes were performed using the M0-62X functional with the 6-31+G(d) basis set, followed by the frequency calculations at the same level of theory. All stationary points were characterized as minima or transition structures based on normal vibrational mode analysis. Thermal corrections were computed from unscaled frequencies, assuming a standard state of 298.15 K and 1 atm. Representative transition states were also linked to their corresponding minima through intrinsic reaction coordinate (IRC) calculations.27 All-s-transoid conformations of the octatetraenes have been used to calculate the energies of the reactants. For the substituents (–OH and –CHO) exhibiting more than one conformation, lowest energy conformers have been provided here.Author contributions
Nur Hazimah B. Z. Arfan: data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing. Malai Haniti S. A. Hamid: funding acquisition, resources, software, co-supervision, writing – review & editing. Nadeem S. Sheikh: conceptualization, methodology, funding acquisition, project administration, resources, software, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank Universiti Brunei Darussalam for the research grant (UBD/RSCH/1.4/FICBF(b)/2022/049) and Ministry of Education, Brunei Darussalam for offering scholarship to N. H. B. Z. A.Notes and references
- For the selected reviews, see: (a) H. Cao, F. Chen, S. Su and L. Yu, Adv. Synth. Catal., 2020, 362, 438 CrossRef CAS; (b) X. Xie, W. Huang, C. Peng and B. Han, Adv. Synth. Catal., 2018, 360, 194 CrossRef CAS; (c) O. Boutureira, M. I. Matheu, Y. Díaz and S. Castillón, Chem. Soc. Rev., 2013, 42, 5056 RSC.
- Y.-J. Hu, L.-X. Li, J.-C. Han, L. Min and C.-C. Li, Chem. Rev., 2020, 120, 5910 CrossRef CAS PubMed.
- Y. Kanda, H. Nakamura, S. Umemiya, R. K. Puthukanoori, V. R. M. Appala, G. K. Gaddamanugu, B. R. Paraselli and P. S. Baran, J. Am. Chem. Soc., 2020, 142, 10526 CrossRef CAS PubMed.
- Y.-L. Jiang, H.-X. Yu, Y. Li, P. Qu, Y.-X. Han, J.-H. Chen and Z. Yang, J. Am. Chem. Soc., 2020, 142, 573 CrossRef CAS PubMed.
- D. Q. Thach, Z. G. Brill, H. K. Grover, K. V. Esguerra, J. K. Thompson and T. J. Maimone, Angew. Chem., Int. Ed., 2020, 59, 1532 CrossRef CAS PubMed.
- L. Min, X. Lin and C.-C. Li, J. Am. Chem. Soc., 2019, 141, 15773 CrossRef CAS PubMed.
- M. Bian, L. Li and H. Ding, Synthesis, 2017, 49, 4383 CrossRef CAS.
- H. Quintela-Varela, C. S. Jamieson, Q. Shao, K. N. Houk and D. Trauner, Angew. Chem., Int. Ed., 2020, 59, 5263 CrossRef CAS PubMed.
- S. L. Drew, A. L. Lawrence and M. S. Sherburn, Chem. Sci., 2015, 6, 3886 RSC.
- A. K. Miller and D. Trauner, Angew. Chem., Int. Ed., 2005, 44, 4602 CrossRef CAS PubMed.
- (a) D. F. Vargas, E. L. Larghi and T. S. Kaufman, Nat. Prod. Rep., 2019, 36, 354 RSC; (b) N. S. Sheikh, Org. Biomol. Chem., 2015, 13, 10774 RSC; (c) M. A. Tius, in Stereoselective Synthesis of Drugs and Natural Products, ed. V. Andrushko and N. Andrushko, 2013, vol. 1, p. 521 Search PubMed; (d) E. L. Myers and D. Trauner, in Comprehensive Chirality, ed. E. M. Carreira and H. Yamamoto, 2012, vol. 2, p. 563 Search PubMed; (e) S. Thompson, A. G. Coyne, P. C. Knipe and M. D. Smith, Chem. Soc. Rev., 2011, 40, 4217 RSC; (f) B. Gasper and D. Trauner, in Science of Synthesis, Stereoselective Synthesis, ed. G. J. De Vries, G. A. Molander and P. A. Evans, 2011, vol. 3, p. 383 Search PubMed; (g) J. Burnley, M. Ralph, P. Sharma and J. E. Moses, in Biomimetic Organic Synthesis, ed. E. Poupon and B. Nay, Wiley-VCH: Weinheim, 2011, vol. 1, p. 591 Search PubMed; (h) C. M. Beaudry, J. P. Malerich and D. Trauner, Chem. Rev., 2005, 105, 4757 CrossRef CAS PubMed; (i) J. C. Namyslo and D. E. Kaufmann, Chem. Rev., 2003, 103, 1485 CrossRef CAS PubMed; (j) T. Durst and L. Breau, in Comprehensive Organic Synthesis, ed. B. M. Trost, I. Fleming and L. A. Paquette, Pergamon, Oxford, 1991, vol. 5, p. 665 Search PubMed; (k) E. N. Marwell, Thermal Electrocyclic Reactions, Academic Press, New York, 1980, ch. 5, p. 124 Search PubMed.
- B. M. Trost, Science, 1991, 254, 1471 CrossRef CAS PubMed.
- (a) I. Fleming, Molecular Orbitals and Organic Chemical Reactions, John Wiley & Sons, 2011 Search PubMed; (b) R. Hoffmann, Angew. Chem., 1982, 94, 725 (Angew Chem. Int. Ed. Engl., 1982, 21, 711) CrossRef; (c) R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Verlag Chemie, Weinheim, 1970 Search PubMed; (d) R. B. Woodward and R. Hoffmann, Angew. Chem., 1969, 81, 797 (Angew Chem. Int. Ed. Engl., 1969, 8, 781) CrossRef; (e) R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395 CrossRef CAS.
- (a) P. S. Lee, X. Zhang and K. N. Houk, J. Am. Chem. Soc., 2003, 125, 5072 CrossRef CAS PubMed; (b) B. E. Thomas, J. D. Evanseck and K. N. Houk, J. Am. Chem. Soc., 1993, 115, 4165 CrossRef CAS; (c) E. A. Kallel, Y. Wang, D. C. Spelmeyer and K. N. Houk, J. Am. Chem. Soc., 1990, 112, 6759 CrossRef CAS; (d) D. C. Spelmeyer and K. N. Houk, J. Am. Chem. Soc., 1988, 110, 3412 CrossRef; (e) K. Rudolf, D. C. Spelmeyer and K. N. Houk, J. Org. Chem., 1987, 52, 3708 CrossRef CAS; (f) N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1985, 107, 2099 CrossRef CAS.
- B. Lecea, A. Arrieta and F. P. Cossío, J. Org. Chem., 2005, 70, 1035 CrossRef CAS PubMed.
- T. D. Goldfarb and L. Lindqvist, J. Am. Chem. Soc., 1967, 89, 4588 CrossRef CAS.
- C. Hoult, S. Amiri, G. Blond, P. R. Schreiner and J. Suffert, J. Am. Chem. Soc., 2009, 131, 13387 CrossRef PubMed.
- A. Patel and K. N. Houk, J. Org. Chem., 2014, 79, 11370 CrossRef CAS PubMed.
- N. S. Sheikh, RSC Adv., 2016, 6, 25503 RSC.
- T.-Q. Yu, Y. Fu, L. Liu and Q.-X. Guo, J. Org. Chem., 2006, 71, 6157 CrossRef CAS PubMed.
- (a) B. E. Thomas, J. D. Evanseck and K. N. Houk, Isr. J. Chem., 1993, 33, 287 CrossRef CAS; (b) K. N. Houk, Y. Li and J. D. Evanseck, Angew Chem. Int. Ed. Engl., 1992, 31, 682 CrossRef.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, U.K., 1989 Search PubMed.
- M. J. Frisch, et al., GAUSSIAN16, (Revision C.01), Gaussian, Inc., Wallingford CT, 2019, the full reference can be found in the ESI.† Search PubMed.
- R. Denningtom, T. Keith and J. Millam, GaussView (Version 6), Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- (a) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Chem. Phys., 1994, 98, 11623 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS; (d) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- (a) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523 CrossRef CAS; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1989, 90, 2154 CrossRef CAS; (c) K. Fukui, Acc. Chem. Res., 1981, 14, 363 CrossRef CAS; (d) Due to unsuccessful IRC calculations for some cases, the transition state structures were linked to their corresponding minima via perturbing their structures in the direction along the vibrational coordinate linked with the imaginary frequency, followed by optimization..
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05127g |
| This journal is © The Royal Society of Chemistry 2023 |