DOI:
10.1039/D3RA05251F
(Paper)
RSC Adv., 2023,
13, 27792-27800
Effect of modulation by adsorption and doping on the quantum capacitance of borophene
Received
3rd August 2023
, Accepted 12th September 2023
First published on 20th September 2023
Abstract
Electric double-layer supercapacitors (EDLCs) have attracted much attention in the energy storage field due to their advantages such as high output power, long service life, safety and high efficiency. However, their low energy density limits their application. Aiming at the problem of the low energy density of EDLCs, improving quantum capacitance (CQ) of electrode materials is an effective strategy. In this paper, we systematically studied the effects of vacancy, doping, and metal atom adsorption on the CQ of borophene using first-principles calculations. The results show that S and N doping greatly enhance the charge accumulation of borophene at positive and negative potential, respectively. The maximum CQ values of S-doped and N-doped borophene are 157.3 μF cm−2 (0.38 V) and 187.8 μF cm−2 (−0.24 V), respectively. Both of them can serve as ideal candidates for the positive (S-doped one) and negative (N-doped one) electrodes of EDLCs. Besides, metal Al atom-adsorbed borophene can also effectively enhance the CQ, with a maximum value of 109.1 μF cm−2.
1. Introduction
With the increasingly serious environmental pollution and the rapid depletion of non-renewable energy, it is urgent to develop sustainable and clean energy sources.1 However, the production of renewable energy (such as wind and solar energy) is discontinuous due to regional and temporal factors.2 Therefore, the development of reliable, higher energy density and low-cost energy conversion and storage devices is rather important.3 Among various energy storage devices, electric double-layer supercapacitors (EDLCs) have attracted much attention due to their high-power density and long cycle life. However, EDLCs usually exhibit lower energy densities.4 Studies have shown that the electrode material of EDLCs is one of the most important factors limiting the energy density.5,6
Two-dimensional (2D) materials have promising application prospects as electrode materials due to their unique physical and chemical properties, including high specific surface area and good conductivity.7–11 For 2D electrode materials, the total interfacial capacitance (CT) can be expressed as 1/CT = 1/CQ + 1/CD, where CQ is the quantum capacitance, and CD is the electric double layer capacitance.12–14 The CQ limits the total interface capacitance as much as the electric double layer capacitance. Therefore, it is necessary to improve the CQ of 2D electrode materials. In recent years, researchers have modulated the CQ of two-dimensional materials such as graphene, silicene and germanene by means of defects and doping,15–17 which makes a high density of electron states at the Fermi level.
Boron is the adjacent element of carbon. It has the same short covalent radius and the flexibility to adopt sp2 hybridization as carbon.18 There are three valence electrons in the outer layer of boron, which could form a typical 2D configuration of borophene. Ab initio calculations were used by Boustania and Quandt to predict a variety of stable borophenes and boron nanotubes, which opened the curtain to the study of 2D boron sheets.19,20 Different from graphene, intrinsic borophene is metallic and has electron density of states at the Fermi level.21 Theoretical studies have shown that borophene may have a variety of allotropes. The common structures of borophene allotropes are triangular, hexagonal and triangular–hexagonal mixed structures.22–24 Borophene can be made by various methods, such as chemical vapor decomposition on a metal substrate, molecular beam epitaxy, and liquid exfoliation, to produce 2D flat boron.25–29 In 2015, Mannix et al.30 successfully prepared wrinkled triangular borophene (2-Pmmn) on Ag (111) surface by experiments. In the same year, Tai et al.31 prepared γ-B28 with direct band gap on copper foils surface by chemical vapor deposition. In particular, Hou et al.32 demonstrate that hydrogenated borophenes in large quantities can be prepared without any metal substrates by a stepwise in situ thermal decomposition of sodium borohydride under hydrogen as the carrier gas. And Liu et al.33 confirmed though a CO-functionalized scanning tunneling microscopy that borophene is a chemically discrete two-dimensional material as opposed to a surface reconstruction or alloy with the underlying Ag(111) growth substrate. In addition, the single crystal boron nanoplane prepared by Zhai et al.34 is a p-type semiconductor with a carrier modulus of 1.26 × 10−1 cm2 V−1 s−1, which has excellent electrical conductivity. The latest results that a 2D borophene supercapacitor prepared by Abdi et al.35 reached a high specific capacitance of 350 μF g−1, which clarified the application prospect of borophene-based supercapacitors.
In recent years, many studies have suggested that vacancy defects, atom doping, and functional group adsorption caused by chemical treatment during growth can effectively enhance the CQ of the electrode materials. For instance, Zhou et al.36 introduced vacancy defects into graphene, increasing the maximum CQ from 21.34 μF cm−2 to 120.72 μF cm−2. In our previous studies, introducing dopants into silicene with monovacancy defects also improved the CQ.16 The latest theoretical research shows that the CQ of monolayer δ-6 borophene is 203.09 μF cm−2.37 However, there is no detailed report on the effects of defects and doping on the CQ of borophene.
In this work, we perform the first-principles method to investigate the effects of vacancy defects, metal atom adsorption (Ag, Au, Cu, Ti, Al) and doping (C, N, O, P, S) on the electronic structure and CQ of 2-Pmmn borophene. By analyzing its electronic structure and fitting the changes of CQ and surface storage charge with potential difference, its energy storage properties were explored. In addition, the co-doping of S (N) and Al and the adsorption of Al atoms on vacancy defects were studied. The results show that borophene has the best adsorption effect on Al, and the maximum CQ is 103.4 μF cm−2. S doping significantly improves the CQ of borophene, and the maximum value reaches 120.2 μF cm−2. When the concentration of S is increased to 4.17%, the CQ is further increased to 157.3 μF cm−2. Therefore, doping and adsorption can be used as an effective way to improve the energy storage performance of borophene-based supercapacitors.
2. Computational methods
In this work, we use the VASP package to perform first-principles calculations.38–40 Projected augmented wave (PAW) method was used to optimize the geometric structure of the modulated borophene.41 The exchange correlation energy of the interaction between electrons is expressed by the Perdew–Burke–Ernzerhoff (PBE) functional with the generalized gradient approximation (GGA).42,43 In order to avoid the interaction between the layers, 20 Å vacuum layers were added. The K-point sampling in the Brillouin zone used the Monkhorst–Pack method. The energy convergence criterion of atomic relaxation was 10−6 eV, and the cutoff energy was set to 450 eV. The spin polarization was considered in our calculations. The van der Waals (vdW) interaction is considered with dispersion correction via the vdW-DF method.
The optimized lattice constants of 2-pmmn borophene are a = 1.617 Å and b = 2.867 Å, which are consistent with the previously reported theoretical and experimental results.37,44–46 Based on the original cell (1 × 1), a 4 × 4 supercell is constructed. The adsorption energy of metal atoms adsorbed on intrinsic borophene is calculated by the following formula:
| | |
ΔEad(x) = EBor–M(x) − EBor − μM
| (1) |
EBor and
EBor–M are the total energy of intrinsic borophene and adsorbed by metal atoms, respectively, and
μM is the chemical potential of a single adsorbing atom (Ag, Au, Cu, Ti, Al).
The doping concentration is controlled by changing the size of the supercell. Formation energy was calculated to determine the stability of the defect structures. The formation energies of borophene with monovacancy, divacancy and dopants of C, N, O, P, S atoms are:
| | |
ΔEf = EBor–SV − (n − 1)μB
| (2) |
| | |
ΔEf = EBor–DV − (n − 2)μB
| (3) |
| | |
ΔEf = EBor–X − (n − 1)μB − μX
| (4) |
where
EBor–SV and
EBor–DV represent the total energy of borophene with monovacancy and divacancy,
n is the number of B atoms in the original borophene,
μB is the energy of a single B atom, and
μX represents the energy of one doping atom (C, N, O, P, S).
The CQ can be expressed as CQ = dσ/dΦ, where dσ and dΦ represent the surface charge density and local potential, respectively.47,48 According to the formula μ = eΦ, the electrochemical potential μF can move rigidly through the local potential Φ. On the electrode, the excess charge density can be expressed as:49
| |
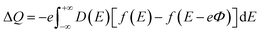 | (5) |
D(
E) represent the electron density of states,
e is the basic charge (
e = 1.6 × 10
−19 C), and
f(
E) is the Fermi–Dirac distribution function.
E is the relative energy of the Fermi level.
16,49 From this, the expression of
CQ is:
| |
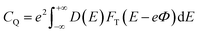 | (6) |
where
FT(
E) is a thermal broadening function, denoted by:
| |
FT(E) = (4kBT)−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sech2(E/2kBT) sech2(E/2kBT)
| (7) |
kB is the Boltzmann constant, and
T is set to room temperature (300 K).
3. Results and discussion
3.1 The vacancy defects and adsorption of borophene
The structure of 2-Pmmn borophene shows a curved hexagonal structure (Fig. 1a), unlike silicene, its six-membered ring center is occupied by a boron atom. Each B atom in borophene is bonded to six adjacent atoms, the B1–B2 bond length on the same plane is 1.617 Å, which is slightly shorter than the B1–B3 (2.098 Å) on different planes. The two kinds of bond angles for each B atom are 67.33° and 45.33°, respectively.
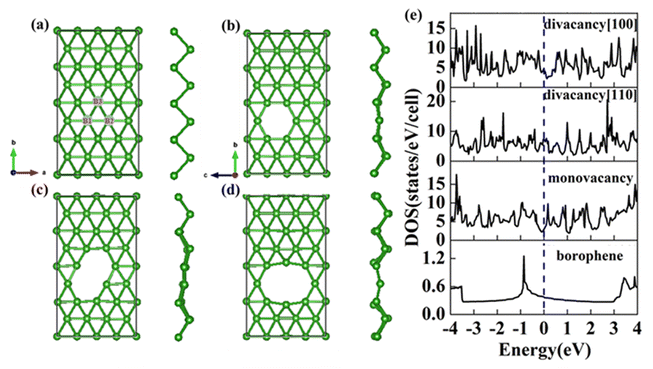 |
| | Fig. 1 Top view and side view of (a) pristine; (b) monovacancy; (c) divacancy [110]; (d) divacancy [100] borophene structures with a supercell of (4 × 4). (e) Electron density of states of the above four borophene structures. | |
In this section, we consider the monovacancy and two possible divacancy defects of 2-Pmmn borophene, as shown in Fig. 1b–d. The B1 and B2 atoms in the adjacent planes are deducted to form divacancy [110] (shown in Fig. 1c), and the absence of B1 and B3 atoms in the same plane is recorded as divacancy [100] (shown in Fig. 1d). Fig. 1e shows the density of states of the four systems, since there is no band gap, the intrinsic borophene is metallic, which is consistent with the previous reports.19,30,50 The density of states of monovacancy and divacancy [110] borophene near the Fermi level appear obvious decrease which is caused by the unoccupied state caused by the defect vacancy. We calculate the formation energy to describe the stability of different defects (Fig. 2a). In addition, four possible adsorption sites of borophene are marked in Fig. 2b. As we expected, defects are likely to cause instability of the 2D material structure. Contrary to what was thought, the divacancy seems to be more stable than the monovacancy for borophene, because of the formation energies of the two double-vacant structures are about six times lower than that of the monovacancy.
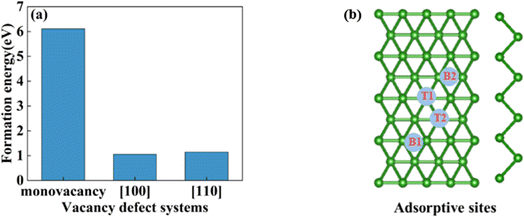 |
| | Fig. 2 (a) The formation energy of monovacancy, [110], [100] defect borophene; (b) four adsorption sites of borophene. | |
The CQ with potential of intrinsic, monovacancy, divacancy [110] and [100] borophene is shown in Fig. 3a. The CQ of intrinsic borophene shows an inclined straight line, which is stable with the increase of potential. For monovacant, divacant [110] and [100] borophene, the local maximum values of CQ are 73.0 μF cm−2 (−0.17 V), 83.8 μF cm−2 (0.24 V) and 84.6 μF cm−2 (0.43 V), respectively. According to the relationship between surface charge density and potential calculated in Fig. 3b, the charge accumulation effect of intrinsic borophene is better than that of borophene structure after introducing vacancies. Different from other 2D materials, the influence of CQ of borophene on vacancy defects is relatively stable.
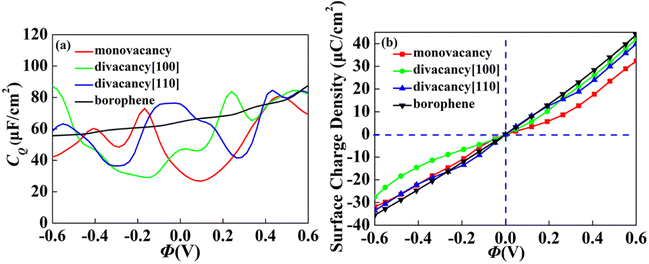 |
| | Fig. 3 The (a) quantum capacitance and (b) surface charge density changes of intrinsic, monovacancy, divacancy [110], divacancy [100] borophene with potential. | |
In view of the high conductivity of transition metal atoms (Au, Ag, Cu, Ti, Al), we will discuss its adsorption effect on various adsorption sites of borophene. As schematic models shown in Fig. 2b, borophene has four adsorption sites, T1: above the top atom; T2: above the bottom atom; B1: above the top B–B bond; B2: above the bottom B–B bond. Similarly, we will judge the most stable situation of each atom in the above four positions by adsorption energy (Table 1). The negative adsorption energy advocates the feasibility of transition metal atoms adsorption. The adsorption energy of Ag, Cu, Al at T1 position is the lowest and the configuration is the most stable, but Au and Ti are most stable at B1 and B2 positions, respectively. Based on the stable adsorption of the above atoms on intrinsic borophene, we further studied their effects on the electronic structure and CQ (Fig. 4a and b). The adsorption is carried out on 4 × 4 intrinsic borophene. Compared with pristine borophene, the adsorption of Au, Ag, Cu caused a decrease in the density of states near the Fermi level, resulting in a decrease in the CQ at zero potential, and the overall trend was relatively the same, but the Au adsorption system had a relatively good effect on charge accumulation (Fig. 4c). The adsorption of Ti and Al atoms improves the CQ of borophene, and the local maximum values are 103.5 μF cm−2 (−0.48 V) and 109.1 μF cm−2 (0.45 V), respectively. This is attributed to the local electronic state formed near the zero potential. At the same time, the charge stored from their surface can verify that Ti, Al doped borophene has the potential to be a symmetrical supercapacitor electrode.
Table 1 The adsorption energy (eV) of Au, Ag, Cu, Ti and Al atoms adsorbed on borophene at T1, T2, B1 and B2 sites
| ΔEad |
Au |
Ag |
Cu |
Ti |
Al |
| T1 |
−1.989 |
−1.663 |
−2.333 |
−4.184 |
−2.429 |
| T2 |
−2.015 |
−1.815 |
−2.723 |
−4.827 |
−2.728 |
| B1 |
−2.117 |
−1.704 |
−2.324 |
−3.236 |
−2.431 |
| B2 |
−2.068 |
−1.778 |
−2.591 |
−5.173 |
−2.676 |
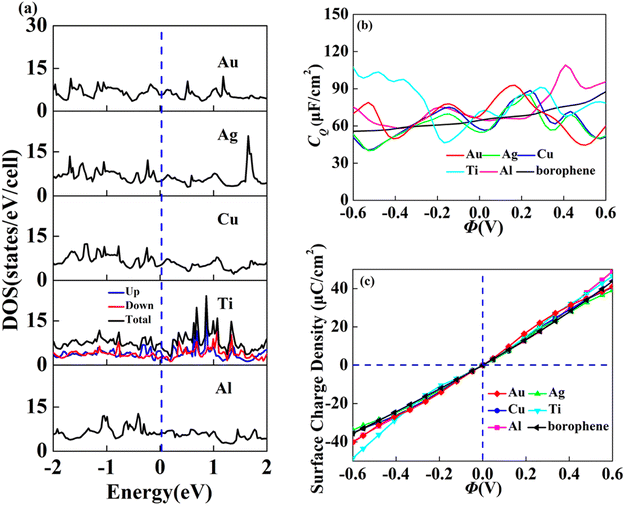 |
| | Fig. 4 The (a) electronic density of states, (b) quantum capacitance and (c) surface charge density of borophene adsorbing Au, Ag, Cu, Ti, Al. | |
On the whole, the effect of intrinsic borophene adsorbing Al is the best. Therefore, we consider adsorbing Al in borophene containing vacancy defects. The adsorption configuration on monovacancy, divacancy [100] and divacancy [110] is shown in Fig. 5a–c. The stable adsorption site is at top of monovacancy for monovacancy borophene (Fig. 5a), the center of vacancy for divacancy [100] (Fig. 5b), and the off-center of vacancy for divacancy [110] (Fig. 5c), respectively. In order to intuitively show the electronic properties, we draw the energy band structure diagram of three kinds of vacancy adsorption Al in Fig. 6a–c. The energy band of these three materials cross the Fermi level and exhibit metallic character. The CQ and charge density of divacancy [100] borophene are enhanced under negative potential after adsorbing Al, the capacitance value is 87.8 μF cm−2 (−0.096 V), while the CQ of [110] borophene peaked at 83.1 μF cm−2 at 0.12 V (Fig. 7a). Through surface charge storage (Fig. 7b), it is found that Al adsorbed [100] and [110] borophene are suitable for the negative and positive electrodes of supercapacitors, respectively.
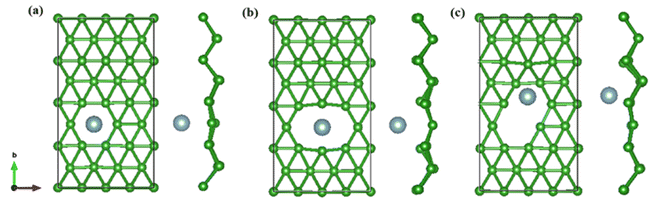 |
| | Fig. 5 The optimized structure of (a) monovacancy, (b) divacancy [100], (c) divacancy [110] borophene adsorbed Al in 4 × 4 supercell. | |
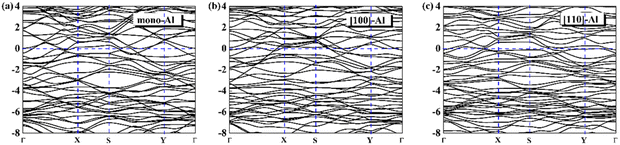 |
| | Fig. 6 The band structure diagram of (a) monovacancy, (b) divacancy [100], (c) divacancy [110] borophene adsorbed Al. | |
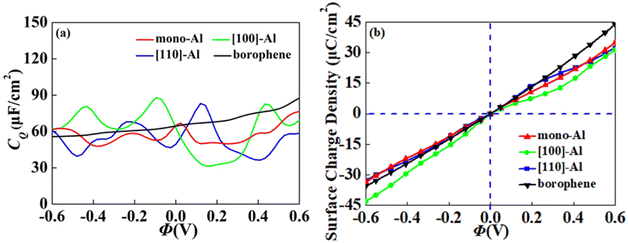 |
| | Fig. 7 The (a) quantum capacitance and (b) surface charge density of Al adsorbed on vacancy borophene. | |
3.2 The doping and co-doping of borophene
For 2D materials, the light element (such as N, P, S) doping is one of the common strategies usually used to regulate the electronic properties of materials. Combined with the characteristics of B, we take C and O into account and consider the effect of doping on the CQ of borophene. Fig. 8a–e depicted the quantum capacitance of C, N, O, P, S doped borophene. Firstly, we calculated the defect formation energy, as shown in Fig. 9a, and concluded that the formation energy of O doping is the lowest. For intrinsic borophene, when the local potential is zero, a lower CQ appears, and the trend is symmetrical U-shaped. The local maximum values of the doped CQ are 83.8 μF cm−2 (0.05 V), 90.3 μF cm−2 (−0.29 V), 94.5 μF cm−2 (0.17 V), 110.9 μF cm−2 (0.17 V) and 120.2 μF cm−2 (0.05 V), respectively. Obviously, the introduction of non-metallic atoms improves the CQ of intrinsic borophene. The improvement of CQ is due to the downward shift of Fermi level and the formation of nearby localized states. Fig. 9b and c shows the change of surface charge density with potential. Under positive potential, the charge accumulation effect of S and N doping is obviously enhanced, in particular, the surface charge density of the S-doped system reaches 60 μC cm−2 at 0.6 V, and the enhancement effect of N doping is the best under negative potential. It shows that S and N doped borophene have the potential to be used as positive and negative electrodes for supercapacitors, respectively. In order to further analyze the effect of doping on the electronic structure of borophene, we plotted the energy band diagram of the doped structure as shown in Fig. 10a–f. The band structure of intrinsic borophene again verifies its metallicity, but doped atoms not only produce deep localized states, but also make the electronic structure redistributing. The doping of P and S leads to higher local states near the Fermi level. The density of states shows a downward trend near the conduction band minima, indicating that the electrons occupying the lower part are delocalized. But in general, doping does not change the metallic behavior of borophene. From Pauling's chemical bond theory, this is because boron is an electron-deficient substance, and the doped atoms do not affect the conjugated π bond in borophene, and the electronic structure of borophene will not change significantly.51
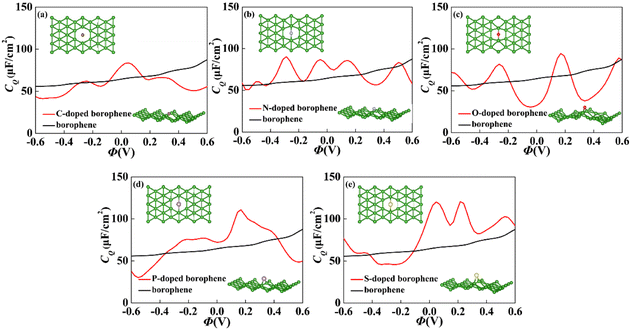 |
| | Fig. 8 The crystal structure and change of quantum capacitance of (a) C, (b) N, (c) O, (d) P, (e) S doped borophene with potential. | |
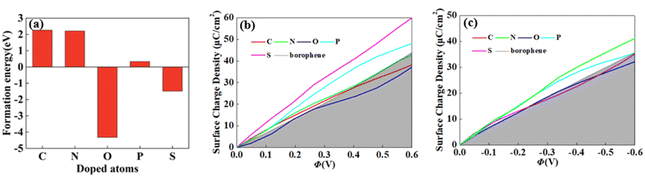 |
| | Fig. 9 The (a) formation energy and change of surface charge density with (b) positive, (c) negative potential of C, N, O, P, S doped brophene. | |
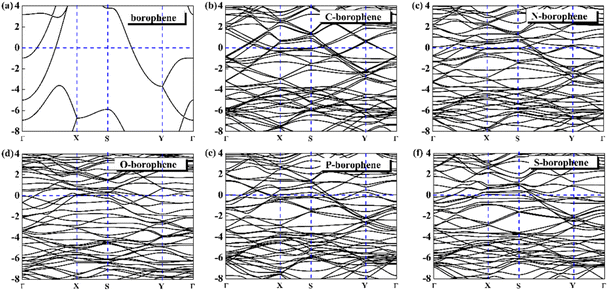 |
| | Fig. 10 The band structure diagram of (a) intrinsic borophene and doped (b) C, (c) N, (d) O, (e) P, (f) S atom. | |
In order to further explore the concentration effect of doping on borophene CQ, we construct the 4 × 4, 4 × 3 and 3 × 3 supercell structures, corresponding concentration of 3.13%, 4.17% and 5.56%, respectively. When the S doping concentration is 4.17% and 5.56%, the CQ values of 157.3 μF cm−2 (0.38 V) and 122.7 μF cm−2 (−0.31 V) are higher, which are twice the intrinsic CQ at the same potential. The charge accumulation effect after S doping, as shown in Fig. 11b, is significantly enhanced at 4.17% positive potential. Under negative potential, 5.56% S doping has the best enhancement effect. Therefore, borophene can be applied to the positive and negative electrodes of supercapacitors by controlling the N doping concentration. After N doping, the CQ value gradually increases with the increase of concentration. When the doping concentration is 5.56%, the CQ increases most obviously, reaching a maximum value of 187.8 μF cm−2 (−0.24 V). The surface charge density in Fig. 11d also corresponds to it, indicating that borophene with N doping concentration of 4.17% has more advantages in the negative electrode of supercapacitors.
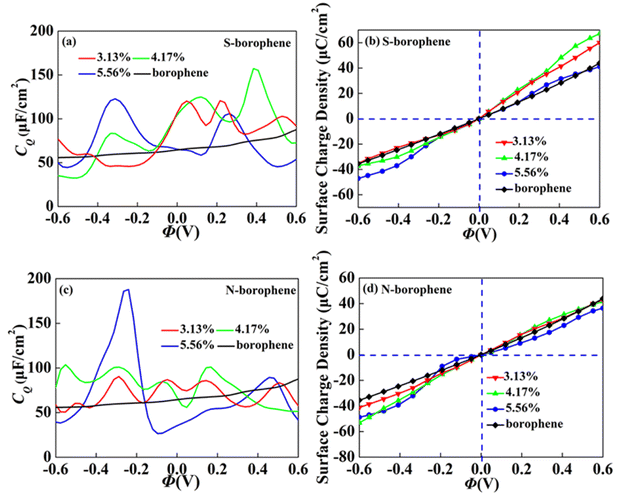 |
| | Fig. 11 The relationship between (a and c) quantum capacitance and (band d) surface charge density and potential of S, N doped borophene with different concentrations. | |
Combined with the excellent energy storage effect of Al adsorbed borophene mentioned above, we combined it with S and N doped borophene with different concentrations. The synergistic effect both of aspects are considered. We selected the doping borophene structure (4 × 3 and 3 × 3 borophene structure doped with S and N, respectively) with higher CQ to adsorbed. The 4 × 3 S doped borophene supercell with Al adsorption, 4 × 3 S doped borophene supercell with Al adsorption, and 4 × 3 N doped borophene supercell with Al adsorption are denoted 43SAl, 33SAl and 33NAl, respectively. After co-doping, the CQ of 33SAl doped borophene reaches the maximum value of 113.6 μF cm−2 (−0.24 V) at positive potential, but decreases sharply at negative potential, and the CQ value is unstable, which may be caused by the local state of density of states (Fig. 12). Unfortunately, Al does not have a good positive effect on S and N-doped borophene, but the short-term improvement of 33SAl proves that co-doping is still a direction to be explored.
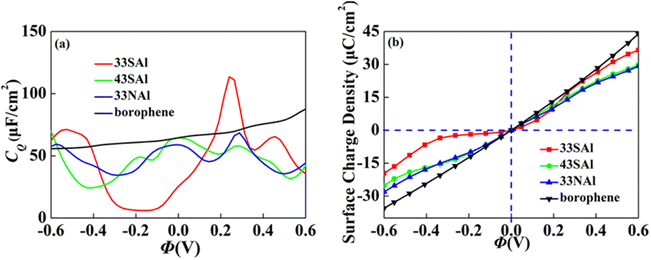 |
| | Fig. 12 The (a) quantum capacitance and (b) surface charge density of S, N doped borophene adsorbed Al. | |
4. Conclusions
In summary, we systematically studied the effects of vacancy, adsorbed transition metal atoms (Au, Ag, Cu, Ti, Al) and doping (C, N, O, P, S) on the electronic structure and CQ of borophene through first-principles calculations to improve the energy storage properties of borophene-based electrode materials. The results show that the vacancy defects have little effect on the CQ of borophene electrode materials, but doping and adsorption can still effectively regulate the electronic structure of borophene, thereby improving its CQ. In the system of metal atoms adsorbed borophene, the Al-adsorbed borophene exhibits excellent energy storage properties, and the CQ reaches 109.1 μF cm−2. In the doped system, the maximum CQ of S-doped borophene is 120.2 μF cm−2. Further increase the S doping concentration to 4.17%, the CQ value is 157.3 μF cm−2. And by controlling the concentration of S-doped, borophene can be applied to the positive (4.17% one) and negative (5.56% one) electrodes of EDLCs respectively. The CQ of N-doped borophene increases with the increase of concentration, and reaches the maximum value of 87.8 μF cm−2 at the concentration of 5.56%, however, the surface charge density is the largest when the concentration is 4.17%. Nevertheless, N-doped borophene can still be regarded as an ideal anode material for supercapacitors.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
This work was supported by the Natural Science Foundation of Jilin Province (Grant No. YDZJ202201ZYTS576).
References
- S. T and K. Tarafder, Phys. B, 2021, 604, 412676 CrossRef.
- R. M. Hu and J. X. Shang, Appl. Surf. Sci., 2019, 496, 143659 CrossRef CAS.
- C. Hou, G. Tai, Y. Liu, Z. Wu, X. Liang and X. Liu, Nano Res. Energy, 2023, 2, e9120051 CrossRef.
- C. Wang, Y. Zhou, L. Sun, Q. Zhao, X. Zhang, P. Wan and J. Qiu, J. Phys. Chem. C, 2013, 117, 14912–14919 CrossRef CAS.
- L. L. Zhang and X. S. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2283 CrossRef.
- B. Biel, X. Blase, F. Triozon and S. Roche, Phys. Rev. Lett., 2009, 102, 096803 CrossRef PubMed.
- C. Liu, Z. Yu, D. Neff, A. Zhamu and B. Z. Jang, Nano Lett., 2010, 10, 4863–4868 CrossRef CAS PubMed.
- H. M. Jeong, J. W. Lee, W. H. Shin, Y. J. Choi, H. J. Shin, J. K. Kang and J. W. Choi, Nano Lett., 2011, 11, 2472–2477 CrossRef CAS PubMed.
- Y. Chen, X. Zhang, D. Zhang, P. Yu and Y. Ma, Carbon, 2011, 49, 573–580 CrossRef CAS.
- J. Xia, F. Chen, J. Li and N. Tao, Nat. Nanotechnol., 2009, 4, 505–509 CrossRef CAS PubMed.
- A. J. Pak, E. Paek and G. S. Hwang, Phys. Chem. Chem. Phys., 2013, 15, 19741–19747 RSC.
- G. M. Yang, H. Z. Zhang, X. F. Fan and W. T. Zheng, J. Phys. Chem. C, 2015, 119, 6464–6470 CrossRef CAS.
- S. M. Mousavi-Khoshdel and E. Targholi, Carbon, 2015, 89, 148–160 CrossRef CAS.
- X. Si, Z. Li, S. Q. Wang, Q. Xu, J. Y. Lin and G. M. Yang, Appl. Surf. Sci., 2022, 605, 154673 CrossRef CAS.
- G. M. Yang, Q. Xu, X. F. Fan and W. T. Zheng, J. Phys. Chem. C, 2018, 122, 1903–1912 CrossRef CAS.
- X. Si, W. She, Q. Xu, G. Yang, Z. Li, S. Wang and J. Luan, Materials, 2022, 15, 103 CrossRef CAS PubMed.
- H.-J. Zhai, Y.-F. Zhao, W.-L. Li, Q. Chen, H. Bai, H.-S. Hu, Z. A. Piazza, W.-J. Tian, H.-G. Lu, Y.-B. Wu, Y.-W. Mu, G.-F. Wei, Z.-P. Liu, J. Li, S.-D. Li and L.-S. Wang, Nat. Chem., 2014, 6, 727–731 CrossRef CAS PubMed.
- I. Boustani, A. Quandt, E. R. Hernández and Á. Rubio, J. Chem. Phys., 1999, 110, 3176–3185 CrossRef CAS.
- I. Boustani, A. Quandt and Á. Rubio, IEEE J. Solid-State Circuits, 2000, 154, 269–274 CAS.
- H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501 CrossRef PubMed.
- B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568 CrossRef CAS PubMed.
- J. He, D. F. Li, Y. Ying, C. B. Feng, J. J. He, C. Y. Zhong, H. B. Zhou, P. Zhou and G. Zhang, npj Comput. Mater., 2019, 5, 47 CrossRef.
- C. Hou, G. Tai, Y. Liu, Z. Wu, Z. Wu and X. Liang, J. Mater. Chem. A, 2021, 9, 13100–13108 RSC.
- S.-Y. Xie, Y. Wang and X.-B. Li, Adv. Mater., 2019, 31, 1900392 CrossRef PubMed.
- T. Z. Wen, A. Z. Xie, J. L. Li and Y. H. Yang, Int. J. Hydrogen Energy, 2020, 45, 29059–29069 CrossRef CAS.
- C. Li, A. K. Tareen, K. Khan, J. Long, I. Hussain, M. F. Khan, M. Iqbal, Z. Xie, Y. Zhang, A. Mahmood, N. Mahmood, W. Ahmad and H. Zhang, Prog. Solid State Chem., 2023, 70, 100392 CrossRef CAS.
- Y. Jiao, F. Ma, J. Bell, A. Bilic and A. Du, Angew Chem. Int. Ed., 2016, 55, 10292–10295 CrossRef CAS PubMed.
- J. Joseph, V. S. Sivasankarapillai, S. Nikazar, M. S. Shanawaz, A. Rahdar, H. Lin and G. Z. Kyzas, ChemSusChem, 2020, 13, 3754–3765 CrossRef CAS PubMed.
- A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- G. Tai, T. Hu, Y. Zhou, X. Wang, J. Kong, T. Zeng, Y. You and Q. Wang, Angew. Chem., Int. Ed., 2015, 54, 15473–15477 CrossRef CAS PubMed.
- C. Hou, G. Tai, J. Hao, L. Sheng, B. Liu and Z. Wu, Angew. Chem., Int. Ed., 2020, 59, 10819–10825 CrossRef CAS PubMed.
- X. Liu, L. Wang, S. Li, M. S. Rahn, B. I. Yakobson and M. C. Hersam, Nat. Commun., 2019, 10, 1642 CrossRef PubMed.
- J. Xu, Y. Chang, L. Gan, Y. Ma and T. Zhai, Adv. Sci., 2015, 2, 1500023 CrossRef PubMed.
- Y. Abdi, A. Mazaheri, S. Hajibaba, S. Darbari, S. J. Rezvani, A. D. Cicco, F. Paparoni, R. Rahighi, S. Gholipour, A. Rashidi, M. M. Byranvand and M. Saliba, ACS Mater. Lett., 2022, 4, 1929–1936 CrossRef CAS.
- Q. X. Zhou, W. W. Ju, Y. X. Liu, J. H. Li and Q. Zhang, Appl. Surf. Sci., 2020, 510, 145448 CrossRef CAS.
- H. Kolavada, S. Singh, I. Lukačević, P. N. Gajjar and S. K. Gupta, Electrochim. Acta, 2023, 439, 141589 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- B. Peng, H. Zhang, H. Z. Shao, Y. F. Xu, R. J. Zhang and H. Y. Zhua, J. Mater. Chem. C, 2016, 4, 3592–3598 RSC.
- H. X. Zhong, K. X. Huang, G. D. Yu and S. J. Yuan, Phys. Rev. B, 2018, 98, 054104 CrossRef CAS.
- Q. X. Zhou, L. Wang, W. W. Ju, Y. L. Yong, S. L. Wu, S. T. Cai and P. C. Li, Electrochim. Acta, 2022, 433, 141261 CrossRef CAS.
- E. Paek, A. J. Pak, K. E. Kweon and G. S. Hwang, J. Phys. Chem. C, 2013, 117, 5610–5616 CrossRef CAS.
- X. Si, Q. Xu, J. Lin and G. Yang, Appl. Surf. Sci., 2023, 618, 156586 CrossRef CAS.
- D. L. John, L. C. Castro and D. L. Pulfrey, J. Appl. Phys., 2004, 96, 5180–5184 CrossRef CAS.
- P. Xiang, X. Chen, W. Zhang, J. Li, B. Xiao, L. Li and K. Deng, Phys. Chem. Chem. Phys., 2017, 19, 24945–24954 RSC.
- L. C. Pauling, Nature of the Chemical Bond, Cornell University Press, Ithaca, NY, 1939 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article b and
Jianyan Lin
b and
Jianyan Lin *a
*a
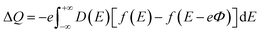
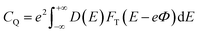
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sech2(E/2kBT)
sech2(E/2kBT)












