Open Access Article
Open Access ArticleNew polymorphic phase of arachidic acid crystal: structure, intermolecular interactions, low-temperature stability and Raman spectroscopy combined with DFT calculations†
Luanny M. B. Cardosoa,
João G. de Oliveira Neto b,
Gilberto D. Saraivac,
Fábio F. Leite
b,
Gilberto D. Saraivac,
Fábio F. Leite d,
Alejandro P. Ayala
d,
Alejandro P. Ayala e,
Adenilson O. dos Santosb and
Francisco F. de Sousa
e,
Adenilson O. dos Santosb and
Francisco F. de Sousa *a
*a
aInstitute of Exact and Natural Sciences, Federal University of Para – UFPA, Belém, Pará CEP 66075-110, Brazil. E-mail: ffs@ufpa.br
bCenter for Social Sciences, Health, and Technology, Federal University of Maranhao – UFMA, Imperatriz, Maranhão CEP 65900-410, Brazil
cPhysics Course, State University of Ceara – UECE, Campus FECLESC, Quixadá, Ceará CEP 63900-000, Brazil
dDepartment of Exact and Technological Sciences, Federal University of Amapá – UNIFAP, Macapá, Amapá CEP 68903-419, Brazil
eDepartment of Physics, Federal University of Ceara – UFC, Fortaleza, Ceará CEP 65455-900, Brazil
First published on 21st November 2023
Abstract
Saturated monocarboxylic fatty acids with long carbon chains are organic compounds widely used in several applied fields, such as energy production, thermal energy storage, antibactericidal, antimicrobial, among others. In this research, a new polymorphic phase of arachidic acid (AA) crystal was synthesized and its structural and vibrational properties were studied by single-crystal X-ray diffraction (XRD) and polarized Raman scattering. The new structure of AA was solved at two different temperature conditions (100 and 300 K). XRD analysis indicated that this polymorph belongs to the monoclinic space group P21/c (C2h5), with four molecules per unit cell (Z = 4). All molecules in the crystal lattice adopt a gauche configuration, exhibiting a R22(8) hydrogen bond pattern. Consequently, this new polymorphic phase, labeled as B form, is a polytype belonging to the monoclinic symmetry, i.e., Bm form. Complementarily, Hirshfeld's surfaces were employed to analyze the intermolecular interactions within the crystal lattice of this polymorph at temperatures of 100 and 300 K. Additionally, density functional theory (DFT) calculations were performed to assign all intramolecular vibration modes related to experimental Raman-active bands, which were properly calculated using a dimer model, considering a pair of AA molecules in the gauche configuration, according to the solved-crystal structure.
1. Introduction
In recent years, fatty acids (FAs) have played an important role in materials science and engineering due to their physical, chemical, and biological properties.1–3 For instance, composites containing carbon nanotubes, graphene and FA eutectic mixtures for energy storage have been developed.4–7 Furthermore, structural and kinetic studies revealed that these compounds can inhibit phospholipase A(2), thus being an anti-inflammatory agent.8,9 According to the literature,10,11 these compounds can be used to graft polymers and produce carriers for non-viral gene delivery.Chemically, FAs are commonly described as organic substances duly consisting of a carbon chain (skeletal) attached to a methyl group (CH3) and a carboxylic group (COOH), also often found in the form of esters.12 In addition, in the crystalline state, these compounds are duly arranged in crystalline structures forming dimers through intermolecular interactions, mainly hydrogen bonds (H–O⋯H), which have an essential role in the formation of saturated FA crystals. The crystal structure of monocarboxylic FAs is formed by packed molecules via hydrogen bonds with dimers predominantly adopting an all-trans or a gauche configuration that generally allow three-dimensionally ordering from a typical R22(8) hydrogen bond pattern for monocarboxylic FAs.13,14 These molecular configurations are responsible for the polymorphism phenomenon; so, FAs can crystallize in more than one crystal structure.15–18
According to the literature, molecular systems formed by monocarboxylic acids with an even number of carbon atoms, such as capric acid (C10H20O2),19 lauric acid (C12H24O2),20 myristic acid (C14H28O2),21 palmitic acid (C16H32O2),22 stearic acid (C18H36O2),23 arachidic acid (C20H40O2),24 behenic acid (C22H44O2),25 and lignoceric acid (C24H48O2),26 can be crystallized in different polymorphic phases: A1, A2, A3, Asuper, Bo/m, C, and Eo/m, depending on the conditions of temperature, pressure, solvent, among others.27,28 Amidst these polymorphic phases, the C form is the most stable at high temperatures. Moreover, the A phases have a triclinic system, the Bo and Eo structures are found in the orthorhombic symmetry, and the Bm/Em and C forms belong to the monoclinic system. It is important to notice that the indices “o” and “m” are associated with two polytypes belonging to the orthorhombic and monoclinic structures, respectively.29 As mentioned above, the dimers formed through O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds of each pair of molecules influence the polymorphism at saturated monocarboxylic FAs. Such a phenomenon is duly associated with the molecular configurations into the crystal lattice. Thereby, the polymorphic phases named by A and B exhibit a gauche configuration while the E and C forms present an all-trans configuration.15,17,30
C hydrogen bonds of each pair of molecules influence the polymorphism at saturated monocarboxylic FAs. Such a phenomenon is duly associated with the molecular configurations into the crystal lattice. Thereby, the polymorphic phases named by A and B exhibit a gauche configuration while the E and C forms present an all-trans configuration.15,17,30
Arachidic acid (AA), also known as eicosanoic acid, is a saturated fatty acid with the chemical formula C20H40O2. It is classified as a long-chain fatty acid due to its skeletal structure containing more than 13 carbon atoms; it can be found in the human organism from the plasma phospholipid; it is an almost hydrophobic compound, i.e., it is practically insoluble in water.24 Among various saturated fatty acids, AA is present in lower quantities in cupuaçu butter, cocoa butter, perilla oil, peanut oil, and corn oil. It also constitutes approximately 7.0% of the fats found in Durio graveolens fruit.31,32 It is also found naturally in cannabis, fish, and other plant oils. In the area of materials development, AA is used to produce detergents, lubricants, and photographic materials.33
Due to its high melting point, differently of unsaturated FAs, the AA is highly stable from a physicochemical point of view, since the carbon chain does not have double bonds.34 In a study reported by B. Rogers et al.,33 the influence of temperature on the composition and thermo-oxidative stability of AA in Arabica coffee oil was investigated. The analyzed samples showed that the thermal treatment does not significantly affect the grains.34 Besides that, this FA can be used in processes involving high temperatures, such as non-ambient conditions employed in the food industries.35 However, even in the face of these concepts and properties, AA was superficially investigated in the literature, with a lack of results associated with polymorphic variations, structural and spectroscopic characterizations.
In this paper, we report the crystal growth of a new AA polymorph (Bm form) by slow evaporation method in acetone and its structure determination through single-crystal X-ray diffraction (XRD) at 100 and 300 K. Complementarily, we performed a computational study using crystal voids and Hirshfeld's surfaces to describe the intermolecular interactions present in this new polymorphic phase. In addition, spectroscopic analyses using polarized Raman spectroscopy at two scattering geometries were performed to evaluate the crystalline system's inter- and intramolecular vibration modes. Furthermore, the correct assignment of intramolecular Raman modes was described through quantum chemical calculation based on density functional theory (DFT) using a dimer system as model, which is formed by two molecules of AA in the gauche configuration.
2. Experimental and theoretical methods
2.1 Growth of AA crystals
The arachidic acid was supplied by Sigma Aldrich with high purity (>99%). It was crystallized by slow evaporation method using 0.1 g of AA solved in 30 mL of ketone solvent under magnetic stirring (280 rpm) for 30 min. Then, the final solution with pH 5.1 was filtered and then kept under ambient conditions for the solid-phase nucleation.2.2 Single-crystal XRD and structural experiments
A single crystal was analyzed on a Bruker D8 Venture diffractometer with a Photon II CPAD detector and an ImS 3.0 Incoatec MoKα (λ = 0.71073 Å) microfocus source. The sample was kept at constant temperature during data collection, using an Oxford Cryostream cryostat (800 series Cryostream Plus) attached to the diffractometer. The APEX 4 software was used for data acquisition.36 The data reduction and global cell refinement were done using Bruker SAINT+ software package,37 and a numerical absorption correction was performed with SADABS.38 Using the Olex2 (ref. 39) interface program to the SHELX suite, the structure was solved by intrinsic phasing method implemented in ShelXT40 allowing the location of most of the non-hydrogen atoms. The remaining non-hydrogen atoms were located from difference Fourier maps calculated from successive full-matrix least-squares refinement cycles on F2 with ShelLX41 and refined using anisotropic displacement parameters. Hydrogen atoms were placed according to geometrical criteria and treated using riding model. MERCURY software42 was used to prepare the crystallographic information file (CIF) and artwork representations for publication. The CIF file was deposited in the Cambridge Crystallographic Structural Database (CCSD) under the codes 2177008 (100 K) and 2177009 (300 K). Copies of the data can be obtained, free of charge, via https://www.ccdc.cam.ac.uk/structures/. Other structural parameters are given in Tables S1–S10 of ESI,† as well as experimental patterns with respective crystalline planes for the temperatures of 100 K and 300 K are shown in Fig. S1.†2.3 Crystal voids and Hirshfeld surfaces
Void spaces were identified through crystal electronic density isosurfaces of 0.002 a.u., as suggested by Bader et al.,43 using the CrystalExplorer software.44 Hirshfeld's surfaces and 2D fingerprint graphs were also obtained using the CrystalExplorer software to analyze the crystal intermolecular contacts between the chemical species present. The Hirshfeld's surface plots were mapped with the normalized distance property (dnorm), which is defined in terms of the distances from a given point on the surface to the nearest external (de) and internal (di) atom and van der Waals radius.45,46 In addition, using these same computational calculations, the shape index and the curvedness of the molecular unit were generated for a topological study of the contacts.47 The 2D-fingerprint plots were presented as a function of the distance from a given point on the Hirshfeld's surface in terms of de and di. The calculated patterns encompass all intermolecular interactions, quantifying the specific contacts.482.4 Raman spectroscopy technique
Room-temperature Raman spectra were recorded on an AA single crystal in the 40–3000 cm−1 region using a LabRAM spectrometer (HR Evolution Horiba) with a charge-coupled device (CCD) detection system thermoelectrically refrigerated based on a Peltier-cooled device. A red He–Ne laser (λ = 633 nm) was used as an excitation source, with laser power near 6.0 mW. In addition, each spectrum was obtained with a counting time of 60 s, 4 accumulations, and a spectral resolution of 4 cm−1.2.5 Density functional theory calculations
Quantum-chemical calculations were performed using Gaussian09 (ref. 49) suite to determine the optimized molecular geometry and the Raman-active frequencies using a pair of AA molecules in the Bm form as model. Initial atomic coordinates at two different temperatures (100 and 300 K) were taken from the XRD data. The crystal structure was obtained through the single-crystal XRD experiments, as aforementioned, and it was duly relaxed using a DFT method with a hybrid B3LYP (Becke exchange with Lee, Yang, and Parr correlation) functional in 6-31G(d,p) computational level.50–52 After optimization, harmonic-vibration modes were evaluated at the same level of theory and then scaled to 0.974 (between 700 and 1760 cm−1) and 0.947 (between 2900 and 3250 cm−1) for the Raman spectra at both temperatures of 100 and 300 K. These values are in agreement with NIST – Standard Reference Database.53,54 The Raman activities (Si) obtained were converted to relative Raman intensities (Ii) using the following equation derived from the intensity theory of Raman scattering:55,56| I = f(ν0 − νi)4·νi(−1)·Bi(−1)·Si |
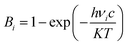 | (1) |
3. Results and discussion
3.1 Structural properties by single-crystal XRD
The new polymorph phase of AA crystal was obtained by the slow evaporation method as above-mentioned. A tiny platelet, with average dimensions of 0.092 × 0.091 × 0.042 mm3 was used in the single-crystal XRD analysis.The AA crystals grown in this study have a lozenge-like shape, resembling a small transparent plate. They typically exhibit the B-form crystal structure with monoclinic symmetry, specifically the polytype Bm. Fig. 1 exhibits the simulated morphology from the CIF file (code 2177009 for 300 K) using the Mercury program, showing that the crystal has grown as platelets with a lozenge-like prismatic shape. Fig. 1 shows the crystal terminal planes corresponding to the main crystallographic planes. It is worth noting that the acute angles are visibly distinguished. According to the literature,59 the two internal acute angles are near 75° (smaller acute angle between the two angles) and 105° (larger acute angle between the two angles).
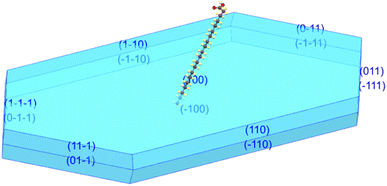 | ||
| Fig. 1 Growth habit of AA crystal showing that the crystal has grown in the Bm form and it has a lozenge-like morphology. | ||
Table 1 presents the structural data associated with the final atomic parameters determined for this sample. From single-crystal XRD results' analysis, the polymorphic phase of AA crystal belongs to the polytype Bm form, corresponding to monoclinic symmetry with P21/c (C2h5) space group, with the AA molecules in the crystal lattice adopting a gauche configuration, as shown in Fig. 2. Additionally, it was verified that the crystalline structure remains stable down to 100 K. However, the unit cell parameters (a, b, and c) undergo a contraction effect with the cooling and, consequently, the volume of unit cell decreases from 2004.5(2) to 1912.0(6) Å3.
| Temperature | 100 K | 300 K |
| Empirical formula | C20H40O2 | C20H40O2 |
| Formula weight | 304.47 g mol−1 | 304.47 g mol−1 |
| Crystal system | Monoclinic | Monoclinic |
| Space group | P21/c (C2h5) | P21/c (C2h5) |
| a (Å) | 48.445(7) | 48.478(19) |
| b (Å) | 7.1499(10) | 7.400(3) |
| c (Å) | 5.5267(8) | 5.597(2) |
| β (°) | 92.785(5) | 93.301(9) |
| V (Å3) | 1912.0(6) | 2004.5(2) |
| Z | 4 | 4 |
| Radiation | MoKα (λ = 0.71073 Å) | MoKα (λ = 0.71073 Å) |
| R-factor (%) | 6.84 | 9.50 |
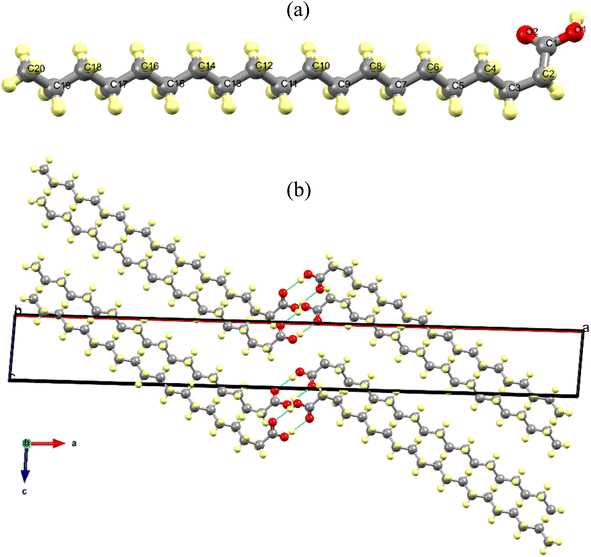
Fig. 2a shows the AA molecule in the gauche configuration at 300 K, viewed along the c-axis, with all carbon and oxygen atoms duly numbered. Additionally, it illustrates the presence of a saturated carbon chain and a carboxylic group in the monomer, which is connected to carbon chain via the C1 atom. Fig. 2b shows the arrangement of AA molecular units in the Bm form, where the dimers form alternating monolayers composed of carboxylic and methyl terminal groups along the [001] direction.
In addition, in the crystal lattice, the monomers interact through the hydrogen bonds between the carboxylic groups (O–H⋯O/O⋯H–O) with a distance of 6.981 Å and an angle of 140.94° at 300 K, which change to 6.845 Å and 146.09°, respectively, when the temperature reaches 100 K. This structural phenomenon can be also interpreted as tri-axial contraction undergone by unit cell at 100 K, which leads to a compaction of the AA units within the crystal lattice. As expected, the cryogenic effect induces a shorting in the lengths of the intermolecular bonds, promoting modifications such that the two molecules belonging to a dimer approach each other.
In order to detail the atomic packing of AA molecules in the unit cell, crystal void surfaces were generated and analyzed at both temperatures of 100 and 300 K. Fig. 3a–c shows the unit cell projected in the ab plane without void surfaces and with void centers in the unit cell at 100 K (Fig. 3b) and 300 K (Fig. 3c). The void spaces are described through gray electronic density isosurfaces, where the free volume in the unit cells, the surface areas, the percentages of voids present in the lattice, and the globularity index were calculated.
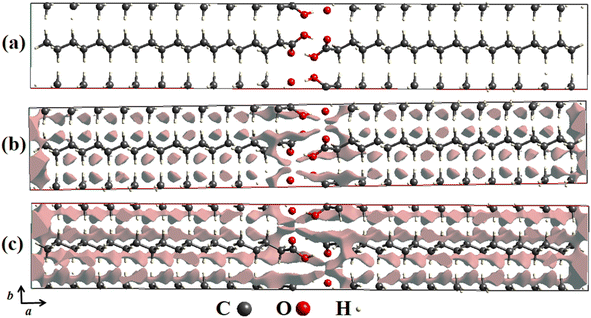 | ||
| Fig. 3 (a) Crystal voids viewed along the ab plane in the unit cell of AA in the Bm form without presence of isosurfaces. (b) At 100 K and (c) 300 K with presence of isosurfaces. | ||
According to our computational calculations, at 100 K the Bm form of AA has a void volume of 64.60 Å3, equivalent to 3.38% void centers, and a void surface area of 373.63 Å2, as pictured in Fig. 3b, while at 300 K (see Fig. 3c) higher values are observed for these parameters, such as a percentage of 6.89% of free space, corresponding to a volume of 138.17 Å3, and a surface area of 719.68 Å2. This change in unit cell volume can be clarified by different temperatures measured. In both cases, there are four molecules per unit cell, but the AA molecules are closer together at 100 K owing to volume compaction, so there are fewer void centers in the crystal lattice. This also justifies the disparity between the surface area values, as at 300 K there is a greater free volume; thus, the electronic isosurfaces occupy a greater area.
Another important descriptor was calculated from the crystal voids: the globularity (G).60 This index property describes the measurement of the degree to which the isosurface area differs from that of a perfect sphere with the same volume, being equivalent to 1.0 as it is thoroughly spherical, and progressively less than a unit as the isosurface becomes more structured. For the AA polymorph, values of G = 0.208 and G = 0.180 were obtained for temperatures of 100 and 300 K, respectively, suggesting that at lower temperatures, the isosurfaces have more rounded shapes than those noticed at 300 K.
3.2 Hirshfeld surface analysis
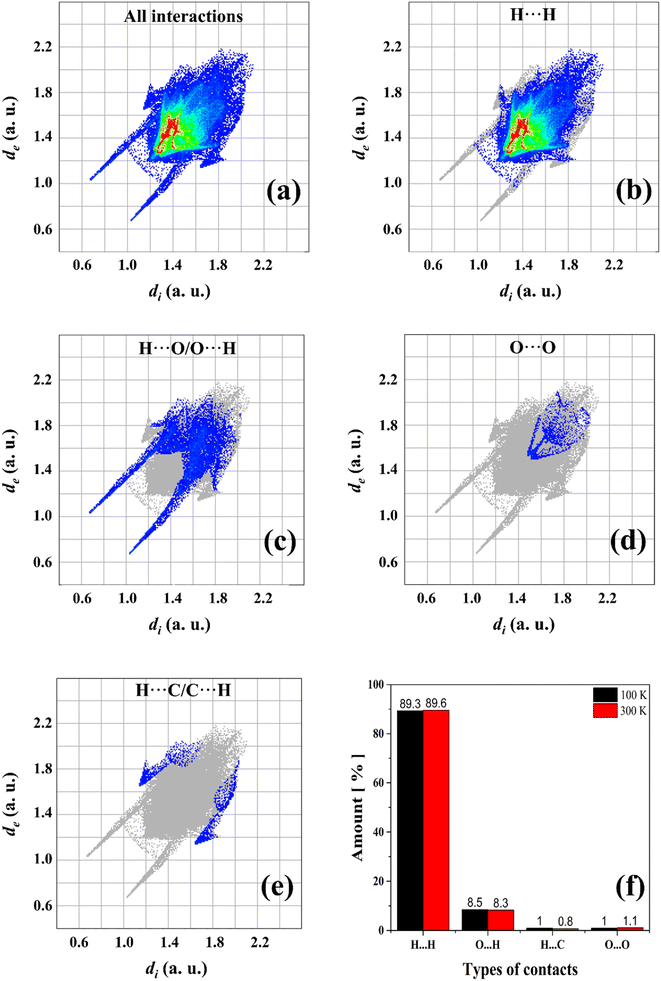
To better visualize and analyze the intermolecular interactions in the crystal structure of the Bm form of AA, three-dimensional Hirshfeld surfaces were generated, as shown in Fig. 4. As can be noticed, Fig. 4a exhibits the Hirshfeld surface given in terms of dnorm with the main contacts involved between the neighboring units that form the crystal lattice, in which the H⋯H induced-dipole interactions are established from the H atoms belonging to the carbon chains (red dashed line). The established color pattern indicates the intensity of the interatomic contacts between molecular units: blue regions – intermolecular interactions with distances greater than the van der Waals radii; white regions – interatomic contacts with distances equivalent to van der Waals radii; red regions – intermolecular interactions with distances shorter than the van der Waals radii. In the crystal structure at both temperatures, the strongest interactions represented by the red color are located around the O atoms belonging to the COOH groups, with a predominance of O⋯H/O⋯H hydrogen bonds. In addition, the white areas are related to H⋯H, H⋯C, and O⋯O weaker contacts on the Hirshfeld surface.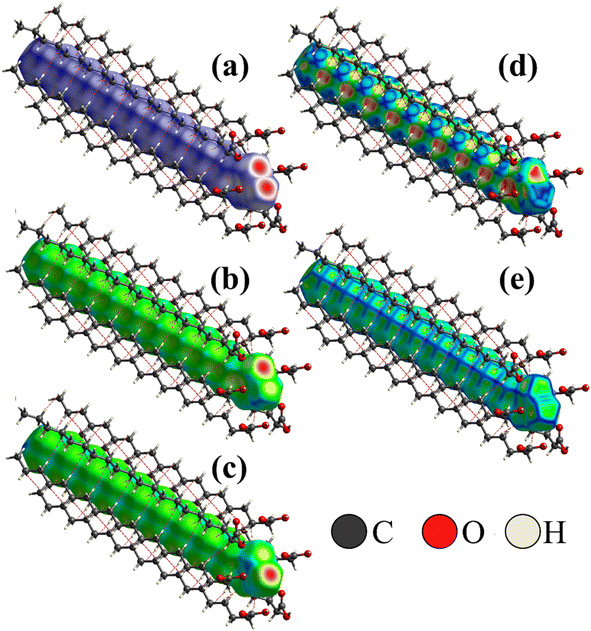 | ||
| Fig. 4 (a) Hirshfeld surface of AA crystal in the Bm form at 300 K given in terms of dnorm, (b) de, and (c) di; (d) shape index; (e) curvedness of crystal structure. | ||
Complementarily, the distances from the Hirshfeld surface to the nearest atoms outside (de) and inside (di) the surface, as displayed in Fig. 4b and c, are given in terms of de and di, respectively. On the de surface shown in Fig. 4b, the red region around O atom indicates the receptor site of intermolecular contacts, while on the di surface displayed in Fig. 4c, the red area presented under the OH group reveals a hydrogen donor zone. Furthermore, in the main chain that appears on the Hirshfeld surface mapped in terms of de and di, slightly yellowish portions are verified, corresponding to the recipient and donor contacts of the CH2 groups, respectively, which are established between the neighboring units. Both areas complement each other for the formation of hydrogen bonds and structural stabilization of the packing of AA units into the unit cells.
Fig. 4d and e shows the shape index and curvedness of the AA molecule, which are unique surfaces that provide information about the topology of the contacts. The shape index is particularly sensitive to even subtle changes in surface shape. In this representation, warm-colored regions indicate concave locations, while cool-colored regions are associated with convex areas. These two surfaces complement each other, identifying the points where two AA surfaces come into contact to facilitate intermolecular interactions. As seen in Fig. 4d, the concave regions of AA molecule are found between the C–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O units, while the convex areas predominate over the CH3, CH2, and C–OH groups; thus, these zones form the structural lattice through the hydrogen bonds performed between dimers.
O units, while the convex areas predominate over the CH3, CH2, and C–OH groups; thus, these zones form the structural lattice through the hydrogen bonds performed between dimers.
The curvedness surface is a measurement that details the crystal shape. In Fig. 4e, the flat areas, depicted in green, correspond to the regions with low curvedness values. On the other hand, the areas delineated by blue edges are indicative of high curvedness values. Furthermore, these edges serve as dividers, demarcating the surface into distinct parts and indicating the locations where neighboring molecules interact with each other. This observation aligns with the findings of McKinnon et al.,45 who described the core of n-alkanes. The close approach of identical atoms (H⋯H) produces flat areas in the Hirshfeld surface clearly evidenced in the curvedness index mapping. In addition, the flat areas enhance the sensibility of the shape index to minor changes in the surface as the set of blue spots characteristic of the approach of CH2 groups from adjacent molecules.
A computational study based on Hirshfeld surfaces was also performed to calculate the percentage of contacts present in AA units. Fig. 5a–e shows the cumulative and stratified 2D-fingerprint plots from the intermolecular interactions between the chemical species in the crystalline system. The same pattern is obtained for both temperatures of 100 and 300 K, where four different types of contacts are revealed: H⋯H, H⋯O/O⋯H, O⋯O, and H⋯C/C⋯H, which correspond to the following intermolecular interactions: induced dipole, hydrogen bonds, induced dipole, and dipole–dipole, respectively. These interactions contribute for the structural stability of AA crystal. In addition, the fraction of colored dots (red and yellow) highlighted in Fig. 5b characterizes specific close contacts (H⋯H) and the blue and green dots represent distant contacts (O⋯O and H⋯C/C⋯H). However, as observed in Fig. 5f, slight variations are verified in relation to the percentage contributions of the contacts in the two temperatures measured herein. At 100 K, the H⋯O/O⋯H hydrogen bonds are favored, while the H⋯H induced-dipole interactions suffer a little reduction, owing to the contraction effect in the unit cell.
Furthermore, the long and thin peaks in the lower regions of de–di values in the fingerprint plots represent strong and greater contacts on the surfaces, as shown in Fig. 5c. Indeed, hydrogen bonds are predominant intermolecular forces in the crystalline lattice of FAs, even though they are not the main contact in terms of percentages. On the other hand, hydrogen bonds in terms of percentage exhibit a more significant amount in other compounds based on organic molecules such as amino acids and their complexes.61,62
3.3 Group theory and vibrational properties at temperatures of 300 and 100 K
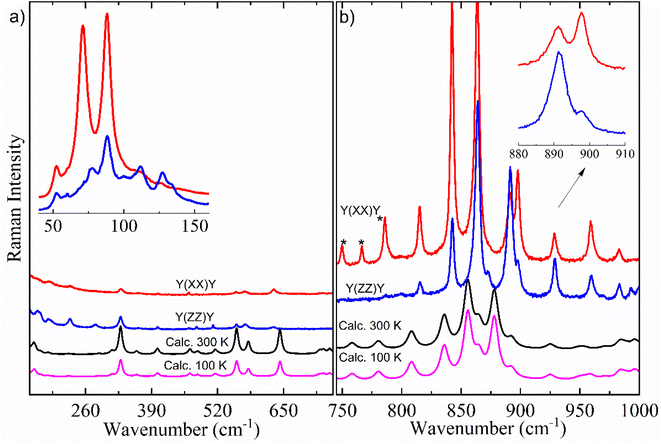
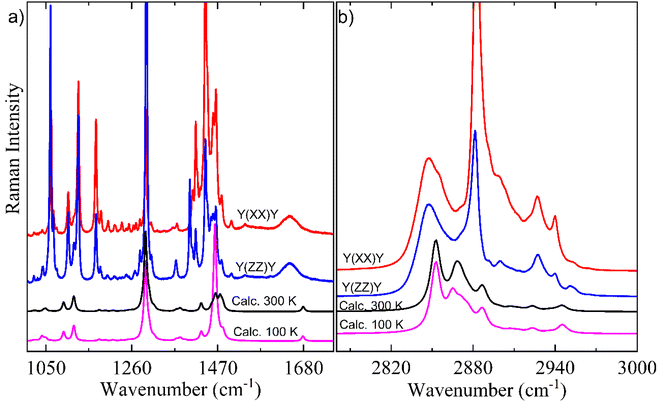
Here, it is done a comparison between experimental Raman spectra obtained in the y(xx)y (red spectrum) and y(zz)y (blue spectrum) scattering geometries and calculated Raman spectra in both temperatures of 300 K (black spectrum) and 100 K (pink spectrum). The dimer model used in our DFT calculations is provided in Fig. S2.† For a better discussion, the Raman spectra are divided into four distinct wavenumber regions: 30–690 cm−1; 700–980 cm−1; 1100–1690 cm−1; and 2780–3000 cm−1, as shown in Fig. 6 and 7.
Fig. 6a exhibits the Raman spectra containing inter- and intramolecular vibration modes in the region of 160–690 cm−1, which includes an inset with experimental Raman spectra between 40 and 155 cm−1 in both y(xx)y and y(zz)y scattering geometries. All bands that appeared in this wavenumber region (40–155 cm−1) are associated with lattice modes, which can give important information to understand the intermolecular interactions, thermodynamic stability, and physicochemical properties of organic systems, as well as polymorphism in materials in the crystalline state.15,16,64–66 According to the literature,15 these vibration modes have coupling with hydrogen bonds belonging to dimers responsible for the crystalline lattice. The inset of Fig. 6a shows little differences in the Raman spectra profile and relative intensity in the lattice vibration bands due to the polarization effect. In particular, the bands centered at 112, 127 and 133 cm−1 were not observed at y(xx)y geometry.
According to literature,15,29 the set of bands that appears within the 200–1000 cm−1 spectral range (Fig. 6a and b) is intrinsically characteristic of the Bm form of saturated FAs. This spectral region has predominant contribution from deformations of CH2 units. These vibrations are influenced by monoclinic angle β of the unit cell, as well as molecular configuration strongly impacts in the positions and intensities of intramolecular Raman bands in the 200–1000 cm−1 range. Indeed, when we compared the number and profiles of bands from the Bm-Raman spectrum with the Raman spectrum of the C form of other saturated FAs, one can notice that such an C polymorphic phase has a spectrum with number of bands minor than the Bm form.15,29 This suggests that the molecular configuration of dimers has an essential role on alterations in the Raman bands related to the CH2 groups, consequently, the Raman spectra of both polymorphic phases are well distinct. Table 2 presents the Raman modes of the Bm form of AA, both experimental and calculated at T = 300 K.
| ωy(zz)y | ωy(xx)y | ωcal. | Assignments (VMARD)a |
|---|---|---|---|
| a Nomenclature: τ-torsion; δ-bending; sc-scissoring; ν-stretching; γ-out-of-plane deformation. | |||
| 2953 | 2953 | 2945 | ν(C121H122) + ν(C121H123) + ν(C121H124) |
| 2940 | 2940 | 2939 | ν(C121H123) + ν(C121H124) |
| 2927 | 2927 | 2923 | ν(C64H72) |
| 2900 | 2900 | 2886 | ν(C121H124) + ν(C121H123) + ν(C121H122) |
| 2883 | 2882 | 2867 | ν(C92H98) + ν(C92H99) + ν(C92H100) |
| 2848 | 2848 | 2853 | ν(C77H85) |
| 1647 | 1647 | 1679 | ν(C2O10) + ν(C71O80) |
| 1503 | 1503 | 1490 | sc(H16C11H17) + sc(H6C15H25) + sc(H42C32H43) |
| 1479 | 1478 | 1476 | γ(H4C3H5C12) |
| 1466 | 1465 | 1463 | τ(C115C116C121H124) |
| 1440 | 1440 | 1429 | τ(C37C46C55H63) |
| 1416 | 1416 | 1391 | sc(C87C92H100) + sc(C87C92H98) + sc(C87C92H99) |
| 1370 | 1368 | 1368 | δ(C55C64H72) |
| 1294 | 1296 | 1293 | δ(H89C84C91) |
| 1235 | — | 1233 | δ(C109C112H114) |
| 1217 | — | 1214 | τ(C46C55C64C71) |
| 1200 | 1201 | 1196 | τ(H9O1C2C7) |
| 1184 | 1184 | 1181 | τ(C112C115C116H119) |
| 1129 | 1129 | 1118 | δ(C109C112C115) |
| 1105 | 1105 | 1093 | ν(C3C12) |
| 1068 | 1067 | 1049 | ν(C55C64) |
| 1063 | 1040 | 1040 | ν(C3C12) |
| — | 993 | 996 | ν(C31C40) |
| 983 | 983 | 983 | ν(C37C46) |
| 959 | 959 | 953 | ν(C84C91) |
| 929 | 929 | 925 | ν(C64C71) |
| 898 | 898 | 892 | δ(C55C64H73) |
| 892 | 892 | 878 | ν(C77C87) + ν(C87C92) + δ(C87C92H100) |
| — | 873 | 865 | τ(H9O1C2O10) |
| 864 | 864 | 855 | ν(C14C23) |
| 843 | 843 | 835 | ν(C64C71) |
| 815 | 815 | 808 | ν(C71O81) |
| 786 | — | 780 | τ(C32C41C50C59) |
| 766 | — | 758 | τ(C3C12C20C28) |
| 631 | 632 | 642 | δ(O1C2O10) + δ(C64C71O80) |
| 575 | 575 | 580 | δ(C46C55C64) |
| 557 | 557 | 557 | δ(C64C71O81) |
| — | 511 | 515 | δ(C58C67C76) |
| — | 480 | 480 | δ(C23C31C40) |
| 463 | — | 465 | δ(O1C2C7) |
| 402 | 402 | 401 | δ(C109C112C115) |
| 329 | 329 | 328 | δ(O1C2C7) |
| — | 280 | 285 | δ(O1C2O10) |
| 229 | 229 | 226 | τ(O10C2C7H13) |
| 186 | 186 | 186 | δ(C55C64H73) |
| — | 166 | 157 | Lattice |
| 132 | 134 | 135 | Lattice |
| 126 | — | 128 | Lattice |
| 111 | — | 113 | Lattice |
| — | 108 | 105 | Lattice |
| 88 | 87 | 84 | Lattice |
| 76 | 71 | 60 | Lattice |
| 59 | 58 | 60 | Lattice |
| 52 | 52 | 53 | Lattice |
As mentioned above, the Raman vibrational calculations were also performed for the AA structure in the Bm form at 100 K; however, significant changes between the Raman spectra profile and peak positions were not observed when the calculated Raman bands were compared to the experimental bands, indicating that inter- and intramolecular vibration modes of the Bm form of the crystal are stable under lower-temperature conditions.
According to our DFT calculations, intramolecular vibration modes in the wavenumber region between 300 and 690 cm−1 (Fig. 6a) appear mainly related to motions from bending of skeletal chain. One can notice that the calculated modes' positions exhibit a good agreement with experimental modes in both y(xx)y and y(zz)y scattering geometries (Table 2).
Comparing the vibration bands' profile in the 708–860 cm−1 range (Fig. 6b) between experimental Raman spectra in both scattering geometries, three bands located at about 750, 766 and 785 cm−1 (marked by *) in the y(zz)y geometry have higher intensity due to polarization effect. Interestingly, a similar phenomenon also occurs in the spectral profile of the polarized-Raman spectra of the C form of stearic- and palmitic-acid crystals within the same wavenumber region.15 Furthermore, when we compare the two scattering geometries, it is possible to observe differences in the relative intensity of bands related to the vibration modes at about 843, 864, 892, 898, 929 and 959 cm−1 as shown in the inset of Fig. 6b.
The Raman vibration modes located within the 800–1100 cm−1 region are mostly related to the stretching vibrations of C–C units, which are very sensitive to carbon chain modifications. The literature has shown the relation between gauche C–C stretching peak position and chain length for saturated FAs.15,29 Indeed, the gauche configuration influences the C–C bonds around COOH groups, which directly connect with hydrogen bonds leading in the Raman spectrum. It is worth noting that in the 30–1000 cm−1 spectral range significant differences could not be observed between the calculated Raman spectra profile at temperatures of 100 K and 300 K, suggesting a good structural stability for the AA crystal under low-temperature conditions.
Fig. 7a shows a characteristic peak located nearly 1105 cm−1 corresponding to gauche C–C stretching for a C20 chain length, in agreement with literature.67 The spectral region of 1100–1400 cm−1 is mainly composed of vibration modes of rocking/twisting types (see Table 2) and exhibits a high number of modes due to the chain configuration of Bm form. The shape of CH2-deformations’ modes of the scissoring type within 1400–1500 cm−1 spectral region is the only difference observed between the calculated Raman spectra at 300 K and 100 K. Another important point can be noticed in the low intensity broad bands nearly 1645 and 1646 cm−1 corresponding to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration which was well corroborated by DFT calculations.
O stretching vibration which was well corroborated by DFT calculations.
Fig. 7b shows the high-wavenumber region which is mainly related to the large bands associated with stretching vibrations due to the CH, CH2, and CH3 units. This region presents a good agreement between experimental Raman spectra and calculated Raman spectra in both 300 K and 100 K temperatures. It is worth noting that in the 2800–3000 cm−1 range no difference were evidenced between calculated Raman spectra at different temperatures, which supports the good stability of AA chain under low temperature.
4. Conclusions
In this study, the structure of the synthesized AA crystal was analyzed using single-crystal XRD at two different temperatures, 100 K and 300 K. The results revealed that the crystal belongs to the Bm form, where all molecules within the lattice adopt a gauche configuration. Interestingly, the crystal maintained its symmetry even at the lower temperature of 100 K, indicating good structural stability under low-temperature conditions. The evaluation of Hirshfeld's surfaces provided insights into the intermolecular bonds of the AA crystal in both 100 K and 300 K temperatures. The analyses indicated only minor changes in the intermolecular interactions, which can be attributed to the high stability of H⋯H, H⋯O/O⋯H, and O⋯O contacts. In addition, the vibrational properties were studied using polarized Raman scattering in the y(xx)y and y(zz)y geometries. The DFT calculations were performed in a pair of molecules of AA in the Bm form in the two temperatures of 100 and 300 K, in order to obtain all Raman modes of the new polymorph phase and their respective assignments, as well as indicated a good accordance with experimental Raman results. Overall, this study successfully determined the structure of the AA crystal, highlighting its polymorphic Bm form and structural stability at low temperatures. Studies of intermolecular bonds and vibrational properties further enhanced our understanding of this crystalline system.Author contributions
J. G. Oliveira Neto: synthesis of crystals, carried out the computational calculations of Hirshfeld surfaces and crystal voids, experimental data treatment, and analyses & writing-review. L. M. B. Cardoso: investigation and formal analysis of vibrational data. G. D. Saraiva: investigation and formal analysis of Raman results, conceptualization, writing-review & editing. F. F. Leite: theoretical methodology, conceptualization, formal analysis of DFT results & writing-review. A. P. Ayala: experimental methodology and investigation of single-crystal XRD, structural data collection and analysis, conceptualization, writing-review & editing. A. O. Santos: investigation and formal analysis of structural data, resources, conceptualization, writing-review & editing. F. F. Sousa: carried out the Raman spectroscopy experiments, experimental methodology of Raman spectroscopy, investigation and formal analysis of Raman data, conceptualization, writing–overviewed the manuscript, supervision, writing-review & editing. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank the following Brazilian agencies: Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – CAPES-Finance Code 001, Conselho Nacional de Desenvolvimento Científico e Tecnológico – MCT/CNPq (Grants #312926/2020-0, 309688/2019-1 and 308789/2022-9), and Fundação de Amparo à Pesquisa e ao Desenvolvimento Científico e Tecnológico do Maranhão – FAPEMA (BPD-12643/22). Also, J. G. Oliveira Neto, PhD, acknowledges the scholarship from FAPEMA. F. F. Leite, PhD, acknowledges the support from Grupo Amazônico de Materiais e Energias Renováveis – GAMER.References
- B. Bharath, K. Perinbam, S. Devanesan, M. S. AlSalhi and M. Saravanan, J. Mol. Struct., 2021, 1235, 130229, DOI:10.1016/j.molstruc.2021.130229.
- N. Ngamakeue and P. Chitprasert, Food Bioprocess Technol., 2016, 9, 1735–1745, DOI:10.1007/s11947-016-1756-4.
- N. Zhang, Y. Yuan, Y. Yuan, X. Cao and X. Yang, J. Sol. Energy, 2014, 110, 64–70, DOI:10.1016/j.solener.2014.09.003.
- I. Baskar, C. Bhuvanesh, K. S. Kavithanjali and U. Sanjana, Mater. Today: Proc., 2022, 69, 950–956, DOI:10.1016/j.matpr.2022.07.380.
- V. A. Veloso, D. L. Silva, P. L. Gastelois, C. A. Furtado and A. P. Santos, Mater. Chem. Phys., 2022, 285, 126162, DOI:10.1016/j.matchemphys.2022.126162.
- V. Veloso, F. Cotting, D. Silva and A. Santos, Prog. Org. Coat., 2022, 172, 107146, DOI:10.1016/j.porgcoat.2022.107146.
- F. M. R. Cruz, R. Q. Solórzano and M. S. Cantú, Int. J. Energy Res., 2022, 46, 19548–19565, DOI:10.1002/er.8526.
- F. J. M. Molenberg, J. Goede, A. J. Wanders, P. L. Zock, D. Kromhout and J. M. Geleijnse, Am. J. Clin. Nutr., 2017, 106, 895–901, DOI:10.3945/ajcn.117.157826.
- V. Aparna, K. V. Dileep, P. K. Mandal, P. Karthe, C. Sadasivan and M. Haridas, Chem. Biol. Drug Des., 2012, 80, 434–439, DOI:10.1111/j.1747-0285.2012.01418.x.
- J. G. S. Santos, A. Macedo-Filho, A. M. Silva, F. F. De Sousa, E. W. S. Caetano, M. B. Da Silva and V. N. Freire, J. Mol. Model., 2021, 27, 145, DOI:10.1007/s00894-021-04752-x.
- G. Zerbi, G. Minoni and A. P. Tulloch, J. Chem. Phys., 1982, 78, 5853–5862, DOI:10.1063/1.444604.
- D. H. Wang and T. J. Brenna, Fatty Acids: Structural and Quantitative Analysis, in Mass Spectrometry for Lipidomics, Wiley-VCH GmbH, 2023, pp. 291–315, DOI:10.1002/9783527836512.ch11.
- M. C. Etter, J. C. Mc Donald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262, DOI:10.1107/S0108768189012929.
- G. M. Florio, T. S. Zwier, E. M. Myshakin, K. D. Jordan and E. L. Sibert, J. Chem. Phys., 2003, 118, 1735–1746, DOI:10.1063/1.1530573.
- L. F. L. Silva, T. Andrade-Filho, P. T. C. Freire, J. M. Filho, J. G. Da Silva Filho, G. D. Saraiva, S. G. C. Moreira and F. F. De Sousa, J. Phys. Chem., 2017, 121, 4830–4842, DOI:10.1021/acs.jpca.7b04117.
- L. F. L. Silva, W. Paschoal, G. S. Pinheiro, J. G. Da Silva Filho, P. T. C. Freire, F. F. De Sousa and S. G. C. Moreira, CrystEngComm, 2019, 21, 297–309, 10.1039/c8ce01402g.
- E. Moreno, R. Cordobilla, T. Calvet, M. A. C. Diarte, G. Gbabode, P. Negrier, D. Mondieig and H. A. J. Oonk, New J. Chem., 2007, 31, 947–957, 10.1039/b700551b.
- E. M. Calvo, T. Calvet, M. A. C. Diarte and D. Aquilano, Cryst. Growth Des., 2010, 10, 4262–4271, DOI:10.1021/cg901436p.
- W. P. Gurgel, A. Correa, C. C. Santos, A. O. Santos, G. D. Saraiva, P. T. C. Freire, C. E. S. Nogueira, S. G. C. Moreira and F. F. De Sousa, Spectrochim. Acta, Part A, 2023, 287, 122068, DOI:10.1016/j.saa.2022.122068.
- G. D. S. Souza, A. M. Amado, A. M. R. Teixeira, P. T. C. Freire, G. D. Saraiva, G. S. Pinheiro, S. G. C. Moreira, F. F. De Sousa and C. E. S. Nogueira, Cryst. Growth Des., 2020, 20, 281–290, DOI:10.1021/acs.cgd.9b01164.
- J. R. S. Miranda, A. J. R. De Castro, J. G. Da Silva Filho, P. T. C. Freire, G. S. Pinheiro, S. G. C. Moreira, G. D. Saraiva and F. F. De Sousa, Spectrochim. Acta, Part A, 2019, 208, 97–108, DOI:10.1016/j.saa.2018.09.065.
- F. F. De Sousa, C. E. S. Nogueira, P. T. C. Freire, S. G. C. Moreira, A. M. R. Teixeira, A. S. De Menezes, J. Mendes Filho and G. D. Saraiva, Spectrochim. Acta, Part A, 2016, 161, 162–169, DOI:10.1016/j.saa.2016.02.035.
- F. F. De Sousa, P. T. C. Freire, A. S. De Menezes, G. S. Pinheiro, L. P. Cardoso, P. Alcantara Jr, S. G. C. Moreira, F. E. A. Melo, J. Mendes Filho and G. D. Saraiva, Spectrochim. Acta, Part A, 2015, 148, 280–288, DOI:10.1016/j.saa.2015.04.003.
- E. M. Calvo, G. Gbabode, R. Cordobilla, T. Calvet, M. À. C. Diarte, P. Negrier and D. Mondieig, Eur. J. Chem., 2009, 15, 13141–13149, DOI:10.1002/chem.200901831.
- S. Abrahamsson and E. von Sydow, Acta Crystallogr., 1954, 7, 591–592, DOI:10.1107/S0365110X54001910.
- T. Kajiyama, R. Tominaga, K. Kojio and K. Tanaka, Bull. Chem. Soc. Jpn., 2001, 74, 765–771, DOI:10.1246/bcsj.74.765.
- G. Zerbi, G. Conti, G. Minoni, S. Pison and A. Bigotto, J. Phys. Chem., 1987, 91, 2386–2393, DOI:10.1021/j100293a038.
- F. Kaneko, M. Kobayashi, M. Kitagawa and Y. Matsuura, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 1490–1492, DOI:10.1107/s0108270189012679.
- D. C. Abreu, P. F. F. Filho, G. S. Pinheiro, P. T. C. Freire, S. G. C. Moreira, A. O. Dos Santos and F. F. De Sousa, Vib. Spectrosc., 2022, 121, 103402, DOI:10.1016/j.vibspec.2022.103402.
- F. Kaneko, K. Tashiro and M. Kobayashi, J. Cryst. Growth, 1999, 198–199, 1352, DOI:10.1016/S0022-0248(98)01011-2.
- E. M. Moore, C. Wagne and S. Komarnytsky, Front. Pharmacol., 2020, 11, 785, DOI:10.3389/fphar.2020.00785.
- G. S. Jamieson, A. N. Baughman, G. S. Jamieson, W. F. Baughman and D. H. Brauns, J. Am. Chem. Soc., 1921, 43, 1372–1381, DOI:10.1021/ja01439a020.
- J. L. B. Rogers, A. Dieffenbacher and J. V. Holm, Pure Appl. Chem., 2001, 73, 685–744, DOI:10.1351/pac200173040685.
- N. K. Adam and J. W. Dyer, J. Chem. Soc., Trans., 1925, 127, 70–73, 10.1039/CT9252700070.
- D. N. Raba, D. R. Chambre, D. M. Copolovici, C. Moldovan and L. O. Copolovici, PLoS One, 2018, 13, 1–13, DOI:10.1371/journal.pone.0200314.
- Bruker AXS Inc., APEX4 Data Collection Software (Version 2021.4-0), Madison, Wisconsin, USA, 2021 Search PubMed.
- SAINT Data Reduction Software, Version 8.36, Madison, Wisconsin, USA, 2019 Search PubMed.
- L. Krause, R. Herbst-Irmer, G. M. Sheldrick and D. Stalke, J. Appl. Crystallogr., 2015, 48, 3–10, DOI:10.1107/S1600576714022985.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341, DOI:10.1107/S0021889808042726.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8, DOI:10.1107/S2053273314026370.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122, DOI:10.1107/S0108767307043930.
- C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235, DOI:10.1107/S160057671901409242.
- R. F. W. Bader, W. H. Henneker and P. E. Cade, J. Chem. Phys., 1967, 46, 3341–3363, DOI:10.1063/1.1841222.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011, DOI:10.1107/S1600576721002910.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2004, 60, 627–668, DOI:10.1107/S0108768104020300.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32, 10.1039/b818330a.
- J. J. Koenderink and A. J. van Doorn, Image Vis. Comput., 1992, 10, 557–564, DOI:10.1016/0262-8856(92)90076.
- S. L. Tan, M. M. Jotani and E. R. T. Tiekink, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2019, 75, 308–318, DOI:10.1107/S2056989019001129.
- G. J. Zheng, L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima and Y. Honda, et al., Gaussian 09, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4, 297–306, DOI:10.1021/CT700248K/SUPPL_FILE/CT700248K-FILE002.PDF.
- Y. Ünal, W. Nassif, B. C. Özaydin and K. Sayin, Vib. Spectrosc., 2021, 112, 103189, DOI:10.1016/j.vibspec.2020.103189.
- CCCBDB introduction navigation, https://cccbdb.nist.gov/, accessed 2023-03-15.
- P. L. Polavarapu, J. Phys. Chem., 2002, 94, 8106–8112, DOI:10.1021/j100384a024.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513, DOI:10.1021/jp960976r.
- D. Michalska and R. Wysokiński, Chem. Phys. Lett., 2005, 403, 211–217, DOI:10.1016/j.cplett.2004.12.096.
- F. Teixeira and M. N. D. S. Cordeiro, J. Chem. Theory Comput., 2019, 15, 456–470, DOI:10.1021/ACS.JCTC.8B00439.
- K. Sato and M. Okada, J. Cryst. Growth., 1977, 45, 259–263, DOI:10.1016/0022-0248(77)90204-4.
- A. Y. Meyer, Chem. Soc. Rev., 1986, 15, 449–474, 10.1039/CS9861500449.
- I. F. S. Reis, J. R. Viana, J. G. De Oliveira Neto, S. R. Stoyanov, J. W. D. M. Carneiro, M. R. Lage and A. O. Dos Santos, J. Mol. Model., 2022, 28, 1–11, DOI:10.1007/s00894-022-05168-x.
- N. Tyagi, H. Yadav, A. Hussain and B. Kumar, J. Mol. Struct., 2021, 1224, 129190, DOI:10.1016/j.molstruc.2020.129190.
- D. L. Rousseau, R. P. Bauman and S. P. S. Porto, J. Raman Spectrosc., 1981, 10, 253–290, DOI:10.1002/JRS.1250100152.
- T. S. Baldez, C. M. R. Remédios, A. S. De Menezes, A. O. Dos Santos and F. F. De Sousa, Spectrochim. Acta, Part A, 2019, 214, 294–301, DOI:10.1016/j.saa.2019.02.043.
- N. S. Santana, A. F. Gomes, H. S. Santana, G. D. Saraiva, P. R. S. Ribeiro, A. O. Santos and F. F. De Sousa, Cryst. Growth Des., 2021, 21, 3602–3613, DOI:10.1021/acs.cgd.1c00375.
- B. A. Zakharov, E. A. Losev and E. V. Boldyreva, CrystEngComm, 2013, 15, 1693–1697 RSC.
- K. Czamara, K. Majzner, M. Z. Pacia, K. Kochan, A. Kaczor and M. Baranska, J. Raman Spectrosc., 2015, 17, 4–20, DOI:10.1002/jrs.4607.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2177008 and 2177009. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ra05388a |
| This journal is © The Royal Society of Chemistry 2023 |