Open Access Article
Open Access ArticleA density functional theory study on the adsorption of different organic sulfides on boron nitride nanosheet†
Zhengjian Hou‡
a,
Xufeng Lin‡ *ab,
Ke Wuc,
Hua Chia,
Wumin Zhanga,
Lishuang Ma
*ab,
Ke Wuc,
Hua Chia,
Wumin Zhanga,
Lishuang Ma *a and
Yanyan Xid
*a and
Yanyan Xid
aCollege of Chemistry and Chemical Engineering, China University of Petroleum (East China), Qingdao 266580, China. E-mail: hatrick2009@upc.edu.cn; hxmals@upc.edu.cn; Tel: +86-532-86981975
bState Key Laboratory of Heavy Oil Processing, China University of Petroleum (East China), Qingdao 266580, China
cChangqing Engineering Design Co. Ltd., PetroChina Changqing Oilfield Company, Xi'an 710000, Shanxi, China
dAdvanced Chemical Engineering and Energy Materials Research Center, China University of Petroleum (East China), Qingdao 266580, China
First published on 30th October 2023
Abstract
The adsorption of methanethiol (MT), thiophene (T), benzothiophene (BT), dibenzothiophene (DBT) on hexagonal boron nitride (h-BN) has been investigated by the framework of the density functional theory (DFT) calculations in this work. The prefer adsorption sites and interfacial angles of different sulfur compounds on the surface of the h-BN are investigated and analyzed. The adsorption energy results indicated that the adsorption of MT (Ead ≈ −6 kcal mol−1), T (Ead ≈ −10 kcal mol−1), BT (Ead ≈ −15 kcal mol−1), and DBT (Ead ≈ −21 kcal mol−1) on monolayer h-BN is physical interaction, and the value of Ead on bilayer h-BN is more than that on monolayer h-BN 0.05%. Adsorptive conformations show that sulfides prefer to be adsorbed on center B atoms rather than N atoms. Meanwhile, thiophene and its analogues tend to be adsorbed parallel on h-BN plane. Energy decomposition, natural population analysis (NPA), and electrostatic potential (ESP) analysis used to better understand the nature of adsorption on h-BN. van der Waals force plays a dominant role in adsorption process. Due to the π–π interactions, T, BT, and DBT have larger van der Waals forces than MT and the value of adsorption energy is negative correlated to the number of benzene rings. These findings are helpful for deeper understanding the adsorptive desulfurization mechanism and help develop better adsorbents for desulfurization in the future.
1. Introduction
Ultra-deep desulfurization of commercial fuel is of growing concern nowadays. The sulfur (S)-containing species in oil are not only harmful to environmental livings, but also poisonous for metal-based catalysts in the oil-refining and petrochemical processes. Therefore, many researchers are devoted to reduce the S content in fuel,1–3 and the present desulfurization methods includes hydrodesulfurization (HDS),4 oxidative desulfurization (ODS),5,6 extraction desulfurization,7 bio-desulfurization (BDS)8 and adsorptive desulfurization (ADS).9–12 Among them, ADS has attracted extensive attentions especially for ultra-low S oils because of its mild process conditions and low operation cost.Up to now, several types of adsorbent have been successfully applied for ADS, such as metal oxides,13,14 zeolites,15–17 activated carbons,18 metal organic frameworks (MOF),19,20 boron nitride (BN)21–23 including hexagonal boron nitride (h-BN)24,25 and so on. BN-based materials in general, like their carbon-based analogues, can existed in various nanostructures including nanotubes,23 nanosheets,26 nanobowls,27 are potentially useful materials in the field of adsorbent–adsorbate interactions like pollutant removal and drug delivery. In particular, the h-BN-based adsorbents have gained particular attentions because of its unique layer–structure properties, high specific surface area, remarkable durability and adsorption capacity. These characteristics make h-BN become a promising carrier for dispersion of active species.1,4 Li et al.28 introduced Sn-based deep eutectic solvents (DESs) into h-BN to obtain superior adsorption performance. Sn-BN showed an adsorption capacity of 17.93 mg S g−1. Sun et al.29 prepared the Cu-intercalated layered h-BN/N-doped carbon-nanofiber composite films (PAN-Cu/ABN-CNFs). Its adsorption capacity was up to 78.38 mg S g−1 and the adsorption capacity after a four-time regeneration recycling still maintained at 74.894 mg S g−1. In short, h-BN is a promising adsorbent for ADS and it is of great importance to study its adsorption mechanism to further improve its performance.
However, it is difficult to study the adsorption mechanisms and active sites through experimental method due to high costs. In contrast, computational chemistry provides powerful tools for investigating adsorption mechanism. For example, Li et al.30 investigated the dibenzothiophene (DBT) adsorption strength on the pristine and O-doped h-BN monolayer by density functional theory (DFT) calculations. Larijani et al. studied the adsorption of glycine amino acid and its zwitterionic form on graphene, h-BN and silicon carbide (h-SiC).31 The interaction of sulfur mustard, a chemical warfare agent, with the surface of C24, C12Si12, Al12N12, Al12P12, Be12O12, B12N12 and Mg12O12 nanocages was studied using the dispersion corrected density functional theory (DFT-D3) method.32 In addition, Xiong et al. found that the strong interaction between DBT and the graphene-like BN or BN nanowire came from the occupied π-electrons of the B atoms orbitals.22 The driven force for adsorption of aromatic compounds on h-BN is qualitatively proposed to be π–π interaction.33
Modified h-BN and other adsorbents are often used to adsorb only one sulfide according to previous researches. However, there are many different sulfur compounds needs to be adsorbed and separated in reality. The study on adsorption behaviors of different molecules has a significant effect on separation and purification in chemical engineering, as well as in molecular recognition.33 For example, CO and CO2 are recovered from blast furnace exhaust gas, BZ and DBT are separated and removed in petrochemical industry. Therefore, it is necessary to study the adsorption mechanisms of adsorbents for different sulfur compounds. Though the adsorptive energies of several sulfurs on h-BN and graphene were previously studied, the comprehensive analyses of the interaction nature between the adsorbates and adsorbents are still inadequate.
In this work, adsorption mechanisms of different sulfur compounds adsorbed on the surface of model h-BN sheets were investigated through the density functional theory (DFT). A series adsorption model of sulfur compounds adsorbed on h-BN with different sites and interfacial angles was obtained and optimized.34 The adsorption energy (Eads) of different structures were compared and the mechanism of ADS was analyzed.
2. Computational methods
DFT calculations including the Grimme's D3 dispersion correction (DFT-D3BJ) were performed using the Gaussian 09 program suite35 to investigate the adsorption mechanism of various sulfur compounds on the h-BN. All geometries including the sulfur compounds, h-BN, as well as their adsorption complexes were fully optimized using the B3LYP-D3BJ functional with the 6-31G(d,p) basis set. Vibrational frequency analyses were also performed at the same level of theory to confirm that the obtained structures are true minima with no imaginary frequencies. The B3LYP functional had been demonstrated to be a reliable commonly used theoretical level for studying adsorption of different nanostructures.36–39 It has proven that the B3LYP/6-31G(d,p) is a suitable theoretical method for medium systems to provide acceptable results with low cost.39 To avoid the underestimation of the interaction between sulfur compound and BN nanosheet due to dispersion problem,40,41 the D3BJ dispersion correction was applied for all DFT calculations.42The model S compounds studied in this work include methanethiol (MT), thiophene (T), benzothiophene (BT), and dibenzothiophene (DBT). To represent the h-BN sheet, a slab of hexagonal lattice composed of 27B and 27N atoms were constructed, where the dangling bonds were saturated with hydrogen atoms to minimize the edge effect. The global charge of the model S compounds, the model h-BN sheet, and their adsorption systems are zero. The spin multiplicity of them are 1 since all S compounds have closed-shell electronic configuration, and the model h-BN sheet has a singlet ground state compared to its triplet state.
The adsorption energy (Ead) was calculated as follows,
| Ead = Esulfur/BN − EBN − Esulfur + EBSSE | (1) |
In order to further support the rationality of the basis set as well as the B3LYP-D3BJ method used in this work, the Ead of MT adsorbed on the above described B27N27 sheet (with η1 conformation, vide infra) using the 6-31G(d,p) basis sets was compared to that using the 6-311G(d,p) basis set. The small error (0.7 kcal mol−1, see first two line of Table S1 in the ESI†) supports the rationality of using the 6-31G(d,p) basis sets for description of the adsorption system interested in this work. Furthermore, a benchmark calculation on the Ead of MT on a B3N3 ring was also carried out with the results being collected in Table S2.† From Table S2† it can be seen the presently used B3LYP-D3BJ/6-31G(d,p) level predicts a rather close Ead compared to another popular method of M06-2X-D3. More importantly, B3LYP-D3BJ/6-31G(d,p) also predicts a quite close Ead compared to post-SCF levels of MP2/AGU-CC-PVDZ, with the error of less than 1.0 kcal mol−1. These comparisons show that using B3LYP-D3BJ method is appropriate for studying the adsorption systems interested in this work.
3. Results and discussion
3.1 Adsorptive conformations and energies of the sulfides on a monolayer h-BN sheet
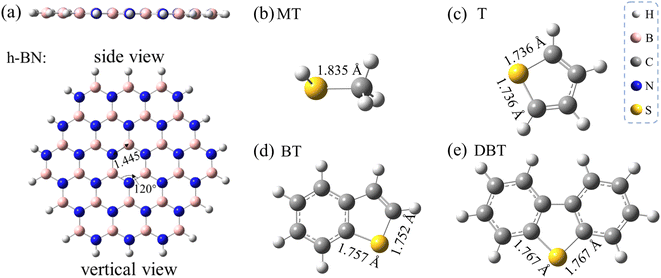
In this section, the adsorption conformations and energies of the sulfur adsorbates on the monolayer h-BN, as well as the influence of different possible adsorptive sites are discussed. Fig. 1a shows the optimized structure of a slab of hexagonal lattice composed of 27B and 27N atoms. The B27N27 sheet was selected to represent the h-BN monolayer, which has been proven to be reliable to study the adsorption performance of h-BN nanosheets toward various adsorbates.33 The interested sulfur adsorbates in this work, including methanethiol (MT), thiophene (T), benzothiophene (BT), and dibenzothiophene (DBT), are also shown in Panels b–e in Fig. 1.As the h-BN sheet has a polar surface with non-uniform charge distribution due to the difference in the polarity of B and N, the h-BN sheet can offer more differentiated adsorptive sites than the graphene sheet. On a given h-BN monolayer, the electronegative sulfur ad-atoms can interact with BN surface either through a point-to-point site of an electropositive B atom (denoted as η1:B-site) or through an on-top site of a six-membered B3N3 ring (denoted as η6-site). In addition, the π–π stacking interaction cannot be ignored for the aromatic sulfur adsorbates. By taking the above factors into consideration, the stable adsorptive conformations were obtained as illustrated in Fig. 2–4. Note that all these conformations were fully optimized without any structural restrictions. Hereafter in this paper, the notation of XX/h-BN (where XX represent a certain adsorbate of MT, T, BT or DBT) is used to represent the adsorption complexes of different sulfides on an h-BN sheet. A suffix of “-mono” or “-bi” represents the h-BN sheet is a monolayer or bilayer one. This paper mainly contains the result of a monolayer h-BN sheet (except Section 3.2), so when no suffix was used, the notation refers to the monolayer case. A suffix of “-ηn” (where n = 1, 2 and 6 in this work) represent different type of adsorption conformation for a certain adsorption system. For example, the notation of MT/h-BN-ηn (n = 1, 2 and 6 in this work) is used to define the adsorption complex where the MT occupies the ηn site, and the η1 below will specifically represent the η1:B-site.
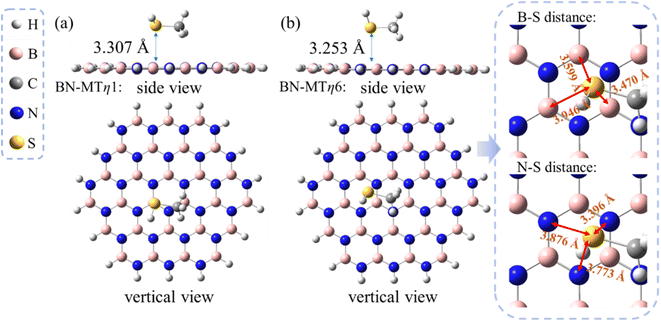
The calculated results show that two most stable conformations of MT/h-BN in which the sulfur atom located at the η1:B-site and the η6-site of h-BN exhibit close adsorption energies, i.e. −5.8 and −6.0 kcal mol−1 respectively (see Table 1). This suggests that the η6-site and the η1:B site may compete in stabilizing the sulfide/h-BN complex. As can be seen from the geometry parameters shown in Fig. 2, the equilibrium distance from the S atom to the hexagonal BN plane in the MT/h-BN-η1 complex is 3.307 Å, and meanwhile the geometry parameters (bond length and bond angles) of the complex remained almost unchanged compared with the individual MT and h-BN, which indicates the non-covalent physisorption characteristic between the two entities. The MT/h-BN-η6 complex shows a physisorption conformation since the B–S distances between the S atom and the closest BN hexagon vary in the range of 3.47–3.95 Å, and the S–N distances are in the range of 3.40–3.88 Å.
| Species | Adsorptive site | Interfacial angles | Ead (kcal mol−1) |
|---|---|---|---|
| MT/h-BN | η1 | — | −5.8 |
| η6 | — | −6.0 | |
| T/h-BN | η1 | 0 | −10.1 |
| η1 | 15 | 0.4 | |
| η1 | 60 | 0.5 | |
| η1 | 90 | 1.1 | |
| η6 | 0 | −10.1 | |
| BT/h-BN | η1 | 0 | −15.7 |
| η6 | 0 | −15.0 | |
| DBT/h-BN | η1 | 0 | −21.3 |
| η6 | 0 | −21.3 |
Since in practice ADS is often carried out in oil like gasoline or diesel, the Ead of MT on the BN sheet with gas phase model was compared to the those with the solvation models using n-heptane (representing gasoline) and using n-dodecane (representing diesel). The Ead with the gas phase model (the 1st entry in Table S1†) is quite close to those of the solvation model (the 3rd and 4th entries in Table S1†), showing in these ADS systems oil solvents play trivial roles. On the other hand, besides the adsorption of MT on the central BN ring in the B27N27 model (Fig. 2a), the possible edge effect was also investigated by comparing the Ead of MT on different sites with η1 conformation (Fig. S1 in ESI†). The Ead results listed in Table S1† show that the Ead values are quite close for these different sites. Therefore, the solvation effect and edge effect on the adsorption behavior and energy were no longer considered for other adsorption systems in this work.
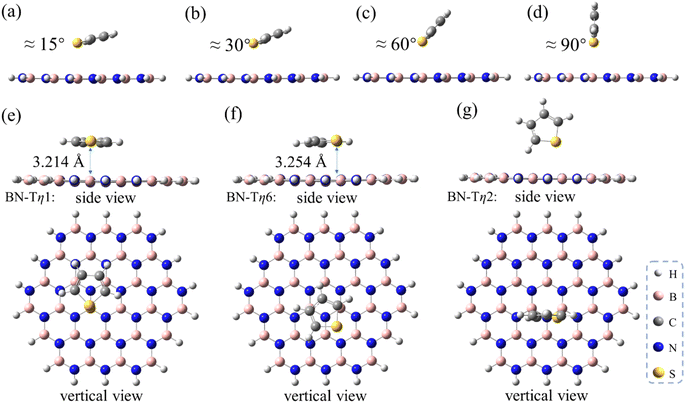
Besides the aliphatic methanthiol MT, the aromatic sulfur compounds such as T, BT and DBT adsorbates were also investigated, in order to explore the influence of the π–π interaction during the ADS process. For this purpose, we first performed a series of optimizations by fixing the interfacial angle (Φ) between T and h-BN from 15° to 90°, and the B–S distances being fixed at 3.30 Å (panels a–d in Fig. 3). As shown in Table 1, the adsorption strength gradually decreases as the dihedral angle Φ increases and the π–π interaction strength decreases. These changes indicate that the π–π interaction plays an important role in the ADS process. It is worth noting that the adsorption energy of T/h-BN-η1 with Φ = 90° (−4.8 kcal mol−1) is smaller than that of MT/h-BN-η1 (−5.8 kcal mol−1), partly due to the weaker electronegativity of sulfur atom on T than MT. When global optimization was performed for the T/h-BN complex without any constraints, three energy minima were obtained including T/h-BN-η1, T/h-BN-η6 and T/h-BN-η2 as shown in panels e–g in Fig. 3. The calculated results show that the T/h-BN-η2 structure with a perpendicular orientation has an adsorption energy of −6.7 kcal mol−1, which is obviously lower than that of the T/h-BN-η1 structure with Φ = 90°. Not surprisingly, the π–π stacked T/h-BN-η1 and the T/h-BN-η6 conformations exhibit similar stabilities with low adsorption energies (−10.06 and −10.07 kcal mol−1). These calculated results indicate that the π–π stacking interaction plays an important role in the ADS process on the h-BN adsorbent.
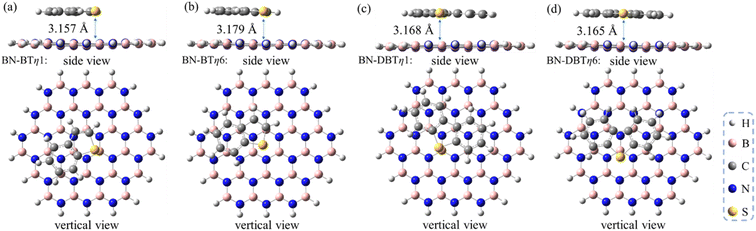
To further evaluate the influence of the strength of π–π interaction on stabling the sulfur/h-BN complex, the BT and DBT adsorbates having two and three aromatic rings, respectively, were also studied. It was found that on the one hand, the π–π stacked η1-site- and η6-site-adsorptive conformations are also the two most energetically favorable ones with similar adsorption energies for the cases of BT and DBT adsorbates (Fig. 4). On the other hand, the adsorption energy increase with the order of MT < T < BT < DBT, ranging from −6.0 to −21.4 kcal mol−1 (Table 1). In addition, the distances between all sulfides and BN plane become closer around 3.2–3.3 Å (see geometries of adsorbed MT, T, BT and DBT shown in Fig. 1–4). This suggests that the more aromatic the sulfide is, the significantly stronger the adsorption interaction will be.
 | ||
| Fig. 4 Optimized structures of (a) BT/h-BN-η1, (b) BT/h-BN-η6, (c) DBT/h-BN-η1 and (d) DBT/h-BN-η6. All distances are indicated in angstroms. | ||
3.2 Adsorptive conformations and energies of the sulfides on a bilayer h-BN sheet
In this section, the adsorptive conformations and energies of the sulfides on bilayer h-BN was explored to understand the effect of BN layer stacking on adsorption desulfurization performance. As shown in Fig. 5, the so-called AA′ stacking conformation, where the B atoms on lower layer are eclipsed by the N atoms on upper layer and vice versa, has been reported to be the most favorable pattern among the five possible ones, i.e. AA, AA′, AB, AB′ and A′B, for a bilayer h-BN sheet.47 So the AA′-stacked bilayer h-BN was considered as the other interested adsorbent in this paper. The formation energy of this bilayer h-BN was calculated to be −96.3 kcal mol−1 by using the following formula,| Eform = Ebilayer −2Emonolayer | (2) |
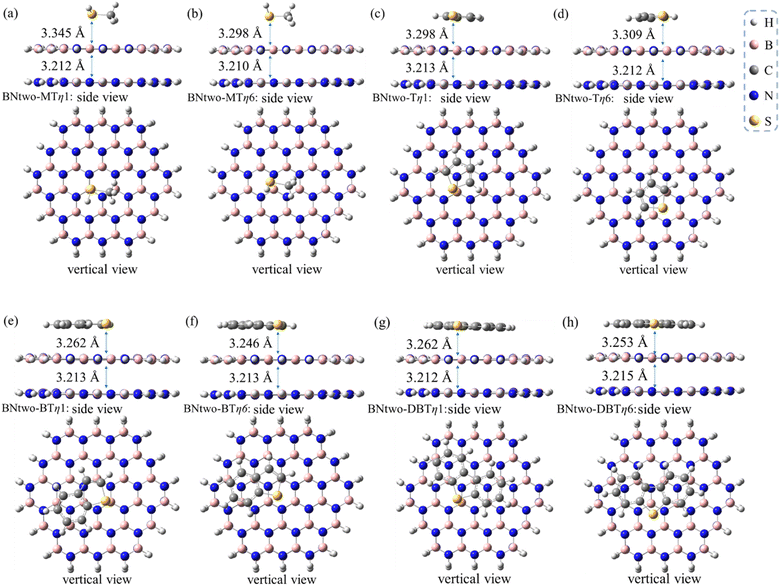
The adsorptive conformations systematically become more stabilized with the order of MT, T, BT and DBT, similar as the results of monolayer h-BN case (Table 2 compared to Table 1). The adsorption energies are ranged from −6.0 to −21.4 kcal mol−1 which is also same as the results of monolayer h-BN. Therefore, π–π effects also plays an important role in bilayer systems. Meanwhile, there are also two competitive adsorptive conformations (η1 and η6) for the bilayer h-BN systems (see Fig. 6). The distance from sulfides to bilayer h-BN is slightly larger than that of the monolayer case (Table 3), indicating a second h-BN layer has a weakening effect for the sulfide adsorption on the h-BN adsorbents.
| Species | Adsorptive site | Ead (kcal mol−1) |
|---|---|---|
| MT/h-BN-bi | η1 | −6.3 |
| η6 | −6.3 | |
| T/h-BN-bi | η1 | −10.8 |
| η6 | −10.6 | |
| BT/h-BN-bi | η1 | −16.6 |
| η6 | −15.9 | |
| DBT/h-BN-bi | η1 | −22.6 |
| η6 | −22.6 |
| Species | Adsorption conformation | dmonolayer (Å) | dbilayer (Å) |
|---|---|---|---|
| MT/h-BN | η1 | 3.307 | 3.345 |
| η6 | 3.253 | 3.298 | |
| T/h-BN | η1 | 3.214 | 3.298 |
| η6 | 3.254 | 3.309 | |
| BT/h-BN | η1 | 3.157 | 3.262 |
| η6 | 3.179 | 3.246 | |
| DBT/h-BN | η1 | 3.168 | 3.262 |
| η6 | 3.165 | 3.253 |
3.3 Further analysis for the nature of adsorption on h-BN
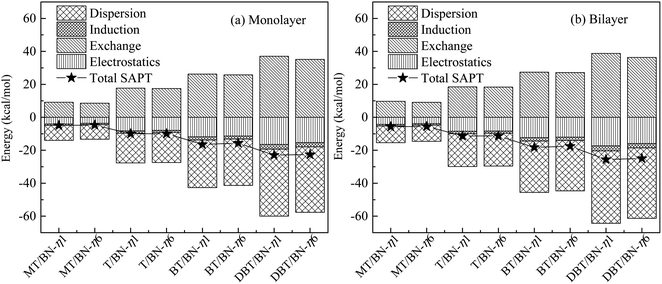 | ||
| Fig. 7 Symmetry adapted perturbation theory (SAPT) energy decomposition of (a) sulfide/h-BN-mono and (b) sulfide/h-BN-bi adsorption systems, where, sulfide represents one of MT, T, BT or DBT. | ||
The electrostatics and dispersion effect contribute the most to the interaction among four interactions. Dispersion effect dominates in the adsorption system, and electrostatics is smaller. Therefore, electrostatics and dispersion play main role in the adsorption system studied above, and are discussed in the following part. The electrostatics effect comes from the positive and negative charges in adsorption system, and the dispersion effect comes from the weak van der Waals force and π–π interaction.
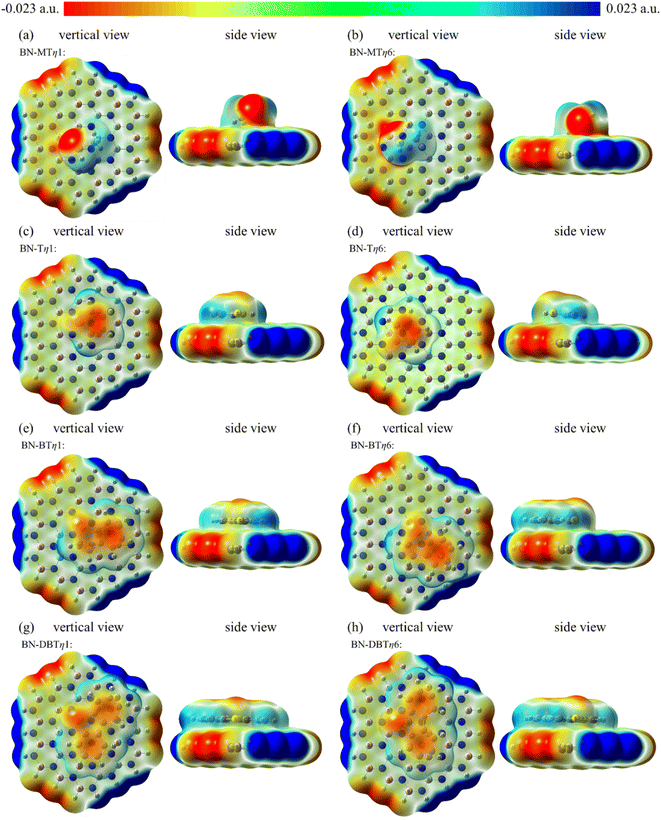
Both electrostatics and dispersion energy increase as the adsorbate changing from MT to DBT, and the dispersion increases more. On the one hand, the negative charge of S atom is partly dispersed due to the aromatic properties in sulfides. Thus the negative region contacting with h-BN plane increases. Accordingly, the electrostatic effect increases. For example, the charge of C and H on DBT is more negative than that on MT because of conjugation. Otherwise, it can be concluded that electrostatics of η1 is stronger than η6. This may be due to the negative charge center of S atom is closer to B atom in η1, and the charge effect is stronger. On the other hand, lager adsorbate could result in increasing van der Waals force (dispersion force). In addition, the aromatic ring on adsorbate will form π–π mode with the six-membered ring on h-BN, which further strengthens the van der Waals force.
Therefore, the adsorption of T, BT and DBT on h-BN is stronger than MT, and the effect mainly attribute to dispersion and electrostatics. The π–π interaction between sulfides and h-BN will increase with more benzene rings. The monolayer and bilayer of h-BN adsorption systems have the same properties.
The results above are in line with the adsorption energies (the Ead decrease in order MT, T, BT and DBT) as well as the stabilities of the sulfur/h-BN complexes. While the charge transfers are both below 0.05e, indicating that the charge effect is not strong. And it is similar to electrostatics in the energy decomposition analysis. The results of bilayer h-BN system are consistent with the monolayer system.
| Structure | Adsorption conformation | ΔQ (e) | |
|---|---|---|---|
| h-BN | Adsorbate | ||
| MT/h-BN-mono | η1 | −0.018 | 0.018 |
| η6 | −0.009 | 0.009 | |
| T/h-BN-mono | η1 | −0.029 | 0.029 |
| η6 | −0.026 | 0.026 | |
| BT/h-BN-mono | η1 | −0.034 | 0.034 |
| η6 | −0.031 | −0.031 | |
| DBT/h-BN-mono | η1 | −0.044 | 0.044 |
| η6 | −0.034 | 0.034 | |
| MT/h-BN-bi | η1 | −0.022 | 0.022 |
| η6 | −0.013 | 0.013 | |
| T/h-BN-bi | η1 | −0.034 | 0.034 |
| η6 | −0.030 | 0.030 | |
| BT/h-BN-bi | η1 | −0.039 | 0.039 |
| η6 | −0.038 | 0.038 | |
| DBT/h-BN-bi | η1 | −0.052 | 0.052 |
| η6 | −0.041 | 0.041 | |
The negative charge on S atom is dispersed due to the existence of large conjugate structure (panels c–h in Fig. 8). Whereas S atom is still the center where the negative charge of sulfide is concentrated to interact with B atom. As a result, the adsorption sites of T, BT and DBT are the same as MT. It can be seen from Fig. 8 that the adsorption area of DBT and the negatively charged area of the system are the largest one. This is the reason why the value of adsorption energy of DBT on h-BN is most negative among four sulfides.
4. Conclusions
In summary, the adsorption behavior and nature of four S-containing compounds on model h-BN nanosheets were systematically investigated with DFT calculations. Primary conclusions can be drawn as follows.(i) Sulfides can be adsorbed on h-BN with two energetically competitive conformations, namely point-to-point (η1, through S⋯B interaction) and point-to-ring-center (η6) ones. The plane of T, BT or DBT tends to be adsorbed parallel on h-BN plane. Besides, the adsorption energies increase with the order of MT < T < BT < DBT. There rules are feasible for both of the monolayer and bilayer h-BN cases.
(ii) Electrostatic effects, the interactions between positive and negative charges, play an important role in the adsorption process. The S atom tends to adsorbed near to the positively charged B atom. Therefore, electrostatic effect in the conformation η1, where negative center of sulfide S atom is closer to the B atom, is stronger than that of η6.
(iii) van der Waals force plays a dominant role in adsorption process. Compared with the case of MT, the π–π interaction of T, BT and DBT with h-BN strengthens the van der Waals force. This effect increases with increasing number of benzene rings in the adsorbate.
The above findings provide deeper understandings about sulfides adsorption mechanism on BN type absorbents in particular, and on wider types of absorbents in general. The new understandings may help design better adsorbent for adsorptive desulfurization in the future.
Author contributions
Zhengjian Hou: calculation performing, results analysis, writing and organization; Xufeng Lin: idea development, research funding provision, writing and organization; Ke Wu: discussion, writing; Hua Chi: discussion, writing; Wumin Zhang: discussion, revision; Lishuang Ma: funding provision, discussion; Yanyan Xi: discussion.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support from the National Natural Science Foundation of China (22003076, 21576291) and the Fundamental Research Funds for the Central Universities (23CX03007A, 22CX06012A) is gratefully acknowledged.References
- H. Li, H. Ran, Y. Li, N. Lv, J. Yin, J. Zhang, C. Wang, W. Jiang, W. Zhu, H. Li and H. Ji, J. Environ. Chem. Eng., 2021, 9, 105886–105899 CrossRef CAS.
- S. A. Ganiyu and S. A. Lateef, Fuel, 2021, 294, 120273–120295 CrossRef CAS.
- Z. Chen, L. Ling, B. Wang, H. Fan, J. Shangguan and J. Mi, Appl. Surf. Sci., 2016, 387, 483–490 CrossRef CAS.
- A. Tanimu and K. Alhooshani, Energy Fuels, 2019, 33, 2810–2838 CrossRef CAS.
- W. Jiang, H. Jia, H. Li, L. Zhu, R. Tao, W. Zhu, H. Li and S. Dai, Green Chem., 2019, 21, 3074–3080 RSC.
- W. Jiang, K. Zhu, H. Li, L. Zhu, M. Hua, J. Xiao, C. Wang, Z. Yang, G. Chen, W. Zhu, H. Li and S. Dai, Chem. Eng. J., 2020, 394, 124831–124839 CrossRef CAS.
- R. Abro, A. A. Abdeltawab, S. S. Al-Deyab, G. Yu, A. B. Qazi, S. Gao and X. Chen, RSC Adv., 2014, 4, 35302–35317 RSC.
- G. Mohebali and A. S. Ball, Int. Biodeterior. Biodegrad., 2016, 110, 163–180 CrossRef CAS.
- Y. Li, N. Lv, C. Wang, J. Zhang, W. Fu, J. Yin, H. Li, W. Zhu and H. Li, J. Mol. Graph. Model., 2020, 101, 107715–117725 CrossRef CAS.
- Y. X. Li, J. X. Shen, S. S. Peng, J. K. Zhang, J. Wu, X. Q. Liu and L. B. Sun, Nat. Commun., 2020, 11, 3206–3215 CrossRef CAS.
- T. Feng, Y. Wang, Y.-n. Wu, D. M. Kabtamu, K. László and F. Li, J. Mater. Chem. A, 2020, 8, 8678–8683 RSC.
- P. Tan, Y. Jiang, L.-B. Sun, X.-Q. Liu, K. AlBahily, U. Ravon and A. Vinu, J. Mater. Chem. A, 2018, 6, 23978–24012 RSC.
- R. Menzel, D. Iruretagoyena, Y. Wang, S. M. Bawaked, M. Mokhtar, S. A. Al-Thabaiti, S. N. Basahel and M. S. P. Shaffer, Fuel, 2016, 181, 531–536 CrossRef CAS.
- R. Neubauer, M. Husmann, C. Weinlaender, N. Kienzl, E. Leitner and C. Hochenauer, Chem. Eng. J., 2017, 309, 840–849 CrossRef CAS.
- B. S. Crandall, J. Zhang, V. Stavila, M. D. Allendorf and Z. Li, Ind. Eng. Chem. Res., 2019, 58, 19322–19352 CrossRef CAS.
- R. Mahmoudi and C. Falamaki, Fuel, 2016, 173, 277–284 CrossRef CAS.
- M. Moradi, R. Karimzadeh and E. S. Moosavi, Fuel, 2018, 217, 467–477 CrossRef CAS.
- X. N. Li, S. S. Peng, L. N. Feng, S. Q. Lu, L. J. Ma and M. B. Yue, Microporous Mesoporous Mater., 2018, 261, 44–50 CrossRef CAS.
- N. A. Khan, J. W. Yoon, J. S. Chang and S. H. Jhung, Chem. Comm., 2016, 52, 8667–8670 RSC.
- J.-X. Qin, P. Tan, Y. Jiang, X.-Q. Liu, Q.-X. He and L.-B. Sun, Green Chem., 2016, 18, 3210–3215 RSC.
- J. Xiong, W. Zhu, H. Li, W. Ding, Y. Chao, P. Wu, S. Xun, M. Zhang and H. Li, Green Chem., 2015, 1647–1656 RSC.
- J. Xiong, L. Yang, Y. Chao, J. Pang, M. Zhang, W. Zhu and H. Li, ACS Sustainable Chem. Eng., 2018, 6(8), 9912–9920 CrossRef.
- E. C. Anota, G. H. Cocoletzi and A. M. G. Tapia, Open Chem., 2015, 13, 734–742 Search PubMed.
- H. Ji, J. Sun, P. Wu, Y. Wu, J. He, Y. Chao, W. Zhu and H. Li, Fuel, 2018, 213, 12–21 CrossRef CAS.
- P. Wu, Y. Wu, L. Chen, J. He, M. Hua, F. Zhu, X. Chu, J. Xiong, M. He, W. Zhu and H. Li, Chem. Eng. J., 2020, 380, 122526–122534 CrossRef CAS.
- E. C. Anota, SN Appl. Sci., 2022, 4, 295 CrossRef CAS.
- M. C. F. Bautista, D. Cortés-Arriagada, E. Shakerzadeh and E. C. Anota, J. Mol. Liq., 2022, 355, 118980 CrossRef.
- H. Li, J. Zhang, J. Yi, J. Luo, S. Zhu, L. Sun, J. Xiong, W. Zhu and H. Li, Chem. Eng. Res. Des., 2019, 144, 11–18 CrossRef CAS.
- X.-L. Sun, Z. Liu and Z.-L. Cheng, J. Alloys Compd., 2021, 885, 160976–160988 CrossRef CAS.
- H. Li, Y. Zhang, N. Lv, J. Yin, J. Zhang, H. Ran, M. Zhang, W. Jiang, W. Zhu and H. Li, J. Environ. Chem. Eng., 2021, 9, 106463–106475 CrossRef CAS.
- H. T. Larijani, M. Jahanshahi, M. D. Ganji and M. H. Kiani, Phys. Chem. Chem. Phys., 2017, 19, 1896–1908 RSC.
- H. Jouypazadeh and H. Farrokhpour, J. Mol. Struct., 2018, 1164, 227–238 CrossRef CAS.
- H. Li, C. Wang, S. Xun, J. He, W. Jiang, M. Zhang, W. Zhu and H. Li, J. Mol. Graph. Model., 2018, 82, 93–100 CrossRef CAS.
- Y. Sun, S. Gao, F. Lei and Y. Xie, Chem. Soc. Rev., 2015, 44, 623–636 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian Inc., Wallingford, CT, 2013 Search PubMed.
- K. M. Eid and H. Y. Ammar, Appl. Surf. Sci., 2011, 257, 6049–6058 CrossRef CAS.
- J. Beheshtian, A. A. Peyghan and Z. Bagheri, Appl. Surf. Sci., 2012, 258, 8171–8176 CrossRef CAS.
- J. Beheshtian, A. A. Peyghan, M. B. Tabar and Z. Bagheri, Appl. Surf. Sci., 2013, 266, 182–187 CrossRef CAS.
- G. I. Csonka, J. Mol. Struct. Theochem., 2002, 584, 1–4 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- Y. X. Yu, J. Mater. Chem. A, 2014, 2, 8910–8917 RSC.
- J. Li, H. Gan, Y. Xu, C. Wang, Y. Pei, F. L. Gu and G. Wang, CrystEngComm, 2018, 20, 6775–6785 RSC.
- M. A. Spackman and A. S. Mitchell, Phys. Chem. Chem. Phys., 2001, 3, 1518–1523 RSC.
- D. G. A. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A. M. James, S. Lehtola, J. P. Misiewicz, M. Scheurer, R. A. Shaw, J. B. Schriber, Y. Xie, Z. L. Glick, D. A. Sirianni, J. S. O'Brien, J. M. Waldrop, A. Kumar, E. G. Hohenstein, B. P. Pritchard, B. R. Brooks, H. F. Schaefer III, A. Yu. Sokolov, K. Patkowski, A. E. DePrince III, U. Bozkaya, R. A. King, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Phys., 2020, 152, 184108 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD – visual molecular dynamics, J. Mol. Graphics, 1996, 14.1, 33–38 CrossRef PubMed.
- U. Paliwal, G. Sharma and K. B. Joshi, Mater. Today Proc., 2022, 50, 301–306 CrossRef CAS.
- O. Karalti, D. Alfe, M. J. Gillan and K. D. Jordan, Phys. Chem. Chem. Phys., 2012, 14, 7846–7853 RSC.
- J. G. McDaniel, K. Yu and J. R. Schmidt, J. Phys. Chem. C, 2012, 116, 1892–1903 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05718f |
| ‡ These two authors contribute equally to this paper. |
| This journal is © The Royal Society of Chemistry 2023 |