Open Access Article
Open Access ArticleIntrinsic half-metallicity in two-dimensional Cr2TeX2 (X = I, Br, Cl) monolayers†
Jun Zhanga,
Zixin Hea,
Chuchu Gaoa,
Yanyan Taoa,
Feng Lianga,
Guannan Lia,
Benling Gao *a and
Guang Song
*a and
Guang Song *ab
*ab
aDepartment of Physics, Huaiyin Institute of Technology, 1 Meicheng East Road, Huaian 223003, China. E-mail: jsblgao@163.com; gsong@hyit.edu.cn
bDepartment of Physics, Nanjing University, 22 Hankou Road, Nanjing 210093, China
First published on 10th October 2023
Abstract
Two-dimensional (2D) materials with intrinsic half-metallicity at or above room temperature are important in spin nanodevices. Nevertheless, such 2D materials in experiment are still rarely realized. In this work, a new family of 2D Cr2TeX2 (X = I, Br, Cl) monolayers has been predicted using first-principles calculations. The monolayer is made of five atomic sublayers with ABCAB-type stacking along the perpendicular direction. It is found that the energies for all the ferromagnetic (FM) half-metallic states are the lowest. The phonon spectrum calculations and molecular dynamics simulations both demonstrate that the FM states are stable, indicating the possibility of experimentally obtaining the 2D Cr2TeX2 monolayers with half-metallicity. The Curie temperatures from Monte Carlo simulations are 486, 445, and 451 K for Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 monolayers, respectively, and their half-metallic bandgaps are 1.72, 1.86 and 1.90 eV. The corresponding magnetocrystalline anisotropy energies (MAEs) are about 1185, 502, 899 μeV per Cr atom for Cr2TeX2 monolayers, in which the easy axes are along the plane for the Cr2TeBr2 and Cr2TeCl2 monolayers, but being out of the plane in the Cr2TeI2. Our study implies the potential application of the 2D Cr2TeX2 (X = I, Br, Cl) monolayers in spin nanodevices.
I. Introduction
The discovery of graphene in 2004 has greatly promoted the research upsurge on two-dimensional (2D) materials because of their prominent advantages in electronics, magnetism, spintronics, optoelectronics, batteries and sensors due to the quantum confinement effect.1–8 In spintronic nanodevices, the 2D ferromagnetic (FM) materials with half-metallicity, are desired as perfect candidates for producing full spin polarization, injection, and transport.2,9 However, most of the pristine 2D materials are short of magnetism, and the inevitable inhomogeneity of magnetism obtained by doping, defecting, edging, etc., is disadvantageous to spintronics, so it is very necessary to obtain pristine 2D materials with the intrinsic magnetism.10–13It is known that obtaining the 2D materials with intrinsic magnetism is difficult because the magnetic order of the 2D isotropic Heisenberg model at finite temperatures is forbidden according to the Mermin–Wagner (M–W) theorem.14 The 2D anisotropic crystals can effectively overcome the limitation of M–W principle. The 2D CrI3 and Cr2Ge2Te6 with the FM structure obtained experimentally in recent years are the outstanding progress of the long-range FM ordering in atomic thin materials.15,16 However, their Curie temperatures (TC) of 45 and 20 K are too low, which obviously confines the applications in practice.
Accordingly, it is particularly urgent to search for the 2D FM materials with high Curie temperatures. Through continuous-unremitting and arduous efforts, in recent years, some 2D materials with high TC have been realized theoretically or experimentally, whose values are far exceeding the liquid-nitrogen transition temperature and even reaching room temperature.17–26 These are extremely important progress. However, among these high TC 2D FM materials, some are semiconductors,17–21 while others are normal FM metals rather than FM half-metals.22–26
Considering the practical applications in spintronics, it is perfect for a 2D FM half-metal to have wide half-metal bandgaps and large magnetocrystalline anisotropy energy (MAE) besides possessing the high TC. That is to say, the 2D FM half-metals with three distinguishing features: high TC, wide half-metal bandgaps, and sizeable MAEs, are essentially pursued for the realization of the practical spintronic devices. So far, many 2D intrinsic half-metals have been proposed, such as 2D CoGa2X4 (X = S, Se, or Te),27 Mn2CF2 MXene,28 Cr3X4 (X = S, Se, Te),29 Co2O3,30 Fe2CF2,31 Fe4N2 pentagon crystal,32 Cr2C,33 Janus monolayer V2XN (X = P, As),34 etc., but the vast majority of these materials only have some of the three factors and few can fully meet all these requirements. Therefore, exploring new 2D half-metallic materials with higher Curie temperatures, wider half-metallic bandgaps, and larger MAEs has always been a very important and meaningful work.
In this paper, we propose a new family of 2D Cr2TeX2 (X = I, Br, Cl) monolayers. It is composed of five trigonal atomic sublayers X1–Cr1–Te–Cr2–X2 with ABCAB-type stacking along the z-direction (c-axis), shown as Fig. 1(a). Two antiferromagnetic (AFM) configurations besides the FM (as Fig. 1(b)) are named as AFM-1 and AFM-2 (as Fig. 1(c) and (d)), in which AFM-1 means that the intra- and inter-sublayers are FM and AFM, respectively, but in AFM-2, the intra-sublayers are AFM, and the magnetic states in two Cr-sublayers are same. The lowest energy states are found to be FM half-metal. In the Cr2TeX2 monolayers, the Curie temperature and the direction of the magnetization easy axis are related to the type of halogen atoms. Our Monte Carlo simulations based on the classic Heisenberg model show that the Curie temperatures are about 486, 445, and 451 K for Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 monolayers, respectively. The large MAEs show their potential applications in magnetic memory and storage, in which the easy axe directions are along the plane for the Cr2TeBr2 and Cr2TeCl2 monolayers, but is out of plane in Cr2TeI2. Besides, they also have considerable half-metal bandgaps. These properties make the 2D Cr2TeX2 (X = I, Br, Cl) monolayers have good potential application in spin nanodevices.
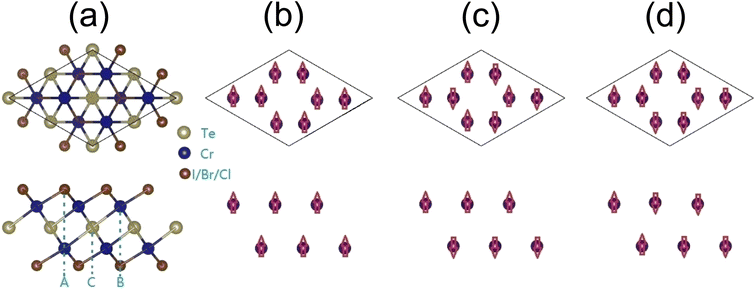 | ||
| Fig. 1 Geometric and magnetic configurations of Cr2TeX2 monolayers from top (above) and side (below) views: (a) structures of 2 × 2 × 1 supercell, (b) FM, (c) AFM-1, and (d) AFM-2. | ||
II. Method and computational details
Our calculations based on the first-principles of density functional theory (DFT) are carried out by using the VASP code.35,36 The projector augmented wave method is adopted for describing the ion–electron interaction and the plane-wave cutoff energy is set to be 550 eV. The Brillouin-zone integration is sampled on a 21 × 21 × 1 Monkhorst–Pack k-point mesh grid for geometry optimization.37 The generalized gradient approximation (GGA) in the version of Perdew–Burke–Ernzerholf (PBE) is used for the electron exchange and correlation.38,39 For the structural optimization of different magnetic states, a collinear initial magnetic moment configuration is adopted as shown in Fig. 1, and when calculating the MAE of the FM state, the spin–orbit coupling (SOC) effect is considered. The effective on-site interaction Ueff = 2.0 eV is used to describe the Hubbard correction, and the selection of the Ueff is mainly based on the consideration that in similar structures in many other works, such values on Cr atoms can make the calculation results better approximate or agree with the experiment.40–42The periodic boundary conditions are adopted and a vacuum layer of 25 Å in the non-periodic c-axis direction is used to eliminate the interactions between the periodic images. The energy convergence is set to 10−7 eV for the electron relaxation and the structure optimization is stopped until the force acting on each atom is less than 0.005 eV Å−1. Dynamic stabilities and phonon dispersion curves are obtained using the phonopy code based on the density functional perturbation theory (DFPT).43 Ab initio molecular dynamics (AIMD) simulations are used to check the thermal stability of the structures using a Nosé–Hoover thermostat.44 In all the molecular dynamics simulations, the time step is 1 fs and the total time lasts for 10 ps. In order to estimate the Curie temperature, Monte Carlo (MC) simulations are implemented based on the Heisenberg model of 40 × 40 × 1 supercell.
III. Results and discussions
The Cr2TeX2 monolayers possess the geometric structure with a D3d symmetry (P3m1) space group, as shown in Fig. 1(a). Each Cr atom is connected to three X and three Te atoms, and each X atom is connected to three Cr atoms, while each Te atom is coordinated with six Cr atoms. To study the preferred coupling of magnetic moments in Cr2TeX2 monolayers, we consider three typical magnetic coupling configurations in a 2 × 2 × 1 supercell. Three spin configurations include one FM coupling and two AFM couplings shown in Fig. 1(b) and (c), which are called AFM-1 and AFM-2, respectively. The Cr atoms in the two adjacent rows from top (above) view in Fig. 1 correspond to two different Cr sublayers, indicating two different c-axis coordinates. Table 1 shows the relative energies between the FM and AFMs. Among all monolayers, the FM state has the lowest energy, meaning that the Cr2TeX2 monolayers have a FM ground state. The total magnetic moments are about 8μB for the FM states, showing large spin polarizations in the 2D Cr2TeX2 monolayers.| FM, meV | AFM1, meV | AFM2, meV | Ecoh, eV | MAE1, μeV | MAE2, μeV | J1, meV | J2, meV | |
|---|---|---|---|---|---|---|---|---|
| Cr2TeI2 | 0.0 | 2359.2 | 1963.1 | 2.660 | 1185 | 1191 | 9.193 | 24.575 |
| Cr2TeBr2 | 0.0 | 2506.3 | 1701.9 | 2.898 | −502 | −490 | 6.770 | 26.107 |
| Cr2TeCl2 | 0.0 | 2516.7 | 1728.8 | 3.114 | −899 | −888 | 6.952 | 26.216 |
The optimized structure parameters of the FM ground states are summarized in Table 2 for the unit cell of Cr2TeX2 monolayers. One can see that the lattice constant (a, b) and thickness (dX) of Cr2TeX2 monolayers increase with the radius of halogen atom increasing, while the distance (dCr) between the two planes of Cr atoms decreases. This is because the interactions of the bigger halogen atoms with the Cr atoms are weaker, which leads to more stronger attraction of Cr to Te atoms.
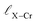 and
and 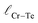 represent the nearest distances between X and Cr atoms, and between Cr and Te atoms, respectively. The lengths are in units of Å
represent the nearest distances between X and Cr atoms, and between Cr and Te atoms, respectively. The lengths are in units of Å
In order to investigate the relative stability of the 2D Cr2TeX2 (X = I, Br, Cl) monolayers, we calculate the cohesive energy defined as Ecoh = (2ECr + 2EX + ETe − ECr2TeX2)/5 with ECr, EX, ETe and ECr2TeX2 being the energies of a single atom of Cr, X, Te, and of one unit of ECr2TeX2 monolayer, respectively. The obtained cohesive energies of the Cr2TeX2 (X = I, Br, Cl) monolayers are 2.66, 2.90, and 3.11 eV per atom for the FM states, respectively, which are comparable to those of V3X8 (X = I, Br, Cl) monolayers (2.92, 3.38, and 3.84 eV per atom),45 indicating that the Cr2TeX2 monolayers should be stable.
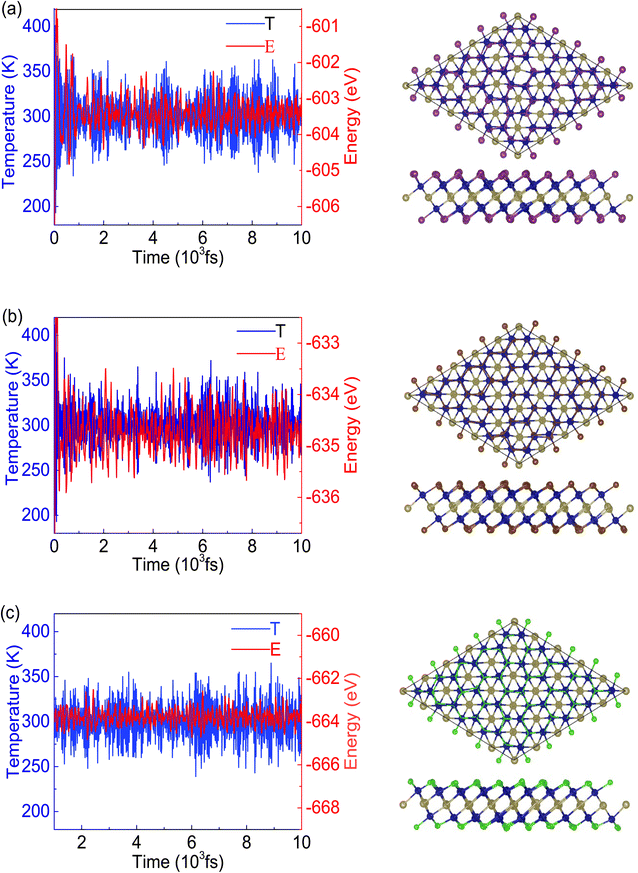
To demonstrate the dynamical stabilities of the Cr2TeX2 (X = I, Br, Cl) monolayers, we calculate their phonon spectra. From the results shown in Fig. 2, one can see that there exist no negative vibrational frequencies in the phonon dispersions, confirming that the three structures with the FM states are stable for all monolayers. The thermal stabilities of these FM monolayers are also investigated by AIMD simulations. In the simulations, a 5 × 5 × 1 supercell containing 125 atoms is considered. At the temperature of 300 K, the Nosé–Hoover temperature and energy changes with time are shown in Fig. 3, in which the two physical quantities vary with time always around a stable value. Moreover, it can be seen from the top-side views that there is no chemical bond fracture and structural reconstruction after 10 ps. This implies that the three FM monolayers are thermally stable.
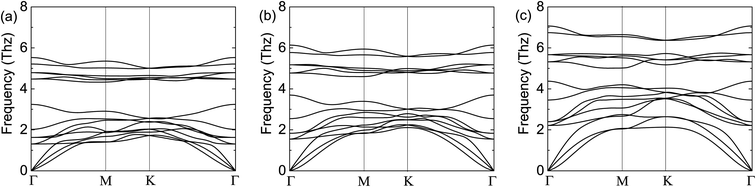 | ||
| Fig. 2 Calculated phonon spectra of the FM states: (a) for Cr2TeI2, (b) for Cr2TeBr2, and (c) for Cr2TeCl2. In the calculation, the expansion of 3 × 3 × 1 for the primitive cell Cr2TeX2 is adopted. | ||
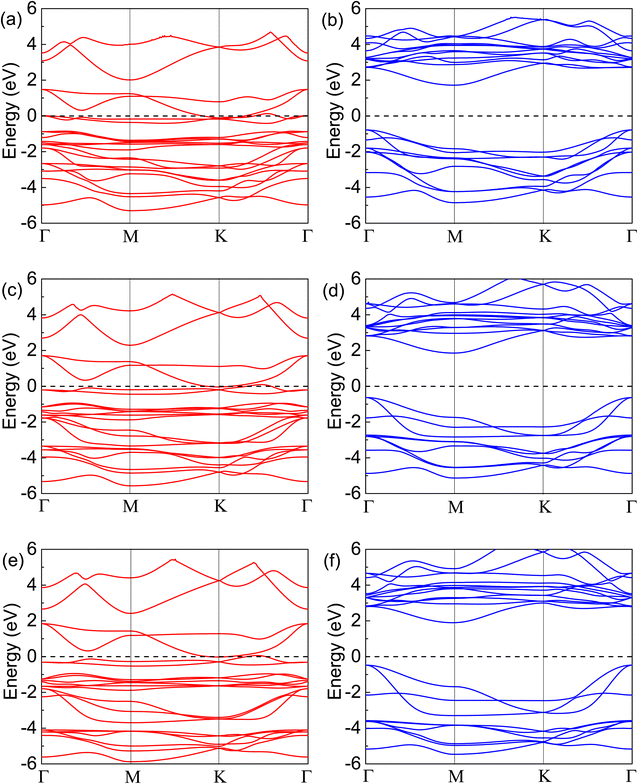
To further understand the magnetism of the FM ground states, the spin-resolved band structures have been calculated and plotted in Fig. 4. It can be seen that the spin-up states are all metallic, while the spin-down ones exhibit semiconductor characteristics. The energy gaps of the spin-down states from Fig. 4(b), (d) and (f) are 2.50, 2.49, and 2.37 eV for the Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 monolayers, respectively, showing the indirect bandgaps between the Γ point of the valence band top and the M point of the conduction band bottom. Compared with the spin-down ones, the spin-up states are occupied by more electrons below the Fermi energy. There are two bands crossing the Fermi energy twice, which are mainly contributed by the orbitals of Cr-eg and X-p from Fig. 5, making half of the two bands below the Fermi energy. Together with the extra seven full bands, the occupied number of the spin-up states is about 8 more than that of the spin-down ones below the Fermi level, thus resulting in the magnetic moment of about 8.0μB per cell. As the SOC may open a bandgap and make metals transform into semiconductors, in order to verify the rigidity of half-metallic properties, we have also calculated the band structure considering SOC, and the results show that there are several energy bands passing through the Fermi level, indicating the reliability of the half-metallicity of the Cr2TeX2 monolayers (see Fig. S1 in ESI†).
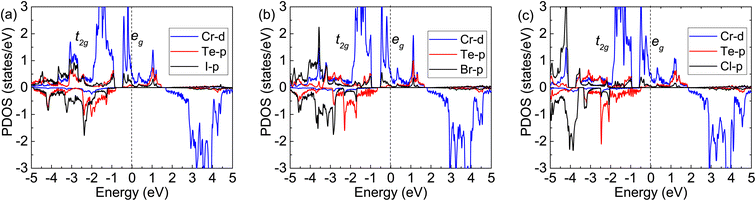 | ||
| Fig. 5 Calculated partial density of states with FM: (a) for Cr2TeI2, (b) for Cr2TeBr2, and (c) for Cr2TeCl2. The dashed-black line at zero eV denotes the Fermi energy Ef. | ||
In order to determine the stability of the half-metallicity, we calculate the half-metallic bandgap, which is defined as the energy gap from the Fermi level to the conduction band minimum in spin-down channel and represents the preventing ability that a electron at Fermi level flips its spin from the spin-up channel to the spin-down one. The half-metallic bandgaps are 1.72, 1.86, and 1.90 eV for the Cr2TeI2, Cr2TeBr2 and Cr2TeCl2 monolayers, being comparable to those (1.55, 1.94, and 1.78 eV) of Mn2X3 (X = Te, Se, S) monolayers46 and 1.53 eV of YN2 monolayer,47 and such large values mean that half-metallic properties have high stability and 100% spin polarization can be easily maintained. In order to verify the reliability of the half-metallicity of the three monolayers, we have also conducted a calculation with Ueff = 3.0 eV. The results show that all ground states of the three monolayers are still ferromagnetic under Ueff = 3.0 eV, and all band structures (see Fig. S2 in ESI†) also exhibit half-metallicity with wide half-metallic bandgaps (2.08, 2.27, and 2.33 eV for the Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 monolayers, respectively). This indicates that the characteristic of the FM half-metallicity with wide half-metallic bandgaps do not change with the changes of Ueff.
In order to further explain the FM ground states, the specific orbital densities of states of the Cr, Te and X atoms are calculated and shown in Fig. 5. The maximum contribution to the states near the Fermi level is from the d-orbitals of Cr atoms. In the Cr2TeX2 monolayers, each Cr atom forms octahedral coordination with three Te atoms and three X ligands, which causes the Cr-d orbitals to split into two parts: the t2g (dxy, dxz, and dyz) and eg (dz2 and dx2−y2) manifolds. Each Cr atom can provide two electrons on its outer orbitals to form bonds with X and Te atoms. Meanwhile, the remaining four electrons are divided into two parts, in which three electrons half occupy the lower t2g orbitals and one will half occupy the higher eg orbitals and lead to a magnetic moment of about 4μB per Cr atom (see Fig. 5). It is seen that the angles (θCr–Te–Cr and θCr–X–Cr) Cr–Te–Cr and Cr–X–Cr in the three monolayers are all close to 90° from the results of the structural optimizations. Based on the Goodenough–Kanamori–Anderson (GKA) rules,48–50 the electronic configuration is helpful to the formation of FM exchange between the nearest-neighbor (NN) Cr atoms. On the other hand, the half-occupied eg orbitals pass through the Fermi energy, resulting in the emergence of half-metallicity.
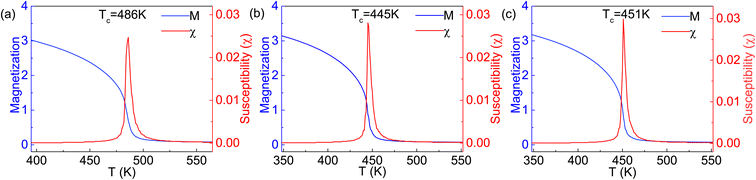
The Curie temperature TC is an important physical parameter for the constituent materials of spintronic devices, because the magnetism can only be maintained at temperatures below TC. In order to overcome the drawback of overestimating the Curie temperature by mean field method and obtain a more accurate value of TC, we carry out the MC simulations with the MC code based on the 2D Heisenberg model,51 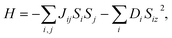 in which S is the magnetic moment of a single Cr atoms, Jij is the exchange parameter between the i-th and j-th Cr atoms, and D is the magnetic anisotropy parameter. The sum of i, j in the formula includes the nearest neighbors in the intra- and inter-sublayer, and the corresponding exchange parameters are denoted as J1 and J2, respectively. To calculate J1 and J2, we choose the relative energies of the FM and the above AFM-1 and AFM-2 orders, and make use of the following equations,
in which S is the magnetic moment of a single Cr atoms, Jij is the exchange parameter between the i-th and j-th Cr atoms, and D is the magnetic anisotropy parameter. The sum of i, j in the formula includes the nearest neighbors in the intra- and inter-sublayer, and the corresponding exchange parameters are denoted as J1 and J2, respectively. To calculate J1 and J2, we choose the relative energies of the FM and the above AFM-1 and AFM-2 orders, and make use of the following equations,
| EFM = E0 − (24J1 + 12J2)S2, | (1) |
| EAFM-1 = E0 − (24J1 − 12J2)S2, | (2) |
| EAFM-2 = E0 − (−8J1 + 4J2)S2. | (3) |
The obtained parameters of J1 and J2 are listed in Table 1. It can be seen from the J1 and J2 values that the intralayer coupling is obvious weaker than the interlayer one, similar to the case of 2D Cr2C monolayers,52 in which the next-nearest-neighbor coupling is stronger than the nearest-neighbor one. Due to the fact that in the same Cr sublayer, a Cr atom has six nearest-neighbor Cr atoms, while a Cr atom has three nearest-neighbor Cr atoms between two Cr sublayers, the contribution of J1 to the Curie temperature will be significantly greater than that of J2 if the changes of J1 and J2 are similar. In our simulations, the spins on arbitral Cr atoms can flip freely in positive or negative directions. The magnetic moment and susceptibility of the 2D supercell at equilibrium under each given temperature are calculated, as shown in Fig. 6. The estimated values of TC are about 486, 445, and 451 K for the Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 monolayers, respectively, which are considerably higher than the room temperature of 300 K. Due to the different spin directions of the three monolayers, we have also calculated the relative energies of the three magnetic states with SOC, and then obtained the exchange parameters J1 and J2 (see Table S1 in ESI†). From the parameters, we have performed the MC simulations again, and the obtained values of TC with SOC are 475, 438, and 445 K for the Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 monolayers, respectively (see Fig. S3 in ESI†). This indicates that the Curie temperature remains basically unchanged when considering the spin direction, showing that the results of the FM transition temperature above room temperature are reliable, and implying that the Cr2TeX2 (X = I, Br, Cl) monolayers may have the application probability in practice.
Finally, let's calculate the magnetocrystalline anisotropy energy (MAE), defined as MAE1/2 = E(100)/(010) − E(001), which is a signature of ability for the magnetic order to resist thermal disturbances and also is an important parameter related to the thermal stability of magnetic information storage. A large MAE mean storing more information, which is more conducive to device miniaturization. The calculated MAE1/2 are 1185/1191, −502/−490, and −899/−888 μeV per Cr atom for Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 FM states, respectively, which are significantly higher than those of some previously reported monolayers such as CrBr3 (186 μeV per Cr),17 CrOBr (290 μeV per Cr),18 CrSBr (146 μeV per Cr),19 Cr3Te4 (150 μeV per Cr),29 etc., and also have comparability with those of the InCrTe3 (1442 μeV per Cr)21 and Cr2O3 (900 μeV per Cr)30 monolayers. The differences between MAE1 and MAE2 are 6, 12, and 11 μeV per Cr atom for Cr2TeI2, Cr2TeBr2, and Cr2TeCl2 FM states, respectively, showing in-plane magnetic crystal anisotropy. Due to the tiny difference, the effect on Curie temperature and magnetic susceptibility can be ignored. As one can see, the MAE value of the Cr2TeI2 in the three monolayers is the biggest because the I atom is the heaviest and its SOC strength is much stronger than those of the other atoms. It is particularly noted that the easy axe (magnetization direction) is out of the plane for the Cr2TeI2 monolayer, and the direction along the out-of-plane is better to the storage and adjustment of information, while the axes are in plane for the Cr2TeBr2 and Cr2TeCl2 monolayers. However, although the Br atom is heaver than the Cl one, the MAE of the Cr2TeBr2 is smaller than that of the Cr2TeCl2. This can be explained by the MAE formula from the second-order perturbation theory,53,54 and it can be expressed as, 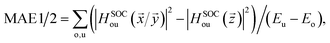 here Eu (Eo) is the energy of occupied (nonoccupied) state o (u), and
here Eu (Eo) is the energy of occupied (nonoccupied) state o (u), and 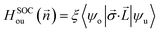 is the SOC matrix element, in which ξ is the SOC strength, are Pauli matrics, and
is the SOC matrix element, in which ξ is the SOC strength, are Pauli matrics, and 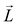 is the orbital angular momentum operator. It can be seen that the MAE is not only related to the size of transition-matrix elements between two states, but also to the energy differences in between. Although the SOC in the Cr2TeBr2 may be stronger than that in the Cr2TeCl2, it is possible that the MAE in the Cr2TeBr2 monolayer is smaller than that in the Cr2TeCl2. And the similar phenomena also occur in other structures, such as the GdX2 and GdX (X = Cl, Br) monolayers, in which the MAEs of the GdCl2 and GdCl monolayers are bigger than those of the GdBr2 and GdBr ones.55,56 The large out-of-plane MAE makes the Cr2TeI2 monolayer possessing potential applications in high-density information storage.
is the orbital angular momentum operator. It can be seen that the MAE is not only related to the size of transition-matrix elements between two states, but also to the energy differences in between. Although the SOC in the Cr2TeBr2 may be stronger than that in the Cr2TeCl2, it is possible that the MAE in the Cr2TeBr2 monolayer is smaller than that in the Cr2TeCl2. And the similar phenomena also occur in other structures, such as the GdX2 and GdX (X = Cl, Br) monolayers, in which the MAEs of the GdCl2 and GdCl monolayers are bigger than those of the GdBr2 and GdBr ones.55,56 The large out-of-plane MAE makes the Cr2TeI2 monolayer possessing potential applications in high-density information storage.
IV. Summary
By performing first-principles DFT calculations, we have predicted that the 2D Cr2TeX2 (X = I, Br, Cl) monolayers with ABCAB-type stacking along the perpendicular direction are FM half-metals. The structures are dynamically stable. The Curie temperatures are all above room temperature, as obtained from the Monte Carlo simulations based on the Heisenberg model. Especially, they possess wide half-metallic bandgaps and sizeable MAEs, and the magnetization direction of the Cr2TeI2 monolayer is out of plane, showing their potential application value in spin nanodevices and information storages. Our study implies that the 2D Cr2TeX2 (X = I, Br, Cl) monolayers may have the potential application in realizing spin nanodevices.Conflicts of interest
The authors have no conflicts of interest to disclose.Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11774296 and 11974296.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488 CrossRef CAS PubMed.
- Z. Guo, S. Chen, Z. Wang, Z. Yang, F. Liu, Y. Xu, J. Wang, Y. Yi, H. Zhang and L. Liao, Adv. Mater., 2017, 29, 1703811 CrossRef PubMed.
- X. Yang, X. Zhang, J. Deng, Z. Chu, Q. Jiang, J. Meng, P. Wang, L. Zhang, Z. Yin and J. You, Nat. Commun., 2018, 9, 570 CrossRef PubMed.
- R. Wang, X. Li, Z. Wang and H. Zhang, Nano Energy, 2017, 34, 131 CrossRef CAS.
- Y. Zhang, B. Zheng, C. F. Zhu, X. Zhang, C. L. Tan, H. Li, B. Chen, J. Yang, J. Z. Chen, Y. Huang, L. H. Wang and H. Zhang, Adv. Mater., 2015, 27, 935 CrossRef CAS PubMed.
- S. Q. Zhang, R. Z. Xu, N. N. Luo and X. L. Zou, Nanoscale, 2021, 13, 1398 RSC.
- X. Jiang, Q. X. Liu, J. P. Xing, N. S. Liu, Z. F. Liu and J. J. Zhao, Appl. Phys. Rev., 2021, 8, 031305 CAS.
- N. Miao and Z. Sun, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 12, e1545 CrossRef PubMed.
- S. Jiang, L. Li, Z. Wang, K. F. Mak and J. Shan, Nat. Nanotechnol., 2018, 13, 549 CrossRef CAS PubMed.
- R. R. Nair, M. Sepioni, I. L. Tsai, O. Lehtinen, J. Keinonen, A. V. Krasheninnikov, T. Thomson, A. K. Geim and I. V. Grigorieva, Nat. Phys., 2012, 8, 199 Search PubMed.
- S. Dutta, A. K. Mann and S. K. Pati, Phys. Rev. Lett., 2009, 102, 096601 CrossRef PubMed.
- X. Hong, K. Zou, B. Wang, S. H. Cheng and J. Zhu, Phys. Rev. Lett., 2012, 108, 226602 CrossRef CAS PubMed.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133 CrossRef CAS.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. D. Xu, Nature, 2017, 546, 270 CrossRef CAS PubMed.
- C. Gong, L. Li, Z. L. Li, H. W. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Z. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265 CrossRef CAS PubMed.
- W. B. Zhang, Q. Qu, P. Zhu and C. H. Lam, J. Mater. Chem. C, 2015, 3, 12457 RSC.
- N. Miao, B. Xu, L. Zhu, J. Zhou and Z. Sun, J. Am. Chem. Soc., 2018, 140, 2417 CrossRef CAS PubMed.
- H. Wang, J. S. Qi and X. F. Qian, Appl. Phys. Lett., 2020, 117, 083102 CrossRef CAS.
- N. Sivadas, M. W. Daniels, R. H. Swendsen, S. Okamoto and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235425 CrossRef.
- G. Song, D. S. Li, H. F. Zhou, C. F. Zhang, Z. W. Li, G. N. Li, B. W. Zhang, X. K. Huang and B. L. Gao, Appl. Phys. Lett., 2021, 118, 123102 CrossRef CAS.
- X. Jiang, Q. X. Liu, J. P. Xing and J. J. Zhao, J. Phys. Chem. Lett., 2019, 10, 7753 CrossRef CAS PubMed.
- Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J. H. Chu and X. Xu, Nat. Mater., 2018, 17, 778 CrossRef CAS PubMed.
- Y. Deng, Y. Yu, Y. Song, J. Zhang, N. Z. Wang, Z. Sun, Y. Yi, Y. Z. Wu, S. Wu, J. Zhu, J. Wang, X. H. Chen and Y. B. Zhang, Nature, 2018, 563, 94 CrossRef CAS PubMed.
- H. Wang, Y. Liu, P. Wu, W. Hou, Y. Jiang, X. Li, C. Pandey, D. Chen, Q. Yang, H. Wang, D. Wei, N. Lei, W. Kang, L. Wen, T. X. Nie, W. S. Zhao and K. L. Wang, ACS Nano, 2020, 14, 10045 CrossRef CAS PubMed.
- Y. J. Niu, K. Zhang, X. F. Cui, X. J. Wu and J. L. Yang, Nano Lett., 2023, 23, 2332 CrossRef CAS PubMed.
- S. Q. Zhang, R. Z. Xu, W. H. Duan and X. L. Zou, Adv. Funct. Mater., 2019, 29, 1808380 CrossRef.
- J. J. He, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 11143 RSC.
- X. Zhang, B. Wang, Y. Guo, Y. Zhang, Y. Chen and J. Wang, Nanoscale Horiz., 2019, 4, 859 RSC.
- A. Hashmi, K. Nakanishi, M. U. Farooq and T. Ono, npj 2D Mater. Appl., 2020, 4, 39 CrossRef CAS.
- Y. Hu, X. Y. Liu, Z. H. Shen, Z. F. Luo, Z. G. Chen and X. L. Fan, Nanoscale, 2020, 12, 11627 RSC.
- K. Zhang, M. L. Chen, D. Y. Wang, H. F. Lv, X. J. Wu and J. L. Yang, Nanoscale, 2021, 13, 19493 RSC.
- S. Das, A. Kabiraj and S. Mahapatra, Nanoscale, 2022, 14, 9409 RSC.
- W. Wan, B. T. Fu, C. Liu, Y. F. Gea and Y. Liu, Phys. Chem. Chem. Phys., 2023, 25, 9311 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. L. Lado and J. Fernández-Rossier, 2D Mater., 2017, 4, 035002 CrossRef.
- C. X. Huang, J. S. Feng, F. Wu, D. Ahmed, B. Huang, H. J. Xiang, K. M. Deng and E. J. Kan, J. Am. Chem. Soc., 2018, 140, 11519 CrossRef CAS PubMed.
- X. B. Lu, R. X. Fei and L. Yang, Phys. Rev. B, 2019, 100, 205409 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635 CrossRef.
- H. B. Xiao, X. N. Wang, R. L. Wang, L. F. Xu, S. H. Liang and C. P. Yang, Phys. Chem. Chem. Phys., 2019, 21, 11731 RSC.
- C. J. Yu, X. Y. Li, X. X. Li and J. L. Yang, J. Phys. Chem. Lett., 2021, 12, 11790 CrossRef CAS PubMed.
- Z. F. Liu, J. Y. Liu and J. J. Zhao, Nano Res., 2017, 10, 1972 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1950, 79, 350 CrossRef.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87 CrossRef CAS.
- L. Liu, X. Ren, J. Xie, B. Cheng, W. Liu, T. An, H. Qin and J. Hu, Appl. Surf. Sci., 2019, 480, 300 CrossRef CAS.
- C. Si, J. Zhou and Z. M. Sun, ACS Appl. Mater. Interfaces, 2015, 7, 17510 CrossRef CAS PubMed.
- D. S. Wang, R. Q. Wu and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 14932 CrossRef CAS PubMed.
- G. H. O. Daalderop, P. J. Kelly and M. F. H. Schuurmans, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 9989 CrossRef CAS PubMed.
- S. J. Li, W. Jiang, Y. F. Hou, F. W. Zheng, X. H. Shao and P. Zhang, J. Appl. Phys., 2021, 130, 043902 CrossRef CAS.
- Y. W. Wang, X. C. Zhang, Z. H. Gao, T. F. Cao, J. Q. Shi and X. L. Fan, J. Phys. Chem. C, 2023, 127, 4643 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra05780a |
| This journal is © The Royal Society of Chemistry 2023 |