Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation of pyramidal structures through mixing gold and platinum atoms: the AuxPty2+ clusters with x + y = 10†
Bao-Ngan Nguyen-Ha ab,
Cam-Tu Phan Dang
ab,
Cam-Tu Phan Dang cd,
Long Van Duong
cd,
Long Van Duong be,
My Phuong Pham-Hofg,
Minh Tho Nguyen
be,
My Phuong Pham-Hofg,
Minh Tho Nguyen *ab and
Nguyen Minh Tam
*ab and
Nguyen Minh Tam *h
*h
aLaboratory for Chemical Computation and Modeling, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: ngan.nguyenhabao@vlu.edu.vn; minhtho.nguyen@vlu.edu.vn
bFaculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
cFaculty of Natural Sciences, Duy Tan University, Da Nang, Vietnam
dInstitute of Research and Development, Duy Tan University, Da Nang, Vietnam
eAtomic Molecular and Optical Physics Research Group, Science and Technology Advanced Institute, Van Lang University, Ho Chi Minh City, Vietnam
fFaculty of Chemical Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, District 10, Ho Chi Minh City, Vietnam
gVietnam National University Ho Chi Minh City, Linh Trung Ward, Thu Duc City, Ho Chi Minh City, Vietnam
hFaculty of Basic Sciences, University of Phan Thiet, 225 Nguyen Thong, Phan Thiet City, Binh Thuan, Vietnam. E-mail: nmtam@upt.edu.vn
First published on 8th November 2023
Abstract
The geometric and electronic structures of a small series of mixed gold and platinum AuxPty2+ clusters, with x + y = 10, were investigated using quantum chemical methods. A consistent tetrahedral pyramid structure emerges, displaying two patterns of structural growth by a notable critical point at y = 5. This affects the clusters' electron population, chemical bonding, and stability. For the Pt-doped Au clusters with y values from 2 to 5, the bonds enable Pt atoms to assemble into symmetric line, triangle, quadrangle, and tetragonal pyramidal Pty blocks, respectively. For the Au-doped Pt clusters, with larger values of y > 5, the structures are more relaxed and the d electrons of Pt atoms become delocalized over more centers, leading to lower symmetry structures. A certain aromaticity arising from delocalization of d electrons over the multi-center framework in the doped Pt clusters contributes to their stability, with Pt102+ at y = 10 exhibiting the highest stability. While the ground electronic state of the neutral platinum atom [Xe]. 4f145d96s1 leads to a triplet state (3D3), the total magnetic moments of AuxPty2+ are large increasing steadily from 0 to 10 μB and primarily located on Pt atoms, corresponding to the increase of the number of Pt atoms from 0 to 10 and significantly enhancing the magnetic moments. An admixture of both Au and Pt atoms thus emerges as an elegant way of keeping a small pyramidal structure but bringing in a high and controllable magnetic moment.
Introduction
The element gold and gold-based clusters have several unique electronic,1–3 optical,4–8 chemical,9,10 and catalytic11–15 properties that have been, and still are, triggering an explosive growth in both experimental and theoretical studies so far. Gold has an electronic configuration of 5d106s1 but in contrast to other coinage metal atoms, the gold atom exhibits a typical sd hybridization, resulting from a strong relativistic effect of the heavy element16 and emphasizing numerous specific and customized properties, particularly in its geometric and electronic structures. As a result, stable frameworks of pure gold clusters with intriguing structures have emerged such as 2D-planar,17 flat cage,18,19 tubular,20 icosahedral,21–24 core–shell,25 star-like shape,26,27 and tetrahedral structures. In the latter, the tetrahedron stands out by a completely filled electronic shell.16,28–30Through the use of a combination of photoelectron spectroscopic techniques and relativistic density functional theory (DFT) calculations, a tetrahedral cluster of 20 gold atoms was identified as an ideal building block for gold surfaces.31 The distinctive Au20 cluster exhibits a notably large HOMO–LUMO energy gap (1.8 eV) exceeding that of the well-known C60 fullerene. This characteristic contributes to the cluster's exceptional inertness and stability in both its geometric and electronic structures. The Au20 pyramid can also be considered as a superatom with an electronic shell-closure. Its distinctive features include a (16c-16e) superatomic Au-core connected to four vertical Au atoms via a SD3 hybridization,16 resulting in a closed electron shell configuration of (1S21P62S21D10) of Au20 giving rise to its magic number of 20 valence electrons.28 This pyramidal superatomic cluster could be used as building blocks for assembling cluster-based materials.
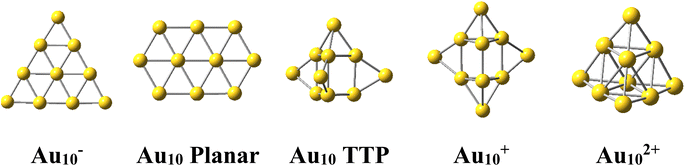
The Au10 clusters in different charge states were expected to also have a tetrahedral skeleton like Au20. However, it was found that the neutral Au10 favors a 2D planar structure of elongated hexagon17 (Scheme 1). Recently, Nhat et al.32 reported that both the 2D elongated hexagonal and 3D tetra-capped trigonal prism (TTP) isomers of Au10 are likely to exist together in experimental molecular beams at temperatures between 100 and 300 K.32 On the other hand, the Au10− monoanion was observed to prefer a 2D-planar structure,1,33,34 whereas the Au10+ monocation possesses a quasi-tetrahedral TTP shape35–37 (Scheme 1). It is well known that while the negative charge tends to favour the planar form of atomic clusters, the positive charge induces 3D shapes.
For its part, the dicationic Au102+ cluster is of particular interest due to its magic number of 8 valence electrons, which forms a closed electron shell of (1S21P6) and an exceptionally large HOMO–LUMO energy gap of 3.9 eV.29 The geometrical structure of Au102+ dication has theoretically been determined to be a tetrahedral pyramid with Td symmetry29 (Scheme 1) and is considered as a tetravalent SP3-Au6 core decorated with four capping Au atoms.38 The coincidence of both the same geometric symmetry and a magic electron shell makes both Au102+ and Au20 clusters equivalent superatoms.30 However, this magic character invariably causes these clusters to have no magnetic properties.
In order to induce magnetism in these clusters, the possibility of incorporating additional elements, particularly transition metals, into the gold tetrahedral Au20 and Au102+ clusters was considered.30,39,40 While doping of some transition metals can cause significant geometric transformations to form endohedral structures, the M@Au19 having 19-Au atoms doped with lighter transition metals such as Cr, Mn, Fe, Co, Ni and Cu still maintain their tetrahedral framework.39 Among these clusters, CrAu19 exhibits the largest magnetic moment of 5 μB with its 20 delocalized valence electrons forming a stable electron shell of (1S21P62S21D10) and the 3d-Cr atomic shell is partially filled by its five remaining localized electrons, resulting in a total magnetic moment of 5 μB.40 A recent investigation29 explored the effects of first-row transition metal M doping on the Au92+ dication and found that the total spin magnetic moment of the metal doped MAu92+ dication is induced mainly by electrons on the 3d-AOs of dopant M atoms and is, as expected, strongly dopant-dependent, varying from the smallest value of 0 μB for ScAu92+ to the largest value of 5 μB for CrAu92+.30 Despite shape variations in ScAu92+ and TiAu92+, the tetrahedral framework is maintained in the remaining MAu92+ clusters.
The platinum element which has an electronic configuration of [Xe]4f145d96s1 and a triplet ground state (3D3), is located next to gold on the Periodic Table. Unlike the gold Au10, the pure platinum Pt10 cluster exhibits a highly stable tetrahedral shape and is regarded as a magic cluster41 at a nonet spin state.42,43 A planar isomer of Pt10 is much higher in energy. For its part, the Pt10− anion has been reported to follow the [Pt6@Pt4]− model,44 which, similar to Au102+, imitates the tetrahedral arrangement of the methane molecule with the Pt6 core substituting for the carbon center. What makes this even more intriguing is that both the significant magnetic moment and tetrahedral pyramid framework are present in all three charged states of Pt10.45–47 This suggests that Pt could be a suitable dopant which could either preserve the tetrahedral framework and/or improve the magnetic moment of gold cluster through its unpaired electrons. In other words, substitution of Au atom(s) in the pure Au102+ dication by Pt atom(s) in a stepwise manner, could open the Au102+ closed electron shell and thereby increase its magnetic moment while keeping the pyramidal shape. In this context, we set out to perform a detailed and systematic investigation on the binary AuxPty2+ clusters with x + y = 10, making use of quantum chemical computations to scrutinize their geometries as well as their corresponding electronic and magnetic properties. It is clear that when x < y, the Au atom plays the role of dopant on Pt clusters. Our goal is to understand the factors governing the formation of a tetrahedral pyramid as the most stable isomer following mixture of a small number of Au and Pt atoms.
Computational methods
All standard electronic structure calculations are performed using the Gaussian 09 package.48 In theoretical studies of the heavy atoms and their cluster systems, it is important to properly account for relativistic effects,15,23,37,49–51 in particular that of the gold atom.15,23,52 This is in fact an issue of concern, because in density functional theory (DFT) methods, even they are favored over wavefunction methods thanks to their lower computational cost and decently accurate outcome, there is no global functional which can accurately describe the properties of both Au and Pt atoms.37,53 Several DFT functionals have been applied to these metals including the BP86,33,35 TPSS,54 BPE,55,56 BLYP,32 B2PLYP,37 M0x (x = 5, 6, 8) as well as M0x with variously modified Hartree–Fock exchange57 such as M05-2X,58 M06-L,59 etc. to interpret the experimental results of transition metals.19,33,35,37,54–57In previous studies of dicationic gold clusters29 as well as both pure and doped Pt clusters,42,60–63 the hybrid B3PW91 functional has been extensively used. This functional has been well calibrated and has demonstrated good agreement with experimental results for doped Pt clusters.61 Furthermore, the BP86 and revTPSS functionals are also commonly employed when studying Au and transition metal (TM)-doped Au clusters,32,64 while the TPSSh functional has been utilized for Ptn clusters.43,65 Hence to ensure consistency and facilitate comparison, we employ the B3PW91, BP86, TPSSh, and revTPSS functionals in our current investigation to explore stable species of the binary clusters AuxPty2+ with x + y = 10.
The low-lying isomers of a cluster are located on the corresponding potential energy surface which is explored using an intensive search procedure covering as many atomic arrangements as possible. Our search for energy minima of clusters is conducted using two different approaches. First, all possible structures of AuxPty2+ clusters are generated using a stochastic algorithm66 which was improved from the previously reported random kick procedure.67 By another way, initial structures of AuxPty2+ are manually built by either replacing y Pt atoms into various positions belonging to local minimum structures of both neutral and charged states of Au10,1,17,29,32–35 or doping y Pt atoms onto the surfaces of the pure Aux+/0/− clusters,1,2,17,33–35 and conversely by doping x Au atoms into the Pty+/0/− clusters alike.42,60 These initial structures are first optimized at different multiplicities using the B3PW91, BP86, TPSSh, and revTPSS functional in conjunction with the small LANL2DZ basis set. Subsequently, the local energy minima identified from both search approaches with relative energies of <5 eV with respect to the lowest-lying minimum of each size are all re-optimized using the same functional but with the larger aug-cc-pVTZ-PP basis set, in which PP stands for an effective core potential including the relativistic effects for heavy atoms. Harmonic vibrational frequencies are then calculated at the same level to identify equilibrium geometries and evaluate their zero-point energy (ZPE) corrections.
The natural bond orbital (NBO) analysis is performed by the NBO 5.0 program68 to investigate the electronic configurations and populations thereby the chemical bonding and magnetic properties of the clusters considered. The results of NBO calculation are further analyzed69 using the Multiwfn program70 to study bonding characteristics of the AuxPty2+ clusters.
Results and discussion
Lower-lying structures
Let us first evaluate the performance of difference density functionals on the relative energies between isomers. Fig. 1 illustrates the assessment of low-lying structures within the Au102+ cluster, by combining the CCSD(T) method with the cc-pVDZ-PP basis set and the B3PW91, BP86, TPSSh, and revTPSS functionals in conjunction with the aug-cc-pVTZ-PP basis set. The results unequivocally support the conclusion that the pyramidal configuration stands out as the sole and most stable structure for the Au102+ clusters.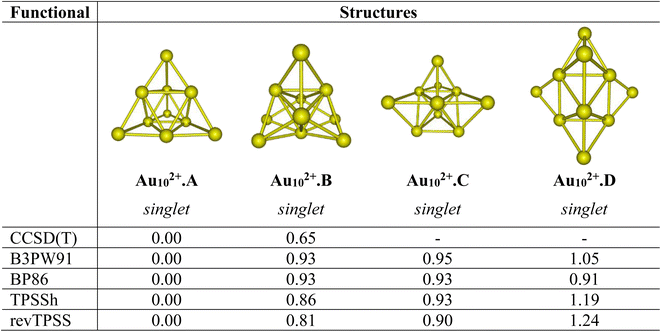 | ||
| Fig. 1 Relative energies ΔE (eV) of the low-lying Au102+ isomers using CCSD(T)/cc-pVDZ-PP and B3PW91, TPSSh, BP86 and revTPSS functionals with the aug-cc-pVTZ-PP bais set and ZPE corrections. | ||
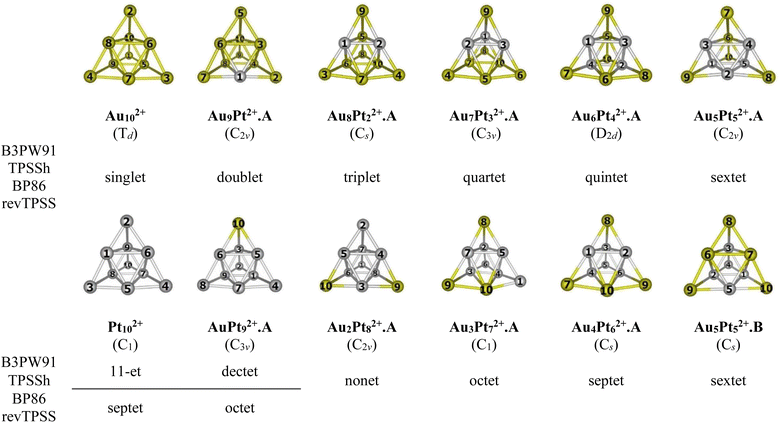
For the AuxPty2+ (x + y = 10), due to the abundance of local minima on the potential energy surface for each cluster size, we selectively include only the lowest-lying isomers with relative energies in proximity to the most stable structure (with a difference of <1.00 eV in relative energy).71,72 The shapes of the AuxPty2+ equilibrium structures, their spin states and their relative energies obtained at the B3PW91, BP86, TPSSh, or revTPSS with the aug-cc-pVTZ-PP basis set and ZPE corrections are displayed in Fig. 2, S1 and S2 (ESI file).†
As for a convention, the AuxPty2+.Z label is used to denote the isomers where x is the number of Au atoms, y the number of Pt atoms and Z = A, B, C,… accords to the isomers with increasing relative energy. Hence, the notation AuxPty2+.A invariably stands for the most stable isomer A of the AuxPty2+ dication.
In general, regardless of the specific numbers of Au or Pt atoms (represented by x and y) and the calculation methods employed, it has been observed that the most stable isomer for each size (x, y) consistently exhibits a tetrahedral pyramid structure (Fig. 2). This indicates a strong preference for this geometric skeleton within this series of small binary clusters. Previous studies suggested that Au102+ comprises a hybridized tetravalent SP3-Au62+ core with an octahedral central structure, adorned by four extra Au atoms on the Au3 faces of this core (Scheme 1).29,38 However, in the case of Pt-doped Au clusters, the use of a [Au6X4]2+ model38 cannot adequately explain the shapes of these AuxPty2+ dications. This is due to the fact that Au atoms in core positions are successively replaced by Pt atoms, even before the Au atoms at the top positions of the tetrahedron (cf. Fig. 2). This is because (i) the Pt–Pt bond is stronger than the Au–Au bond (cf. section “thermodynamic stability” hereafter) and (ii) d-electrons of Au atoms do not join to a formation of multi-center bonds, but d-electrons of Pt atoms do (cf. section “chemical bonding” hereafter). In other words, Pt atoms tend to gather into small groups in such a way that their electrons can move more freely around them. Such a preference for Pt atoms placed in the core and Au atoms at the surface can also explain why the core Au6 is not fixed in place.
Accordingly, two tendencies emerge in the formation of binary structures with a critical point at size x = y = 5. In the first trend, the Pty blocks in the lowest-lying structures Au9Pt2+.A, Au8Pt22+.A, Au7Pt32+.A, Au6Pt42+.A and Au5Pt52+.A regularly develop from a spot, a line, a triangle, a quadrangle and a tetragonal pyramid as y increases from 1 to 5, respectively (cf. Fig. 2). Each of these blocks constitutes the octahedral center which is located inside the pyramid. However, in the second trend of y = 6–9, replacement of Pt no longer follows the same pattern of structural growth as that of y = 1–5, and some Pt atoms tend to occupy outer vertices rather than apexes of the inner core (cf. Fig. 2). In fact, in this series where y > x, the mixed systems can better be regarded as Au-doped Pt clusters, and Pt atoms assemble forming the cores of the pyramid. The lowest-lying structures at sizes y = 6–9, namely Au4Pt62+.A, Au3Pt72+.A, Au2Pt82+.A and AuPt92+.A follow a similar pattern that can be traced back to the shape of the Au5Pt52+.B isomer and are achieved by sequentially replacing the remaining Au atoms in Au5Pt52+.B by Pt atoms. It is worth noting that both isomers Au5Pt52+.A and Au5Pt52+.B are in competition for the global minimum structure, given their small relative energy gap of only ∼0.1eV with a marginal energy preference for the Au5Pt52+.A (cf. Fig. S2†). This energy gap is, in fact, smaller than the expected error margin of ±0.3 eV, typically associated with energetic parameters derived from DFT computations.71,72 To further validate these findings, the energies of these two isomers are also calculated using the CCSD(T)/cc-pVDZ-PP method, yielding results consistent with an energy difference of ∼0.1 eV. This additional analysis reinforces the assumption of energy degeneracy between the two geometric structures.
In the transitional size, five Au atoms of Au5Pt52+.B are arranged as a triangle corner, where two atoms reside at the core, while the remaining three atoms occupy the outer vertices. This triangular arrangement forms one of the three faces of a tetrahedron (cf. Fig. 2). Following the same framework as Au5Pt52+.B, the Au4Pt62+.A isomer which has more Pt atom than Au, is formed by replacing one of the two Au atoms at the core of the Au5Pt52+.B with a Pt atom. Consequently, Au4Pt62+.A is now composed of five Pt atoms in the internal core and one Pt atom locating at an external vertex and with Au atoms serving as dopants (cf. Fig. 2). This substitution leads to a relaxation towards Cs symmetry.
A similar phenomenon is witnessed in the Au3Pt72+.A, where the substitution of Au atoms with Pt atoms takes place at an external vertex of Au4Pt62+.A, resulting in the attainment of C1 symmetry. Continuing this trend, replacing the last Au atom at the internal core of the Au3Pt72+.A with a Pt atom, we obtain the Au2Pt82+.A. By further sequentially substituting Au atom(s) in Au2Pt82+.A with Pt atom(s), we eventually arrive at the AuPt92+.A and the Pt102+ clusters (cf. Fig. 2).
Thermodynamic stability
The B3PW91/aug-cc-pVTZ-PP + ZPE method is utilized to investigate the thermodynamic stability of the clusters. The inherent thermodynamic stability of the 10-atom clusters is evaluated by the average binding energies (Eb). In this work, the average binding energies (Eb) of all lowest-lying structures of AuxPty2+ can conventionally be defined using the following formula (eqn (1)–(3)):| Eb(AuxPty2+) = [xE(Au) + (y − 2)E(Pt) + 2E(Pt+) − E(AuxPty2+)]/10 | (1) |
Particularly for two dicationic clusters Au102+ and AuPt92+, the Eb can be defined as eqn (2) and (3), respectively:
| Eb(Au102+) = [8E(Au) + 2E(Au+) − E(Au102+)]/10 | (2) |
| Eb(Au9Pt2+) = [8E(Au) + E(Au+) + E(Pt+) − E(Au9Pt2+)]/10 | (3) |
 | ||
| Fig. 3 Average binding energies of AuxPty2+ clusters with x + y = 10, obtained at the B3PW91/aug-cc-pVTZ-PP + ZPE level. | ||
The mixed clusters exhibit varying levels of stability, with the Au8Pt22+ cluster being the least stable due to energetic degeneracy between singlet and triplet states. Mixed clusters with a limited number of Pt atoms (y = 1–6) exhibit lower stability as compared to the original Au102+. This could be attributed to the insufficiency of Pt–Pt bonds due to the limited number of Pt atoms and the deficiency of multi-center bonds formed between atomic orbitals (AOs) of Pt and Au atoms. In these cases, some distortion in the overall bonds (10c-1e) occurs because of the contamination in S and P-MOs within the mixed clusters in comparison to the pure Au102+ clusters (cf. section “chemical bonding” hereafter).
However, as the number of Pt atoms increases beyond y = 2, the mixed clusters exhibit a linear stabilization (see Fig. 3). Notably, starting at y = 7, where it resembles a doped Pt cluster, the stability of the mixed clusters surpasses that of the Au102+ cluster. At y = 10, which corresponds to a pure Pt cluster, Pt102+ emerges as the most stable configuration. This suggests that a Pt cluster, even with the same number of atoms as its Au counterpart, is inherently more stable.
The underlying reason for this enhanced stability lies in the intrinsic strength of the Pt–Pt bond, boasting a bond energy of 2.91 eV, as compared to the Au–Au (2.03 eV) and Au–Pt (2.04 eV) bond energy. As the number of Pt atoms increases, this strength is amplified, resulting in the formation of more robust Pt–Pt bonds. Consequently, these stronger bonds contribute to greater stability within the mixed clusters.
It's worth noting that the prevalence of stronger Pt–Pt bonds leads Pt atoms to congregate together, forming small Pt blocks within the clusters. This arrangement facilitates the movement of d-electrons between the Pt atoms, resulting in a creation of smaller aromatic regions characterized by free d-electrons in the Pt blocks. These exists alongside the primary aromaticity arising from in S and P-MOs throughout the entire AuxPty2+ clusters (cf. section “chemical bonding” hereafter).
Magnetic moments
In terms of spin state, the total and local magnetic moments (TMMs and LMMs, respectively) are determined by calculating the difference between the number of spin-up and spin-down electrons occupying the molecular or atomic orbitals.When using the B3PW91 and TPSSh functionals, an increase in the number of Pt atoms in the mixed clusters, due to the intrinsic triplet ground state of Pt atom, invariably leads to a higher multiplicity of their most stable isomers. In other words, as the size of Pt increases from 0 to 10, the corresponding total magnetic moment of the AuxPty2+ steadily increases from 0 to 10 μB (cf. Fig. 4). The electronic configuration of pure Au102+, as mentioned earlier, is a closed-shell singlet state with four bonds formed by the SP3-Au62+ core bonded with four 6s electrons of four external Au atoms using the eight shared valence electrons,38 leading to a completely quenched total magnetic moment. When Pt atoms replace Au in Au102+, the closed-shell electronic configuration becomes defective due to the deficiency of one electron on each Pt 5d-AO. NBO results confirm that the magnetic moment mainly localizes on Pt atoms (as shown in Table 1) with a spin density range of 0.7–1.2 electron for each Pt atom and the unpaired d-electron is fixed on each Pt atom. As each Pt atom donates one single electron, an increase in the number of Pt atoms results in an increasing number of unpaired electrons in the cluster, and thereby leads to a significant increase in magnetic moments.
| No | Au9Pt2+.A (doublet) | Au8Pt22+.A (triplet) | Au7Pt32+.A (quartet) | Au6Pt42+.A (quintet) | Au5Pt52+.A (sextet) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Pt | 0.8 | Pt | 1.0 | Pt | 0.9 | Pt | 0.9 | Pt | 0.9 |
| 2 | Au | 0.1 | Pt | 0.9 | Pt | 0.9 | Pt | 0.9 | Pt | 1.0 |
| 3 | Au | 0.0 | Au | 0.0 | Pt | 0.9 | Pt | 0.9 | Pt | 0.9 |
| 4 | Au | 0.0 | Au | 0.0 | Au | 0.1 | Pt | 0.9 | Pt | 0.9 |
| 5 | Au | 0.0 | Au | 0.1 | Au | 0.0 | Au | 0.0 | Pt | 0.9 |
| 6 | Au | 0.0 | Au | 0.0 | Au | 0.0 | Au | 0.0 | Au | 0.0 |
| 7 | Au | 0.1 | Au | 0.0 | Au | 0.0 | Au | 0.1 | Au | 0.1 |
| 8 | Au | 0.0 | Au | 0.0 | Au | 0.1 | Au | 0.1 | Au | 0.1 |
| 9 | Au | 0.0 | Au | 0.0 | Au | 0.1 | Au | 0.1 | Au | 0.1 |
| 10 | Au | 0.0 | Au | 0.0 | Au | 0.0 | Au | 0.1 | Au | 0.1 |
| Total | 1.0 | Total | 2.0 | Total | 3.0 | Total | 4.0 | Total | 5.0 | |
| No | Au4Pt62+.A (septet) | Au3Pt72+.A (octet) | Au2Pt82+.A (nonet) | AuPt92.A (dectet) | AuPt92+.A (octet) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Pt | 1.0 | Pt | 0.8 | Pt | 0.7 | Pt | 1.2 | Pt | 1.0 |
| 2 | Pt | 1.0 | Pt | 1.0 | Pt | 0.7 | Pt | 0.7 | Pt | 0.3 |
| 3 | Pt | 1.1 | Pt | 1.0 | Pt | 1.0 | Pt | 1.1 | Pt | 1.1 |
| 4 | Pt | 1.0 | Pt | 1.2 | Pt | 1.1 | Pt | 0.7 | Pt | 0.4 |
| 5 | Pt | 0.7 | Pt | 1.1 | Pt | 1.1 | Pt | 1.1 | Pt | 1.1 |
| 6 | Pt | 1.0 | Pt | 0.7 | Pt | 1.1 | Pt | 1.1 | Pt | 1.1 |
| 7 | Au | 0.1 | Pt | 1.0 | Pt | 1.2 | Pt | 1.2 | Pt | 0.7 |
| 8 | Au | 0.1 | Au | 0.1 | Pt | 1.1 | Pt | 0.7 | Pt | 0.4 |
| 9 | Au | 0.1 | Au | 0.1 | Au | 0.1 | Pt | 1.2 | Pt | 1.0 |
| 10 | Au | 0.0 | Au | 0.1 | Au | 0.1 | Au | 0.0 | Au | 0.0 |
| Total | 6.0 | Total | 7.0 | Total | 8.0 | Total | 9.0 | Total | 7.0 | |
| No | Pt102+ (11-et) | Pt102+ (septet) | ||
|---|---|---|---|---|
| 1 | Pt | 1.2 | Pt | 1.1 |
| 2 | Pt | 0.7 | Pt | 0.5 |
| 3 | Pt | 0.7 | Pt | 0.5 |
| 4 | Pt | 0.7 | Pt | 0.5 |
| 5 | Pt | 1.2 | Pt | 1.1 |
| 6 | Pt | 1.2 | Pt | 1.1 |
| 7 | Pt | 1.2 | Pt | 0.5 |
| 8 | Pt | 1.2 | Pt | 0.5 |
| 9 | Pt | 1.2 | Pt | 0.5 |
| 10 | Pt | 0.7 | Pt | −0.3 |
| Total | 10.0 | Total | 6.0 | |
However, when utilizing the BP86 and revTPSS methods, the magnetic moments reach their peak at y = 8 (eight Pt atoms) with a value of 8 μB, and then gradually decrease to 6 μB when y = 10 (ten Pt atoms) (cf. Fig. 4).
Both the Pt102+ clusters with septet and 11-et spin states and the AuPt92+ clusters with octet and dectet spin states, the relative energy gaps among all four DFT methods considered, as listed in Fig. S2,† are very small (<0.1 eV). This indicates that these spin states can be considered to be energetically degenerate, arising from the closely spaced energy levels of the d-orbitals within these clusters.
The high spin states exhibited by these clusters pose a challenge for the coupled-cluster method calculations as well, primarily due to an increasing spin contamination, resulting from its unrestricted Hartree–Fock (UHF) wavefunctions, whose spin contamination tends to lead to a slow and deceptive convergence of the coupled-cluster expansions, and thereby incorrect total energies. Consequently, determination of a reliable method for these systems becomes a complex task, in particular for system having multi-reference character.
Chemical bonding
For a rationalization of the chemical bonding of these Au-Pt mixed clusters, the electronic configuration of each lowest-lying isomer AuxPty2+.A displayed in Fig. 2 is analyzed using NBO at the B3PW91/cc-pVTZ-PP theory level and related adaptive natural density partitioning (AdNDP) analysis.70 Conventionally, the (nc-me) label specifies the number n of atomic centers and the number m of electrons moving within those centers. For instance, (10c-1e) indicates one electron moving over ten atomic centers in the cluster.The binary AuxPty2+ clusters, with y varying from 0 to 10, prominently exhibit a spherical aromaticity. This aromaticity arises from the presence of (10c-2e) bonds in case of the Au102+ and (10c-1e) bonds in both the alpha and beta electron sides of the AuxPty2+ clusters (y = 1–10). Specifically, in the case of the Au102+, eight electrons are distributed across over one S-MO and three P-MOs, while in the case of the AuxPty2+ clusters (y = 1–10) four electrons similarly delocalized over one S-MO and three P-MOs on each side (cf. Fig. 4, and S3–S14†). As the Pt size increases from y = 1 to y = 10, these beta (10-1e) bonds become impure due to a certain contamination with d-AOs of Pt atoms, as shown in Fig. S4–S14.† Nevertheless, the binary AuxPty2+ (y = 1–10) species still possess a (1S21P6) shell and adopt a tetrahedral pyramid similar to that of the Au102+, as depicted in Fig. S3–S14.† The preference for a tetrahedral shape in these binary dications can be attributed to the stability and electronic structure associated with this geometry. The tetrahedral arrangement allows for efficient bonding interactions between the Au and Pt atoms while maintaining the desired electronic configuration and stability for the clusters.
In addition to the prominent (10c-1e) bonds of spherical aromaticity, the AuxPty2+ (y = 1–10) clusters also display a variety of smaller multi-center bonds (cf. Fig. 5 and S4–S14†). These bonds result from the overlapping of equivalent atomic orbitals with similar symmetry and approximate energy levels of the d-electrons of Pt atoms. The presence and nature of these multi-center bonds depend on the specific positions of the Pt atoms within the cluster. By virtue of their spatial arrangement, these bonds contribute to the overall bonding pattern and electronic structure of the AuxPty2+ clusters. The formation of these multi-center bonds adds further complexity to the bonding interactions and highlights the role of Pt d-electrons in influencing the properties of these clusters.
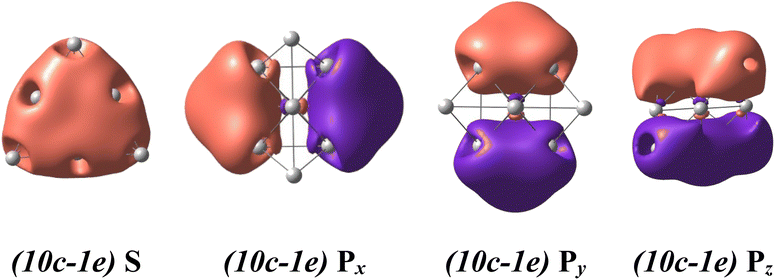 | ||
| Fig. 5 The metal aromaticity arising from (10c-1e) bonds of dicationic AuxPty2+ (y ranges from 1 to 10) clusters via AdNDP analysis at B3PW91/cc-pVTZ-PP theory level. | ||
The formation of bonds in AuxPty2+ is basically influenced by two trends based on their character, Au vs. Pt clusters, and thereby their structural tendencies with the critical point at y = 5. In the first trend which is observed for Au clusters (y ranging from 2 to 5), the Pt dopants tend to cluster together into symmetric blocks, with a preference for being located at the octahedral core. Since the number of d-electrons at these sizes is still small, one common d-electron is shared between two adjacent Pt dopants by an overlap of two equivalent atomic orbital having similar symmetry on the beta side to form one bond between two Pt centers (2c-1e) (cf. Fig. 6 and S5–S8†). In the second trend, with larger y values ranging from 5 to 10 giving rise to a series of Au-doped Pt clusters, the dominance and increased flexibility of the d-electrons on Pt atoms enable them to form numerous bonds that involve the delocalization of d electrons over more multiple centers, including (3c-1e) and (6c-1e). This is in contrast to the Au clusters (with y < 6). The increase in the number of d-AOs provided by Pt atoms leads to significant contamination and heavier distortion of the S and P-MOs. (cf. Fig. S9–S14†).
In the AuxPty2+ clusters, it is observed in both alpha and beta side that each Au atom wholly retains five (1c-1e) electrons localized on its five d-orbitals, indicating that the d-electrons of Au atoms are not involved in muti-center bond formation (cf. Fig. S3–S14†). This contrasts with the behaviour of Pt atoms, whose beta d-electrons are more flexible and can participate in multi-center bonds, allowing them to connect with neighbouring Pt atoms. As a result, Pt atoms have a propensity to preferentially occupy the core of the binary clusters.
This discrepancy in behaviour between Au and Pt atoms can be attributed to the differences in their electronic structures and bonding capabilities. The localized nature of Au's d-electrons restricts their involvement in multi-center bonding, while the more flexible d-electrons of Pt enable them to engage in such bonding interactions. This distinction influences the preferred placement of Pt atoms in the core of the binary clusters, where they can effectively form multi-center bonds and establish connections with neighbouring Pt atoms.
In addition, Fig. S15† illustrates that the density of states (DOS) maps of the AuxPty2+ exhibit two distinct trends, which correspond to their respective structures with the critical point at x = y = 5, showing the structural impact on global population of electron. Notably, Au102+ has the highest density of states, followed by a gradual decrease towards the Pt102+. The DOS on the mixed AuxPty2+ is primarily contributed by the d-electrons of Au and Pt atoms, with Au making a more significant contribution. As the number of Au atoms in the cluster decreases from x = 10 to x = 0, there is a significant reduction in the DOS of AuxPty2+, especially from the critical point at y = 5 onward. Furthermore, the downward shift of the SOMO–LUMO gap on the beta side results in a reduced gap size (almost half) compared to the alpha side (see Table 2). This shift facilitates electron movement between the frontier orbital levels, ultimately causing an energetic degeneracy among the spin states within the clusters considered.
| Clusters | Spin states | SOMO–LUMO (α) | SOMO–LUMO (β) |
|---|---|---|---|
| Au102+ | Singlet | 3.88 | |
| Au9Pt2+ | Doublet | 3.56 | 1.85 |
| Au8Pt22+ | Triplet | 3.55 | 1.46 |
| Au7Pt32+ | Quartet | 3.54 | 2.54 |
| Au6Pt42+ | Quintet | 3.46 | 2.15 |
| Au5Pt52+ | Sextet | 3.45 | 2.01 |
| Au4Pt62+ | Septet | 3.37 | 2.07 |
| Au3Pt72+ | Octet | 3.38 | 1.74 |
| Au2Pt82+ | Nonet | 3.47 | 1.95 |
| AuPt92+ | Dectet | 3.58 | 1.79 |
| Pt102+ | 11-et | 3.52 | 1.82 |
Concluding remarks
In the present theoretical study, the binary gold-platinum clusters AuxPty2+ containing ten atoms with x + y = 10 were systematically studied using DFT calculations with the B3PW91, TPSSh, revTPSS and BP86 functionals in conjunction with the aug-cc-pVTZ-PP basis set. The main results demonstrated that all the most stable structures of the AuxPty2+ clusters follow the tetrahedral pyramid pattern. In their dicationic state, a mixture of ten Au and Pt atoms consistently holds the pyramidal shape of both pure clusters. A critical point at y = 5 marks the onset of two distinct tendencies in the structural growth that characterize their chemical bonding.For y = 2, 3, 4, and 5 where the AuxPty2+ are basically Au clusters, the Pt atoms gather together into symmetric Pty blocks as a line, a triangle, a quadrangle, and a tetragonal pyramid, respectively, located at the inner octahedral core of the cluster. At these sizes, some d-electrons of Pt atoms tend to form (2c-1e) bonds. Meanwhile, larger y = 6–10 leading to the doped Pt clusters, Pt atoms substitute Au atoms in the structure of the Au5Pt52+.B isomer and form larger multi-center d-electron bonds.
All ten-atom binary AuxPty2+ clusters are characterized by bonds whose electrons are delocalized on S-MO and P-MOs for each alpha and beta stream. The S-MO and P-MOs are more distorted when the number of Pt atoms rise due to contaminations with d-AOs of Pt atoms. For the number of Pt atoms y = 1–6, the mixed clusters AuxPty2+ are less stable than the pure gold Au102+ cluster (in terms of dissociation energy) but from y = 7 onwards, the system becomes Pt clusters, and they can be more stabilized by the formation of the stronger Pt–Pt bonds. In fact, the pure platinum Pt102+, corresponding to y = 10, exhibits the highest thermodynamic stability. Furthermore, the substitution of Pt atoms into the pure Au102+ cluster increases significantly the magnetic property. The spin density of the AuxPty2+ clusters is mainly located on Pt atoms and the total magnetic moment increase steadily from 0 to 10 μB, corresponding to the number y of Pt atoms increased from 0 to 10 with calculations using B3PW91 and TPSSh functionals. Overall, admixture of both Au and Pt atoms within a small size emerges as an elegant way of keeping the small pyramidal structure but bringing in a high and controllable magnetic moment.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
BNNH, LVD and MTN are grateful to Van Lang University. NMT thanks Prof. Nguyen Thanh Tung and Ngo Thi Lan at VAST Ha Noi for helpful discussion. This work is funded by VinGroup Vietnam and supported by VinGroup Innovation Foundation (VinIF) under project code VinIF.2020.DA21.References
- L.-M. Wang and L.-S. Wang, Probing the electronic properties and structural evolution of anionic gold clusters in the gas phase, Nanoscale, 2012, 4(14), 4038–4053 RSC.
- U. N. Kurelchuk, O. S. Vasilyev and P. V. Borisyuk, Structure and electronic properties of small gold clusters, J. Phys.: Conf. Ser., 2019, 1238(1), 012021 CrossRef CAS.
- Y. Zhao, J. Wang, H.-C. Huang, J. Li, X.-X. Dong, J. Chen, Y.-X. Bu and S.-B. Cheng, Tuning the Electronic Properties and Performance of Low-Temperature CO Oxidation of the Gold Cluster by Oriented External Electronic Field, J. Phys. Chem. Lett., 2020, 11(3), 1093–1099 CrossRef CAS PubMed.
- A. N. Gloess, H. Schneider, J. M. Weber and M. M. Kappes, Electronically excited states and visible region photodissociation spectroscopy of Aum+·Arn clusters (m = 7–9): molecular dimensionality transition?, J. Chem. Phys., 2008, 128(11), 114312 CrossRef PubMed.
- S. Lecoultre, A. Rydlo, C. Félix, J. Buttet, S. Gilb and W. Harbich, UV-visible absorption of small gold clusters in neon: Aun (n = 1–5 and 7–9), J. Chem. Phys., 2011, 134(7), 074302 CrossRef CAS PubMed.
- N. V. Karimova and C. M. Aikens, Optical Properties of Small Gold Clusters Au8L82+ (L = PH3, PPh3): Magnetic Circular Dichroism Spectra, J. Phys. Chem. C, 2017, 121(35), 19478–19489 CrossRef CAS.
- S. Goel, K. A. Velizhanin, A. Piryatinski, S. A. Ivanov and S. Tretiak, Ligand Effects on Optical Properties of Small Gold Clusters: A TDDFT Study, J. Phys. Chem. C, 2012, 116(5), 3242–3249 CrossRef CAS.
- V. Kaydashev, P. Ferrari, C. Heard, E. Janssens, R. L. Johnston and P. Lievens, Optical Absorption of Small Palladium-Doped Gold Clusters, Part. Part. Syst. Charact., 2016, 33(7), 364–372 CrossRef CAS.
- V. G. Yarzhemsky, Y. A. D’yakov, A. D. Izotov and V. O. Izotova, Chemical Properties of Gold Clusters as Dependent on the Structure and Doping by 5d Elements, Russ. J. Inorg. Chem., 2019, 64(10), 1242–1248 CrossRef CAS.
- S. Kenzler and A. Schnepf, Metalloid gold clusters – past, current and future aspects, Chem. Sci., 2021, 12(9), 3116–3129 RSC.
- J. H. Teles, S. Brode and M. Chabanas, Cationic Gold(I) Complexes: Highly Efficient Catalysts for the Addition of Alcohols to Alkynes, Angew. Chem., Int. Ed., 1998, 37(10), 1415–1418 CrossRef CAS.
- M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, Gold catalysts prepared by coprecipitation for low-temperature oxidation of hydrogen and of carbon monoxide, J. Catal., 1989, 115(2), 301–309 CrossRef CAS.
- R. M. P. Veenboer, S. Dupuy and S. P. Nolan, Stereoselective Gold(I)-Catalyzed Intermolecular Hydroalkoxlation of Alkynes, ACS Catal., 2015, 5(2), 1330–1334 CrossRef CAS PubMed.
- M. Rudolph and A. S. K. Hashmi, Heterocycles from gold catalysis, Chem. Commun., 2011, 47(23), 6536–6544 RSC.
- H. Häkkinen, Atomic and electronic structure of gold clusters: understanding flakes, cages and superatoms from simple concepts, Chem. Soc. Rev., 2008, 37(9), 1847–1859 RSC.
- L. Cheng, X. Zhang, B. Jin and J. Yang, Superatom–atom super-bonding in metallic clusters: a new look to the mystery of an Au20 pyramid, Nanoscale, 2014, 6(21), 12440–12444 RSC.
- B. R. Goldsmith, J. Florian, J.-X. Liu, P. Gruene, J. T. Lyon, D. M. Rayner, A. Fielicke, M. Scheffler and L. M. Ghiringhelli, Two-to-three dimensional transition in neutral gold clusters: The crucial role of van der Waals interactions and temperature, Phys. Rev. Mater., 2019, 3(1), 016002 CrossRef CAS.
- S. Bulusu and X. C. Zeng, Structures and relative stability of neutral gold clusters: Aun (n = 15–19), J. Chem. Phys., 2006, 125(15), 154303 CrossRef PubMed.
- P. Gruene, M. Rayner David, B. Redlich, F. G. van der Meer Alexander, T. Lyon Jonathan, G. Meijer and A. Fielicke, Structures of Neutral Au7, Au19, and Au20 Clusters in the Gas Phase, Science, 2008, 321(5889), 674–676 CrossRef CAS PubMed.
- W. Fa and J. Dong, Possible ground-state structure of Au26: a highly symmetric tubelike cage, J. Chem. Phys., 2006, 124(11), 114310 CrossRef.
- M. P. Johansson, D. Sundholm and J. Vaara, Au32: A 24-Carat Golden Fullerene, Angew. Chem., Int. Ed., 2004, 43(20), 2678–2681 CrossRef CAS PubMed.
- A. J. Karttunen, M. Linnolahti, T. A. Pakkanen and P. Pyykkö, Icosahedral Au72: a predicted chiral and spherically aromatic golden fullerene, Chem. Commun., 2008, 4, 465–467 RSC.
- W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, Relativistic Effects and the Unique Low-Symmetry Structures of Gold Nanoclusters, ACS Nano, 2008, 2(5), 897–904 CrossRef CAS PubMed.
- I. L. Garzón, K. Michaelian, M. R. Beltrán, A. Posada-Amarillas, P. Ordejón, E. Artacho, D. Sánchez-Portal and J. M. Soler, Lowest Energy Structures of Gold Nanoclusters, Phys. Rev. Lett., 1998, 81(8), 1600–1603 CrossRef.
- N. Shao, W. Huang, Y. Gao, L.-M. Wang, X. Li, L.-S. Wang and X. C. Zeng, Probing the Structural Evolution of Medium-Sized Gold Clusters: Aun− (n = 27−35), J. Am. Chem. Soc., 2010, 132(18), 6596–6605 CrossRef CAS PubMed.
- P. V. Nhat, N. T. Si, V. G. Kiselev, A. Fielicke, H. T. Pham and M. T. Nguyen, Unexpected structures of the Au17 gold cluster: the stars are shining, Chem. Commun., 2022, 58(38), 5785–5788 RSC.
- P. V. Nhat, N. T. Si, A. Fielicke, V. G. Kiselev and M. T. Nguyen, A new look at the structure of the neutral Au18 cluster: hollow versus filled golden cage, Phys. Chem. Chem. Phys., 2023, 25(13), 9036–9042 RSC.
- A. Muñoz-Castro and R. B. King, Au20. Effect of a Strong Tetrahedral Field in a Spherical Concentric Bonding Shell Model, J. Phys. Chem. C, 2017, 121(10), 5848–5853 CrossRef.
- P. M. Petrar, M. B. Sárosi and R. B. King, Au102+: A Tetrahedral Cluster Exhibiting Spherical Aromaticity, J. Phys. Chem. Lett., 2012, 3(22), 3335–3337 CrossRef CAS.
- N. T. Lan, N. T. Mai, D. D. La, N. M. Tam, S. T. Ngo, N. T. Cuong, N. V. Dang, T. T. Phung and N. T. Tung, DFT investigation of Au9M2+ nanoclusters (M = Sc-Ni): The magnetic superatomic behavior of Au9Cr2+, Chem. Phys. Lett., 2022, 793, 139451 CrossRef CAS.
- J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Au20: A Tetrahedral Cluster, Science, 2003, 299(5608), 864–867 CrossRef CAS PubMed.
- P. V. Nhat, N. T. Si, N. T. N. Hang and M. T. Nguyen, The lowest-energy structure of the gold cluster Au10: planar vs. nonplanar?, Phys. Chem. Chem. Phys., 2022, 24(1), 42–47 RSC.
- F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, The structures of small gold cluster anions as determined by a combination of ion mobility measurements and density functional calculations, J. Chem. Phys., 2002, 117(15), 6982–6990 CrossRef CAS.
- H. Häkkinen, B. Yoon, U. Landman, X. Li, H.-J. Zhai and L.-S. Wang, On the Electronic and Atomic Structures of Small AuN− (N = 4–14) Clusters: A Photoelectron Spectroscopy and Density-Functional Study, J. Phys. Chem. A, 2003, 107(32), 6168–6175 CrossRef.
- S. Gilb, P. Weis, F. Furche, R. Ahlrichs and M. M. Kappes, Structures of small gold cluster cations (Aun+, n < 14): ion mobility measurements versus density functional calculations, J. Chem. Phys., 2002, 116(10), 4094–4101 CrossRef CAS.
- P. Ferrari, H. A. Hussein, C. J. Heard, J. Vanbuel, R. L. Johnston, P. Lievens and E. Janssens, Effect of palladium doping on the stability and fragmentation patterns of cationic gold clusters, Phys. Rev. A, 2018, 97(5), 052508 CrossRef CAS.
- P. Ferrari and K. Hansen, Computing gold cluster energies with density functional theory: the importance of correlation, Phys. Chem. Chem. Phys., 2021, 23(27), 14830–14835 RSC.
- A. Muñoz-Castro and R. B. King, Au6 clusters: superatomic molecules bearing an SP3-hybrid Au6 core, Int. J. Quantum Chem., 2017, 117(5), e25331 CrossRef.
- N. M. Tam, N. T. Mai, H. T. Pham, N. T. Cuong and N. T. Tung, Ultimate Manipulation of Magnetic Moments in the Golden Tetrahedron Au20 with a Substitutional 3d Impurity, J. Phys. Chem. C, 2018, 122(28), 16256–16264 CrossRef CAS.
- N. M. Tam, N. T. Cuong, H. T. Pham and N. T. Tung, Au19M (M = Cr, Mn, and Fe) as magnetic copies of the golden pyramid, Sci. Rep., 2017, 7(1), 16086 CrossRef PubMed.
- V. Fung and D.-e. Jiang, Exploring Structural Diversity and Fluxionality of Ptn (n = 10–13) Clusters from First-Principles, J. Phys. Chem. C, 2017, 121(20), 10796–10802 CrossRef CAS.
- N. B. Singh and U. Sarkar, Structure, vibrational, and optical properties of platinum cluster: a density functional theory approach, J. Mol. Model., 2014, 20(12), 2537 CrossRef PubMed.
- R. Li, M. Odunlami and P. Carbonnière, Low-lying Ptn cluster structures (n = 6–10) from global optimizations based on DFT potential energy surfaces: Sensitivity of the chemical ordering with the functional, Comput. Theor. Chem., 2017, 1107, 136–141 CrossRef CAS.
- Y. Jia, X. Yu, H. Zhang, L. Cheng and Z. Luo, Tetrahedral Pt10− Cluster with Unique Beta Aromaticity and Superatomic Feature in Mimicking Methane, J. Phys. Chem. Lett., 2021, 12(21), 5115–5122 CrossRef CAS PubMed.
- A. S. Chaves, G. G. Rondina, M. J. Piotrowski, P. Tereshchuk and J. L. F. Da Silva, The Role of Charge States in the Atomic Structure of Cun and Ptn (n = 2–14 atoms) Clusters: A DFT Investigation, J. Phys. Chem. A, 2014, 118(45), 10813–10821 CrossRef CAS.
- D. Bumüller, A. G. Yohannes, S. Kohaut, I. Kondov, M. M. Kappes, K. Fink and D. Schooss, Structures of Small Platinum Cluster Anions Ptn−: Experiment and Theory, J. Phys. Chem. A, 2022, 126(22), 3502–3510 CrossRef PubMed.
- T. R. Henninen, M. Bon, F. Wang, D. Passerone and R. Erni, The Structure of Sub-nm Platinum Clusters at Elevated Temperatures, Angew. Chem., Int. Ed., 2020, 59(2), 839–845 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, J. R. Cheeseman, G. Scalmani, M. Caricato, H. P. Hratchian, X. Li, V. Barone, J. Bloino, G. Zheng, T. Vreven, J. A. Montgomery Jr, G. A. Petersson, G. E. Scuseria, H. B. Schlegel, H. Nakatsuji, A. F. Izmaylov, R. L. Martin, J. L. Sonnenberg, J. E. Peralta, J. J. Heyd, E. Brothers, F. Ogliaro, M. Bearpark, M. A. Robb, B. Mennucci, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, A. Rendell, R. Gomperts, V. G. Zakrzewski, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao and H. Nakai, Gaussian 09, Revision A.01, 2009 Search PubMed.
- P. Schwerdtfeger, L. F. Pašteka, A. Punnett and P. O. Bowman, Relativistic and quantum electrodynamic effects in superheavy elements, Nucl. Phys. A, 2015, 944, 551–577 CrossRef CAS.
- H. Tatewaki, S. Yamamoto and Y. Hatano, Relativistic Effects in the Electronic Structure of Atoms, ACS Omega, 2017, 2(9), 6072–6080 CrossRef CAS.
- J. Autschbach, Perspective: Relativistic effects, J. Chem. Phys., 2012, 136(15), 150902 CrossRef PubMed.
- P. Pyykko, Relativistic effects in structural chemistry, Chem. Rev., 1988, 88(3), 563–594 CrossRef CAS.
- K. H. Lee, Q. Van Vuong, V. Fung, D.-e. Jiang and S. Irle, Density-Functional Tight-Binding for Platinum Clusters and Bulk: Electronic vs. Repulsive Parameters, MRS Adv., 2019, 4(33), 1821–1832 CrossRef CAS.
- M. P. Johansson, A. Lechtken, D. Schooss, M. M. Kappes and F. Furche, 2D-3D transition of gold cluster anions resolved, Phys. Rev. A, 2008, 77(5), 053202 CrossRef.
- S. Bulusu, X. Li, L.-S. Wang and X. C. Zeng, Evidence of hollow golden cages, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(22), 8326–8330 CrossRef CAS PubMed.
- P. Ferrari, G.-L. Hou, O. V. Lushchikova, F. Calvo, J. M. Bakker and E. Janssens, The structures of cationic gold clusters probed by far-infrared spectroscopy, Phys. Chem. Chem. Phys., 2020, 22(20), 11572–11577 RSC.
- C. J. Cramer and D. G. Truhlar, Density functional theory for transition metals and transition metal chemistry, Phys. Chem. Chem. Phys., 2009, 11(46), 10757–10816 RSC.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions, J. Chem. Theory Comput., 2006, 2(2), 364–382 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions, J. Chem. Phys., 2006, 125(19), 194101 CrossRef PubMed.
- L. Xiao and L. Wang, Structures of Platinum Clusters: Planar or Spherical?, J. Phys. Chem. A, 2004, 108(41), 8605–8614 CrossRef CAS.
- P. Ferrari, J. Vanbuel, N. M. Tam, M. T. Nguyen, S. Gewinner, W. Schöllkopf, A. Fielicke and E. Janssens, Effects of Charge Transfer on the Adsorption of CO on Small Molybdenum-Doped Platinum Clusters, Chem.–Eur. J., 2017, 23(17), 4120–4127 CrossRef CAS PubMed.
- T. Li and P. B. Balbuena, Computational Studies of the Interactions of Oxygen with Platinum Clusters, J. Phys. Chem. B, 2001, 105(41), 9943–9952 CrossRef CAS.
- R. L. T. Parreira, G. F. Caramori, S. E. Galembeck and F. Huguenin, The Nature of the Interactions between Pt4 Cluster and the Adsorbates ·H, ·OH, and H2O, J. Phys. Chem. A, 2008, 112(46), 11731–11743 CrossRef CAS PubMed.
- Q. Du, X. Wu, P. Wang, D. Wu, L. Sai, R. B. King, S. J. Park and J. Zhao, Structure Evolution of Transition Metal-doped Gold Clusters M@Au12 (M = 3d–5d): Across the Periodic Table, J. Phys. Chem. C, 2020, 124(13), 7449–7457 CrossRef CAS.
- G. Sun and P. Sautet, Toward Fast and Reliable Potential Energy Surfaces for Metallic Pt Clusters by Hierarchical Delta Neural Networks, J. Chem. Theory Comput., 2019, 15(10), 5614–5627 CrossRef CAS PubMed.
- H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, The 2D-to-3D geometry hopping in small boron clusters: The charge effect, Chem. Phys. Lett., 2013, 577, 32–37 CrossRef CAS.
- M. Saunders, Stochastic search for isomers on a quantum mechanical surface, J. Comput. Chem., 2004, 25(5), 621–626 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.G, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2004 Search PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10(34), 5207–5217 RSC.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed.
- E. J. Baerends, V. Branchadell and M. Sodupe, Atomic reference energies for density functional calculations, Chem. Phys. Lett., 1997, 265(3), 481–489 CrossRef CAS.
- S. Pittalis, S. Kurth and E. K. U. Gross, On the degeneracy of atomic states within exact-exchange (spin-) density functional theory, J. Chem. Phys., 2006, 125(8), 084105 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: (i) The low-lying structures, their relative energies and spin states of the AuxPty2+ (x + y = 10) clusters, (ii) AdNDP analysis of the AuxPty2+ clusters with x + y = 10 (B3PW91/cc-pVTZ-PP), (iii) calculated density of states (DOS) of the AuxPty2+ (x + y = 10) at B3PW91/aug-cc-pVTZ-PP level, and (iv) geometric shapes and Cartesian coordinates of the lowest-energy isomers. See DOI: https://doi.org/10.1039/d3ra06000d |
| This journal is © The Royal Society of Chemistry 2023 |