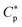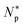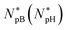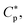Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modeling selectivity of antimicrobial peptides: how it depends on the presence of host cells and cell density
Suemin Lee†
a,
Bethany R. Schefter b,
Sattar Taheri-Araghic and
Bae-Yeun Ha
b,
Sattar Taheri-Araghic and
Bae-Yeun Ha *a
*a
aDepartment of Physics and Astronomy, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada. E-mail: byha@uwaterloo.ca
bDepartment of Physics and Astronomy, University of Western Ontario, London, Ontario N6A 3K7, Canada
cDepartment of Physics and Astronomy, California State University, Northridge, CA 91330, USA
First published on 22nd November 2023
Abstract
Antimicrobial peptides (AMPs), naturally-occurring peptide antibiotics, are known to attack bacteria selectively over the host cells. The emergence of drug-resistant bacteria has spurred much effort in utilizing optimized (more selective) AMPs as new peptide antibiotics. Cell selectivity of these peptides depends on various factors or parameters such as their binding affinity for cell membranes, peptide trapping in cells, peptide coverages on cell membranes required for membrane rupture, and cell densities. In this work, using a biophysical model of peptide selectivity, we show this dependence quantitatively especially for a mixture of bacteria and host cells. The model suggests a rather nontrivial dependence of the selectivity on the presence of host cells, cell density, and peptide trapping. In a typical biological setting, peptide trapping works in favor of host cells; the selectivity increases with increasing host-cell density but decreases with bacterial cell density. Because of the cell-density dependence of peptide activity, the selectivity can be overestimated by two or three orders of magnitude. The model also clarifies how the cell selectivity of AMPs differs from their membrane selectivity.
1. Introduction
Antimicrobial peptides (AMPs) are naturally-occurring peptide antibiotics used in the host defense of living organisms (e.g., animals, plants, …).1,2 They are relatively short, typically consisting of 20–50 amino acids. In the bulk, they often resemble random coils, but when inserted in membranes, they assume compact, amphiphilic structures (e.g., α helices), as required for their antimicrobial activity (e.g., membrane perturbation). AMPs are mostly cationic and thus utilize the unique ‘design feature’ of microbial membranes,1 enriched with anionic lipids.1–3 Cationic AMPs preferentially attach to and rupture microbial membranes over host cell membranes; in the latter case, anionic lipids are segregated to their inner layer (see Fig. 1). Once they gain entry into the cytoplasm, they can target key intra-cellular components (e.g., DNA and proteins), leading to intra-cellular killing of microbes.1,2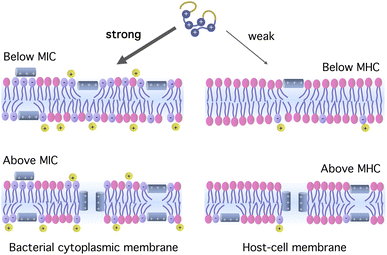 | ||
| Fig. 1 Origin of peptide selectivity. Cationic antimicrobial peptides interact more strongly with bacterial membranes enriched with anionic lipids. Bound peptides can form pores in the membrane when the bulk concentration is at or above the MIC or MHC. In the figure, the membranes are only schematically illustrated, leaving out such details as membrane proteins and the presence of cholesterol in the host-cell membrane. The figure is inspired by ref. 1, 2 and 10. | ||
There has been much interest in developing enhanced AMPs as potent peptide antibiotics, especially for fighting drug-resistant bacteria.1–5 Membrane-targeting AMPs are advantageous.1–4,6 They act via physical mechanisms such as pore formation1–4,6 or anionic-lipid clustering3 in membranes, which bacteria cannot easily avoid. In addition to rupturing bacterial membranes, they act as metabolic inhibitors1,2 and/or immunomodulators.7 Even though pathogens can, in principle, evolve antimicrobial resistance,8,9 the therapeutic potential of these multitasking molecules deserves much consideration.4,5
Cationic AMPs can single out bacteria through their stronger binding affinity for bacterial membranes.1–4,6 The resulting selectivity can be quantified by the ratio of two concentrations: the minimum hemolytic concentration (MHC) and the minimum inhibitory concentration (MIC).10,11 At or beyond this concentration, peptides can form pores in their binding membranes, as illustrated in Fig. 1. The larger the ratio MHC/MIC is for a given peptide, the more selective the peptide is. In a sizeable range of peptide concentration (∼μM) between MIC and MHC, the peptide is active against bacteria while leaving the host cells unharmed.
The selectivity of AMPs is influenced by a number of factors or parameters such as their binding affinity for cell membranes, peptide trapping in (dead) cells,12–14 cell density,11–18 and a peptide coverage on cell membranes required for membrane rupture.19–21 Let P/L denote the molar ratio of bound peptides to lipids. At the MIC or MHC, P/L reaches a threshold value, P/L*. The value of P/L* depends on the type of peptide and lipid19–21 and is typically larger for membranes containing lipids with smaller headgroups such as phosphatidylethanolamine (PE) as in bacterial membranes. Recent studies suggest that at P/L*, each cell consumes a certain number of peptides with some of them trapped in the cell.12–14 This implies that the MIC or the MHC increases with increasing cell density; as a result, the ratio MHC/MIC is cell-density dependent.11–13,16–18 The cell-density dependence is often referred to as an inoculum effect12–15 and is known to enhance population survivability.14
A natural consequence of the cell-density dependence of peptide activity and selectivity is that the selectivity depends on the way it is measured.16–18 For instance, it can be obtained by combining MIC and MHC measured separately from bacteria-only and host-cell-only solutions, respectively. In this work, the resulting selectivity is referred to as “noncompetitive” selectivity. More realistically, it can be measured from a mixture of both types of cells: “competitive” selectivity. In this case, the presence of host cells raises the MIC and influences the ratio MHC/MIC.13,16,22 These two approaches generally lead to different levels of selectivity. This implies that the selectivity reflects the biological setting of infected sites (e.g., the degree of infection, …).
According to what is discussed above, peptide selectivity not only reflects peptide's intrinsic properties such as peptide charge and hydrophobicity, but it also depends on external parameters such as cell density and the presence of host cells. Does this mean that the selectivity should be measured for a wide range of cell density and various combinations of host cell and bacterial cell density? Recent modeling efforts, however, suggest that these two aspects (intrinsic and extrinsic) are well separated.16,18 With an appropriate model, one can figure out the selectivity with varying cell density, once it is known at a low cell-density limit or at conveniently-chosen density. Furthermore, in the past, model lipid membranes, mimicking cell membranes, were often used for peptide activity or selectivity experiments.10,19–21 How does the resulting membrane selectivity differ from cell selectivity measured for cells (bacteria versus host cells)? Peptide trapping is one of the determining factors in the latter12–14,16 but is expected to be insignificant in the former.
Recently, we examined theoretically peptide selectivity and clarified the effects of peptide trapping on the selectivity, MHC/MIC.16 This effort is relevant in the presence of an excess amount of host cells or for a homogeneous solution of either bacteria or host cells. Here, we extend this effort and offer a more complete picture of the activity and selectivity of AMPs, which can be used to interpret selectivity measurements or to assist with our endeavor in finding optimized peptides.
This work builds on earlier studies.12–16 The results reported in this work, which are relevant for melittin-like peptides, suggest a rather nontrivial dependence of the selectivity on the presence of host cells, peptide trapping, and cell density. Peptide trapping can enhance or reduce the selectivity depending on how cell (host and bacterial) density is chosen. In most cases, it works in favor of the host cells, enhancing the selectivity. The presence of an excess amount of host cells (5 × 109 cells per mL) as in whole blood can raise the MIC more than 10-fold, proportionally with the density of bacterial cells. The resulting MIC still falls in a low-μM range as long as the bacterial cell density is somewhat smaller than 5 × 107 cells per mL.
Let CB and CH be the density of bacteria and the density of host cells, respectively, and Np the number of peptides trapped per cell. As we raise CB and CH coherently so that CB = CH, the selectivity decreases in both noncompetitive and competitive cases. Similarly, in the presence of an excess amount of host cells, the selectivity decreases with increasing CB in both cases, more so for larger Np. In contrast, when the bacterial cell density is fixed at CB = 5 × 104 cells per mL or CB = 108 cells per mL, the selectivity increases with increasing CH, more rapidly for larger Np. Compared to the competitive one, the noncompetitive selectivity can be overestimated by more than two orders of magnitude, depending on how CB and CH are chosen (see refs. 11 and 16 for related discussions).
We also clarify how the cell selectivity of AMPs differs from their membrane selectivity. While the selectivity based on model membranes is typically larger than the corresponding cell selectivity, the (relative) difference between competitive and noncompetitive selectivity is generally larger in the latter. Except for some differences, membrane selectivity and cell selectivity of AMPs are qualitatively similar to each other. If interpreted with care, the former can provide useful information about the latter.
In this work, we will focus our effort on presenting a selectivity model in a pedagogical but yet systematic manner. In our consideration, one of the main differences between model membranes and cells comes from peptide trapping in the latter. Nevertheless, we will use membrane density and cell density interchangeably; also MICs and MHCs refer to peptide concentration beyond which membranes are ruptured, whether they are model membranes or cell membranes.
This paper is organized as follows: in Section 2, we present a simple picture of how the activity and selectivity of AMPs vary with cell density for a noncompetitive and competitive medium. Section 3 introduces a Langmuir model of peptide binding. Section 4 summaries the results for peptide activity and selectivity as a function of cell density; the effect of peptide trapping is highlighted, and membrane selectivity and cell selectivity are compared. All the symbols and acronyms are defined in Table 1.
2. Cell and membrane selectivity of antimicrobial peptides
In this section, we present a pedagogical approach to peptide activity and selectivity, which shows how peptide selectivity depends on cell density and peptide trapping in cells. We start with a homogeneous system of either bacterial or host cells, referred to as a noncompetitive case, and turn to a mixture of both types of cells, referred to as a competitive case.Before proceeding further, we introduce several parameters relevant for peptide activity and selectivity. A key “extrinsic” parameter is the number density of peptides, denoted as Cp; so is the density of cells, Ccell.12,14,17,18 The surface area of each cell, Acell, matters.17 In terms of the number of membrane-bound peptides, doubling Acell for given Ccell is equivalent to doubling Ccell for given Acell. The peptide selectivity arises primarily from the difference in binding energy, denoted as w, between bacterial membranes and host-cell membranes.1,16–18 Membrane rupture occurs in an all-or-none Ccell-dependent manner.19,20,23 Recall that P/L is the molar ratio of membrane-bound peptides to lipids. At a certain value of Cp, i.e., 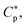 P/L reaches a threshold value required for membrane rupture, P/L*;10,19–21
P/L reaches a threshold value required for membrane rupture, P/L*;10,19–21 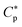 is either MIC or MHC. Finally, Np denotes the number of trapped peptides per cell. This needs to be taken with caution. Below
is either MIC or MHC. Finally, Np denotes the number of trapped peptides per cell. This needs to be taken with caution. Below 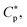 we assume that Np = 0. In this case, penetration of peptides into a cell is expected to be a rare event, since it involves overcoming a large free energy barrier for crossing an otherwise intact cell membrane. At
we assume that Np = 0. In this case, penetration of peptides into a cell is expected to be a rare event, since it involves overcoming a large free energy barrier for crossing an otherwise intact cell membrane. At 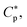 half of the cell membranes are ruptured. Thus, Np can be interpreted as the number of peptides trapped in each dead cell. Alternatively, it can be considered as the “average” number of peptides trapped per cell at
half of the cell membranes are ruptured. Thus, Np can be interpreted as the number of peptides trapped in each dead cell. Alternatively, it can be considered as the “average” number of peptides trapped per cell at 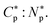 Here, we employ this definition of Np, which is half of the number of trapped peptides in a dead cell. Beyond, Np can be larger than
Here, we employ this definition of Np, which is half of the number of trapped peptides in a dead cell. Beyond, Np can be larger than 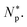 But we ignore the possible weak dependence of Np on Cp (see Section 2.2 for further discussion). As a result, for
But we ignore the possible weak dependence of Np on Cp (see Section 2.2 for further discussion). As a result, for 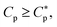 we use Np and
we use Np and 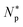 interchangeably, unless otherwise indicated. Finally, the subscript ‘B’ or ‘H’ will be used to refer to bacteria and host cells, respectively, as in NpB, NpH,
interchangeably, unless otherwise indicated. Finally, the subscript ‘B’ or ‘H’ will be used to refer to bacteria and host cells, respectively, as in NpB, NpH, 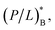 and
and 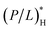 (see Table 1). Similarly, CB is the bacterial cell density and AB is the bacterial cell surface area; aB and aH are the lipid headgroup area of bacterial and host-cell membranes, respectively; the binding energy wB and wH can be interpreted similarly.
(see Table 1). Similarly, CB is the bacterial cell density and AB is the bacterial cell surface area; aB and aH are the lipid headgroup area of bacterial and host-cell membranes, respectively; the binding energy wB and wH can be interpreted similarly.
2.1 Homogeneous case
Fig. 2 illustrates how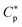 depends on cell density Ccell in a homogeneous or noncompetitive case, consisting of either bacteria or host cells. Here, two concentric circles represent cells (membrane bilayers enclosing cells), whereas small circles stand for peptides; if filled ones are free or trapped, unfilled ones are membrane-bound. The fraction of bound peptides is controlled by the balance between entropy and energy24 (also see ref. 25). At a low peptide concentration, peptides are mostly free, because of a large entropic penalty for binding even in a single-cell limit (Fig. 2(i)). As the peptide concentration Cp increases, the balance is swayed toward energy, which favors binding. As a result, the surface coverage of peptides P/L (molar ratio of bound peptides to lipids) also increases. Eventually, Cp reaches
depends on cell density Ccell in a homogeneous or noncompetitive case, consisting of either bacteria or host cells. Here, two concentric circles represent cells (membrane bilayers enclosing cells), whereas small circles stand for peptides; if filled ones are free or trapped, unfilled ones are membrane-bound. The fraction of bound peptides is controlled by the balance between entropy and energy24 (also see ref. 25). At a low peptide concentration, peptides are mostly free, because of a large entropic penalty for binding even in a single-cell limit (Fig. 2(i)). As the peptide concentration Cp increases, the balance is swayed toward energy, which favors binding. As a result, the surface coverage of peptides P/L (molar ratio of bound peptides to lipids) also increases. Eventually, Cp reaches 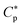 (either MIC or MHC), at which P/L = P/L*. Even in the single cell limit shown in (i),
(either MIC or MHC), at which P/L = P/L*. Even in the single cell limit shown in (i), 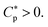
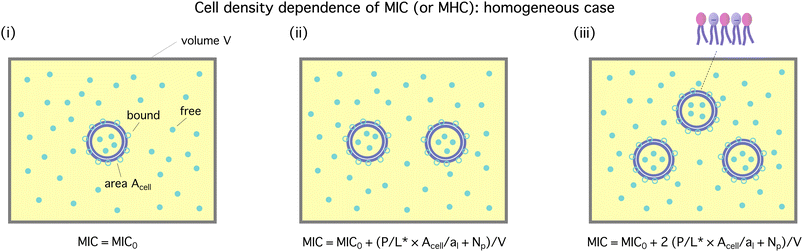 | ||
Fig. 2 Cell-density dependence of 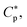 i.e., either MIC or MHC: a homogeneous or noncompetitive case. Cells are represented by two concentric circles and peptides by filled (free or trapped) or unfilled circles (membrane-bound). As the peptide concentration Cp increases, their surface coverage P/L (molar ratio of peptides to lipids) also increases and eventually reaches a threshold P/L* at i.e., either MIC or MHC: a homogeneous or noncompetitive case. Cells are represented by two concentric circles and peptides by filled (free or trapped) or unfilled circles (membrane-bound). As the peptide concentration Cp increases, their surface coverage P/L (molar ratio of peptides to lipids) also increases and eventually reaches a threshold P/L* at 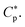 Even in the single-cell limit shown in (i), Even in the single-cell limit shown in (i), 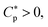 because of the entropy of peptides, which favors unbinding. Imagine introducing a second cell in (i), converting the system into the one in (ii). The number of peptides the first cell consumed is equal to (P/L* × Acell/a1 + Np), where al is the area of each lipid. In order to remain at P/L*, the same number of peptides should be supplied. This will raise because of the entropy of peptides, which favors unbinding. Imagine introducing a second cell in (i), converting the system into the one in (ii). The number of peptides the first cell consumed is equal to (P/L* × Acell/a1 + Np), where al is the area of each lipid. In order to remain at P/L*, the same number of peptides should be supplied. This will raise 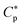 by P/L* × Acell/al + Np/V, where V is the volume of the system: by P/L* × Acell/al + Np/V, where V is the volume of the system: 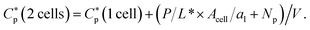 The progression from (i) to (iii) shows that The progression from (i) to (iii) shows that 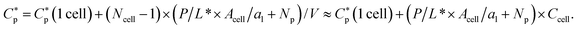 When applied to bacteria, this equation become MIC(Ccell) = MIC0 + (P/L* × Acell/al + Np)Ccell, where MIC0 is MIC in the low-cell density limit: Ccell → 0. Figure adapted with permission from ref. 17. Copyright 2015 American Chemical Society; Reproduced with modifications from ref. 18 with permission from the Royal Society of Chemistry. When applied to bacteria, this equation become MIC(Ccell) = MIC0 + (P/L* × Acell/al + Np)Ccell, where MIC0 is MIC in the low-cell density limit: Ccell → 0. Figure adapted with permission from ref. 17. Copyright 2015 American Chemical Society; Reproduced with modifications from ref. 18 with permission from the Royal Society of Chemistry. | ||
As the cell density increases, different cells compete for peptides. Even though the binding is driven by energy, this competition is entropic in origin and does not involve cell–cell interactions. This is responsible for the cell-density dependence of 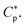 It can be worked out progressively as shown in Fig. 2. Now imagine introducing a second cell in Fig. 2(i), converting the system into the one in Fig. 2(ii). Because of the presence of the first cell, there will be less peptides for the second one: at
It can be worked out progressively as shown in Fig. 2. Now imagine introducing a second cell in Fig. 2(i), converting the system into the one in Fig. 2(ii). Because of the presence of the first cell, there will be less peptides for the second one: at 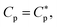 the number of peptides the first cell consumed is equal to
the number of peptides the first cell consumed is equal to 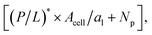 where al is the area of each lipid; recall Acell is the surface area of each cell. The presence of a second cell in (ii) is equivalent to removing [(P/L)* × Acell/al + Np] peptides in (i), which is at
where al is the area of each lipid; recall Acell is the surface area of each cell. The presence of a second cell in (ii) is equivalent to removing [(P/L)* × Acell/al + Np] peptides in (i), which is at 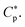 In order to remain at P/L*, an extra number of peptides should be supplied. The required number of peptides is equal to [(P/L)* × Acell/al + Np]. This will raise
In order to remain at P/L*, an extra number of peptides should be supplied. The required number of peptides is equal to [(P/L)* × Acell/al + Np]. This will raise 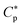 by [(P/L)* × Acell/al + Np]/V, where V is the volume of the system:
by [(P/L)* × Acell/al + Np]/V, where V is the volume of the system:
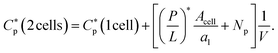 | (1) |
Here, 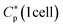 is either MIC or MHC in the single-cell case.
is either MIC or MHC in the single-cell case.
The progression from (i) to (iii) shows how this analysis can be extended to the Ncell-cell case:
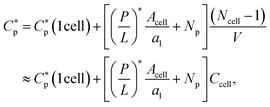 | (2) |
Eqn (2) becomes
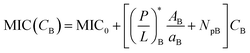 | (3a) |
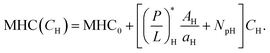 | (3b) |
Here MIC0 and MHC0 are, respectively, the MIC and MHC in the low-cell density limit: 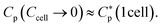
Eqn (3) can be viewed as a function of Ccell: CB or CH. Both the MIC and the MHC increase linearly with the cell density CB and CH, respectively. The slope of the relation in eqn (3), [(P/L)* Acell/al + Np], is the total number of peptides consumed per cell at P/L = (P/L)*. This is larger for larger Np; peptide trapping in cells makes 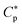 increase more rapidly with Ccell. The ‘y’-axis intercept, either MIC0 or MHC0, is set by the interaction of peptides with membranes among others (see Section 3). The value of P/L* reflects membrane curvature (peptide parameters as well).19–21 It is larger for PE (phosphatidylethanolamine)-containing bacterial membranes, which tend to develop a negative curvature. However, this does not change P/L* by an order of magnitude. For the peptide melittin, for instance,
increase more rapidly with Ccell. The ‘y’-axis intercept, either MIC0 or MHC0, is set by the interaction of peptides with membranes among others (see Section 3). The value of P/L* reflects membrane curvature (peptide parameters as well).19–21 It is larger for PE (phosphatidylethanolamine)-containing bacterial membranes, which tend to develop a negative curvature. However, this does not change P/L* by an order of magnitude. For the peptide melittin, for instance, 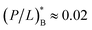 and
and 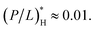 19–21
19–21
Imagine combining MHC and MIC values obtained separately for homogeneous solutions. The ratio MHC/MIC increases with CH: the larger CH is, the larger the selectivity is. As evidenced below, this does not correctly represent the selectivity in a biological-relevant medium (e.g., a mixture of host cells and bacteria) but tends to overestimate it.
2.2 Competitive case
The homogeneous-case analysis in Fig. 2 can be extended to a mixture of bacterial and host cells, referred to as a competitive case, as shown in Fig. 3. If the concentric circles in blue represent bacterial cells, the pink ones stand for the host cells. Fig. 3(i) shows a single bacterial cell at the MIC. The introduction of a host cell in Fig. 3(ii) will reduce the amount of peptides for the bacterial cell. The extra number of peptides to maintain Cp at the MIC is equal to [(P/L)H × AH/aH + NpH]; similarly, in Fig. 3(iii), the number of peptides that should be added is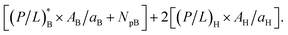
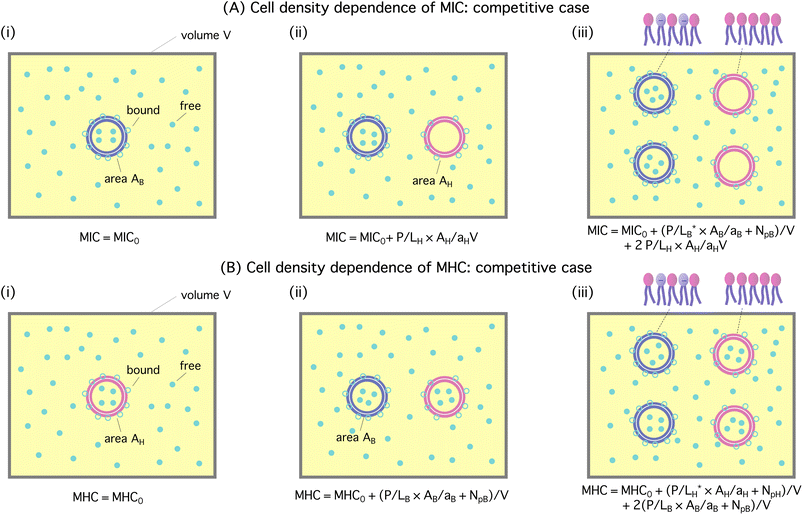 | ||
Fig. 3 Cell-density dependence of MIC (A) and MHC (B): competitive case. Cells are represented by two concentric circles and peptides by filled (free or trapped) or unfilled circles (membrane-bound); if the blue circles represent bacterial cells, the pink ones stand for host cells. Let Acell = AB or AH be the bacterial or host cell surface area, respectively; aB and aH the lipid headgroup area of the bacterial or host-cell membranes, respectively; NpB and NpH the number of trapped peptides in each bacterial and host cell, respectively; (P/L)B and (P/L)H are the molar ratio of bound peptides to lipids on the bacterial and host-cell membranes, respectively. (A) The progression from (i) to (iii) suggests that 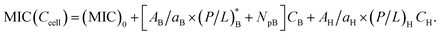 (B) Using a similar line of reasoning, we arrive at (B) Using a similar line of reasoning, we arrive at 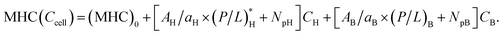 Figure adapted with permission from ref. 17. Copyright 2015 American Chemical Society; Reproduced with modifications from ref. 18 with permission from the Royal Society of Chemistry. Figure adapted with permission from ref. 17. Copyright 2015 American Chemical Society; Reproduced with modifications from ref. 18 with permission from the Royal Society of Chemistry. | ||
The progression from (i) to (iii) suggests that
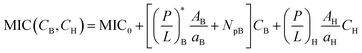 | (4a) |
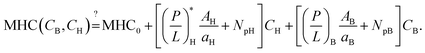 | (4b) |
If Np is set to zero as for model membranes, the second equation in eqn (4) can be obtained from the first one by swapping the role of bacteria with that of host cells. Here (P/L)H in eqn (4a) is the surface coverage of peptides on the host cells evaluated at Cp = MIC, whereas (P/L)B in eqn (4b) is the surface coverage of peptides on bacteria evaluated at Cp = MHC.
Note that these two lines of equations in eqn (4) are not fully symmetric with respect to the exchange in role between host cells and bacteria for the obvious reason: as Cp increases, the MIC will be reached first. This explains why the last term in eqn (4a) does not contain NpH. In other words, 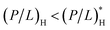 in eqn (4a). In contrast,
in eqn (4a). In contrast, 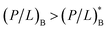 in eqn (4b). As a result, over a sizeable Cp range, the peptide under consideration is active against bacteria only and is thus selective.
in eqn (4b). As a result, over a sizeable Cp range, the peptide under consideration is active against bacteria only and is thus selective.
Also, eqn (4b) needs to be understood with caution. Beyond 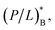 some of bound peptides start to rupture the membranes by forming pores, for instance. The last term in these equations may be interpreted as the total amount of bound peptides whether on the membrane surface or in pores. As a result, the binding energy wB needs to be interpreted accordingly. As it turns out, the term inside […] in eqn (4) is dominated by Np (see below). Furthermore, wH, which governs peptide binding and influences (P/L)H, is not constant but can vary with (P/L)H. The main source of this dependence is the electrostatic interaction between bound peptides. But this dependence is generally weak, since the distance between bound peptides for (P/L) ≤ (P/L)* ≈ 0.01 is typically larger than the Debye screening length, rD, beyond which the electrostatic interaction is exponentially screened.25 At (P/L)* = 0.01, the typical distance between the adjacent peptides is
some of bound peptides start to rupture the membranes by forming pores, for instance. The last term in these equations may be interpreted as the total amount of bound peptides whether on the membrane surface or in pores. As a result, the binding energy wB needs to be interpreted accordingly. As it turns out, the term inside […] in eqn (4) is dominated by Np (see below). Furthermore, wH, which governs peptide binding and influences (P/L)H, is not constant but can vary with (P/L)H. The main source of this dependence is the electrostatic interaction between bound peptides. But this dependence is generally weak, since the distance between bound peptides for (P/L) ≤ (P/L)* ≈ 0.01 is typically larger than the Debye screening length, rD, beyond which the electrostatic interaction is exponentially screened.25 At (P/L)* = 0.01, the typical distance between the adjacent peptides is 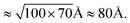 This is appreciably larger than the screening length under physiological conditions (e.g., in the presence of 100 mM of monovalent salts): rD ≈ 10 Å. Finally, in eqn (4b), NpB is the number of trapped peptides in each cell above the MIC. The value of this parameter will eventually be determined by chemical equilibrium between trapped peptides and those on the membrane or in the bulk. The energetics of this is unknown and can be influenced by a number of factors such as peptide's interaction with cellular components and crowding in the cell. As mentioned in Section 2, in our consideration, we ignore this complexity and approximate NpB in eqn (4b) by
This is appreciably larger than the screening length under physiological conditions (e.g., in the presence of 100 mM of monovalent salts): rD ≈ 10 Å. Finally, in eqn (4b), NpB is the number of trapped peptides in each cell above the MIC. The value of this parameter will eventually be determined by chemical equilibrium between trapped peptides and those on the membrane or in the bulk. The energetics of this is unknown and can be influenced by a number of factors such as peptide's interaction with cellular components and crowding in the cell. As mentioned in Section 2, in our consideration, we ignore this complexity and approximate NpB in eqn (4b) by 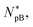 i.e., NpB at MIC.
i.e., NpB at MIC.
It is worth noting that eqn (3) and (4) are a special case of the following relations:
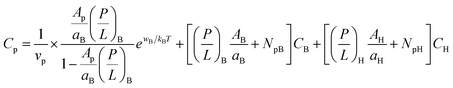 | (5a) |
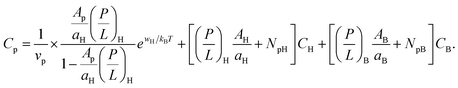 | (5b) |
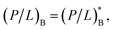 the first term on the right hand side of eqn (5a) is MIC0; the first term in eqn (5b) can be interpreted similarly. Strictly speaking, both wB and wH have a weak dependence on P/L. At the relevant range of P/L around P/L*, however, this dependence can be neglected as discussed above.
the first term on the right hand side of eqn (5a) is MIC0; the first term in eqn (5b) can be interpreted similarly. Strictly speaking, both wB and wH have a weak dependence on P/L. At the relevant range of P/L around P/L*, however, this dependence can be neglected as discussed above.
The meaning of Np in eqn (5) is somewhat different from that in eqn (4). As noted above, eqn (5) is more general in the sense that Cp on the left hand side does not have to be equal to 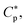 which is either MIC or MHC. As a result, Np in eqn (5) varies with P/L and is generally different from
which is either MIC or MHC. As a result, Np in eqn (5) varies with P/L and is generally different from 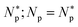 for (P/L) = (P/L)* and Np = 0 for (P/L) < (P/L)* Accordingly, NpH = 0 in eqn (5a), when Cp = MIC (<MHC). Eqn (5a) then reduces to the MIC expression in eqn (4a). Similarly, eqn (5b) becomes the MHC expression in eqn (4b) in an appropriate limit.
for (P/L) = (P/L)* and Np = 0 for (P/L) < (P/L)* Accordingly, NpH = 0 in eqn (5a), when Cp = MIC (<MHC). Eqn (5a) then reduces to the MIC expression in eqn (4a). Similarly, eqn (5b) becomes the MHC expression in eqn (4b) in an appropriate limit.
For given values of Cp and cell density (CB and CH), the two equations in eqn (5) can be solved simultaneously for P/L: (P/L)B and (P/L)H. Initially, we set Np = 0 and increase Cp gradually from zero. At some value of Cp, (P/L)B reaches 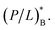 The resulting value of Cp with NpB set to
The resulting value of Cp with NpB set to 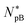 is the MIC. We then increase Cp further until
is the MIC. We then increase Cp further until 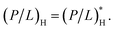 The resulting Cp with
The resulting Cp with 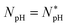 is the MHC. In this step, (P/L)B in eqn (5) is larger than
is the MHC. In this step, (P/L)B in eqn (5) is larger than 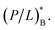 In reality, pore formation in bacterial membranes can complicate the energetics of peptide binding to the membrane. But this complication will not change the MHC in any significant way, since (P/L)B (AB/aB) ≪ NpB at or above the MHC, as discussed in ref. 16 (also see below); the main source of inoculum effects is the trapping of peptides in cells rather than peptide adsorption to membranes. For model membranes, however, this reasoning is not applicable. In our coarse-grained model, all the details governing peptide binding are subsumed into the parameter w (wB and wH). As noted above, w has a weak dependence on P/L and can also be influenced by pore formation. In a Langmuir-type model such as the one employed here, w is often approximated by its representative value. With a similar spirit, we will use a standard value of Np, as discussed in Section 3.
In reality, pore formation in bacterial membranes can complicate the energetics of peptide binding to the membrane. But this complication will not change the MHC in any significant way, since (P/L)B (AB/aB) ≪ NpB at or above the MHC, as discussed in ref. 16 (also see below); the main source of inoculum effects is the trapping of peptides in cells rather than peptide adsorption to membranes. For model membranes, however, this reasoning is not applicable. In our coarse-grained model, all the details governing peptide binding are subsumed into the parameter w (wB and wH). As noted above, w has a weak dependence on P/L and can also be influenced by pore formation. In a Langmuir-type model such as the one employed here, w is often approximated by its representative value. With a similar spirit, we will use a standard value of Np, as discussed in Section 3.
Let's analyze the relative significance of peptide trapping in determining the cell-density dependence of MIC or MHC. For this, we essentially repeat the earlier analysis in ref. 16. Compare the two terms with each other inside […] in eqn (4): the number of membrane-bound peptides and the number of absorbed peptides per cell. For the representative bacterium E. coli, AB ≈ 12 μm2, which is twice the area of the inner or outer layer of the cytoplasmic membrane.16,17 Since aB ≈ aH ≈ 70 Å2, AB/aB ≈ 1.7 × 107. For the peptide melittin, 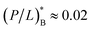 and
and 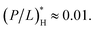 19–21 We thus find
19–21 We thus find 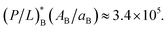 This number is much smaller than NpB ≈ 107 to 108.14 For the outer E. coli membrane,
This number is much smaller than NpB ≈ 107 to 108.14 For the outer E. coli membrane, 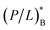 is several fold larger,10,26 but this does not change the picture. For human red blood cells as representative host cells, AH ≈ 17AB and AH/aH ≈ 2.9 × 108. As a result, we obtain
is several fold larger,10,26 but this does not change the picture. For human red blood cells as representative host cells, AH ≈ 17AB and AH/aH ≈ 2.9 × 108. As a result, we obtain 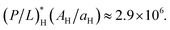 This is smaller than NpH ≈ 107.12,13 The main source of inoculum effects is the trapping of peptides inside dead cells at or above (P/L)*.
This is smaller than NpH ≈ 107.12,13 The main source of inoculum effects is the trapping of peptides inside dead cells at or above (P/L)*.
The analysis above implies that only the last term in eqn (4a) has a noticeable, explicit dependence on the binding energy wH for given MHC0. As a result, the MIC in eqn (4a) can be sensitive to wH, whereas the MHC in eqn (4b) is not. For similar reasons, both the MIC and the MHC in eqn (4) and (3) are not sensitive to wB for a fixed value of MIC0. For the homogeneous case in eqn (3), none of the MIC and the MHC is “explicitly” sensitive to wB or wH.
Similarly to what was observed in the homogenous case in Section 2.1, peptide trapping in cells (the main inoculum effect) makes 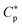 increase more rapidly with Ccell. It makes steeper the slope of a
increase more rapidly with Ccell. It makes steeper the slope of a 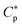 curve versus Ccell.
curve versus Ccell.
2.3 Limiting cases
It proves instructive to take some mathematical limits and simplify eqn (4). First, consider the case CB = CH. In the low cell-density limit, i.e., CB = CH → 0, the MIC and MHC in eqn (4) reduce to MIC0 and MHC0, respectively, as there is no competition between different cells (or membranes) to bind peptides. As a result, the distinction between the competitive and noncompetitive cases disappears in this limit.In the high-cell-density case, for simplicity, let's assume that AB = AH and Np = 0, as is often the case for lipid bilayers, and aB = aH ≈ 70 Å2, which is a good approximation (if AH ≠ AB, this analysis is applicable to the case: ABCB = AHCH). The competitive selectivity, MHC/MIC, becomes cell-density independent: 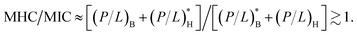 To understand the origin of the inequality, note that (P/L)B in the numerator is larger than
To understand the origin of the inequality, note that (P/L)B in the numerator is larger than 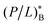 in the denominator, whereas (P/L)H in the denominator is smaller than
in the denominator, whereas (P/L)H in the denominator is smaller than 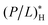 in the numerator. Thus MHC/MIC in this limit will get saturated at some constant larger than 1.
in the numerator. Thus MHC/MIC in this limit will get saturated at some constant larger than 1.
In the noncompetitive case with CB = CH, however, the ratio MHC/MIC approaches the following constant: 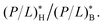 The threshold P/L is better known for lipid bilayers mimicking cell membranes than for cell membranes. As noted in Section 2.1, because of the presence of PE (phosphatidylethanolamine) in bacterial cell-membrane mimics,
The threshold P/L is better known for lipid bilayers mimicking cell membranes than for cell membranes. As noted in Section 2.1, because of the presence of PE (phosphatidylethanolamine) in bacterial cell-membrane mimics, 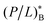 is somewhat larger than
is somewhat larger than 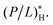 In the large cell-density limit in the noncompetitive case, we thus have MHC/MIC ≲ 1. There is a noticeable difference between the competitive and noncompetitive cases in the large cell-density limit; the selectivity is higher in the former case.
In the large cell-density limit in the noncompetitive case, we thus have MHC/MIC ≲ 1. There is a noticeable difference between the competitive and noncompetitive cases in the large cell-density limit; the selectivity is higher in the former case.
If CH ≫ CB, eqn (4) can be simplified as MIC ≈ (MIC)0 + AH/aH × (P/L)HCH and 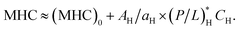 Note that the MIC in this case is much larger than the MIC for the corresponding bacteria-only case and the MHC here is approximately equal to the MHC for the corresponding host-cell-only case, as illustrated in Fig. 4. Accordingly, the ratio MHC/MIC is roughly independent of CB and approaches a constant of order 1, as CH → ∞ (while CB is held fixed).
Note that the MIC in this case is much larger than the MIC for the corresponding bacteria-only case and the MHC here is approximately equal to the MHC for the corresponding host-cell-only case, as illustrated in Fig. 4. Accordingly, the ratio MHC/MIC is roughly independent of CB and approaches a constant of order 1, as CH → ∞ (while CB is held fixed).
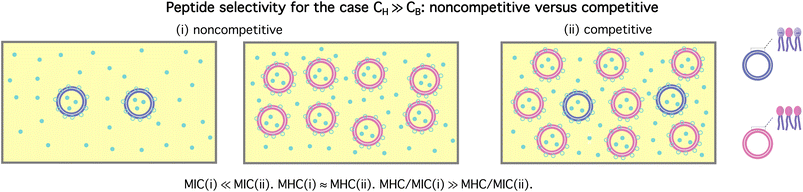 | ||
| Fig. 4 Peptide selectivity for a noncompetitive (homogeneous) (i) versus competitive (heterogeneous) case (ii). It is assumed that CH ≫ CB. In this case, whether the selectivity is measured noncompetitively (i) or competitively (ii) has a profound impact on the selectivity. It can be excessively overestimated in the noncompetitive case (i) with reference to the corresponding competitive case (ii), since the MIC is much larger for the latter case. The opposite is true if CH ≪ CB. Figure adapted with permission from ref. 17. Copyright 2015 American Chemical Society; Reproduced with modifications from ref. 18 with permission from the Royal Society of Chemistry. | ||
Imagine combining two sets of data: one set for bacteria only and one set for host cells only, i.e., two homogeneous cases in eqn (3). If CH ≫ CB, MHC/MIC → ∞ as CH → ∞. This limiting behavior in the homogeneous case is opposite to the one obtained for the corresponding competitive case (see Fig. 4). It explains how the selectivity can be excessively overestimated.
When Np ≠ 0 and AB ≠ AH, our analysis should reflect these inequalities. But the difference caused by them is often quantitative rather than qualitative, as evidenced in Section 4.
A full analysis of eqn (4) is involved. As discussed earlier,16 in some relevant limits, we can simplify eqn (4) (see ref. 16). This is particular the case for CH ≫ CB as in whole blood. In this case, eqn (4) can be approximated as
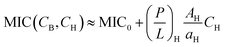 | (6a) |
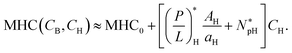 | (6b) |
Notice the obvious difference the competitive MIC in eqn (6a) and the noncompetitive one in eqn (3a). As discussed earlier in Section 2.3 and in Fig. 4, for CH ≫ CB, the competitive MIC is much larger than the noncompetitive one. In contrast, the MHC is approximately the same for both cases. This results in much larger selectivity in the noncompetitive case compared to the corresponding competitive case. This finding is consistent with the analysis above with Np set to zero.
For the case CH ≫ CB, the ratio MHC/MIC becomes
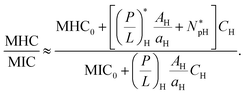 | (7) |
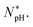 Since the second term inside […] in the numerator of eqn (7) is larger than the first term roughly by an order of magnitude (see Section 2.2), the effect of peptide trapping on the selectivity is up to about 10-fold.
Since the second term inside […] in the numerator of eqn (7) is larger than the first term roughly by an order of magnitude (see Section 2.2), the effect of peptide trapping on the selectivity is up to about 10-fold.
So far, we have used a simple biophysical picture, based on Fig. 2–4 to explore how peptide selectivity depends on cell density (CB or CH) and on the way it is measured (i.e., competitive versus noncompetitive). The y-intercepts, MIC0 and MHC0, may be considered as fitting parameters. They can also be related to more microscopic parameters. In the next section, we recapture the main results in this section; we then relate MIC0 and MHC0 to the biophysical parameters of peptides and membranes.
3. Langmuir binding model
In this section, using a Langmuir-type model for molecular binding,25 we derive the main results presented in Section 2 and relate MIC0 and MHC0 to the biophysical parameters of peptides and membranes. Note that such a model was already considered recently.17,18 Here, we recapture the essence of this consideration and generalize it to include peptide trapping in a cell. It suffices to focus on the homogeneous case, since the dependence of peptide activity on cell density in the competitive case is already obvious from eqn (4).In this model, peptides are either “free” (in the bulk) or “bound”; bound peptides are further classified as adsorbed to the cell surface or trapped inside a cell (see Fig. 2); trapped ones can bind to intracellular components. Initially, peptide binding occurs on the outer membrane layer or the outmost one in the case of Gram-negative bacteria. Adsorbed peptides will be eventually symmetrically distributed between the two layers after or even prior to membrane rupture27,28 (also see ref. 17). For simplicity, we ignore peptide trapping below 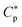 within typical experimental time scales. Indeed, it was shown that a large amount of trapped peptides were observed in dead bacterial cells, but not in dividing cells.14 At and beyond
within typical experimental time scales. Indeed, it was shown that a large amount of trapped peptides were observed in dead bacterial cells, but not in dividing cells.14 At and beyond 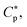 the amount of bound peptides is determined by chemical equilibrium between free and bound states.
the amount of bound peptides is determined by chemical equilibrium between free and bound states.
Let w and u be the adsorption and trapping energy, respectively. The value of w is typically more negative for bacterial membranes containing a large fraction of anionic lipids. It is worth noting that w is an effective parameter in which the effect of lipid demixing and peptide–peptide interactions on the membrane surface are subsumed (see ref. 18 for details). Similarly, u takes into account the interactions of trapped peptides with intracellular components as well as their mutual interactions inside the cell; it is also influenced by molecular crowding in the cell.29,30
Let Cp be the total concentration of peptides whether free or bound, σp [=(P/L)/al] the planar density of adsorbed peptides and Ap the area occupied by a bound peptide; np the number density of trapped peptides, and vp the volume of each peptide; np = 0 when P/L < P/L* and np = Np/Vcell when P/L = P/L*, where Vcell is the volume of each cell. In our Langmuir model, the chemical potential of bound peptides μbound at and above P/L* can readily be obtained as
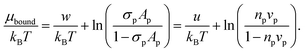 | (8) |
The chemical potential of free peptides is
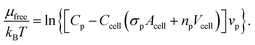 | (9) |
By equating the two chemical potentials in eqn (8) and (9), we obtain
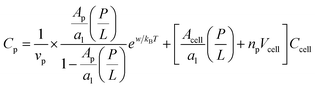 | (10a) |
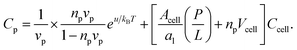 | (10b) |
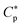 ), eqn (10a) with np = 0 describes chemical equilibrium between free and adsorbed peptides; eqn (10b) becomes irrelevant.
), eqn (10a) with np = 0 describes chemical equilibrium between free and adsorbed peptides; eqn (10b) becomes irrelevant.
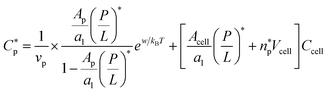 | (11a) |
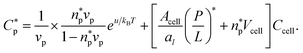 | (11b) |
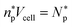 is the (average) number of peptides trapped in each cell at
is the (average) number of peptides trapped in each cell at 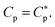
Comparison between eqn (11) and (3) leads to the following relation
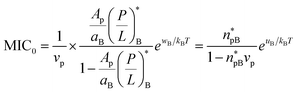 | (12a) |
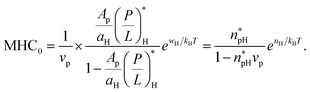 | (12b) |
It is worth mentioning that we will not attempt to solve eqn (10) for np, partly because the energetics involved in peptide trapping (i.e., u) is not well known. Instead, we will use suitable values of 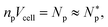 the number of peptides trapped in each cell, inspired by recent experiments.12–14 With this simplification, eqn (10) can readily be extended to the competitive case shown in Fig. 3. The cell-density dependence of
the number of peptides trapped in each cell, inspired by recent experiments.12–14 With this simplification, eqn (10) can readily be extended to the competitive case shown in Fig. 3. The cell-density dependence of 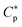 is already obvious in light of the discussion in Section 2.2; one can readily write down eqn (5).
is already obvious in light of the discussion in Section 2.2; one can readily write down eqn (5).
4. Results
In this section, we present the results for peptide activity and selectivity obtained for model membranes (Section 4.1) and cells (Section 4.2). Recall that one of the main differences between the two comes from peptide trapping in the latter case. As detailed below, MIC0 and MHC0 are chosen differently for the two cases. If calculated values of these quantities are used for model membranes, they are chosen appropriately for cells.4.1 Membrane selectivity
Following Section 2, we first present our results for peptide activity and selectivity without taking into account peptide trapping using peptide parameters relevant for a melittin-like peptide:17,18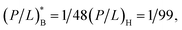 19–21 vp = 333 Å3, and Ap = 400 Å2.17,18 For this peptide, w was mapped out for model membranes, mimicking bacterial and host-cell membranes: wB = −16.6kBT and wH = −6.72kBT.18 Also, aB = 71 Å2 (al for bacterial membranes), aH = 74 Å2 (al for host-cell membranes),19–21 AB = 1.2 ×109 Å2 = 12 μm2 (suitable for E. coli), and AH = AB or AH = 17AB (as for human red blood cells).17 Note here that this value of AB is two times the surface area of E. coli (≈6 μm2).31 This is to reflect the symmetrical binding of peptides on the inner and outer layers of the cytoplasmic membrane, as discussed in Section 3. Finally, we set Np = 0 as expected for model membranes. In reality, Np ≠ 0 at or beyond (P/L)*. But practically, it can be set to zero, since the majority of peptides would remain ‘free’; trapped peptides in model membranes are outnumbered by those in the bulk.
19–21 vp = 333 Å3, and Ap = 400 Å2.17,18 For this peptide, w was mapped out for model membranes, mimicking bacterial and host-cell membranes: wB = −16.6kBT and wH = −6.72kBT.18 Also, aB = 71 Å2 (al for bacterial membranes), aH = 74 Å2 (al for host-cell membranes),19–21 AB = 1.2 ×109 Å2 = 12 μm2 (suitable for E. coli), and AH = AB or AH = 17AB (as for human red blood cells).17 Note here that this value of AB is two times the surface area of E. coli (≈6 μm2).31 This is to reflect the symmetrical binding of peptides on the inner and outer layers of the cytoplasmic membrane, as discussed in Section 3. Finally, we set Np = 0 as expected for model membranes. In reality, Np ≠ 0 at or beyond (P/L)*. But practically, it can be set to zero, since the majority of peptides would remain ‘free’; trapped peptides in model membranes are outnumbered by those in the bulk.
We have solved eqn (3) for the noncompetitive case and eqn (4) for the competitive case (both together with eqn (12)). This is equivalent to solving eqn (5) for P/L at and found Cp at which P/L is equal to P/L*, as discussed below eqn (5). In Fig. 5, the resulting 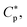 either MIC or MHC, as well as the ratio MHC/MIC are shown as a function of cell density: CB or CH. When CH (CB) is held fixed, the x axis represents CB (CH); for the case CH = CB, it indicates both CH and CB. If the competitive cases are represented by dashed lines with filled symbols, the noncompetitive ones are described by solid lines with open symbols.
either MIC or MHC, as well as the ratio MHC/MIC are shown as a function of cell density: CB or CH. When CH (CB) is held fixed, the x axis represents CB (CH); for the case CH = CB, it indicates both CH and CB. If the competitive cases are represented by dashed lines with filled symbols, the noncompetitive ones are described by solid lines with open symbols.
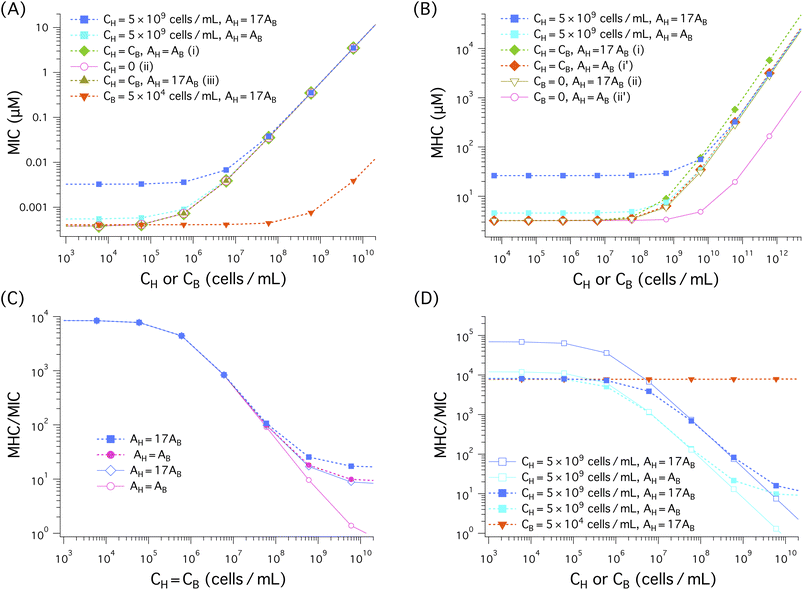 | ||
Fig. 5 Cell (membrane) density dependence of MIC, MHC, and MHC/MIC for the noncompetitive and competitive cases, represented by solid lines with unfilled symbols and dashed lines with filled symbols, respectively. When CH (CB) is held fixed, the ‘x’ axis represents CB (CH); for the case CH = CB, it stands for both CH and CB. We have chosen the parameter as follows: the bacterial cell surface area AB = 12 μm2 (suitable for E. coli); the host cell surface area AH = AB and AH = 200 μm2 ≈ 17 × AB (as for human red blood cells); aB = 71 Å2 and aH = 74 Å2; 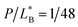 and and 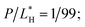 19–21 vp = 333 Å3 and Ap = 400 Å2;17,18 wB = −16.6 kBT and wH = −6.72 kBT18 as for the peptide melittin. (A)–(B) In all cases, both MICs and MHCs increase with increasing CH or CB, as expected from eqn (4a). Also, the presence of a large amount of hot-cell membranes (CH = 5 × 109 cells per mL) raises both the MIC and the MIC, almost by an order of magnitude for the case AH = 17AB as long as CH ≫ CB. There is no essential difference between the three cases labelled as (i), (ii), and (iii) in the legend in (A): the presence of an equal amount of host-cell membranes (CH = CB) or the value of AH does not influence the MIC in any noticeable way. As shown in (B), the MHC is larger for larger AH (i.e., AH = 17AB). For this, compare a curve obtained with AH = AB with the corresponding one obtained with AH = 17AB. Also, the MHC curve labelled as (i) lies somewhat above the one labelled as (ii), both obtained with AH = 17AB. In this case, the presence of an equal amount of bacterial membranes (CH = CB) increases slightly the MHC. When AH = AB represented as (i’) and (ii’), however, it has a more appreciable impact on the MHC. The competitive MHC in the presence of 5 × 104 cells per mL of bacterial membranes with AH = 17AB is almost identical to the corresponding noncompetitive one (i.e., CB = 0) (data not shown for simplicity). The selectivity in (C), as measured by MHC/MIC, decreases as the membrane density increases; in both competitive and noncompetitive cases, we chose CH = CB. The difference between the competitive and noncompetitive cases becomes obvious when the cell density is ≳ 108 cells per mL, in which the selectivity is higher for the former case. Also the selectivity is higher for the larger AH case as long as CB = CH ≳ 108 cells per mL. In (D), except for the red dashed curve with inverted filled triangles, CH = 5 × 109 cells per mL but CB varies. Similarly to what the graph in (C) suggests, the selectivity in (D) decreases as CB decreases. Compared to the competitive case represented by the blue dashed curve with filled squares, the corresponding noncompetitive case overestimates the selectivity by about one order of magnitude at a low CB range of CB ≲ 105 cells per mL. The red dashed line with inverted triangles obtained with CB = 5 × 104 cells per mL is nearly flat in the CH range shown. 19–21 vp = 333 Å3 and Ap = 400 Å2;17,18 wB = −16.6 kBT and wH = −6.72 kBT18 as for the peptide melittin. (A)–(B) In all cases, both MICs and MHCs increase with increasing CH or CB, as expected from eqn (4a). Also, the presence of a large amount of hot-cell membranes (CH = 5 × 109 cells per mL) raises both the MIC and the MIC, almost by an order of magnitude for the case AH = 17AB as long as CH ≫ CB. There is no essential difference between the three cases labelled as (i), (ii), and (iii) in the legend in (A): the presence of an equal amount of host-cell membranes (CH = CB) or the value of AH does not influence the MIC in any noticeable way. As shown in (B), the MHC is larger for larger AH (i.e., AH = 17AB). For this, compare a curve obtained with AH = AB with the corresponding one obtained with AH = 17AB. Also, the MHC curve labelled as (i) lies somewhat above the one labelled as (ii), both obtained with AH = 17AB. In this case, the presence of an equal amount of bacterial membranes (CH = CB) increases slightly the MHC. When AH = AB represented as (i’) and (ii’), however, it has a more appreciable impact on the MHC. The competitive MHC in the presence of 5 × 104 cells per mL of bacterial membranes with AH = 17AB is almost identical to the corresponding noncompetitive one (i.e., CB = 0) (data not shown for simplicity). The selectivity in (C), as measured by MHC/MIC, decreases as the membrane density increases; in both competitive and noncompetitive cases, we chose CH = CB. The difference between the competitive and noncompetitive cases becomes obvious when the cell density is ≳ 108 cells per mL, in which the selectivity is higher for the former case. Also the selectivity is higher for the larger AH case as long as CB = CH ≳ 108 cells per mL. In (D), except for the red dashed curve with inverted filled triangles, CH = 5 × 109 cells per mL but CB varies. Similarly to what the graph in (C) suggests, the selectivity in (D) decreases as CB decreases. Compared to the competitive case represented by the blue dashed curve with filled squares, the corresponding noncompetitive case overestimates the selectivity by about one order of magnitude at a low CB range of CB ≲ 105 cells per mL. The red dashed line with inverted triangles obtained with CB = 5 × 104 cells per mL is nearly flat in the CH range shown. | ||
The results in Fig. 5(A) and (B) suggest that both MICs and MHCs increase with increasing cell density (CH or CB), as expected from eqn (3) and (4). For AH = 17AB, the presence of a large amount of host-cell membranes (CH = 5 × 109 cells per mL) raises the MIC by an order of magnitude as long as CB ≲ 5 × 105 cells per mL, compared to the case CH = 0; for AH = AB, however, its impact on the MIC appears to be minor. There is no essential difference between the three cases in (A): (i) CH = CB, AH = AB, (ii) CH = 0, AH = AB, and (iii) CH = CB, AH = 17AB (labelled as (i), (ii), (iii), respectively, in the legend); in these cases, the MIC is insensitive to the presence of an equal amount of host-cell membranes or the value of AH. As CB increases, the MIC curves eventually collapse onto each other. In this case, it is dominated by the CB-dependent term in eqn (4a). This applies to all the curves shown except the one in tangerine for which CB is held fixed.
As shown Fig. 5(B), in the presence of a large amount of host-cell membranes (CH = 5 × 109 cells per mL), the MHC obtained with AH = 17AB is about ten times larger than MHC0 ≈ 3 μM (i.e., the y-intercept of the curve labelled as (ii) or (ii’)), as long as CB ≲ 108 cells per mL. Similarly, in the other cases shown, the MHC is larger for larger AH = 17AB than for AH = AB, as long as CH ≳ 108cells per mL. For this, compare a curve obtained with AH = AB with the corresponding one obtained with AH = 17AB (e.g., the curves labelled as (i) and (i′) or those labelled as (ii) and (ii′)). The difference between (i) and (i′) seems somewhat minor, but the difference between (ii) and (ii′) (in the absence of bacterial membranes) is pronounced. Also, the MHC curve labelled as (i) lies somewhat above the one labelled as (ii), both obtained with AH = 17AB. In this case, the presence of an equal amount of bacterial membranes (CH = CB) increases slightly the MHC. When AH = AB (see the curves labelled as (i′) and (ii′)), however, the presence of an equal amount of bacterial membranes has a more appreciable impact on the MHC. In other words, the presence of an equal amount of bacterial cells increases the MHC more effectively when AH = AB. This is consistent with eqn (3) or 4, which suggests that the MHC is more sensitive to CB if AH is smaller. The presence of 5 × 104 cells per mL of bacterial membranes (AH = 17AB) does not have any noticeable impact on the MHC (the data not shown for simplicity).
The MIC and MHC results in Fig. 5(A) and (B) suggest that the presence of an equal amount of bacterial membranes influences MHCs more effectively than the presence of an equal amount of host cell membranes influences MICs. For this, compare the two curves labeled as (i) CH = CB, AH = AB and (ii) CH = 0, AH = AB in (A) as well as those labelled as (i’) CH = CB, AH = AB and (ii′) CB = 0, AH = AB in (B). The two in (A) tend to collapse onto each other, whereas in (B) the curve obtained with CB = 0, AH = AB falls well below the other one. This difference can be attributed to the stronger binding of peptides to bacterial membranes.
In the competitive case with an excessive amount of host cells (CH = 5 × 109 cells per mL), however, the MIC in Fig. 5(A) and the MHC in Fig. 5(B) are much larger than in the other cases as long as CB ≪ CH. This is consistent with what eqn (4) suggests: the presence of a large amount of host cells increases both the MIC and the MHC (see the relevant discussion in Section 2.3). These equation also suggest that the MIC or the MHC is generally larger for AH = 17AB than for AH = AB, unless the AH-independent terms dominate. For this, compare the two curves in blue and cyan in (A) or (B), for instance. As discussed in Section 2, increasing AH is equivalent to increasing CH. This explains the observation of larger MIC and MHC values for larger AH.16,17
The ratio MHC/MIC measures peptide selectivity. Our results for this ratio are shown in Fig. 5(C) and (D). In (C), CB = CH; in (D), except for the red dashed line, CH = 5 × 109 cells per mL but CB is allowed to vary. In all cases, the selectivity decreases (or remains flat), as the cell density increases as discussed in Section 2. In (C), the difference between the competitive and noncompetitive cases for AH = AB becomes obvious when the cell density is ≳ 108 cells per mL, in which the selectivity is higher for the former case. This is correlated with the observation that the MHC is higher for the competitive case in this range of cell density as shown in Fig. 5(B). Also, the selectivity is higher for the larger AH case.
The competitive cases in (D), except for the red dashed line, contain a large amount of host cells (CH = 5 × 109 cells per mL) in addition to bacterial cells with variable CB. In the noncompetitive measurement, MHCs obtained with the choice CH = 5 × 109 cells per mL were combined with MICs. Similarly to what the graphs in (C) suggests, the selectivity in (D) decreases as CB increases. However, the selectivity in the noncompetitive case is overestimated compared to the corresponding competitive case, as long as CB ≲ 107 to 108 cells per mL ≪ CH. For the large AH case, it is overestimated by up to an order of magnitude. When CB is held fixed at CB = 5 × 104 cells per mL, the (competitive) selectivity remains roughly flat in the CH range shown.
This finding is well aligned with the view that the selectivity measured in a noncompetitive manner (with CH ≫ CB) can be an experimental illusion.11 This is not the case for the competitive selectivity. Even in the presence of a large amount of host cells, the selectivity measured in a competitive environment is not an experimental artifact. It just reflects the cell-density dependence of the selectivity, presented in Section 2.
4.2 Cell selectivity: inoculum effects
We have solved eqn (4) with realistic choices of Np and mapped out various scenarios for peptide activity and selectivity. One of the challenges in this effort is that the parameters in these equations are not well known for real cells. In particular, wB for Gram-negative bacteria is also influenced by the peptide interaction with their outer membrane (OM); recall that this is an effective parameter, in which microscopic details (e.g., peptide charge, peptide interaction with the OM) are subsumed (see Section 3). This quantity has only recently been mapped out theoretically for the interaction of melittin-like peptides with model membranes.18 For the reasons explained in Section 2, however, the dependence of peptide activity on wB is reflected mainly through MIC0. Furthermore, the MIC and the MHC in the homogeneous case in eqn (3) do not depend sensitively on wB or wH for given MIC0 and MHC0.Here we do not attempt to calculate the effective binding energy w (either wB or wH) for real cells and use it in the computation of MIC0 and MHC0. Instead, we start with conveniently-chosen but biophysically-relevant values of MIC0 and MHC0: MIC0 = 1 μm and MHC0 = 5 μm (see ref. 14 and 15, for instance, for MIC0). For simplicity, the number of trapped peptides Np is chosen to be the same for bacteria and host cells: Np = 0, 107, 5 × 107. Otherwise, we choose the same parameters used in Fig. 5: the bacterial cell surface area AB = 12 μm2 (suitable for E. coli); the host cell surface area AH = 200 μm2 ≈ 17 × AB (as for human red blood cells); aH = 71 Å2 and aH = 74 Å2; wB = −16.6 kBT and wH = −6.72 kBT;18 vp = 333 Å3 and Ap = 400 Å2.17,18
Fig. 6 displays the results for the MIC (A) and the MHC (B) for the noncompetitive and competitive cases, represented by solid lines with unfilled symbols or unfilled symbols and dashed lines with filled symbols, respectively. As in Fig. 5, when CH (CB) is held fixed, the ‘x’ axis represents CB (CH); for the case CH = CB, it stands for both CH and CB.
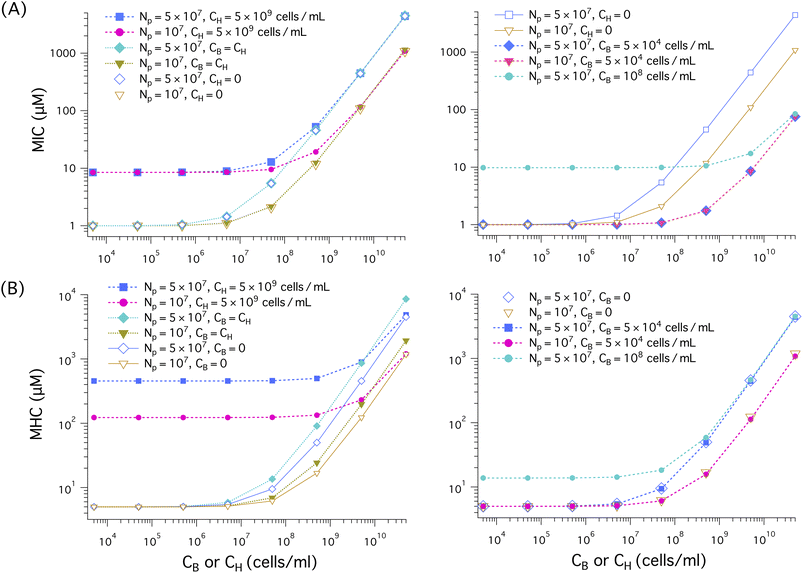 | ||
| Fig. 6 Cell-density dependence of MIC (A) and MHC (B) for the noncompetitive and competitive cases, represented by solid lines with unfilled symbols (or unfilled symbols) and dashed lines with filled symbols, respectively. When CH (CB) is held fixed, the ‘x’ axis represents CB (CH); for the case CH = CB, it indicates both CH and CB (as indicated in the legends of (A), (B), and (C)). We have chosen the parameters as follows: MIC0 = 1 μm and MHC0 = 5 μm; wB = −16.6 kBT and wH = −6.72 kBT, as for a melittin-like peptide; the bacterial cell surface area AB = 12 μm2 (suitable for E. coli); the host cell surface area AH = 200 μm2 ≈ 17 × AB (as for human red blood cells); the lipid headgroup area aB = 71 Å2 and aH = 74 Å2; vp = 333 Å3 and Ap = 400 Å2. In all cases shown in (A) and (B), both the MIC and MHC increase with increasing cell density (CH or CB), as expected from eqn 4(a) and (b). (A) (Left) The presence of a large amount of host cells as in whole blood increases the MIC up to ten-fold, as long as CB ≲ 5 × 108 cells per mL; for this, compare the curve obtained with CH = 5 × 109 cells per mL with the corresponding one obtained with CH = 0. Also the MIC increases more rapidly, if Np is larger. The MIC remains ≲ 10 μm if CB ≲ 5 × 107 cells per mL. If CB ≳ 5 × 108 cells per mL, the presence of host cells does not have a significant impact on the MIC; in this case, peptide trapping in bacterial cells is a determining factor. For the same value of Np, different curves representing different values of CH collapse onto each other for sufficiently large CB: CB ≳ 5 × 108 cells per mL. There is no noticeable difference between the two cases: CB = CH and CH = 0 for given Np. In this case, the main source of inoculum effects is the trapping of peptides in bacterial cells. (A) (right) When CB is held fixed at CB = 5 × 104 cells per mL, the MIC is insensitive to the value of Np used, as if bacterial cells are in the low-cell density limit (i.e., their presence creates a minimal inoculum effect). At the MIC, host cells are below the MHC. As a result, the binding of peptides to the host-cell membrane is responsible for the slow increase of the MIC with CH. The presence of a large amount of bacterial cells (CB = 108 cells per mL) increases the MIC about ten-fold as long as CH ≲ 108 cells per mL (the two homogenous MIC curves from the graph in the left are also included for comparison purposes.) (B) (left) In all cases, the MHC increases with increasing cell densities: either CB or CH. When CH = 5 × 109 cells per mL, the MHC is large and remains roughly flat as CB increases up to CB = 109 cells per mL. It is obviously larger for the larger Np case (squares or diamonds); it can be two orders of magnitude larger than MHC0. Also the MHC is larger for the competitive case CB = CH compared to the corresponding noncompetitive case CB = 0: at the MHC, the bacterial cells are above the MIC and the resulting peptide trapping in the bacterial cells raises the MHC. (B) (right) The presence of a small concentration of bacteria (i.e., CB = 5 × 104 cells per mL) does not alter the MHC in any significant way. Also the MHC increases faster with CH for larger Np, as expected from eqn (4b). In the presence of a large amount of bacterial cells (CB = 108 cells per mL), the MHC is about three times as large as in the corresponding host-cell only case, as long as CH ≲ 107 cells per mL. | ||
In all cases shown in Fig. 6(A) and (B), both MICs and MHCs increase linearly with increasing cell density (CH or CB), similarly to what is shown for model membranes in Fig. 5. This is a natural consequence of the cell-density dependence shown in eqn (4).
As indicated in the graph on the left in Fig. 6(A), the presence of an excess amount of host cells raises the MIC, more so for larger Np as long as CB ≲ 5 × 108 cells per mL; for this, compare the curve obtained with CH = 5 × 109 cells per mL with the one obtained with CH = 0. Nevertheless, the MIC remains somewhat smaller than 10 μm if CB ≲ 5 × 107 cells per mL. When CB ≳ 5 × 108 cells per mL, the presence of host cells does not have a significant impact on the MIC; in this case, peptide trapping in bacterial cells is a determining factor. For the same value of Np, different curves representing different values of CH collapse onto each other for sufficiently large CB: CB ≳ 5 × 108 cells per mL. Also, the MIC obtained with Np = 5 × 107 increases more rapidly with cell density than the corresponding one obtained with Np = 107 does, as suggested by eqn (4). Finally, for given Np, there is no noticeable difference between the two cases: CB = CH (competitive) and CH = 0 (bacterial-cell only). The presence of an equal amount of host cells has an insignificant impact on the MIC. At the MIC, the host cells are above the MHC (no trapping in the cells) and their effect on the MIC is expected to be minor (see Section 2.2. for the relative significance of membrane association of peptides versus peptide trapping in cells).
As shown in the graph on the right in Fig. 6, when CB is held fixed at CB = 5 × 104 cells per mL, the MIC is insensitive to the value of Np used, as if bacterial cells are in the low-cell density limit (i.e., their presence creates a minimal inoculum effect). At the MIC, the host cells, which are present together with bacterial cells, are below the MHC. As a result, the binding of peptides to the host-cell membrane is responsible for the slow increase of the MIC with CH. The presence of a large amount of bacterial cells (CB = 108 cells per mL) increases the MIC about ten-fold as long as CH ≲ 108 cells per mL (the two homogenous MIC curves from the graph in the left are also included for comparison purposes).
Fig. 6(B) shows how the MHC varies as a function of cell density: CB or CH. In all cases, the MHC increases with increasing cell density. When CH = 5 × 109 cells per mL, the MHC is large and remains roughly flat as CB increases up to CB = 109 cells per mL. This is consistent with eqn (4b), which suggests that the MHC is roughly independent of CB, as long as CH is sufficiently larger than CB. The MHC is obviously larger for the larger Np case (squares or diamonds). Finally, the MHC is somewhat larger in the presence of an equal amount of host cells (CB = CH) compared to the host-cell only case CB = 0. Peptide trapping in the bacterial cells is responsible for this.
As shown in the graph on the right in Fig. 6, the presence of a small concentration of bacteria (i.e., CB = 5 × 104 cells per mL) does not alter the MHC in any significant way. For this, compare open diamonds and filled squares or between open inverted triangles and filled circles. Similarly to the other cases shown on the left in Fig. 6(B), the MHC increases faster with CH for larger Np, as expected from eqn (4b). The presence of a large amount of bacterial cells (CB = 108 cells per mL) increases the MHC about three-fold from the corresponding host-cell only case, long as CH ≲ 107 cells per mL. For this, compare the dashed curve with filled circles in cyan with open diamonds in blue.
Fig. 7 shows the results for MHC/MIC. The dashed lines with filled symbols represent competitive selectivity, whereas the solid lines with unfilled symbols describe noncompetitive selectivity; in the latter case, MHCs and MICs, obtained for host-cell only and bacteria-only solutions, respectively, are combined into MHC/MIC.
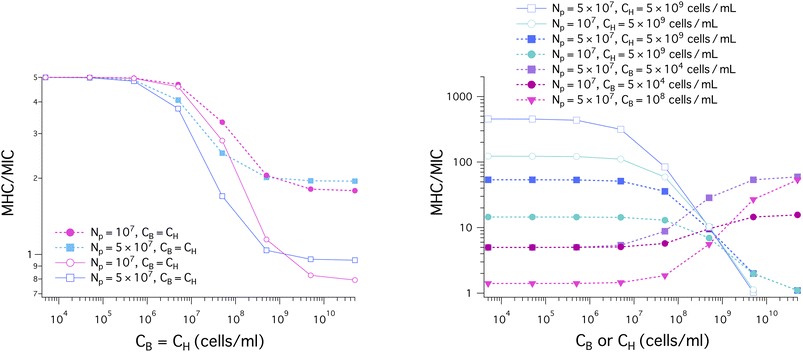 | ||
| Fig. 7 Cell-density dependence of MHC/MIC for the noncompetitive and competitive cases, represented by solid lines with unfilled symbols and dashed lines with filled symbols, respectively. In the graph on the left, CH = CB; in the graph on the right, the ‘x’ axis represents CB (CH), when CH (CB) is held fixed. We have chosen the same parameters as in Fig. 6: MIC0 = 1 μm and MHC0 = 5 μm; wB = −16.6 kBT and wH = −6.72 kBT as for melittin; the bacterial cell surface area AB = 12 μm2 (suitable for E. coli); the host cell surface area AH = 200 μm2 ≈ 17 × AB (as for human red blood cells); aB = 71 Å2 and aH = 74 Å2; vp = 333 Å3 and Ap = 400 Å2. (left) In all cases shown, CH = CB. The selectivity, MHC/MIC, decreases as the cell density increases. It is larger for the competitive case (filled symbols), more so for larger CH = CB. For CH = CB ≲ 109 cells per mL, the selectivity is somewhat larger when Np is smaller; in this case, peptide trapping works in bacteria's favor by increasing the MIC. (right) The selectivity obtained with CH = 5 × 109 cells per mL decreases with increasing CB, more rapidly for larger Np. In this case, peptide trapping enhances the selectivity as long as CB ≲ 5 × 109 cells per mL (competitive) or CB ≲ 5 × 108 cells per mL (noncompetitive) but does not seem to have a noticeable impact outside this range. In contrast, it increases with CH, more rapidly for larger Np, when CB is held fixed at CB = 5 × 104 cells per mL or CB = 108 cells per mL. The selectivity is smaller for the latter choice of CB. With the parameter choices used, the noncompetitive selectivity can be an order of magnitude larger than the corresponding competitive one; depending on how the selectivity is measured, it can be two or three order of magnitude different; for this, compare the blue solid line with open squares with the magenta dashed curve with inverted filled triangles. | ||
In the graph on the left in Fig. 7, we have chosen CH = CB. In all cases shown in the graph, the selectivity, MHC/MIC, decreases from the initial value MHC0/MIC0 as the cell density increases. It is larger for the competitive case (filled symbols) than for the corresponding noncompetitive case so that the difference between the two cases is more pronounced for larger CH = CB. For CH = CB ≲ 109 cells per mL, the selectivity is somewhat larger when Np is smaller; in this case, peptide trapping works in bacteria's favor by increasing the MIC.
As shown in the graph on the right in Fig. 7, the selectivity obtained with CH = 5 × 109 cells per mL decreases with increasing CB, more rapidly when Np is larger. In this case, peptide trapping enhances the selectivity for CB ≲ 5 × 109 cells per mL (competitive) or CB ≲ 5 × 108 cells per mL (noncompetitive) but does not seem to have a noticeable impact outside this range, as it approaches MHC0/MIC0. In contrast, it increases with CH, more so for larger Np, when CB is held fixed at CB = 5 × 104 cells per mL or CB = 5 × 108 cells per mL. The selectivity is smaller for the latter choice of CB. The presence of host cells in the competitive case works in favor of the host cells by enhancing the selectivity, more effectively for larger Np.
The results in Fig. 7 show how the selectivity can be overestimated. With the parameter choices used, the noncompetitive selectivity can be an order of magnitude larger than the corresponding competitive one. Furthermore, depending on how the selectivity is measured, it can be two or three order of magnitude different; for this, compare the solid line with unfilled squares in blue (noncompetitive) and the dashed line with filled squares in purple (competitive).
The picture offered by the graph on the right in Fig. 7 is not only consistent with the earlier observation that the selectivity can be excessively overestimated11 (see ref. 16 for a theoretical basis) but also clarifies further how peptide selectivity is influenced by various factors or even the way it is measured: competitive, noncompetitive, the presence of host cells, peptide trapping in dead cells.
4.3 Membrane versus cell selectivity
There are both similarities and differences between membrane selectivity (Fig. 5) and cell selectivity (Fig. 7) of antimicrobial peptides. In both cases, the membrane-density or cell-density dependence of the selectivity is well manifested. If we set CH = CB, both membrane and cell selectivity decrease with CH = CB. In the presence of 5 × 109 cells per mL of host cells or neutral membranes (mimicking host cell membranes) as in whole blood, the selectivity decreases as CB increases. In both cases, the selectivity tends to be overestimated in a noncompetitive environment with reference to the corresponding competitive case; when AH = AB, however, the difference between competitive and noncompetitive selectivity against model membranes appears to be minor, especially when CB ≲ 109 cells per mL (Fig. 5). When CB is held fixed at CB = 5 × 104 cells per mL, the membrane selectivity remains nearly flat as a function of CH, whereas the cell selectivity increases up to about 10 folds for Np = 5 × 107; if Np = 0, the selectivity would remain nearly flat (the data not shown).It is worth noting that the MICs for bacterial membranes in Fig. 5 are much smaller than those for bacterial cells in Fig. 6. In contrast, the MHCs in the two figures are comparable. In the case of E. coli, the outer membrane enclosing the cell tends to raise MIC0. In addition, peptide trapping in dead cells is also responsible for the differences between membranes and cells. Nevertheless, the qualitative picture offered from membranes (Fig. 5) is generally consistent with the one obtained for cells.
5. Discussions and conclusions
We have presented a biophysical model of peptide activity and selectivity by combining a pedagogical approach with a Langmuir-type model. If the former captures the cell-density dependence of peptide activity and selectivity in an intuitively-obvious way, the latter relates peptide binding (or trapping) to an effective binding (or trapping) energy.Using the model, we have clarified how the presence of host cells and peptide trapping influence peptide selectivity and how competitive selectivity differs from noncompetitive selectivity. If the competitive selectivity represents a mixture of bacteria and host cells, the noncompetitive one is obtained by combining MICs and MHCs for bacterium-only and host-cell-only solutions, respectively. In this work, we chose parameters relevant for the peptide melittin (see refs. 19–21 and relevant references therein).
The results based on the model suggest a rather nontrivial dependence of the selectivity on the presence of host cells, cell density, and peptide trapping; these factors or effects can enhance or reduce the selectivity depending on how the density of host cells and that of bacterial cells are chosen. When CB = CH, the selectivity is somewhat smaller for larger Np, unless CB = CH is sufficiently large (left graph in Fig. 7). In more general cases (right graph in Fig. 7), however, peptide trapping tends to enhance the selectivity; also the presence of host cells works in favor of the host cells, but it raises the MIC up to about 10-fold (Fig. 6(A)).
When CB = CH, the selectivity decreases from the initial value MHC0/MIC0, with increasing CB = CH, more rapidly for the noncompetitive case; the selectivity is higher for the competitive case and is not sensitive to the choice of Np. In the presence of a large amount of host cells (CH = 5 × 109 cells per mL), the selectivity decreases with increasing CB in both competitive and noncompetitive cases. The noncompetitive selectivity can be one-order of magnitude larger than the corresponding competitive one. When CB is held fixed at CB = 5 × 104 cells per mL or at CB = 108 cells per mL, the competitive selectivity increases with CH; the selectivity is smaller for the latter choice of CB. Depending on how cell density is chosen, the selectivity can be overly overestimated – almost by three orders of magnitude.
Our work also clarifies how the cell selectivity of AMPs differs from their membrane selectivity. The selectivity based on model membranes is typically larger than the one measured for cells. In both cases (membranes and cells), noncompetitive selectivity is typically larger than the corresponding competitive one, except for the case CB = CH.
The results in this work suggest that the selectivity reflects not only peptide-membrane parameters but also cell density, peptide trapping, and even the way the selectivity is measured (competitive vs. noncompetitive). This is a natural consequence of MICs and MHCs that vary with cell density and Np. Mapping out possible scenarios of peptide activity and selectivity thus would involve exploring wide ranges of CB and CH, which are not easily realized in experiments.
If the involved peptide-membrane parameters are characterized, our model described by eqn (4) can be used as a predictive model. It enables one to calculate MICs, MHCs, and MHC/MIC, as a function of cell density: CB or CH, the density of bacterial and host cells, respectively.
Alternatively, eqn (3) can be used as a fitting model for analyzing MIC and MHC data obtained in a noncompetitive manner: the ‘y’-intercept and the ‘slope’ can be extracted by fitting MIC or MHC data to eqn (3a) or (3b), respectively. This enables one to determine MIC0 or MHC0. Eqn (12) shows how these quantities are related to peptide's binding energy w (wB or wH) and 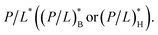 It is worth noting that P/L* has been measured for various model membranes19–21 as well as for cells.10 Once P/L* is known, MIC0 and MHC0 can be converted into wB and wH, respectively. Conversely, if w is known, P/L* can be estimated. If all this information is used in the ‘slope,’ the value of Np can be extracted.
It is worth noting that P/L* has been measured for various model membranes19–21 as well as for cells.10 Once P/L* is known, MIC0 and MHC0 can be converted into wB and wH, respectively. Conversely, if w is known, P/L* can be estimated. If all this information is used in the ‘slope,’ the value of Np can be extracted.
The information from the homogeneous analysis above can be used in eqn (4), which represents a competitive case. Accordingly, one can quantify peptide selectivity for a biologically relevant setting, which reflects the degree and location of infection. For instance, CB ranges from 1 colony-forming unit (CFU mL−1) (in blood stream, where CH ≈ 5 × 109 cells per mL) to 109 CFU mL−1 (in soft tissue or peritonea) (see a recent review12 and relevant references therein).
To advance our model and to take fuller advantage of its predictive power, computational and experimental methods can be employed to evaluate further the respective roles of host cells, cell density, and peptide trapping in the selectivity of AMPs (see Fig. 6). Because of their complexity, peptide-cell systems are not so amenable to microscopic computational modeling based on molecular dynamics simulations.32 A concerted effort between theoretical modeling, computational approaches, and experiments would be desired. Along the line of what was done in recent studies,14 in which a number of key parameters including Np were extracted, parameters for multi-species cultures can be mapped out and used in eqn (4) or its variation.
In this work and in a typical experimental setting, the total number of AMPs is treated as a constant. In reality, however, it is influenced by the expression of AMPs by the host14 and peptide degradation by protease.12,22 Furthermore, earlier studies highlight the stochastic nature of eliminating bacteria with AMPs and its impact on the survivability of a population.14 It was shown that below the MIC, two sub-populations emerged: one group that stopped dividing and another group that could grow unharmed and divide. To clarify the roles of these population fluctuations, stochastic modeling of population dynamics can be employed.33,34
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by NSERC (Canada) (B-YH) and NIH (R15GM124640) (ST-A).References
- M. Zasloff, Antimicrobial peptides of multicellular organisms, Nature, 2002, 415, 389–395 CrossRef CAS PubMed.
- K. A. Brogden, Antimicrobial peptides: pore formers or metabolic inhibitors in bacteria?, Nat. Rev. Microbiol., 2005, 3, 238–250 CrossRef CAS PubMed.
- R. M. Epand and R. F. Epand, Biophysical analysis of membrane-targeting antimicrobial peptides: membrane properties and the design of peptides specifically targeting Gram-negative bacteria, in Antimicrobial Peptides Discovery, Design and Novel Therapeutic Strategies, ed. G. Wang, Cabi, 2010 Search PubMed.
- N. Mookherjee, M. A. Anderson, H. P. Haagsman and D. J. Davidson, Antimicrobial host defence peptides: functions and clinical potential, Nat. Rev. Drug Discovery, 2020, 19, 311–332 CrossRef CAS PubMed.
- R. E. W. Hancock and H.-G. Sahl, Antimicrobial and host-defense peptides as new anti-infective therapeutic strategies, Nat. Biotechnol., 2006, 24, 1551–1557 CrossRef CAS PubMed.
- K. Matsuzaki, Why and how are peptide-lipid interactions utilized for self-defense? Magainins and tachyplesins as archetypes, Biochim. Biophys. Acta, 1999, 1462, 1–10 CrossRef CAS PubMed.
- R. E. Hancock, E. F. Haney and E. E. Gill, The immunology of host defence peptides: beyond antimicrobial activity, Nat. Rev. Immunol., 2016, 16, 321–334 CrossRef CAS PubMed.
- G. G. Perron, M. Zasloff and G. Bell, Experimental evolution of resistance to an antimicrobial peptide, Proc. Biol. Sci., 2006, 273, 251–256 CAS.
- A. Peschel and H. G. Sahl, The co-evolution of host cationic antimicrobial peptides and microbial resistance, Nat. Rev. Microbiol., 2006, 4, 529–536 CrossRef CAS PubMed.
- M. N. Melo, R. Ferre and M. A. R. B. Castanho, Antimicrobial peptides: linking partition, activity and high membrane-bound concentrations, Nat. Rev. Microbiol., 2009, 7, 245–250 CrossRef CAS PubMed.
- K. Matsuzaki, Control of cell selectivity of antimicrobial peptides, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 1687–1692 CrossRef CAS PubMed.
- F. Savini, S. Bobone, D. Roversi, M. L. Mangoni and L. Stella, From liposomes to cells: filling the gap between physicochemical and microbiological studies of the activity and selectivity of host-defense peptides, Peptide Sci., 2018, 110, e24041 CrossRef.
- F. Savini, V. Luca, A. Bocedi, R. Massoud, Y. Park, M. L. Mangoni and L. Stella, Cell-density dependence of host-defense peptide activity and selectivity in the presence of host cells, ACS Chem. Biol., 2017, 12, 52–56 CrossRef CAS PubMed.
- M. Snoussi, J. P. Talledo, N.-A. D. Rosario, S. Mohammadi, B.-Y. Ha, A. Košmrlj and S. Taheri-Araghi, Heterogeneous absorption of antimicrobial peptide LL37 in Escherichia coli cells enhances population survivability, eLife, 2018, 7, e38174 CrossRef PubMed.
- M. R. Loffredo, F. Savini, S. Bobone, B. Casciaro, H. Franzyk, M. L. Mangoni and L. Stella, Inoculum effect of antimicrobial peptides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2014364118 CrossRef CAS PubMed.
- B. R. Schefter, S. Nourbakhsh, S. Taheri-Araghi and B.-Y. Ha, Modeling cell selectivity of antimicrobial peptides: how is the selectivity influenced by intracellular peptide uptake and cell density, Front. Med. Technol., 2021, 22, 626481 CrossRef PubMed.
- A. Bagheri, S. Taheri-Araghi and B.-Y. Ha, How cell concentrations are implicated in cell selectivity of antimicrobial peptides, Langmuir, 2015, 31, 8052–8062 CrossRef CAS PubMed.
- S. Nourbakhsh, S. Taheri-Araghi and B.-Y. Ha, Toward building a physical model for membrane selectivity of antimicrobial peptides: making a quantitative sense of the selectivity, Soft Matter, 2019, 15, 7509–7526 RSC.
- H. W. Huang, Molecular mechanism of antimicrobial peptides: the origin of cooperativity, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 1292–1302 CrossRef CAS PubMed.
- M. Lee, W. Hung, F. Chen and H. W. Huang, Many-Body effect of antimicrobial peptides: on the correlation between Lipid's spontaneous curvature and pore formation, Biophys. J., 2005, 89, 4006–4016 CrossRef CAS PubMed.
- M.-T. Lee, F.-Y. Chen and H. W. Huang, Energetics of pore formation induced by membrane active peptides, Biochemistry, 2004, 43, 3590–3599 CrossRef CAS PubMed.
- C. G. Starr, J. He and W. C. Wimley, Host cell interactions are a significant barrier to the clinical utility of peptide antibiotics, ACS Chem. Biol., 2016, 11, 3391–3399 CrossRef CAS PubMed.
- S. M. Gregory, A. Cavenaugh, W. Journigan, A. Pokorny and P. F. F. Almeida, A quantitative model for the all-or-none permeabilization of phospholipid vesicles by the antimicrobial peptide cecropin A, Biophys. J., 2008, 94, 1667–1680 CrossRef CAS PubMed.
- When the peptide concentration is low, the propensity for them to remain unbound is high because of the substantial entropic penalty for binding. Entropy is a measure of the number of microscopic arrangements subject to a macroscopic constraint (e.g., total energy,…). In the context of our model in this work, in the low peptide concentration limit, the multitude of possible unbound states for the peptides results in a much larger entropy, contrasted with the smaller number of bound states. The entropy of peptides favors unbound states. This argument is most obvious in light of Eqs. 8 and 9, as is particularly the case for Ccell = 0. When Ccell = 0, these equations suggest that the entropic free energy cost for peptide binging per peptide, denoted as ΔFent, is given by
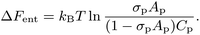 The smaller Cp is, the larger the entropic penalty is..
The smaller Cp is, the larger the entropic penalty is.. - K. Dill and S. Bromberg, Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience, Garland Science, 2nd edn, 2010 Search PubMed.
- L. Ding, L. Yang, T. M. Weiss, A. J. Waring, R. I. Lehrer and H. W. Huang, Interaction of antimicrobial peptides with lipopolysaccharides, Biochemistry, 2003, 42, 12251–12259 CrossRef CAS PubMed.
- K. Matsuzaki, O. Murase, N. Fujii and K. Miyajima, An antimicrobial peptide, magainin 2, induced rapid flip-flop of phospholipids coupled with pore formation and peptide translocation, Biochemistry, 1995, 34, 6521–6526 CrossRef CAS PubMed.
- M.-T. Lee, W.-C. Hung, F.-Y. Chen and H. W. Huang, Mechanism and kinetics of pore formation in membranes by water-soluble amphipathic peptides, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5087 CrossRef CAS PubMed.
- S. B. Zimmerman and A. P. Minton, Macromolecular crowding: biochemical, biophysical, and physiological consequences, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 27–65 CrossRef CAS PubMed.
- H.-X. Zhou, G. Rivas and A. P. Minton, Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences, Annu. Rev. Biophys., 2008, 37, 375–397 CrossRef CAS PubMed.
- See for instance R. Philips, J. Kondev, J. Theriot and H. G. Garcia, Physical Biology of the Cell, Garland Science, 2nd edn, 2013, ch. 2 Search PubMed.
- E. Luna, S. Kim, Y. Gao, G. Widmalm and W. Im, Influences of vibrio cholerae lipid a types on LPS bilayer properties, J. Phys. Chem. B, 2021, 125, 2105–2112 CrossRef CAS PubMed.
- J. Coates, B. R. Park, D. Le, E. Şimşek, W. Chaudhry and M. Kim, Antibiotic-induced population fluctuations and stochastic clearance of bacteria, eLife, 2018, 7, e32976 CrossRef PubMed.
- R. Erban, J. Chapman and P. Maini, A practical guide to stochastic simulations of reaction-diffusion processes, arXiv, 2007, preprint, arXiv:0704.1908, DOI:10.48550/arXiv.0704.1908.
Footnote |
| † Current address: Biophysics Program and Institute for Physical Science and Technology, University of Maryland, College Park 20742, USA |
| This journal is © The Royal Society of Chemistry 2023 |