 Open Access Article
Open Access ArticleNonlinear dielectric response of dilute protein solutions
Dmitry V. Matyushov *
*
School of Molecular Sciences, Department of Physics, Arizona State University, PO Box 871504, Tempe, Arizona 85287-1504, USA. E-mail: dmitrym@asu.edu
First published on 24th October 2023
Abstract
A theory for the nonlinear dielectric response of dilute protein solutions is presented. The field-dependent dielectric function of the protein solution changes linearly with the electric field squared in the lowest order. The slope of this dependence is expressed in terms of the protein dipole moment M0, its volume fraction in solution η0, and the second osmotic virial coefficient. For practical conditions, the nonlinear dielectric response scales as η03M08. This strong dependence on the protein dipole moment and concentration establishes a sharp contrast between the nonlinear response of solvated proteins relative to the surrounding polar solvent. Nonlinear dielectric response can serve as a sensitive tool for monitoring protein conformations and physiological activity.
1 Introduction
Consider a particle carrying the dipole moment M0 immersed in a polar liquid with the dielectric constant εs (subscript “0” stands for solute properties). When an external (Maxwell1) field E is applied to the solution along the laboratory axis z, the dipole moment orients along the field to allow an average dipole projection on the field 〈M0z〉E, where 〈…〉E specifies a statistical ensemble average in the presence of the field. The Maxwell field E = ϕ/d, given as the ratio of the voltage ϕ at a plane capacitor to the distance d between the plates, is related to the vacuum field of external charges Evac trough the static dielectric constant of the solution εsol as Evac = εsolE ≃ εsE.If the response of the dipole is linear in the applied field, the standard perturbation theory yields the following result2–4
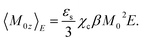 | (1) |
Proteins typically carry large dipole moments of the order of several hundreds of Debye units due to asymmetric distributions of charged residues exposed to water and charges of the N- and C-termini.6–8 The value of the cavity-field susceptibility was estimated as χc ≃ 1.1–1.2 for proteins.9,10 With these numbers, one arrives at
| 〈M0z〉E/M0 ≃ 0.23E (kV−1 cm−1), | (2) |
Measuring NDE in bulk polar liquids requires much stronger electric fields, ∼100 kV cm−1.11 The gap in field magnitudes between bulk liquids and protein solutions suggests that NDE can be used to probe the protein component separately from a much weaker nonlinear response of the surrounding solvent. Given that the dipole moment is sensitive to protein's conformations and physiological activity,12–16 NDE can potentially monitor alterations in the protein structure, phosphorylation, and redox reactions. Despite some preliminary reports on cells17,18 and membrane-bound proteins,19 NDE of proteins in solution has not been measured and the formalism proposed here remains a theoretical prediction at this moment.
The NDE is quantified by the dielectric function of the solution εsol(E) depending on the applied electric field, in contrast to the linear dielectric constant (a material property) εsol independent of the field. The difference εsol(E) − εsol is linear in E2 in the lowest order. The proportionality constant a is the Piekara coefficient11,20–22
| Δε(E) = εsol(E) − εsol = aE2. | (3) |
The theory presented here calculates a for low-concentration protein solutions when interaction between individual protein molecules are sufficiently weak to be viewed as perturbations (see below). It shows that Δε(E) changes its scaling from ∝cpM04 at low concentrations to ∝cp3M08 at larger protein concentrations cp (in g L−1). The slope of the dielectric constant vs. cp at cp → 0 provides access to the ratio, M04/Mp, of the fourth power of the protein dipole moment M0 and the protein molar mass Mp.
A strong dependence of the protein NDE on the protein dipole moment provides high contrast of solvated proteins relative to a much weaker background signal from the solvent. Linear dielectric spectroscopy of solutions also allows6 access to M02 from the slope of the solution dielectric increment εsol − εs vs. the protein concentration (Oncley's formula23). A much stronger scaling Δε(E) ∝ cp3M08 compared to εsol − εs ∝ cpM02 grants a much higher sensitivity of the NDE to the presence of proteins in solution compared to linear dielectric spectra.
2 Model
A general formulation of the problem of nonlinear dielectric polarization24 represents the Piekara coefficient in eqn (3) in terms of the parameter describing non-Gaussian fluctuations of the dipole moment projection M0z
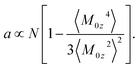 | (4) |
The term in the brackets in eqn (4) describes non-Gaussian statistics of the dipole moment projection. It vanishes for a macroscopic sample with a large number of dipoles N as stipulated by the central limit theorem. This is avoided by multiplying the bracket term with N thus resulting in a finite value of the Piekara coefficient a.
Non-Gaussian statistics of the dipole moment can arise from both internal protein motions, such as conformational transitions, and from correlated rotations of the protein dipoles in solution. The present formulation considers only the latter mechanism, leaving the possibility of intrinsic conformations and field-induced opening of membrane-bound protein pumps18,25,26 as a source of non-Gaussian statistics to future studies. Nevertheless, conformational transitions altering the protein dipole moment should project to an altering NDE.
Assuming that proteins behave as rigid dipoles, the fourth-order statistical central moment in eqn (4) introduces dipolar correlations of up to the fourth order. Some of these correlations decouple, allowing one to cast the Piekara coefficient in terms of the second, third, and fourth-order correlations of the protein dipoles24,27
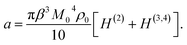 | (5) |
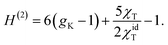 | (6) |
In this equation, gK is the Kirkwood factor of protein dipoles describing short-ranged binary orientational correlations and defined by the following expression
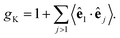 | (7) |
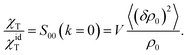 | (8) |
When the density of dipoles is low, the Kirkwood factor gK in eqn (6) can be calculated as a series expansion in the dimensionless density of protein dipoles2,3 commonly appearing in dielectric theories
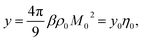 | (9) |
The lowest-order perturbation expansion of gK in terms of y0η0 reads33
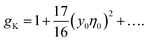 | (10) |
From eqn (9) and (10), one obtains for the Piekara coefficient
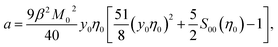 | (11) |
The ideal-gas limit for S00(η0) is the Poisson fluctuations of the protein density leading to S00 = 1 at η0 → 0 in eqn (8). This limit does not, however, apply to charged proteins in electrolyte solutions: the ideal-gas limit is not reached even when there are no interactions between the protein molecules.34 The reason is that electroneutrality condition imposes a constrain on the protein density fluctuations, which become coupled to corresponding density fluctuations of the electrolyte. Following Stockmayer34 and Asthagiri et al.35 one can calculate S00 from the derivative of the protein density over the protein chemical potential μ0
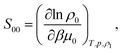 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte (e.g., NaCl), one can write the equations for the chemical potentials of the protein and electrolyte ions, which are coupled to each other through the electroneutrality condition. Finding the derivative in eqn (12) becomes a matrix inversion problem.34 Assuming ideal electrolyte on non-interacting ions, one arrives at
1 electrolyte (e.g., NaCl), one can write the equations for the chemical potentials of the protein and electrolyte ions, which are coupled to each other through the electroneutrality condition. Finding the derivative in eqn (12) becomes a matrix inversion problem.34 Assuming ideal electrolyte on non-interacting ions, one arrives at
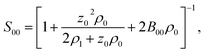 | (13) |
| S00 = [1 + 2B0η0]−1, | (14) |
| B0 = 4B00/BHS00 + z02/(ρ1BHS00). | (15) |
One finally arrives at the following equation for the Piekara coefficient
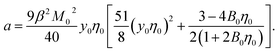 | (16) |
3 Discussion and model calculations
A positive NDE (a > 0) is found here for a dilute protein solution. In contrast, the NDE is typically negative (a < 0) for bulk polar liquids, thus leading to a dielectric decrement in the applied field.11 While a negative NDE is often related to dielectric saturation through the Langevin equation,2 an exact theoretical formalism27 leading to eqn (5) assigns negative NDE to multi-dipolar correlations responsible for a negative H(3,4) in eqn (5), which exceeds in magnitude the typically positive binary term H(2). The binary term can in principle be negative for a sufficiently large positive second virial osmotic coefficient (B0 in eqn (16)), which can lead to rather complex concentration dependencies for the NDE of binary mixtures of polar and nonpolar liquids.22For typically large protein dipole moments, the polar term, 6 (gK − 1), dominates in eqn (5) and (6) thus leading to a positive NDE. This result is generally consistent with an increment of dielectric constant of protein solutions over that of the solvent,6 also arising from a large protein dipole moment. The strong polarity of proteins in solution is allowed by reorientations of the protein dipole to align along the applied field. When the protein is immobilized, its internal dielectric constant is low,41 εp ≃ 4, because the internal dipoles are restricted, by the protein fold, from aligning along the field.
The present theory is not limited to protein solutions and can be applied to test the widely accepted dielectric saturation paradigm2 for the NDE. The Langevin equation used to describe dipole's saturation predicts a linear scaling,2,24 −a ∝ β3M04ρ0 ∝ ρ0, of a negative Piekara coefficient with the solute concentration. The derivation of the Langevin equation is performed for a single dipoles and specific assumptions need to be imposed when the theory is extended to an ensemble of dipoles. While those are often omitted, it is implicitly assumed that dipoles are placed on a rigid lattice with a low compressibility (χT ≪ χidT) and they do not interact (gK = 1).2 Eqn (5) then reduces to a result, a = −πβ3M04ρ0/10, very close to the result of the Langevin model, which additionally requires adopting a specific form for the cavity-field susceptibility χc (see eqn (1)).24
Saturation prescribed by the Langevin framework can be distinguished from correlations advocated here by measuring NDE of dilute solutions of dipolar particles (dipolar molecules, proteins, or ferroelectric nanoparticles42) in less polar or nonpolar solvents. A positive Piekara coefficient in the present formulation scales linearly with the concentration in the infinite dilution limit, a = 3πβ3M04ρ0/20, but becomes proportional to the third power of the concentration, a ∝ ρ03, when binary dipolar correlations start dominating over the compressibility term in the brackets of eqn (16). The distinction in the sign and in the concentration scaling should allow one to discriminate between saturation and binary correlations when dielectric measurement are performed at sufficiently low frequencies below the frequency of solute tumbling.
The positive Donnan term in eqn (15) can be neglected at sufficiently large electrolyte concentrations and pH close to the isoelectric point. The second osmotic coefficient becomes negative at high pH and high electrolyte concentrations.30,31 A negative B00 is a good predictor of protein crystallization36,43 or of the liquid–liquid phase separation.38,39 For a negative value of B0 in eqn (15), the truncation of the osmotic virial expansion produces a divergence in the structure factor S00 in eqn (14) at 1 + 2B0η0 → 0. Such a singularity, reached at the critical point or at the spinodal line, might signal the onset of the liquid–liquid phase separation of the protein solution32,38,39 or arise from the failure of the truncated expansion for the osmotic pressure. The range of protein concentrations is chosen to ensure 1 + 2B0η0 > 0 in the present calculations.
It is clear that the second term in the brackets in eqn (16) dominates over the first term at η0 → 0. Given that B00 is of the order of BHS00,36,44 and η0 < 0.2 at typical protein concentrations <20 g L−1,37,39 the first term gains in importance at 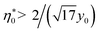 . With the typical values of y0 for proteins (Table 1), this condition puts
. With the typical values of y0 for proteins (Table 1), this condition puts 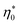 within the range of protein concentrations studied by light scattering35,38–40 and dielectric spectroscopy45,46 of protein solutions. One can, therefore, anticipate a crossover from the linear scaling, a ∝ M04cp, to a cubic dependence a ∝ M08cp3. However, by virtue of being multiplied with η0 in the Piekara coefficient in eqn (16), the low-concentration range is not prominent in the overall dependence a(cp).
within the range of protein concentrations studied by light scattering35,38–40 and dielectric spectroscopy45,46 of protein solutions. One can, therefore, anticipate a crossover from the linear scaling, a ∝ M04cp, to a cubic dependence a ∝ M08cp3. However, by virtue of being multiplied with η0 in the Piekara coefficient in eqn (16), the low-concentration range is not prominent in the overall dependence a(cp).
| Proteina | z0 | Ω0, nm3 | M0, D | y0 | B0/4 |
|---|---|---|---|---|---|
| a Lys = lysozyme, BSA = bovine serum albumin.b Second virial coefficient at pH = 7 and c1 = 7 mM is taken from ref. 35.c Data at pH = 6 and c1 = 0.1 M from ref. 30.d Data taken at pH = 7 and c1 = 15 mM from ref. 40 where corrections for the Donnan term were implemented.e Values ≃−2.4 at c1 = 7 mM were reported in the presence of trivalent salts.38,39 | |||||
| Lysb | 8 | 24 | 208 | 61 | 29 |
| Lysc | −0.87 | ||||
| BSAd | −8 | 137 | 384 | 36 | 4.5e |
Fig. 1 shows a(cp)/|aw| normalized with the Piekara coefficient for bulk water at 293 K:47 aw = −0.8 × 10−15 m2 V−2. The calculations are done for lysozyme (Lys, second line in Table 1) and bovine serum albumin (BSA) proteins (Table 1). The full calculation according to eqn (16) (solid lines) is compared to the results with the second term in the brackets, containing the second osmotic coefficient, dropped (dashed lines). At concentrations cp > 10 g L−1, one can neglect the virial coefficient component and approximate the Piekara coefficient by the dipolar term
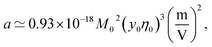 | (17) |
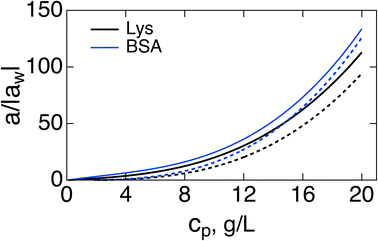 | ||
| Fig. 1 Reduced Piekara coefficient a/|aw| (aw = −0.8 × 10−15 m2 V−2 is the Piekara coefficient for bulk water) vs. the protein concentration cp (g L−1) for Lys (black, second line in Table 1) and BSA (blue). The solid lines indicate calculations based on eqn (16) and dashed lines refer to calculations with the second term in the brackets (involving the second virial coefficient) dropped. | ||
If the purpose of measuring the Piekara coefficient is to gain access to the protein dipole moment, a better strategy might be to plot a/cp vs. cp2. Both the slope and intercept should provide access to M0: the intercept becomes (3π/20)β2M04NA/Mp, where Mp is the protein molar mass and NA is the Avogadro number. Extrapolation from high concentrations can be of limited value because of the curvature of the plot at cp → 0, as is seen in Fig. 2 for BSA. The slope (17/5)β5M08(πNA/(3Mp))3, provides a more robust access to M0. A strong temperature dependence of the slope, ∝T−5, can be used to test theory predictions.
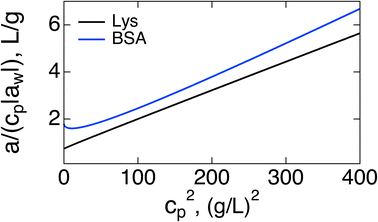 | ||
| Fig. 2 a/(|aw|cp) vs. cp2 for Lys (black, second line in Table 1) and BSA (blue). | ||
From a general perspective, the Piekara coefficient quantifies the non-linear dielectric response and non-Gaussian statistics of the sample dipole moment24 (eqn (4)). In bulk dipolar materials, the NDE arises from rotations of individual non-interacting dipoles (Langevin model) or from mutual correlations of dipoles (the present description). Non-Gaussian statistics of the dipole moment can also arise from intrinsic conformational transitions of the protein. Intrinsically disordered proteins or disordered domains of folded proteins48 can potentially be good candidates for observing the NDE. The field required to observe protein NDE, ≃1–10 kV cm−1, is comparable to the field strength of protein capture on nanopores by another nonlinear dielectric effect, the protein dielectrophoresis.49,50 Extending the theory to the response of entire cells18 requires modeling the field-induced changes of the membrane-bound protein pumps.26
4 Conclusions
An analytical theory for the nonlinear dielectric response of protein solutions developed here shows high contrast between the nonlinear response of proteins in solution and surrounding water. The contrast arises from a strong scaling, ∝cp3M08, of the nonlinear response with the large protein dipole. The Piekara coefficient of proteins in solution exceeds that of surrounding water by two orders of magnitude at the typical protein concentrations used in light-scattering and dielectric measurements.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was supported by the National Science Foundation (CHE-2154465). Discussions with Ranko Richert are gratefully acknowledged.Notes and references
- J. D. Jackson, Classical Electrodynamics, Wiley, New York, 2nd edn, 1975 Search PubMed.
- C. J. F. Böttcher, Theory of Electric Polarization, in Dielectrics in Static Fields, Elsevier, Amsterdam, 1973, vol. 1 Search PubMed.
- B. K. P. Scaife, Principles of Dielectrics, Clarendon Press, Oxford, 1998 Search PubMed.
- D. V. Matyushov, J. Chem. Phys., 2012, 136, 085102 CrossRef PubMed.
- D. V. Matyushov, Manual for Theoretical Chemistry, World Scientific Publishing Co. Pte. Ltd, New Jersey, 2021 Search PubMed.
- E. H. Grant, R. J. Sheppard and G. P. South, Dielectric Behaviour of Biological Molecules in Solution, Clarendon Press, Oxford, 1978 Search PubMed.
- S. Takashima, Electrical Properties of Biopolymers and Membranes, Adam Hilger, Bristol, 1989 Search PubMed.
- S. Takashima and K. Asami, Biopolymers, 1993, 33, 59–68 CrossRef CAS PubMed.
- S. S. Seyedi and D. V. Matyushov, J. Phys. Chem. B, 2018, 122, 9119–9127 CrossRef CAS PubMed.
- M. Heyden and D. V. Matyushov, J. Phys. Chem. B, 2020, 124, 11634–11647 CrossRef CAS PubMed.
- R. Richert, Adv. Chem. Phys., 2015, 156, 101–195 CrossRef CAS.
- T. Kamei, M. Oobatake and M. Suzuki, Biophys. J., 2002, 82, 418–425 CrossRef CAS PubMed.
- Y. Ajaj, M. Wehner and H. Weingärtner, Z. Phys. Chem., 2009, 223, 1105–1118 CrossRef CAS.
- S. Khodadadi and A. P. Sokolov, Soft Matter, 2015, 11, 4984–4998 RSC.
- L. Bourgeat, L. Pacini, A. Serghei and C. Lesieur, Structure, 2021, 29, 1419–1429 CrossRef CAS PubMed.
- L. Bourgeat, A. Serghei and C. Lesieur, Sci. Rep., 2019, 9, 17988 CrossRef PubMed.
- A. M. Woodward and D. B. Kell, J. Electroanal. Chem. Interfacial Electrochem., 1990, 299, 83–100 CrossRef.
- A. Palanisami, G. T. Mercier, J. Fang and J. H. Miller Jr, Biosensors, 2011, 1, 46–57 CrossRef CAS PubMed.
- J. Fang, A. Palanisami, K. Rajapakshe, W. R. Widger and J. H. Miller, Biosensors, 2011, 1, 13–22 CrossRef CAS PubMed.
- A. Piekara, Proc. R. Soc. London, Ser. A, 1939, 172, 360–383 CAS.
- A. Piekara and A. Chelkowski, J. Chem. Phys., 1956, 25, 794–795 CrossRef CAS.
- A. Chełkowski, Dielectric Physics, Elsevier Scientific Pub. Co, Amsterdam, 1980 Search PubMed.
- J. L. Oncley, Chem. Rev., 1942, 30, 433–450 CrossRef CAS.
- D. V. Matyushov, J. Chem. Phys., 2015, 142, 244502 CrossRef PubMed.
- B. Robertson and R. D. Astumian, Biophys. J., 1990, 57, 689–696 CrossRef CAS PubMed.
- A. M. Woodward and D. B. Kell, FEMS Microbiol. Lett., 1991, 84, 91–96 CrossRef CAS.
- D. V. Matyushov, J. Chem. Phys., 2022, 157, 164501 CrossRef CAS PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, Amsterdam, 4th edn, 2013 Search PubMed.
- S.-H. Chen and D. Bendedouch, Methods Enzymol., 1986, 130, 79–116 CAS.
- O. D. Velev, E. W. Kaler and A. M. Lenhoff, Biophys. J., 1998, 75, 2682–2697 CrossRef CAS PubMed.
- J. D. Gunton, A. Shiryayev and D. L. Pagan, Protein Condensation, Cambridge University Press, Cambridge, UK, 2007 Search PubMed.
- M. Wolf, F. Roosen-Runge, F. Zhang, R. Roth, M. W. Skoda, R. M. Jacobs, M. Sztucki and F. Schreiber, J. Mol. Liq., 2014, 200, 20–27 CrossRef CAS.
- C. G. Gray and K. E. Gubbins, Theory of Molecular Liquids, Clarendon Press, Oxford, 1984, vol. 1 Search PubMed.
- W. H. Stockmayer, J. Chem. Phys., 1950, 18, 58–61 CrossRef CAS.
- D. Asthagiri, A. Paliwal, D. Abras, A. M. Lenhoff and M. E. Paulaitis, Biophys. J., 2005, 88, 3300–3309 CrossRef CAS PubMed.
- A. C. Dumetz, A. M. Snellinger-O'Brien, E. W. Kaler and A. M. Lenhoff, Protein Sci., 2007, 16, 1867–1877 CrossRef CAS PubMed.
- P. Mereghetti, R. R. Gabdoulline and R. C. Wade, Biophys. J., 2010, 99, 3782–3791 CrossRef CAS PubMed.
- O. Matsarskaia, F. Roosen-Runge, G. Lotze, J. Möller, A. Mariani, F. Zhang and F. Schreiber, Phys. Chem. Chem. Phys., 2018, 20, 27214–27225 RSC.
- F. Surfaro, R. Maier, K.-F. Pastryk, F. Zhang, F. Schreiber and R. Roth, J. Chem. Phys., 2023, 158, 164902 CrossRef CAS PubMed.
- S. Yadav, S. J. Shire and D. S. Kalonia, Pharm. Res., 2011, 28, 1973–1983 CrossRef CAS PubMed.
- H. Lozano, R. Fabregas, N. Blanco-Cabra, R. Millán-Solsona, E. Torrents, L. Fumagalli and G. Gomila, Nanoscale, 2018, 10, 19188–19194 RSC.
- Y. Cho, J. Mater. Res., 2011, 26, 2007–2016 CrossRef CAS.
- A. George, Y. Chiang, B. Guo, A. Arabshahi, Z. Cai and W. W. Wilson, Methods Enzymol., 1997, 276, 100–110 CAS.
- P. Prinsen and T. Odijk, J. Chem. Phys., 2004, 121, 6525–6537 CrossRef CAS PubMed.
- A. Oleinikova, P. Sasisanker and H. Weingärtner, J. Phys. Chem. B, 2004, 108, 8467 CrossRef CAS.
- C. Cametti, S. Marchetti, C. M. C. Gambi and G. Onori, J. Phys. Chem. B, 2011, 115, 7144–7153 CrossRef CAS PubMed.
- A. E. Davies, M. J. van der Sluijs, G. P. Jones and M. Davies, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 571–578 RSC.
- B. Schuler, A. Soranno, H. Hofmann and D. Nettels, Annu. Rev. Biophys., 2015, 45, 1–25 Search PubMed.
- R. Pethig, Dielectrophoresis. Theory, Methodology and Biological Applications, Wiley, Hoboken, NJ, 2017 Search PubMed.
- T. Colburn and D. V. Matyushov, J. Appl. Phys., 2023, 133, 164701 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |
