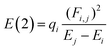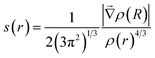Molecular orbital and topological electron density study of n → π* interactions: amides and thioamides cases

Abstract

The n → π* interactions were studied in amides and thioamides systems models, through the analysis of the electron density topology along with the Natural Bonding Orbital (NBO) approach. The effect of the dispersion terms was assessed using different DFT functionals. The NBO, independent gradient model (IGM), and the analysis of the reduced density gradient outcomes show that dispersion forces play a significant role in the strength of n → π* interactions. The IGM results indicate that δg height values for n → π* interactions do not extend beyond 0.025. All the methods used in this work predict that n → π* interaction between pairs of thioamides is stronger than those between amides. However, the electron density topology-based methods were not able to replicate the trends in the relative force of this interaction found in the experimental and NBO results.

---

1. Introduction

The n → π* interaction is a type of orbital donor–acceptor interaction with a widespread presence in chemistry, material science, and biology, and identified in aromatic, amide, and thioamide systems.^1–9 In a n → π* interaction, a lone-pair electron density is donated into the empty π* orbital of a neighbouring acceptor group, such as a carbonyl moiety. From this orbital mixing, energy is released resulting in an attractive interaction. The n → π* interactions are weak; however, they could make a significant contribution to the relativity stability on systems where energy differences are low or where this sort of interaction is abundant. Currently, the carbonyl–carbonyl n → π* interactions have been detected in amino acids, and its occurrence is widely spread in the backbones of proteins and peptoids.^1–9 Because of its abundance, this type of interaction makes a significant contribution to protein stability. It has been estimated that a third of residues in folded proteins engage in this kind of interaction and it contributes with 10 kcal mol⁻¹ for a 100-residue protein.^2–9 It is well known that in carbonyl–carbonyl interaction, the attractive force arises from the charge distribution, leading to Coulomb and dipolar interaction, along with n → π* donor–acceptor interaction. Dipolar and coulombic contributions are well-described by most molecular force fields used in theoretical protein studies, but they do not consider the contributions from electron donation. Nonetheless, efforts have been made to understand and quantify the donor–acceptor contribution and to include it in force field parameterizations.^1,4

The n → π* donation has also been identified in β-alanine using microwave spectroscopy in gas-phase.¹⁰ Four lowest-energy conformers were identified and characterized with one conformer being stabilized by n → π* interaction between the carboxylic acid fragment and the amino nitrogen.¹⁰

The n → π* interaction was first observed by Bürgi and Dunitz on nucleophilic attack to carbonyl groups.¹ In this reaction, the electron donation occurs along the so-called Bürgi–Dunitz trajectory, where a filled orbital overlaps a nearby empty orbital leading to energy stabilization. Since then, the quantum mechanical nature of the n → π* interactions has been supported by experimental and theoretical evidence.^1–9

Within the hyperconjugation model, the energetic stabilization produced by a n → π* donation depends on two main factors: the degree of the orbital mixing and the energy gap between the n and π* molecular orbitals. In the former, the Bürgi–Dunitz trajectory maximizes the orbital overlap. Due to the shorter distances necessary to form a n → π* interactions, the acceptor fragment must be highly polarized to minimize the Pauli repulsion that arises from a filled orbital in the acceptor. Therefore, amides and thioamides functional groups are very good n → π* acceptors.

Since the cis/trans and exo/endo stereochemistry in the proline system affect the stability of the collagen triple helix, the prolines are a prototype that allows to characterize energetic relationships of significance to protein structure.^2,4 For this reason, several groups have used prolines, amides, and thioamides as structure models to study the main features of the n → π* electron donor interaction.^2,4,11–17 Raines et al.⁴ developed a computational and experimental work to study the n → π* interactions in a group of six proline derived systems.¹ Their experimental and computational results show the electron donation nature of n → π* interactions, demonstrating the importance of this interaction in the stability of protein structure. According to their results, the contribution is ≥0.27 kcal mol⁻¹ per interaction.⁴

Theoretically, the n → π* interactions are studied using the Natural Bond Orbital (NBO) protocol.¹⁸ In NBO analysis, the delocalized canonical orbitals are transformed into localized Lewis-type orbitals. This methodology brings tools to obtain an estimate of the donor–acceptor interaction energy.

The topological analysis of the electron density using the Non-Covalent Interactions (NCI) index approach and the Quantum Theory of Atoms in Molecules (QTAIM) have been used to confirm the presence of NCI in molecules. The main advantage of this methodology is that electron density is a more fundamental concept than molecular orbital. In QTAIM method,¹⁹ the electron density (ρ(r)) is studied through its Laplacian, which is used to identify critical points (QTAIM-cp) in ρ(r); (∇ρ(r) = 0). The eigenvalue of the Hessian matrix at QTAIM-cp enables us to classify them according to their sign, as a Bond Critical Point (BCP), a Nuclear Critical Point (NCP), and a Ring Critical Point (RCP). The BCP is always found between all pairs of nuclei that are linked by a chemical bond. However, the NCI are not always associated with a QTAIM-cp in the electron density. The non-covalent index method was developed by Johnson et al. with the purpose to characterize the NCI.^20,21 This method focuses on the study of the reduced density gradient, s(r), instead of the bare electron density. In the NCI index method, the critical points in s(r) correspond to NCI presents in a molecule and it distinguishes the interaction types by colours, corresponding to the values of mapped function sign(λ₂)ρ on the isosurfaces. The main challenge with this methodology is the absence of a formal method to calculate the energy interactions and the incapacity to isolate one NCI from others present in the system. Recently, the Independent Gradient Model (IGM) has been proposed with advantages over the NCI index method,²² such as isolating the interactions, allowing to study them independently. The IGM technique is based on measuring, for two given fragments, the difference between a virtual upper limit of the electron density gradient norm (|∇ρ^IGM|) and the true gradient norm (|∇ρ|). The (|∇ρ^IGM|) corresponds to a non-interacting system, whereas |∇ρ| is associated with real systems. A local descriptor, δg, is defined as the difference between (|∇ρ^IGM|) and |∇ρ| and it can be interpreted as the electron shared caused by the electron density interactions between two subunits. The two subunits involved in δg can be defined by the user to reveal intra-fragment and inter-fragment interactions. In this way, one can isolate specific interactions and study them without interference from other interactions. The IGM was originally developed to work with a pro-molecular electron density. However, it was recently proposed a new variant based on the analysis of ρ(r) from DFT calculations. With this improvement, IGM has a more rigorous physical background and it allows to explore interactions in a wide variety of chemical systems.²² Numerous efforts have been made to estimate the strength of the NCI through different scheme integration in specific ranges in IGM.²² However, the small values in the interaction energy in NCI make that, even the slightest error could affect the results and compromise the interaction energy prediction.

All the electron density analysis methods described above have been calibrated numerously in NCI, such as hydrogen bonding, π–π stacking, and van der Waals forces. However, less attention has been given to the capacity of these protocols to predict and describe donor–acceptor interactions, such as the n → π*. This study would make possible to assess the ability of IGM method to represent and estimate the strength of this kind of interaction, as well as to determine their IGM fingerprints.

Therefore, in this article we propose to study the n → π* interactions in the proline models, synthesized by Raines et al.⁴ since the electron-donor nature of the carbonyl interactions in these compounds has been established. Additionally, we propose to carry out the study using the NBO protocol, to compare with the IGM results and to gain a deeper insight. Finally, to explore the effect of the dispersion terms contributions, the calculations were performed using hybrid functional B3LYP and B3LYP-D3, and their results were compared.²³ In addition, we use the M06-2X, ωB97X-V, and the ωB97X-D4 functionals.^24–26 The meta-GGA functional M06-2X is one of the most reliable functionals. It treats non-covalent interactions and dispersion via parametrization terms by using training sets;²⁴ whereas the ωB97X-V and the ωB97X-D4 functionals are recommended for studying the NCI.^24–26

2. Experimental

2.1. Computational details

All the calculations were performed at 298.15 K and 1 atm and carried out with the ORCA 5.0.4. code.²⁷ Full geometry optimizations for all the stationary points were performed. To explore the effect of the theoretical methods, we employ the M06-2X, B3LYP, B3LYP-D3, ωB97X-D4, and ωB97X-V functionals, along with 6-311+G(2d,p) basis set. Normal vibrational mode analyses were performed to characterize the stationary points at the same computational level. Zero-point vibrational energy corrections were applied without scaling for all stationary points. We have used the DEFGRID2 angular grid scheme for the numerical integration, with a SCF convergence tolerance of 1.0 × 10⁻⁶ a.u. for single point calculations and 1.0 × 10⁻⁸ a.u. for geometry optimizations.²⁷

The n → π* interactions were studied using the NBO protocol as implemented in the NBO 6.0 program.²⁸ The stabilization energy E(2) associated with the electron delocalization was estimated using a second-order perturbation as:

where q_i is the orbital occupancy, E_i and E_j are the diagonal elements (orbital energies), and F_i,j is the off-diagonal NBO Fock matrix element. Finally, the NBO visualization was achieved with the UCSF Chimera 1.16 software.²⁹

To study the acceptor–donor interactions from the analysis of the electron density topology, firstly a calculation of the Non-Covalent Interactions (NCI), based on the reduced density gradient (s(r)), was performed.

The reduced density gradient is a dimensionless quantity especially suited to identifying non-covalent interactions that picture the inhomogeneity of the density. According to this method, roots of s(r) correspond to NCI and they can be of two types. The first type occurs where the gradient of the electron density equates to zero. These points are also considered in the QTAIM. In the second type, roots are found where a complex balance exists between the electron density hessian and the von Weizsäcker kinetic terms.²¹ Such points are usually blind to QTAIM analysis and correspond to intramolecular weak interactions, as well as lone pair interactions.

The maximum variation in the contributions to the Laplacian, along with the axes, corresponds to the eigenvalues (λ_t) of the electron-density Hessian matrix. The sign λ₂ enables us to distinguish between different types of weak interactions, attractive and repulsive, while the electron density lets us assess the interaction's strength. The NCI calculations were performed using the NCIPLOT4 and Multiwfn 3.8 programs.^21,30 The isosurfaces were visualized using the UCSF Chimera 1.16 software,²⁹ according to the following color code: blue for attractive interactions, green for dispersive interactions (attractive or repulsive), and red for repulsive interactions.

The third approach used in this work to study the n → π* interactions is the Independent Gradient Model (IGM). In this approach, a local descriptor δg is defined as

δg = |∇ρ^IGM| − |∇ρ|

where |∇ρ| is the electron density gradient of the system under study and |∇ρ^IGM| represents the electron density gradient of the equivalent non-interacting system. |∇ρ^IGM| is defined as the sum of the absolute value of the density gradient of each atom in its isolated state, in such a way that |∇ρ^IGM| is the upper limit of the true density gradient (|∇ρ|). The bonding region can be revealed by isosurfaces at a convenient δg value. Therefore, in the IGM method, an interaction region is defined as the zone where the δg value is different from zero. In this stage, the IGMplot 3.0 software was used²² and the resulting isosurfaces were visualized using the UCSF Chimera 1.16 software.²⁹

The IGM approach uses the second eigenvalue of the electron density hessian to differentiate two sorts of interactions: λ₂ > 0 for nonbonding and λ₂ < 0 for bonding. In this method, when two fragments have been defined, it is possible to separate the inter/intra interactions. δg is not a dimensionless quantity and it has been found that its height has a positive correlation with the interaction strength, allowing rank of interactions. The NCI are in the range of δg values between 0 a.u. and 0.1 a.u. with the H-bonding about 0.1.

Besides, the Wiberg Bond Index (WBI)³¹ was calculated at the same level of theory using the Multiwfn 3.8 code.³⁰ To obtain the WBI, first the basis function was orthogonalized using the Löwdin method and then the Mayer bond analysis was performed. By summing up the interatomic bond order the total bond order between two fragments is obtained.

3. Results & discussion

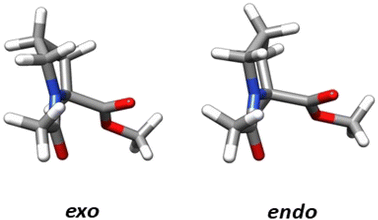
The structural parameters, related to n → π* interactions, used to evaluate the effect of the level of calculation are shown in Fig. 1. Since the n → π* interactions are only feasible in the trans isomer, only this isomer was considered in the geometrical optimization. All the structures were fully optimized in the endo and exo pucker of its pyrrolidine ring (Fig. 2).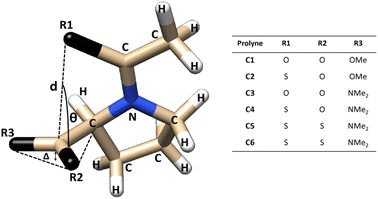

Fig. 1 Compounds used to evaluate n → π* interactions and the structural parameters denoting pyramidalization of carbonyl groups due to n → π* donation.

Fig. 2 Compound 1 showing the exo and endo ring pucker.

The n → π* donation weakens the π bond system in the carbonyl moiety reducing the planarity of the carbonyl group, this induces a pyramidalization (Δ) (Fig. 1), which can be seen as a hallmark of their strength. In the case of the proline systems studied here (Fig. 1), the pyramidalization in compounds C5 (trans, endo), C6 (trans, endo) and C6 (trans, exo) were measured by Raines et al. using X-ray diffraction.⁴ Therefore, the geometrical parameters calculated in our optimized geometries, at different levels of theory in the compound C5-endo, C6-endo, and C6-exo, were compared with those measured in ref. 4 The results are shown in Table 1 along with the E(2) value of the n → π* interactions calculated using the NBO protocol. The theoretical methods predict the compound C6 in the exo geometry, as the one with the highest value of pyramidalization property. Besides, the calculated Δ value shows that the pyramidalization of C6 in both conformations is greater than in C5-endo, in agreement with the experimental results. However, the computational outcomes forecast a higher difference in the Δ values between the C6-endo and C5-endo than in those measured in the X-ray diffraction experiment. Further, the theoretical results do not reproduce the experimental trends in the donor–acceptor d distance. Since the computational optimization was performed in the gas phase, these differences could be related to the crystal pack effect, to which the experimental samples are exposed.

Table 1 Theoretical and experimental structural parameters along the E(2) energy for selected compounds calculated using 6-311+G(2d,p) basis set

method	compound	d (Å)	θ	Δ (Å)	E(2) (kcal mol^−1)
Experimental^4	5-endo	3.526(12)	92.19(4)	0.0237(8)
	6-endo	3.4248(16)	96.11(6)	0.0243(17)
	6-exo	3.243(15)	101.92(7)	0.0392(16)
B3LYP	5-endo	3.145	117.55	0.019	0.3
	6-endo	3.433	109.49	0.028	1.0
	6-exo	3.317	109.05	0.036	1.5
B3LYP-D3	5-endo	3.023	113.21	0.015	0.6
	6-endo	3.325	107.42	0.028	1.4
	6-exo	3.213	106.79	0.036	2.2
M06-2X	5-endo	2.920	110.77	0.014	1.0
	6-endo	3.315	106.92	0.025	1.7
	6-exo	3.194	105.80	0.029	3.4
ωB97X-D4	5-endo	2.947	110.67	0.014	1.2
	6-endo	3.256	106.13	0.027	2.6
	6-exo	3.154	105.72	0.034	3.8
ωB97X-V	5-endo	2.973	112.01	0.015	1.1
	6-endo	3.319	106.72	0.027	2.1
	6-exo	3.210	106.47	0.034	3.2

---

Since the E(2) values show the following order C6-exo > C6-endo > C5-endo, the Δ values are consistent with the trends in the strength of n → π* interactions. The fact that Δ value in C6-endo is lesser than in C6-exo, indicates that the exo ring pucker promotes stronger donor–acceptor interactions, which is reflected in the E(2) tendency. Consistently, all methods predict a higher E(2) value in exo geometry than in endo geometry for the compound shown in Table 1. Furthermore, all the calculated values for E(2) (Table 2), predict that E(2) in the endo conformation is lower than its value calculated for the exo, except compound 4. In this specific case, the M06-2X, ωB97X-D4 and ωB97X-V functionals predict the opposite tendency.

Table 2 E_n→π* energies (kcal mol⁻¹) calculated using 6-311+G(2d,p) basis set and the ORCA 5.0.4 code²⁷

Comp.	B3LYP			B3LYP-D3			M06-2X			ωB97X-D4			ωB97X-V
	E(2) endo	E(2) exo	En→π*	E(2) endo	E(2) exo	En→π*	E(2) endo	E(2) exo	En→π*	E(2) endo	E(2) exo	En→π*	E(2) endo	E(2) exo	En→π*
1	0.3	1.2	0.61	0.5	1.5	0.84	0.9	1.9	1.26	0.9	2.5	1.46	0.8	2.4	1.38
2	0.8	2.0	1.21	1.2	2.7	1.70	1.5	3.2	2.11	2.0	4.1	2.68	1.6	3.5	2.22
3	0.2	0.6	0.30	0.1	0.9	0.39	0.3	1.3	0.64	1.1	1.3	1.15	1.0	1.3	1.13
4	0.7	1.0	0.80	1.2	1.3	1.21	1.6	1.5	1.60	1.8	1.6	1.71	1.5	1.4	1.51
5	0.3	0.6	0.39	0.6	0.8	0.65	1.0	1.2	1.07	1.2	1.7	1.40	1.1	1.5	1.25
6	1.0	1.5	1.16	1.4	2.2	1.67	1.7	3.4	2.29	2.6	3.9	3.03	2.1	3.2	2.48

---

In Table 2, if we compare the B3LYP results with those found with B3LYP-D3, we can observe the effect of including dispersion terms in the study of hyperconjugation interactions. The results show that the inclusion of dispersive forces increases the E(2) value but it has little effect on Δ value. This is noteworthy, since the pyramidalization is believed to be a measure of the strength of the n → π* interactions. However, the donor–acceptor distances predicted by B3LYP-D3 are shorter than those predicted by B3LYP, which produce an increase in the calculated strength of the n → π* interaction, due to a more effective orbital overlap.

Accordingly, we compare the orbital overlap, calculated with B3LYP, with those calculated with B3LYP-D3. The value of the orbital overlap increases when the dispersion terms are considered (Table S1†), whereas the energy gap between the n and π* orbital remains almost unchanged in most of the cases. Regarding the values of the overlap integrals calculated with M06-2X, ωB97X-D4, and ωB97X-V functionals, all the values are greater than those calculated with B3LYP. Likewise, the calculated energy difference between the donor and acceptor orbitals using B3LYP has the lowest value. Some studies have suggested that dispersion forces play a significant role in the strength of n → π* interactions due to dispersion-corrected DFT calculations provide better geometries, with a closer donor–acceptor distances which enhance the orbital overlap.^3,32–34 Our results support these conclusions. Therefore, it is expected that n → π* interaction energy value, calculated in geometries optimized with methods that include dispersive terms, were more reliable than those calculated with methods that do not include dispersion corrections.

In the proline system, the endo/exo ratio has been determined previously as ∼66% in endo fold and ∼34% in exo fold.⁴ This feature was used to estimate the E_n→π* energy for the compounds studied in this paper. The smaller E_n→π* energy (Table 2) are those calculated with B3LYP, which is consistent with the fact that in B3LYP contribution of the dispersive forces is missing.³⁵ Furthermore, the range-separate hybrid functionals ωB97X-D4 and ωB97X-V predict higher values for E_n⃑π* energy among the functionals studied here. The ωB97X-V functional is a reparametrized version of the range-separated functional ωB97X.²⁵ This functional captures the London-dispersion energy effects using a density-dependent nonlocal-correlation component, the VV10 kernel. These methods can be very accurate in treating dispersion effects but come with a greater computational cost due to the evaluation of the nonlocal kernel. The ωB97X-D4 is an extension of the ωB97X-D3(BJ), with atomic-charge dependent dispersion coefficients providing an improvement over ωB97X-D3(BJ) variant.²⁶ Both functionals are very accurate in handling the dispersion contributions, and therefore, our results suggest that the stabilization energy due to each n → π* interaction is higher than previously estimated⁴ in protein systems.

A topic of interest is to test the ability of the different models to correctly predict the expected trends due to functional group replacement. In this respect, since the sulfur atom is a better electron pair donor than the oxygen atom, the thioamide would improve the n → π* interaction, incrementing electron donation. Therefore, it is anticipated that the interaction in compound C2 will be higher than in compound C1 (E²_n→π* > E¹_n→π*), as shown by Raines et al.⁴ All the methods employed here were able to predict ceorrectly the tendency mentioned above. The lesser energetic difference, E²_n→π* > E¹_n→π* was calculated with the B3LYP approach (0.596 kcal mol⁻¹), meanwhile, the greatest energetic difference was obtained with the ωB97X-D4 (1.220 kcal mol⁻¹). In addition, it is well known that the ester group has a higher electrophilicity than the amide acceptor. Therefore, the n → π* interaction is expected to be stronger in compound C1 than in compound C3. This is illustrated in the calculated E_n→π* values, as all the methods employed in this work correctly predict E¹_n→π* > E³_n→π*. The greatest energetic difference was calculated with the M06-2X approach (E¹_n→π* > E³_n→π* = 0.623). Once more, a lesser difference was found using the B3LYP functional (0.309). In the work done by Raines et al.⁴ the donor in compound C3 was replaced by a thioamide to give compound C4 and the value of the ratio of the isomers, K_trans/cis was increased, which is consistent with an increase in the n → π* interaction in compound C4, relative to compound C3. This feature was correctly predicted by all methods (Table 2). In Fig. 3 we plot the orbital rendering showing the overlap of n and π* orbitals, calculated with the NBO method along with the corresponding s(r) and δg isosurfaces associated with the n → π* interaction. Over each isosurface, the sign(λ₂)ρ was plotted using the color code mentioned in the material and method section. For simplicity, only the M06-2X results in endo and exo pucker are shown. All the methods are capable of revealing the n → π* interaction in both, s(r) and δg isosurfaces. The n → π* interaction is identified as a green flat disc in the middle of the interaction zone. From Fig. 3, it is clear the advantage of the IGM methodology over the NCI index method, as the δg isosurfaces are capable to isolate the n → π* interaction from the other interactions, whereas the NCI method is not. By defining the fragments involved in the n → π* interaction, the IGM approach can isolate this interatomic interaction and their associated δg^intra height peaks.

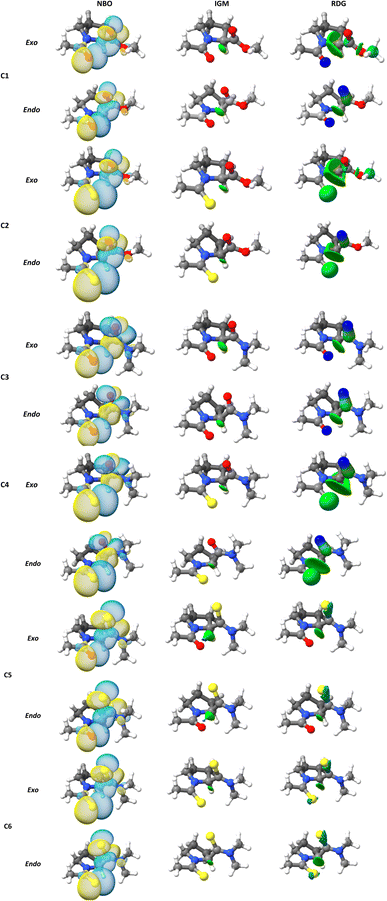Fig. 3 (NBO) three-dimensional orbital rendering, (NCI) s(r), and (IGM) δg isosurfaces associated with the n → π* interactions obtained at M06-2X/6-311+G(2d,p) level of theory.

For simplicity, only the (ρ, δg^intra) fingerprints-plots obtained using the M06-2X functional in endo and exo pucker are shown (Fig. 4). In all the cases, the peak associated with the n → π* interaction always appears at around the interval of −0.02 < sign(λ₂)ρ < −0.01 a.u. The δg^intra is always higher in the exo pucker, which is consistent with the finding that the exo geometry promotes stronger donor–acceptor interactions in these compounds. Interestingly, if we compare the plots for compounds C1, C3, and C5 with the results for compounds C2, C4, and C6 we note that when the donor atom is the sulfur instead of the oxygen atom, the peak is shifted to values slightly below.

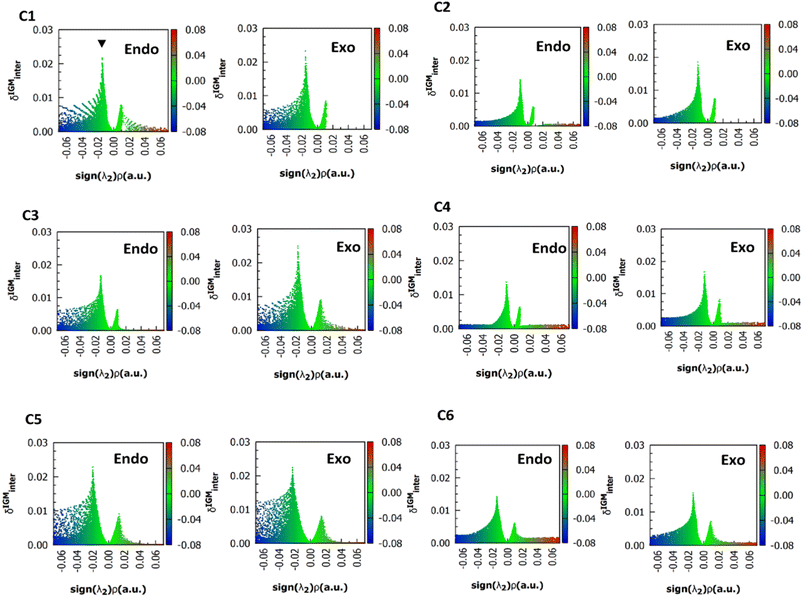Fig. 4 (ρ, δg) 2D fingerprints plots obtained at M06-2X/6311+G(2d,p) level of theory, the black arrow shows the peaks associated to n → π* interactions.

All the methods predict a δg height peak less than 0.1 a.u., as it is expected for NCI interactions and the calculated values do not extend beyond 0.025 a.u. As it was noted in Fig. 4, the δg height peak in exo pucker is higher than in the endo geometry, showing that the exo pucker promotes stronger donor–acceptor interactions. For each calculated compound, B3LYP predicts lesser values of δg peak indicating that the B3LYP functional predicts the lesser interaction energy, which is in according with the NBO results. However, δg values do not agree with the trends found in the strength of the n → π* interaction calculated using the NBO protocol. For instance, the δg value (Table 3) computed for compound C2 is lesser than compound C1, predicting that the n → π* interaction in compound C1 will be higher than compound C2. This is not in agreement with the sulfur atom, as a better electron pair-donor than the oxygen atom. The same conclusions can be reached when we compare the δg values between compounds C1 and C3, and between compounds C3 and C4. In all cases, the δg values are unable to reflect the experimental trends in these compounds.

Table 3 δg^intra (a.u.) associated to n → π* interaction, calculated using 6-311+G(2d,p) basis set and the ORCA 5.0.4 code

Compound	B3LYP		B3LYP-D3		M06-2X		ωB97X-D4		ωB97X-V
	endo	exo	endo	exo	endo	exo	endo	exo	endo	exo
1	0.01438	0.01585	0.01662	0.01830	0.02164	0.02328	0.01946	0.02137	0.01787	0.02099
2	0.01130	0.01856	0.01300	0.02363	0.01407	0.01863	0.01533	0.01932	0.01393	0.01854
3	0.01407	0.01543	0.01547	0.01918	0.01710	0.02501	0.02190	0.02486	0.02119	0.02360
4	0.01340	0.01445	0.01317	0.01590	0.01375	0.01695	0.01562	0.01795	0.01398	0.01648
5	0.01664	0.01630	0.01759	0.01776	0.02284	0.02227	0.02021	0.02049	0.01931	0.01966
6	0.01332	0.01676	0.01240	0.02283	0.01395	0.02416	0.01454	0.02461	0.01343	0.01962

---

To achieve a IGM base descriptor that may be able to reproduce the trends obtained by the NBO method, an integration of the δg associated with the n → π* interaction was performed. Within the IGM approach the integral of δg has been proposed as a descriptor of the force interactions.²²

∫δg^intra dV

To focus on attractive interaction, only the grid points with λ₂ < 0 and 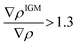were considered for the integration.

Table 4 shows the results for the above integral evaluation in the n → π* region of interaction. Like the δg results, all the methods were incapable to reproduce the NBO trends and the experimental tendency. This failure could be due to the electron density displaying additional effects that are being captured in δg values. To examine this hypothesis, the Wiberg bond index³¹ was calculated in the atoms involved in the n → π* donation. Subsequently, the results were compared with E(2) and δg values to analyze their correlation. Since the Wiberg bond order measures the electron population overlap between two atoms or fragments, it is expected to reflect some additional contribution from the whole wave function beyond the one associated with the n → π* interaction. For simplicity, henceforth only the M06-2X results will be analysed.

Table 4 Integrated δg^intra values for the n → π* interaction, calculated using 6-311+G(2d,p) basis set and the IGMplot code

Compound	B3LYP		B3LYP-D3		M06-2X		ωB97X-D4		ωB97X-V
	endo	exo	endo	exo	endo	exo	endo	exo	endo	exo
1	0.03792	0.02869	0.04075	0.03140	0.05441	0.04042	0.04620	0.03617	0.04733	0.03769
2	0.03546	0.03126	0.03725	0.03381	0.04134	0.04253	0.03773	0.03468	0.03789	0.03838
3	0.04577	0.03643	0.04783	0.04114	0.04854	0.05397	0.04827	0.05045	0.04787	0.04898
4	0.03923	0.03845	0.04139	0.04217	0.03652	0.04858	0.03464	0.04295	0.03719	0.04428
5	0.05657	0.05754	0.05137	0.05539	0.06318	0.07985	0.05061	0.06225	0.05281	0.06545
6	0.04717	0.05533	0.04323	0.05974	0.06620	0.06072	0.04659	0.06312	0.05009	0.07432

---

The calculated WBI values lie between 0.02 and 0.15, showing poor electron sharing (Fig. S1†). Due to the exo ring pucker promotes stronger donor–acceptor interactions, the calculated values of WBI in the exo pucker are higher than in the endo geometry. A good correlation between the computed E(2) values and the computed WBI values was found, however, no correlation was established between δg and WBI values. Therefore, no additional effects from the whole wave function beyond the one associated with the n → π* interaction were found.

The QTAIM analysis show that there are no critical points associated with the n → π* interaction. In Fig. 5 we depicted the Laplacian of the electron density (∇²ρ) contour maps, plotted in a plane defined by the atom donor and the atoms in thioamide and amide electron acceptor for selected compounds. For compound C1, ∇²ρ shows a zone of charge concentration in the vicinity of the oxygen electron donor, pointing to the charge depletion region around the carbon atom of the carbonyl group. This feature is found in both exo and endo ring pucker. In compound C2, when the donor oxygen atom is replaced by a sulfur atom, the charge concentration in the vicinity of the S atom is increased; indicating that the S atom is a better electron pair donor than the O atom. This suggests an improvement in the electron donation, which is in agreement with the n → π* interaction in compound C2 as higher than compound C1. In compound C3 the carbonyl acceptor group was replaced with a thioamide to give compound C5. Since the S atom is less electronegative than O atom, the charge depletion in the C atom is reduced in compound C5 (red arrow in Fig. 5), decreasing the interaction with the donor and producing that E³_n→π* > E⁵_n→π*. In compound C6 the acceptor and the donor are both thioamides, we can observe the effect in the Laplacian contour maps. It is noteworthy to mention that even though a thioamide acceptor overlaps less than a carbonyl acceptor (Table S1†), the n → π* interaction in compound C6 is stronger. This is an apparent contradiction, however, checking the value of the energy gap between the donor and acceptor for all compounds studied here, we found that all the methods predict the energy gap in compound C6 as the smaller one. Thus, all the methods predict that the pair of thioamides present a stronger n → π* interaction than do pair of amides, mainly due to a smaller energy gap between the donor and acceptor atoms. This smaller energy gap produces a more effective mixing between the donor and acceptor orbitals, since the energy mixing is inversely proportional to this energy gap. Therefore, the thioamides pair participate in a stronger n → π* interaction than the pairs of amides, as was outlined before.⁴

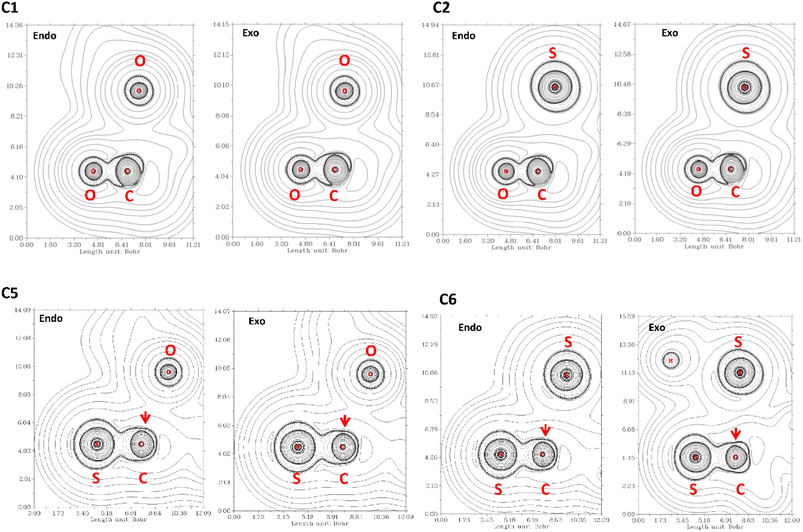Fig. 5 ∇²ρ contour maps at the plane defined by the atom donor and the atoms in thioamide and amide electron acceptor. Solid and dashed lines correspond to positive and negative region, respectively.

4. Conclusions

In summary, using the NBO protocol all DFT methods correctly predict trends in the relative strength of the n → π* interaction. The results revealed that dispersion forces play a significant role in the calculation of the strength of this interaction. Our results suggest that the stabilization energy due to each n → π* interaction is higher than previously estimated. This underestimation of the strength of the n → π* interaction, found with the B3LYP functional, is also revealed in the calculated values for δg and ∫δg^intra dV within the IGM approach. Besides, the δg height values for the n → π* interaction do not exceed a value of 0.25. However, the IGM approach is not able to reproduce the trends in the relative force of this interaction found in the experimental and NBO results. Finally, all the DFT functional used in this work predict that n → π* interaction between pair of thioamides is stronger than those between amides.

Author contributions

Conceptualization, R. F. Q.-Q.; formal analysis, R. F. Q.-Q., M. Q.-R., and F. M. M. B.-V.; funding acquisition, R. F. Q.-Q., M. Q.-R., D. C.-C., G. J. M.-R., G. M.-L., and R. M. C.; investigation, R. F. Q.-Q., F. M. M. B.-V.; writing—original draft, R. F. Q.-Q. Writing—review & editing, R. F. Q.-Q., G. J. M.-R., M. Q.-R., R. M. C., D. C.-C., and G. M.-L.; methodology, R. F. Q.-Q., F. M. M. B.-V.; resources, R. F. Q.-Q., G. J. M.-R., R. M. C., D. C.-C., and G. M.-L.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by research project 4-2023, granted by the Laboratorio Nacional de Cómputo de Alto Desempeño (LANCAD). Molecular graphics and analyses were performed with UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco, with support from NIH P41-GM103311.

Notes and references

1. H. B. Bürgi, J. D. Dunitz and E. Shefter, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1517–1527.
2. R. W. Newberry and R. T. Raines, Acc. Chem. Res., 2017, 50, 1838–1846.
3. S. K. Singh and A. Das, Phys. Chem. Chem. Phys., 2015, 17, 9596.
4. R. W. Newberry, B. VanVeller, I. A. Guzei and R. T. Raines, J. Am. Chem. Soc., 2013, 135(21), 7843–7846.
5. J. Sandoval-Lira, J. M. Solano-Altamirano, O. Cortezano-Arellano, S. Cruz-Gregorio, R. L. Meza-León, J. M. Hernández-Pérez and F. Sartillo-Piscil, J. Org. Chem., 2019, 84(4), 2126–2132.
6. J. F. Tamez-Fernández, F. M. Soto-Suárez, Y. D. Estrada-Chavarría, R. F. Quijano-Quiñones, R. A. Toscano, F. Cuétara-Guadarrama, F. Cuétara-Guadarrama, V. Duarte-Alaniz, T. R. Ibarra-Rivera, B. Quiroz-García, D. Martínez-Otero, K. Ramírez-Gualito, J. E. Barquera-Lozada, V. M. Rivas-Galindo and G. Cuevas, J. Org. Chem., 2021, 86(14), 9540–9551.
7. H. Chen, X. Tang, H. Ye, X. Wang, H. Zheng, Y. Hai, X. Cao and L. You, Org. Lett., 2021, 23(1), 231–235.
8. B. Khatri, P. Majumder, J. Nagesh, A. Penmatsa and J. Chatterjee, Chem. Sci., 2020, 11, 9480.
9. S. Jena, J. Dutta, K. D. Tulsiyan, A. K. Sahu, S. S. Choudhury and H. S. Biswal, Chem. Soc. Rev., 2022, 51, 4261–4286.
10. M. E. Sanz, A. Lesarri, M. I. Peña, V. Vaquero, V. Cortijo, J. C. López and J. L. Alonso, J. Am. Chem. Soc., 2006, 128(11), 3812–3817.
11. M. P. Hinderaker and R. T. Raines, Protein Sci., 2003, 12(16), 1188–1194.
12. A. Choudhary, D. Gandla, G. R. Krow and R. T. Raines, J. Am. Chem. Soc., 2009, 131(21), 7244–7246.
13. J. A. Hodges and R. T. Raines, Org. Lett., 2006, 8(21), 4695–4697.
14. L.-S. Sonntag, S. Schweizer, C. Ochsenfeld and H. Wennemers, J. Am. Chem. Soc., 2006, 128(45), 14697–14703.
15. Y. C. Chiang, Y. J. Lin and J. C. Horng, Protein Sci., 2009, 18(9), 1967–1977.
16. R. S. Erdmann and H. Wennemers, J. Am. Chem. Soc., 2012, 134(41), 17117–17124.
17. A. K. Pandey, D. Naduthambi, K. M. Thomas and N. J. Zondlo, J. Am. Chem. Soc., 2013, 135(11), 4333–4363.
18. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
19. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, United Kingdom, 1st ed., 1990.
20. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132(18), 6498–6506.
21. R. A. Boto, F. Peccati, R. Laplaza, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-Garcia, J. Chem. Theory Comput., 2020, 16, 4150–4158.
22. C. Lefebvre, J. Klein, H. Khartabil, J.-C. Boisson and E. Hénon, J. Comput. Chem., 2023, 44(20), 1750–1766.
23. S. T. Schneebeli, A. D. Bochevarov and R. A. Friesner, J. Chem. Theory Comput., 2011, 7(3), 658–668.
24. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
25. N. Mardirossiana and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924.
26. A. Najibi| and L. Goerigk, J. Comput. Chem., 2020, 41, 2562–2572.
27. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
28. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013.
29. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 13, 1605–1612.
30. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
31. I. Mayer, J. Comput. Chem., 2007, 28, 204–221.
32. B. W. Gung, Y. Zou, Z. Xu, J. C. Amicangelo, D. G. Irwin, S. Ma and H. C. Zhou, J. Org. Chem., 2008, 73, 689–693.
33. J. C. Amicangelo, B. W. Gung, D. G. Irwin and N. C. Romano, Phys. Chem. Chem. Phys., 2008, 10, 2695–2705.
34. S. K. Singh, S. Kumar and A. Das, Phys. Chem. Chem. Phys., 2014, 16, 8819–8827.
35. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzanoa and P. Ugliengoa, CrystEngComm, 2008, 10, 405–410.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06038a

---