Open Access Article
Open Access ArticleDynamics of droplet motion over hydrophobic surfaces with functionalized and non-functionalized ferro particles†
Ghassan Hassan ac,
Bekir Sami Yilbas
ac,
Bekir Sami Yilbas *abcd,
Abba Abdulhamid Abubakar
*abcd,
Abba Abdulhamid Abubakar ae,
Hussain Al-Qahtaniab and
Abdullah Al-Sharafiabc
ae,
Hussain Al-Qahtaniab and
Abdullah Al-Sharafiabc
aMechanical Engineering Department, King Fahd University of Petroleum and Minerals (KFUPM), Dhahran 31261, Saudi Arabia. E-mail: bsyilbas@kfupm.edu.sa
bIRC for Renewable Energy and Power, King Fahd University of Petroleum and Minerals (KFUPM), Dhahran 31261, Saudi Arabia
cK. A. CARE Energy Research & Innovation Center, Dhahran 31261, Saudi Arabia
dTurkish Japanese University of Science and Technology, Istanbul, Turkey
eInterdisciplinary Research Center for Advanced Materials, King Fahd University of Petroleum and Minerals, Dhahran, 31261, Saudi Arabia
First published on 29th November 2023
Abstract
Dynamically manipulating droplet motion on hydrophobic surfaces is crucial in various fields, including biomedical, sensing, actuation, and oil–water separation applications. Ferrofluid droplets can be manipulated and controlled using external magnetic forces. The creation of ferrofluids involves multiple procedures that can affect the functionality and stability of droplet manipulation, limiting their use in sustainable applications. This study investigates the dynamics of droplet motion over functionalized and non-functionalized ferroparticles, considering different droplet volumes, ferroparticle layer widths, and wt% concentrations. The translational and sliding velocities of the droplets are measured using high-speed camera recording with a tracker application. The finding revealed the transformation of a droplet sliding motion into a rolling motion with propulsion under the magnetic influence. The sliding velocity increases for the droplets moving over the ordinary ferroparticles on the hydrophobic surface. However, the droplet motion is dominated by rolling in the case of hydrophobic ferro particles. The droplet sliding velocity rises sharply at high concentrations (or layer width) of ferroparticle as the magnetic bond number rises sharply to 3. A newborn droplet adheres to the magnet surface during droplet rolling and sliding motion.
Introduction
An applied magnetic flux can control the position of ferro-droplets due to the strong liquid/magnetic field interaction.1 Creating ferrofluids involves several procedures, such as ultrasonic agitation, mixing, and homogenization.2 However, due to the vast surface area of nanoscale ferroparticles, they tend to clump together within the droplet fluid, and surfactants are added to minimize this phenomenon.Nevertheless, adding surfactants to the solution can alter the magnetic characteristics, especially at elevated temperatures.3 In addition, ferroparticles under magnetic fields modify fluid characteristics such as viscosity, surface free energy, adhesion, and density.4 Therefore, ferrofluid droplet stability remains critical for such applications. Recent research shows that the ratio between magnetic (Fm) and adhesion (Fpin) forces (known as magnetic bond number (Bo)) is necessary to identify the shape of the droplet under the magnetic influence.5 The droplet shape symmetry occurs at Bo values less than unity, while a shape disturbance happens at Bo values greater than unity. As the concentration of ferroparticles increases, they tend to pin to the surface, slowing down droplet mobility due to the increased magnetic. Interestingly, a magnet can further alter the wetting characteristics of ferrofluid droplets on hydrophobic surfaces, causing them to experience significant deformations and acquire pointed shapes with less wettable surface edges.6 The magnet attracts the ferro colloidal particles inside the water droplet, generating a magnetic field that affects the force acting on the moving droplet, which can drag or deform the droplet into the translation motion.6 Droplet motion on channels or hydrophobic surfaces can be controlled by encasing them in magnetically charged hydrophobic colloids. This arrangement makes transporting liquids across hydrophobic surfaces in microelectronics and biomedicine applications possible, which is essential.7 Earlier studies have evaluated the impact of ferroparticle concentrations on droplet motion.8
Research on magnetic fluids and their applications has generated interest in several fields,9 including actuators,10 liquid extractions,11 water separation,12 therapy,13 and solar energy harvesting.14 NASA utilized ferrofluids as seals on rotating shafts in satellites. In addition, the utilization of ferrofluids in other disciplines, such as microfluidics and thermal management, has recently received much attention.15 Triboelectric wetting (TEW) is a method for precise liquid manipulation. It eliminates the need for complex circuitry by using molecular layers to generate and store triboelectric charges, allowing for controlled water droplet manipulation on various surfaces. This innovation has broad applications, including controlled chemical reactions and surface defogging.16 Droplet motion can be manipulated and controlled using a magnetic field in several ways. Applying a magnetic field pattern allows the droplet to move in a specific direction or be forced to split or coalesce.17 Additionally, an external magnetic field can control the post-impact dynamics of ferrofluid droplets.18 Magnetic fields can also influence the droplet's shape and surface tension. The droplet's motion can be altered by manipulating the surface tension, allowing for better control over the droplet's movement.17 Other methods of manipulating droplet motion using a magnetic field include using a rotating magnetic field to create a vortex motion within the droplet and using an external electric field to control the droplet's motion.19 Furthermore, a magnetic field can also be used to induce electro-kinetic forces in the droplet, allowing for the manipulation of the droplet's surface tension.20 In recent works, magnetic fields have been used to create a lattice structure of ferrofluid droplets, which could be used to control fluid motion in microfluidic channels.21 Lately, a magnetic field has been used to induce an acoustic field in the water droplet, allowing the droplet's acoustic properties manipulation.22 Therefore, recent research focuses on effectively controlling ferro-droplet motion using an external magnetic flux. Although droplet mobility under magnetic flux has been considered earlier, manipulating lower-concentration ferrofluid droplets on the hydrophobic surface is postponed. The limitations of ferrofluid droplets, such as their temperature sensitivity, high cost, and instability, hinder the utilization of ferrofluid droplets for many applications. Besides the high development costs, ferrofluids may become magnetically saturated and lose their magnetic properties at higher temperatures. Moreover, ferrofluids tend to be unstable, and their properties can change over time or interact with other substances, adversely affecting their properties and making them less reliable for use in specific applications. Consequently, there is a need to develop other procedures for effectively manipulating droplet motion under magnetic influence via lower concentrations of ferrofluid droplets.
The fluid velocity inside the droplet can be strongly influenced by droplet fluid penetrating into surface texture spacing. This leads to different interfacial shear and droplet pinning behavior across the affected surface. When an external magnetic field is applied to hydrophobized surfaces, the interfacial characteristics of ferrofluid droplets on those surfaces are different from those of liquid droplets. Magnetic particles impact the surface and interfacial tensions of the droplet fluid, hence influencing the size of the droplet meniscus in response to the magnetic field. Because of the additional magnetic forces generated within the droplet fluid, the contact angle of the ferrofluid droplets changes under the effect of magnetism. This becomes crucial when the surface texture profile varies over the surface.23 Ferrofluid droplet deformation dynamics, including puddling, can be influenced by the magnetic field. As long as there is a difference in deformation at the droplet's rear edge due to the magnetic influence, the effects of gravity and magnetism on the droplet's deformation become similar.24 With the use of an external magnetic field, the rolling and sliding motion of ferrofluid droplets across the hydrophobic surface may be adjusted and controlled. On the other hand, the droplet mobility over the surface can be increased by utilizing the lubricant oil that accommodates the ferrofluid droplet. A range of droplet volumes, namely those in the range of 2 μL < V < 12 μL, does not affect the maximum droplet velocity.25 Ferrofluid droplets can be utilized in oil–gas separation to attenuate and encapsulate undesirable contaminants from the soil surface. While permitting the oil droplets to move through a magnetic field, the semi-fluorinated ligand can aid in the integration of the nanoparticles into the oil phase.26 Digital microfluidics devices can also make use of the ferrofluid droplets. The fluids in microfluidic devices can be controlled nonlinearly by the applied magnetic field.27
The present study investigates the droplet dynamic behavior and movement over nano-sized ferroparticles residing on the hydrophobic surfaces for various droplet volumes and ferroparticle layer widths (or concentrations). A high-speed video recording is employed to capture the movement of the droplets on the hydrophobic surface with and without ferroparticles presence. A tracker software calculates the droplet sliding and rolling velocities from the recorded data. The force-based formulas are developed for the droplet rolling and sliding velocities to compare and evaluate the experimental results and the predicted droplet rolling velocities. Additionally, the study assesses how normal and hydrophobic ferroparticles affect the droplet rolling and sliding motion over the hydrophobized surfaces.
Experimental
The experiment measures transparent glass samples (80 mm × 30 mm × 1.5 mm, length × width × thickness). Functionalized silica nanoparticles coated the glass surface to modify the surface wettability. The tetraethyl orthosilicate (TEOS) functionalizes the silica particle using the dip-coating technique adopted in early work.28,29 The dip-coating method applied synthesized silica nanoparticles to the glass (Biolin Scientific). An ethanol solution, ammonium hydroxide, and desalinated water were mixed thoroughly during the initial preparation. The mixture was agitated for eight hours after adding TEOS and isobuthytrimethoxysilane with a molar ratio of (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) to the prepared solution. A JEOL 6460 SEM was used to investigate the microstructure, and a goniometer (Data-physics, Model: OCA11) was used to assess the surface free energy.
4) to the prepared solution. A JEOL 6460 SEM was used to investigate the microstructure, and a goniometer (Data-physics, Model: OCA11) was used to assess the surface free energy.
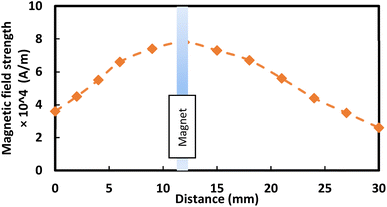
In addition, nanoscale (<50 nm) ferroparticles consisting of iron oxide, Fe3O4, and Sigma Aldrich were functionalized using the silica nanoparticles solution. A monolayer of the modified ferroparticles is distributed on the surface of the water droplets before each droplet experiment. The hydrophobized ferroparticles alter the droplets' wetting states on the superhydrophobic surface. The study's tests use a neodymium iron boron (NdFeB) magnetic core (K&J Magnetics Inc., USA) with an ultimate magnetic attraction of 11.806 × 105 A m−1 was used in the test. The variation of the magnetic field intensity along the hydrophobic glass surface is measured using a digital Tesla meter with a sensitivity of 10 T. Fig. 1 shows the experimental setup diagram, indicating the location of the modified ferroparticles and the magnet. A micropipette attached to a syringe pump deposits water droplets, passing through a monolayer of modified ferro particles before being attracted by the magnet. A fixture is designed to ensure the attraction of the droplet above the surface of the hydrophobic glass. Different droplet sizes are tested on ferroparticle layers with widths of 3 mm, 6 mm, and 12 mm. Fig. 1a demonstrates the magnet's location and the droplet's movements on the ferro-particles layer. In contrast, Fig. 1b displays an isometric optical view of the experimental design. A high-speed recording (Speed Sense 9040) captures the motion of droplets on the superhydrophobic plate, and tracking software is applied to assess the motion. The camera records the movements at a rate of 5000 frames per second (fps) with a high resolution of 1280 × 800 pixels, and the data is extracted at 800 fps to enhance data quality.
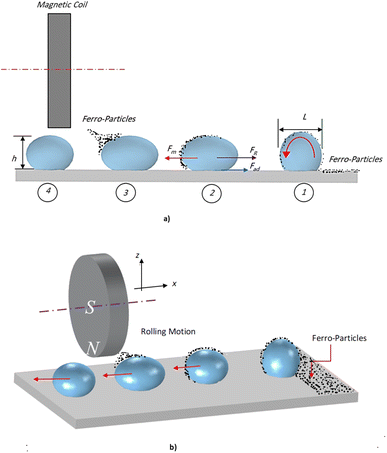 | ||
| Fig. 1 Schematic diagram of the experimental setup: (a) description of magnet-induced droplet rolling on a hydrophobic surface, and (b) an isometric view. | ||
Results and discussion
This study investigates the behaviour of water droplets on hydrophobic substrates covered with modified ferroparticles and subjected to an external magnetic field. The effect of ferroparticles width and concentration on the translation velocities of different droplet sizes is considered concerning the self-cleaning application. Additionally, the study evaluates rolling/sliding dynamics of the droplets on the ferroparticles under magnetic excitation, comparing the results for both cases as-received and surface modified by ferroparticles.Hydrophobized surfaces
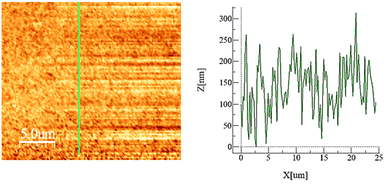
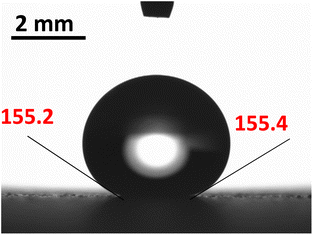
The hydrophobic silica coating is depicted in SEM micrographs in Fig. 2, and the surface's AFM and line scan diagrams are shown in Fig. 3. The hydrophobic surface is made up of 50 nm-sized nanoparticles. The surface line scan exposes nanoscale pillars and gaps in the texture morphology because particles form nonuniform aggregations on the surface (Fig. 3). About 250 nm is the maximum pillar height, while the nonuniform aggregates limit the space between pillars. The roughness parameter and average surface roughness are examined for each sample and attain values of 0.62 and 150 nm, respectively. The ratio of the covered pillars to the projected surface area (r) establishes the roughness parameter (r). Although the roughness parameter varies by 2%, the average roughness varies by no more than 5 nm. Generally, a surface with r = 0 is smooth, whereas a surface with r > 0 has texture.The SEM micrograph of the coated hydrophobic ferroparticle is also shown in Fig. 4. Due to the hierarchical textural morphology of the coated surface, a uniform hydrophobic condition is maintained over the surface. The transition from hierarchical to arbitrary textural morphology leads to a shift in wetting states. After ten repetitions, the expected error in the contact angle measurement is ±3°. Fig. 5 depicts the wetting assessment of the hydrophobic coating. The contact angle of water on the hydrophobic coating is approximately 155° ± 2°, with a hysteresis of 1 ± 2°.
Hydrophobic ferrofluids behavior in the magnetic field
Minor variations in surface tension and density of ferro particles can cause the contact angle of ferro droplets to deviate from the regular contact angle.8 However, when a hydrophobic ferroparticle layer is placed on top of a hydrophobic coating, the droplet contact angle increases by approximately 5° after 15 repeatability tests. The measured water droplet contact angle in the presence of a hydrophobic ferroparticles layer is around 155° (Fig. 5), which is more than the water droplet contact angle for the hydrophobic surface without modified ferroparticles (150°).30 Fig. 1 shows the droplet movement on the hydrophobic coating while the magnet is present. The droplet initially moves through a hydrophobic layer of ferroparticles, allowing it to roll in the direction of the magnet. As the droplet moves, it slides and rolls toward the magnetic source, increasing its velocity.31 Droplet mobility on a hydrophobic coating is governed by the balance of forces and contact angle hysteresis. Thus, the droplet can be pulled under body forces due to gravity, magnetic, and acoustic fields. However, opposing forces such as air drag, interfacial shear, adhesion, and friction hinder the droplet's motion. Large rolling droplets undergo puddling/wobbling behaviour; hence, the location of the centre of mass of the droplet changes considerably during its movement. Therefore, the droplet size becomes crucial for rolling due to the puddle thickness. A droplet's ability to squirm reduces as its diameter approaches the capillary length. As a result, the droplet rolls as a sphere of marble without any obvious puddling. Elastic deformation occurs in a rolling droplet on a hydrophobic surface. The hydrophobic surface's surface roughness prevents the rolling droplet from slipping. Therefore, rolling action dominates its motion because of the effect of inertia forces.Moreover, the moving droplet shape change significantly differs between the advancing/receding angles. Balancing energies along the superhydrophobic surface was formulated earlier.32 However, assuming that the droplet has a spherical shape, the droplet's rolling inertial force under magnetic influence satisfies the following requirement:
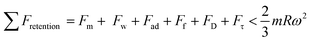 | (1) |
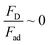 and
and 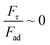 ) obtains the condition for the onset of droplet rolling:
) obtains the condition for the onset of droplet rolling:
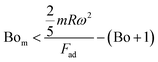 | (2) |
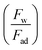 , Bom is the magnetic bond number
, Bom is the magnetic bond number  .
.
The adhesion force highly influences droplet mobility on the hydrophobic surface. It is proportional to important droplet characteristics such as the fluid surface tension, contact length scale, and advancing and receding contact angles. The adhesion force is expressed as:33
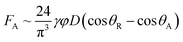 | (3) |
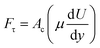 | (4) |
| Ff = μdmg | (5) |
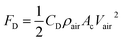 | (6) |
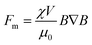 | (7) |
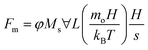 | (8) |
As the droplet passes a magnet, the magnetic force exceeds the retention forces and pulls the ferrodroplet in that direction. The net force acting on the water droplet gives the differential equation regulating:
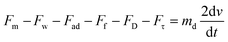 | (9) |
The magnetic disturbance of the 30 μL droplet makes sliding velocity substantially lower than rolling speed (with Re = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 and We = 142), given that the ferroparticle concentration is 0.11 wt%. As a result, drag and shear forces terms have significant impacts. Nevertheless, the air and sliding velocities (Vd) above the sliding droplet are in the same order. A numerical solution can be ensured every time step by utilizing practical inputs such as droplet position, dropping/receding contact angles, and magnetic force intensity. This method makes it possible to anticipate the droplet's speed while the magnetic effect is at play. It is possible to identify the retention force that has the most significant impact by doing a scale analysis of the forces' effects on droplet motion.
200 and We = 142), given that the ferroparticle concentration is 0.11 wt%. As a result, drag and shear forces terms have significant impacts. Nevertheless, the air and sliding velocities (Vd) above the sliding droplet are in the same order. A numerical solution can be ensured every time step by utilizing practical inputs such as droplet position, dropping/receding contact angles, and magnetic force intensity. This method makes it possible to anticipate the droplet's speed while the magnetic effect is at play. It is possible to identify the retention force that has the most significant impact by doing a scale analysis of the forces' effects on droplet motion.
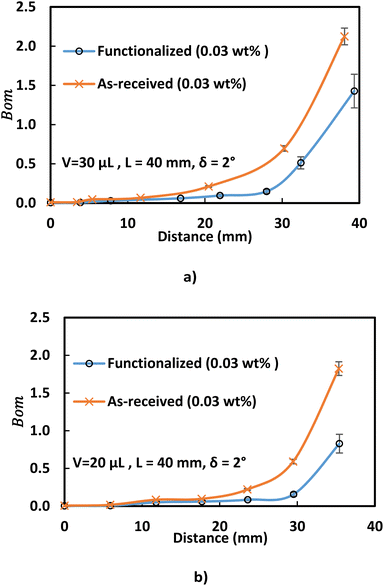
Analyzing forces that affect a droplet's mobility can help determine the most influential retention force. For a 30 μL droplet of ferro-liquid, with a concentration of hydrophobized particles at 0.03% by weight and positioned 4.0 mm away from the magnet, the magnetic force is about 2.0 × 10−4 N, and the adhesion force is roughly 2.0 × 10−4 N (measured at R = 128° and A = 105°). The pinning (adhesion) force has a negative value, acts against the magnetic force, and hinders the droplet's mobility on the surface. Two significant factors, the magnetic and adhesion forces, strongly affect the rolling/sliding dynamics of the droplet. Fig. 7 demonstrates the fluctuation of forces as the droplet moves on the hydrophobic plate under different ferroparticle conditions. The investigations prove that the water droplet remains stationary on the surface when positioned 40 mm away from the magnet. The data from high-speed recording indicates that the droplet stays sessile on the hydrophobic plate if the adhesion force overcomes the magnetic force (see Fig. 7). The movement of the drop is initiated by the gradual increase in the magnetic field strength as the drop approaches the magnet and the small inclination angle of the hydrophobic surface (2°). The experiment shows that 40 mm is the critical distance from the magnet, the magnetic force acting on it becomes stronger, and this force overcomes the pinning forces that initially held the drop stationary. This results in the drop starting to move.
The magnetic bond number can be determined as the magnetic to the adhesion forces ratio. As illustrated in Fig. 7a, the magnetic bond number 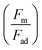 for droplets to initiate sliding motion under the current investigation's magnetic field is approximately 0.4. In addition, the concentration of modified ferroparticles increases the magnetic bond number (Bom). The magnetic force gradually increases as the droplet rolls and alters its shape. The pinning (adhesion) force exhibits fluctuations due to changes in the contact area and droplet shape. However, the value of Bom is more significant for droplets containing as-received ferroparticles than those containing functionalized ones due to the applied magnetic force's influence. The pinning force slightly differs between hydrophobic surfaces for as-received and hydrophobic ferroparticles. When the water droplet reaches the magnet, the value of Bom rises with droplet volume and reaches its maximum after 40 mm (the magnet's location).
for droplets to initiate sliding motion under the current investigation's magnetic field is approximately 0.4. In addition, the concentration of modified ferroparticles increases the magnetic bond number (Bom). The magnetic force gradually increases as the droplet rolls and alters its shape. The pinning (adhesion) force exhibits fluctuations due to changes in the contact area and droplet shape. However, the value of Bom is more significant for droplets containing as-received ferroparticles than those containing functionalized ones due to the applied magnetic force's influence. The pinning force slightly differs between hydrophobic surfaces for as-received and hydrophobic ferroparticles. When the water droplet reaches the magnet, the value of Bom rises with droplet volume and reaches its maximum after 40 mm (the magnet's location).
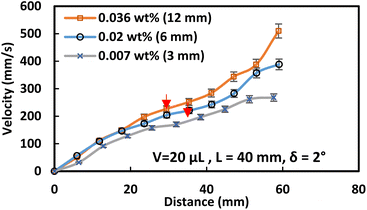
As a droplet approaches a magnet, the magnetic flux rises due to the accumulation of magnetized particles towards the magnet. This causes a change in the clustered particle orientation, resulting in a magnetically altered structure with a significant magnetic flux exposure inside the droplet fluid. The water droplet's slide velocity rises as the distance between it and the magnet gets smaller because the magnetic force opposes the droplet's retention forces and pulls the clumped ferroparticles to the magnet's surface. The water droplet's motion changes to pure rolling when the clustered ferroparticles are eliminated, and its translational velocity rises as its distance from the magnet shortens on the hydrophobic substrate. Fig. 8 depicts the translational droplet velocity for different ferroparticle concentrations on a horizontal hydrophobic surface. With rising ferroparticle concentrations, the translation velocity fluctuation becomes more perceptible, significantly when the droplet-magnet distance shrinks. As the volume of the droplet fluid increases to 30 μL, the number of ferroparticles within the droplet also increases, which eventually increases magnetic force, even though the adhesion force increases due to a greater contact area on the surface compared to the 20 μL droplet. The magnetic force becomes dominant as the droplet gets closer to the magnet, causing the 30 μL droplet to slide faster than the 20 μL. The velocity of the water droplet rises rapidly near the magnet due to the magnetic flux exceeding the pinning force. However, when the water droplet and magnet approach the critical spacing, the magnet picks up the ferroparticles from the droplet, causing its motion to change from sliding motion to rolling motion. Despite the increasing magnetic force, the droplet's shape remains unchanged, but its pressure decreases gradually.35 The in-plane/out-of-plane droplet motion is controlled by dynamic force after the magnet picks up the ferroparticles, causing the hydrophobic droplet to wobble in the early stages of rolling. The wobbling is caused by gravity and the droplet's elastic reaction, as observed in the high-speed camera photographs. The initial acceleration of the droplet before rolling creates a significant moment of inertia to sustain its motion. However, the droplet velocity decreases after the wobbling stops due to pinning and capillary forces. The spreading coefficient can determine how fast water spreads over ferroparticles, and it can be expressed as:36
| S = γP − γ − γP–w | (10) |
Additionally, the sustained capillary force (F) responsible for the ferroparticles' retention inside the water droplet may be approximated as follows:38
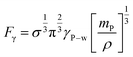 | (11) |
The strong attraction between ferroparticles and water causes the water droplet to divide into two droplets to separate the particles. Fig. 8 monitors the location of ferroparticle mitigation in the newly formed droplet. Droplet volume or ferroparticle content causes an increase in the new droplet volume. The magnetic force acting on the droplet is determined to be 9.82 × 10−5 N at a distance of 8.5 mm. As the ferroparticle only weighs 0.05% of the fluid, a gravitational force of 1.38 × 10−6 N is needed to counteract the magnetic attraction. According to the experimental results, the neonatal droplet (which contains ferro-particles) is 1.57 μL in volume or 5% of the 30 L droplet volume. The newborn droplet, therefore, weighs 1.32 × 10−5 N is less than the magnetic force applied at its beginning. Hence, the newborn droplet's weight (1.32 × 10−5 N) is heavier than the neonatal droplet's magnetic force mitigation force (9.82 × 10−5 N at 8.5 mm from the magnet surface).
The volume of the new-formed droplet grows by 98% as the ferrofluid concentration is raised from about 0.05 to 0.1 wt% for the 30 μL droplet. At 0.05 wt% ferrofluid concentration, and with lower droplet volume (from 30 to 20 μL), decreases the neonatal droplet volume by 17%. After the droplet forms, some ferroparticles are found in the fluid. Residues may include hydroxyl ligaments and charged particle repulsion, demagnetizing a few ferroparticles in the droplet.39
As a droplet breaks from its parent, its shape changes to a distinctive wobbly spherical rolling droplet shape, and the droplet's velocity changes from sliding to rolling motion. A rolling droplet's range and maximum height are depicted in Fig. 9. The ferroparticle content influences the droplet height while rolling in the droplet fluid. This is related to the droplet motion when a new droplet emerges from a sliding droplet, which leads to an unstable droplet motion and the beginning of droplet rolling. Notably, the modest interfacial force between the ferroparticle and the droplet causes the newborn droplet separation to occur early. Also, the hydrophobic surface's maximum rolling droplet height can be observed there; the water droplet with the minimum concentration of functionalized ferroparticles starts rolling before the one with the greatest concentration. This is due to the separation of newborn droplets occurring in the droplet with the low ferroparticle concentration sliding late. The inability to entirely remove magnetic particles is primarily attributed to interfacial forces that act between the particles and the droplet interface. These forces can be particularly strong, making it difficult to achieve complete separation, especially when it exceeds the applied magnetics force. As a result, a higher concentration droplet may wobble before reaching the location where the highest droplet height occurs. This location is where droplet rolling begins. This might lead to a droplet with a shorter maximum height and a maximum concentration of ferroparticles.
 | ||
| Fig. 9 Droplet height variation under the influence of ferro-particles for 20 μL. The initial distance between the droplet and the magnetic is 40 mm, and the tilt angle is 2°. | ||
Moreover, when ferroparticle concentration increases, the maximum and minimum heights of the droplet change in location and distance. As a result, the high-concentration droplet wobbles first along the hydrophobic surface, then the low-concentration droplet. In this case, the maximum droplet height, which is also affected by the ferroparticle concentrations, may be utilized to assess the wobbling state of the droplet.
The droplet translation velocity can be predicted from the energy balance equation as:40
| Etotal − Eloss = Ekinetic | (12) |
Hence, the translational droplet velocity can be expressed as:25
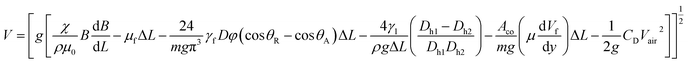 | (13) |
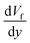 is the fluid's strain, χ is the magnetic susceptibility, μ0 is the air's permittivity, and B is the density of the magnetic field.
is the fluid's strain, χ is the magnetic susceptibility, μ0 is the air's permittivity, and B is the density of the magnetic field.
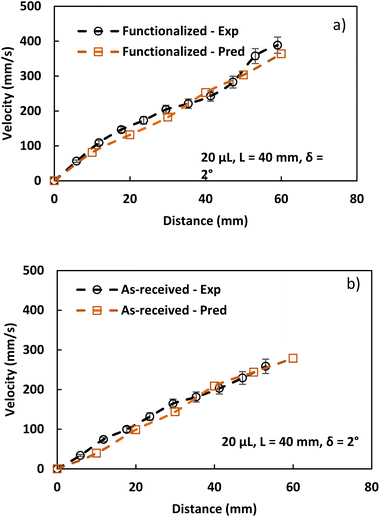
A program continually executes the prediction of droplet rolling velocity using the parameter inputs (such as rolling droplet distance, receding and advancing angles, hydraulic diameter, and magnetic intensity). These features were determined experimentally using high-speed droplet motion data recorded during the rolling phase. Fig. 10 displays the experimental findings and the early formulation's velocity estimate for several ferro-particle scenarios.
Hydrophobic ferroparticle droplets exhibit a faster translational velocity increase than the as-received droplets. However, the gap between the experimental and predicted droplet velocities diverges for the modified ferroparticles due to the interaction between ferroparticles inside the water droplet when the droplet's position alters on the hydrophobic plate, resulting in an incredibly nonlinear magnetic effect on the droplet's motion. As a result, the assumptions made when formulating the droplet's translational velocity were modified to account for the effects of the initial water droplet activity on the wobbling while rolling. The tests are conducted 15 times to ensure the accuracy of the reported data, and although there is less variation between the expected and experimental droplet velocities, both results confirm that the surface is hydrophobic. The findings are consistent, and any minor discrepancies may be attributed to errors in the experiment and assumptions made when calculating the droplet's translational velocity.
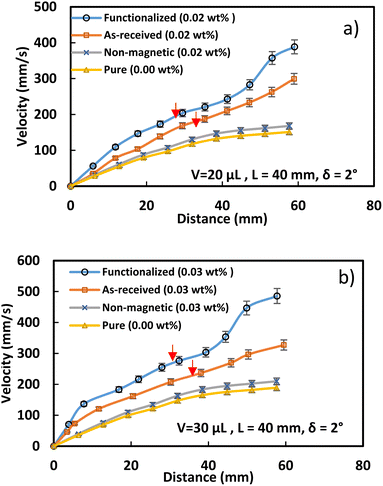
The velocity of the water droplet rises with the functionalized ferroparticle compared to the normal ferroparticle due to the reduced adhesion forces. Fig. 11 shows the translational velocity under the influence of ferro particles for different ferro particles layer widths. The translational velocity increases gradually with the ferroparticle layer width due to increased magnetic influence with the ferro-particle influence. Fig. 12 shows the measured translational velocity under the influence of different ferroparticles conditions. The translational velocities under both as-received and modified ferroparticles are higher than the velocities of pure water droplets due to the pulling effect of the magnetic force for all droplet volumes. However, the functionalized ferroparticles reduce the pining forces; consequently, the translational velocity is more significant than in all other cases. The water droplet mixed with functionalized (hydrophobic) ferro particles will enhance the translation velocity of the droplet due to the reduction of the pining forces between the droplet and the solid surfaces. This is because the hydrophobic ferro particles that cover the droplet surface have low surface free energy. In conclusion, the ferroparticles conditions and concentrations play a vital role in controlling the motion of the water droplets, which is considered a significant feature for many applications.
Conclusions
This study aims to investigate the behaviour of normal/modified ferro droplets on hydrophobic substrates under the influence of a magnetic force. The magnetic field causes slight fluctuations in the contact angle of the droplet on the hydrophobic surface, which is small and mostly remains within the measurement error range of 150° despite varying by approximately 5°. The specific findings are listed below:(1) The magnetic flux can alter the droplet dynamics from sliding into rolling on the surface. The sliding velocity of the droplet increases significantly with higher concentrations of ferroparticles (0.11 wt%), and the bond number rises non-linearly with the water droplet's distance from the magnet.
(2) The ferroparticles in the droplet fluid form an agglomerated structure as the distance between the magnet and the droplet becomes small. Some particles departing from the droplet under the magnetic force, can break a small droplet on the magnet surface. This is more pronounced in the case of a large percentage of ferroparticles (90 wt%). This droplet adheres to the surface of the magnet due to the surface tension force between the droplet and ferroparticles. Ferroparticle separation and the generation of new droplets can happen at a faster rate at higher concentrations of ferroparticles (0.11 wt%) inside the water droplet. After separation, the newborn droplet rolls with significant wobbling on the surface, and its transverse velocity decreases over time. Higher concentrations of ferroparticles inside the droplet fluid lead to a minimum height of the droplet's wobbling.
(3) The water droplet mixed with functionalized (hydrophobic) ferro particles will enhance the translation velocity of the droplet due to the reduction of the pining forces between the droplet and the solid surfaces. Therefore, the translational velocity of functionalized ferrofluid, which is 400 mm s−1, is greater than it is in every other scenario. Because of the weak interfacial force, the newborn droplet from a functionalized ferro droplet is substantially smaller than a regular ferro fluid droplet.
Author contributions
Ghassan Hassan: did the experimental work and wrote the main manuscript text. Abba Abdulhamid Abubakar: did the experimental work. Bekir S. Yilbas: wrote the original draft of the main manuscript text. Hussain Al-Qahtani: reviewed and edited the main manuscript. Abdullah Al-Sharafi: reviewed and edited the main manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the financial support of IRC Renewable Energy and Power System at King Fahd University of Petroleum and Minerals (KFUPM) and King Abdullah City for Atomic and Renewable Energy (K. A. CARE) to accomplish this work.References
- B. Assadsangabi, M. S. M. Ali and K. Takahata, Bidirectional actuation of ferrofluid using micropatterned planar coils assisted by bias magnetic fields, Sens. Actuators, A, 2012, 173, 219–226 CrossRef CAS.
- S. Campelj, D. Makovec and M. Drofenik, Preparation and properties of water-based magnetic fluids, J. Phys.: Condens. Matter, 2008, 20, 204101 CrossRef CAS PubMed.
- W. Yu and H. Xie, A review on nanofluids: preparation, stability mechanisms, and applications, J. Nanomater., 2012, 435873 Search PubMed.
- U. Banerjee and A. K. Sen, Shape evolution and splitting of ferrofluid droplets on a hydrophobic surface in the presence of a magnetic field, Soft Matter, 2018, 14, 2915–2922 RSC.
- M. Latikka, M. Backholm, J. V. I. Timonen and R. H. A. Ras, Wetting of ferrofluids: Phenomena and control, Curr. Opin. Colloid Interface Sci., 2018, 36, 118–129 CrossRef CAS.
- A. Zakinyan, O. Nechaeva and Y. Dikansky, Motion of a deformable drop of magnetic fluid on a solid surface in a rotating magnetic field, Exp. Therm. Fluid Sci., 2012, 39, 265–268 CrossRef.
- J. Jin and N. T. Nguyen, Manipulation schemes and applications of liquid marbles for micro total analysis systems, Microelectron. Eng., 2018, 197, 87–95 CrossRef CAS.
- B. S. Yilbas, et al., Sliding and Rolling Motion of a Ferro-Liquid Droplet on the Hydrophobic Surface under Magnetic Influence, Langmuir, 2022, 38, 3925–3935 CrossRef CAS PubMed.
- A. Syafiq, A. K. Pandey, N. N. Adzman and N. A. Rahim, Advances in approaches and methods for self-cleaning of solar photovoltaic panels, Sol. Energy, 2018, 162, 597–619 CrossRef.
- M. A. Bijarchi, A. Favakeh, E. Sedighi and M. B. Shafii, Ferrofluid droplet manipulation using an adjustable alternating magnetic field, Sens. Actuators, A, 2020, 301, 111753 CrossRef CAS.
- J. Saien, H. Bamdadi and S. Daliri, Liquid-liquid extraction intensification with magnetite nanofluid single drops under oscillating magnetic field, J. Ind. Eng. Chem., 2015, 21, 1152–1159 CrossRef CAS.
- J. Zhang, et al., Synthesis of magnetic iron oxide nanoparticles onto fluorinated carbon fabrics for contaminant removal and oil–water separation, Sep. Purif. Technol., 2017, 174, 312–319 CrossRef CAS.
- P. Das, M. Colombo and D. Prosperi, Recent advances in magnetic fluid hyperthermia for cancer therapy, Colloids Surf., B, 2019, 174, 42–55 CrossRef CAS PubMed.
- H. R. Yun, D. J. Lee, J. R. Youn and Y. S. Song, Ferrohydrodynamic energy harvesting based on air droplet movement, Nano Energy, 2015, 11, 171–178 CrossRef CAS.
- M. Zarei Saleh Abad, M. Ebrahimi-Dehshali, M. A. Bijarchi, M. B. Shafii and A. Moosavi, Visualization of pool boiling heat transfer of magnetic nanofluid, Heat Transfer Res., 2019, 48, 2700–2713 CrossRef.
- W. Xu, Y. Jin, W. Li, Y. Song, S. Gao, B. Zhang, L. Wang, M. Cui, X. Yan and Z. Wang, Triboelectric wetting for continuous droplet transport, Sci. Adv., 2022, 8(51), eade2085 CrossRef CAS PubMed.
- G.-P. Zhu, Q.-Y. Wang, Z.-K. Ma, S.-H. Wu and Y.-P. Guo, Droplet Manipulation under a Magnetic Field: A Review, Biosensors, 2022, 12, 156 CrossRef CAS PubMed.
- J.-X. Zhou, et al., Controlling post-impact dynamics of ferrofluid droplets with magnetic field, Phys. Fluids, 2022, 34, 122117 CrossRef CAS.
- L. Cha, N. Wang, M. Prodanović and M. T. Balhoff, Fluid droplet deformation in ferrofluid exposed to a rotating magnetic field, J. Magn. Magn. Mater., 2022, 555, 169331 CrossRef CAS.
- S. Ganguly, S. Sarkar, T. K. Hota and M. Mishra, Thermally developing combined electroosmotic and pressure-driven flow of nanofluids in a microchannel under the effect of magnetic field, Chem. Eng. Sci., 2015, 126, 10–21 CrossRef CAS.
- S. Ishida, Y. Yang, F. Meng and D. Matsunaga, Field-controlling patterns of sheared ferrofluid droplets, Phys. Fluids, 2022, 34, 63309 CrossRef CAS.
- K. Liu, et al., Bubbling of Ferrofluid Droplets via Coupled Magnetic and Sound Fields, Adv. Mater. Interfaces, 2023, 2201724 CrossRef CAS.
- S. Guba, B. Horváth and I. Szalai, Examination of contact angles of magnetic fluid droplets on different surfaces in uniform magnetic field, J. Magn. Magn. Mater., 2020, 498, 166181 CrossRef CAS.
- H. Asakura, A. Nakajima, M. Sakai, S. Suzuki, Y. Kameshima and K. Okada, Deformation and motion by gravity and magnetic field of a droplet of water-based magnetic fluid on a hydrophobic surface, Appl. Surf. Sci., 2007, 253(6), 3098–3102 CrossRef CAS.
- P. K. Roy, E. Bormashenko, M. Frenkel, I. Legchenkova and S. Shoval, Magnetic field induced motion of water droplets and bubbles on the lubricant coated surface, Colloids Surf., A, 2020, 597, 124773 CrossRef CAS.
- G. Alp, E. Alp and N. Aydogan, Magnetic liquid marbles to facilitate rapid manipulation of the oil phase: Synergistic effect of semifluorinated ligand and catanionic surfactant mixtures, Colloids Surf., A, 2020, 585, 124051 CrossRef CAS.
- L. Mats, R. Young, G. T. T. Gibson and R. D. Oleschuk, Magnetic droplet actuation on natural (Colocasia leaf) and fluorinated silica nanoparticle superhydrophobic surfaces, Sens. Actuators, B, 2015, 220, 5–12 CrossRef CAS.
- W. Y. D. Yong, Z. Zhang, G. Cristobal and W. S. Chin, One-pot synthesis of surface functionalized spherical silica particles, Colloids Surf., A, 2014, 460, 151–157 CrossRef CAS.
- L. Mats, R. Young, G. T. T. Gibson and R. D. Oleschuk, Magnetic droplet actuation on natural (Colocasia leaf) and fluorinated silica nanoparticle superhydrophobic surfaces, Sens. Actuators, B, 2015, 220, 5–12 CrossRef CAS.
- G. Hassan, B. S. Yilbas, S. Bahatab, A. Al-Sharafi and H. Al-Qahtani, A water droplet-cleaning of a dusty hydrophobic surface: influence of dust layer thickness on droplet dynamics, Sci. Rep., 2020, 10(1), 14746 CrossRef CAS PubMed.
- M. Ali Bijarchi, A. Favakeh, E. Sedighi and M. B. Shafıi, Ferrofluid droplet manipulation using an adjustable alternating magnetic field, Sens. Actuators, A, 2020, 301, 111753 CrossRef.
- G. Hassan, B. S. Yilbas, A. Al-Sharafi, H. Al-Qahtani and N. Al-Aqeeli, Water droplet on inclined dusty hydrophobic surface: influence of droplet volume on environmental dust particles removal, RSC Adv., 2019, 9, 3582–3596 RSC.
- D. G. Venkateshan and H. V. Tafreshi, Modelling droplet sliding angle on hydrophobic wire screens, Colloids Surf., A, 2018, 538, 310–319 CrossRef CAS.
- G. Paul, P. K. Das and I. Manna, Motion, deformation and pearling of ferrofluid droplets due to a tunable moving magnetic field, Soft Matter, 2020, 16, 1642–1652 RSC.
- M. Jamali and H. V. Tafreshi, Measuring force of droplet detachment from hydrophobic surfaces via partial cloaking with ferrofluids, Langmuir, 2020, 36, 6116–6125 CrossRef CAS PubMed.
- N. D. DiPietro, C. Huh and R. G. Cox, The hydrodynamics of the spreading of one liquid on the surface of another, J. Fluid Mech., 1978, 84, 529–549 CrossRef.
- N. M. Farhan and H. V. Tafreshi, Using magnetic field to measure detachment force between a nonmagnetic droplet and fibers, Langmuir, 2019, 35, 8490–8499 CAS.
- M. Shikida, K. Takayanagi, H. Honda, H. Ito and K. Sato, Development of an enzymatic reaction device using magnetic bead-cluster handling, J. Micromech. Microeng., 2006, 16, 1875 CrossRef.
- M. Jamali, K. S. Mehta, H. Holweger, M. M. Amrei and H. V. Tafreshi, Controlling detachment residue via magnetic repulsion force, Appl. Phys. Lett., 2021, 118, 191601 CrossRef CAS.
- B. S. Yilbas, et al., Water droplet dynamics on a hydrophobic surface in relation to the self-cleaning of environmental dust, Sci. Rep., 2018, 8, 2984 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06073j |
| This journal is © The Royal Society of Chemistry 2023 |