Open Access Article
Open Access ArticleIntrinsically dominated anomalous Hall effect in pulsed laser deposited epitaxial Co2MnGe ferromagnetic full Heusler alloy thin films†
Ekta Yadav and
Sunil Kumar *
*
Department of Physics, Indian Institute of Technology Delhi, New Delhi 110016, India. E-mail: kumarsunil@physics.iitd.ac.in
First published on 13th October 2023
Abstract
Large size epitaxial thin films of ferromagnetic Co2MnGe full Heusler alloy are grown over MgO(100) substrate by using pulsed laser deposition technique under optimized growth conditions. Metallic behavior is confirmed from the longitudinal resistivity-temperature data, while a minimum in the resistivity at ∼25 K is attributed to the disorder-induced weak localization effect. Importantly, a dominating intrinsic anomalous Hall conductivity value of ∼21 S cm−1 against an overall anomalous Hall conductivity value of ∼36 S cm−1 at the room temperature has been estimated for the epitaxial Co2MnGe film. The dominating intrinsic mechanism is also evident from the near temperature-independent behavior of the overall anomalous Hall conductivity.
1. Introduction
Search for novel materials with potential for advanced technological applications has always been driving the research efforts by material scientists and engineers. Heusler alloys are one of the important breakthrough materials which were discovered for the first time in year 1903,1 since when the number of possible compositions having physical properties spanning multiple fields of the material science has enormously grown. Every time, new observations in one or more of their types, for example, the half-metallicity,2 nontrivial topological states,3 superconductivity,4 have been regenerating the interest in these systems. Co-based ferromagnetic full Heusler alloys are quite interesting systems due to their remarkable characteristics, including the high Curie temperature (Tc), and tunable electronic and magnetic properties.5–7 They possess unique half-metallic property wherein bands of one type spin exhibit metallic nature while the bands of the other are semiconducting or insulating.2,8 Among the possible Co-based ferromagnetic full Heusler alloys, the ternary Co2MnGe has been shown, both theoretically and experimentally, to exhibit half-metallicity2,9,10 along with high Curie temperature, Tc ∼ 905 K (ref. 11) and large saturation magnetization, Ms ∼ 5μB f.u.−1.12 Such properties deem it to be fit for use in spintronic devices, for example, magnetic electrodes in magnetic tunnel junctions13 and magnetic memory devices.10,14,15 The possibility of Co2MnGe as being a Weyl semimetal is strengthened from a recent theoretical study on a clean Co2MnGe system16 and another experimental study using angle-resolved photoemission spectroscopy (ARPES) on Co2MnGe single crystal,9 where two topological cones near the Fermi level could be located. The presence of Berry curvature in the topological non-trivial band structure of a material system is expected to give rise to several unique transport phenomena, including the large anomalous Hall effect (AHE) and chiral anomaly effect.9,17–19In the Hall measurements, AHE manifests itself as an additional contribution in the developed transverse voltage. Fundamentally, the interaction between a spontaneous magnetization (M) and spin–orbit coupling (SOC) in the system is the origin for AHE,20–22 where extrinsic and intrinsic mechanisms are involved. The extrinsic contribution to AHE arises from asymmetric scattering events, such as skew scattering and side jumps, from defects/disorders. On the other hand, the intrinsic mechanism elucidates the role of SOC in the electronic band structure of the ferromagnetic metal. The Karplus and Luttinger theory (KL theory) in terms of Berry phase20,21,23,24 is popularly used to analyze the intrinsic behavior of the AHE. To distinguish between the intrinsic and extrinsic mechanisms contributing to the AHE, experimentally measured anomalous Hall resistivity is analyzed by certain scaling relation with the longitudinal resistivity.19,25,26 While many studies in the literature have explored AHE in Co-based Heusler alloys,3,27–29 there exists only one such study on the Co2MnGe system, where Obaida et al.30 reported AHE in polycrystalline Co2MnGe thin film grown by sputtering. It was inferred from those results that AHE is predominantly influenced by extrinsic scattering, specifically, the skew scattering in the sample. More such studies on the other forms, viz., the epitaxial films and single crystals of Co2MnGe are highly desirable.
In the present study, we report intrinsically dominated AHE in epitaxial Co2MnGe thin films grown on MgO(100) substrate by pulsed laser deposition (PLD) technique under optimized growth conditions. While the epitaxial growth of the Co2MnGe thin films were previously reported using molecular beam epitaxy (MBE)12 and sputtering techniques,31,32 however, the same by using PLD technique on MgO substrate are lacking. Structural properties were investigated by X-ray diffraction and ϕ-scan measurements to establish the epitaxial nature of the films. The dominating intrinsic AHE in the films is established by fitting the experimental results from magnetotransport measurements with appropriate scaling relations. Thus obtained value of the anomalous Hall conductivity (AHC) is found to be of the same order as the theoretically predicted value.16 Since, intrinsic AHE is one of the characteristics of Weyl semimetals,33,34 hence, the dominating intrinsic AHE in epitaxial Co2MnGe thin film indicates the presence of a non-negligible Berry curvature in its electronic structure. Further experiments, such as ARPES on the epitaxially grown films of the Co2MnGe, will be required to affirm the same. Nevertheless, our results from transport measurements provide further linkages for the Co2MnGe Heusler alloy to be categorized as a Weyl semimetal.
2. Experimental details
Co2MnGe thin films were grown on (100)-oriented MgO single crystal substrates using the PLD technique. Base pressure of ∼10−7 mbar was maintained in the deposition chamber inside which, a bulk target (Co: 50%, Mn: 25%, Ge: 25%) was continuously hit by pulsed laser light from an excimer KrF laser (Coherent Inc.) at 248 nm wavelength and variable repetition rate and energy. The laser beam was incident on the target at a 45° incident angle to avoid any plume disorientation. To ensure film homogeneity, the target surface was continuously rotated and toggled at a fixed distance (∼4 cm) below the substrate. Vacuum environment of ∼10−6 mbar was maintained during the deposition process. A range of the growth temperatures, the laser fluences and the laser repetition rates were implemented for the initial optimization process. The optimized growth conditions for epitaxial thin films were with the growth temperature of 773 K, laser fluence of 2.6 J cm−2 and pulse repetition rate of 7 Hz. An in situ post-annealing was conducted at the same temperature for 1 hour to further enhance the crystallinity and chemical ordering.An X-ray diffractometer (PANalytical X'Pert) having Cu-Kα radiation source (λ = 1.5406 Å) was used for analyzing crystal structure and crystalline quality of the Co2MnGe films. ϕ-scan measurements helped to confirm the epitaxial quality of the films while thickness, density, and surface roughness for the film were determined from X-ray reflectivity (XRR) data. Elemental composition of the Co2MnGe film was determined by using electron probe microanalysis (EPMA) as described in the ESI Section S2.† An atomic force microscope (AFM by Asylum Research) was used to investigate the films' surface morphology at room temperature. Magnetization measurements were performed using a magnetic property measurement system (MPMS by Quantum Design, USA). Transport measurements for longitudinal resistivity, magnetoresistance, and AHE were carried out by using a physical property measurement system (PPMS by Quantum Design, USA).
3. Results and discussion
3.1. Structural analysis
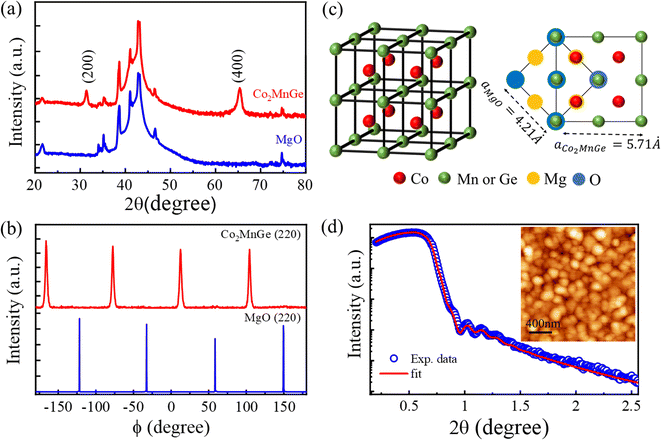
The XRD pattern at room temperature is shown in Fig. 1(a). For a comparison, the data for the bare substrate is also presented. The presence of (200) and (400) reflections at 2θ = 31.34° and 65.3°, respectively, indicates formation of an epitaxial Co2MnGe film with a B2-type structure oriented along (100) direction of the substrate. The absence of any extra peaks is strong evidence of the phase purity of the thin film sample. From these results, we determine the value of the lattice constant to be aCo2MnGe = 5.71 Å, which is in good agreement with the literature.35,36 We estimate mean size of the highly oriented crystallites in the plane of the film to be ∼15 nm from the Scherrer's formula, D = [0.9λ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ], where β is the full width at half-maximum of the diffraction peak, λ is the X-ray wavelength in nm, and θ is the diffraction angle in degrees. Results from ϕ-scan measurements carried out along the (220) plane (2θ = 45.3° and χ = 45°) of the Co2MnGe film and along the (220) plane (2θ = 62.3° and χ = 45°) of the MgO substrate, are shown in Fig. 1(b). Four well-defined peaks, periodically separated from one another with an angular difference of 90°, clearly demonstrate an underlying fourfold crystalline symmetry. To substantiate the epitaxial growth of the Co2MnGe film on the MgO(100) substrate, we also recorded ϕ-scans along the (111) planes (2θ = 27.3° and χ = 54.7°) in which no reflections were observed. From all the above, it can be concluded that (100)-oriented Co2MnGe epitaxial thin film with B2-type crystalline ordering was grown by PLD.
θ], where β is the full width at half-maximum of the diffraction peak, λ is the X-ray wavelength in nm, and θ is the diffraction angle in degrees. Results from ϕ-scan measurements carried out along the (220) plane (2θ = 45.3° and χ = 45°) of the Co2MnGe film and along the (220) plane (2θ = 62.3° and χ = 45°) of the MgO substrate, are shown in Fig. 1(b). Four well-defined peaks, periodically separated from one another with an angular difference of 90°, clearly demonstrate an underlying fourfold crystalline symmetry. To substantiate the epitaxial growth of the Co2MnGe film on the MgO(100) substrate, we also recorded ϕ-scans along the (111) planes (2θ = 27.3° and χ = 54.7°) in which no reflections were observed. From all the above, it can be concluded that (100)-oriented Co2MnGe epitaxial thin film with B2-type crystalline ordering was grown by PLD.
As inferred from the X-ray analysis in the above paragraph, schematic unit cell structure is shown in Fig. 1(c) in which, the crystallographic orientations of Co2MnGe on the MgO substrate are also indicated. In the figure, the picture on the left represents unit cell of the B2-ordered Co2MnGe crystal, where anti-site disorder is present at Mn and Ge positions, while the image on the right is the top-view showing the Co2MnGe unit cell, positioned diagonally on the MgO substrate. The XRR data for the thin film is presented in Fig. 1(d), where the solid red curve is the best fit obtained by following recursive Parratt formalism.37 From the fitting, we obtain the film thickness of 45 ± 1.5 nm and roughness of 3 ± 0.3 nm. The relatively high roughness here can be attributed to the large grain size, as evidenced from the AFM image of the film. The same is presented as inset in Fig. 1(d), from which we estimate an average grain size of ∼180 nm. From the AFM image, the root mean square roughness is estimated to be ∼3.2 nm, a value consistent with the result obtained from the XRR analysis.
3.2. Magnetization, electrical resistivity, and magnetoresistance
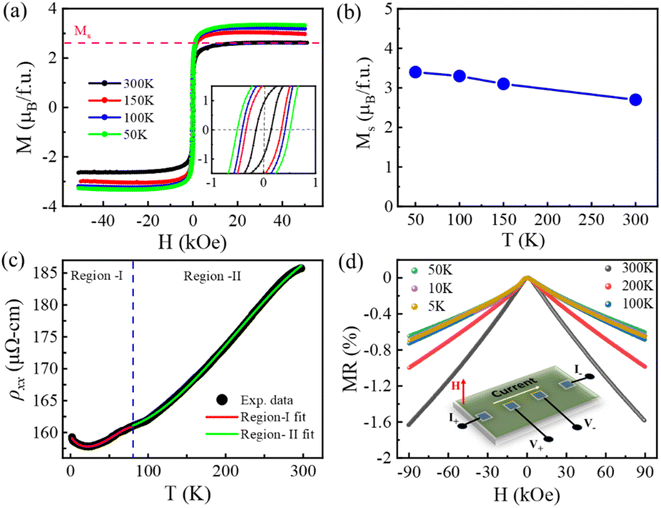
A soft ferromagnetic behavior with coercivity value of 140 Oe at 300 K is evident from the M–H curves recorded at different sample temperatures as shown in Fig. 2(a). We estimate the value of the saturation magnetization to be Ms ∼ 2.7μB f.u.−1 at 300 K and Ms ∼ 3.4μB f.u.−1 at 50 K. These values are smaller than those reported in the literature for L21-phase Co2MnGe.32,38 Indeed, the smaller value of the saturation moment in the present case is consistent with the reduced chemical ordering in the B2-phase Co2MnGe.30,38 Fig. 2(b) shows the variation of Ms with sample temperature. A slight increment in Ms with the decreasing temperature can be attributed to the pinning of magnetic moments at low temperatures.Fig. 2(c) illustrates the behavior of the longitudinal resistivity (ρxx) vs. sample temperature (2–300 K) in the absence of any external magnetic field. The experimentally measured resistivity-temperature curve shows metallic nature of the epitaxial Co2MnGe film. A minimum in the resistivity in the vicinity of 25 K is followed by an upturn as the temperature decreases further. Such type of low-temperature anomaly in the resistivity can be attributed to the disorder-enhanced coherent backscattering of conduction electrons due to weak localization.28,39 The residual resistivity near the lowest temperature of 2 K, due to scattering from the impurities and structural imperfections, is ρxx,0 ∼ 160 μΩ cm. From this result, we obtain residual resistivity ratio [RRR = ρxx(300 K)/ρxx(2 K)] of about 1.2, a value close to the previously reported ones for epitaxial thin films of different Co-based full Heusler alloys.12,39,40
Owing to the spin polarization of conduction electrons at the Fermi energy for one spin channel in half-metallic Heusler alloys, the spin flipping related single magnon scattering is prohibited at low temperatures. The possible scattering mechanisms to affect the temperature-dependent resistivity of a ferromagnet are (a) electron–electron scattering (T2-dependence), (b) electron–phonon scattering (T-dependence), and (c) double magnon scattering (T9/2-dependence at low temperatures and T7/2-dependence at higher temperatures).41 In addition, scattering from disorders is accounted for by a T1/2-dependent term. A careful observation of the experimental data in Fig. 2(c) necessitates fitting in two temperature regions, identified as region-I and region-II that are separated by a demarcation dashed line drawn at temperature of ∼80 K. The continuous curves in Fig. 2(c) are fittings to the data obtained as follows.
The best theoretical fit to the resistivity data in region-I (2–80 K) is obtained by using a relation, ρxx = ρxx,0 − AT1/2 + BT2 + CT9/2. Here ρxx,0 represents the residual resistivity, while the coefficients A, B, and C represent the strengths of the weak localization, electron–electron, and double magnon scattering processes, respectively. Similarly, the best fit to the data in region-II (80–300 K) is obtained by using a relation, ρxx = ρxx,0 + DT + ET2 + FT7/2, where the coefficients D, E and F represent the electron–phonon scattering, electron-magnon scattering and double magnon scattering strengths, respectively. At higher temperatures (region-II), it is imperative to add electron-magnon scattering term to obtain the best fit to the data. Therefore, unlike the case at low-temperatures (region-I), the single magnon scattering becomes viable at high temperatures (region-II) in half-metallic Heusler alloys.42 Moreover, we find that below a certain temperature in region-I, the A-term of ρxx due to weak localization dominates over others before the electron–electron scattering catches up with the increasing temperature. This leads to dip-like shape in region-I of the resistivity-temperature curve. On the other hand, in region-II, the D-term of ρxx due to electron–phonon scattering is dominant over the other processes. Double magnon scattering contributes to the T9/2-dependence at low temperatures (region-I) and T7/2-dependence at higher temperatures (region-II).43 Therefore, half-metallic nature of the Co2MnGe epitaxial film is evidenced from the resistivity-temperature data in the entire range of 2–300 K.
Results for the magnetoresistance (MR) of the Co2MnGe epitaxial film are obtained by sweeping out-of-plane magnetic field from H = −90 kOe to +90 kOe. The same recorded at different sample temperatures are presented in Fig. 2(d). The linear four-probe geometry used for these measurements is also shown schematically in the inset of the figure. The MR in percentage is defined as 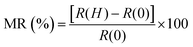 , where R(0) is the resistance of the film at H = 0 kOe. It can be seen from the figure that the MR value is quite small and negative at all the investigated temperatures, from the lowest of 5 K to the highest of the room temperature. The above seems a usual behavior of the MR in different ferromagnetic Heusler alloys.19,44
, where R(0) is the resistance of the film at H = 0 kOe. It can be seen from the figure that the MR value is quite small and negative at all the investigated temperatures, from the lowest of 5 K to the highest of the room temperature. The above seems a usual behavior of the MR in different ferromagnetic Heusler alloys.19,44
3.3. Anomalous Hall effect
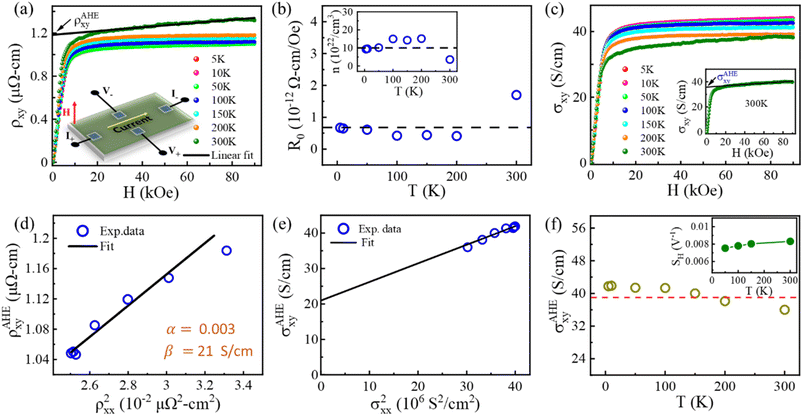
Dominating intrinsic AHE in epitaxial Co2MnGe thin films is established here from detailed magnetotransport measurements performed over a temperature range of 5–300 K. The results for experimentally measured Hall resistivity ρxy are presented in Fig. 3(a) for different sample temperatures in the entire range. For these measurements, a rectangular piece of the sample having dimensions of 5 mm × 3 mm was utilized on which electrical contacts were made in the Hall geometry, as shown schematically in the inset of Fig. 3(a). Contributions from voltage probe misalignment are avoided by averaging for opposite fields in the form,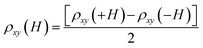 . The magnetic field was swept from H = −90 kOe to +90 kOe and measurements were repeated at different temperatures. A minimal dc charge current of 100 μA was used in these experiments. As can be seen from Fig. 3(a), the Hall resistivity initially increases sharply up to a field of ∼10 kOe, before the slope of the curves changes drastically. Therefore, two regions in the Hall resistivity curves can be clearly distinguished. Such a behaviour of total ρxy in a ferromagnetic system can be expressed in terms of an ordinary Hall resistivity, ρOHExy and anomalous Hall resistivity, ρAHExy, via the following relation20,45
. The magnetic field was swept from H = −90 kOe to +90 kOe and measurements were repeated at different temperatures. A minimal dc charge current of 100 μA was used in these experiments. As can be seen from Fig. 3(a), the Hall resistivity initially increases sharply up to a field of ∼10 kOe, before the slope of the curves changes drastically. Therefore, two regions in the Hall resistivity curves can be clearly distinguished. Such a behaviour of total ρxy in a ferromagnetic system can be expressed in terms of an ordinary Hall resistivity, ρOHExy and anomalous Hall resistivity, ρAHExy, via the following relation20,45| ρxy = ρOHExy + ρAHExy = R0H + 4πRSM | (1) |
Fig. 3(b) displays the values of R0 at all temperatures obtained by the fitting procedure as discussed above. Positive values of R0 indicate that holes are majority charge carriers in the whole temperature range. Using the relation, n = 1/R0e, where e is electronic charge, we have also calculated the hole concentration n in the film at different temperatures as shown in the inset of Fig. 3(b). The mean value of the hole concentration in the film at all temperatures is n ∼ 1022 to 1023 cm−3, which is sufficiently large to provide metal-like behaviour in the electrical resistivity, as discussed earlier.
Magnetic field-dependent Hall conductivity, σxy(H) can be obtained by using the relation46
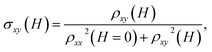 | (2) |
The temperature dependent anomalous Hall resistivity is now analysed here. We first plot the ρAHExy as a function of the squared longitudinal resistivity, ρxx2 at the varying sample temperatures, as shown in Fig. 3(d). To extract the contributions from the intrinsic and extrinsic mechanisms in the AHE, a scaling relation as proposed by Tian et al.25 and popularly known as the TYJ model is used, according to which,
| ρAHExy(T) = αρxx,0 + βρxx2(T) | (3) |
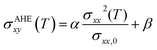 , where
, where 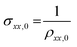 ,
, 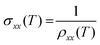 , and the intercept value β directly providing the numerical value of the intrinsic anomalous Hall conductivity. The corresponding result and linear fit are shown in Fig. 3(e) and the same value of σAHE,inxy ∼ 21 S cm−1 is obtained from it in the limit of σxx → 0. By comparing thus obtained values of σAHE,inxy and overall σAHExy (300 K), we conclude that intrinsically dominated AHE occurs in epitaxial Co2MnGe thin film in the current study. Furthermore, by following the procedure in eqn (2) and the results in Fig. 3(c) for each individual sample temperature, the values of σAHExy at all temperatures are plotted in Fig. 3(f). From such a representation33,50 and the observation of nearly temperature independent σAHExy, we get further evidence of intrinsically dominating AHC. We note that almost same temperature-dependent behavior is shown by the saturation magnetization MS in Fig. 2(b) and the anomalous Hall conductivity σAHExy in Fig. 3(f). Therefore, σAHExy is approximately proportional to MS, indicating constant behaviour of the scaling coefficient,
, and the intercept value β directly providing the numerical value of the intrinsic anomalous Hall conductivity. The corresponding result and linear fit are shown in Fig. 3(e) and the same value of σAHE,inxy ∼ 21 S cm−1 is obtained from it in the limit of σxx → 0. By comparing thus obtained values of σAHE,inxy and overall σAHExy (300 K), we conclude that intrinsically dominated AHE occurs in epitaxial Co2MnGe thin film in the current study. Furthermore, by following the procedure in eqn (2) and the results in Fig. 3(c) for each individual sample temperature, the values of σAHExy at all temperatures are plotted in Fig. 3(f). From such a representation33,50 and the observation of nearly temperature independent σAHExy, we get further evidence of intrinsically dominating AHC. We note that almost same temperature-dependent behavior is shown by the saturation magnetization MS in Fig. 2(b) and the anomalous Hall conductivity σAHExy in Fig. 3(f). Therefore, σAHExy is approximately proportional to MS, indicating constant behaviour of the scaling coefficient, 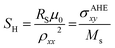 with respect to the temperature. Here, μ0 is the vacuum permeability. The same can be evidenced from our results as shown in the inset of Fig. 3(f), thereby, confirming the dominating intrinsic contribution to AHC.29,51
with respect to the temperature. Here, μ0 is the vacuum permeability. The same can be evidenced from our results as shown in the inset of Fig. 3(f), thereby, confirming the dominating intrinsic contribution to AHC.29,51
4. Conclusions
To summarize, we have synthesized epitaxial thin films of ferromagnetic Co2MnGe Heusler alloy on MgO(100) substrate by using PLD under optimized growth conditions. Structural and morphological investigations have revealed uniformly oriented large-size grains in B2-phase. An in-plane saturation magnetization value of ∼3.4μB f.u.−1 at 50 K, and ∼2.7μB f.u.−1 at 300 K was measured for the above metallic thin film whose longitudinal electrical resistivity is minimum around temperature of ∼25 K due to the presence of a weak localization effect. An expanded scaling mechanism has been performed to analyze the experimentally measured anomalous Hall resistivity, which confirms a dominating intrinsic origin of AHE in the epitaxial Co2MnGe thin film.Author contributions
SK supervised the work. EY performed the experiments. SK and EY analyzed the results and wrote the manuscript.Conflicts of interest
The authors declare no conflict of interests.Acknowledgements
SK acknowledges the Science and Engineering Research Board (SERB), Department of Science and Technology, Government of India, for financial support through Project No. CRG/2020/000892. Joint Advanced Technology Center, IIT Delhi is also acknowledged for support through EMDTERA#5 project. EY acknowledges the University Grant Commission, Government of India, for Senior Research Fellowship. We acknowledge the Central Research Facility, IIT Delhi for PPMS measurements, and the Physics Department, IIT Delhi for PLD, MPMS, AFM and XRD facilities.References
- F. Heusler, Verh. Dtsch. Phys. Ges., 1903, 5, 219 CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429 CrossRef.
- I. Belopolski, K. Manna, D. S. Sanchez, G. Chang, B. Ernst, J. Yin, S. S. Zhang, T. Cochran, N. Shumiya, H. Zheng, B. Singh, G. Bian, D. Multer, M. Litskevich, X. Zhou, S.-M. Huang, B. Wang, T.-R. Chang, S.-Y. Xu, A. Bansil, C. Felser, H. Lin and M. Z. Hasan, Science, 2019, 365, 1278–1281 CrossRef CAS PubMed.
- J. Goraus, J. Czerniewski, K. Prusik and M. Fijałkowski, J. Alloys Compd., 2021, 867, 159078 CrossRef CAS.
- T. Graf, C. Felser and S. S. P. Parkin, Prog. Solid State Chem., 2011, 39, 1–50 CrossRef CAS.
- H. C. Kandpal, G. H. Fecher and C. Felser, J. Phys. D: Appl. Phys., 2007, 40, 1507 CrossRef CAS.
- J. Kübler, G. H. Fecher and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024414 CrossRef.
- R. A. de Groot, F. M. Mueller, P. G. v. Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024–2027 CrossRef CAS.
- T. Kono, M. Kakoki, T. Yoshikawa, X. Wang, K. Goto, T. Muro, R. Y. Umetsu and A. Kimura, Phys. Rev. Lett., 2020, 125, 216403 CrossRef CAS PubMed.
- S. Picozzi, A. Continenza and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 094423 CrossRef.
- T. Taira, T. Ishikawa, N. Itabashi, K.-i. Matsuda, T. Uemura and M. Yamamoto, Appl. Phys. Lett., 2009, 94, 072510 CrossRef.
- T. Ambrose, J. J. Krebs and G. A. Prinz, Appl. Phys. Lett., 2000, 76, 3280–3282 CrossRef CAS.
- D. Asakura, T. Koide, S. Yamamoto, K. Tsuchiya, T. Shioya, K. Amemiya, V. R. Singh, T. Kataoka, Y. Yamazaki, Y. Sakamoto, A. Fujimori, T. Taira and M. Yamamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 184419 CrossRef.
- K. Gross, P. Szary, O. Petracic, F. Brüssing, K. Westerholt and H. Zabel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 054456 CrossRef.
- S. Jena, M. Zzaman, V. K. Verma, K. Ishigami, G. Shibata, T. Ishikawa, G. f. Li, M. Yamamoto, R. Shahid, T. Koide, A. Fujimori and V. R. Singh, Phys. B, 2022, 627, 413619 CrossRef CAS.
- A. Sharan, F. Crasto de Lima, S. Khalid, R. H. Miwa and A. Janotti, Phys. Status Solidi - Rapid Res. Lett., 2022, 16, 2100652 CrossRef CAS.
- M. Hirschberger, S. Kushwaha, Z. Wang, Q. Gibson, S. Liang, C. A. Belvin, B. A. Bernevig, R. J. Cava and N. P. Ong, Nat. Mater., 2016, 15, 1161–1165 CrossRef CAS PubMed.
- T. Suzuki, R. Chisnell, A. Devarakonda, Y. T. Liu, W. Feng, D. Xiao, J. W. Lynn and J. G. Checkelsky, Nat. Phys., 2016, 12, 1119–1123 Search PubMed.
- K. Manna, L. Muechler, T.-H. Kao, R. Stinshoff, Y. Zhang, J. Gooth, N. Kumar, G. Kreiner, K. Koepernik, R. Car, J. Kübler, G. H. Fecher, C. Shekhar, Y. Sun and C. Felser, Phys. Rev. X, 2018, 8, 041045 Search PubMed.
- N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539–1592 CrossRef.
- R. Karplus and J. M. Luttinger, Phys. Rev., 1954, 95, 1154–1160 CrossRef.
- S. Onoda, N. Sugimoto and N. Nagaosa, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165103 CrossRef.
- R. Takahashi and N. Nagaosa, Phys. Rev. B, 2015, 91, 245133 CrossRef.
- D. Xiao, M.-C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959–2007 CrossRef CAS.
- Y. Tian, L. Ye and X. Jin, Phys. Rev. Lett., 2009, 103, 087206 CrossRef PubMed.
- L. Wu, K. Zhu, D. Yue, Y. Tian and X. Jin, Phys. Rev. B, 2016, 93, 214418 CrossRef.
- Y. Zhang, Y. Yin, G. Dubuis, T. Butler, N. V. Medhekar and S. Granville, npj Quantum Mater., 2021, 6, 17 CrossRef CAS.
- S. Husain, A. Kumar, S. Akansel, P. Svedlindh and S. Chaudhary, J. Magn. Magn. Mater., 2017, 442, 288–294 CrossRef CAS.
- S. Roy, R. Singha, A. Ghosh, A. Pariari and P. Mandal, Phys. Rev. B, 2020, 102, 085147 CrossRef CAS.
- M. Obaida, K. Westerholt and H. Zabel, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184416 CrossRef.
- T. Ishikawa, T. Marukame, K.-i. Matsuda, T. Uemura, M. Arita and M. Yamamoto, J. Appl. Phys., 2006, 99, 08J110 CrossRef.
- M. Yamamoto, T. Marukame, T. Ishikawa, K. Matsuda, T. Uemura and M. Arita, J. Phys. D: Appl. Phys., 2006, 39, 824–833 CrossRef CAS.
- Q. Wang, Y. Xu, R. Lou, Z. Liu, M. Li, Y. Huang, D. Shen, H. Weng, S. Wang and H. Lei, Nat. Commun., 2018, 9, 3681 CrossRef PubMed.
- K. Manna, Y. Sun, L. Muechler, J. Kübler and C. Felser, Nat. Rev. Mater., 2018, 3, 244–256 CrossRef CAS.
- M. Özduran, A. Candan, S. Akbudak, A. K. Kushwaha and A. İyigör, J. Alloys Compd., 2020, 845, 155499 CrossRef.
- S. Ishida, S. Fujii, S. Kashiwagi and S. Asano, J. Phys. Soc. Jpn., 1995, 64, 2152–2157 CrossRef CAS.
- L. G. Parratt, Phys. Rev., 1954, 95, 359–369 CrossRef.
- A. Rajanikanth, Y. K. Takahashi and K. Hono, J. Appl. Phys., 2007, 101, 023901 CrossRef.
- Q. Wang, Z. Wen, T. Kubota, T. Seki and K. Takanashi, Appl. Phys. Lett., 2019, 115, 252401 CrossRef.
- A. Markou, D. Kriegner, J. Gayles, L. Zhang, Y.-C. Chen, B. Ernst, Y.-H. Lai, W. Schnelle, Y.-H. Chu, Y. Sun and C. Felser, Phys. Rev. B, 2019, 100, 054422 CrossRef CAS.
- L. Bainsla, K. G. Suresh, A. K. Nigam, M. Manivel Raja, B. S. D. C. S. Varaprasad, Y. K. Takahashi and K. Hono, J. Appl. Phys., 2014, 116, 203902 CrossRef.
- C. G. F. Blum, C. A. Jenkins, J. Barth, C. Felser, S. Wurmehl, G. Friemel, C. Hess, G. Behr, B. Büchner, A. Reller, S. Riegg, S. G. Ebbinghaus, T. Ellis, P. J. Jacobs, J. T. Kohlhepp and H. J. M. Swagten, Appl. Phys. Lett., 2009, 95, 161903 CrossRef.
- S. Chatterjee, J. Sau, S. Samanta, B. Ghosh, N. Kumar, M. Kumar and K. Mandal, Phys. Rev. B, 2023, 107, 125138 CrossRef CAS.
- D. Zhang, Z. Hou and W. Mi, Appl. Phys. Lett., 2022, 120, 232401 CrossRef CAS.
- M. S. Gabor, M. Belmeguenai, T. Petrisor, C. Ulhaq-Bouillet, S. Colis and C. Tiusan, Phys. Rev. B, 2015, 92, 054433 CrossRef.
- S. Tong, Z. Xupeng, D. Wei and J. Zhao, Phys. Rev. B, 2020, 101, 184434 CrossRef CAS.
- K. I. A. Khan, R. S. Yadav, H. Banxgar, A. Kumar, N. Chowdhury, P. K. Muduli and P. K. Muduli, Nanoscale, 2022, 14, 8484–8492 RSC.
- L. Ye, M. Kang, J. Liu, F. von Cube, C. R. Wicker, T. Suzuki, C. Jozwiak, A. Bostwick, E. Rotenberg, D. C. Bell, L. Fu, R. Comin and J. G. Checkelsky, Nature, 2018, 555, 638–642 CrossRef CAS PubMed.
- J. Shen, Q. Yao, Q. Zeng, H. Sun, X. Xi, G. Wu, W. Wang, B. Shen, Q. Liu and E. Liu, Phys. Rev. Lett., 2020, 125, 086602 CrossRef CAS PubMed.
- G. K. Shukla, J. Sau, N. Shahi, A. K. Singh, M. Kumar and S. Singh, Phys. Rev. B, 2021, 104, 195108 CrossRef CAS.
- Q. Wang, S. Sun, X. Zhang, F. Pang and H. Lei, Phys. Rev. B, 2016, 94, 075135 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06132a |
| This journal is © The Royal Society of Chemistry 2023 |