Open Access Article
Open Access ArticleUnsupervised deep learning for molecular dynamics simulations: a novel analysis of protein–ligand interactions in SARS-CoV-2 Mpro†
Jessica Mustali a,
Ikki Yasudab,
Yoshinori Hirano
a,
Ikki Yasudab,
Yoshinori Hirano b,
Kenji Yasuokab,
Alfonso Gautieria and
Noriyoshi Arai
b,
Kenji Yasuokab,
Alfonso Gautieria and
Noriyoshi Arai *b
*b
aDepartment of Electronics, Information and Bioengineering, Politecnico di Milano, Italy
bDepartment of Mechanical Engineering, Keio University, Japan. E-mail: arai@mech.keio.ac.jp
First published on 22nd November 2023
Abstract
Molecular dynamics (MD) simulations, which are central to drug discovery, offer detailed insights into protein–ligand interactions. However, analyzing large MD datasets remains a challenge. Current machine-learning solutions are predominantly supervised and have data labelling and standardisation issues. In this study, we adopted an unsupervised deep-learning framework, previously benchmarked for rigid proteins, to study the more flexible SARS-CoV-2 main protease (Mpro). We ran MD simulations of Mpro with various ligands and refined the data by focusing on binding-site residues and time frames in stable protein conformations. The optimal descriptor chosen was the distance between the residues and the center of the binding pocket. Using this approach, a local dynamic ensemble was generated and fed into our neural network to compute Wasserstein distances across system pairs, revealing ligand-induced conformational differences in Mpro. Dimensionality reduction yielded an embedding map that correlated ligand-induced dynamics and binding affinity. Notably, the high-affinity compounds showed pronounced effects on the protein's conformations. We also identified the key residues that contributed to these differences. Our findings emphasize the potential of combining unsupervised deep learning with MD simulations to extract valuable information and accelerate drug discovery.
Introduction
The landscape of drug discovery has been traditionally characterized by profound challenges, such as escalating costs and protracted timelines. At present, the costs associated with drug development have escalated to exceed US$2.8 billion, and the process requires an average of 14 years to reach fruition.1–3 To overcome these hurdles, computational methods have become increasingly prevalent in pipelines for expediting drug–discovery processes.4–6 Among these methods, molecular dynamics (MD) simulations have pushed the confines of computationally driven drug discovery and design over the past decades, owing to the increasing availability of computational power and suitable software.7,8 Offering a dynamic, atomistic view of protein–ligand interactions, MD simulations represent a powerful tool in biophysics research.The successful discovery and design of therapeutic agents significantly depends on the depth of our understanding of protein–ligand interactions.9 The profound influence of these interactions on the pharmacodynamics and pharmacokinetics of drugs provides a rationale for the major emphasis laid on their study in the field of drug discovery and design.10,11 Comprehensive characterization of the protein–ligand interaction landscape can guide the optimization of lead compounds, facilitate predictions of drug responses, and help avoid undesirable off-target effects.12,13 However, decoding the intricate dynamics of protein–ligand interactions poses a formidable challenge owing to their inherent complexity and multifaceted nature.14,15 The classic static view of protein–ligand interactions, based primarily on the structures obtained from X-ray crystallography and NMR spectroscopy, does not capture the conformational dynamics and energetic nuances of protein–ligand crosstalk. MD simulations can provide perspectives beyond this static view, explore the dynamic behavior of protein–ligand systems in atomistic detail, and capture their temporal evolution.16 These simulations can unravel the thermodynamic and kinetic properties of protein–ligand interactions by incorporating structural flexibility and entropic effects. Thus, they provide insights into both enthalpic and entropic contributions to the binding free energy.17–19 However, the inherent complexity of the data generated by MD simulations and the high computational cost of long-duration simulations remain substantial challenges.16,20
The synergy of machine learning (ML), particularly deep learning, with MD simulations represents a promising frontier in molecular system research. The applications of ML and deep-learning methods in MD simulations are diverse and growing. They range from deriving classical potential energy surfaces from quantum mechanical calculations21–27 to enhancing MD sampling by learning bias potentials,28–32 and even include generating samples from the equilibrium distribution of a molecular system without performing MD altogether, as exemplified by Boltzmann generators.33,34 Recently emerged graph neural network (GNN)-based machine learned potentials (MLPs) have demonstrated excellent accuracy in predicting forces directly from atomic structures of biomolecules as well as small molecules.35–38 ML algorithms that perform tasks such as dimensionality reduction, clustering, regression, and classification have also been proven to be conceptually potent tools for analyzing the large datasets obtained from MD simulations.8,39–41
While these applications enshrine the potential of ML and deep learning in this field, their specific application to the analysis of MD simulation data in the context of protein–ligand interactions has emerged only recently. Significant progress has been made in this direction using supervised training. Supervised machine-learning algorithms were successfully applied to the classification of ligand-determined GPCR conformational properties by Plante et al.42 This and other studies43–45 have outlined the potential of ML to extract valuable functional information from MD simulation trajectories of protein–ligand complexes, setting the stage for future advances in this field. Despite this promise, the lack of labeled data represents a major limitation in the implementation of supervised deep-learning approaches,46,47 and other issues that may affect the prediction quality of supervised deep neural networks include the dependence on the dataset and thus on experimental conditions. Thus, the need for data standardization and curation precedes the construction of robust predictive models.48 Consequently, the implementation of unsupervised techniques to circumvent these concerns offers distinct advantages.49,50 Deep neural networks (DNNs) within unsupervised frameworks can learn the hierarchical representations of data and identify complex patterns in unlabelled high-dimensional MD data. This enables the capture of intricate protein–ligand interaction dynamics, which are often challenging to identify through traditional means. By producing a compact, lower-dimensional representation of MD data, these models facilitate in-depth exploration of system dynamics. Furthermore, the application of deep-learning models can reveal relationships between protein conformational dynamics and ligand-binding affinities, which would otherwise be difficult to identify. Considering this potential, a novel approach using unsupervised DNNs to extract features from the MD trajectory data of protein–ligand complexes was introduced in a previous paper.51 Their study showed that differences in protein dynamics induced by ligands are indicative of binding energy. However, the benchmarks in that study were limited to bromodomain 4, a rigid protein with diverse ligand structures, and protein tyrosine phosphatase 1B, a flexible loop-containing protein with a similar ligand structure. Therefore, these methods have not yet been validated against flexible proteins with various ligand structures.
In this study, we demonstrate the potency of this approach for the analysis of more complex flexible protein systems through a case study of the SARS-CoV-2 main protease (Mpro). Mpro is a key target for drug design against SARS-CoV-2 because of its critical role in mediating viral replication and transcription, high sequence conservation with other coronaviruses, and lack of human homologs.52 An oral drug named Paxlovid (nirmatrelvir and ritonavir) has been approved for the inhibition of Mpro,53,54 but its application is limited because of drug–drug interactions55 and rebound effects.56,57 Understanding the dynamics of Mpro, both in its ligand-free form and when bound to potential inhibitors, is of significant interest in the ongoing efforts to develop extended and alternative treatments against SARS-CoV-2.
With the research presented here, we aim to offer valuable insights into the complex interplay between dynamic protein conformations and ligand binding by utilizing an advanced analytical framework that employs unsupervised deep learning for MD simulations. We believe that the innovative approach presented in this study holds significant potential for transforming the current landscape of protein–ligand complex analyses and drug discovery.
Materials and methods
In this study, we analyzed the structural and dynamic patterns induced by 11 different ligands on the SARS-CoV-2 main protease (Mpro or 3CLpro). The success of our machine learning-driven analysis relies on a substantial dataset obtained through extensive MD simulations, providing rich temporal information on the protein–ligand interactions. Our deep learning model calculated Wasserstein distance between different simulation data via unsupervised learning. Here, MD simulation data is used to train the deep learning model, and Wasserstein distance is calculated for the same dataset by iteratively training the model.58 We performed three independent simulations, each spanning one microsecond, for each of the 11 protein–ligand systems, which we believe produce a sufficient amount of data. These simulations captured a diverse range of conformational states and ligand-induced dynamics (Fig. 1). The molecular dynamics simulations exhibited a performance rate of 310 ns day−1, resulting in an approximate runtime of 77 hours for each simulation. Subsequently, the ML-driven analysis of the MD trajectories was completed within a single day. It's worth noting that while our approach may entail a relatively longer processing time compared to supervised learning methods, it doesn't rely on the availability of labeled data. In this section, we present methods for MD simulations, extracting features, refining MD data, and briefly introduce the ML approach.51Molecular dynamics simulations
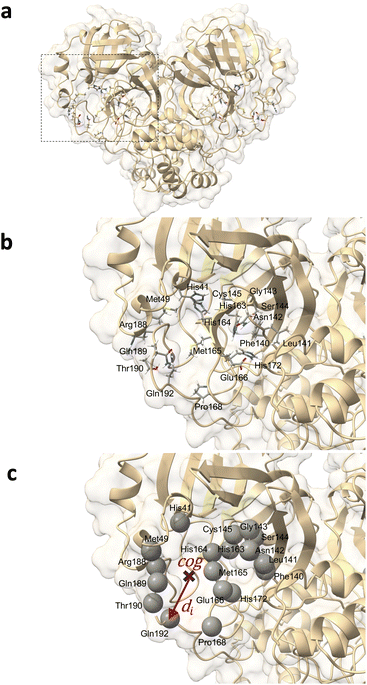
We performed MD simulations of Mpro in the apo- and ligand-binding forms (1a). Mpro is a homodimeric cysteine protease composed of 306 amino acids per monomer. Each monomer contains three subdomains; domains I and II (residues 8–101 and 102–184, respectively) are characterized mainly by β-barrel motifs, whereas domain III (residues 201–306) primarily consists of α-helices.59–61 The substrate-binding region is located at the interface of domains I and II and consists of the key active-site residues Met49, Gly143, His163, His164, Glu166, Pro168, and Gln189, as well as Tyr54, Gly143, His163, which form an oxyanion loop. In addition, the Mpro active site cleaves peptide bonds using a catalytic dyad formed by a cysteine residue (Cys145) and a histidine residue (His41).The structures of the apo- and holo-SARS-CoV-2 main protease (Mpro) were obtained from the Protein Data Bank62 (PDB ID: 6M03, 6M2N, 6XMK, 6Y2F, 7JU7, 7K6D, 7K40, 7JYC, 6LZE, 6M0K, and 6WTK7,59,61,63–70). The inhibitors of Mpro we considered in this study have various molecular weights, ranging from 270.24 g mol−1 to 709.98 g mol−1, and a broad spectrum of IC50 values, ranging from 0.04 μM to 10.7 μM (Table 1). Missing atoms from these structures were added using the homology model module of the molecular operating environment (MOE) software.71 The protonation state of the amino acids in the 6M03 system (apo structure) was set to pH 7 using protonate 3D in MOE. The protonation states of the amino acids of other protein structures were fitted to those of the 6M03 system, and the number of amino acids was set to 712 (homodimer of 306). These initially modeled protein structures were referred to as the initial structures, and their pocket conformations were nearly identical to those of the corresponding X-ray crystallographic (PDB) structures. Each ligand was responsible for recognizing the N-terminal fragments of the substrate peptide non-covalently occupying the active-site cleft of each Mpro monomer. The total charge of each ligand was set to neutral. To compare the effects of ligand charge on Mpro, we also prepared a 7JU7 system with a positively charged (pos) ligand in addition to a neutral one. The force fields of Mpro and each ligand were amber14SB72 and the general AMBER force field (GAFF),73 respectively. The partial charges for each ligand were calculated at the RHF/6-31G** level using Gaussian 16 software74 and fitted by restrained electrostatic potential (RESP) charge fitting in the antechamber on AmberTools18.75
| Cpd | PDB | Ligand | MW (g mol−1) | IC50 (μM) | Refs. |
|---|---|---|---|---|---|
| 1 | 6M0K | FJC | 464.49 | 0.04 | 61 |
| 2 | 6LZE | FHR | 452.55 | 0.053 | 61 |
| 3 | 6WTK | UED | 405.49 | 0.4 | 70 |
| 4 | 6XMK | QYS | 527.58 | 0.48 | 83 |
| 5 | 6Y2F | O6K | 595.69 | 0.67 | 59 |
| 6 | 6M2N | 3WL | 270.24 | 0.94 | 84 |
| 7 | 7JU7 | G65 | 498.64 | 2.5 | 85 |
| 8 | 7K40 | U5G | 521.69 | 4.13 | 86 |
| 9 | 7JYC | NNA | 709.98 | 5.73 | 86 |
| 10 | 7K6D | SV6 | 681.87 | 10.7 | 87 |
The following steps for MD simulations were performed using GROMACS 2023.76 The apo-protein and protein–ligand complexes were solvated in a periodic cubic water box of 10 nm, with TIP3P77 water molecules used as the solvent model. The systems were then neutralized with the addition of Cl− ions and Na+ ions, with the ionic strength set to 0.15 M, resulting in a total of ≈100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. Preliminary system energy minimisations were performed using the steepest descent algorithm for 10
000 atoms. Preliminary system energy minimisations were performed using the steepest descent algorithm for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, until the maximum force was reduced to less than 10.0 kJ mol−1. Subsequently, the systems were equilibrated in the NVT ensemble for 200 ps at 310 K using the velocity-rescaling method,78 followed by NPT equilibration at 1 bar for 200 ps using the Berendsen barostat.79 The heavy atoms of the protein were restrained in equilibrium processes with a spring constant of 1000 kJ per mol nm.2 Nonbonding interactions were computed using a cutoff value for the neighbor list at 1 nm, and the potential-shift-Verlet approach with a cutoff of 1.0 nm was used to handle van der Waals interactions, whereas the particle-mesh Ewald method was applied to describe electrostatic interactions. The LINCS algorithm was used to constrain the h-bonds, thus allowing a time step of 2 fs. The production phase consisted of three independent MD replicates for each system with a random initial velocity. Each simulation had a duration of 1 μs, and was performed using the velocity-rescaling method for temperature control and a Parinello-Rahman barostat.80 The coordinates are saved every 2 ps, resulting in 500
000 steps, until the maximum force was reduced to less than 10.0 kJ mol−1. Subsequently, the systems were equilibrated in the NVT ensemble for 200 ps at 310 K using the velocity-rescaling method,78 followed by NPT equilibration at 1 bar for 200 ps using the Berendsen barostat.79 The heavy atoms of the protein were restrained in equilibrium processes with a spring constant of 1000 kJ per mol nm.2 Nonbonding interactions were computed using a cutoff value for the neighbor list at 1 nm, and the potential-shift-Verlet approach with a cutoff of 1.0 nm was used to handle van der Waals interactions, whereas the particle-mesh Ewald method was applied to describe electrostatic interactions. The LINCS algorithm was used to constrain the h-bonds, thus allowing a time step of 2 fs. The production phase consisted of three independent MD replicates for each system with a random initial velocity. Each simulation had a duration of 1 μs, and was performed using the velocity-rescaling method for temperature control and a Parinello-Rahman barostat.80 The coordinates are saved every 2 ps, resulting in 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps.
000 steps.
The stability of the system was assessed by monitoring the convergence of the root mean square deviation (RMSD) of the protein. To determine the structural elasticity and residual fluctuation, the root mean square fluctuation (RMSF) profiles of the Cα atoms in the MD-simulated ensembles were calculated. To monitor the movement of the ligands relative to the binding pocket, we used the RMSD of the heavy atoms of the ligand after superimposing the backbone-binding site residues onto the reference structure.
The figures in the article were generated using VMD81 and UCSF Chimera,82 while the analysis was performed via scripts written in Python 3.11 using the matplotlib libraries for plotting, and pandas, numpy, and scipy for data handling and statistics.
Descriptors of molecular systems from MD data
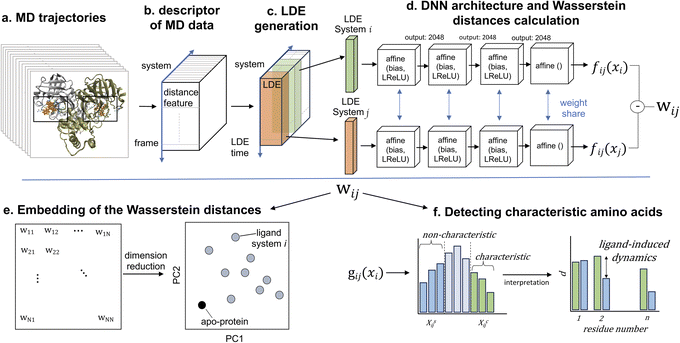
After obtaining trajectory data from MD simulations, a pivotal step is the selection of an appropriate trajectory-derived descriptor. This descriptor adequately represents the systems of interest for subsequent analyses using the DNN (Fig. 1b). We focused our analysis on the binding-site residues of these proteins. The rationale behind this choice relies on the ability to capture the difference in protein behavior in the context of ligand binding while dramatically reducing the dimensionality and computational cost considering the trajectories of all particles in the system. In a previous study,51 the protein fluctuation of binding-site residues in Cartesian coordinates was selected. However, in contrast to the relatively rigid proteins considered in that study, Mpro is highly flexible because its binding pocket consists of flexible loops,88–92 meaning that the fitting of structures may cause biases, and significant conformational changes can occur. Therefore, our descriptor was required to overcome two challenges: (1) the descriptor should avoid dependency on coordinate changes, and (2) conformations associated with the dynamics should be considered. After testing both coordinates and distance, we selected the distance between the center of mass of the binding-pocket residues (binding-site residue determination is discussed below) and the center of geometry of the binding-pocket. The selected distance conveys relevant information regarding Mpro structural and dynamic differences, providing a robust description of the thermodynamic and kinetic properties of the systems.11,93,94 In addition, the distance representation of the trajectory is not affected by mixing the overall rotation and internal motion, which are issues that affect Cartesian coordinates.95 Comparisons of different types of descriptors are presented in the results section.Selection of the binding-pocket residues
The binding-site residues were selected by an analysis using the AmberTools CPPTRAJ nativecontacts module combined with the GROMACS distance module and VMD for visual inspection. For this purpose, trajectories spanning the last 200 ns were considered to determine protein–ligand atom pairs closer than 4.5 Å using CPPTRAJ native contacts. This distance cutoff value was demonstrated to be optimal, with performance equivalent to that of more sophisticated methods relying on residue–residue interaction energies.96 The output file was processed using Python 3.11 scripts. This enabled the isolation of atom pairs engaged in protein–ligand hydrogen bonds (namely, oxygen–oxygen, nitrogen–oxygen, sulfur–oxygen, sulfur–nitrogen, and nitrogen–nitrogen) and those present in over 75% of the examined 200 ns timeframe. In-depth contact analysis of the identified atom pairs was performed using the GROMACS distance module supplemented by VMD visual validation. The Mpro residues that manifested from the contact analysis in both monomers of the dimeric Mpro across any simulated system were designated as binding-pocket residues. From this comprehensive analysis, 36 residues were identified for the dimeric Mpro (18 residues for each binding site) (Fig. 2). For subsequent analyses, the trajectories of the centers of mass of the binding-site residues were extracted from the total MD trajectory after fitting to the Cα of the binding-site residues of the apo-protein reference structure.Selection of MD trajectory time windows for local dynamics ensemble generation
Flexible proteins adopt various atomistic conformations, some of which lead to ligand disassociation. To harness this effectively and extract highly stable conformations around the stable protein–ligand complex, this trajectory should be refined by strategically selecting time windows. This selection process aims to represent nuanced local changes in the protein–ligand system, with an emphasis on periods where ligand interactions occur within the binding pocket, particularly during the most stable conformations of the system. To streamline this selection, we applied principal component analysis (PCA) to the distance features. In this context, the utility of PCA relies on its ability to distinguish relevant temporal patterns and transitions from extensive MD trajectory data.97,98 By mapping the MD frames onto these principal components, we could discern the specific structural variations. More importantly, this allowed us to pinpoint the time windows characterized by the adoption of stable conformations by the system. Using the insights derived from PCA, we chose distinct 300 ns intervals. These selected intervals became the foundation for constructing the local dynamics ensemble (LDE) trajectories. By narrowing our focus to these intervals, we enhanced the ability of LDE to encapsulate relevant conformational changes associated with ligand binding and bolstered the efficiency of the ensuing machine-learning analyses.Analysis of protein conformation dynamics using ML
Here, we briefly introduce the machine-learning methods (for a detailed description, please refer to previous works51,99,100). The LDE, which is defined as an ensemble of short-term trajectories related to a descriptor of interest, was generated from the distance in the previous section. Derived from the MD simulation data, the LDE portrays the temporal evolution of this descriptor, thereby offering a snapshot of localized changes in the protein–ligand system over time. Mathematically, the LDE from the starting time step t0 is represented as a time series of configurations:| x = [d(t0 + Δ), …, d(t0 + δ)] | (1) |
| x = [d(t0 + Δ) − d(t0), …, d(t0 + δ) − d(t0)] | (2) |
Upon computing the LDE for every particle present in the binding site, a high-dimensional matrix is obtained (Fig. 1c). This matrix is a comprehensive representation of the structural and dynamic behavior of the system. The rows represent distinct particles within the binding site, with each row encapsulating the temporal evolution of the distance descriptor for that specific particle and providing a trajectory of its behavior over the course of the simulation. The matrix columns correspond to specific time points in the MD simulation and offer a cross-sectional overview of the structural configuration of the system at each time point. In essence, the matrix obtained by calculating the LDE for all the particles of the binding site encapsulated the temporal evolution of each particle and the state of the entire system at each time point.
For pairs of LDEs across all systems, the differences in LDEs were computed on the basis of the Wasserstein distance, which is the distance between two probability distributions, using the approximation of the optimal transport function by DNNs (Fig. 1d):
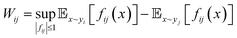 | (3) |
In this formula, 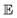 symbolizes the expectation over the probability distribution, x is the sampled short-term trajectory of the system i, yi is the probability distribution of x, and fij represents a function approximated by the DNN with the supremum taken over all 1-Lipschitz functions fij. The DNNs consisted of multilayer perceptrons used in a previous study,51 and the training of the networks was performed via unsupervised learning.
symbolizes the expectation over the probability distribution, x is the sampled short-term trajectory of the system i, yi is the probability distribution of x, and fij represents a function approximated by the DNN with the supremum taken over all 1-Lipschitz functions fij. The DNNs consisted of multilayer perceptrons used in a previous study,51 and the training of the networks was performed via unsupervised learning.
By computing the Wasserstein distance for all pairs of N systems, a distance matrix of (N, N) was obtained (Fig. 1e). This matrix provides a comprehensive view of the differences in protein dynamics owing to the presence of different ligands. The subsequent nonlinear dimensionality reduction and PCA resulted in the creation of an embedding map, thereby simplifying the visualization.
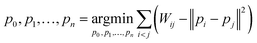 | (4) |
Here, pi represents a three-dimensional vector corresponding to system i, where Wij denotes the Wasserstein distance between systems i and j. Embedding optimization employs a two-pronged approach using simulated annealing for global-minimum exploration, followed by gradient descent for swift convergence.51 This embedding cycle was iterated multiple times, and the most favorable result—having the least distance loss—was selected. Finally, PCA was performed on the set of embeddings; hence, the embedded vectors were used to represent the systems using principal components 1 and 2. This provides a compact and insightful representation of the complex high-dimensional dynamics inherent in the protein–ligand interactions. By facilitating the extraction of simple features, this embedding can deepen our understanding of global differences in systems.
In addition, the characteristic dynamics were extracted using the function g(xi) (Fig. 1f). This function quantifies the contribution of a single short-term trajectory (the trajectory of the distance descriptor of one specific binding pocket residue) to the overall differences between the two systems. When juxtaposing the LDE trajectory of system i with that of reference system j, the function is represented as
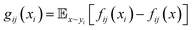 | (5) |
Here lies the utility of g(x): it quantitatively evaluates the uniqueness of a given short-term trajectory in comparison to the average trajectory of another system. For instance, a small g(x) value for a trajectory in system i relative to system j suggests that system i's trajectory closely mirrors the general behavior observed in system j and vice versa. Building on this, because gij(xi) encompasses short-term trajectories that span numerous residues, we can derive the residues that significantly affect the Wasserstein distance between systems, effectively shedding light on the contrasting protein differences (Fig. 1f). According to gij(xi), the short-term trajectories of system i are classified into three distinct groups: system i-characteristic, denoted as XCij; system j-similar, denoted as XSij; and middle XMij:
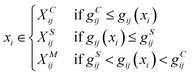 | (6) |
The higher and lower thresholds gCij and gSij are determined by the top and bottom deciles of all sampled values of gij(xi). In contrast to a previous study that utilized only fluctuation,51 we focused on fluctuating conformations represented by residue–residue distances, taking distance-based interpretations. If the average distance between the center of mass of residue k and the center of the geometry of the binding pocket is very different between groups XCij and XSij, the Wasserstein distance Wij is highly influenced by residue k. Through this analysis, we identified the residues whose dynamics were highly affected by ligand binding.
Results and discussion
Flexibility of SARS-CoV-2 Mpro
To compare the local conformational dynamics of Mpro in the presence and absence of 11 inhibitors, we conducted simulations of dimeric Mpro in inhibitor-unbound (apo state) and inhibitor-bound (holo state) states. We performed three MD simulations of 1 μs for each of the 12 systems (apo-protein system and 11 protein–ligand systems). To monitor the structural stability of Mpro during the simulations, we measured the RMSD of the Cα atoms from the starting crystallographic coordinates. As shown in the ESI (Fig. S2†), the plotted RMSD for MD run 1 provides evidence that all the simulated systems have reached convergence. The residue-based RMSF through the trajectory was calculated to assess the flexibility of the residues (RMSF plot of MD run 1 in Fig. 3). We computed the RMSF for each chain of the dimeric Mpro in every system and calculated the mean RMSF values between the two monomers. The overall RMSF analysis of the systems confirmed the structural flexibility of Mpro. The conformational flexibility of Mpro was experimentally assessed by Kneller et al.88 The structural heterogeneity of Mpro has also been highlighted in other studies using computational methods.89–92 The flexibility of the protein structure plays a significant role in determining the thermodynamic properties of drug binding. This underscores the importance of considering intrinsic conformational flexibility and conformational selection when studying protein–ligand interactions.101,102 The RMSF data showed that the region from residue 45 to 53 and the region from residue 185 to 200 of the two protomers had a high RMSF. The largest differences in fluctuations between the systems were associated with these regions. Our findings find support in the study by Gorgulla et al.91 which revealed the differences in the conformation and position of the Gln189-containing loop and the short Ser46-containing a-helix between three apo structures and five structures in the complex with inhibitors. These regions correspond to the two loops that enclose the catalytic pocket and physically occlude the path toward the catalytic site. The ligand-free system showed higher fluctuations than some protein–ligand systems and lower fluctuations than others. In conjunction with the RMSF data, this finding suggests that ligand binding cannot be simply correlated with the higher/lower induced fluctuation of Mpro residues. The approach proposed in this paper can overcome these challenges. Unsupervised deep learning can elucidate complex dynamic properties by detecting hidden patterns in MD data that conventional analysis methods such as RMSF cannot uncover. The RMSF plots for MD runs 2 and 3 are presented in the ESI (Fig. S5 and S6†).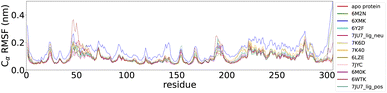 | ||
| Fig. 3 Residue-based root mean squared fluctuation (RMSF) of the protein backbone averaged between monomer A and monomer B in the first 1 μs MD simulation for the 12 systems. | ||
Selection of binding-site residues and MD trajectory time windows
For effective analysis of the MD trajectory data, three core parameters must be determined: binding-site residues, appropriate time windows, and input type (descriptor and definition of LDE). The selection of the binding-site residues and time windows is rooted in MD analyses, while the input types require testing because of their dependence on the nature of the protein.The binding-pocket residues of Mpro were determined through contact analysis, as detailed in the Methods section. The selected residues were as follows: His41, Met49, Phe40, Leu141, Asn142, Gly143, Ser144, Cys145, His163, His164, Met165, Glu166, Pro168, His172, Arg188, Gln189, Thr190, and Gln192. A comprehensive list of the amino acids in contact with each ligand over the three simulations is presented in Table 2.
| Cpd | System | Residues |
|---|---|---|
| 1 | 6M0K | [41, 49, 140–145, 163, 164, 165, 166, 172, 188, 189] |
| 2 | 6LZE | [41, 140–145, 163, 164, 165, 166, 172, 188] |
| 3 | 6WTK | [140–145, 163, 164, 166, 172] |
| 4 | 6XMK | [140–144, 163, 164, 165, 166, 172, 188–190] |
| 5 | 6Y2F | [41, 140–145, 163, 164, 165, 166, 172, 189, 190] |
| 6 | 6M2N | [140–142, 144, 145, 163, 164, 166, 172] |
| 7 | 7JU7neu | [41, 49, 140, 141, 144, 145, 163–166, 172, 189] |
| 7 | 7JU7pos | [41, 49, 140, 141, 144, 145, 163–166, 172, 189, 190] |
| 8 | 7K40 | [41, 142, 165, 166, 167, 188–190, 192] |
| 9 | 7JYC | [41, 140, 142, 143, 145, 164–166, 189, 190, 192] |
| 10 | 7K6D | [41, 49, 141–145, 163–168, 188–192] |
The next core step involved the selection of frame windows guided by PCA. In the context of our MD simulations, PCA helped distinguish stable molecular conformations from fluctuations, ensuring that the chosen time intervals accurately represented the local changes induced by ligand binding. First, we visually inspected the MD trajectories using the VMD tool, supplemented by ligand RMSD plots available in the ESI (Fig. S8†). These plots were instrumental in monitoring the ligand movement relative to Mpro. A noteworthy observation was made for the system 6M2N: the ligands, initially situated at the binding site of the two monomers, migrated out of the pocket in all three simulations. One potential contributor to this behavior may be the lower molecular weight of the ligand in the system 6M2N. Consequently, it was not possible to identify the pertinent period of ligand interaction within the binding pocket of one of the protomers, and this system was excluded from further analysis. Our primary objective for using PCA was to identify the time windows that embodied stable conformations during pivotal ligand interaction events. Through this analysis, we identified a window of 300 ns demonstrating the enhanced structural stability of the protein–ligand complex. A visual illustration of our PCA results is provided in Fig. 4 for apo-protein system and a protein–ligand system as an example. The PCA plots of the selected frame windows, representative of stable conformations, for all the simulated systems are displayed in the ESI (Fig. S7†). In conclusion, contact analysis and PCA-based selection of time windows were central to guiding the relevance and efficiency of the LDE trajectories, ensuring that our analysis captured the most relevant and stable interactions between ligands and proteins.
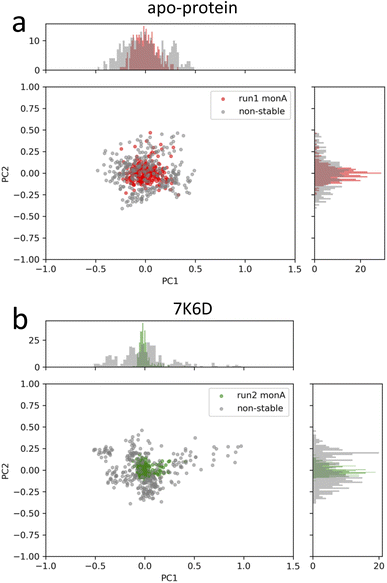 | ||
| Fig. 4 PCA plots of the stable-structure data selected for the generation of the LDEs of (a) apo-protein and (b) system 7K6D. In grey, PCA plots of non-stable-structure data for comparison. | ||
Unsupervised deep learning-based insights into protein–ligand dynamics
Unsupervised deep learning offers the advantages of discovering hidden patterns and providing insights into complex datasets without prior labeling or categorization. Leveraging this approach, we sought to uncover the subtle protein–ligand interaction dynamics in the studied systems. Regarding the two other parameters for LDE, we selected the residue-pocket center distance and time series distances. For this selection, we assumed that both structure and fluctuation are important for representing flexible proteins, and fitting coordinates may result in a large bias for larger deformations.Central to our methodology is the Wasserstein distance matrix derived from LDE. This matrix provides a quantitative measure of differential ligand-induced changes across systems. The color-coded representation of this matrix shows the relative distances between the systems, with system 7JYC distinctly separated from the other systems (Fig. 5a). This observation suggests that system 7JYC exhibits unique trajectories that were captured and highlighted by our unsupervised deep-learning methodology. Because we considered the time series of the distance to generate the LDE, the Wasserstein distance compares the probability distributions of the two LDEs, quantifying the differences in the conformations of the systems. While RMSD considers only the average difference between conformations, the Wasserstein distance also considers protein flexibility and is therefore more suitable for conveying a comprehensive view of fluctuating structures. Using the Wasserstein distance matrix, we constructed an embedding map that spatially arranges the system. In this map, each system was represented as a point and its color corresponded to the experimental binding-affinity values (pIC50). A meaningful pattern emerged: systems with lower affinity values were situated closer to the apo-protein, indicating structural and dynamic behavior similar to that of the ligand-free state. Conversely, high-affinity systems were positioned further along PC2, indicating distinct ligand-influenced structures and dynamics (Fig. 5b). We also noticed that the two systems with higher affinities, 6M0K and 6LZE, showed great similarities in the chemical structures of the ligands and were characterized by the same PC2 values. To reinforce the insights drawn from the embedding map, we correlated the experimental binding-affinity values (pIC50) with PC2 values from the embedding map. We observed a Pearson's correlation coefficient of 0.7 and a Spearman's correlation coefficient of 0.4. While the separation between high- (blue) and low-affinity (red) systems based on PC2 is evident, the classification of systems with moderate affinity seems complicated. This observation explains the differences between the two correlation metrics. The significant correlation between PC2 and IC50 for high- and low-affinity ligands, reflected by a Pearson's correlation of 0.7, indicates the potential of our deep-learning approach in highlighting the subtle shifts in ligand-induced trajectories within Mpro (Fig. 6).
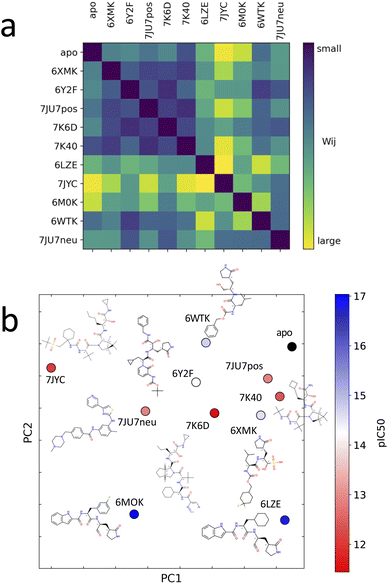 | ||
| Fig. 5 (a) Distance matrix of Wasserstein distances between the probability distributions of the LDEs for system pairs. A large Wasserstein distance (yellow) corresponds to a large difference in the protein structure and dynamics. (b) Embedded points of the distance matrix and chemical structure of the corresponding system. The points are colored according to the experimental binding-affinity values (pIC50). pIC50 corresponds to −log(IC50). IC50 values can be found in the Table 1. | ||
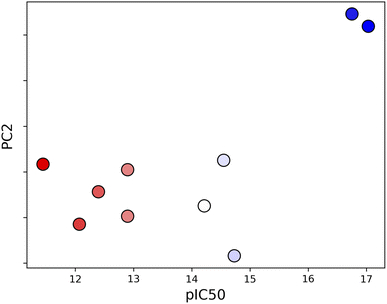 | ||
| Fig. 6 Correlation between PC2 and experimental binding-affinity data (pIC50). The correlation, quantified using Pearson coefficient, is 0.7. | ||
In addition to the time-series distance used as the descriptor of the MD, we investigated three other types of inputs: (1) time-series displacements of residue–pocket center distance, (2) time-series residue–pocket center xyz displacement, and (3) time-series displacements of residue–pocket center xyz displacement. The use of time-series displacements has demonstrated success in the previous study on rigid proteins,51 exhibiting a notable correlation with binding affinities. Time-series displacements primarily consider fluctuations, whereas time-series distances consider conformations. In the case of (1), although apo-proteins could not be distinguished from high-affinity ligands, low-affinity ligands were separated from high-affinity ligands (Fig. S9a†). In case (2), high-affinity ligands were separated from low-affinity ligands within the embedding map (Fig. S9b†). In case (3), 7K6D overlapped with 6M0K (Fig. S9c†). These results indicate that the fluctuations themselves are insufficient to estimate binding-affinity-related features, and conformation is also important in the context of flexible proteins. When employing Cartesian coordinates, careful consideration must be given to the selection of fitting parameters. For example, if fitting encompasses terminal regions or involves the other monomer of the dimer, it can affect the Cartesian coordinates of the binding site regardless of the conformations of the binding pocket. In cases where the binding site undergoes significant changes, it is better to include the global protein conformations. Note that in contrast to the normal mode analysis, this embedding map does not have specific physical meanings in the PC axis.
In contrast to the correspondence between PC1 and binding affinity observed in this study, a previous study indicated a correlation between binding affinity and PC1 for rigid proteins.51 Because PCs are determined to find the axes with the largest deviation, they depend on the number and nature of the systems. Hence, the ability to differentiate systems should be determined based on embedding maps to compare complex systems, although a single axis may be useful, as shown in Fig. 6. In addition, flexible proteins have a high degree of freedom, which may lead to a situation where a single Wasserstein distance is not sufficient to represent the various differences among the systems. Generally, if two high-dimensional manifolds are significantly different, the meaning of the distance becomes vague.
Interpretation of the contribution of residues to ligand-induced dynamics
The unsupervised deep-learning approach employed in this study enabled the extraction of significant features from the protein–ligand systems. Notably, the correlation between the PC2 component of the embedding map and pIC50 indicates PC2's role in capturing conformational differences related to ligand-binding affinity. To delve deeper into the molecular underpinnings of this observation, we aimed to identify specific amino acids that showed prominent dynamic disparities between the highest and lowest binding-affinity systems. Using the function g(x) (detailed in the Methods section, see eqn (5)), we examined the characteristic behavior differences between high- and low-affinity systems. This function allowed us to discern the characteristic dynamics of each system and to identify the residues that exhibited the most significant variations. First, according to the metrics derived from function gij(x), the short-term trajectories of the LDE of system i are classified into three g(x) groups, XCij (high, characteristic of system i), XSij (low, similar to system j) and XMij (mid, non-characteristic of system i neither similar to system j). Then, the average value of the distance descriptor was calculated for each residue included in the LDE trajectories of the system i for each of the three LDE groups XCij, XMij, XSij. Fig. 7 shows the average distance from the center of the pocket for each LDE-residue of system 6M0K (with high binding affinity) when compared to system 7JYC (low binding-affinity system). The characteristic behavior XCij in system 6M0K exhibited large movements in residues Met49 and Arg188-Gln189-Thr190. The largest differences between groups XCij and XSij corresponded to residues Arg188-Gln189-Thr190 and Met49. We also compared the characteristic trajectories of system 6M0K and system 6LZE (Fig. 7b). In this case, large differences in the residues Arg188-Gln189-Thr190 between the characteristic (high) and similar (low) groups were absent, whereas the distinctions in residue Met49 persisted. The interpretation of this result in combination with visual inspection of the embedding map led us to conclude that (1) residues Met49 and Arg188-Gln189-Thr190 are highly influenced by the ligand-binding Mpro; (2) the conformation of residues Arg188-Gln189-Thr190, which is highly different between high- and low-affinity ligands, is predominantly represented in the PC2 feature; and (3) the conformation of residue Met49 is captured in PC1.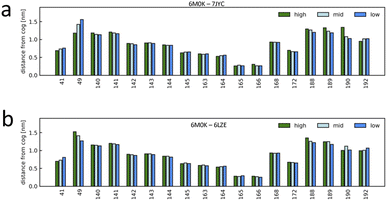 | ||
| Fig. 7 Characteristic dynamics were compared for selected system pairs, and the contributions of the binding-site residues were interpreted. The short-term trajectories of system i were classified into characteristic (high, characteristic of system i), non-characteristic (low, similar to system j), and others (mid), and the average value of the distance from the pocket center was calculated for each binding-site residue. (a) Characteristic dynamics analysis for system 6M0K (high-affinity system) compared to system 7JYC (low-affinity system). (b) Characteristic dynamics analysis for system 6M0K compared to system 6LZE (both high-affinity systems). | ||
To support our findings, we referred to studies that offer complementary insights. MacDonald et al.103 described how changes in substrate accommodation can cause significant alterations in catalytic efficiency. A widened active-site cleft between the Mpro residues Met49 and Asn142 led to decreased catalytic efficiency for the nsp8/9 substrate. This observation underscores Met49's critical role in ligand recognition and binding dynamics, consistent with our findings. Through binding free-energy decomposition analysis, Hamed et al.104 highlighted the pivotal role of specific residues in ligand interactions. In addition to identifying Asp187 and Asp48 as essential for β-blocker agents, this study also highlighted the important roles of Met49 and Thr190, further validating our observations. A comprehensive analysis conducted by Amamuddy et al.105 identified heightened mobility in residues such as Met49 and Tyr54, supporting our findings concerning Met49's significant movements. Furthermore, the identification of residues Asp187, Arg188, Gln189, Thr190, and Ala191 as flexible in slower modes indicates the importance of these residues in functional motion, which is consistent with our conclusions. Investigating Mpro mutations, Yang et al.106 highlighted residues such as Met49 and Arg188-Gln189-Thr190 as pivotal for protein–ligand interactions. Their analysis of mutations affecting nirmatrelvir binding, particularly at Gln189 and Arg188, resonated with our findings, emphasizing the importance of these residues in ligand interaction and potential drug resistance. The shared insights across these independent studies bolster the robustness of our conclusions, contributing to a more comprehensive understanding of the dynamics governing protein–ligand interactions in Mpro.
Conclusions
In modern drug discovery, protein–ligand interactions play a crucial role in determining the efficacy and specificity of potential therapeutic agents. Traditional methods such as X-ray crystallography and NMR spectroscopy provide structural snapshots but often lack the capability to capture the dynamic nature of these interactions. MD simulations have emerged as a valuable tool in the drug-discovery process by providing a detailed characterization of the temporal evolution of protein–ligand systems at the atomic level. However, analyzing the vast datasets generated by MD simulations remains challenging. In this context, the integration of deep-learning techniques with MD simulations is a promising approach. Unsupervised deep-learning approaches can efficiently handle high-dimensional data and extract meaningful patterns and relationships. In this study, we adopted an unsupervised deep-learning framework specifically tailored for the analysis of MD simulation data of flexible protein–ligand complexes. We assessed the ability of our ML approach to capture patterns in MD trajectories induced by 11 different ligands of the SARS-CoV-2 main protease. To enhance both the relevance and efficiency of MD data analysis using ML, we focused on selected binding-pocket residues and time windows in stable protein conformations. The third core parameter to be determined for an effective analysis is the type of input: the descriptor (distance or coordinates) and the definition of LDE (time series or time displacements). After testing different types of inputs, we selected the time series of the distance between the centers of mass of the binding-site residues and the center of geometry of the binding pocket. As discussed in the previous section, Cartesian coordinates exhibited sub-optimal performance due to susceptibility to fitting selection and subsequent issues with coordinate rotations, which can compromise the representation of protein conformational landscapes. In future investigations, it would be intriguing to incorporate bond angles and assess the performance of our method using this equivariant model as input.36,37,107 Other types of features of protein complexes, such as surface volume, and features of ligands, such as molecular weights, have been used in previous works.8,45,108,109 In a supervised learning framework, these features are useful after normalization and the determination of optimal weight parameters. However, within our unsupervised learning framework, seamlessly incorporating such information into the coordinates of the protein is a complex task. We hypothesize that a self-supervised learning scheme might offer a viable avenue for achieving this, and we view it as a promising direction for our future research. Subsequently, Wasserstein distances between the LDE trajectories of the residue–pocket center distance were calculated using DNNs across all system pairs. Dimensionality-reduction techniques were employed to extract relevant variables. The distances between the systems in the embedding map were interpreted and related to the experimental binding affinities. Systems with lower affinity values were located closer to the apo-protein, whereas high-affinity systems were positioned further along PC2. We found a significant Pearson's correlation coefficient (0.7 between the ligand-induced dynamics reflected in PC2 and the experimental binding-affinity data). This finding implies that the most active compounds have the maximum impact on the local structure and dynamics of the target protein, resulting in them being further distanced from the ligand-free system. Moreover, we determined the binding-site residues that contributed the most to the ligand-induced changes in Mpro. These findings are consistent with the latest literature on this topic.In a previous study, the DNN approach was employed for relatively rigid proteins,51 while in this study, it was tested and adopted for Mpro, a protein known for its high degree of flexibility (as discussed in the Results section). A recent study by Gu et al.110 demonstrated that the application of classical machine-learning algorithms to MD trajectory-derived descriptors significantly enhanced the prediction performance of binding affinities for protein targets exhibiting considerable structural flexibility. The importance of using MD-generated descriptors instead of static 3D structural data of protein–ligand complexes as inputs has also been demonstrated by Ash and Fourches.111 Additionally, complementary studies45,112,113 further resonated with our approach, where a combination of DNNs with MD was deployed to capture the complex, nonlinear relationships in high-dimensional MD simulation data to leverage the intricate dynamics induced by the ligand. In the domain of methodologies that leverage deep learning for trajectory analysis, a noteworthy mention goes to the VAMPNet framework.49 VAMPNet framework has indeed made significant contributions to the field by employing the variational approach for Markov processes (VAMP) to acquire a kinetic model from MD data. However, we would like to emphasize that there are notable distinctions with our approach that reflect their specific applications and capabilities. VAMPNets excel at extracting metastable structures and determining the rate of conformational transition within a single system. In contrast, our method specifies the time scale of dynamics, and dynamical conformations are analyzed among multiple systems. This allows us to examine how dynamics vary across a set of systems. It's worth noting that we envision a potential synergy between our approach and VAMPNets, where the use of VAMPNets to extract input features for our method holds promise for enhancing the analysis of variances in conformational transitions. This underscores the complementary nature of our approach within the landscape of trajectory analysis methodologies. While our results are promising, it is important to acknowledge possible limitations and the directions for future work. Firstly, it is noteworthy that our approach is dependent on the initial conditions, specifically the initial structure of the protein and the chosen input feature. Additionally, our study focused on a set of 11 ligands. Expanding this dataset to encompass a wider range of ligands will be crucial for a more comprehensive understanding of the method's capabilities. Moreover, the sampling of MD simulations and the associated computational time are recognized as limitations. Efforts to optimize sampling strategies and potentially employ more efficient simulation techniques, such as metadynamics, are areas for future consideration.114,115 Looking ahead, we believe that the unsupervised deep-learning framework utilized in this study will be highly valuable in the early stages of drug discovery. When binding-affinity data are not yet available, this method may help identify the most promising compounds to prioritize for further analysis. The versatility of our approach offers potential extensions also to diverse protein–ligand interactions, including allosteric events, and holds promise for lead optimization. Using our approach, the effects of different variants of the same ligand can be analyzed to gain insights into the influence of ligand modifications on the dynamics of the target protein. Future work will also focus on extending our method to other datasets, and on leveraging the power of deep learning for feature selection. Integrating feature selection directly into the automated machine-learning component of our model will not only enhance the model's adaptability but also align it more closely with the objective of achieving a truly unsupervised approach. By harnessing the strengths of deep learning and MD simulations, we envision that our novel methodology will not only accelerate drug discovery but will also contribute to a deeper understanding of molecular mechanisms, thus paving the way for more targeted and efficient therapeutic interventions.
Conflicts of interest
The authors declare no competing interests.Acknowledgements
I. Y. is supported by JSPS KAKENHI Grant No. 202322314.Notes and references
- O. J. Wouters, M. McKee and J. Luyten, JAMA, 2020, 323, 844–853 CrossRef PubMed.
- M. Schlander, K. Hernandez-Villafuerte, C.-Y. Cheng, J. Mestre-Ferrandiz and M. Baumann, PharmacoEconomics, 2021, 39, 1243–1269 CrossRef PubMed.
- J. P. Hughes, S. Rees, S. B. Kalindjian and K. L. Philpott, Br. J. Pharmacol., 2011, 162, 1239–1249 CrossRef CAS PubMed.
- W. L. Jorgensen, Science, 2004, 303, 1813–1818 CrossRef CAS PubMed.
- G. Sliwoski, S. Kothiwale, J. Meiler and E. W. Lowe, Pharmacol. Rev., 2014, 66, 334–395 CrossRef PubMed.
- A. Ganesan, M. L. Coote and K. Barakat, Drug Discovery Today, 2017, 22, 249–269 CrossRef CAS PubMed.
- Y. Zhao, Y. Zhu, X. Liu, Z. Jin, Y. Duan, Q. Zhang, C. Wu, L. Feng, X. Du and J. Zhao, et al., Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2117142119 CrossRef CAS PubMed.
- Y. Wang, J. M. L. Ribeiro and P. Tiwary, Curr. Opin. Struct. Biol., 2020, 61, 139–145 CrossRef CAS PubMed.
- J. D. Durrant and J. A. McCammon, BMC Biol., 2011, 9, 1–9 CrossRef PubMed.
- I. Buch, T. Giorgino and G. De Fabritiis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10184–10189 CrossRef CAS PubMed.
- N. Plattner, S. Doerr, G. De Fabritiis and F. Noé, Nat. Chem., 2017, 9, 1005–1011 CrossRef CAS PubMed.
- R. A. Copeland, D. L. Pompliano and T. D. Meek, Nat. Rev. Drug Discovery, 2006, 5, 730–739 CrossRef CAS PubMed.
- C. G. Ricci, J. S. Chen, Y. Miao, M. Jinek, J. A. Doudna, J. A. McCammon and G. Palermo, ACS Cent. Sci., 2019, 5, 651–662 CrossRef CAS PubMed.
- X. Du, Y. Li, Y.-L. Xia, S.-M. Ai, J. Liang, P. Sang, X.-L. Ji and S.-Q. Liu, Int. J. Mol. Sci., 2016, 17, 144 CrossRef PubMed.
- M. Wilchek, E. A. Bayer and O. Livnah, Immunol. Lett., 2006, 103, 27–32 CrossRef CAS PubMed.
- S. A. Hollingsworth and R. O. Dror, Neuron, 2018, 99, 1129–1143 CrossRef CAS PubMed.
- P. Cozzini, G. E. Kellogg, F. Spyrakis, D. J. Abraham, G. Costantino, A. Emerson, F. Fanelli, H. Gohlke, L. A. Kuhn and G. M. Morris, et al., J. Med. Chem., 2008, 51, 6237–6255 CrossRef CAS PubMed.
- M. De Vivo, M. Masetti, G. Bottegoni and A. Cavalli, J. Med. Chem., 2016, 59, 4035–4061 CrossRef CAS PubMed.
- M.-H. Seo, J. Park, E. Kim, S. Hohng and H.-S. Kim, Nat. Commun., 2014, 5, 3724 CrossRef CAS PubMed.
- R. O. Dror, R. M. Dirks, J. Grossman, H. Xu and D. E. Shaw, Annu. Rev. Biophys., 2012, 41, 429–452 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Chem. Sci., 2017, 8, 3192–3203 RSC.
- F. Brockherde, L. Vogt, L. Li, M. E. Tuckerman, K. Burke and K.-R. Müller, Nat. Commun., 2017, 8, 872 CrossRef PubMed.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 13890 CrossRef PubMed.
- O. Valsson and M. Parrinello, Phys. Rev. Lett., 2014, 113, 090601 CrossRef CAS PubMed.
- L. Bonati, Y.-Y. Zhang and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17641–17647 CrossRef CAS PubMed.
- J. Zhang, Y. I. Yang and F. Noé, J. Phys. Chem. Lett., 2019, 10, 5791–5797 CrossRef CAS PubMed.
- J. McCarty and M. Parrinello, J. Chem. Phys., 2017, 147, 20 CrossRef PubMed.
- M. M. Sultan and V. S. Pande, J. Chem. Theory Comput., 2017, 13, 2440–2447 CrossRef PubMed.
- F. Noé, S. Olsson, J. Köhler and H. Wu, Science, 2019, 365, eaaw1147 CrossRef PubMed.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Ann. Rev. Phys. Chem., 2020, 71, 361–390 CrossRef PubMed.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579 CrossRef CAS PubMed.
- A. Musaelian, A. Johansson, S. Batzner and B. Kozinsky, 2023, preprint, arXiv:2304.10061, DOI:10.48550/arXiv.2304.10061.
- C. Chen and S. P. Ong, Nat. Computat. Sci., 2022, 2, 718–728 CrossRef.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 1–11 Search PubMed.
- A. Glielmo, B. E. Husic, A. Rodriguez, C. Clementi, F. Noé and A. Laio, Chem. Rev., 2021, 121, 9722–9758 CrossRef CAS PubMed.
- F. Noé, Mach. Learn. Meets Quantum Phys., 2020, 331–372 Search PubMed.
- S. Kaptan and I. Vattulainen, Adv. Phys.: X, 2022, 7, 2006080 Search PubMed.
- A. Plante, D. M. Shore, G. Morra, G. Khelashvili and H. Weinstein, Molecules, 2019, 24, 2097 CrossRef CAS PubMed.
- M. Ferraro, E. Moroni, E. Ippoliti, S. Rinaldi, C. Sanchez-Martin, A. Rasola, L. F. Pavarino and G. Colombo, J. Phys. Chem. B, 2020, 125, 101–114 CrossRef PubMed.
- F. Marchetti, E. Moroni, A. Pandini and G. Colombo, J. Phys. Chem. Lett., 2021, 12, 3724–3732 CrossRef CAS PubMed.
- S. Jamal, A. Grover and S. Grover, Front. Pharmacol., 2019, 10, 780 CrossRef CAS PubMed.
- D. M. Camacho, K. M. Collins, R. K. Powers, J. C. Costello and J. J. Collins, Cell, 2018, 173, 1581–1592 CrossRef CAS PubMed.
- J. Kim, S. Park, D. Min and W. Kim, Int. J. Mol. Sci., 2021, 22, 9983 CrossRef CAS PubMed.
- M. A. Thafar, R. S. Olayan, H. Ashoor, S. Albaradei, V. B. Bajic, X. Gao, T. Gojobori and M. Essack, J. Cheminform., 2020, 12, 1–17 CrossRef PubMed.
- A. Mardt, L. Pasquali, H. Wu and F. Noé, Nat. Commun., 2018, 9, 5 CrossRef PubMed.
- T. Xie, A. France-Lanord, Y. Wang, Y. Shao-Horn and J. C. Grossman, Nat. Commun., 2019, 10, 2667 CrossRef CAS PubMed.
- I. Yasuda, K. Endo, E. Yamamoto, Y. Hirano and K. Yasuoka, Commun. Biol., 2022, 5, 481 CrossRef CAS PubMed.
- S. Ullrich and C. Nitsche, Bioorg. Med. Chem. Lett., 2020, 30, 127377 CrossRef CAS PubMed.
- D. R. Owen, C. M. Allerton, A. S. Anderson, L. Aschenbrenner, M. Avery, S. Berritt, B. Boras, R. D. Cardin, A. Carlo and K. J. Coffman, et al., Science, 2021, 374, 1586–1593 CrossRef CAS PubMed.
- J. Hammond, H. Leister-Tebbe, A. Gardner, P. Abreu, W. Bao, W. Wisemandle, M. Baniecki, V. M. Hendrick, B. Damle and A. Simón-Campos, et al., N. Engl. J. Med., 2022, 386, 1397–1408 CrossRef CAS PubMed.
- C. Marzolini, D. R. Kuritzkes, F. Marra, A. Boyle, S. Gibbons, C. Flexner, A. Pozniak, M. Boffito, L. Waters and D. Burger, et al., Clin. Pharmacol. Ther., 2022, 112, 1191–1200 CrossRef CAS PubMed.
- L. Wang, N. A. Berger, P. B. Davis, D. C. Kaelber, N. D. Volkow and R. Xu, medRxiv, 2022, preprint, DOI:10.1101/2022.06.21.22276724.
- Y. Wang, X. Chen, W. Xiao, D. Zhao and L. Feng, J. Infect., 2022, 85, e134–e136 CrossRef CAS PubMed.
- M. Arjovsky, S. Chintala and L. Bottou, International Conference on Machine Learning, 2017, pp. 214–223 Search PubMed.
- L. Zhang, D. Lin, X. Sun, U. Curth, C. Drosten, L. Sauerhering, S. Becker, K. Rox and R. Hilgenfeld, Science, 2020, 368, 409–412 CrossRef CAS PubMed.
- Z. Jin, X. Du, Y. Xu, Y. Deng, M. Liu, Y. Zhao, B. Zhang, X. Li, L. Zhang and C. Peng, et al., Nature, 2020, 582, 289–293 CrossRef CAS PubMed.
- W. Dai, B. Zhang, X.-M. Jiang, H. Su, J. Li, Y. Zhao, X. Xie, Z. Jin, J. Peng and F. Liu, et al., Science, 2020, 368, 1331–1335 CrossRef CAS PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- B. Zhang, Y. Zhao, Z. Jin, X. Liu, H. Yang and Z. Rao, The Crystal Structure of COVID-19 Main Protease in Apo Form, Publ, 2020 Search PubMed.
- H. Su, W. Zhao, M. Li, H. Xie and Y. Xu, PDB Protein Data Bank, 2020 Search PubMed.
- H.-x. Su, S. Yao, W.-f. Zhao, M.-j. Li, J. Liu, W.-j. Shang, H. Xie, C.-q. Ke, H.-c. Hu and M.-n. Gao, et al., Acta Pharmacol. Sin., 2020, 41, 1167–1177 CrossRef CAS PubMed.
- A. D. Rathnayake, J. Zheng, Y. Kim, K. D. Perera, S. Mackin, D. K. Meyerholz, M. M. Kashipathy, K. P. Battaile, S. Lovell and S. Perlman, et al., Sci. Transl. Med., 2020, 12, eabc5332 CrossRef CAS PubMed.
- K. Tan, N. Maltseva, L. Welk, R. Jedrzejczak and A. Joachimiak, The Crystal Structure of SARS-CoV-2 Main Protease in Complex with Masitinib, 2020 Search PubMed.
- N. Drayman, J. K. DeMarco, K. A. Jones, S.-A. Azizi, H. M. Froggatt, K. Tan, N. I. Maltseva, S. Chen, V. Nicolaescu and S. Dvorkin, et al., Science, 2021, 373, 931–936 CrossRef CAS PubMed.
- B. Andi, D. Kumaran, D. F. Kreitler, A. S. Soares, J. Keereetaweep, J. Jakoncic, E. O. Lazo, W. Shi, M. R. Fuchs and R. M. Sweet, et al., Sci. Rep., 2022, 12, 12197 CrossRef CAS PubMed.
- W. Vuong, M. B. Khan, C. Fischer, E. Arutyunova, T. Lamer, J. Shields, H. A. Saffran, R. T. McKay, M. J. van Belkum and M. A. Joyce, et al., Nat. Commun., 2020, 11, 4282 CrossRef CAS PubMed.
- C. C. G. Inc., Molecular Operating Environment (MOE), 2016 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. e. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson, H. Nakatsuji, et al., Gaussian 16, revision C. 01, 2016 Search PubMed.
- D. Case, I. Ben-Shalom, S. Brozell, D. Cerutti, T. Cheatham III, V. Cruzeiro, T. Darden, R. Duke, D. Ghoreishi, M. Gilson, et al., AMBER 2018, University of California, San Francisco, 2018 Search PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack Jr, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo and S. Ha, et al., J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 1 CrossRef PubMed.
- H. J. Berendsen, J. v. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38 CrossRef CAS PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- A. D. Rathnayake, J. Zheng, Y. Kim, K. D. Perera, S. Mackin, D. K. Meyerholz, M. M. Kashipathy, K. P. Battaile, S. Lovell and S. Perlman, et al., Sci. Transl. Med., 2020, 12, eabc5332 CrossRef CAS PubMed.
- H.-x. Su, S. Yao, W.-f. Zhao, M.-j. Li, J. Liu, W.-j. Shang, H. Xie, C.-q. Ke, H.-c. Hu and M.-n. Gao, et al., Acta Pharmacol. Sin., 2020, 41, 1167–1177 CrossRef CAS PubMed.
- N. Drayman, K. A. Jones, S.-A. Azizi, H. M. Froggatt, K. Tan, N. I. Maltseva, S. Chen, V. Nicolaescu, S. Dvorkin, K. Furlong, et al., bioRxiv, 2020, preprint, DOI:10.1101/2020.08.31.274639.
- C. Ma, M. D. Sacco, B. Hurst, J. A. Townsend, Y. Hu, T. Szeto, X. Zhang, B. Tarbet, M. T. Marty and Y. Chen, et al., Cell Res., 2020, 30, 678–692 CrossRef CAS PubMed.
- B. J. Anson, M. E. Chapman, E. K. Lendy, S. Pshenychnyi, T. Richard, K. J. Satchell and A. D. Mesecar, Eur. J. Pharmacol., 2021, 890, 173664 CrossRef PubMed.
- D. W. Kneller, G. Phillips, H. M. O'Neill, R. Jedrzejczak, L. Stols, P. Langan, A. Joachimiak, L. Coates and A. Kovalevsky, Nat. Commun., 2020, 11, 3202 CrossRef CAS PubMed.
- B. Dehury, S. Mishra and S. Pati, J. Cell. Biochem., 2023, 124, 861–876 CrossRef CAS PubMed.
- M. Bzówka, K. Mitusińska, A. Raczyńska, A. Samol, J. A. Tuszyński and A. Góra, Int. J. Mol. Sci., 2020, 21, 3099 CrossRef PubMed.
- C. Gorgulla, K. M. P. Das, K. E. Leigh, M. Cespugli, P. D. Fischer, Z.-F. Wang, G. Tesseyre, S. Pandita, A. Shnapir and A. Calderaio, et al., iScience, 2021, 24(2), 102021 CrossRef CAS PubMed.
- T. Sztain, R. Amaro and J. A. McCammon, J. Chem. Inform. Model., 2021, 61, 3495–3501 CrossRef CAS PubMed.
- G. Diez, D. Nagel and G. Stock, J. Chem. Theory Comput., 2022, 18, 5079–5088 CrossRef CAS PubMed.
- W. Deng, C. Breneman and M. J. Embrechts, J. Chem. Inf. Comput. Sci., 2004, 44, 699–703 CrossRef CAS PubMed.
- F. Sittel, A. Jain and G. Stock, J. Chem. Phys., 2014, 141(1), 014111 CrossRef PubMed.
- X.-Q. Yao, M. Momin and D. Hamelberg, J. Chem. Inf. Model., 2019, 59, 3222–3228 CrossRef CAS PubMed.
- C. C. David and D. J. Jacobs, Protein Dynamics: Methods and Protocols, 2014, 193–226 Search PubMed.
- R. Bro and A. K. Smilde, Anal. Methods, 2014, 6, 2812–2831 RSC.
- K. Endo, D. Yuhara, K. Tomobe and K. Yasuoka, Nanoscale, 2019, 11, 10064–10071 RSC.
- I. Yasuda, Y. Kobayashi, K. Endo, Y. Hayakawa, K. Fujiwara, K. Yajima, N. Arai and K. Yasuoka, ACS Appl. Mater. Interfaces, 2023, 15, 8567–8578 CrossRef CAS PubMed.
- M. Amaral, D. Kokh, J. Bomke, A. Wegener, H. Buchstaller, H. Eggenweiler, P. Matias, C. Sirrenberg, R. Wade and M. Frech, Nat. Commun., 2017, 8, 2276 CrossRef CAS PubMed.
- D. D. Boehr, R. Nussinov and P. E. Wright, Nat. Chem. Biol., 2009, 5, 789–796 CrossRef CAS PubMed.
- E. A. MacDonald, G. Frey, M. N. Namchuk, S. C. Harrison, S. M. Hinshaw and I. W. Windsor, ACS Infect. Dis., 2021, 7, 2591–2595 CrossRef CAS PubMed.
- M. I. Hamed, K. M. Darwish, R. Soltane, A. Chrouda, A. Mostafa, N. M. A. Shama, S. S. Elhady, H. S. Abulkhair, A. E. Khodir and A. A. Elmaaty, et al., RSC Adv., 2021, 11, 35536–35558 RSC.
- O. Sheik Amamuddy, G. M. Verkhivker and O. Tastan Bishop, J. Chem. Inf. Model., 2020, 60, 5080–5102 CrossRef CAS PubMed.
- K. S. Yang, S. Z. Leeuwon, S. Xu and W. R. Liu, J. Med. Chem., 2022, 65, 8686–8698 CrossRef CAS PubMed.
- Z. Wang, H. Wu, L. Sun, X. He, Z. Liu, B. Shao, T. Wang and T.-Y. Liu, J. Chem. Phys., 2023, 159(3), 035101 CrossRef CAS PubMed.
- D. D. Wang, L. Ou-Yang, H. Xie, M. Zhu and H. Yan, Comput. Struct. Biotechnol. J., 2020, 18, 439–454 CrossRef CAS PubMed.
- D. D. Wang, M. Zhu and H. Yan, Briefings Bioinf., 2021, 22, bbaa107 CrossRef PubMed.
- S. Gu, C. Shen, J. Yu, H. Zhao, H. Liu, L. Liu, R. Sheng, L. Xu, Z. Wang and T. Hou, et al., Briefings Bioinf., 2023, 24, bbad008 CrossRef PubMed.
- J. Ash and D. Fourches, J. Chem. Inf. Model., 2017, 57, 1286–1299 CrossRef CAS PubMed.
- O. Yakovenko and S. J. Jones, J. Comput.-Aided Mol. Des., 2018, 32, 299–311 CrossRef CAS PubMed.
- W. D. Bennett, S. He, C. L. Bilodeau, D. Jones, D. Sun, H. Kim, J. E. Allen, F. C. Lightstone and H. I. Ingólfsson, J. Chem. Inf. Model., 2020, 60, 5375–5381 CrossRef CAS PubMed.
- R. C. Bernardi, M. C. Melo and K. Schulten, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 872–877 CrossRef CAS PubMed.
- Y. I. Yang, Q. Shao, J. Zhang, L. Yang and Y. Q. Gao, J. Chem. Phys., 2019, 151(7), 070902 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra06375e |
| This journal is © The Royal Society of Chemistry 2023 |