Open Access Article
Open Access ArticleDelocalization quantitatively mapped for prototypic organic nitroanions as well as azidoform anions†
Anatoly M. Belostotskii
Department of Chemistry, Bar-Ilan University, Ramat-Gan, 5290002, Israel. E-mail: belostot@biu.ac.il
First published on 17th November 2023
Abstract
Delocalization of occupied orbitals impacts the chemical bonding in the simplest known pernitroanions [(NO2)3C]− (1) and [(NO2)2N]− (2) as well as other functionalized organic anions. By quantitatively mapping it onto molecular backbones of 1, 2, [CH2NO2]− (3), [CH3NNO2]− (4) and [C(N3)]− (6) anions (all modeled by QM calculations), the Weinhold's NBO analysis refines their chemical structure, enabling to explain and even predict their essential chemical behaviour. In detail, the HOMO of 1 and 2 is associated with the central atom to the degree of 70.7% and 80.4%, respectively, while the HOMO localization on O atoms for 3 and 4 is 85.3% and 81.1%, respectively. Predomination of C-alkylation for 1 and that of O-alkylation for 3 in non-coordinating solvents thus becomes clear. The important news is that the easiness of homolytically disrupting the N–N bond in 2, a constituent of inexpensive powerful explosives, is because of the occupancy of the related σ*orbital increases with stretching this bond. The same is true for electrocyclic extrusion of NO3− from this molecule. This antibonding effect may be assumed to be the common cause of the proneness of aliphatic nitro compounds to decompose. Pyramidal anion 6 is a highly localized carbanion. Its isomer of molecular symmetry CS has a unique chemical structure of its azido substituents: each of them is represented by one high-weight resonance structure, e.g., N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N. The prediction is that the dinitrogen-eliminating decomposition of this isomer is more facile than of the isomer of C3 symmetry. In summary, this study affords three novel particular insights into the chemical structure and reactivity of these anions: chemically telling delocalization-augmented molecular structures, a reasonable hypothesis of the common cause of thermally triggered instability of aliphatic nitro compounds, and discovered one-resonance structure azido groups.
N. The prediction is that the dinitrogen-eliminating decomposition of this isomer is more facile than of the isomer of C3 symmetry. In summary, this study affords three novel particular insights into the chemical structure and reactivity of these anions: chemically telling delocalization-augmented molecular structures, a reasonable hypothesis of the common cause of thermally triggered instability of aliphatic nitro compounds, and discovered one-resonance structure azido groups.
Introduction
Nitroformate [(NO2)3C]− (1) and dinitroamide [(NO2)2N]− (2) are the only known anions whose molecular structure is one atom bearing nitro groups. Their salts are easily available high-energy compounds and the thoroughly selected ones (e.g., hydrazinium nitroformate, ammonium dinitroamide, and hydrazinium dinitroamide) are an inexpensive chief component of excellent explosives and propellants. In view of this important practical circumstance as well as the general interest in the structure of prototypic molecules, anions 1 and 2 have been the focus of many structural studies (mainly by XRD1,2 and quantum mechanics (QM) molecular modeling1a,2b,c,3a,4–7 as well as episodically by 13C, 14N, 15N NMR,1c,3a IR3a,4 and Raman spectroscopies3a,4). Astonishingly, chemical bonding in these homoleptic anions has remained inadequately understood.Their chemical structure is mainly considered as a significantly delocalized anion;2b,c,3,5,6a a near-ideal planarity of the central elementary molecular fragment (C)NNN in 1 urges to accept this view. Among them, QM calculations undertaken for anion 2 using Bader's atoms-in-molecules approach are notable: they show that the π bonding is dissipated along the whole molecular backbone.2c,5 An extreme viewpoint is that anion 1 is a Y-aromatic system;6a the number n of the Hückel's aromaticity criterion (4n + 2) is 0 in this case as it is for the archetypal Y-aromatic molecule of trimethylenemethane dication.6b Unfortunately, the convenient magnetic shielding-based criterion of aromaticity (abbreviated to TSNMRS) is unable to prove or disprove this.6c Contradicting the aromaticity hypothesis, early DFT calculations characterize anion 1 to be not sizably delocalized.7 Thus, while establishing the fact of delocalization of anions 1 and 2, the undertaken molecular modeling2b,c,3a,b,5–7 does not unambiguously conclude what the degree of this delocalization is.
Obviously, conclusions regarding the chemical bonding in anions 1 and 2, which were drawn from age-old QM calculations, require verification because these studies have used either insufficiently accurate calculation methods, or unbalanced basis sets, or an unsuccessful combination of them. For instance, in modeling anion 2, Pople's basis sets together with various post-HF calculation methods were sometimes used or tried.3a,4 This combination rather delivers an essentially corrupted molecular geometry if applied to conjugated systems.8
The description of anions 1 and 2 as a σ-bonded molecular backbone enforced by a framework of substantially delocalized π-bonding is not in line with their considerable chemical instability: as a rule, their salts are explosive substances sensitive to storing and handling conditions (except the cases where crystal packing stabilizes the salt1e,3c). Also, the central atom in anions 1 and 2, though carrying substituents both of a potent −I and −M effect, shows an appreciable nucleophilicity. Tetrafluoroammonium salt NF4SbF6 oxidizes anion 2 in SO2 at −64 °C with forming fluorodinitroamine FN(NO2)2.9 This low-temperature fluorination does not surprise only if assuming a poor delocalization of the N-anion. On the other hand, an extremely high acidity of both parent C–H and N–H acid-trinitromethane (pKa = 0.17) and dinitraminic acid (pKa = −5.0) – is a rationale in favor of the hypothesis of a sheer anion delocalization.
Herein, homoleptic nitroanions 1 and 2 (Fig. 1) are computationally revisited with quantitatively mapping delocalization in their molecular backbones by means of the Weinhold's natural bond orbital (NBO) method10 that analyses chemical structure with ‘translating’ orbital consideration to that in chemical bond terms. Conformational dynamics of these anions is modeled as well. Their mononitro analogs, nitronate anion [CH2NO2]− (3), N-methyl nitramide anion [CH3NNO2]− (4), tris(dimethylboranyl)methane anion [(Me2B)3C]− (5), and azidoform anion [CN3]− (triazidomethane anion; 6) are similarly approached. The chemistry of anions 1–4, 6 is considered in the light of the calculated orbital delocalization.
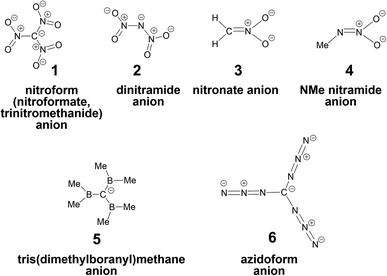 | ||
| Fig. 1 Chemical structure of anions 1–6 shown in a plain notation of localized bonds. This formal view is very far from reflecting the chemical bonding in 1–6. | ||
Results and discussion
Studied molecules are modeled for vacuum conditions with using the Dunning basis set aug-cc-pVTZ or Karlsruhe basis set QZVP. The Møller–Plesset post-HF calculation methods are exploited; that of the second-order perturbation –MP2– for anions 1, 2, 5 and that of the third-order perturbation –MP3– for anions 1 and 2. As expected, it is possible to model molecular geometry of these anions within the limits of harmonic approximation. When examining applicability of the latter on the example of anion 2, only insignificant differences are found to distinguish between the vibrationally averaged molecular geometry and the equilibrium geometry (e.g., the difference is 7 × 10−4 nm for the N–N bond length and 0.09° for the bond angle N–N–N; ESI†). MP2/aug-cc-pVTZ and B2PLYP/QZVP calculations provide a very similar molecular geometry for anion 6, and this double-hybrid functional in combination with this quadruple-zeta basis set has been chosen for analyzing orbital delocalization in this anion.Quantitative orbital delocalization is computed in the form of natural semi-localized molecular orbitals (NLMOs), where each NLMO is a linear combination of the parent natural bond orbital (NBO) and the delocalization tail (contributions of the parent NBO to other, vacant NBOs10). Notably, in spite of its apparently easy interpretability, this ‘light construction’, NLMO, is not a step-down theoretical simplification: it does not decrease the accuracy of the ab initio theory in representing the wave function.
Chemical bonding in anions 3 and 4
Computational screening of the PES for 3 (including initial structures with a pyramidal C atom) shows that this molecule is planar as well as single-shaped in the ground state (Fig. 2), confirming less accurate early calculations.11 NBO analysis of the chemical structure of anion 3 shows that there are two NLMOs in bonding the C and N atoms, both of two-electron occupancy near 100%, while there is no occupied NLMO solely related to the C atom. Thus, the carbon and nitrogen are both σ- and π-bonded (Lewis structure C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), as usually accepted for this anion. This chemical structure does not point to the still considerable C-nucleophilicity12 in SN2 reactions in aprotic solvents of low polarity.
N), as usually accepted for this anion. This chemical structure does not point to the still considerable C-nucleophilicity12 in SN2 reactions in aprotic solvents of low polarity.
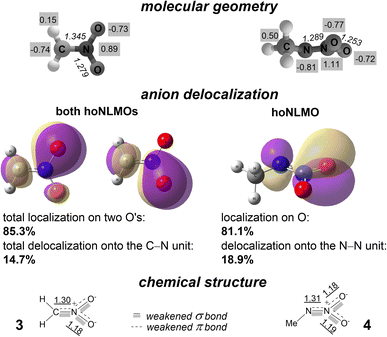 | ||
| Fig. 2 Molecular geometries of anions 3 and 4 (numbers in italics display bond lengths, Å, while those with gray background show CHELPG atomic charges14), hoNLMOs with quantitatively mapped anion delocalization, and Lewis structures of anions with the bonding that reflects the weakening effect of partial σ* and π* antibonds. Underlined numbers show calculated bond orders (as Wiberg indexes). | ||
The chemical structure C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N does not accurately describe the bonding of the C and N atoms in 3. For each O atom, there is a remarkable, 7.3% delocalization tail of one NLMO occupied by a pair of p electrons. Thus, the O,O-anion delocalization is 14.7% (Fig. 2). These two NLMOs of the same energy are the highest occupied NLMOs (hoNLMOs) for 3. For each of these NLMOs, the delocalization tail is due to a partial donation of unshared electrons of these O's from the p orbital to the π* orbital of the C
N does not accurately describe the bonding of the C and N atoms in 3. For each O atom, there is a remarkable, 7.3% delocalization tail of one NLMO occupied by a pair of p electrons. Thus, the O,O-anion delocalization is 14.7% (Fig. 2). These two NLMOs of the same energy are the highest occupied NLMOs (hoNLMOs) for 3. For each of these NLMOs, the delocalization tail is due to a partial donation of unshared electrons of these O's from the p orbital to the π* orbital of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit; the related orbital interaction energy is large (109.7 kcal mol−1 for each pair of the p and π* NBOs). A weighty 0.58 occupancy of this π* orbital means that the bonding of the C and N atoms is appreciably weakened vs. pure bonding C
N unit; the related orbital interaction energy is large (109.7 kcal mol−1 for each pair of the p and π* NBOs). A weighty 0.58 occupancy of this π* orbital means that the bonding of the C and N atoms is appreciably weakened vs. pure bonding C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N formally assigned earlier to this fragment.13 Also, the NBO analysis rejects the single bond structure N–O ‘canonized’ (ibid) for both diatomic N,O units of anion 3. There is a n → π* vicinal donation that strengthens the bonding of the N and both O atoms by ‘connecting’ them by a partial π bond (in addition to the σ bond N–O; Fig. 2).
N formally assigned earlier to this fragment.13 Also, the NBO analysis rejects the single bond structure N–O ‘canonized’ (ibid) for both diatomic N,O units of anion 3. There is a n → π* vicinal donation that strengthens the bonding of the N and both O atoms by ‘connecting’ them by a partial π bond (in addition to the σ bond N–O; Fig. 2).
Hyperconjugation also affects the chemical bonding in 3. Each pair of p electrons of both O atoms, which does not participate in occupation of the π orbital of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit, partially occupies the σ* orbital of the C–N (each related stabilization energy is 8.6 kcal mol−1). In addition, one of these pairs of both oxygens is in part donated to the σ* orbital of the geminal N–O unit (each related stabilization energy is 22.3 kcal mol−1). Stabilizing the molecule as a whole, this delocalization of the O,O unshared valence electrons weakens the σ bonding both in C–N and N–O units. With including these delocalizations of lone electron pairs, the bonding of the C and N atoms in nitronate anion 3 appears the ‘sum’ σ bond + partial σ* antibond + π bond + partial π* antibond, and the bonding of the N and O atoms appears σ bond + partial σ* antibond + partial π* bond. Bond orders calculated for 3 confirm that the bonding in its C, N fragment is significantly weaker than that of the pure double bond C
N unit, partially occupies the σ* orbital of the C–N (each related stabilization energy is 8.6 kcal mol−1). In addition, one of these pairs of both oxygens is in part donated to the σ* orbital of the geminal N–O unit (each related stabilization energy is 22.3 kcal mol−1). Stabilizing the molecule as a whole, this delocalization of the O,O unshared valence electrons weakens the σ bonding both in C–N and N–O units. With including these delocalizations of lone electron pairs, the bonding of the C and N atoms in nitronate anion 3 appears the ‘sum’ σ bond + partial σ* antibond + π bond + partial π* antibond, and the bonding of the N and O atoms appears σ bond + partial σ* antibond + partial π* bond. Bond orders calculated for 3 confirm that the bonding in its C, N fragment is significantly weaker than that of the pure double bond C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N (σ bond + π bond), and the bonding in its N, O fragment is stronger than that in the single bond N–O.
N (σ bond + π bond), and the bonding in its N, O fragment is stronger than that in the single bond N–O.
Structural conclusions are similar for nitramide anion 4. There are two doubly occupied NLMOs associated with bonding the two nitrogen atoms; they both do not have a considerable delocalization tail. Thus, this anion is a diazenium-1,1-diolate (Fig. 2). The performed NBO analysis adds more detail to the familiar chemical structure [MeN = N(O)O]− deduced from IR spectra and early ab initio calculations.15 There is a highly stabilizing n → π* electron donation from the both O's to the unit N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N: the π* orbital of this unit has a 0.65 occupancy while the occupancy of this donating n orbital of each O atom decreases to 1.65. As the related NLMOs show, delocalization of this partially donated lone electron pair is 18.9% for the trans-positioned oxygen and 15.6% for the cis-positioned oxygen. The other p electron pair of both O atoms also is not O-localized. This pair is partially donated to the π* orbital of the N
N: the π* orbital of this unit has a 0.65 occupancy while the occupancy of this donating n orbital of each O atom decreases to 1.65. As the related NLMOs show, delocalization of this partially donated lone electron pair is 18.9% for the trans-positioned oxygen and 15.6% for the cis-positioned oxygen. The other p electron pair of both O atoms also is not O-localized. This pair is partially donated to the π* orbital of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N fragment as well as to the σ* orbital of the N–O fragment with the related stabilization energies of 13.4 and 14.8 kcal mol−1, respectively. That is, the bonding which binds the N atoms in 4 is σ bond + partial σ* antibond + π bond + partial π* antibond, and the bonding which ties the atoms N and O of the nitro group is σ bond + partial σ* antibond + partial π* bond (Fig. 2).
N fragment as well as to the σ* orbital of the N–O fragment with the related stabilization energies of 13.4 and 14.8 kcal mol−1, respectively. That is, the bonding which binds the N atoms in 4 is σ bond + partial σ* antibond + π bond + partial π* antibond, and the bonding which ties the atoms N and O of the nitro group is σ bond + partial σ* antibond + partial π* bond (Fig. 2).
Chemical bonding in anions 1 and 2
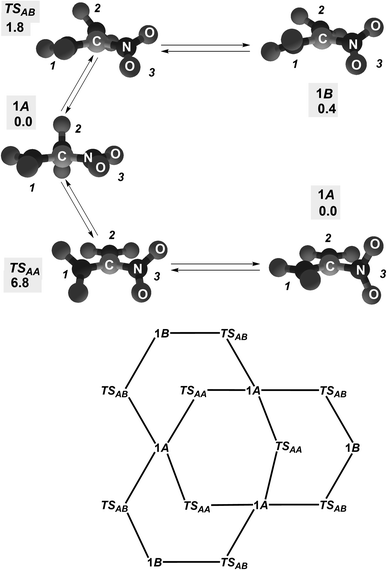
There are two conformers 1A (molecular symmetry D3) and 1B (molecular symmetry C2V) for 1; they interconvert with synchronously rotating the C substituents and changing interatomic distances C⋯N (Fig. 2 and 3).‡ Transformation 1A ⇆ 1B is associated with rotating all three NO2 groups in the conrotatory fashion, while degenerate transformation 1A ⇆ 1A is provided by rotating two NO2 groups conrotatory and one in the opposite direction. Diastereomerization 1A ⇆ 1B appears a very fast intramolecular process: the calculated barrier ΔG#AB is 1.8 kcal mol−1 at 298 K (the barrier corresponds to transition state TSAB in Fig. 3). Interconversion of degenerate (structurally identical) conformers 1A occurs slower (calculated barrier ΔG#AA = 6.8 kcal mol−1; the related transition state is TSAA in Fig. 3) while degenerate conformers 1B do not directly interconvert. In total, stereodynamics of anion 1 occurs as interconversion of six degenerate structures 1A and six degenerate structures 1B.The NLMO associated with the C lone electron pair is the hoNLMO for both conformers. It is significantly C-localized, tough somewhat differently for them (Fig. 4). That is, in contrast to the mononitro analog 3, anion 1 is a carbanion with a 29.3%- and 33%-delocalization for conformers 1A and 1B, respectively. Its essential C-localization indicates that this molecule cannot be assigned to Y-aromatic systems. A strong Y-aromaticity for 1 would require the delocalization tail to be of the 65–75% magnitude, i.e., the contribution of each related molecular fragment (the carbon atom and three NO2 groups) into this hoNLMO should be more or less equal.
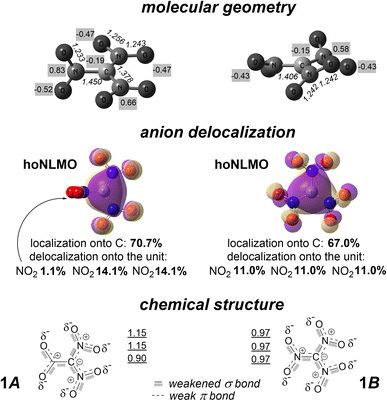 | ||
| Fig. 4 Conformers 1A and 1B: calculated molecular geometry (numbers in italics point out interatomic distances, Å; numbers with gray background present CHELPG atomic charges14), the hoNLMO with quantitatively mapped carbanion delocalization, and Lewis structure with indicating the bond weakening due to partial occupancy of σ* and π* antibonding orbitals. Underlined numbers display calculated C–N bonding orders (as Wiberg indexes). | ||
Together with this, the delocalization tail of the hoNLMO both for 1A and 1B is not negligible. The occupancy of the parent C-localized NBO for conformers 1A and 1B is substantially less than 2 (1.42 and 1.32, respectively). This deficiency in the orbital occupancy mainly is because of partially accommodating these p electrons of the C atom in the antibonding π* NBOs of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O units, as the distinctively high values of the stabilization energy for these n donor and π* acceptor NBOs show (more than 130 kcal mol−1 for each of three nitro group in 1B and 260 kcal mol−1 for each of two coplanar nitro groups in 1A). Thus, there is a partial π bonding in connecting the C atom with each of the three N atoms in 1B while this π bonding connects the C atom with only two N atoms in 1A. This orbital interaction also explains why C–N bond lengths both in 1A and 1B are different for their nitro groups differently oriented rotationally: the considered bond-shortening conjugation is maximal at the coplanar disposition of three atoms of the nitro group and the carbon atom (Fig. 4).
O units, as the distinctively high values of the stabilization energy for these n donor and π* acceptor NBOs show (more than 130 kcal mol−1 for each of three nitro group in 1B and 260 kcal mol−1 for each of two coplanar nitro groups in 1A). Thus, there is a partial π bonding in connecting the C atom with each of the three N atoms in 1B while this π bonding connects the C atom with only two N atoms in 1A. This orbital interaction also explains why C–N bond lengths both in 1A and 1B are different for their nitro groups differently oriented rotationally: the considered bond-shortening conjugation is maximal at the coplanar disposition of three atoms of the nitro group and the carbon atom (Fig. 4).
The hoNLMO delocalization tails for 1A and 1B expose that the carbanion delocalization is dissimilar for them: the delocalization onto one among their NO2 groups is 1.1% and 11.0% for 1A and 1B, respectively (Fig. 4). In particular, this means that the conformers of ambident anion 1 possess somewhat different C-nucleophilicity. Nevertheless, it would be rather impossible to discern this difference in experiments. Nucleophilic reactions of this anion are not controlled conformationally: the kinetic barrier of interconversion of 1A and 1B is very low (Fig. 3).
Unshared electron pairs of the oxygen atoms of 1 are not localized. There is a partial donation of one p electron pair of each O atom of each nitro group to the σ* orbital of the corresponding C–N fragment [with energy of 16.0 kcal mol−1 for the electron pair in 1B and 15.8 kcal mol−1 (in average) for the electron pair in 1A]. Summarizing all these delocalizations propagated to this diatomic fragment, one can conclude that the bonding that ties the C and N atoms in 1 is σ bond + partial π bond + partial σ* antibond for 1B as well as for the two coplanar nitro groups of 1A. While the aforementioned vicinal n → π* conjugation reinforces this bonding, the n → σ* hyperconjugation weakens it (see Fig. 4 for the calculated bond orders) together with strengthening the bonding between the N and O atoms. The bonding that ties the central C atom and the nitro group of 1A, which is orthogonal to the other NO2 groups, is σ bond + partial σ* antibond.
Concerning the nitro groups of 1 themselves, the bonding in N,O units is identical in each NO2 group of conformer 1B. Similarly, it is the same in the two coplanar NO2 groups of conformer 1A. In each of these nitro groups, there are both N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–O units with oxygen lone electron pairs partially delocalized in the NO2 fragment. For 1A, the delocalization includes high energy n → π* vicinal donation from the N–O unit to the N
O and N–O units with oxygen lone electron pairs partially delocalized in the NO2 fragment. For 1A, the delocalization includes high energy n → π* vicinal donation from the N–O unit to the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit (188.8 kcal mol−1 for each from two coplanar NO2 groups and 283.9 kcal mol−1 for the NO2 group orthogonal to them). Such a donation characterized by a 241.0 kcal mol−1 energy for each NO2 group of 1B. In other words, there is an essential partial π bonding in each N–O unit of anion 1.
O unit (188.8 kcal mol−1 for each from two coplanar NO2 groups and 283.9 kcal mol−1 for the NO2 group orthogonal to them). Such a donation characterized by a 241.0 kcal mol−1 energy for each NO2 group of 1B. In other words, there is an essential partial π bonding in each N–O unit of anion 1.
Anion 2 is more localized on the central atom (80.4%; Fig. 5) than carbanion 1. Nevertheless, it is not a highly localized N-anion. The 19.6% delocalization tail of the hoNLMO associated with one unshared electron pair of the central N encompasses both nitro groups, i.e., this lone electron pair is involved by almost one fifth in forming the bonding which ‘attaches’ each NO2 substituent to the central N atom.
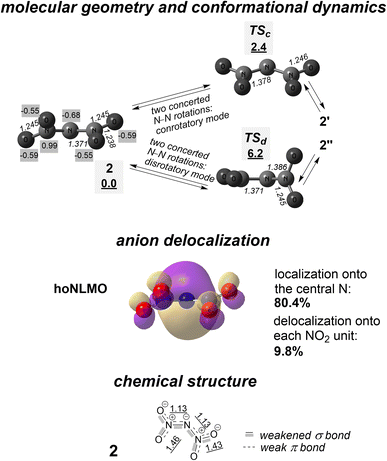 | ||
| Fig. 5 Anion 2 and interconversion of degenerate conformers 2, 2′ and 2′′ through transition states TSc and TSd. Shown are calculated molecular geometry (numbers in italics point out interatomic distances, Å; numbers with gray background present CHELPG atomic charges14), relative free energies (underlined numbers with gray background; kcal mol−1), the hoNLMO with quantitatively mapped N-anion delocalization, and Lewis structure with indicating bond weakening due to partial σ* and π* antibonds. Underlined numbers show calculated bond orders (as Wiberg indexes). | ||
The performed NBO analysis indicates that each NO2 group has both the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N–O unit (correspondingly, the N⋯O distances are different for them). The mentioned p electron pair of the central N atom is in part donated to the π* orbital of the N
O and N–O unit (correspondingly, the N⋯O distances are different for them). The mentioned p electron pair of the central N atom is in part donated to the π* orbital of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit of each nitro group, diminishing the occupation of the donating n NBO to 1.61. That is, the additional, delocalization-delivered bonding in the σ-bonded fragment N–N–N is a partial π bonding (see Fig. 5 for the calculated bond orders). Correspondingly, both interatomic distances N⋯N are decreased, and N⋯O distances in both units N
O unit of each nitro group, diminishing the occupation of the donating n NBO to 1.61. That is, the additional, delocalization-delivered bonding in the σ-bonded fragment N–N–N is a partial π bonding (see Fig. 5 for the calculated bond orders). Correspondingly, both interatomic distances N⋯N are decreased, and N⋯O distances in both units N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O are increased.
O are increased.
Similarly, for each nitro group, there is a high stabilization energy (more than 160 kcal mol−1) donation of one p electron pair of the O atom of the N–O unit to the π* orbital of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O unit of the same nitro group (the resulting occupation of this antibonding orbital is 0.54). In chemical bond terms, a partial π bond, in addition to the σ bond, ties the N and O atoms in both N–O units.
O unit of the same nitro group (the resulting occupation of this antibonding orbital is 0.54). In chemical bond terms, a partial π bond, in addition to the σ bond, ties the N and O atoms in both N–O units.
Together with this, hyperconjugation n → σ* slightly weakens the σ bond framework in anion 2. Both oxygens of each NO2 group partially donate one lone electron pair to the σ* orbital of the related N–N fragment (the orbital interaction energy is ∼16.7 kcal mol−1 for each of the N–O oxygens and 22.8 kcal mol−1 for each of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxygens). The occupancy of this antibonding orbital of both N–N fragments is further increased to 0.08 due to the partial n → σ* donation (with energy of 2 × 12.7 kcal mol−1) of the unshared N electron pair which does not participate in occupying the π* orbital of the N
O oxygens). The occupancy of this antibonding orbital of both N–N fragments is further increased to 0.08 due to the partial n → σ* donation (with energy of 2 × 12.7 kcal mol−1) of the unshared N electron pair which does not participate in occupying the π* orbital of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O units. For both N–O units, one O atom partially donates (with energy of 20.9 kcal mol−1) to the σ* orbital of the N
O units. For both N–O units, one O atom partially donates (with energy of 20.9 kcal mol−1) to the σ* orbital of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragment of this NO2 group, while the O atom of the N
O fragment of this NO2 group, while the O atom of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragment similarly donates a p electron pair to the σ* orbital of the geminal N–O unit with stabilization energy of 22.8 kcal mol−1. When describing these delocalizations of lone electron pairs in terms of chemical bonding, chemical structure of anion 2 appears somewhat different from that considered12,13 earlier. The bonding of the N atoms is σ bond + partial π bond + partial σ* antibond. The bonding in the N
O fragment similarly donates a p electron pair to the σ* orbital of the geminal N–O unit with stabilization energy of 22.8 kcal mol−1. When describing these delocalizations of lone electron pairs in terms of chemical bonding, chemical structure of anion 2 appears somewhat different from that considered12,13 earlier. The bonding of the N atoms is σ bond + partial π bond + partial σ* antibond. The bonding in the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O units is σ bond + π bond + partial σ* antibond + partial π* antibond, while the bonding in the N–O units is σ bond + partial σ* bond + partial π* antibond. Clearly, there are two opposite tendencies in bonding atoms in units N–N and N–O: the bond weakening due to the n → σ* hyperconjugation and its strengthening due to the n → π* conjugation. The calculated bond orders for these diatomic units (Fig. 5) reflect the final balance of these tendencies.
O units is σ bond + π bond + partial σ* antibond + partial π* antibond, while the bonding in the N–O units is σ bond + partial σ* bond + partial π* antibond. Clearly, there are two opposite tendencies in bonding atoms in units N–N and N–O: the bond weakening due to the n → σ* hyperconjugation and its strengthening due to the n → π* conjugation. The calculated bond orders for these diatomic units (Fig. 5) reflect the final balance of these tendencies.
Chemical bonding in some other methanide anions
Delocalization of tri(dimethylboranyl) methanide anion 5 (Fig. 6) is the single orbital interaction significantly stabilizing the structure; others are of essentially lower energy. It is a poccupied → pvacant orbital interaction that takes place in diatomic fragments of neighboring proper atoms, another type of formal electron donation.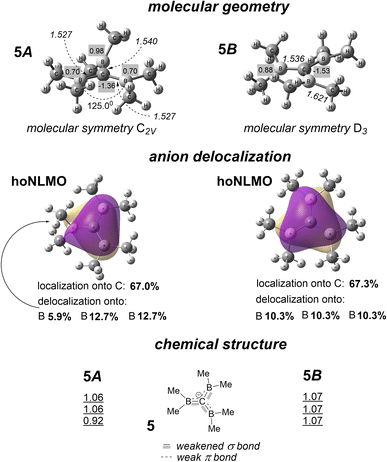 | ||
| Fig. 6 Conformers 5A and 5B (designations are the same as they are in Fig. 4). Calculated bond orders are shown for diatomic C–B units. | ||
This orbital interaction is highly expedient energetically in borane-stabilized C anions,16 where such 1,2-positioned occupied (for C) and vacant (for B) p orbitals are separated by a modest energy gap and their Cn symmetry axes are coplanar or near-coplanar. Both conformers 5A and 5B have the geometrical motif of conformers 1A and 1B, and their donor and acceptor p orbitals are almost coplanar for 5B and coplanar for two C substituents of 5A. Nevertheless, anion 5 is not Y-aromatic. The delocalization of this anion comprises the four-atom fragment C(B3), and the anion is localized there onto the C atom by 67.0% in one conformer and by 67.3% in the other (Fig. 6), similarly to anion localization in 1. The example of anions 1 and 5 that have different channels of strong electron donation indicates that carbanions bearing three substituents of the same chemical structure have a certain, carbon-specific and substituent-invariant, limit in delocalization magnitude (∼30% of delocalization). That is, Y-aromaticity is not inherent in triply substituted methanide anions.
Azidoform anion 6, one of the simplest geminal azide molecules,19 is unknown. It is difficult to a priori judge whether, e.g., salt Li+˙ 6 could be prepared in a short way, for instance, from the parent, very unstable azidoform17 with using neopentyl lithium (a non-nucleophilic organolithium reagent) or from triazidocarbenium tetrafluroborate18 if reducing this salt by Li/NH3 or lithium naphthalene. Nevertheless, QM modeling of this methanide anion is undertaken here in order to reveal what is the degree of its delocalization; the starting hypothesis is that the n–π* conjugation similar to that in vinyl azides20 stabilizes this energy-rich molecule.
The results are unexpected. The molecular shape of two most stable, near-energy isomers 6A and 6B of 6§ is a trigonal pyramid, pointing out that this anion is delocalized insignificantly. In addition, C–N bonds in anion 6 (Fig. 7) are slightly longer than the C–N bond in methyl azide,21 but appreciably longer than that in π, π-conjugated vinyl azides.20
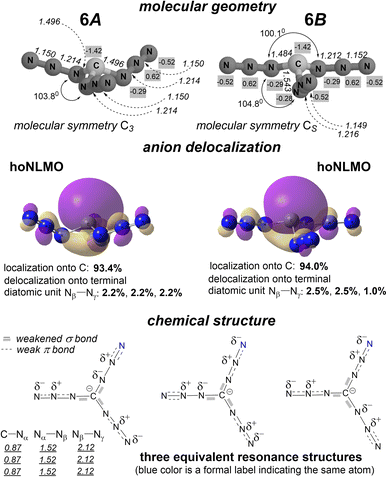 | ||
| Fig. 7 Isomers 6A and 6B: calculated molecular geometry (numbers in italics point out interatomic distances, Å; arc arrows depict NCN bond angles; numbers with gray background present CHELPG atomic charges14), the hoNLMO with quantitatively mapped carbanion delocalization, equivalent resonance structures of isomers of 6 with indicating the bond weakening due to a partial occupation of π* antibonding orbitals, and calculated bond orders (as Wiberg indexes) for isomer 6A (underlined numbers; see ESI† for 6B). The chemical structure of isomer 6A is represented by three displayed resonance structures together, while one of these equivalent structures represents the chemical structure of isomer 6B. | ||
NBO analysis firmly confirms the above guess, demonstrating that there is no such a vicinal interaction of the 2e-occupied p orbital of the carbon and the vacant π* orbital of the Nα–Nβ fragment. Instead, there is localization of the p orbital of the C lone electron pair on this atom by 93.4 and 94.0% for 6A and 6B, respectively (Fig. 7). The small delocalization tail of 6.6 and 6.0%, respectively, is due to a partial electron donation from this occupied orbital of the C atom to the π* orbital of each terminal N–N unit (a long range n → π* electron donation).
For anion 6, NBO analysis endows two azido substituents with the σ and π framework N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N of chemical bonding, and one azido substituent with that of N–N
N of chemical bonding, and one azido substituent with that of N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (for simplicity, formal charges are omitted here). Excluding a 5% delocalization of each C–N bond (see below), both σ and π bonds are largely localized in both isomers 6A and 6B. Essential delocalizations (i)–(iii) are only associated with orbitals of unshared electron pairs of nitrogen atoms. (i) The p orbital of one unshared electron pair of the Nγ atom in each of two N
N (for simplicity, formal charges are omitted here). Excluding a 5% delocalization of each C–N bond (see below), both σ and π bonds are largely localized in both isomers 6A and 6B. Essential delocalizations (i)–(iii) are only associated with orbitals of unshared electron pairs of nitrogen atoms. (i) The p orbital of one unshared electron pair of the Nγ atom in each of two N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N substituents both in 6A and 6B interacts with the vacant π* antibonding orbital of the related Nα = Nβ fragment with decreasing its own localization to 63.9% and populating this antibonding orbital to a significant value of 0.74. The other 2e-occupied p orbital of this nitrogen remains N-localized by 98.5% both for 6A and 6B. (ii) The p orbital of the unshared electron pair of the Nα atom both in N
N substituents both in 6A and 6B interacts with the vacant π* antibonding orbital of the related Nα = Nβ fragment with decreasing its own localization to 63.9% and populating this antibonding orbital to a significant value of 0.74. The other 2e-occupied p orbital of this nitrogen remains N-localized by 98.5% both for 6A and 6B. (ii) The p orbital of the unshared electron pair of the Nα atom both in N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and N–N
N and N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N substituents both in 6A and 6B interacts with the antibonding π* orbital of the corresponding terminal unit Nβ
N substituents both in 6A and 6B interacts with the antibonding π* orbital of the corresponding terminal unit Nβ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Nγ with delocalization of 13.0% (for both N
Nγ with delocalization of 13.0% (for both N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N substituents) and 11.8% (for the N–N
N substituents) and 11.8% (for the N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N substituent), respectively. This formal electron donation, together with the σ → π* donation from the σ orbital of each C–N unit as well as the above mentioned small delocalization tail of the p orbital of the C atom, leads to a 0.32 occupancy of this antibonding orbital for 6A and 0.32 (for two symmetrically positioned azido substituents) as well as 0.34 occupancy (for the third azido substituent) for 6B thus loosening the bonding in each of these diatomic units. The σ → π* donation weakens the σ bond in all C–N units, and the calculated bond orders (Fig. 7) independently ‘detect’ this weakening. (iii) The second lone electron pair of the Nα atom of the N–N
N substituent), respectively. This formal electron donation, together with the σ → π* donation from the σ orbital of each C–N unit as well as the above mentioned small delocalization tail of the p orbital of the C atom, leads to a 0.32 occupancy of this antibonding orbital for 6A and 0.32 (for two symmetrically positioned azido substituents) as well as 0.34 occupancy (for the third azido substituent) for 6B thus loosening the bonding in each of these diatomic units. The σ → π* donation weakens the σ bond in all C–N units, and the calculated bond orders (Fig. 7) independently ‘detect’ this weakening. (iii) The second lone electron pair of the Nα atom of the N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N substituent both of 6A and 6B is copiously donated to the second antibonding π* orbital of the related terminal unit Nβ
N substituent both of 6A and 6B is copiously donated to the second antibonding π* orbital of the related terminal unit Nβ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Nγ with populating it by 0.58 and 0.54, respectively, and delocalizing the parent non-bonding orbital by 27.2% for both conformers. Calculated bond orders well reflect the total decrease of the strength of chemical bonding in diatomic units N–N resulted from weakening their π bonds (Fig. 7 and ESI†).
Nγ with populating it by 0.58 and 0.54, respectively, and delocalizing the parent non-bonding orbital by 27.2% for both conformers. Calculated bond orders well reflect the total decrease of the strength of chemical bonding in diatomic units N–N resulted from weakening their π bonds (Fig. 7 and ESI†).
As mentioned above, NBO analysis supplies the chemical bonding framework N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N to two azido substituents and chemical bonding N–N
N to two azido substituents and chemical bonding N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N to one azido substituent for both structures 6A and 6B (Fig. 7 shows their Lewis chemical structures with taking into account the delocalization of p orbitals of nitrogen lone pairs). However, all three C substituents in isomer 6A of C3 symmetry have the identical molecular geometry (see Fig. 7 for bond lengths), and, hence, the same chemical bonding framework. Neither azido substituent in 6A therefore has the N–N
N to one azido substituent for both structures 6A and 6B (Fig. 7 shows their Lewis chemical structures with taking into account the delocalization of p orbitals of nitrogen lone pairs). However, all three C substituents in isomer 6A of C3 symmetry have the identical molecular geometry (see Fig. 7 for bond lengths), and, hence, the same chemical bonding framework. Neither azido substituent in 6A therefore has the N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N or N
N or N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N chemical structure. Three equivalent resonance structures together (Fig. 7; those also indicate the π bond weakening due to orbital delocalizations) represent the chemical structure of 6A, i.e., each azido substituent of this isomer is represented by two-thirds by chemical connectivity N
N chemical structure. Three equivalent resonance structures together (Fig. 7; those also indicate the π bond weakening due to orbital delocalizations) represent the chemical structure of 6A, i.e., each azido substituent of this isomer is represented by two-thirds by chemical connectivity N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N and by one-third by connectivity N–N
N and by one-third by connectivity N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, both with a weakened π bonding.
N, both with a weakened π bonding.
Concerning isomer 6B of molecular symmetry CS, interatomic distances in diatomic units C–Nα, Nα–Nβ and Nβ–Nγ in two azido substituents, which are mirrorly positioned in the molecule, are identical. The bond lengths of the same diatomic units C–Nα, Nα–Nβ and Nβ–Nγ in the azido substituent, which lies in the symmetry plane of the molecule, differ from the corresponding ones in the above mentioned symmetrically positioned azido substituents (Fig. 7), indicating that the chemical bonding framework in this substituent is distinct from chemical bonding in other two C substituents in this isomer. This azido substituent is supplied by the NBO analysis with chemical bonding N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N; two other substituents have that of N
N; two other substituents have that of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N. Thus, the chemical structure of this isomer is represented by one structure from three equivalent ones shown in Fig. 7. This means that the chemical structure of isomer 6B is more certain than the structure of ordinary alkyl azides. While four classical resonance structures together represent the azido group (see, e.g., ref. 22), each azido substituent of 6B is actually represented by one predominantly highly weighted resonance structure. The clear ‘off-resonance’ chemical structure of the triazide fragment of 6B renders the azide chemistry of this isomer to be more predictable than that of 6A (see below).
N. Thus, the chemical structure of this isomer is represented by one structure from three equivalent ones shown in Fig. 7. This means that the chemical structure of isomer 6B is more certain than the structure of ordinary alkyl azides. While four classical resonance structures together represent the azido group (see, e.g., ref. 22), each azido substituent of 6B is actually represented by one predominantly highly weighted resonance structure. The clear ‘off-resonance’ chemical structure of the triazide fragment of 6B renders the azide chemistry of this isomer to be more predictable than that of 6A (see below).
Chemical structures of 6A and 6B are explicitly not identical; in isomerism terms, 6A and 6B are chemical isomers and not conformers (rapidly interconverting stereoisomers), in contrast to the border case of 1A and 1B explained in distinguishing between chemical isomer–stereoisomer.‡
Interestingly, the deduced chemical structure of isomer 6A (Fig. 7) is related to a diverse group of molecular structures which cannot be adequately filed with exploiting standard formats of computer-readable representation of chemical structure ubiquitously used in cheminformatics (e.g., SMILES, InChI, MDL Mol, etc.). This non-Lewis structures thus is technically problematic for including it into datasets focused on applying computerized AI algorithms to molecular or crystal-level design of high-energy materials (exemplified by datasets used in dozens of related recent studies23). It is an open question whether other geminal polyazides, for instance, tetraazidomethane,24 fall under such a ‘hard nut’ category.
Explainable chemistry of anions 1–4 and chemical predictions for anion 6 (examples). Quantitative mapping of delocalization in anions 1–4, 6 assists in understanding and predicting their chemical reactivity. For instance, in reactions, which involve nitro groups of methanide anion 1, the reactivity of these groups NO2 of distinct rotational orientation in conformer 1A should be somewhat dissimilar. Namely, the nitro group of 1A, which does not essentially delocalize the unshared electron pair of the carbon (Fig. 4), should be more prone to rupturing the C–N bond than two other NO2 groups. Indeed, DFT modeling of decomposition pathways of molecules of K+˙ 1 in both conformations25 shows that the lower barrier of disruption of the C–N bond is for the conformer of geometrical motif of conformer 1A. NO2 groups in molecules of crystalline NH4˙ 4 have different N–N rotational orientations.26 According to this QM modeling, the NO2 group which is near orthogonal to the NNN plane of the molecule, i.e., minimally participates in delocalization of the anion, is kinetically most prone to loss its chemical bonding with the central nitrogen atom, similarly to the above described case of anion 1.
Another example is SN2 reactions of ambident anions 3 and 1 with primary alkyl halides. If very roughly assessing the anion delocalization, the mononitro anion 3 is an O-anion, while the pernitro anion 1 is a C-anion (Fig. 1 and 3). Trivial alkylation of mononitronate anions crucially depends on counterion and solvent, i.e., factors which determine the strength of the heteroatom-cation coordination in solution and thus interfere with the nucleophilicity of the naked anion. Nevertheless, the common experimental conclusion is that the inherent reactivity of nitronate anions is that of the O-anion.27 In contrast, C-alkylation absolutely predominates in similar reactions of trinitromethanide anion 1.28 The quantitatively mapped anion delocalization well explains both experimental observations.
The ‘prominent’ anion 2 is the energy-storing core of superior low-cost explosives forged in the 70 s–80 s and the oxidizing constituent in some modern propellants.29 Both the electrocyclic extrusion of the nitrate anion and homolytically initiated release of gaseous nitrogen oxides in decomposition of this nitroanion are characterized by relatively low kinetic barriers.30 For these barriers, the undertaken calculations provide free energy values ΔG# of 43.0 and 36.3 kcal mol−1, respectively (ESI);† they are satisfactory close to the barrier values calculated earlier.30 The crucial factor of this easiness of molecules of 2 to fall apart is exposed if including orbital delocalization into consideration. As appears, the occupancy of the σ* antibonding orbital in unit N–N of anion 2 archly increases when stretching this diatomic fragment. The same is true for the σ* orbital of unit N–O being stretched, too. Homolytic decomposition of anion 2 starts from dissociation of one N–N bond (Fig. 8). The increase in occupancy from 0.08 (see above for the hyperconjugation in this anion) to 0.62 in the transition state on the route to the intermediate product N2O·N2O4− (ESI)† softens this bond utterly. The occupancy further increases to 0.69 when reaching this supramolecule in the reaction pathway.
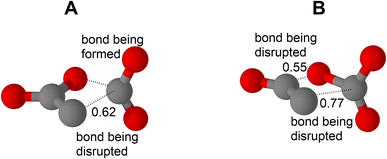 | ||
| Fig. 8 (A) The located transition state in homolytic decomposition of anion 2 (TSlow in ESI†). (B) The located transition state of the concerted electrocyclic decomposition of this anion (ESI†). Numbers show the occupancy of the antibonding σ* orbitals for both A and B. | ||
The above mentioned electrocyclic deintegration of the molecule of 2 requires two bonds, the N–N and N–O, to be concertedly broken (Fig. 8 and ESI†). Thus, the kinetic stability of 2 could be expected to be high while, in fact, it is relatively low, as noticed above. The revealed NO2 group-associated feature of the increase of the occupancy of the σ* orbital under stretching the related σ bond plays a significant role in decomposition of anion 2 also according to this molecular mechanism. In the related transition state (Fig. 8), the σ* orbital occupancy for both bonds being disrupted, namely the N–N bond and the N–O bond, increases to 0.77 and 0.55 (from 0.09 for the parent anion 2), respectively. Not surprisingly, decomposition temperatures for molten salts cation˙ 2 are lower by ∼100 °C and more than those for molten salts cation˙ 4, where the anion has a stronger bonding of a partially double bond character in the N,N unit (Fig. 2).
Both different mechanisms of decomposition of nitroanion 2 are associated with a smooth increase of the occupancy of the antibonding σ* orbital in parallel with stretching the related σ bond. One can reasonably ask whether this molecular feature – the coupling of elongation of a σ bond with a peculiar decrease of the strength of this bond (originated from elevating the σ* orbital occupancy) – is the common cause of proneness of nitro compounds to decompose under thermal impact.
Concerning triazido methanide 6, the established high localization of the anion on the central atom permits to formally separate the chemistry of 6 in that of the C-anion, i.e., a trivial chemistry of carbanions, and that of the azido substituents, i.e., a difficult-to-predict chemistry of geminal polyazides.24,31 However, this anion localization has a clear consequence: the σ bonding framework in the central four-atom fragment (C)NNN of this anion is not reinforced by an additional (i.e., π) bonding, in sharp contrast to the case of nitroanions 1 and 2. Moreover, the elucidated chemical structure of 6 (Fig. 7) reflects that C–N bonds are weakened in this fragment.
In regard to carbanion chemistry, if a salt cation˙ 6 is synthetically available and possesses a considerable stability at moderately low temperatures, one may foresee that one-electron or two-electron oxidation of 6 with producing the corresponding radical (N3)3C˙ or cation (N3)3C+,18 respectively, is quite feasible: the carbanion is only insignificantly delocalized. One can also expect an appreciable C-nucleophilicity for this anion.
The chemical structure of isomer 6B (Fig. 7) prompts that the thermally induced nitrene-generating decomposition of the azido group32 is facilitated for this molecule. Indeed, the single-resonance-structure chemical bonding N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N in one of its azido groups (the absence of appreciably weighted resonance structures which disallow N2 extrusion without rearranging chemical bonding and changing interatomic distances C⋯Nα, Nα⋯Nβ and Nβ⋯Nγ in this substituent; Fig. 6) clearly points out this chemical lability of 6B to be higher than that of 6A, the isomer without azido substituents of a ‘pure’ N–N
N in one of its azido groups (the absence of appreciably weighted resonance structures which disallow N2 extrusion without rearranging chemical bonding and changing interatomic distances C⋯Nα, Nα⋯Nβ and Nβ⋯Nγ in this substituent; Fig. 6) clearly points out this chemical lability of 6B to be higher than that of 6A, the isomer without azido substituents of a ‘pure’ N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N resonance structure.
N resonance structure.
This conclusion can be extended to claiming that isomer 6B is kinetically more labile than any other ordinary alkyl azide. Probably, an isomer of the parent azidoform also has an ‘off-resonance’ structure N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N in its triazide fragment (similar to that in 6B) or the chemical structure with a predominated weight of resonance structure N–N
N in its triazide fragment (similar to that in 6B) or the chemical structure with a predominated weight of resonance structure N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N of one of its azido substituents. This reasonable assumption well explains explosive degradation of azidoform in solution observed at the room temperature.17a Homolytic decomposition of 6 and, thus, azidoform with dissociating the C–N bond and yielding azide radical33 could be scarcely assessed to be a dark reaction possible to occur at this temperature although the σ bonding framework has a diminished strength in this anion as stated above.
N of one of its azido substituents. This reasonable assumption well explains explosive degradation of azidoform in solution observed at the room temperature.17a Homolytic decomposition of 6 and, thus, azidoform with dissociating the C–N bond and yielding azide radical33 could be scarcely assessed to be a dark reaction possible to occur at this temperature although the σ bonding framework has a diminished strength in this anion as stated above.
The ‘pure’ dipolar N−–N+![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N chemical structure of one azido substituent of 6B also indicates an increased reactivity of this isomer in [3 + 2] cycloadditions. Indeed, isomerization of this ‘off-resonance’ structure into reactive 1,3-dipole N−–N
N chemical structure of one azido substituent of 6B also indicates an increased reactivity of this isomer in [3 + 2] cycloadditions. Indeed, isomerization of this ‘off-resonance’ structure into reactive 1,3-dipole N−–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N+ is associated with the energy cost of only changing one interatomic distance Nβ⋯Nγ.
N+ is associated with the energy cost of only changing one interatomic distance Nβ⋯Nγ.
Conclusions
The undertaken QM modelling followed by NBO analysis finds planar nitroanions 1 and 2 to be delocalized to the 33% and 20% extent, respectively. Consequently, the conclusion, which finalizes the long-term discussion on aromaticity suggested for anion 1, is that it is not a Y-aromatic system. The delocalization-prone planar anion 5 is delocalized to the same 33% extent, and, thus, the numerical value of one-third probably is the upper limit of delocalization of homoleptic three-substituted methanide anions. Azidoform anion 6 appears to be pyramidal and is almost entirely C-localized. One from its two lowest energy isomers has a unique chemical structure: one azido substituent possesses the chemical bonding of a ‘pure’ (predominantly highly weighted) resonance structure N–N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N, while two others have the chemical bonding of single resonance structure N
N, while two others have the chemical bonding of single resonance structure N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N highly weighted to the same extent. An important result of these calculations is that the essential chemistry of the studied anions becomes understandable or even predictable when quantitatively mapping orbital delocalization in the molecular backbone. For instance, the outcome of nucleophilic reactions of ambident nitroanions 1 and 3 is clear in the light of the mapped anion delocalization.
N highly weighted to the same extent. An important result of these calculations is that the essential chemistry of the studied anions becomes understandable or even predictable when quantitatively mapping orbital delocalization in the molecular backbone. For instance, the outcome of nucleophilic reactions of ambident nitroanions 1 and 3 is clear in the light of the mapped anion delocalization.
A remarkable example of this ‘through-the-delocalization-prism’ understanding of reactivity is the revealed cause of the easiness of the high-energy anion 2 to initiate its decomposition both via N–N bond homolysis and electrocyclic extrusion of nitrate anion. Delocalization of one 2e-occupied p orbital of both O's of the departing NO2 group onto the antibonding σ* orbital of this bond significantly increases in parallel with stretching this diatomic unit N–N. This finding leads to reasonably conclude that this cause of the proneness of a molecule to start disintegration – the raising increase in the occupancy of the σ* orbital related to the being dissolved σ bond-is probably common for aliphatic nitro compounds.
Calculation methodology
Geometry optimization and frequency calculations were performed at the MP2/aug-cc-pVTZ level (anions 1, 2, and 5), and MP3/aug-cc-pVTZ level (anions 3 and 4) for the gas phase with using harmonic approximation; both MP2/aug-cc-pVTZ and B2PLYP/QZVP calculations were applied to modeling of anion 6 (Gaussian16 calculation package, Revision A.03).34 Anharmonic vibrational frequency calculations were undertaken for anion 2 and both transition states TSc, and TSd. NBO program implemented in Gaussian16 was exploited for NBO analysis with setting the program option Highly Delocalized Structure. A convenient narrow-specialized computer program Chemcraft35 was used for generating files of the Gaussian's cub format from the Gaussian-produced files of the fchk (formatted checkpoint) format. The Gaussian's graphical interface program GaussView6 provided visualization of calculated orbitals.Energy minimization was performed with exploiting the Berny algorithm implemented in the used Gaussian16 version. The GEDIIS algorithm embedded in Gaussian was employed when optimizing the geometry of stable (energy-minimum) structures, while the Rational Function Optimization was the algorithm option involved in optimizing the geometry of transition states.
Transition states TSAB, TSAA, TSc, and TSd were located via generating rotamers by sequential on-the-screen 10°–step rotation of one substituent relative to the other one (GaussianView) and optimizing the geometry of the each resulting rotamer. Transition state TSh of anion 2 were located by randomly varying interatomic distances N1⋯N7 (ESI, page S34†) in the range of 1.8 to 1.9 Å, N2⋯O6 in the range of 1.6 to 1.7 Å, and N1⋯O6 in the range of 1.7 to 1.8 Å, all with increment of 0.1 Å, optimizing the geometry of the each generated structure under ‘freezing’ interatomic distances for the above indicated atom pairs and re-optimizing the resulting geometry with removing geometry constraints. Transition state TSlow was located in the similar way with varying interatomic distances N1⋯N7 (ESI, page S36†) in the range of 1.9 to 2.0 Å, N2⋯O6 in the range of 1.3 to 1.4 Å, and N1⋯O6 in the range of 1.7 to 1.8 Å. The IRC procedure (a Gaussian utility) was applied to establishing the relationship of each located transition state with the corresponding energy-minimum structures.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The governmental KAMEA program coordinated by the Council for Higher Education of Israel has provided the financial ground for this work. The author is always very thankful to a group of civic-minded professors of Israeli universities headed by Prof. Benjamin Fein who, in their times, volunteered to develop and advance this nonsymbolic arrangement in the Israel Academy of Sciences and Humanities and succeeded in their high initiative.References
- (a) M. Göbel and T. M. Klapötke, Potassium-, Ammonium-, Hydrazinium-, Guanidinium-, Aminoguanidinium-, Diaminoguanidinium-, Triaminoguani-dinium- and Melaminiumnitroformate – Synthesis, Characterization and Energetic Properties, Z. Anorg. Allg. Chem., 2007, 633, 1006–1017 CrossRef; (b) J. C. Bryan, M. N. Burnet and A. A. Gakh, Tetrabutylammonium and Caesium Salts of Trinitromethane, Acta Crystallogr., Sect. C, 1998, 54, 1229–1233 CrossRef; (c) A. A. Gakh, J. C. Bryan, M. N. Burnett and P. V. Bonnesen, Synthesis and structural analysis of some trinitromethanide salts, J. Mol. Struct., 2000, 520, 221–228 CrossRef CAS; (d) L. Yang, J. Zhang, T. Zhang, J. Zhang and Y. Cui, Crystal structures, thermal decompositions and sensitivity properties of [Cu(ethylenediamine)2(nitrofor-mate)2] and [Cd(ethylene-diamine)3](nitroformate)2, J. Hazard. Mater., 2009, 164, 962–967 CrossRef CAS; (e) A. F. Baxter, A. Martin, K. O. Christe and R. Haiges, Formamidinium Nitroformate: An Insensitive RDX Alternative, J. Am. Chem. Soc., 2018, 140, 15089–15098 CrossRef CAS PubMed.
- (a) R. D. Gilardi, J. Flippen-Anderson, C. George and R. J. Butcher, A New Class of Flexible Energetic Salts: The Crystal Structures of the Ammonium, Lithium, Potassium, and Cesium Salts of Dinitramide, J. Am. Chem. Soc., 1997, 119, 9411–9416 CrossRef CAS; (b) D. C. Sorescu and D. L. Thompson, Classical and Quantum Mechanical Studies of Crystalline Ammonium Dinitramide, J. Phys. Chem. B, 1999, 103, 6774–6782 CrossRef CAS; (c) E. A. Zhurova, A. Martin and A. A. Pinkerton, Chemical Bonding in Biguanidinium Dinitramide and Biguanidinium Bis-Dinitramide from Experimental X-ray Diffraction Data, J. Am. Chem. Soc., 2002, 124, 8741–8750 CrossRef CAS PubMed; (d) S. Venkatachalam, G. Santhosh and K. N. Ninan, An Overview on the Synthetic Routes and Properties of Ammonium Dinitramide (ADN) and other Dinitramide Salts, Propellants, Explos., Pyrotech., 2004, 29, 178–187 CrossRef CAS.
- (a) V. A. Shlyapochnikov, M. A. Tafipolsky, I. V. Tokmakov, E. S. Baskir, O. V. Anikina, Yu. A. Strelenko, O. A. Luk’yanova and V. A. Tartakovsky, On the structure and spectra of dinitramide salts, J. Mol. Struct., 2001, 559, 147–166 CrossRef CAS; (b) J. C. Bottaro, P. E. Penwell and R. J. Schmitt, 1,1,3,3-Tetraoxo-1,2,3-triazapropene Anion, a New Oxy Anion of Nitrogen: The Dinitramide Anion and Its Salts, J. Am. Chem. Soc., 1997, 119, 9405–9410 CrossRef CAS; (c) L. He, G.-H. Tao, D. A. Parrish and J. M. Shreeve, Impact insensitive dinitromethanide salts, Chem. Commun., 2013, 49, 10329–10331 RSC.
- (a) K. O. Christe, W. W. Wilson, M. A. Petrie, H. H. Michels, J. C. Bottaro and R. Gilardi, The Dinitramide Anion, N(NO2)2−, Inorg. Chem., 1996, 35, 5068–5071 CrossRef CAS PubMed; (b) H. Michels and J. A. Montgomery, Jr., On the Structure and Thermochemistry of Hydrogen Dinitramide, J. Phys. Chem., 1993, 97, 6602–6606 CrossRef CAS.
- J. P. Ritchie, E. A. Zhurova, A. Martin and A. A. Pinkerton, Dinitramide Ion: Robust Molecular Charge Topology Accompanies an Enhanced Dipole Moment in Its Ammonium Salt, J. Phys. Chem. B, 2003, 107, 14576–14589 CrossRef CAS.
- (a) J. Cioslowski, S. T. Mixon and E. D. Fleischmann, Electronic structures of trifluoro-, tricyano-, and trinitromethane and their conjugate bases, J. Am. Chem. Soc., 1991, 113, 4751–4755 CrossRef CAS; (b) A. Dworkin, R. Naumann, C. Seigfred and J. M. Karty, Y-Aromaticity: Stable than the Butadienyl Dication?, J. Org. Chem., 2005, 70, 7605–7616 CrossRef CAS PubMed; (c) E. Kleinpeter and A. Koch, Y-aromaticity – existing: yes or no? An answer given on the magnetic criterion (TSNMRS), Tetrahedron, 2016, 72, 1675–1685 CrossRef CAS.
- H. Brand, J. F. Liebman, A. Schulz, P. Mayer and A. Villinger, Nonlinear, Resonance-Stabilized Pseudohalides: From Alkali Methanides to Ionic Liquids of Methanides, Eur. J. Inorg. Chem., 2006, 4294–4308 CrossRef CAS.
- Energy minimization performed for conformers of anion 1 at the MP2/6-311+G(d,p) level (preliminary calculations in this work) delivers the molecular geometry with an appreciably pyramidal central carbon instead of that with a planar carbon (corresponding to the experimentally established geometry). This ‘deplanarization’ problem probably is due to the intramolecular basis set incompleteness error revealed when modeling planar aromatic systems: D. Moran, A. C. Simmonett, F. E. Leach, W. D. Allen, P. v. R. Schleyer and H. F. Schaefer, Popular Theoretical Methods Predict Benzene and Arenes To Be Nonplanar, J. Am. Chem. Soc., 2006, 128, 9342–9343 CrossRef CAS PubMed.
- K. O. Christe, W. W. Wilson, G. Bélanger-Chabot, R. Haiges, J. A. Boatz, M. Rahm, G. K. S. Prakash, T. Saal and M. Hopfinger, Angew. Chem., Int. Ed., 2015, 54, 1316–1320 CrossRef CAS PubMed.
- F. Weinhold and C. Landis, Valence and Bonding, Cambridge University Press, New-York, 2005 Search PubMed.
- W.-K. Li, An ab initio Molecular Orbital Study of the Nitromethyl Anion, Croat. Chem. Acta, 1990, 63, 127–134 CAS.
- (a) P. G. Gildner, A. A. S. Gietter, D. Cui and D. A. Watson, Benzylation of Nitroalkanes Using Copper-Catalyzed Thermal Redox Catalysis: Toward the Facile C-Alkylation of Nitroalkanes, J. Am. Chem. Soc., 2012, 134, 9942–9945 CrossRef CAS PubMed; (b) K. W. Shimkin and D. A. Watson, Recent developments in copper-catalyzed radical alkylations, Beilstein J. Org. Chem., 2015, 11, 2278–2288 CrossRef CAS PubMed.
- (a) K. E. Edgecombe and R. J. Boyd, Molecular orbital treatment of substituent effects. I. Structures of some carbon acids and their conjugate bases, Can. J. Chem., 1983, 61, 45–49 CrossRef CAS; (b) V. A. Shlyapochnikov, M. A. Tafipolsky, I. V. Tokmakov and G. I. Oleneva, Structure and vibrational spectra of the salts of mononitroalkanes, J. Mol. Struct., 2000, 520, 19–27 CrossRef CAS; (c) R. B. Metz, D. R. Cyr and D. M. Neumark, Study of the2B1 and 2A2 States of CH2NO2 via Ultraviolet Photoelectron Spectroscopy of the CH2NO2− Anion, J. Phys. Chem., 1991, 95, 2900–2907 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, Determining Atom-centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- (a) N. Jonathan, The Infrared Spectra and Structures of O,N-Dimethyl Nitramide and the Silver and Ammonium Salts of Methyl Nitramide, J. Mol. Spectrosc., 1960, 5, 101 CrossRef CAS; (b) V. G. Avakyan, V. A. Shlyapochnikov and A. Chekrygin, Structure of Nitramine Salts, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1972, 21, 902–904 CrossRef.
- R. J. Maza, E. Fernández and J. J. Carbó, Mapping the Electronic Structure and the Reactivity Trends for Stabilized α-Boryl Carbanions, Chem. – Eur. J., 2021, 27, 12352–12361 CrossRef CAS PubMed.
- (a) A. Hassner, M. Stern, H. E. Gottlieb and F. Frolov, Utility of a Polymeric Azide Reagent in the Formation of Di- and Triazidomethane. Their NMR Spectra and the X-ray Structure of Derived Triazoles, J. Org. Chem., 1990, 55, 2304–2306 CrossRef CAS; (b) Y.-H. Joo, Doctoral dissertation, Chemnitz University of Technology, 2007 Search PubMed.
- M. A. Petrie, J. A. Sheehy, J. A. Boatz, G. Rasul, G. K. S. Prakash, G. A. Olah and K. O. Christe, Novel High-Energy Density Materials. Synthesis and Characterization of Triazidocarbenium Dinitramide, -Perchlorate, and -Tetrafluoroborate, J. Am. Chem. Soc., 1997, 119, 8802–8808 CrossRef CAS.
- (a) A. P. Häring and S. F. Kirsch, Synthesis and Chemistry of Organic Geminal Di- and Triazides, Molecules, 2015, 20, 20042–22006 CrossRef PubMed; (b) B. D. Tsyrenova, P. S. Lemport and V. G. Nenajdenko, Di- and polyazides. Synthesis, chemical transformations and practical applications, Russ. Chem. Rev., 2023, 92, 1–48 CrossRef.
- D. J. R. Duarte, M. S. Miranda and J. C. G. E. da Silva, Computational Study on the Vinyl Azide Decomposition, J. Phys. Chem. A, 2014, 118, 5038–5045 CrossRef CAS PubMed.
- (a) B. J. Costa Cabral and M. L. Costa, Density functional study of molecular properties of hydrazoic acid and methyl azide, J. Mol. Struct., 1995, 343, 31–41 CrossRef CAS; (b) R. L. Livingston and C. X. R. Rao, An Electron Diffraction Investigation Of The Molecular Structure Of Methyl Azide, J. Am. Chem. Soc., 1960, 64, 756–759 CAS.
- S. Bräse, C. Gil, K. Knepper and V. Zimmermann, Organic Azides: An Exploding Diversity of a Unique Class of Compounds, Angew. Chem., Int. Ed., 2005, 44, 5188–5240 CrossRef PubMed.
- X. Huang, C. Li, K. Tan, Y. Wen, F. Guo, M. Li, Y. Huang, C. Q. Sun, M. Gozin and L. Zhang, Applying machine learning to balance performance and stability of high energy density materials, iScience, 2021, 24, 102240 CrossRef CAS PubMed.
- K. Banert, Y.-H. Joo, T. Rüffer, B. Walfort and H. Lang, The Exciting Chemistry of Tetraazidomethane, Angew. Chem., Int. Ed., 2007, 46, 1168–1171 CrossRef CAS PubMed.
- F.-L. Zhang, H.-S. Huang and X.-H. Xie, Theoretical Studies on the Thermal Decomposition Mechanism of Potassium Nitroformate, Chin. J. Struct. Chem., 2016, 35, 514–520 CAS.
- M. Rahm and T. Brinck, On the Anomalous Decomposition and Reactivity of Ammonium and Potassium Dinitramide, J. Phys. Chem. A, 2010, 114, 2845–2854 CrossRef CAS PubMed.
- (a) K. W. Shimkin and D. A. Watson, Recent developments in copper-catalyzed radical alkylations of electron-rich π-systems, Beilstein J. Org. Chem., 2015, 11, 2278–2288 CrossRef CAS PubMed; (b) N. Ono, in Organic Nitro Chemistry Series, ed. H. Feuer, Wiley-VCH, New York, NY, 2001, pp. 126–128 Search PubMed.
- (a) G. S. Hammond, W. D. Emmons, C. O. Parker, B. M. Graybill, J. H. Waters and M. F. Hawthorne, Silver Salt Alkylation Reactions And The Preparation of Polynitroalkanes, Tetrahedron, 1963, 19, 177–195 CrossRef CAS; (b) S. A. Shevelev, L. I. Dalinger, V. M. Vinogradov and A. A. Fainzilberg, Alkylation of Alkali Metal Salts of Trinitromethane Under Interphase Catalysis Conditions In Solid Phase–Liquid Systems, Bull. Acad. Sci. USSR, Div. Chem. Sci., 1990, 39, 1647–1650 CrossRef.
- (a) F.-Y. Chen, C.-L. Xuan, Q.-Q. Lu, L. Xiao, J.-Q. Yang, Y.-B. Hu, G.-P. Zhang, Y.-L. Wang, F.-Q. Zhao, G.-Z. Hao and W. Jiang, A review on the high energy oxidizer ammonium dinitramide: Its synthesis, thermal decomposition, hygroscopicity, and application in energetic materials, Def. Technol., 2023, 19, 163–195 CrossRef; (b) S. G. Zlotin, I. L. Dalinger, N. N. Makhova and V. A. Tartakovsky, Nitro compounds as the core structures of promising energetic materials and versatile reagents for organic synthesis, Russ. Chem. Rev., 2020, 89, 1–54 CrossRef CAS; (c) X. Zhang, Y. Liu, F. Wang and X. Gong, A Theoretical Study on the Structure, Intramolecular Interactions, and Detonation Performance of Hydrazinium Dinitramide, Chem.–Asian J., 2014, 9, 229–236 CrossRef CAS PubMed.
- (a) M. Rahm and T. Brinck, Kinetic Stability and Propellant Performance of Green Energetic Materials, Chem. – Eur. J., 2010, 16, 6590–6600 CrossRef CAS PubMed; (b) S. Alavi and D. L. Thompson, Decomposition pathways of dinitramic acid and the dinitramide ion, J. Chem. Phys., 2003, 19, 232–240 CrossRef.
- (a) A. P. Häring and S. F. Kirsch, Synthesis and Chemistry of Organic Geminal Di- and Triazides, Molecules, 2015, 20, 20042–20062 CrossRef PubMed; (b) B. D. Tsyrenova, P. S. Lemport and V. G. Nenajdenko, Di- and polyazides. Synthesis, chemical transformations and practical applications, Russ. Chem. Rev., 2023, 92, RCR5066 CrossRef.
- J. Soto, M. Algarra and D. Peláez, Nitrene formation is the first step of the thermal and photochemical decomposition reactions of organic azides, Phys. Chem. Chem. Phys., 2022, 24, 5109–5115 RSC.
- M. Shee and N. D. P. Singh, Chemical versatility of azide radical: journey from a transient species to synthetic accessibility in organic transformations, Chem. Soc. Rev., 2022, 51, 2255–2312 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- G. A. Zhurko, Chemcraft, Ivanovo, 2005 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates, energies, frequencies for transition states, Wiberg indexes, orbital occupancies, some reaction energy profiles. See DOI: https://doi.org/10.1039/d3ra06708d |
| ‡ Isomers 1A and 1B are a borderline case in classifying isomers either as stereoisomers or as chemical isomers. Traditional understanding of covalent chemical structure (a molecular framework of 2c–2e bonds) only implies full occupation of bonding orbitals. From this perspective, 1A and 1B are conformers (rapidly interconverting stereoisomers – a simplified form of a strict definition of conformer from monograph A. M. Belostotskii, Conformational Concept for Synthetic Chemist's Use, World Scientific Publishing, Singapore, 2015). However, a sizeable donation to a vacant π orbital actually means a partial π bond. Such a 2c–ne bond (n < 1.8) – a bond in the sense of a certain, definable chemical bonding-may be considered the structural determinant to the same extent as the canonical doubly occupied 2c–2e bond is. The molecule of 1A, in contrast to 1B, does not have partially occupied π orbitals for all three diatomic fragments C–N (Fig. 4). Thus, the number of bonds in 1A and 1B is different. From this viewpoint, these structures are chemical isomers. |
| § 6A and 6B are considered as isomers, assuming that a barrier of the height more than 1.5 kcal mol−1 separates these molecular structures in the potential energy surface. |
| This journal is © The Royal Society of Chemistry 2023 |